Abstract
Currently, the best existing molecular dynamics (MD) force fields cannot accurately reproduce the global free-energy minimum which realizes the experimental protein structure. As a result, long MD trajectories tend to drift away from the starting coordinates (e.g., crystallographic structures). To address this problem, we have devised a new simulation strategy aimed at protein crystals. An MD simulation of protein crystal is essentially an ensemble simulation involving multiple protein molecules in a crystal unit cell (or a block of unit cells). To ensure that average protein coordinates remain correct during the simulation, we introduced crystallography-based restraints into the MD protocol. Because these restraints are aimed at the ensemble-average structure, they have only minimal impact on conformational dynamics of the individual protein molecules. So long as the average structure remains reasonable, the proteins move in a native-like fashion as dictated by the original force field. To validate this approach, we have used the data from solid-state NMR spectroscopy, which is the orthogonal experimental technique uniquely sensitive to protein local dynamics. The new method has been tested on the well-established model protein, ubiquitin. The ensemble-restrained MD simulations produced lower crystallographic R factors than conventional simulations; they also led to more accurate predictions for crystallographic temperature factors, solid-state chemical shifts, and backbone order parameters. The predictions for 15N R1 relaxation rates are at least as accurate as those obtained from conventional simulations. Taken together, these results suggest that the presented trajectories may be among the most realistic protein MD simulations ever reported. In this context, the ensemble restraints based on high-resolution crystallographic data can be viewed as protein-specific empirical corrections to the standard force fields.
Keywords: protein structure and dynamics, Molecular Dynamics simulations, force fields, solid-state NMR, protein crystallography, chemical shifts, crystallographic R factors, crystallographic B factors, order parameters, 15N relaxation, ubiquitin
Introduction
Molecular dynamics (MD) is a powerful tool for modeling protein conformational dynamics, with particular emphasis on functionally relevant motions. Importantly, MD simulations can reconstruct the picture of motion in its entirety, including those aspects that cannot be easily probed experimentally. Unfortunately, current MD trajectories tend to drift away from the starting coordinates (e.g., crystallographic structures) during the course of the simulation. This fact has been brought into spotlight by a very recent work of Shaw and coworkers.1 In their study, a number of ultralong (at least 40 µs) MD trajectories have been recorded using state-of-the-art force fields. In all cases, it was found that the simulated structures “moved away” from the true coordinates; in most cases, the structures continued to deteriorate throughout the course of the simulation (sometimes to a substantial degree). This helps to explain the notable lack of successes in many previous attempts to refine protein models by means of unconstrained MD (uMD) simulations in explicit solvent. With the exception of some small, tightly packed proteins,2–4 the uMD approach generally fails to improve the models in the range 1–10 Å from the target structure.5–9 Initially, this situation was blamed on short uMD trajectories that could not adequately sample the conformational phase space. However, the latest results suggest that “the structure that realizes the global free-energy minimum for the force field employed is not the X-ray or NMR structure,”1 i.e. that the force field itself is to blame.
This is a disappointing result which casts a long shadow on the future of conventional protein MD simulations. Clearly, there is need for systematic work on development and redesign of force fields, which remains a major challenge for the foreseeable future. To illustrate the complexity of this challenge, we will mention that the most advanced polarizable force field, AMOEBA, currently fails to maintain the integrity of certain protein structures for more than several nanoseconds.10 As an alternative to such ground-up redesign work, the existing MD force fields can be amended based on experimental data; the emerging trend is to optimize force-field parameters based directly on the data from protein studies.11–13
Here, we propose a more pointed strategy, where protein-specific restraints are introduced directly into the MD simulation. Our motivation is to eliminate the bias in the force field that causes protein structures to drift. Toward this goal, we use the crystallography-based restraints, which are far more complete and accurate than any other experimental data insofar as protein structure is concerned. As crystallographic data pertain to the mean protein structure (averaged over dynamic fluctuations), the corresponding restraints should be applied in a form of ensemble average. In this manner, the simulated protein ensemble remains consistent with X-ray diffraction data (i.e., maintains the correct average structure), whereas the individual protein molecules retain their native-like internal dynamics.
Hydrated protein crystals are uniquely suited to implement this strategy. MD simulations of protein crystals have been the area of interest,14–16 with emerging applications to solid-state NMR (ssNMR) spectroscopy.17,18 An MD simulation of a protein crystal is intrinsically an ensemble simulation, as it involves multiple protein molecules in a crystal unit cell (or a block of unit cells). Therefore, it is straightforward to incorporate the crystallography-based ensemble restraints into the standard MD protocol. In addition to X-ray diffraction, protein crystals offer access to another incredibly rich source of experimental information—ssNMR data. These two types of data are largely orthogonal, as ssNMR can probe internal protein dynamics at the level of detail that is not available to X-ray crystallography. This creates an opportunity for rigorous cross-validation of the obtained results. Briefly, the proposed ensemble-restrained MD (erMD) strategy relies on X-ray data to ensure that the average protein structure remains correct during the course of the simulation, while ssNMR data are used to verify that the resulting trajectories accurately reproduce protein dynamics.
To establish a feasibility of our approach, we have focused on crystalline ubiquitin. Ubiquitin is one of a handful of proteins for which major efforts have been made to characterize protein structure and dynamics by means of ssNMR19–24 and, furthermore, to establish a connection between the NMR and crystallographic samples.25 Implementing ensemble restraints eliminated structural drift in the trajectory of crystalline ubiquitin, while preserving the dynamics of individual ubiquitin molecules. We have found that erMD trajectories produced significantly lower crystallographic R factors than comparable uMD simulations. Furthermore, the erMD simulations were more successful in predicting ssNMR chemical shifts. We have also observed improvements in crystallographic temperature factors and backbone order parameters  . Finally, erMD was at least as accurate as uMD in predicting 15N R1 rates. Taken together, these results suggest that erMD simulations provide a uniquely accurate model of protein structure and dynamics.
. Finally, erMD was at least as accurate as uMD in predicting 15N R1 rates. Taken together, these results suggest that erMD simulations provide a uniquely accurate model of protein structure and dynamics.
Methods
Figure 1 shows the crystal unit cell of ubiquitin based on the recent crystallographic structure 3ONS (six protein molecules per unit cell, one protein molecule per asymmetric unit). Using these coordinates, we have recorded a 1-µs unrestrained MD trajectory of hydrated ubiquitin crystal. The effect of crystal lattice in this simulation is modeled via the periodic-boundary conditions. As it turns out, the average protein coordinates obtained from this MD trajectory deviate by 0.52 Å (backbone rmsd) from the original crystallographic coordinates. The deviation of this magnitude is beyond the uncertainty of high-resolution crystallographic structure. In fact, rmsd becomes progressively worse during the course of the simulation, climbing to 0.7 Å toward the end of the trajectory, see Figure 2(a). The simulated diffraction data also suggest that the quality of the protein structure becomes degraded in the MD simulation, as manifested by the increased R factor.26
Figure 1.
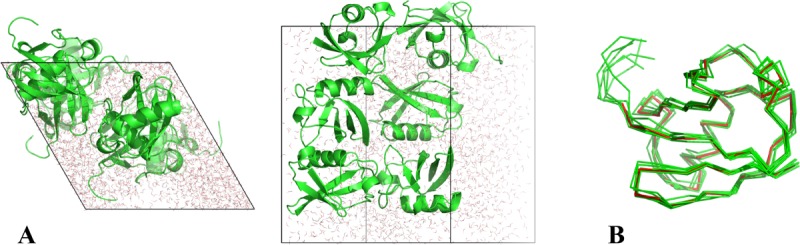
(A) The snapshot from erMD simulation of ubiquitin showing periodic-boundary box (corresponding to the single crystal unit cell, 1U). The unit cell with the primitive trigonal space group P3221 is based on the crystallographic structure 3ONS. The reported dimensions of the cell, a=b and c, are all increased by a factor 1.016 to account for thermal expansion of the protein crystal on transition from 100 K (temperature at which 3ONS was solved) to 301 K (temperature at which ssNMR data were taken).27 Shown are the top view and side view of the unit cell. The MD trajectory was recorded with k0 kcal mol−1 Å−2; the displayed snapshot represents the time point 150 ns. The areas with apparent low water density arise from the periodic-boundary images of ubiquitin molecules. (B) Six ubiquitin molecules from the MD frame, panel A, superimposed according to Eq. (2.1) (green Cα traces). Also shown is the crystallographic structure 3ONS centered according to Eq. (2.2) (red Cα trace). Such superpositions are used to calculate the instantaneous value of Urestraint, Eq. (1). Since protein molecules are superimposed via the symmetry transformations rather than least-square fitting, Urestraint proves to be sensitive to small reorientations of proteins in the simulated unit cell.
Figure 2.
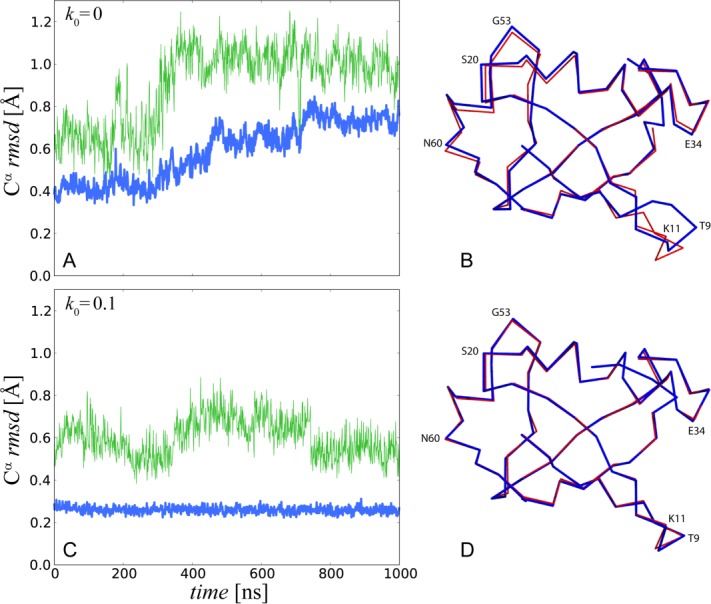
(A) Time course of Cα rmsd for uMD(k0 = 0) trajectory of crystalline ubiquitin. The simulation models a single crystal unit cell (1U) with six ubiquitin molecules. Blue profile represents the ensemble-average rmsd, where protein coordinates  are overlaid according to Eq. (2.1) and then averaged before calculating the rms deviation from
are overlaid according to Eq. (2.1) and then averaged before calculating the rms deviation from 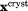 . Green profile represents the rmsd of one individual ubiquitin molecule randomly selected from the ensemble of six. The sampling step is 1 ns. The increase in rmsd observed in this graph does not necessarily mean that the structure will continue further degrading if the simulation is extended. Ubiquitin is one of those small proteins where the structure can be relatively well maintained in the MD simulations. In the recent ultralong solution trajectory, ubiquitin remained within 0.5-1.0 Å of the crystal structure.29 It remains to be seen what is the magnitude of structural drift in long crystal trajectories. (B) Average protein coordinates calculated from the final 100 ns of the uMD trajectory (blue trace) superimposed onto the crystal coordinates (red trace). Structural deviations are found in the area which is known for its plasticity and serves as a ligand-binding interface (loop β1–β2 and C-terminal end the strand β5, lower right part of the molecule). The opposite side of the molecule (β2–α1 loop interacting with the β-turn at the site G53) is affected as well. (C, D) Same as (A) and (B), respectively, for erMD (k0 = 0.1) trajectory.
. Green profile represents the rmsd of one individual ubiquitin molecule randomly selected from the ensemble of six. The sampling step is 1 ns. The increase in rmsd observed in this graph does not necessarily mean that the structure will continue further degrading if the simulation is extended. Ubiquitin is one of those small proteins where the structure can be relatively well maintained in the MD simulations. In the recent ultralong solution trajectory, ubiquitin remained within 0.5-1.0 Å of the crystal structure.29 It remains to be seen what is the magnitude of structural drift in long crystal trajectories. (B) Average protein coordinates calculated from the final 100 ns of the uMD trajectory (blue trace) superimposed onto the crystal coordinates (red trace). Structural deviations are found in the area which is known for its plasticity and serves as a ligand-binding interface (loop β1–β2 and C-terminal end the strand β5, lower right part of the molecule). The opposite side of the molecule (β2–α1 loop interacting with the β-turn at the site G53) is affected as well. (C, D) Same as (A) and (B), respectively, for erMD (k0 = 0.1) trajectory.
This behavior is the manifestation of the coordinate drift, caused by a subtle bias in the MD force field. In addition, one should bear in mind that MD trajectories cannot easily accommodate some of the experimental conditions, such as the presence of protein species with different charges due to titratable side-chain sites. To address this situation, we implemented the MD restraints seeking to ensure that the ensemble of protein molecules contained in the simulation box is on average consistent with the crystallographic structure. In this manner, we use the X-ray crystallography data as ensemble restraints, while retaining the (orthogonal) ssNMR data for the purpose of validation.
Generally speaking, it is desirable to restrain crystal MD simulation directly against the crystallographic diffraction data. Indeed, diffraction data contain the entirety of experimental information, including certain amount of information about the conformational diversity in the system. We have implemented this strategy programmatically and found it unsatisfactory: as it turns out, diffraction-based ensemble restraints are incompatible with bona fide MD simulations. The reasons for this failure are discussed in Supporting Information. In this situation, we pursue a more practical solution, using crystallographic coordinates of a protein to generate ensemble restraints. Specifically, we seek to ensure that the average protein structure, as calculated over the MD ensemble, remains close to the X-ray structure. This is accomplished by introducing the following pseudopotential:
| (1) |
The pseudopotential Urestraint is harmonic with the force constant 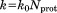 , where Nprot is the number of protein molecules in the simulation. With this choice of
, where Nprot is the number of protein molecules in the simulation. With this choice of 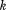 , the pseudoforce acting on an individual atom does not depend on the size of the simulated system.
, the pseudoforce acting on an individual atom does not depend on the size of the simulated system. 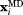 is the vector representing current coordinates of the i-th heavy atom in the MD trajectory and
is the vector representing current coordinates of the i-th heavy atom in the MD trajectory and 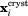 represents the corresponding coordinates in the crystallographic structure. The summation in Eq. (1) is over all atoms contained in the crystallographic structure (typically these are heavy atoms). Because there are multiple protein molecules in the simulated unit cell(s), Figure 1(a), they need to be superimposed prior to comparison with the crystallographic coordinates. This is accomplished by applying symmetry operators as appropriate for the given crystal space group:
represents the corresponding coordinates in the crystallographic structure. The summation in Eq. (1) is over all atoms contained in the crystallographic structure (typically these are heavy atoms). Because there are multiple protein molecules in the simulated unit cell(s), Figure 1(a), they need to be superimposed prior to comparison with the crystallographic coordinates. This is accomplished by applying symmetry operators as appropriate for the given crystal space group:
| 2.1 |
Here, index q enumerates protein molecules in the MD frame, vector 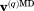 translates the center of mass of the particular protein molecule to the origin of the coordinate frame, and
translates the center of mass of the particular protein molecule to the origin of the coordinate frame, and 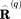 represents the symmetry rotation matrix.28 Subsequent to this manipulation, the coordinates of all protein molecules in the MD frame are averaged,
represents the symmetry rotation matrix.28 Subsequent to this manipulation, the coordinates of all protein molecules in the MD frame are averaged, 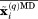 . In turn, the crystallographic structure is also translated to the origin:
. In turn, the crystallographic structure is also translated to the origin:
| 2.2 |
Finally, the deviation between the ensemble-average MD structure and crystallographic structure is used to generate the correcting force according to Eq. (1) (see also Supporting Information). The superposition of multiple protein structures used in calculating Urestraint is illustrated in Figure 1(b).
Clearly, the restraints Eq. (1) are sensitive to the internal dynamics of protein molecules. In addition, they are also sensitive to rigid-body reorientational dynamics (i.e., small-amplitude rocking motion of protein molecules embedded in the crystal lattice). The only motional mode which is left out is translation—the restraints are insensitive to translational displacements of ubiquitin molecules in the crystal lattice.
The restraints set up in this fashion have only mild effect on each individual ubiquitin molecule. In essence, individual molecules are free to move as dictated by the original force field, so long as the ensemble average remains close to the crystallographic structure. When a difference emerges between the ensemble average 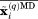 and the crystallographic structure
and the crystallographic structure 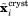 , a small correcting force is applied across the ensemble [one and the same force, derived from the pseudopotential Eq. (1), acts on the i-th atom in all ubiquitin molecules]. Assuming that MD simulation includes a sufficiently large number of protein molecules, this approach should remedy the average structure without stifling the dynamics. As it turns out, our method can actually improve the modeling of dynamics (see below).
, a small correcting force is applied across the ensemble [one and the same force, derived from the pseudopotential Eq. (1), acts on the i-th atom in all ubiquitin molecules]. Assuming that MD simulation includes a sufficiently large number of protein molecules, this approach should remedy the average structure without stifling the dynamics. As it turns out, our method can actually improve the modeling of dynamics (see below).
The pseudopotential Urestraint was incorporated into Amber ff99SB*-ILDN force field in Amber 11 MD simulation package.30 This is one of the most successful protein force fields which includes the backbone helical propensity corrections12 and the ILDN side-chain corrections.31 The initial coordinates for the MD simulations were derived from the recent crystallographic structure of ubiquitin 3ONS, as illustrated in Figure 1. This structure has been solved with the explicit goal to obtain a crystallographic model suitable for the analyses of the ssNMR data.25 Importantly, the sample has been crystallized in the same crystal form as used in the ssNMR experiments.
Prior to the start of the MD trajectory, we have extended the peptide chain of ubiquitin by adding residues 73–76, for which crystallographic coordinates are unavailable. The protein structure was then protonated; the protonation status of Asp and Glu was determined according to the PROPKA32 calculations for crystallization conditions pH 4.2. The results were generally consistent with the estimations using solution pKa,33 except for several residues experiencing the effect of crystal contacts. The unit crystal cell was hydrated using SPC/E water, which has been recommended for protein crystal simulations with Amber ff99SB force field.34 In doing so, the crystallographic water molecules have been retained in their original positions. Finally, the system was neutralized by adding counter ions and equilibrated before the production run. The simulations were conducted at 301 K, which is the temperature used in ssNMR measurements, using the NPT ensemble. The simulated systems ranged from a 1U to a block of four crystal unit cells (4U). In the latter case, the simulations involved 24 ubiquitin molecules and about 8770 water molecules, for the total of 56,240 atoms. For this system, the production rate using NVIDIA GeForce GTX580 cards was 9 ns per card per day. The complete MD protocol is described in the Supporting Information.
Results
Cα rmsd
The data for Cα rms deviation between the different ubiquitin models and the target structure 3ONS are summarized in the first column in Table1. The widely used crystal structure of ubiquitin 1UBQ42 belongs to a different space group than 3ONS. This is manifested in substantial Cα rmsd between the two sets of coordinates, 0.43 Å. The solution-state conformational ensemble 2KOX43 displays a similar level of agreement. In the case of unrestrained solution MD trajectory, the deviation rises to 0.86 Å. The crystal simulation appears to fare better, with average Cα rmsd of 0.52 Å (unrestrained simulation, 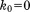 ; here, and in what follows we cite the results from 1U trajectories unless indicated otherwise). One should bear in mind though that the quality of the structure gradually deteriorates through the course of this simulation, Figure 2(a). Ultimately, during the final 100-ns segment of the trajectory average Cα rmsd amounts to 0.71 Å (not including the disordered C-terminus). This is well beyond the intrinsic uncertainty of the crystallographic structure 3ONS. Indeed, the reported resolution of 3ONS is 1.8 Å. At this level of resolution, the accuracy of backbone coordinates is expected to be near 0.2 Å44,45. It is most likely that the elevated rmsd is due to subtle biases in the force-field parameters, as well as the approximate character of the MD setup.
; here, and in what follows we cite the results from 1U trajectories unless indicated otherwise). One should bear in mind though that the quality of the structure gradually deteriorates through the course of this simulation, Figure 2(a). Ultimately, during the final 100-ns segment of the trajectory average Cα rmsd amounts to 0.71 Å (not including the disordered C-terminus). This is well beyond the intrinsic uncertainty of the crystallographic structure 3ONS. Indeed, the reported resolution of 3ONS is 1.8 Å. At this level of resolution, the accuracy of backbone coordinates is expected to be near 0.2 Å44,45. It is most likely that the elevated rmsd is due to subtle biases in the force-field parameters, as well as the approximate character of the MD setup.
Table I.
Comparison Between the Experimental Data from Crystalline Ubiquitin and the Predictions Using Different Structural / MD Models
|
R factorb |
rmsd (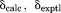 )d (ppm) )d (ppm) |
|||||||
|---|---|---|---|---|---|---|---|---|
| rmsd to 3ONSa (Å) | 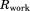 |
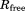 |
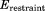 per aac (kcal/mol) per aac (kcal/mol) |
15N | 13Cα | 13Cβ |
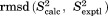 e e
|
|
| 3ONS | 0 | 0.30 | 0.31 | – | 2.39 | 0.75 | 1.11 | – |
| 1UBQ | 0.43 | 0.44 | 0.41 | – | 2.77 | 0.85 | 1.29 | – |
| 2KOX | 0.36 | 0.37 | 0.35 | – | 2.89 | 0.83 | 1.23 | 0.056 |
Solution MD, 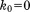 (1 µs) (1 µs) |
0.86 | 0.41 | 0.39 | – | 3.02 | 0.97 | 1.26 | 0.048 |
Solid MD, 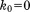 , 1U (1 µs) , 1U (1 µs) |
0.52 | 0.41 | 0.39 | – | 2.96 | 0.92 | 1.15 | 0.056 |
Solid MD, 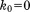 , 4U (200 ns) , 4U (200 ns) |
0.37 | 0.37 | 0.35 | – | 2.91 | 0.92 | 1.12 | 0.062 |
Solid MD,  , 1U (1 µs) , 1U (1 µs) |
0.22 | 0.31 | 0.29 | 0.21 | 2.72 | 0.90 | 1.09 | 0.043 |
Solid MD,  , 4U (200 ns) , 4U (200 ns) |
0.21 | 0.32 | 0.31 | 0.18 | 2.73 | 0.90 | 1.09 | 0.040 |
Solid MD, 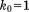 , 1U (1 µs) , 1U (1 µs) |
0.10 | 0.29 | 0.28 | 0.48 | 2.68 | 0.89 | 1.11 | 0.047 |
Solid MD, 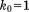 , 4U (200 ns) , 4U (200 ns) |
0.09 | 0.32 | 0.29 | 0.36 | 2.68 | 0.89 | 1.11 | 0.046 |
Solid MD, 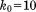 , 1U (1 µs) , 1U (1 µs) |
0.05 | 0.37 | 0.36 | 0.76 | 2.64 | 0.85 | 1.12 | 0.041 |
Solid MD, 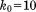 , 4U (200 ns) , 4U (200 ns) |
0.05 | 0.32 | 0.29 | 0.54 | 2.65 | 0.85 | 1.12 | 0.041 |
The shaded rows correspond to the recommended 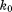 setting.
setting.
Cα rmsd relative to the crystallographic structure. In the case of crystal MD simulations, protein coordinates 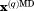 are overlaid according to Eq. (2.1) and then averaged over the entire trajectory; the average coordinates are superimposed onto 3ONS in the least-square sense (via Cα atoms) before calculating the rms deviation from
are overlaid according to Eq. (2.1) and then averaged over the entire trajectory; the average coordinates are superimposed onto 3ONS in the least-square sense (via Cα atoms) before calculating the rms deviation from 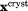 . In other cases, protein coordinates are superimposed onto 3ONS, averaged if necessary, and then used to calculate the rmsd.
. In other cases, protein coordinates are superimposed onto 3ONS, averaged if necessary, and then used to calculate the rmsd.
In calculating crystallographic R, all per-atom B factors have been omitted. This was done to facilitate the comparison between MD models (which encode local dynamics) and static structures (which are dynamics-free). Furthermore, no attempt was made to calculate reflections from explicit water molecules. In the case of crystal MD trajectories, each protein molecule was first transformed according to Eq. (2.1). Then, structure factors 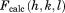 were computed using the fmodel tool in PHENIX.35 In doing so, the flat bulk-solvent contribution was included with
were computed using the fmodel tool in PHENIX.35 In doing so, the flat bulk-solvent contribution was included with 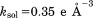 and
and 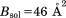 , as recommended by Fokine and Urzhumtsev.36 The obtained values
, as recommended by Fokine and Urzhumtsev.36 The obtained values 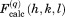 from individual ubiquitin molecules have been averaged (with phases) to determine the intensities of reflections,
from individual ubiquitin molecules have been averaged (with phases) to determine the intensities of reflections, 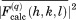 , which were in turn averaged over the entire trajectory. The result was then subjected to the overall scaling to account for the effect of lattice vibrations (translational movement of the protein molecules).37 The degree of overall anisotropy, as reported in 3ONS, is modest; therefore, we chose to use the isotropic scaling whereby a single
, which were in turn averaged over the entire trajectory. The result was then subjected to the overall scaling to account for the effect of lattice vibrations (translational movement of the protein molecules).37 The degree of overall anisotropy, as reported in 3ONS, is modest; therefore, we chose to use the isotropic scaling whereby a single 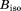 value was optimized using a designated script. Finally, the results were correlated to
value was optimized using a designated script. Finally, the results were correlated to 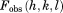 and the crystallographic R factor was calculated in a standard manner. When calculating
and the crystallographic R factor was calculated in a standard manner. When calculating 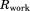 and
and 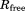 , we used the same subsets of reflections as listed for 3ONS. For structural models other than crystal MD trajectories, the protein coordinates were first superimposed onto 3ONS in the least-square sense (via Cα atoms); the remaining calculations followed the same procedure as described above.
, we used the same subsets of reflections as listed for 3ONS. For structural models other than crystal MD trajectories, the protein coordinates were first superimposed onto 3ONS in the least-square sense (via Cα atoms); the remaining calculations followed the same procedure as described above.
The restraint energy per residue, 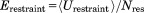 , where Urestraint is calculated according to Eq. (1) and subsequently averaged over all snapshots in the trajectory and
, where Urestraint is calculated according to Eq. (1) and subsequently averaged over all snapshots in the trajectory and 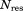 is the number of residues for which crystallographic restraints are available,
is the number of residues for which crystallographic restraints are available,  .
.
Chemical shifts were calculated using the program SHIFTX2 version 1.07.38 A customized version of the program, where ubiquitin was excluded from the training set to avoid biasing the results, was kindly provided by B. Han. The program was used on static structures as well as MD frames, processing one protein structure at a time (disregarding small shifts across protein-protein interface, e.g., due to ring current shifts). Taking intermolecular effects into consideration leads to a slight improvement in 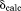 (e.g., by ca. 0.05 ppm for 15N nuclei). In the case of MD data, every 10-th snapshot was included in the chemical shift calculations, corresponding to 50-ps sampling step. The control calculations using 5-ps sampling step produced the results that were virtually identical. The experimental data were obtained from the studies by Igumenova et al.39 (13C) and Schanda et al.23 (15N); we found that there was no need to re-reference these chemical shifts.
(e.g., by ca. 0.05 ppm for 15N nuclei). In the case of MD data, every 10-th snapshot was included in the chemical shift calculations, corresponding to 50-ps sampling step. The control calculations using 5-ps sampling step produced the results that were virtually identical. The experimental data were obtained from the studies by Igumenova et al.39 (13C) and Schanda et al.23 (15N); we found that there was no need to re-reference these chemical shifts.
15N-1HN dipolar order parameters for crystal trajectories were computed using the following protocol. First, symmetry transformations Eq. (2.1) have been applied to all ubiquitin molecules in the periodic boundary box. Then, 15N-1HN vectors were extracted from the transformed coordinates; the vectors pertaining to each individual residue were arranged in a long array. The array had an effective length of 6 × 1 = 6 µs in the case of 1U simulations and 0.2 × 24 = 4.8 µs in the case of 4U simulations. Finally, the standard Brüschweiler's formula40 has been applied to these arrays to calculate 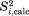 values. The experimental data
values. The experimental data 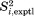 are from the recent solid-state NMR experiments by Haller and Schanda,41 which is the revision of the earlier work by Schanda et al.23 Additionally, the table includes the results from solution-state ensemble 2KOX and 1 µs-long solution simulation. For these models,
are from the recent solid-state NMR experiments by Haller and Schanda,41 which is the revision of the earlier work by Schanda et al.23 Additionally, the table includes the results from solution-state ensemble 2KOX and 1 µs-long solution simulation. For these models, 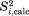 values were obtained by straightforward application of the Brüschweiler's formula.
values were obtained by straightforward application of the Brüschweiler's formula.
To address this problem, we have implemented the erMD protocol, as described above. Already the use of very weak restraints,  kcal mol−1 Å−2, promptly brings rmsd down to the level of 0.22 Å. Bear in mind that this rmsd value describes the deviation between the ensemble-average MD coordinates and the target, the conformational diversity of ubiquitin across the ensemble is retained. This is illustrated in Figure 2(c). Although ensemble-average ubiquitin structure remains within 0.2–0.3 Å of the reference X-ray coordinates (blue trace in the plot), one single ubiquitin molecule which is a part of the ensemble shows much larger deviations (green trace). Furthermore, this one molecule undergoes significant conformational fluctuations. In doing so, it samples certain conformational states that turn out to be sufficiently long-lived (on the order of hundreds of nanoseconds). This behavior demonstrates that individual protein molecules largely retain their native-like internal dynamics in our erMD simulations.
kcal mol−1 Å−2, promptly brings rmsd down to the level of 0.22 Å. Bear in mind that this rmsd value describes the deviation between the ensemble-average MD coordinates and the target, the conformational diversity of ubiquitin across the ensemble is retained. This is illustrated in Figure 2(c). Although ensemble-average ubiquitin structure remains within 0.2–0.3 Å of the reference X-ray coordinates (blue trace in the plot), one single ubiquitin molecule which is a part of the ensemble shows much larger deviations (green trace). Furthermore, this one molecule undergoes significant conformational fluctuations. In doing so, it samples certain conformational states that turn out to be sufficiently long-lived (on the order of hundreds of nanoseconds). This behavior demonstrates that individual protein molecules largely retain their native-like internal dynamics in our erMD simulations.
The simulation results obtained with  kcal mol−1 Å−2 are justified by the accuracy of the X-ray structure. It is reasonable to expect that ensemble-and time-averaged MD coordinates fall within ca. 0.2 Å of the X-ray structure, because the uncertainty margin of the crystallographic coordinates is ca. 0.2 Å. Increasing the force constant from 0.1 to 1.0 kcal mol−1 Å−2 reduces Cα rmsd to 0.10 Å (see Table1). When the restraints are strengthened even further, to 10.0, the rmsd drops to 0.05 Å. The latter situation should be viewed as “over-restraining” as the limited accuracy of the crystal coordinates does not justify excessive tightening of the (average) structure.
kcal mol−1 Å−2 are justified by the accuracy of the X-ray structure. It is reasonable to expect that ensemble-and time-averaged MD coordinates fall within ca. 0.2 Å of the X-ray structure, because the uncertainty margin of the crystallographic coordinates is ca. 0.2 Å. Increasing the force constant from 0.1 to 1.0 kcal mol−1 Å−2 reduces Cα rmsd to 0.10 Å (see Table1). When the restraints are strengthened even further, to 10.0, the rmsd drops to 0.05 Å. The latter situation should be viewed as “over-restraining” as the limited accuracy of the crystal coordinates does not justify excessive tightening of the (average) structure.
Crystallographic R factors
The standard structure-calculation protocol in X-ray crystallography accounts for local protein dynamics via adjustable per-atom B factors. Conversely, if MD trajectory is used as a structural model to interpret X-ray diffraction data then local protein dynamics is taken into consideration explicitly. These two approaches to local dynamics are significantly different, which potentially complicates the comparison between the respective models. To simplify the analyses, we excluded per atom B factors from further consideration (more precisely, for each model we employed a single adjustable 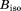 value which was meant to capture the effect of lattice vibrations). This puts different models in Table1 on the same footing, allowing for a clear-cut comparison of the R values.
value which was meant to capture the effect of lattice vibrations). This puts different models in Table1 on the same footing, allowing for a clear-cut comparison of the R values.
Another simplification that we have made in our analyses is the neglect of explicit water. The coordinate set 3ONS includes 91 crystallographic water molecules. Conversely, the MD models include on the order of several thousand water molecules, some of which belong to the protein hydration shell, whereas others are classified as bulk solvent. Once again, the situation is asymmetric. To simplify the treatment, we have chosen to ignore the explicit water and instead use flat bulk solvent correction for the portion of space that is not occupied by protein molecules.36,37
Clearly, the above simplifications degrade the performance of the original crystallographic model. The original deposition 3ONS reports Rwork = 0.18 and Rfree = 0.21. With our simplified protocol, these values rise to 0.30 and 0.31, respectively. The importance of this result is that it provides the point of reference for further comparative analyses. In particular, the unrestrained MD simulation of the ubiquitin crystal produces the R factors 0.41 and 0.39, which is significantly worse than the static crystallographic structure. This means that uMD trajectory provides an inferior structural model, as judged on the basis of the experimental diffraction data. When restraints are turned on, the situation is improved. Both  and 1.0 trajectories of a single unit cell (1U) produce R values that are essentially the same as in the case of 3ONS. Thus, the erMD simulation can at least match the quality of the crystallographic model in this rubric, if not surpass it. Further strengthening of the restraints,
and 1.0 trajectories of a single unit cell (1U) produce R values that are essentially the same as in the case of 3ONS. Thus, the erMD simulation can at least match the quality of the crystallographic model in this rubric, if not surpass it. Further strengthening of the restraints, 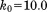 , can make the results worse. As it appears, the excessive force leads to MD artifacts—specifically, the individual ubiquitin molecules in 1U trajectory become slightly reoriented (while the ensemble-average structure remains near-perfect). As already indicated, the value
, can make the results worse. As it appears, the excessive force leads to MD artifacts—specifically, the individual ubiquitin molecules in 1U trajectory become slightly reoriented (while the ensemble-average structure remains near-perfect). As already indicated, the value 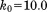 corresponds to over-restraining and thus should be rejected.
corresponds to over-restraining and thus should be rejected.
The lowest R factors obtained in the erMD simulations are seemingly unimpressive, about 0.30. Note, however, that including explicit water should significantly reduce this value. Also bear in mind that low R factors, about 0.20, that are customary for high-resolution X-ray crystallography are obtained with the help of per-atom B factors, which effectively create a very large number of fitting parameters. In the current treatment, these fitting parameters have been eliminated. Interestingly, MD trajectories listed in Table1 display the values of Rfree that tend to be slightly lower than Rwork. As it turns out, this is a statistical effect which depends on the specific subset of reflections used to calculate Rfree. Additional calculations using randomly chosen subsets of 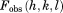 led us to conclude that Rwork and Rfree are equal within the statistical error. Of note, this situation is different from crystallographic refinement where
led us to conclude that Rwork and Rfree are equal within the statistical error. Of note, this situation is different from crystallographic refinement where  is subject to minimization and thus tend to be somewhat lower than Rfree.
is subject to minimization and thus tend to be somewhat lower than Rfree.
Restraint energy
Listed in Table1 are the average restraint energies as registered in the series of erMD simulations (per mole of ubiquitin per residue). The lowest energies, ∼0.2 kcal mol−1 per residue, are found in  trajectories. In the strongly restrained simulations, the energies increase by threefold to fourfold. The value 0.2 kcal mol−1 is comparable to intrinsic uncertainties of the existing force fields. For instance, the accuracy of MD-based calculations for hydration free energies of amino-acid side chains is no better than about 1 kcal mol−1.46 Similarly, the MD-based predictions for change in protein thermal stability upon point mutations
trajectories. In the strongly restrained simulations, the energies increase by threefold to fourfold. The value 0.2 kcal mol−1 is comparable to intrinsic uncertainties of the existing force fields. For instance, the accuracy of MD-based calculations for hydration free energies of amino-acid side chains is no better than about 1 kcal mol−1.46 Similarly, the MD-based predictions for change in protein thermal stability upon point mutations 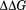 are accurate only to within ca. 1 kcal mol−1.47 Thus, it can be assumed that erMD restraints serve as a (partial) correction for small errors inherent in the standard force fields, rather than produce an unreasonably large new energy term.
are accurate only to within ca. 1 kcal mol−1.47 Thus, it can be assumed that erMD restraints serve as a (partial) correction for small errors inherent in the standard force fields, rather than produce an unreasonably large new energy term.
In this connection, it is also instructive to compare erMD method to other types of restrained simulations. In the erMD protocol, the pseudoforce acting on an individual heavy atom in a given protein molecule is proportional to 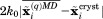 (see Supporting Information). Hence, the value of
(see Supporting Information). Hence, the value of 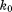 is directly comparable to the force constants associated with NOE restraints in the context of protein structure refinement. In the explicit-solvent refinement protocols,
is directly comparable to the force constants associated with NOE restraints in the context of protein structure refinement. In the explicit-solvent refinement protocols, 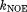 is typically set to 30–50 kcal mol−1 Å−2,48 which is much higher than the setting
is typically set to 30–50 kcal mol−1 Å−2,48 which is much higher than the setting  kcal mol−1 Å−2 advocated in this work. It is also important to keep in mind that in our approach the force is only generated when the average coordinates
kcal mol−1 Å−2 advocated in this work. It is also important to keep in mind that in our approach the force is only generated when the average coordinates 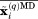 deviate from the crystallographic template. A structural fluctuation in one individual protein molecule generates very little force. From this perspective, Urestraint implemented in the erMD algorithm should be viewed as a “gentle” version of distance restraint.
deviate from the crystallographic template. A structural fluctuation in one individual protein molecule generates very little force. From this perspective, Urestraint implemented in the erMD algorithm should be viewed as a “gentle” version of distance restraint.
At this point, we reaffirm the choice of  as the recommended setting for the erMD simulations. This choice leads to the reasonable value of rms deviation between the ensemble-average protein coordinates and the target crystallographic structure. It also yields a relatively low value of crystallographic R factor. Other things being equal, we favor the low value of Erestraint as found in the erMD simulations with
as the recommended setting for the erMD simulations. This choice leads to the reasonable value of rms deviation between the ensemble-average protein coordinates and the target crystallographic structure. It also yields a relatively low value of crystallographic R factor. Other things being equal, we favor the low value of Erestraint as found in the erMD simulations with  ; low restraint energy ensures that the simulated system retains its native-like dynamics. In what follows, we validate the erMD (
; low restraint energy ensures that the simulated system retains its native-like dynamics. In what follows, we validate the erMD ( ) approach, primarily focusing on comparison with the traditional uMD simulations.
) approach, primarily focusing on comparison with the traditional uMD simulations.
Chemical shifts
Chemical shifts were computed by processing protein coordinates using the prediction program SHIFTX2.38 In this program, the module SHIFTX+ deals with the conformational dependence of chemical shifts while SHIFTY+ relies on sequence homology. To elucidate the dependence of chemical shifts on protein structure / dynamics, we limited the analyses to SHIFTX+. In the case of conformational ensembles and MD trajectories, the results are averaged over multiple conformers or MD frames.
When the static high-resolution structure 3ONS is used to predict chemical shifts, the rms deviations from the experimental ssNMR shifts amount to 2.39, 0.75, and 1.11 ppm for 15N, 13Cα, and 13Cβ, respectively. This is very much in line with the typical performance demonstrated by SHIFTX+.38 Of note, when 1UBQ is used as a structural model, the quality of predictions clearly deteriorates (see Table1). This is a significant result—it provides an independent confirmation that 3ONS is indeed a superior model for analyses of ssNMR data.
When solution-state MD trajectory is used as an input for chemical shift calculations, the quality of the predictions proves to be rather poor. Turning to unrestrained solid-state MD trajectory, 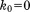 , improves the situation somewhat. Further improvement is obtained using a weakly restrained solid-state trajectory,
, improves the situation somewhat. Further improvement is obtained using a weakly restrained solid-state trajectory,  . At this stage, the quality of the predictions is comparable to that obtained with the static structure 1UBQ. Strengthening the restraints to
. At this stage, the quality of the predictions is comparable to that obtained with the static structure 1UBQ. Strengthening the restraints to 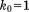 and then to
and then to 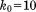 leads to further incremental improvements. The comparison of 15N chemical shifts on per-residue basis is illustrated in Supporting Information, Figure S1—there is good overall agreement between
leads to further incremental improvements. The comparison of 15N chemical shifts on per-residue basis is illustrated in Supporting Information, Figure S1—there is good overall agreement between 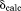 and
and 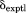 , with several residues showing distinct improvement in going from
, with several residues showing distinct improvement in going from 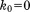 to
to  . We conclude that our erMD strategy leads to a better, more realistic representation of the protein crystal, most likely reflecting the improvements in the average protein structure (cf. first column in Table1).
. We conclude that our erMD strategy leads to a better, more realistic representation of the protein crystal, most likely reflecting the improvements in the average protein structure (cf. first column in Table1).
Interestingly, even though the erMD simulations lead to the average protein coordinates in close agreement with 3ONS (rms deviation 0.2 Å or less), the quality of 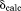 still falls somewhat short of what is obtained using the original static crystallographic structure. Naively, one may expect just the opposite—indeed, not only the average coordinates are faithfully reproduced in the erMD simulations, but also the local dynamics is successfully modeled (see below). What is the reason for this less-than-perfect outcome?
still falls somewhat short of what is obtained using the original static crystallographic structure. Naively, one may expect just the opposite—indeed, not only the average coordinates are faithfully reproduced in the erMD simulations, but also the local dynamics is successfully modeled (see below). What is the reason for this less-than-perfect outcome?
SHIFTX2, just like other chemical shift prediction programs, has been trained on static crystallographic structures and solution chemical shifts. Here, we apply SHIFTX2 to the snapshots from MD trajectories with the goal to reproduce solid-state chemical shifts. Thus, strictly speaking, the program is used outside its domain of validity. We believe that this explains the relative underperformance of the prediction algorithm.
Generally, the prediction program which is trained on high-resolution crystallographic structures would likely produce the best results when applied to another high-resolution crystallographic structure. In doing so, the atomic fluctuations, that are strongly structure-dependent,49 are likely taken into consideration in implicit fashion. From this perspective, the use of an MD model as an input for chemical shift prediction programs probably leads to double counting of the local protein dynamics. As a consequence, the MD models can match the level of δcalc accuracy demonstrated by high-quality crystallographic structures, but cannot significantly outperform them.50,51*
Order parameters
Finally, let us turn to discussion of the dipolar order parameters, 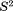 , as listed in the right-most column of Table1. These parameters have been computed using the orientational dependence of 15N-1HN vectors as extracted from the MD trajectories. The ubiquitin coordinates were used “as is,” subject only to crystal symmetry transformations. In this manner, the extracted
, as listed in the right-most column of Table1. These parameters have been computed using the orientational dependence of 15N-1HN vectors as extracted from the MD trajectories. The ubiquitin coordinates were used “as is,” subject only to crystal symmetry transformations. In this manner, the extracted 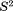 values reflect both local protein dynamics and small-amplitude rocking motion of the protein as a whole (with protein molecules embedded in the crystal lattice).54 The inspection of the data in Table1 shows that unrestrained MD trajectory leads to
values reflect both local protein dynamics and small-amplitude rocking motion of the protein as a whole (with protein molecules embedded in the crystal lattice).54 The inspection of the data in Table1 shows that unrestrained MD trajectory leads to 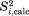 values that are appreciably different from
values that are appreciably different from 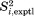 , as manifested by rmsd 0.056. The situation is to a certain degree improved in the erMD simulation using
, as manifested by rmsd 0.056. The situation is to a certain degree improved in the erMD simulation using  , rmsd 0.043. Strengthening of the restraints does not offer any significant improvement. The meaning and the importance of these results are discussed in the next sections.
, rmsd 0.043. Strengthening of the restraints does not offer any significant improvement. The meaning and the importance of these results are discussed in the next sections.
Dipolar correlation functions
The survey of Table1 suggests that most promising results are obtained in the simulations using weak restraints,  . As already discussed, further strengthening the restraints brings ensemble-average coordinates to within 0.05–0.1 Å of the target crystallographic structure, which is not justified by the accuracy of the crystallographic model. Other measures of quality do not show any significant improvement beyond what is achieved with
. As already discussed, further strengthening the restraints brings ensemble-average coordinates to within 0.05–0.1 Å of the target crystallographic structure, which is not justified by the accuracy of the crystallographic model. Other measures of quality do not show any significant improvement beyond what is achieved with  . In addition, we expect that 4U setup should be preferable to 1U. Conceptually, the erMD method is better suited for large molecular ensembles, where the average coordinates are statistically well-defined. Furthermore, the 4U model should be less vulnerable to potential artifacts associated with periodic-boundary conditions. There are certain indications that this indeed may be the case; in particular, 4U simulations consistently produce lower restraint energies, compared to Table1. Based on all of these observations, we choose to focus on
. In addition, we expect that 4U setup should be preferable to 1U. Conceptually, the erMD method is better suited for large molecular ensembles, where the average coordinates are statistically well-defined. Furthermore, the 4U model should be less vulnerable to potential artifacts associated with periodic-boundary conditions. There are certain indications that this indeed may be the case; in particular, 4U simulations consistently produce lower restraint energies, compared to Table1. Based on all of these observations, we choose to focus on  , 4U erMD simulation, comparing it with the conventional 4U uMD simulation. To obtain a better grasp on the issue of convergence, both of these trajectories have been extended from 200 to 400 ns.
, 4U erMD simulation, comparing it with the conventional 4U uMD simulation. To obtain a better grasp on the issue of convergence, both of these trajectories have been extended from 200 to 400 ns.
Figure 3(a) shows the typical 15N-1HN dipolar correlation function as derived from 400-ns-long 4U uMD simulation. Red curve in the plot represents  for residue I61 as extracted directly from the MD data (after averaging over 24 ubiquitin molecules contained in 4U periodic-boundary box). The blue curve is the result of least-square fitting using four-exponential function,
for residue I61 as extracted directly from the MD data (after averaging over 24 ubiquitin molecules contained in 4U periodic-boundary box). The blue curve is the result of least-square fitting using four-exponential function, 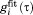 . Note that the specifics of the best-fit curve are inconsequential so long as it nicely reproduces the shape of the original correlation function.55 The plateau of the correlation function is identified with dipolar order parameter. This paves the way for an alternative definition of the order parameter, i.e. it can be equated with the value of
. Note that the specifics of the best-fit curve are inconsequential so long as it nicely reproduces the shape of the original correlation function.55 The plateau of the correlation function is identified with dipolar order parameter. This paves the way for an alternative definition of the order parameter, i.e. it can be equated with the value of 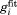 at the time point corresponding to the full length of the trajectory,
at the time point corresponding to the full length of the trajectory, 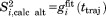 . This definition is clearly empirical, but we find it useful in the context of the following discussion.
. This definition is clearly empirical, but we find it useful in the context of the following discussion.
Figure 3.
15N-1HN dipolar correlation functions from two 400-ns-long simulations of crystalline ubiquitin: (a,b) 4U, k0 = 0 uMD simulation and (c,d) 4U, k0 = 0.1 erMD simulation. Red profiles represent the numerically calculated MD correlation functions  (after averaging over 24 ubiquitin molecules found in 4U periodic-boundary box). Blue curves are the result of 4-exponential fitting
(after averaging over 24 ubiquitin molecules found in 4U periodic-boundary box). Blue curves are the result of 4-exponential fitting 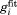 , as conducted over the interval from 0 to 85% of the total simulation length. The residue I61 shows typical convergence behavior as observed in the uMD simulation (its convergence parameter Δ corresponds to the median value in the list comprising the simulated data for residues 1–72). The residue K11 shows the worst convergence behavior in the uMD simulation (highest Δ value). All of the obtained correlation functions are remarkably smooth, which reflects good statistical properties of the simulations containing 24 ubiquitin molecules.
, as conducted over the interval from 0 to 85% of the total simulation length. The residue I61 shows typical convergence behavior as observed in the uMD simulation (its convergence parameter Δ corresponds to the median value in the list comprising the simulated data for residues 1–72). The residue K11 shows the worst convergence behavior in the uMD simulation (highest Δ value). All of the obtained correlation functions are remarkably smooth, which reflects good statistical properties of the simulations containing 24 ubiquitin molecules.
To address the issue of convergence, we have introduced the parameter 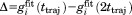 . For those correlation functions that show a well-established plateau, Δ is close to zero. For example, the correlation function shown in Figure 3(a) is characterized by Δ=0.005. This result is representative of the uMD trajectory where most of the correlation functions are well-converged. Specifically, half of the residues in this trajectory display even better convergence properties than I61 (i.e., smaller Δ values).
. For those correlation functions that show a well-established plateau, Δ is close to zero. For example, the correlation function shown in Figure 3(a) is characterized by Δ=0.005. This result is representative of the uMD trajectory where most of the correlation functions are well-converged. Specifically, half of the residues in this trajectory display even better convergence properties than I61 (i.e., smaller Δ values).
At the same time, there are several residues in uMD trajectory which lack convergence. The correlation function with the worst convergence properties belongs to residue K11 [shown in Fig. 3(b), Δ=0.15]. The failure to converge is due to rare conformational transitions involving the loop β1–β2 and, to a certain degree, also due to the “structural drift” affecting this region (see Fig. 2). Under these circumstances, the extracted value of the order parameter should be viewed merely as an estimate. The problem cannot be easily resolved—in particular, doubling the length of the trajectory does not help; for instance, using the first 200 ns of the uMD trajectory, we obtain the order parameter 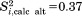 for residue K11, whereas using the full-length 400 ns trajectory the value is 0.39. In both calculations,
for residue K11, whereas using the full-length 400 ns trajectory the value is 0.39. In both calculations,  fails to reach a plateau [cf. Fig. 3(b)]. A considerably longer simulation would be needed to achieve good convergence for this residue.
fails to reach a plateau [cf. Fig. 3(b)]. A considerably longer simulation would be needed to achieve good convergence for this residue.
It is worth noting, however, that the correlation-function-based order parameters 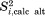 are consistent with
are consistent with 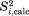 calculated with the help of Brüschweiler's formula (see footnote in Table1). For example, in the case of residue K11, the calculation based on full-length uMD trajectory yields
calculated with the help of Brüschweiler's formula (see footnote in Table1). For example, in the case of residue K11, the calculation based on full-length uMD trajectory yields 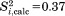 , consistent with
, consistent with 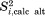 results discussed above. Similar good agreement is found throughout the protein sequence. In this situation, we choose to use
results discussed above. Similar good agreement is found throughout the protein sequence. In this situation, we choose to use 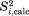 data for the purpose of further analysis, while relying on parameter Δ to indicate convergence.
data for the purpose of further analysis, while relying on parameter Δ to indicate convergence.
Let us now turn to the results in Figure 3(c,d) that illustrate the effect from introducing soft ensemble restraints,  kcal mol−1 Å−2. Characteristically, the correlation function of residue I61 remains unchanged. The order parameter determined for this residue is near-identical to the one previously found in the uMD simulation (in fact it turns out to be slightly lower, 0.86 vs. 0.87). This is generally the case for most residues in ubiquitin, where uMD and erMD simulations produce identical or near-identical results. Conversely, the behavior of residue K11 has undergone a significant change, cf. Fig. 3(b) and 3(d). Although the order parameter remains relatively low,
kcal mol−1 Å−2. Characteristically, the correlation function of residue I61 remains unchanged. The order parameter determined for this residue is near-identical to the one previously found in the uMD simulation (in fact it turns out to be slightly lower, 0.86 vs. 0.87). This is generally the case for most residues in ubiquitin, where uMD and erMD simulations produce identical or near-identical results. Conversely, the behavior of residue K11 has undergone a significant change, cf. Fig. 3(b) and 3(d). Although the order parameter remains relatively low, 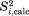 =0.68, the slowly decaying component of the correlation function is less pronounced, Δ=0.04. In general, the picture emerging from Figure 3(d) is that of a mobile loop with motions mostly on subnanosecond time scale, plus presumably a certain limited amount of µs-time-scale dynamics (cf. the remaining downward trend in
=0.68, the slowly decaying component of the correlation function is less pronounced, Δ=0.04. In general, the picture emerging from Figure 3(d) is that of a mobile loop with motions mostly on subnanosecond time scale, plus presumably a certain limited amount of µs-time-scale dynamics (cf. the remaining downward trend in  , as seen in the plot). As it turns out, this picture is largely consistent with the available experimental evidence (discussed below).
, as seen in the plot). As it turns out, this picture is largely consistent with the available experimental evidence (discussed below).
Order parameters (continued)
The survey of the results in Table1 suggests that 4U,  erMD simulation achieves a better agreement with experimental order parameters compared to the equivalent uMD simulation (rmsd 0.040 vs. 0.062). Extending both trajectories from 200 to 400 ns does not change this result (rmsd 0.039 vs. 0.065). To appreciate the significance of these improvements, let us compare the
erMD simulation achieves a better agreement with experimental order parameters compared to the equivalent uMD simulation (rmsd 0.040 vs. 0.062). Extending both trajectories from 200 to 400 ns does not change this result (rmsd 0.039 vs. 0.065). To appreciate the significance of these improvements, let us compare the 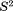 values on per-residue basis. Figure 4(a) shows
values on per-residue basis. Figure 4(a) shows 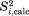 data as obtained from the crystal uMD simulation
data as obtained from the crystal uMD simulation  (blue symbols) in comparison with the recent experimental results by Haller and Schanda41 (red symbols).
(blue symbols) in comparison with the recent experimental results by Haller and Schanda41 (red symbols).
Figure 4.
Comparison of the experimental and predicted 15N-1HN dipolar order parameters in crystalline ubiquitin. Experimental data (red symbols) are from Haller and Schanda.41 The simulated data (blue symbols) are from: (A) the uMD simulation,  , and (B) the erMD simulation, k0 = 0.1 kcal mol−1 Å−2. Each MD trajectory involves a block of four crystal unit cells (4U, 24 ubiquitin molecules) and has a total duration of 400 ns. The residues for which the correlation function lacks convergence, Δ > 0.03, are indicated by cyan filled circles. Of note, the MD-derived correlation functions for residues 72–76 also lack convergence; for these residues we have no experimental data since their signals are absent from the ssNMR spectra (presumably due to slow motions). The secondary-structure regions are represented by the shaded areas and labeled at the top of the plot.
, and (B) the erMD simulation, k0 = 0.1 kcal mol−1 Å−2. Each MD trajectory involves a block of four crystal unit cells (4U, 24 ubiquitin molecules) and has a total duration of 400 ns. The residues for which the correlation function lacks convergence, Δ > 0.03, are indicated by cyan filled circles. Of note, the MD-derived correlation functions for residues 72–76 also lack convergence; for these residues we have no experimental data since their signals are absent from the ssNMR spectra (presumably due to slow motions). The secondary-structure regions are represented by the shaded areas and labeled at the top of the plot.
Generally, good agreement is observed on per-residue basis, although computed values tend to be slightly higher than the experimental ones. However, the plot also reveals one major problem area, loop β1–β2, where molecular dynamics seriously exaggerates the amount of backbone motion. Other areas with significant discrepancies are the boundary between α2 and β3, the turn following β4, and the terminal residue in β5. Of note, all the affected regions coincide with the areas of dynamic instability. The residues following glycines, for example, K11 and R54, are especially problematic. The corresponding correlation functions tend to be poorly converged [cyan circles in Fig. 4(a)], which is indicative of µs-time-scale motions. Experimentally, all these sites stand out, featuring elevated R2 rates and in some cases direct evidence of millisecond dynamics.24,41
Introducing ensemble restraints which act on the average protein structure leads to better overall agreement with the experiment, Figure 4(b) (  ). Importantly, most of the calculated order parameters remain virtually unchanged. Specifically, for 40 residues the
). Importantly, most of the calculated order parameters remain virtually unchanged. Specifically, for 40 residues the 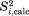 values derived from erMD and uMD simulations fall within 0.01 of each other. Furthermore, for 29 residues the order parameters derived from the ensemble-restrained trajectory are actually slightly lower than their uMD counterparts. Hence, we conclude that the native-like local dynamics is largely preserved in the erMD simulations.
values derived from erMD and uMD simulations fall within 0.01 of each other. Furthermore, for 29 residues the order parameters derived from the ensemble-restrained trajectory are actually slightly lower than their uMD counterparts. Hence, we conclude that the native-like local dynamics is largely preserved in the erMD simulations.
For those sites where uMD simulation shows poor agreement with the experiment, the erMD achieves a significant improvement. The most pronounced improvement is observed for β1–β2 loop, specifically for residues G10 and T12. With regard to K11, one has to keep in mind that (i) ssNMR relaxation dispersion measurements showed that K11 signal is broadened by an exchange process on the time scale <100 µs;24 (ii) K11 is one of those rare residues where solid-state 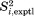 is significantly lower than solution-state
is significantly lower than solution-state 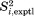 ;41 (iii) similarly, RDC-based
;41 (iii) similarly, RDC-based 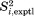 for K11 in solution is substantially lower than the relaxation-based
for K11 in solution is substantially lower than the relaxation-based 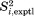 ;56 (iv) the adjacent residues L8 and T9 are both unobservable in the ssNMR experiment due to exchange broadening.23 In agreement with all these observations, the erMD correlation function for K11 contains a slowly-decaying component [characteristic time about 6 µs, see Fig. 3(d)]. To obtain a better handle on microsecond motions involving K11, one would need to record a considerably longer erMD trajectory.57 It is likely that such extended simulation would lead to even better agreement with the experimental result.
;56 (iv) the adjacent residues L8 and T9 are both unobservable in the ssNMR experiment due to exchange broadening.23 In agreement with all these observations, the erMD correlation function for K11 contains a slowly-decaying component [characteristic time about 6 µs, see Fig. 3(d)]. To obtain a better handle on microsecond motions involving K11, one would need to record a considerably longer erMD trajectory.57 It is likely that such extended simulation would lead to even better agreement with the experimental result.
Another area where erMD simulation produces partial improvement is the stretch of residues 52–54 which interconverts between type II and type I β-turn conformation. Severe line broadening due to µs time scale conformational exchange has been observed in residue G53 in solution, while T55 displays a moderate amount of broadening both in solution and in solid.24,58,59 We have scanned the trajectory for the evidence of transitions between type II and type I conformations (the indicative angles are ψ in D52 and ϕ in G5359). Although the current simulation is relatively short, 400 ns, it contains 24 ubiquitin molecules, thus offering respectable statistics. In the erMD trajectory, we have found four transitions between type II and type I conformations.† These transitions are responsible for the slowly-decaying component in the correlation function of G53, which has characteristic time of about 6 µs [cf. Fig. 4(b), where this residue is classified as lacking convergence]. The presence of µs dynamics at this site is consistent with the experimental data.
Of note, erMD simulation produces small but appreciable decrease in the order parameters for residues D52 and G53, along with a small increase for R54, resulting in better agreement with experiment. This is an instructive example which demonstrates that ensemble restraints do not necessarily reduce the amount of motion in the system; on the contrary, sometimes the amount of dynamics is increased. This can be readily understood from a thermodynamic perspective. For intrinsically unstable regions, such as the discussed β turn in ubiquitin, small imperfections in the force field (on the order of 1 kcal mol−1) can significantly alter the population balance between two or more local conformations, resulting in underestimation or overestimation of the order parameters. This is partially corrected by the ensemble restraints, which effectively play the role of empirical force-field corrections.
The findings presented in this section are nontrivial. The restraints implemented in our study are aimed at the average structure of the multiple ubiquitin molecules in the crystal unit cell(s). A priori, it is not clear what may be the effect of these restraints on local protein dynamics. In the worst-case scenario, the dynamics may be “stifled,” resulting in exceedingly high 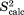 values. Contrary to any such expectations, the modeling of local dynamics is actually preserved and even improved. This result can be viewed as a strong validation of the erMD strategy—the method which relies on structural restraints is validated by the “orthogonal” dynamics data.
values. Contrary to any such expectations, the modeling of local dynamics is actually preserved and even improved. This result can be viewed as a strong validation of the erMD strategy—the method which relies on structural restraints is validated by the “orthogonal” dynamics data.
In this context, it is also interesting to discuss the relationship between solid-and solution-state order parameters. We have previously compared the two sets of order parameters for α-spc SH3 domain, demonstrating a high degree of correlation on per-residue basis.17 Here, we present a similar comparison for ubiquitin, Supporting Information, Figure S2. The agreement on per-residue basis proves to be very good, with low rmsd of 0.035. Thus, the solution 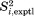 data provide a strong endorsement for their solid-state counterparts. These results also shed additional light on the role of the so-called supra-τc dynamics, that is, internal protein motions on the time scale longer than the protein tumbling time.56 The comparison of solid-and solution-state data from α-spc SH3 previously led us to conclude that supra-τc motions are relatively rare and localize in loop regions or near termini, whereas the structured elements of the protein scaffold remain unaffected.17 The results from the other small globular protein, ubiquitin, are consistent with this view (see Supporting Information, Fig. S2).
data provide a strong endorsement for their solid-state counterparts. These results also shed additional light on the role of the so-called supra-τc dynamics, that is, internal protein motions on the time scale longer than the protein tumbling time.56 The comparison of solid-and solution-state data from α-spc SH3 previously led us to conclude that supra-τc motions are relatively rare and localize in loop regions or near termini, whereas the structured elements of the protein scaffold remain unaffected.17 The results from the other small globular protein, ubiquitin, are consistent with this view (see Supporting Information, Fig. S2).
Crystallographic B factors
An additional opportunity to validate the results of MD simulations is provided by crystallographic B factors. B factors are in a certain sense complementary to dipolar order parameters as they are sensitive to translational displacements of the individual atoms. To compute B factors, all protein molecules in the MD trajectory are superimposed via symmetry transformation and then centered at origin according to Eq. (2.1). As a next step, the average coordinates of each protein atom are calculated, 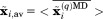 , where overbar denotes averaging over
, where overbar denotes averaging over 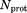 protein molecules and angular brackets indicate the averaging over all frames in the trajectory. Finally, the B factors are calculated via mean square fluctuation of the atomic coordinates:
protein molecules and angular brackets indicate the averaging over all frames in the trajectory. Finally, the B factors are calculated via mean square fluctuation of the atomic coordinates:
| (3) |
The B factors calculated in this fashion can be compared with the experimental values as contained in the crystallographic coordinate set 3ONS. One should bear in mind, however, that such comparison is at best semiquantitative. There are several reasons for this:
The approximate character of the procedure used to derive B factors during the refinement of crystallographic structures. At moderately high level of resolution (1.8 Å in the case of 3ONS), it is standard to assume that atomic fluctuations are isotropic and harmonic, corresponding to the Gaussian probability density. Clearly, these assumptions are crude; in particular, they do not hold well for mobile loops on the surface of the protein and side chains undergoing rotameric jumps.44,60 The general trend is that the reported B factors underestimate the mobility at such sites. Furthermore, various heuristic strategies are used to optimize the B factors (e.g., group atomic displacement parameters, similarity restraints, motional models such as TLS and normal mode analyses, etc.61–64). This makes the reported B factors dependent on the details of the refinement protocol.
In our protocol for calculating the B factors (see above), we subtract out the effect of small translational displacements of the protein relative to the unit crystal cell. The vibrations of the crystal lattice are also disregarded. As a result, one can expect that the calculated B factors are underestimated. It is safe to assume that the two suppressed motional modes are harmonic. Hence their contributions to the B factors should be additive. Thus, one may expect that the B factors obtained from the MD trajectory are subject to a certain constant offset, making them systematically underestimated.
Finally, one should keep in mind that all MD simulations have been conducted at the temperature 301 K, whereas the X-ray diffraction data were collected at 100 K. Assuming that the motion is harmonic, B factors should scale linearly with temperature.65,66 There are also examples of crystals where the dependence of B factors on temperature is piecewise linear with a transition point.67–69 Numerous pairs of X-ray structures can be found in the Protein Data Bank where the coordinates of the same protein have been determined at 100 K as well as at ambient temperature, for example, 1U06 and 2NUZ,70 1GZR and 1GZZ,71 and so forth. As expected, at room temperature the B factors display a systematic shift toward higher values. By the same token, it can be expected that the B factors obtained from the MD trajectory are systematically overestimated. This effect is the opposite of what has been described above, (i) and (ii).
Given all these complications, it is difficult to expect a quantitative agreement between the predicted and experimental B factors. Nevertheless, a semiquantitative agreement can usually be obtained.15 In Figure 5, we present the B factors from the crystal structure 3ONS (red symbols) together with the results from uMD and erMD (  ) simulations (blue symbols). The B factors shown in this plot have not been in any way corrected—the values are taken directly from the coordinate set 3ONS or calculated using Eq. (3).
) simulations (blue symbols). The B factors shown in this plot have not been in any way corrected—the values are taken directly from the coordinate set 3ONS or calculated using Eq. (3).
Figure 5.
Comparison of the experimental and predicted B factors in crystalline ubiquitin. Experimental data (red symbols) are as reported in the coordinate set 3ONS.25 The simulated data (blue symbols) are from: (A) the uMD simulation, 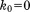 , and (B) the erMD simulation, k0 = 0.1 kcal mol−1 Å−2. Each MD trajectory involves a block of four crystal unit cells (4U, 24 ubiquitin molecules) and has a total duration of 400 ns.
, and (B) the erMD simulation, k0 = 0.1 kcal mol−1 Å−2. Each MD trajectory involves a block of four crystal unit cells (4U, 24 ubiquitin molecules) and has a total duration of 400 ns.
The simulations clearly reproduce the trends seen in the crystallographic study. However, the uMD simulation predicts unreasonably high mobility in the area of β1–β2 loop as well as C-terminal residues 71–72‡ [see Fig. 5(a)]. In erMD simulation, the amount of motion in these regions is reduced, in line with the experimental data [see Fig. 5(b)]. This change leads to a substantial improvement in the rms deviation between the simulated and experimental data, from 18 to 11 Å2. Given all reservations about B factors expressed above, this result should not be overinterpreted. Nevertheless, it is clear that erMD strategy is broadly successful in reproducing the crystallographic B factors. The emerging picture is similar to the one previously obtained from the analysis of 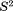 data, leading us to conclude that erMD approach offers an improved description of the local protein dynamics.
data, leading us to conclude that erMD approach offers an improved description of the local protein dynamics.
Of interest, outside the area of β1–β2 loop and C-terminus, the B factors obtained from the erMD simulation tend to be somewhat higher than their uMD counterparts [cf. Fig. 5(a,b)]. As it turns out, this is the consequence of small-amplitude rotational dynamics (rocking motion) which is somewhat more pronounced in the erMD simulation. To quantify this effect, we recalculated the B factors such as to eliminate the effect of rotational fluctuations§. The results of these alternative calculations are shown in Supporting Information, Figure S3. This latter graph demonstrates a very good agreement between the B factors derived from uMD and erMD simulations, except in the area of β1–β2 loop and C-terminus where erMD achieves big improvements and two other sites where minor improvements are obtained. Furthermore, the erMD predictions are in very good agreement with the experiment (up to a scaling factor). Thus, the internal protein dynamics is indeed faithfully captured by the erMD simulation.
The calculation illustrated in Supporting Information, Figure S3 also provides an insight into the amount of orientational disorder in the uMD and erMD trajectories. The mean amplitude of orientational fluctuations experienced by ubiquitin molecules in these two trajectories equals 4.1° and 4.5°, respectively. These are small rotations that have virtually no effect on ssNMR order parameters. However, they can generate up to ca. 1 Å linear displacements for certain protein atoms and thus produce appreciable contributions to B factors. Given the limitations (i–iii) discussed above, it is difficult to further clarify the extent of orientational disorder in this system.
15N R1 rates
Both order parameters and B factors are a measure of motional amplitudes. In contrast, 15N spin relaxation rates depend not only on amplitudes, but also on motional time scales. It is generally more challenging for MD simulations to correctly reproduce motional correlation times than it is to recover the amplitudes. When simulating 15N relaxation rates in solution, it is customary to adjust protein overall tumbling time 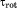 by setting it equal to the experimentally determined value. This ensures a good level of agreement between the simulated and the experimental rates. In solids—where 15N relaxation is controlled by local motions—there is no such readily available option. Furthermore, it is not known a priori if erMD simulations preserve the time scale of local dynamics. One may imagine that restraints lead to stiffening of the system, thus causing a shift toward faster motions. To test this aspect of the erMD model, we turn to the analysis of 15N relaxation data.
by setting it equal to the experimentally determined value. This ensures a good level of agreement between the simulated and the experimental rates. In solids—where 15N relaxation is controlled by local motions—there is no such readily available option. Furthermore, it is not known a priori if erMD simulations preserve the time scale of local dynamics. One may imagine that restraints lead to stiffening of the system, thus causing a shift toward faster motions. To test this aspect of the erMD model, we turn to the analysis of 15N relaxation data.
The 15N R1and 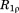 relaxation rates in crystalline ubiquitin (same form as 3ONS) have been measured at multiple fields by Schanda et al. 23 The
relaxation rates in crystalline ubiquitin (same form as 3ONS) have been measured at multiple fields by Schanda et al. 23 The 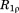 data are not well-suited for the purpose of comparative analysis. Indeed, transverse relaxation rates are a function of the spectral density at zero frequency and thus are highly sensitive to slowly-decaying components of the correlation functions. Given the lack of convergence which has been observed for a number of residues, Figure 3, and the fact that many of the sites are affected by µs motions,24 we are not in a position to accurately predict
data are not well-suited for the purpose of comparative analysis. Indeed, transverse relaxation rates are a function of the spectral density at zero frequency and thus are highly sensitive to slowly-decaying components of the correlation functions. Given the lack of convergence which has been observed for a number of residues, Figure 3, and the fact that many of the sites are affected by µs motions,24 we are not in a position to accurately predict 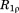 rates on the basis of the current relatively short MD trajectories. In contrast, R1rates are well-suited to draw a comparison between the simulation and experiment. In crystalline samples, 15N R1rates are sensitive to the range of motions from about 10 ps to about 100 ns,72 which is reasonably well-sampled in our MD simulations.
rates on the basis of the current relatively short MD trajectories. In contrast, R1rates are well-suited to draw a comparison between the simulation and experiment. In crystalline samples, 15N R1rates are sensitive to the range of motions from about 10 ps to about 100 ns,72 which is reasonably well-sampled in our MD simulations.
Shown in Figure 6 is the comparison between the experimental and simulated 15N R1rates at static magnetic field strength 11.74 T (proton frequency 500 MHz). The experimental dataset is relatively sparse, 35 residues; in particular, it contains no data from residue K11. At the same time, the measurements are fairly precise—the average uncertainty is estimated to be 7%. The erMD simulation has better success in reproducing the experimental data than uMD, as confirmed by the respective rms deviations, 0.023 versus 0.037 s−1. The decrease in rmsd is mainly due to a single residue, G10. In addition, the erMD simulation seems to better reproduce the experimental R1profile. Even if G10 is removed from the dataset, the erMD-derived rates show a reasonably strong correlation with the experimental data, r=0.68. For uMD simulation, the result is somewhat worse, r=0.63.
Figure 6.
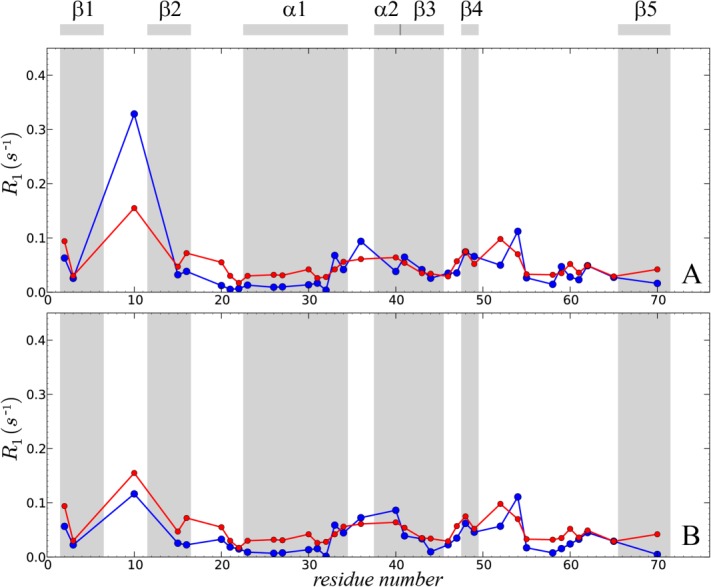
Comparison of the experimental and predicted 15N R1 relaxation rates in crystalline ubiquitin at static magnetic field strength 11.74 T. Experimental data (red symbols) are as reported by Schanda et al.23 The simulated data (blue symbols) are from: (A) the uMD simulation, k0 = 0, and (B) the erMD simulation, k0 = 0.1 kcal mol−1 Å−2. Each MD trajectory involves a block of four crystal unit cells (4U, 24 ubiquitin molecules) and has a total duration of 400 ns.
Similar comparison for data collected at 14.09 T (proton frequency 600 MHz) is illustrated in Figure 7. This data set includes a greater number of residues, 50. However, the measurement error is substantial, on average 13%.23 The agreement with experiment is not as good as previously found with 11.74 T data. The rms deviation between the simulated and experimental rates is 0.047 s−1 for uMD simulation and 0.054 s−1 for erMD simulation. The uMD trajectory, therefore, appears to be somewhat more successful. The difference, however, is due to one single residue, K11. Importantly, this residue shows an anomalous dependence of R1on static magnetic field strength for which we have no satisfactory explanation (see below). If this data point is excluded, the results slightly favor erMD simulation over uMD (rmsd of 0.042 and 0.045 s−1, respectively).
Figure 7.
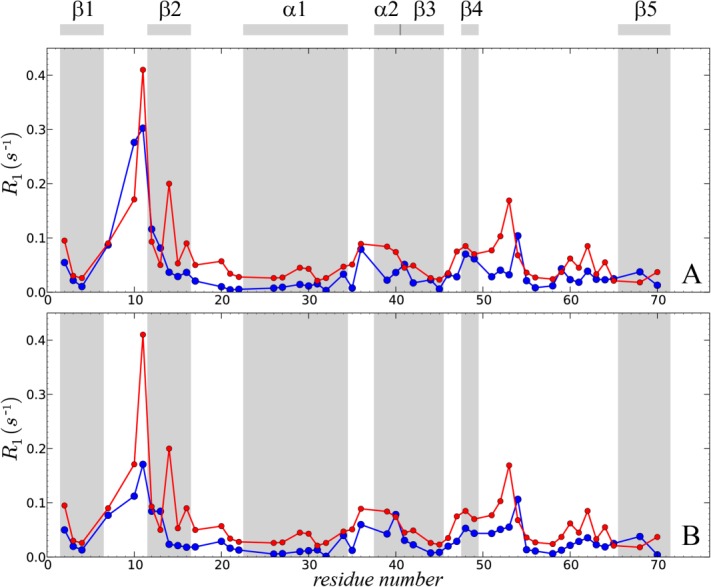
Comparison of the experimental and predicted 15N R1 relaxation rates in crystalline ubiquitin at static magnetic field strength 14.09 T (same plotting conventions as in Fig. 6).
Finally, the results at 19.96 T (850-MHz proton frequency) are illustrated in Supporting Information, Figure S4. This data set is comprised of 54 residues; the error is on average 10%. The rms deviations between the simulated and experimental rates are 0.090 and 0.107 s−1 for uMD and erMD simulations, respectively. The substantial rmsd values are due to one single residue, K11. Of note, both uMD and erMD trajectories cannot successfully reproduce the experimental R1rate for this particular residue (experimental rate 0.90 s−1, uMD rate 0.26 s−1, erMD rate 0.14 s−1). As already pointed out, the experimental data for K11 display an unusual field dependence.23 Specifically, the 15N R1rate for this residue increases from 0.41 ± 0.08 s−1 at 600-MHz spectrometer frequency to 0.90 ± 0.10 s−1 at 850 MHz. Based on what we know about nitrogen relaxation, there is no good explanation for this result (the CSA relaxation mechanism alone is insufficient to explain 2-fold increase in R1rate). It can be suggested that the data involving K11 are contaminated by some sort of experimental error, which may be nontrivial and worthy of further investigation. From our perspective, it is fair to discount or disregard this particular piece of data. With this provision, the performance of erMD model is at least as good, and possibly better than that of the uMD model (cf. Figs. 6 and 7). This result provides a strong validation for the erMD strategy developed in this work.
Concluding Remarks
The applicability of the erMD method is contingent on the assumption that X-ray coordinates faithfully reproduce the average protein structure. Clearly, the very existence of the X-ray coordinates rules out the presence of extensive dynamics such as occurs in disordered proteins. Those elements of the structure that are highly dynamic (e.g., mobile loops or termini) are normally absent from the crystallographic models, so that no restraints are imposed on these mobile fragments (in this sense the erMD approach is “self-regulated”). Likewise, we propose not to impose any restraints on the side chains solved with alternate conformations.
For the major portion of the protein structure, it is safe to assume that the average protein coordinates fall within 0.2–0.3 Å of the high-resolution crystallographic model, which means that erMD approach is fundamentally sound. One caveat, however, is that X-ray coordinates may correspond to the lowest-energy structure, which is not necessarily the same as the average structure. In other words, X-ray coordinates may reproduce the “ground state” of the protein, while ignoring the “excited states” (i.e., the states with locally different conformations that are populated at the level less than ca. 10%). In the context of our study, we do not see this as a major problem. Given that the restraints used in erMD protocol are weak, we believe that individual protein molecules can sample various excited states without incurring any significant energy penalty [cf. Fig. 2(c)].
In this work, we have tested the restraint coefficients of 0, 0.1, 1, and 10 kcal mol−1 Å−2 and concluded that the most meaningful results are obtained with  . This is admittedly a rather ad hoc and coarse-grained approach. Ideally, we would like to fine-tune the restraint force using a certain measure of quality that is independent of the observables that are used to validate the erMD method. However, any such exercise would require at least ca. 10 different protein systems; the results obtained from ubiquitin alone would be of limited value. Given the scarcity of such systems (i.e., small globular proteins thoroughly characterized by ssNMR), this task would be rather demanding, not to mention computationally expensive. Here, we adopt a more qualitative approach, where we demonstrate the feasibility of the erMD method employing weak restraints. The choice of restraint force is dictated primarily by rmsd to crystallographic target and crystallographic R factors, as well as restraint energies. These metrics point toward
. This is admittedly a rather ad hoc and coarse-grained approach. Ideally, we would like to fine-tune the restraint force using a certain measure of quality that is independent of the observables that are used to validate the erMD method. However, any such exercise would require at least ca. 10 different protein systems; the results obtained from ubiquitin alone would be of limited value. Given the scarcity of such systems (i.e., small globular proteins thoroughly characterized by ssNMR), this task would be rather demanding, not to mention computationally expensive. Here, we adopt a more qualitative approach, where we demonstrate the feasibility of the erMD method employing weak restraints. The choice of restraint force is dictated primarily by rmsd to crystallographic target and crystallographic R factors, as well as restraint energies. These metrics point toward  as the most reasonable option. Other types of data have been used to validate the results. In particular, crystallographic B factors and solid-state 15N R1rates have been included post factum (when the manuscript was under revision).
as the most reasonable option. Other types of data have been used to validate the results. In particular, crystallographic B factors and solid-state 15N R1rates have been included post factum (when the manuscript was under revision).
The use of the erMD method is contingent on the existence of crystallographic coordinates. This implies that we can only expect to see a limited amount of dynamics in the erMD trajectories. This is in contrast to more general possibilities offered by conventional MD simulations (assuming for a moment that force field is not an issue). Despite such limitations, the new method can provide valuable insights into functionally important forms of protein motion. Relatively recently, Lange et al. presented a structural ensemble of ubiquitin which samples a multitude of conformational states including those observed in 46 different crystal structures.56 The analysis of this ensemble revealed a dominant motional mode which controls ligand binding via conformational selection mechanism; it also helped to explain the low entropic cost of binding. Later Long and Brüschweiler73 as well as Fenwick et al.43 used MD simulations to further probe the mechanisms of molecular recognition in ubiquitin, including allosteric effects, cooperative transitions, and formation of an encounter complex. It is anticipated that such studies can benefit from use of the new erMD methodology.
This work draws its inspiration from several sources. A number of ensemble simulations employing solution-NMR restraints have been reported in recent years.43,56,74–83 A considerable body of work has also been published on “ensemble refinement” of X-ray crystallographic structures.84–90 Almost all of these simulations, however, consist of short simulated-annealing runs; others are replica-exchange simulations involving high temperatures. In all of these studies, the intention has been to generate structural models with a modicum of conformational diversity; none of them sought to produce a realistic (movie-like) picture of protein motion. This sets our erMD strategy apart from the existing body of work in this area. Of note, our approach is suitable for predicting NMR observables that are dependent on motional correlation times, such as 15N relaxation rates.
The erMD method can be readily generalized for globular proteins in solution, where the crystal structure remains a valid structural template. In principle, protein structure in solution need not necessarily be the same as the X-ray structure obtained from the crystalline sample. Nevertheless, it is generally accepted that crystallographic coordinates provide the best structural models for (single-domain, globular) proteins in solution which are superior to NMR structures.91–93 This is particularly evident given that X-ray structures lead to better predictions of chemical shifts, residual dipolar couplings, and other independently measured parameters.94–98 In the case of solution simulations, we envision a modified version of erMD protocol where multiple simulations are run concurrently, with each simulation representing a single protein molecule in a water box. The overarching restraints are imposed to ensure that the average protein structure remains consistent with the X-ray coordinates.
At this time, the best MD force field potentials cannot match the accuracy afforded by the high-resolution crystallographic structures. This shortcoming has a significant adverse impact on fidelity of protein structure in long MD simulations. From this perspective, the crystallography-based restraints used in this study can be thought of as empirical force-field corrections, which remedy small but not-insignificant defects in the force field.99 Elimination of the “structural drift” is the key achievement of the new erMD methodology. Importantly, the restraints apply only to the ensemble-average coordinates—individual protein molecules in the simulated crystal cell(s) retain their internal dynamics. The restrained MD trajectories recorded in this manner proved to be markedly superior to the conventional unrestrained MD trajectories—they produce better crystallographic R factors, better B factors, better chemical shift predictions, and better predictions for the motional order parameters  . They also predict 15N R1relaxation rates that are at least as accurate as those obtained from the uMD simulations. The restrained trajectories are characterized by uniquely accurate (average) structure as well as a faithful rendition of internal dynamics; as such, they may be among the most realistic protein MD simulations so far reported.
. They also predict 15N R1relaxation rates that are at least as accurate as those obtained from the uMD simulations. The restrained trajectories are characterized by uniquely accurate (average) structure as well as a faithful rendition of internal dynamics; as such, they may be among the most realistic protein MD simulations so far reported.
Acknowledgments
We are thankful to Andrei Fokine and Paul Schanda for valuable discussions. We acknowledge the kind help of Beomsoo Han who prepared for us the customized version of SHIFTX2 software.
Notes
These realizations led to development of the next generation of chemical shift predictors which are trained on MD trajectories and intended for use with MD trajectories.52,53 We have tested one of these newer predictors, PPM,53 on all trajectories listed in Table1. As one may expect, PPM-based predictions using static coordinates 3ONS turn out to be poor. Conversely, the predictions using uMD and erMD k0
 trajectories are of similar overall quality to those obtained via SHIFTX2. More specifically, PPM performs somewhat better for 1HN chemical shifts, somewhat worse for 13Cβ chemical shifts, and on par with SHIFTX2 for 15N and 13Cα chemical shifts.
trajectories are of similar overall quality to those obtained via SHIFTX2. More specifically, PPM performs somewhat better for 1HN chemical shifts, somewhat worse for 13Cβ chemical shifts, and on par with SHIFTX2 for 15N and 13Cα chemical shifts.
The uMD trajectory features no such transitions, although one of the molecules converts into type I conformation during the equilibration stage.
Note that crystallographic coordinates are unavailable for residues 73–76 and ssNMR data are unavailable for residues 72–76.
Toward this end, we implemented the protocol where all ubiquitin molecules from the MD frames were superimposed onto 3ONS in the least-square sense (via secondary-structure Cα atoms). The resulting superposition was then used to calculate B factors according to Eq. (3).
Additional Supporting Information may be found in the online version of this article.
References
- 1.Raval A, Piana S, Eastwood MP, Dror RO, Shaw DE. Refinement of protein structure homology models via long, all-atom molecular dynamics simulations. Proteins. 2012;80:2071–2079. doi: 10.1002/prot.24098. [DOI] [PubMed] [Google Scholar]
- 2.Lee MR, Baker D, Kollman PA. 2.1 and 1.8 angstrom average Cα RMSD structure predictions on two small proteins, HP-36 and S15. J Am Chem Soc. 2001;123:1040–1046. doi: 10.1021/ja003150i. [DOI] [PubMed] [Google Scholar]
- 3.Fan H, Mark AE. Refinement of homology-based protein structures by molecular dynamics simulation techniques. Protein Sci. 2004;13:211–220. doi: 10.1110/ps.03381404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 5.Lee MR, Tsai J, Baker D, Kollman PA. Molecular dynamics in the endgame of protein structure prediction. J Mol Biol. 2001;313:417–430. doi: 10.1006/jmbi.2001.5032. [DOI] [PubMed] [Google Scholar]
- 6.Chen JH, Brooks CL. Can molecular dynamics simulations provide high-resolution refinement of protein structure? Proteins. 2007;67:922–930. doi: 10.1002/prot.21345. [DOI] [PubMed] [Google Scholar]
- 7.Chopra G, Summa CM, Levitt M. Solvent dramatically affects protein structure refinement. Proc Natl Acad Sci USA. 2008;105:20239–20244. doi: 10.1073/pnas.0810818105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.MacCallum JL, Hua L, Schnieders MJ, Pande VS, Jacobson MP, Dill KA. Assessment of the protein-structure refinement category in CASP8. Proteins. 2009;77:66–80. doi: 10.1002/prot.22538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.MacCallum JL, Perez A, Schnieders MJ, Hua L, Jacobson MP, Dill KA. Assessment of protein structure refinement in CASP9. Proteins. 2011;79:74–90. doi: 10.1002/prot.23131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ponder JW, Wu CJ, Ren PY, Pande VS, Chodera JD, Schnieders MJ, Haque I, Mobley DL, Lambrecht DS, DiStasio RA, Head-Gordon M, Clark GNI, Johnson ME, Head-Gordon T. Current status of the AMOEBA polarizable force field. J Phys Chem B. 2010;114:2549–2564. doi: 10.1021/jp910674d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mackerell AD, Feig M, Brooks CL. Extending the treatment of backbone energetics in protein force fields: limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulations. J Comput Chem. 2004;25:1400–1415. doi: 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- 12.Best RB, Hummer G. Optimized molecular dynamics force fields applied to the helix-coil transition of polypeptides. J Phys Chem B. 2009;113:9004–9015. doi: 10.1021/jp901540t. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li DW, Brüschweiler R. NMR-based protein potentials. Angew Chem Int Ed. 2010;49:6778–6780. doi: 10.1002/anie.201001898. [DOI] [PubMed] [Google Scholar]
- 14.Stocker U, Spiegel K, Gunsteren van WF. On the similarity of properties in solution or in the crystalline state: a molecular dynamics study of hen lysozyme. J Biomol NMR. 2000;18:1–12. doi: 10.1023/a:1008379605403. [DOI] [PubMed] [Google Scholar]
- 15.Meinhold L, Smith JC. Fluctuations and correlations in crystalline protein dynamics: a simulation analysis of Staphylococcal nuclease. Biophys J. 2005;88:2554–2563. doi: 10.1529/biophysj.104.056101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Cerutti DS, Freddolino PL, Duke RE, Case DA. Simulations of a protein crystal with a high resolution X-ray structure: evaluation of force fields and water models. J Phys Chem B. 2010;114:12811–12824. doi: 10.1021/jp105813j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Chevelkov V, Xue Y, Linser R, Skrynnikov NR, Reif B. Comparison of solid-state dipolar couplings and solution relaxation data provides insight into protein backbone dynamics. J Am Chem Soc. 2010;132:5015–5017. doi: 10.1021/ja100645k. [DOI] [PubMed] [Google Scholar]
- 18.Mollica L, Baias M, Lewandowski JR, Wylie BJ, Sperling LJ, Rienstra CM, Emsley JW, Blackledge M. Atomic-resolution structural dynamics in crystalline proteins from NMR and Molecular Simulation. J Phys Chem Lett. 2012;3:3657−3662. doi: 10.1021/jz3016233. [DOI] [PubMed] [Google Scholar]
- 19.Martin RW, Zilm KW. Preparation of protein nanocrystals and their characterization by solid state NMR. J Magn Reson. 2003;165:162–174. doi: 10.1016/s1090-7807(03)00253-2. [DOI] [PubMed] [Google Scholar]
- 20.Igumenova TI, Wand AJ, McDermott AE. Assignment of the backbone resonances for microcrystalline ubiquitin. J Am Chem Soc. 2004;126:5323–5331. doi: 10.1021/ja030546w. [DOI] [PubMed] [Google Scholar]
- 21.Lorieau JL, McDermott AE. Conformational flexibility of a microcrystalline globular protein: order parameters by solid-state NMR spectroscopy. J Am Chem Soc. 2006;128:11505–11512. doi: 10.1021/ja062443u. [DOI] [PubMed] [Google Scholar]
- 22.Manolikas T, Herrmann T, Meier BH. Protein structure determination from 13C spin-diffusion solid-state NMR spectroscopy. J Am Chem Soc. 2008;130:3959–3966. doi: 10.1021/ja078039s. [DOI] [PubMed] [Google Scholar]
- 23.Schanda P, Meier BH, Ernst M. Quantitative analysis of protein backbone dynamics in microcrystalline ubiquitin by solid-state NMR spectroscopy. J Am Chem Soc. 2010;132:15957–15967. doi: 10.1021/ja100726a. [DOI] [PubMed] [Google Scholar]
- 24.Tollinger M, Sivertsen AC, Meier BH, Ernst M, Schanda P. Site-resolved measurement of microsecond-to-millisecond conformational exchange processes in proteins by solid-state NMR spectroscopy. J Am Chem Soc. 2012;134:14800–14807. doi: 10.1021/ja303591y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Huang KY, Amodeo GA, Tong LA, McDermott A. The structure of human ubiquitin in 2-methyl-2,4-pentanediol: a new conformational switch. Protein Sci. 2011;20:630–639. doi: 10.1002/pro.584. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kohn JE, Afonine PV, Ruscio JZ, Adams PD, Head-Gordon T. Evidence of functional protein dynamics from X-ray crystallographic ensembles. PLoS Comput Biol. 2010;6:e1000911. doi: 10.1371/journal.pcbi.1000911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Juers DH, Matthews BW. Reversible lattice repacking illustrates the temperature dependence of macromolecular interactions. J Mol Biol. 2001;311(4):851–862. doi: 10.1006/jmbi.2001.4891. [DOI] [PubMed] [Google Scholar]
- 28.Radaelli PG. Symmetry in crystallography: understanding the international tables. Oxford: Oxford University Press; 2011. [Google Scholar]
- 29.Piana S, Lindorff-Larsen K, Shaw DE. Atomic-level description of ubiquitin folding. Proc Natl Acad Sci USA. 2013;110:5915–5920. doi: 10.1073/pnas.1218321110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lindorff-Larsen K, Piana S, Palmo K, Maragakis P, Klepeis JL, Dror RO, Shaw DE. Improved side-chain torsion potentials for the Amber ff99SB protein force field. Proteins. 2010;78:1950–1958. doi: 10.1002/prot.22711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Bas DC, Rogers DM, Jensen JH. Very fast prediction and rationalization of pKa values for protein-ligand complexes. Proteins. 2008;73:765–783. doi: 10.1002/prot.22102. [DOI] [PubMed] [Google Scholar]
- 33.Sundd M, Iverson N, Ibarra-Molero B, Sanchez-Ruiz JM, Robertson AD. Electrostatic interactions in ubiquitin: stabilization of carboxylates by lysine amino groups. Biochemistry. 2002;41:7586–7596. doi: 10.1021/bi025571d. [DOI] [PubMed] [Google Scholar]
- 34.Cerutti DS, Trong Le I, Stenkamp RE, Lybrand TP. Simulations of a protein crystal: explicit treatment of crystallization conditions links theory and experiment in the streptavidin-biotin complex. Biochemistry. 2008;47:12065–12077. doi: 10.1021/bi800894u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Adams PD, Afonine PV, Bunkoczi G, Chen VB, Davis IW, Echols N, Headd JJ, Hung LW, Kapral GJ, Grosse-Kunstleve RW, McCoy AJ, Moriarty NW, Oeffner R, Read RJ, Richardson DC, Richardson JS, Terwilliger TC, Zwart PH. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr Sect D: Biol Crystallogr. 2010;66:213–221. doi: 10.1107/S0907444909052925. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fokine A, Urzhumtsev A. Flat bulk-solvent model: obtaining optimal parameters. Acta Crystallogr Sect D: Biol Crystallogr. 2002;58:1387–1392. doi: 10.1107/S0907444902010284. [DOI] [PubMed] [Google Scholar]
- 37.Afonine PV, Grosse-Kunstleve RW, Adams PD. A robust bulk-solvent correction and anisotropic scaling procedure. Acta Crystallogr Sect D: Biol Crystallogr. 2005;61:850–855. doi: 10.1107/S0907444905007894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Han B, Liu YF, Ginzinger SW, Wishart DS. SHIFTX2: significantly improved protein chemical shift prediction. J Biomol NMR. 2011;50:43–57. doi: 10.1007/s10858-011-9478-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Igumenova TI, McDermott AE, Zilm KW, Martin RW, Paulson EK, Wand AJ. Assignments of carbon NMR resonances for microcrystalline ubiquitin. J Am Chem Soc. 2004;126:6720–6727. doi: 10.1021/ja030547o. [DOI] [PubMed] [Google Scholar]
- 40.Brüschweiler R, Wright PE. NMR order parameters of biomolecules: a new analytical representation and application to the Gaussian Axial Fluctuation model. J Am Chem Soc. 1994;116:8426–8427. [Google Scholar]
- 41.Haller JD, Schanda P. Amplitudes and time scales of picosecond-to-microsecond motion in proteins studied by solid-state NMR: a critical evaluation of experimental approaches and application to crystalline ubiquitin. J Biomol NMR. 2013;57:263–280. doi: 10.1007/s10858-013-9787-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Vijay-Kumar S, Bugg CE, Cook WJ. Structure of ubiquitin refined at 1.8 A resolution. J Mol Biol. 1987;194:531–544. doi: 10.1016/0022-2836(87)90679-6. [DOI] [PubMed] [Google Scholar]
- 43.Fenwick RB, Esteban-Martin S, Richter B, Lee D, Walter KFA, Milovanovic D, Becker S, Lakomek NA, Griesinger C, Salvatella X. Weak long-range correlated motions in a surface patch of ubiquitin involved in molecular recognition. J Am Chem Soc. 2011;133:10336–10339. doi: 10.1021/ja200461n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Vitkup D, Ringe D, Karplus M, Petsko GA. Why protein R-factors are so large: a self-consistent analysis. Proteins. 2002;46:345–354. doi: 10.1002/prot.10035. [DOI] [PubMed] [Google Scholar]
- 45.DePristo MA, Bakker de PIW, Blundell TL. Heterogeneity and inaccuracy in protein structures solved by X-ray crystallography. Structure. 2004;12:831–838. doi: 10.1016/j.str.2004.02.031. [DOI] [PubMed] [Google Scholar]
- 46.Shirts MR, Pitera JW, Swope WC, Pande VS. Extremely precise free energy calculations of amino acid side chain analogs: comparison of common molecular mechanics force fields for proteins. J Chem Phys. 2003;119:5740–5761. [Google Scholar]
- 47.Seeliger D, Groot de BL. Protein thermostability calculations using alchemical free energy simulations. Biophys J. 2010;98:2309–2316. doi: 10.1016/j.bpj.2010.01.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Linge JP, Williams MA, Spronk CAEM, Bonvin AMJJ, Nilges M. Refinement of protein structures in explicit solvent. Proteins. 2003;50:496–506. doi: 10.1002/prot.10299. [DOI] [PubMed] [Google Scholar]
- 49.Halle B. Flexibility and packing in proteins. Proc Natl Acad Sci USA. 2002;99:1274–1279. doi: 10.1073/pnas.032522499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Robustelli P, Stafford KA, Palmer AG. Interpreting protein structural dynamics from NMR chemical shifts. J Am Chem Soc. 2012;134:6365–6374. doi: 10.1021/ja300265w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Li DW, Brüschweiler R. Certification of molecular dynamics trajectories with NMR chemical shifts. J Phys Chem Lett. 2010;1:246–248. [Google Scholar]
- 52.Lehtivarjo J, Tuppurainen K, Hassinen T, Laatikainen R, Perakyla M. Combining NMR ensembles and molecular dynamics simulations provides more realistic models of protein structures in solution and leads to better chemical shift prediction. J Biomol NMR. 2012;52:257–267. doi: 10.1007/s10858-012-9609-6. [DOI] [PubMed] [Google Scholar]
- 53.Li DW, Brüschweiler R. PPM: a side-chain and backbone chemical shift predictor for the assessment of protein conformational ensembles. J Biomol NMR. 2012;54:257–265. doi: 10.1007/s10858-012-9668-8. [DOI] [PubMed] [Google Scholar]
- 54.Lewandowski JR, Sein J, Blackledge M, Emsley L. Anisotropic collective motion contributes to nuclear spin relaxation in crystalline proteins. J Am Chem Soc. 2010;132:1246–1247. doi: 10.1021/ja907067j. [DOI] [PubMed] [Google Scholar]
- 55.Bremi T, Brüschweiler R. Locally anisotropic internal polypeptide backbone dynamics by NMR relaxation. J Am Chem Soc. 1997;119:6672–6673. [Google Scholar]
- 56.Lange OF, Lakomek NA, Farès C, Schröder GF, Walter KFA, Becker S, Meiler J, Grubmüller H, Griesinger C, Groot de BL. Recognition dynamics up to microseconds revealed from an RDC-derived ubiquitin ensemble in solution. Science. 2008;320:1471–1475. doi: 10.1126/science.1157092. [DOI] [PubMed] [Google Scholar]
- 57.Xue Y, Ward JM, Yuwen TR, Podkorytov IS, Skrynnikov NR. Microsecond time-scale conformational exchange in proteins: using long Molecular Dynamics trajectory to simulate NMR relaxation dispersion data. J Am Chem Soc. 2012;134:2555–2562. doi: 10.1021/ja206442c. [DOI] [PubMed] [Google Scholar]
- 58.Massi F, Grey MJ, Palmer AG. Microsecond timescale backbone conformational dynamics in ubiquitin studied with NMR R1ρ relaxation experiments. Protein Sci. 2005;14:735–742. doi: 10.1110/ps.041139505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Sidhu A, Surolia A, Robertson AD, Sundd M. A hydrogen bond regulates slow motions in ubiquitin by modulating a β-turn flip. J Mol Biol. 2011;411:1037–1048. doi: 10.1016/j.jmb.2011.06.044. [DOI] [PubMed] [Google Scholar]
- 60.Garcia AE, Krumhansl JA, Frauenfelder H. Variations on a theme by Debye and Waller: from simple crystals to proteins. Proteins. 1997;29:153–160. [PubMed] [Google Scholar]
- 61.Kundu S, Melton JS, Sorensen DC, Phillips GN. Dynamics of proteins in crystals: comparison of experiment with simple models. Biophys J. 2002;83:723–732. doi: 10.1016/S0006-3495(02)75203-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Poon BK, Chen XR, Lu MY, Vyas NK, Quiocho FA, Wang QH, Ma JP. Normal mode refinement of anisotropic thermal parameters for a supramolecular complex at 3.42-A crystallographic resolution. Proc Natl Acad Sci USA. 2007;104:7869–7874. doi: 10.1073/pnas.0701204104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Afonine PV, Urzhumtsev A, Grosse-Kunstleve RW, Adams PD. atomic displacement parameters (ADPs), their parameterization and refinement in PHENIX. Comput Crystallogr Newsletter. 2010;1:24–31. [Google Scholar]
- 64.Merritt EA. To B or not to B: a question of resolution? Acta Crystallogr Sect D: Biol Crystallogr. 2012;68:468–477. doi: 10.1107/S0907444911028320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Chong SH, Joti Y, Kidera A, Go N, Ostermann A, Gassmann A, Parak F. Dynamical transition of myoglobin in a crystal: comparative studies of X-ray crystallography and Mossbauer spectroscopy. Eur Biophys J. 2001;30:319–329. doi: 10.1007/s002490100152. [DOI] [PubMed] [Google Scholar]
- 66.Schmidt M, Achterhold K, Prusakov V, Parak FG. Protein dynamics of a β-sheet protein. Eur Biophys J. 2009;38:687–700. doi: 10.1007/s00249-009-0427-z. [DOI] [PubMed] [Google Scholar]
- 67.Tilton RF, Dewan JC, Petsko GA. Effects of temperature on protein structure and dynamics: X-ray crystallographic studies of the protein ribonuclease-A at 9 different temperatures from 98 K to 320 K. Biochemistry. 1992;31:2469–2481. doi: 10.1021/bi00124a006. [DOI] [PubMed] [Google Scholar]
- 68.Teeter MM, Yamano A, Stec B, Mohanty U. On the nature of a glassy state of matter in a hydrated protein: relation to protein function. Proc Natl Acad Sci USA. 2001;98:11242–11247. doi: 10.1073/pnas.201404398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Joti Y, Nakasako M, Kidera A, Go N. Nonlinear temperature dependence of the crystal structure of lysozyme: correlation between coordinate shifts and thermal factors. Acta Crystallogr Sect D: Biol Crystallogr. 2002;58:1421–1432. doi: 10.1107/S0907444902011277. [DOI] [PubMed] [Google Scholar]
- 70.Chevelkov V, Faelber K, Diehl A, Heinemann U, Oschkinat H, Reif B. Detection of dynamic water molecules in a microcrystalline sample of the SH3 domain of α-spectrin by MAS solid-state NMR. J Biomol NMR. 2005;31:295–310. doi: 10.1007/s10858-005-1718-z. [DOI] [PubMed] [Google Scholar]
- 71.Brzozowski AM, Dodson EJ, Dodson GG, Murshudov GN, Verma C, Turkenburg JP, Bree de FM, Dauter Z. Structural origins of the functional divergence of human insulin-like growth factor-I and insulin. Biochemistry. 2002;41:9389–9397. doi: 10.1021/bi020084j. [DOI] [PubMed] [Google Scholar]
- 72.Chevelkov V, Zhuravleva AV, Xue Y, Reif B, Skrynnikov NR. Combined analysis of 15N relaxation data from solid-and solution-state NMR spectroscopy. J Am Chem Soc. 2007;129:12594–12595. doi: 10.1021/ja073234s. [DOI] [PubMed] [Google Scholar]
- 73.Long D, Bruschweiler R. In silico elucidation of the recognition dynamics of ubiquitin. PLoS Comput Biol. 2011;7:e1002035. doi: 10.1371/journal.pcbi.1002035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Kim YM, Prestegard JH. Refinement of the NMR structures for Acyl Carrier Protein with scalar coupling data. Proteins. 1990;8:377–385. doi: 10.1002/prot.340080411. [DOI] [PubMed] [Google Scholar]
- 75.Bonvin AMJJ, Boelens R, Kaptein R. Time and ensemble-averaged direct NOE restraints. J Biomol NMR. 1994;4:143–149. doi: 10.1007/BF00178343. [DOI] [PubMed] [Google Scholar]
- 76.Clore GM, Schwieters CD. How much backbone motion in ubiquitin is required to account for dipolar coupling data measured in multiple alignment media as assessed by independent cross-validation? J Am Chem Soc. 2004;126:2923–2938. doi: 10.1021/ja0386804. [DOI] [PubMed] [Google Scholar]
- 77.Tang C, Schwieters CD, Clore GM. Open-to-closed transition in apo maltose-binding protein observed by paramagnetic NMR. Nature. 2007;449:1078–1082. doi: 10.1038/nature06232. [DOI] [PubMed] [Google Scholar]
- 78.Lindorff-Larsen K, Best RB, DePristo MA, Dobson CM, Vendruscolo M. Simultaneous determination of protein structure and dynamics. Nature. 2005;433:128–132. doi: 10.1038/nature03199. [DOI] [PubMed] [Google Scholar]
- 79.Allison JR, Varnai P, Dobson CM, Vendruscolo M. Determination of the free energy landscape of α-synuclein using spin label nuclear magnetic resonance measurements. J Am Chem Soc. 2009;131:18314–18326. doi: 10.1021/ja904716h. [DOI] [PubMed] [Google Scholar]
- 80.Huang JR, Grzesiek S. Ensemble calculations of unstructured proteins constrained by RDC and PRE data: a case study of urea-denatured ubiquitin. J Am Chem Soc. 2010;132:694–705. doi: 10.1021/ja907974m. [DOI] [PubMed] [Google Scholar]
- 81.Robustelli P, Kohlhoff K, Cavalli A, Vendruscolo M. Using NMR chemical shifts as structural restraints in molecular dynamics simulations of proteins. Structure. 2010;18:923–933. doi: 10.1016/j.str.2010.04.016. [DOI] [PubMed] [Google Scholar]
- 82.Esteban-Martin S, Fenwick RB, Salvatella X. Refinement of ensembles describing unstructured proteins using NMR residual dipolar couplings. J Am Chem Soc. 2010;132:4626–4632. doi: 10.1021/ja906995x. [DOI] [PubMed] [Google Scholar]
- 83.Im W, Jo S, Kim T. An ensemble dynamics approach to decipher solid-state NMR observables of membrane proteins. BBA Biomembr. 2012;1818:252–262. doi: 10.1016/j.bbamem.2011.07.048. [DOI] [PubMed] [Google Scholar]
- 84.Kuriyan J, Osapay K, Burley SK, Brunger AT, Hendrickson WA, Karplus M. Exploration of disorder in protein structures by X-ray restrained molecular dynamics. Proteins. 1991;10:340–358. doi: 10.1002/prot.340100407. [DOI] [PubMed] [Google Scholar]
- 85.Burling FT, Brunger AT. Thermal motion and conformational disorder in protein crystal structures: comparison of multi-conformer and time-averaging models. Israel J Chem. 1994;34:165–175. [Google Scholar]
- 86.Gros P, Gunsteren Van WF, Hol WGJ. Inclusion of thermal motion in crystallographic structure by restrained Molecular Dynamics. Science. 1990;249:1149–1152. doi: 10.1126/science.2396108. [DOI] [PubMed] [Google Scholar]
- 87.Clarage JB, Phillips GN. Cross-validation tests of time-averaged molecular dynamics refinements for determination of protein structures by X-ray crystallography. Acta Crystallogr Sect D: Biol Crystallogr. 1994;50:24–36. doi: 10.1107/S0907444993009515. [DOI] [PubMed] [Google Scholar]
- 88.Pellegrini M, Gronbech-Jensen N, Kelly JA, Pfluegl GMU, Yeates TO. Highly constrained multiple-copy refinement of protein crystal structures. Proteins. 1997;29:426–432. doi: 10.1002/(sici)1097-0134(199712)29:4<426::aid-prot3>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- 89.Levin EJ, Kondrashov DA, Wesenberg GE, Phillips GN. Ensemble refinement of protein crystal structures: validation and application. Structure. 2007;15:1040–1052. doi: 10.1016/j.str.2007.06.019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Burnley BT, Afonine PV, Adams PD, Gros P. Modelling dynamics in protein crystal structures by ensemble refinement. eLife Sci. 2012;1:e00311. doi: 10.7554/eLife.00311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Doreleijers JF, Rullmann JAC, Kaptein R. Quality assessment of NMR structures: a statistical survey. J Mol Biol. 1998;281:149–164. doi: 10.1006/jmbi.1998.1808. [DOI] [PubMed] [Google Scholar]
- 92.Garbuzynskiy SO, Melnik BS, Lobanov MY, Finkelstein AV, Galzitskaya OV. Comparison of X-ray and NMR structures: is there a systematic difference in residue contacts between X-ray and NMR-resolved protein structures? Proteins. 2005;60:139–147. doi: 10.1002/prot.20491. [DOI] [PubMed] [Google Scholar]
- 93.Andrec M, Snyder DA, Zhou ZY, Young J, Montellone GT, Levy RM. A large data set comparison of protein structures determined by crystallography and NMR: statistical test for structural differences and the effect of crystal packing. Proteins. 2007;69:449–465. doi: 10.1002/prot.21507. [DOI] [PubMed] [Google Scholar]
- 94.Williamson MP, Kikuchi J, Asakura T. Application of 1H NMR chemical shifts to measure the quality of protein structures. J Mol Biol. 1995;247:541–546. doi: 10.1006/jmbi.1995.0160. [DOI] [PubMed] [Google Scholar]
- 95.Neal S, Nip AM, Zhang HY, Wishart DS. Rapid and accurate calculation of protein 1H, 13C, and 15N chemical shifts. J Biomol NMR. 2003;26:215–240. doi: 10.1023/a:1023812930288. [DOI] [PubMed] [Google Scholar]
- 96.Spronk C, Nabuurs SB, Krieger E, Vriend G, Vuister GW. Validation of protein structures derived by NMR spectroscopy. Prog NMR Spectrosc. 2004;45:315–337. [Google Scholar]
- 97.Bax A. Weak alignment offers new NMR opportunities to study protein structure and dynamics. Protein Sci. 2003;12:1–16. doi: 10.1110/ps.0233303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Simon K, Xu J, Kim C, Skrynnikov NR. Estimating the accuracy of protein structures using residual dipolar couplings. J Biomol NMR. 2005;33:83–93. doi: 10.1007/s10858-005-2601-7. [DOI] [PubMed] [Google Scholar]
- 99.Krieger E, Darden T, Nabuurs SB, Finkelstein A, Vriend G. Making optimal use of empirical energy functions: force-field parameterization in crystal space. Proteins. 2004;57:678–683. doi: 10.1002/prot.20251. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


