Abstract
Objective
This study aimed to evaluate the accuracy and precision of polyurethane (PUT) dental arch models fabricated using a three-dimensional (3D) subtractive rapid prototyping (RP) method with an intraoral scanning technique by comparing linear measurements obtained from PUT models and conventional plaster models.
Methods
Ten plaster models were duplicated using a selected standard master model and conventional impression, and 10 PUT models were duplicated using the 3D subtractive RP technique with an oral scanner. Six linear measurements were evaluated in terms of x, y, and z-axes using a non-contact white light scanner. Accuracy was assessed using mean differences between two measurements, and precision was examined using four quantitative methods and the Bland-Altman graphical method. Repeatability was evaluated in terms of intra-examiner variability, and reproducibility was assessed in terms of inter-examiner and inter-method variability.
Results
The mean difference between plaster models and PUT models ranged from 0.07 mm to 0.33 mm. Relative measurement errors ranged from 2.2% to 7.6% and intraclass correlation coefficients ranged from 0.93 to 0.96, when comparing plaster models and PUT models. The Bland-Altman plot showed good agreement.
Conclusions
The accuracy and precision of PUT dental models for evaluating the performance of oral scanner and subtractive RP technology was acceptable. Because of the recent improvements in block material and computerized numeric control milling machines, the subtractive RP method may be a good choice for dental arch models.
Keywords: Three-dimensional subtractive rapid prototyping, Intraoral scanning, Accuracy, Precision
INTRODUCTION
Conventionally, gypsum-based study models have been used as study models for orthodontic diagnosis or for recording treatment changes. However, they have shortcomings related to storage, because they are heavy and bulky, and retrieval problems, as they are subject to fracture and degradation. One solution may be digital storage, which enhances the ease of storage and facilitates easier access and transfer of the records. In cases where physical storage is needed, the solution may be replacement of plaster models with models fabricated using three-dimensional (3D) additive or subtractive rapid prototyping (RP) methods. While the additive RP method is a process of producing a 3D solid object using additive incremental layering, subtractive RP is a process that removes material from a larger piece of material by milling, turning/lathing, or drilling.
To make dental models using the subtractive RP process, a digital impression system and a computerized numeric control (CNC) milling machine can be used together. The iTero® (iTero; Align Technology, Inc., San Jose, CA, USA), a combination of a digital impression system and a CNC milling machine, can produce a polyurethane (PUT) dental model duplicating the patient's dental arch features, which is beneficial for treatment and storage because it is extremely strong, lightweight, and resistant to abrasion.1 In orthodontic practice, a scanning machine can be used to fabricate an Invisalign® (Align Technology, Inc.) clear aligner product to improve accuracy and patient communication, and to streamline work flow and reduce aligner delivery time.2
In maxillofacial surgery practice, stereolithographic models produced by the additive RP method and 3D computed tomography (CT) have been applied as an adjunct to treatment and planning of surgery. Barker et al.3 compared dried skull and duplicated stereolithographic models and reported a mean difference of 0.85 mm, and Kragskov et al.4 found 0.3-0.8-mm differences between 3D CT scan images and stereolithographic models. Recently, Cuperus et al.5 performed a study, which compared human skulls, digital images, and stereolithographic models, and concluded validity of the models.
Conversely, Lill et al.6 applied subtractive RP based on 3D CT images and reported a mean difference of 1.5 mm between PUT models and dried skull bone. Numerous studies have assessed the accuracy of 3D digital models compared to conventional stone models for orthodontic use, and most have reported smaller linear measurements for digital models, with small differences which could be acceptable for clinical use.7,8,9,10,11,12,13 However, studies on the accuracy and precision of dental arch RP models are scarce. As far as we know, only one study has compared stone, digital, and duplicated dental arch models by the additive RP method; Keating et al.14 assessed models and concluded that the detail and accuracy of RP models may not be sufficient for clinical application, while digital models and plaster models showed good agreement.
This study aimed to evaluate the accuracy and precision of PUT dental arch models fabricated using the 3D subtractive RP method with an oral scanning technique, by comparing the linear measurements of PUT models and conventional plaster models (gold standard).
MATERIALS AND METHODS
Preparing models for the experiment
Ten plaster models were duplicated using a selected standard master model by conventional impression, and 10 PUT models were duplicated using the 3D subtractive RP method with an oral scanner. The selected master model was a standard upper dental arch model reproducing natural teeth without missing teeth or prostheses (500B-1; Nissin Dental Products, Inc., Kyoto, Japan), which was expected to reduce possible errors in the scanning procedure. To duplicate 10 plaster models, a mold was fabricated using additive silicon rubber Deguform® (DeguDent GmbH, Hanau-Wolfgang, Germany). After coating the inside of the mold with wetting agent (Picosilk®; Renfert, Hilzingen, Germany), type IV dental plaster (GC Fujirock® EP; GC Corp, Leuven, Belgium) was mixed with water by directed water/powder ratio for 30 minutes, and inserted using a vibrator in order to avoid formation of air bubbles. The plaster models were removed from the mold after 1 hour and incubated at 22℃ and 45% humidity for 24 hour. To duplicate PUT models, a full arch digital impression was constructed by integrating several scanned images obtained from occlusal, buccal, and mesial sides and 45° angulated lingual and distal sides using the iTero? intraoral scanner. After confirming the completeness of the digital model, the PUT models were fabricated using a computer numerical control (CNC) milling machine (Haas VF-2TR; Haas Automation Inc., Oxnard, CA, USA).
Measurement procedure
A non-contact white light scanner (Identica; Medit Co. Ltd., Seoul, Korea) was used to scan the entire surface of the 20 dental arch models. Models were positioned on a rotary stage and digital images of the full dental arch were obtained in the same way. The data were imported into the Delcam Copycad® (Delcam Plc, Birmingham, UK) and designated linear measurements were obtained between points on the x, y, and z-axes. One week after the first measurements were taken, a second set of measurements were taken to assess intra-examiner reliability.
Measurement of models
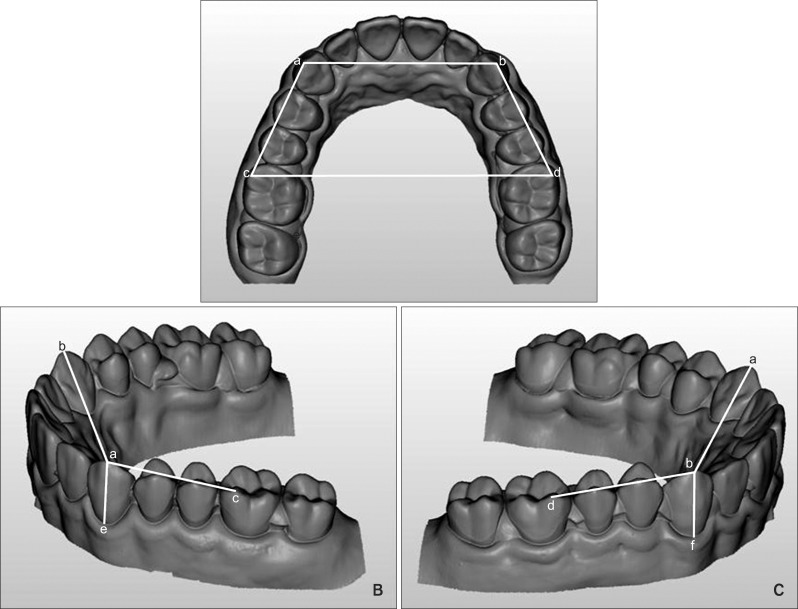
Measurements were evaluated in terms of x, y, and z-axes. In accordance with Creed et al.,15 six points were selected: a and b, the cusp tips of the right and left canines; c and d, the mesiobuccal cusp tips of the right and left first molars; and e and f, the deepest point of the gingival margin of the right and left canines (Figure 1).
Figure 1.
Reference points and linear measurements on the upper full arch model. A, Upper view; B, oblique view from the right side; C, oblique view from left side. See Table 1 for the definition of the reference points.
The following linear measurements on the upper dental arch were surveyed (Table 1):
Table 1.
Definitions of measurements on the upper dental arch
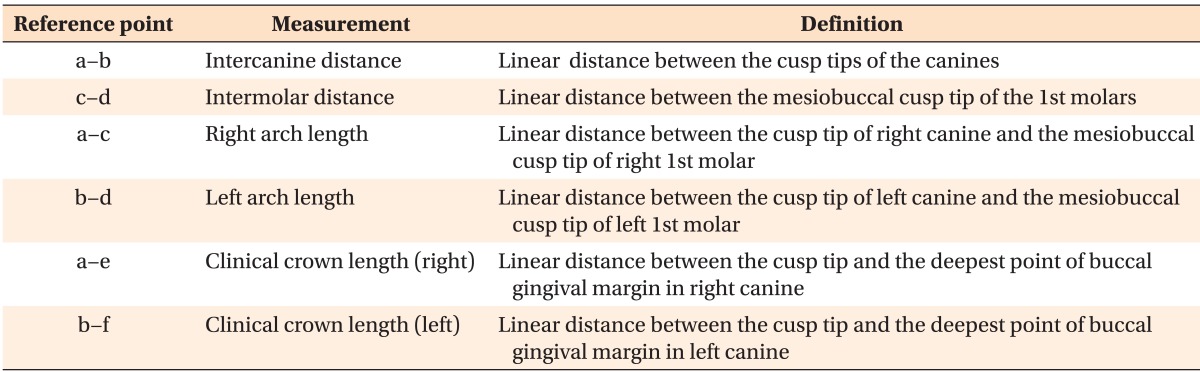
See Figure 1 for the designations of the reference points (a-f ).
From the cusp tip of the right canine to that of the left canine (a to b)
From the mesiobuccal cusp tip of the right first molar to that of the left first molar (c to d)
From the cusp tip of the canine to the mesiobuccal cusp tip of the first molar on the same side (right side a to c, left side b to d)
From the cusp tip to the deepest point of the buccal gingival margin, right and left canines (a to e and b to f, respectively)
Virtual x, y and z-axes were assumed as described in Alcan et al.16 The x and y-axes corresponded to the buccal-lingual and anterior and posterior on an axial plane when the model was positioned with the occlusal plane oriented in the upper direction. The z-axis was defined as the axis perpendicular to the x and y-axes, similar to the height of the teeth (Figure 1).
The measuring procedure was performed on 10 virtual stone models and 10 virtual PUT models by two trained examiners independently, to enable assessment of inter-examiner variability. One week after the main measuring procedure, one of two examiners repeated the same measuring procedure to evaluate intra-examiner variability.
Estimation of accuracy and precision
In the context of this study, accuracy refers to the degree of closeness of measurements of a dimension to that dimension's actual (true) value, and precision refers to the degree to which repeated measurements under unchanged conditions yield the same results. Accuracy was assessed using mean difference between two measurements, under the assumption that the conventional method using stone models, the gold standard, represents the "true" value. Precision was examined using four values evaluating different aspects of agreement: (1) measurement error (ME) as calculated via Dahlberg's formula17; (2) relative measurement error (RME), the percentage value of the ME divided by the mean of two measurements, to assess precision accounting for the measuring unit of the object in order to enhance comparability18; (3) the limit of agreement (LoA) devised by Bland and Altman,19 representing 95% of actual values in the interval; and (4) the intra-class coefficient (ICC). Graphic assessment of agreement between two measurements was performed using the Bland-Altman plot.19 ME, RME, and LoA were calculated using the following formulas:
ME = √(Σdi2/2n)
RME (percent) = [ME/(mean of two corresponding measurements)] × 100
-
LoA: interval of di ± 1.96 (SD of di), where
di = difference between two corresponding measurements
n = number of corresponding pairs
SD = standard deviation
ICC values larger than 0.75 and RME of less than 8% may be regarded as acceptable.18,20
Repeatability was evaluated in terms of intra-examiner variability, and reproducibility was assessed in terms of inter-examiner and inter-method variability.
RESULTS
Repeatability of measurements, intra-examiner variability
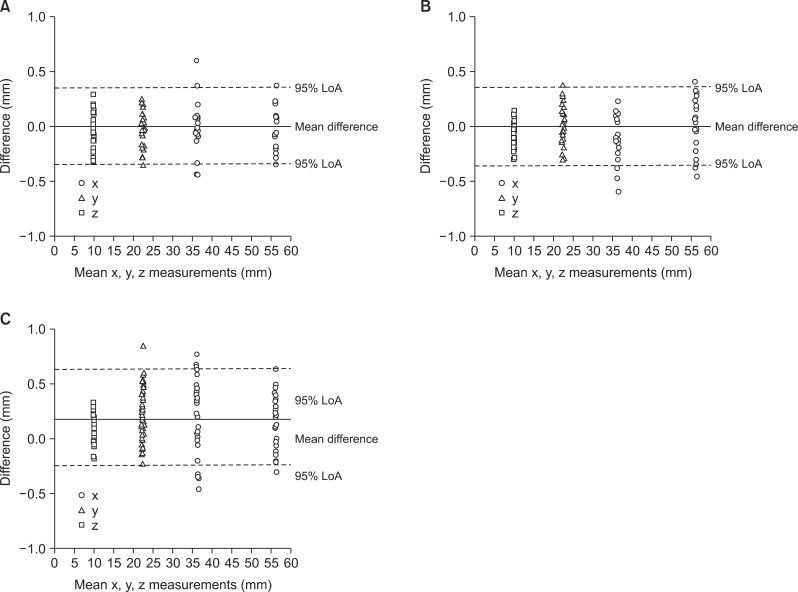
Intra-examiner variability was expressed as ME, RME, LoA and ICC (Table 2). ME ranged from 0.3 mm to 0.74 mm. With regard to intra-examiner variability, the smallest RME of 1.09% was found for the linear distance between c and d (x-axis), while the largest RME of 4.53% was found for the z-axis (b-f). LoA ranged from -0.21 mm to 0.73 mm. All of the ICC values were close to or over 0.8. The Bland-Altman plot showed random dispersion and most observations were located inside the interval of the LoA (Figure 2A).
Table 2.
Intra-examiner variability in assessing the dental arch relationships of 10 stone and 10 polyurethane models
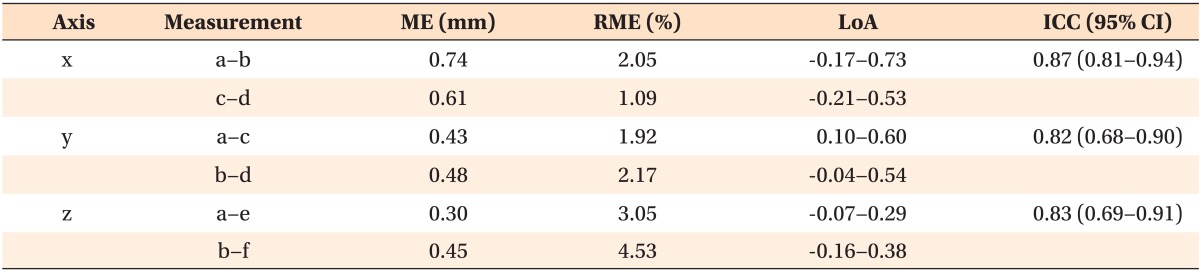
ME, Measurement error; RME, relative measurement error; LoA, the limit of agreement; ICC, the intra-class coefficient; CI, confidence interval.
See Table 1 for the descriptions of the measurements.
Figure 2.
Bland-Altman plot. A, Repeatability, intra-examiner variability; B, reproducibility, inter-examiner variability; C, reproducibility, inter-method variability. '95% limit of agreement (LoA)' represents mean difference ± 1.96 standard deviation.
Reproducibility, inter-examiner variability
Inter-examiner variability is summarized in Table 3. ME ranged from 0.35 mm to 0.78 mm. Similar to the results of inter-examiner variability, the smallest RME of 1.38% was found for the linear distance between c and d (x-axis), while the largest RME of 3.95% was found for the z-axis (b-f). LoA ranged from -0.17 mm to 0.73 mm. The ICC values ranged from 0.75 to 0.81. The Bland-Altman plot showed random dispersion and most observations were located inside the interval of the LoA, with only a few exceptions (Figure 2B).
Table 3.
Inter-examiner variability in assessing the dental arch relationships of 10 stone and 10 polyurethane models
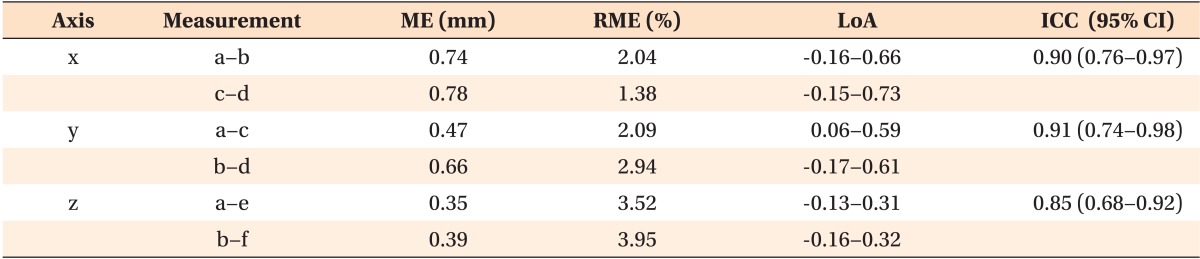
ME, Measurement error; RME, relative measurement error; LoA, the limit of agreement; ICC, the intra-class coefficient; CI, confidence interval.
See Figure 1 for the designations of the reference points (a-f).
Reproducibility, inter-method variability
Table 4 shows the inter-method variability comparing conventional stone models and PUT models. The mean difference between stone and PUT models ranged from 0.07 mm to 0.33 mm. ME ranged from 0.60 mm to 1.77 mm. The smallest RME of 2.21% was found for the linear distance between c and d (x-axis), while the largest RME of 7.60% was found for the y-axis (a-c). ICC values ranged from 0.93 to 0.96. The Bland-Altman plot showed random dispersion and most observations were located inside the interval of the LoA (Figure 2C).
Table 4.
Inter-method variability between 10 stone models and 10 polyurethane models
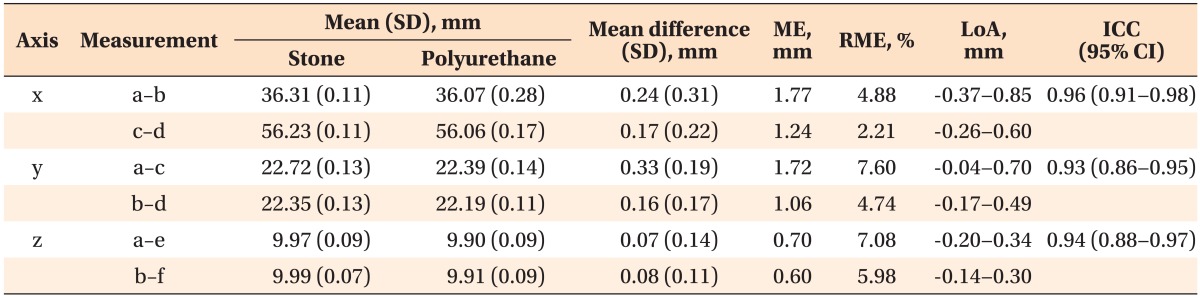
SD, Standard deviation; ME, measurement error; RME, relative measurement error; LoA, the limit of agreement; ICC, the intra-class coefficient; CI, confidence interval.
See Figure 1 for the designations of the measurements.
DISCUSSION
The purpose of this study was evaluation of the accuracy and precision of PUT dental arch models fabricated by 3D subtractive RP methods with an intraoral scanning technique. Assessing the accuracy and precision of the PUT models entails evaluation of two subsequent procedures: oral scanner and subtractive RP technology. Differences in linear measurements between the PUT models and stone models ranged from 0.07 mm to 0.33 mm, which is relatively small compared to the results of some previous studies using RP models, which have reported linear differences of 0.3-1.5 mm.3,4,5,6 Particularly, compared to a study using subtractive RP reported by Lill et al.6 showing 1.5-mm differences, it may be postulated that the accuracy of the subtractive RP method has improved greatly in the last 10 years. Other indices assessing agreement showed good precision of the subtractive RP method: ME ranged from 0.7 mm to 1.77 mm, all of the RME percentages were less than 8%, and all of the ICC values were greater than 0.93. Further, the assessment of intra- and inter-examiner variability suggested consistency of the measuring procedure. As far as we know, this is the first study assessing the accuracy and precision of 3D subtractive RP dental models.
Dahlberg's formula has been used the most frequently in assessing precision in orthodontic studies. BeGole21 reported that Dahlberg's formula had been used in 56% of reliability/error tests among 203 articles in major orthodontic journals published in 1997. The merits of Dahlberg's formula include that the original unit is preserved, and interpretation can be relatively easy because its form is similar to that of standard errors. However, a shortcoming of it may be that there is no standard of acceptable ranges because units of measurements are quite different in different cases. Therefore, we introduced the RME, the percentage of ME of the mean linear measures, to enable direct comparison between measurements with different units. In accordance with Henriksen et al.,18 we deemed that the acceptable range included values below 8%.
Many previous studies7,9,11,12,13,22,23,24 have adopted the paired t-test to assess whether mean differences between two corresponding measurements are statistically significant, and have mistakenly interpreted the results as evidence of agreement. According to Linnet,25 the paired t-test should not be applied uncritically to method comparison data, and the test should only be applied when graphic display suggests a systematic constant difference. Similarly, Donatelli and Lee26 showed typical examples of erroneous conclusions that may be reached via the paired t-test in the context of the Bland-Altman plot.
In this study, linear measurements of PUT models tended to be smaller than those of stone models. One of the reasons for the discrepancy may be related to the geometry of milling burs, including their diameter, and the milling direction. As Reich et al.27 suggested, the diameter of the milling bur may determine the smallest grindable radius, and therefore excessive removal may have occurred on line angles or complicated occlusal surfaces, while more exact removal is expected on flat axial surfaces. Possible errors may arise in the complicated procedure of intra-oral scanning, which requires integration of several oral images taken repeatedly. The iTero® digital impression system used in this study is based on the theory of parallel confocal: a beam of light emitted through a small hole is reflected by the target surface and moves toward the wand. The iTero® system projects 100,000 beams of red light and converts the reflected light into digital data, and therefore it produces accurate imaging data. Another advantage of the system is that there is no need for a reflecting agent powder as the laser can reflect off all oral structures.28
The additive RP method has been more frequently used in craniofacial and maxillofacial fields, owing to its advantages in fabricating physical models with complex structures and cavities as compared to the subtractive RP method. The quality of milled models has historically been poor because soft and brittle PUT foam was used, and there was limited development of the milling machine.6,29 However, the recent use of high strength PUT blocks and multiple-axis milling machines enables production of a variety of complex geometries from a vast array of materials.30 Further studies are required incorporating patients under clinical conditions as subjects, that may involve missing or malpositioned teeth and fixed dental prostheses, because this study was limited to the use of a standard master model and duplicated sample models, in a laboratory setting.
CONCLUSION
We concluded that based on this study, the accuracy and precision of PUT dental models in evaluating the performance of oral scanner and subtractive RP technology was acceptable. Owing to recent improvements in block material and CNC milling machines, the subtractive RP method may now be a good choice for dental arch models.
Footnotes
This work was supported by a Korea University Grant (K1325051).
The authors report no commercial, proprietary, or financial interest in the products or companies described in this article.
References
- 1.Henkel S. A better first impression: manufacturing dental restorations using impressions. J Dent Technology. 2008:13–16. [Google Scholar]
- 2.Jones P. The iTero optical scanner for use with Invisalign: A descriptive review. Dent Implantol Update. 2008;19:1–4. [Google Scholar]
- 3.Barker TM, Earwaker WJ, Lisle DA. Accuracy of stereolithographic models of human anatomy. Australas Radiol. 1994;38:106–111. doi: 10.1111/j.1440-1673.1994.tb00146.x. [DOI] [PubMed] [Google Scholar]
- 4.Kragskov J, Sindet-Pedersen S, Gyldensted C, Jensen KL. A comparison of three-dimensional computed tomography scans and stereolithographic models for evaluation of craniofacial anomalies. J Oral Maxillofac Surg. 1996;54:402–411. doi: 10.1016/s0278-2391(96)90109-3. [DOI] [PubMed] [Google Scholar]
- 5.Cuperus AM, Harms MC, Rangel FA, Bronkhorst EM, Schols JG, Breuning KH. Dental models made with an intraoral scanner: a validation study. Am J Orthod Dentofacial Orthop. 2012;142:308–313. doi: 10.1016/j.ajodo.2012.03.031. [DOI] [PubMed] [Google Scholar]
- 6.Lill W, Solar P, Ulm C, Watzek G, Blahout R, Matejka M. Reproducibility of three-dimensional CT-assisted model production in the maxillofacial area. Br J Oral Maxillofac Surg. 1992;30:233–236. doi: 10.1016/0266-4356(92)90265-k. [DOI] [PubMed] [Google Scholar]
- 7.Santoro M, Galkin S, Teredesai M, Nicolay OF, Cangialosi TJ. Comparison of measurements made on digital and plaster models. Am J Orthod Dentofacial Orthop. 2003;124:101–105. doi: 10.1016/s0889-5406(03)00152-5. [DOI] [PubMed] [Google Scholar]
- 8.Quimby ML, Vig KW, Rashid RG, Firestone AR. The accuracy and reliability of measurements made on computer-based digital models. Angle Orthod. 2004;74:298–303. doi: 10.1043/0003-3219(2004)074<0298:TAAROM>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 9.Zilberman O, Huggare JA, Parikakis KA. Evaluation of the validity of tooth size and arch width measurements using conventional and three-dimensional virtual orthodontic models. Angle Orthod. 2003;73:301–306. doi: 10.1043/0003-3219(2003)073<0301:EOTVOT>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
- 10.Stevens DR, Flores-Mir C, Nebbe B, Raboud DW, Heo G, Major PW. Validity, reliability, and reproducibility of plaster vs digital study models: comparison of peer assessment rating and Bolton analysis and their constituent measurements. Am J Orthod Dentofacial Orthop. 2006;129:794–803. doi: 10.1016/j.ajodo.2004.08.023. [DOI] [PubMed] [Google Scholar]
- 11.Watanabe-Kanno GA, Abrão J, Miasiro Junior H, Sánchez-Ayala A, Lagravère MO. Reproducibility, reliability and validity of measurements obtained from Cecile3 digital models. Braz Oral Res. 2009;23:288–295. doi: 10.1590/s1806-83242009000300011. [DOI] [PubMed] [Google Scholar]
- 12.Leifert MF, Leifert MM, Efstratiadis SS, Cangialosi TJ. Comparison of space analysis evaluations with digital models and plaster dental casts. Am J Orthod Dentofacial Orthop. 2009;136:16.e1–16.e4. doi: 10.1016/j.ajodo.2008.11.019. [DOI] [PubMed] [Google Scholar]
- 13.Mullen SR, Martin CA, Ngan P, Gladwin M. Accuracy of space analysis with emodels and plaster models. Am J Orthod Dentofacial Orthop. 2007;132:346–352. doi: 10.1016/j.ajodo.2005.08.044. [DOI] [PubMed] [Google Scholar]
- 14.Keating AP, Knox J, Bibb R, Zhurov AI. A comparison of plaster, digital and reconstructed study model accuracy. J Orthod. 2008;35:191–201. doi: 10.1179/146531207225022626. [DOI] [PubMed] [Google Scholar]
- 15.Creed B, Kau CH, English JD, Xia JJ, Lee RP. A comparison of the accuracy of linear measurements obtained from cone beam computerized tomography images and digital models. Semin Orthod. 2011;17:49–56. doi: 10.1053/j.sodo.2010.08.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Alcan T, Ceylanoğlu C, Baysal B. The relationship between digital model accuracy and time-dependent deformation of alginate impressions. Angle Orthod. 2009;79:30–36. doi: 10.2319/100307-475.1. [DOI] [PubMed] [Google Scholar]
- 17.Dahlberg G. Statistical methods for medical and biological students. London: George Allen & Unwin Ltd.; 1940. pp. 122–132. [Google Scholar]
- 18.Henriksen M, Lund H, Moe-Nilssen R, Bliddal H, Danneskiod-Samsøe B. Test-retest reliability of trunk accelerometric gait analysis. Gait Posture. 2004;19:288–297. doi: 10.1016/S0966-6362(03)00069-9. [DOI] [PubMed] [Google Scholar]
- 19.Bland JM, Altman DG. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- 20.Fleiss JL. The design and analysis of clinical experiments. New York: John Wiley & Sons; 1986. pp. 76–78. [Google Scholar]
- 21.BeGole EA. Statistics for the orthodontist. In: Graber TM, Vanarsdall RL, editors. Orthodontics: current principles and techniques. 3rd ed. St. Louis: Mosby; 2000. pp. 339–352. [Google Scholar]
- 22.Dalstra M, Melsen B. From alginate impressions to digital virtual models: accuracy and reproducibility. J Orthod. 2009;36:36–41. doi: 10.1179/14653120722905. [DOI] [PubMed] [Google Scholar]
- 23.Mok KH, Cooke MS. Space analysis: a comparison between sonic digitization (DigiGraph Workstation) and the digital caliper. Eur J Orthod. 1998;20:653–661. doi: 10.1093/ejo/20.6.653. [DOI] [PubMed] [Google Scholar]
- 24.Asquith J, Gillgrass T, Mossey P. Three-dimensional imaging of orthodontic models: a pilot study. Eur J Orthod. 2007;29:517–522. doi: 10.1093/ejo/cjm044. [DOI] [PubMed] [Google Scholar]
- 25.Linnet K. Limitations of the paired t-test for evaluation of method comparison data. Clin Chem. 1999;45:314–315. [PubMed] [Google Scholar]
- 26.Donatelli RE, Lee SJ. How to report reliability in orthodontic research: Part 1. Am J Orthod Dentofacial Orthop. 2013;144:156–161. doi: 10.1016/j.ajodo.2013.03.014. [DOI] [PubMed] [Google Scholar]
- 27.Reich S, Uhlen S, Gozdowski S, Lohbauer U. Measurement of cement thickness under lithium disilicate crowns using an impression material technique. Clin Oral Investig. 2011;15:521–526. doi: 10.1007/s00784-010-0414-x. [DOI] [PubMed] [Google Scholar]
- 28.Birnbaum NS, Aaronson HB. Dental impressions using 3D digital scanners: virtual becomes reality. Compend Contin Educ Dent. 2008;29:494, 496, 498–505. [PubMed] [Google Scholar]
- 29.Klein HM, Schneider W, Alzen G, Voy ED, Günther RW. Pediatric craniofacial surgery: comparison of milling and stereolithography for 3D model manufacturing. Pediatr Radiol. 1992;22:458–460. doi: 10.1007/BF02013512. [DOI] [PubMed] [Google Scholar]
- 30.Petrzelka JE, Frank MC. Advanced process planning for subtractive rapid prototyping. Rapid Prototyping J. 2010;16:216–224. [Google Scholar]