Abstract
Males of the bushcricket Mecopoda elongata synchronise or alternate their chirps with their neighbours in an aggregation. Since synchrony is imperfect, leader and follower chirps are established in song interactions; females prefer leader chirps in phonotactic trials. Using playback experiments and simulations of song oscillator interactions, we investigate the mechanisms that result in synchrony and alternation, and the probability for the leader role in synchrony. A major predictor for the leader role of a male is its intrinsic chirp period, which varies in a population from 1.6 to 2.3 s. Faster singing males establish the leader role more often than males with longer chirp periods. The phase-response curve (PRC) of the song oscillators differs to other rhythmically calling or flashing insects, in that only the disturbed cycle is influenced in duration by a stimulus. This results in sustained leader or follower chirps of one male, when the intrinsic chirp periods of two males differ by 150 ms or more. By contrast, the individual shape of the male’s PRC has only little influence on the outcome of chirp interactions. The consequences of these findings for the evolution of synchrony in this species are discussed.
Keywords: Bush cricket, Synchrony, Song oscillator, Phase-response curve, Behavioural simulation
Introduction
Acoustic advertisement signals in orthopteran insects are used to attract mates from a distance, or in competitive interactions between males. However, signalling often occurs in groups (choruses) of many individuals of the same and/or different species. Whatever the proximate and ultimate causes for chorusing may be (for reviews see Alexander 1975; Otte 1977; Thornhill and Alcock 1983; Greenfield 1994a), the result of such aggregations is a complex sonic and ultrasonic background over which individuals must then communicate. Thus each species faces a trade-off between optimum broadcast conditions and the problem of detecting and discriminating individual conspecific signals against a high background noise.
Within insect and anuran choruses, the most impressive interactions occur when the signalling of individuals is influenced by the timing of signalling of other individuals. On the one hand, this can be a solution to the problem of masking interference, when individuals are able to signal in gaps of masking noise (Zelick and Narins 1985). Extreme forms of fine-scale signal timing occur, when neighbouring individuals of discontinuously singing species either synchronise or alternate with the signals of their neighbours, i.e. when the phase angles approximate either 0° or 180°, respectively. Various evolutionary explanations for this phenomenon have been presented: (1) preservation of the species-specific temporal pattern (Walker 1969), (2) concealing of the call in response to acoustically orienting predators and parasitoids (Otte 1977), and (3) synchrony and alternation as a by-product of inter- and intrasexual selection (Alexander 1975; Greenfield 1994a,b, 1997).
When synchronous choruses were analysed with some degree of temporal precision, synchrony was not perfect; rather there was a partial overlap of the two signals with one leading the other in time. Recognising that the amplitude modulation of chirps in synchronising species often contains higher intensities at the end, Greenfield (1994b) suggested that synchrony ultimately results from the value of these exposed chirp endings. Initiating a chirp immediately after hearing the onset of a neighbour’s chirp would conceal the neighbour’s ending, while at the same time exposing the male’s own chirp ending to potential mates. The synchronous chorusing in the katydid Neoconocephalus spiza and the snowy tree cricket Oecanthus fultoni, during which males were found frequently switching the leader and follower role in successive chirp interactions, is consistent with the hypothesis of an ongoing competition for leadership (Walker 1969; Greenfield and Roizen 1993).
However, subsequent studies on the preference of females to synchronising pairs of males in insects and anurans demonstrated that females select for males by timing their chirp such that they most often produce attractive leading signals (reviewed in Klump and Gerhardt 1992; Greenfield 1994a; Grafe 1996; Snedden and Greenfield 1998). Indeed, chorusing in N. spiza was found to be an evolutionary stable outcome of female choice selecting for leaders in a chirp interaction (Greenfield and Roizen 1993; Greenfield et al. 1997).
The very regular individual solo pattern of song timing, and various kinds of observations of song interaction in synchronising or alternating insects resulted in the development of two models that could explain these observations: the phase-delay model (Buck et al. 1981; Hanson 1978) and the inhibitory resetting model (Greenfield 1994a, b). Both the “phase-delay” and the “inhibitory resetting model” assume that the underlying mechanism leading to song production is a neuronal oscillator which, once its excitatory level becomes suprathreshold, starts the production of a chirp. The only difference between the inhibitory resetting and the phase-delay model (as originally described by Hanson 1978 and Buck et al. 1981) is that in inhibitory resetting the male’s rhythm generator is held at the basal level throughout the duration of the stimulus (for detailed reviews see Greenfield 1994b; Gerhardt and Huber 2002). The tonic inhibition was not part of the phase-delay model as originally described by Buck et al. (1981), although a phase shift due to an increased flash duration was already described by Hanson (1978).
There are, however, cases of reported synchrony and alternation which do not fit the above models exactly. Sismondo (1990) investigated the call timing of the Southeast Asian bush cricket Mecopoda elongata (Tettigoniidae) and demonstrated that synchrony and alternation can result from the same underlying mechanism, but one which differs from a phase-delay model. He focused on the role of the phase-response curves (PRCs) of the individual oscillators, and how the slopes of the PRC result either in synchrony and alternation. He also developed a model that would allow one to predict under which conditions stable phase-locking with a phase angle of 180° (stable alternation) would occur. One of the striking differences in synchronous interactions of Mecopoda males compared to N. spiza is the fact that leader and follower roles can be fixed for long periods of song interaction without a “forbidden interval” leading to a regular drop in chirps. Again, female choice experiments have shown that (similar to other synchronising species of insects and anurans), Mecopoda females prefer leaders in such interactions. The choice of females depends on how often, and by what time difference, one male leads the other (Römer et al. 1997).
If sexual selection by female choice so strongly selects for leaders in chirp interactions, it is of prime importance (1) to know exactly what determines the outcome of a male–male interaction and (2) to have information about the variance in parameters within a population of males which determine this outcome. The aim of the present paper was therefore to investigate which features in the song of males are most important for establishing the leader role in synchrony and to examine the variation in these parameters.
Methods
Insects
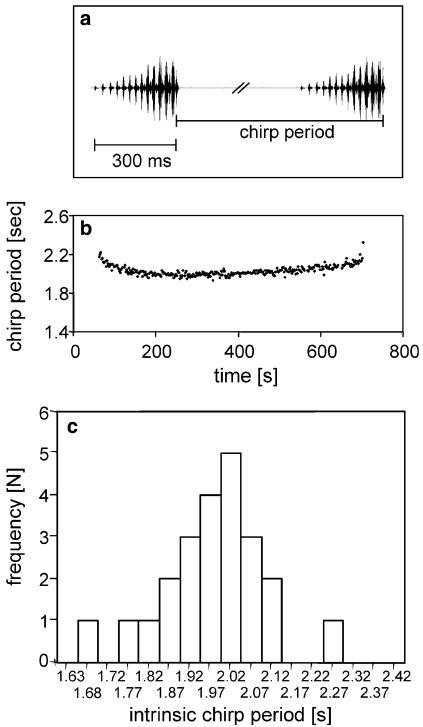
Mecopoda elongata (Orthoptera, Tettigoniidae; Mecopodinae) is a bush cricket commonly found in Southeast Asia. The taxonomic relationship of species in the genus Mecopoda is uncertain, and there are probably several sibling species, which are morphologically indistinguishable, but have distinctly different song patterns. The insects in this study were originally collected from the field in Malaysia; their song is identical to the one described by Sismondo (1990) as “species S”. The insects were reared at 27 °C and 70% relative humidity on a 12:12 h light:dark cycle and were fed ad libitum with fresh lettuce and fish food. Immature development involves eight instar stages and about 2 weeks after the last moult adult males start singing. The calling song of M. elongata consists of chirps with a duration of 250–300 ms, each chirp comprising 10–14 syllables of increasing amplitude (Fig. 1a). When males sing in isolation, chirps are repeated very regularly at intervals of about 2 s. Males start their singing activity shortly before or after the onset of the dark period; over one night they call in singing bouts which last for a highly variable time between 10 and 45 min.
Fig. 1.
Song characteristics of male M. elongata. a The chirp of a male consists of 12–15 syllables of increasing amplitude, about 300 ms in duration. b Chirps are produced in singing bouts lasting for 10 to more than 30 min, where the chirp periods are rather constant except for the start and the end of a singing bout. c The intrinsic chirp period is characteristic for each male and varies in the population between 1.6 and 2.3 s
Song recordings and analysis
Individual adult males at the age of 50–64 days after the last moult were caged in a 7×7×7 cm box surrounded with wire mesh, and transferred to an incubator maintaining a constant temperature of 27°C. The walls of the incubator were covered with acoustic foam to minimise sound reflections. Songs were recorded with a sound level meter (NORIS, NM-3) and digitised at a sampling rate of 1 kHz, which is sufficient to obtain precise information on the onset and end of chirps. The A/D conversion was performed with a CED-board (Cambridge Technology). A custom written Spike2 script was used to obtain the times of chirp ends and transfer them to an Excel sheet. Because the syllables within the chirp increase in amplitude (Fig. 1a), the ends of chirps are easier to measure when compared to the soft syllables found at the beginning. To characterise the intrinsic call rate only the first singing bout of a male over the dark period was analysed. Furthermore, the initiation and the end of a song bout exhibit slower chirp rates (Fig. 1b). Therefore, we excluded the 20 chirps at the beginning and the end of the song bout and calculated the median value of the remaining chirp periods as the intrinsic chirp period for a calling song of a male singing in isolation.
Characterisation of the song oscillator
To characterise the properties of the song oscillators of different males, individual males were placed in the incubator (27°C). After a male started singing spontaneously, a conspecific chirp of 281 ms duration was broadcast via a loudspeaker (dome tweeter, Dynaudio, Denmark) to the singing male. The timing of the broadcast chirp was controlled by a custom-written sequencer script (Cambridge Technology) to playback the stimulus at random phases of the intrinsic cycle of the male’s song. The song of a male was recorded and digitised at 1 kHz, and the changes in cycle length of the disturbed cycle and the following cycle due to the stimulus were calculated. The resulting PRCs were obtained at three different stimulus intensities (50, 60 and 70 dB SPL). The conspecific chirp used as a stimulus was digitised from a recording of a male singing in isolation (CED-board, Cambridge Technology; sampling rate of 250 kHz). Every seventh chirp of the singing male elicited a stimulus, and the last five undisturbed chirps preceding the stimulus were taken to estimate the current intrinsic cycle length of the song oscillator. A custom-written Spike2 script was used to calculate the normalised stimulus phase (Ts/T0) and the normalised response period (Tr/T0) for the generation of the PRCs. This procedure assumes a constant solo CP before and after the stimulus, and sudden changes of CP will scatter the PRC. Therefore, we excluded all data at the beginning and the end of a singing bout showing a deviation in the cycles following the disturbed cycle of more than 0.04 normalised phase units (ranging from 0 to 1). Both the stimulus and the response times were taken from the ends of chirps.
Periodical stimulation
The same equipment was used to record singing bouts entrained to a model song with a fixed CP. A conspecific male chirp was regularly played back at different CPs via a A/D board (DSP Erlangen, Germany) at an intensity of 60 dB SPL at the position of the singing male. Recorded entrained chirps were easily distinguished from the stimulus artefact which was much smaller in amplitude. A custom written Spike2 script was used for the evaluation of the relation of leader (L) to follower (F) chirps and the time difference between them (Δt).
Modelling male duets
For a better understanding of parameters critical for the outcome of signal interactions, a realistic model of mutually coupled oscillators, based on male’s PRCs, was programmed. It allows us to investigate the influence of differences between the PRCs of individual males on chirp timing. Starlogo 2.02 is a shareware program designed for multiagent-based modelling, and although we just modelled the acoustic interaction between two males (Starlogo turtles) in the current study, the simulation environment enables us to increase the number of chorusing participants to a few hundred. Two oscillators were mutually coupled by their PRCs obtained from real experiments as those described above. The left branch refers to responses to stimuli presented shortly after the focal male’s chirp and was described by second- and third-order polynomials. Linear equations or first-order polynomials were used to describe the right branch of PRCs referring to responses to stimuli presented later, but still before the subsequent focal male’s chirp. Uncoupling one oscillator from the other allows one to study oscillator responses upon entrainment to periodical stimuli with a fixed CP.
We used the experimentally obtained PRCs of 11 males to simulate the acoustic interactions between these males. Thus, each song oscillator had its own intrinsic CP and PRC. In every time step (1 ms), the Starlogo observer “asked” both turtles to count down an internal counter representing the actual phase of the oscillator cycle (intrinsic CP). If one counter becomes zero, the end of the male chirp is reached and the CP of the other oscillator is affected according to the PRC of its oscillator. Since the data represented in the PRC were calculated by measuring the stimulus and the response at chirp ends, chirps were only modelled as discrete time events representing chirp ends. In the next time step, the internal counter of the oscillator was set back to the intrinsic CP ± a Gaussian distributed randomness accounting for the variability of the CPs obtained from the constant part of intrinsic songs. The standard deviation of this variation was set to 0.02 phase units (ranging from 0 to 1), which is the average standard deviation obtained from intrinsic songs of 23 males, and which corresponds to the overlap between both branches of PRCs. The y-variability of the branches of a PRC was modelled by multiplication of the normalised disturbed cycle length with a Gaussian distributed randomness having a standard deviation of 0.0168 (given in normalised cycle lengths) for the left branch and 0.009 for the right branch of the PRC. These standard deviations were again obtained from real PRCs by evaluating the deviations of cycle length from curve fittings. For all oscillators, the variability of the intrinsic CP and the variation found in the PRCs was modelled using the same standard deviations as mentioned above. Rate-phase plots were obtained by varying the intrinsic CP of one oscillator while keeping the intrinsic CP of the second oscillator at a constant value. Data represented in the rate-phase plots were obtained from ten interactions. In order to identify bistable couplings, which are sensitive to initial conditions, the simulation was started six times at different initial phases, which were uniformly distributed within a cycle. That is, for each CP of oscillator #1, there were six initial phases which result in a total of 60 interactions. Transient phase couplings were prevented by skipping the first ten interactions.
Recording of song interactions between two males
Acoustic interactions of two males were studied in the same incubator as described above, at a constant temperature of 27°C. Two males, each caged in a 7×7×7 cm box, were positioned along the diagonal axis of the incubator. Five centimetres of acoustic foam between males mimicked an intermale distance of about 5 m, because it attenuates chirp intensities to approximately 70 dB SPL. Although the mean intermale distance for the Mecopoda species under study is unknown and can vary in aggregations of bush crickets substantially (e.g. Thiele and Bailey 1980; Römer and Bailey 1986), an intermale distance of approximately 5 m was frequently observed in male choruses of another Mecopoda species (R. Balakrishnan, personal communication), and in the synchronising bush cricket Neoconocephalus nebrascensis (Meixner and Shaw 1979). Microphones mounted close to each male allowed us to record the acoustic interactions between pairs of males and reduced the cross-talk between both recording channels. All recorded duets between real males were manually evaluated with respect to the timing of their chirps. A total of seven male pairs were examined in this way.
We performed all statistical calculations with Sigmastat 2.03 (SPSS Inc.). All data were evaluated for normal distribution before applying non-parametric tests.
Results
The intrinsic chirp period (CP) of M. elongata males is characterised by only a small cycle-to-cycle variation with a standard deviation of 35–45 ms (about 2% per male) and a characteristic drift towards longer CPs for the last third of the song bout (Fig. 1b). Although the intrinsic CP for a given male exhibits only a small variation, there is a considerable variability in this song parameter between males in a population, all at the same age of 50–64 days after the last moult (Fig. 1c). Most of the males exhibit an intrinsic CP of about 2 s, but the range of variation is from 1.6 to 2.3 s. Thus, some males in the population sing at much higher rates than others.
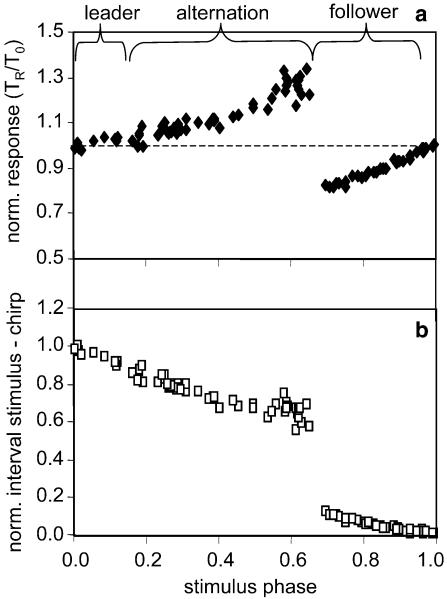
Chirping is assumed to be driven by an underlying song oscillator, which can be characterised by its PRC. The PRCs of the song oscillator of M. elongata males are characterised by an exponentially increasing left branch and a nearly linear right branch (Fig. 2a). Thus, a conspecific stimulus occurring at a phase around 0.5 results in an increase in the disturbed cycle, whereas some time later (at about 0.7–0.9) the disturbed cycle will be shortened.
Fig. 2.
a Phase-response curve (PRC) of the song oscillator of an individual male. The disturbed chirp period of a singing male is either increased or decreased in duration (response phase >1 or <1, respectively) in response to a single conspecific stimulus at 70 dB SPL (black diamonds). b The normalised intervals between stimulus and response chirps (open squares) are very small in response to stimuli late in the period, with the result that follower chirps will be produced
This particular shape of the PRC has predictable consequences for the chirp timing between two interacting males, which is shown by plotting the interval from the stimulus to the next chirp against stimulus phase (Fig. 2b). The right branch of the PRC results in follower situations, where a stimulus is quickly followed by a chirp. In contrast, the outmost left branch is important in the establishment of leader chirps (a stimulus quickly follows a chirp). Only when a stimulus happens in the middle part of the PRC stable alternation can occur. Thus, a stimulus late in the cycle immediately leads to a synchronisation with the stimulus.
Coupling properties of the song oscillator and its influence on chirp timing
By modelling the mutual coupling of two song oscillators, we next analysed the influence of the relative chirp period (time difference between the intrinsic CPs of two oscillators) on phase coupling and on chirp timing. For simplicity and because the intention of the current study focuses on the evaluation of chirp timing properties of the song oscillators rather than the re-examination of the previously described phase locking behaviour (Sismondo 1990), oscillator response was categorised into four different types according to the relative time difference between chirp interactions (Δt): “precise synchronisation”=1:1 coupling with a constant CP (Δt ≤ 50 ms); “leader/follower synchronisation”=1:1 coupling with a constant CP (50 ms <Δt ≤ 300 ms); “alternation”=1:1 locking with a constant CP of both oscillators but non-overlapping chirps (Δt>300 ms); “quasi-periodic dynamics”=a constantly shifting phase relationship between successive periods, where the cycle-to-cycle pattern starts again after n cycles (Glass et al.1980). We defined 50 ms as cut-off for “precise synchrony” because the cycle-to-cycle variation of solo songs was found to show a standard deviation of only 35–45 ms. Since the average chirp duration is about 300 ms and non-overlapping chirps are known to be equally well represented in the nervous system of receivers (Römer et al. 2002), we choose this Δt to distinguish between “leader/follower synchronisation” and “alternation”.
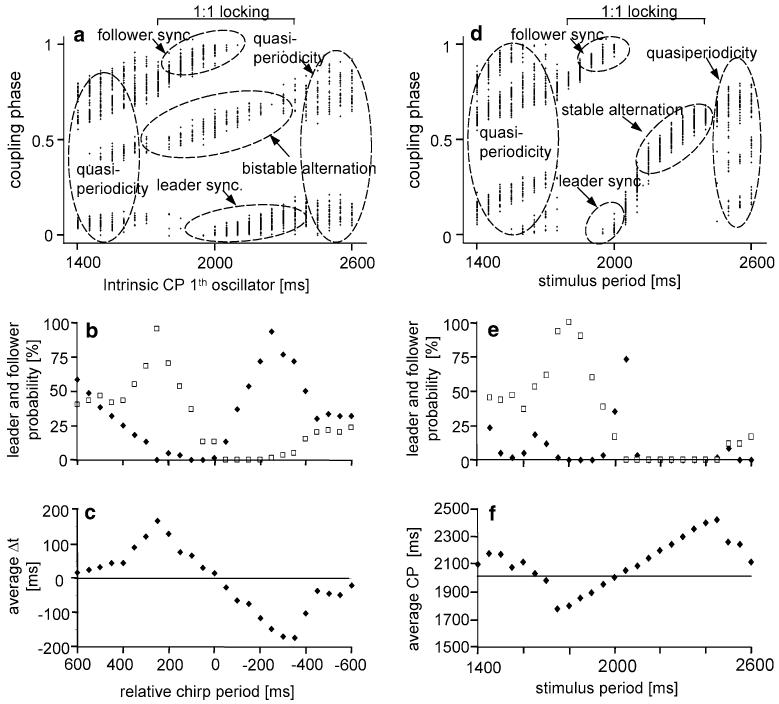
In the first series of simulations, the two coupled oscillators shared the same PRCs (obtained at 70 dB SPL), but differed in their intrinsic CP. In Fig. 3a, the intrinsic CP of oscillator #1 was varied from 1,400 to 2,600 ms, whereas the intrinsic CP of oscillator #2 was maintained at 2,000 ms. Results are given as rate-phase plots of the steady-state phases of coupling of oscillator #2 with six repeated simulations, each simulation starting at a different phase of the fixed oscillator. For example, when the intrinsic CP of oscillator #1 was somewhat higher than the fixed oscillator between 2,100 and 2,300 ms, the result was a stable 1:1 locking with either synchrony (fixed oscillator as leader) or alternation. These two alternatives depend solely on the phase relationship at the starting point of coupling: alternation only occurs at stimulus initial phases between 0.4 and 0.6 (thus the term “bistable alternation, since it depends on the starting conditions, whether alternation or synchrony will be the result; see also Fig. 2a). In contrast, when the intrinsic CP of oscillator #1 was smaller than the fixed oscillator between 1,700 and 1,900 ms, the result was again a stable 1:1 locking with either synchrony or alternation, but here with the fixed oscillator as follower. Thus, 1:1 locking was found over a broad range of CPs, centred around the intrinsic CP of oscillator #2, and covers nearly the complete range of intrinsic CPs characterised for the male population studied here (1,600–2,300 ms; see Fig. 1c).
Fig. 3.
Phase coupling (a) and chirp timing (b, c) in a simulation of chirp interactions between two males differing in their intrinsic chirp period. In a simulation with mutually coupled oscillators, sharing an identical PRC, the intrinsic chirp period of the first oscillator was varied from 1.4 to 2.6 s while keeping the intrinsic chirp period of the second oscillator at a constant period of 2 s. The coupling phases of the first oscillator are shown in the cycle of the second oscillator (a). Synchronisation as well as bistable alternation was found in the range of 1:1 phase locking between both oscillators, whereas quasi-periodicity with permanently changing chirp periods occurs outside this range. Synchronisation to chirp periods greater than the intrinsic chirp period of the second oscillator resulted in a higher probability for leader chirps (b, black diamonds), synchronisation to smaller periods increased the probability for follower chirps (b, open squares). Quasi-periodicity results in a similar probability for leader and follower chirps. In the 1:1 phase locking range Δt is a function of the relative chirp period (c). Entrainment of oscillator two to periodical stimuli with varying periods results either in synchronisation or stable alternation; outside the range of 1:1 phase locking quasi-periodicity occurs (d). Note that the average chirp period in the 1:1 phase locking range matches exactly the stimulus period (f). The range with a high probability for leader chirps (e, black diamonds) is rather narrow whereas the probability for follower chirps (e, open squares) is similar to what was found in the simulation with mutually coupled oscillators (compare with b)
In the example given in Fig. 3a, alternation occurs with a probability of 33% when the intrinsic CP of both oscillators deviate as little as 100 ms (5%). Bistable alternation does always result in a joint CP (i.e. the CP which is established when two oscillators are mutually coupled) of longer duration than the intrinsic CPs of each of the oscillators. This is a consequence of the left branch of the PRC (Fig. 2a), because any stimulus here results in an increase in duration of the disturbed phase. By contrast, synchronisation results in a joint CP similar to the intrinsic CP of the faster oscillator. When the intrinsic CPs of both oscillators diverge even more (difference >400 ms), the interaction may lead to quasiperiodic dynamics as well. In these cases, there is no more 1:1 locking of the chirps.
Phase coupling is a consequence of the shape of the PRCs and strongly affects the timing of chirps. For CPs of longer duration than the intrinsic CP of the second oscillator, the probability of oscillator #2 becoming the leader increases according to the relative CP (intrinsic period of oscillator #2 minus intrinsic period of oscillator #1; Fig. 3b; black diamonds). At the same time CPs shorter than the competing one result in a higher probability for oscillator #2 to become the follower (Fig. 3b, open squares). Further, the average time difference Δt between leader and follower is a function of the relative CP in the range of 1:1 coupling (Fig. 3c). Both the probabilities for leader/follower and the value of Δt are highest for relative chirp periods of ±300 ms, and decrease with still larger relative periods as a result of quasi-periodic couplings (cf. Fig. 3a).
Entrainment of males to periodical stimuli
In a system of two mutually coupled oscillators, each oscillator influences the behaviour of the other. However, if we “deafen” one of the oscillators (#1), it simulates an entrainment of oscillator #2 to a periodical stimulus, which yields a different rate-phase plot (Fig. 3d). The most obvious difference is the existence of a region of stable alternation without the possibility of synchronisation (coupling phase about 0.5). Oscillator #2 simply adopts its CP to the SP of the periodical stimulus over a broad range (Fig. 3f). However, the range of “leader synchronisation” is limited to a narrow range of relative signal periods around the intrinsic CP of the oscillator (Fig. 3e, black diamonds). Whereas in such a one-directional coupling system “leader synchronisation” is much different from what is found for mutually coupled song oscillators, “follower synchronisation” (Fig. 3e, open squares) was found to be rather similar in both coupling systems with respect to follower probability and the amount of Δt.
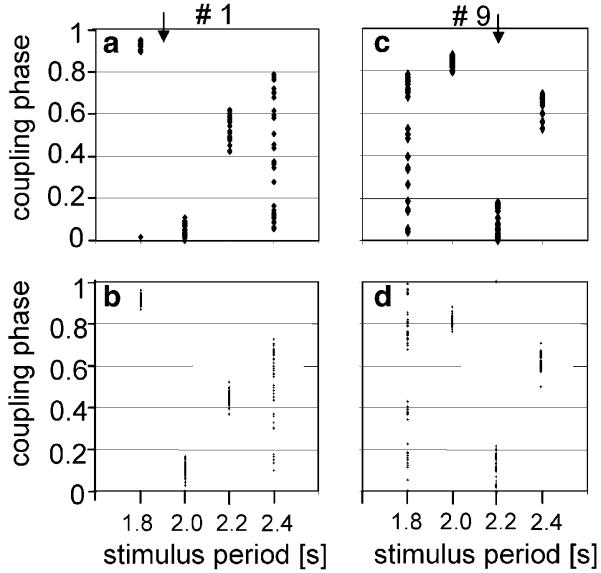
In order to test whether the results of our model match the behaviour found in real males, we entrained males to periodical stimuli of different periods and compared their behaviour with the outcome of simulations, using the PRCs of their song oscillators. As a typical example, Fig. 4 shows the coupling phases for two males (#1 and #9) entrained to different stimulus periods. Male #1 (a) was a fast singer with an intrinsic chirp period of 1,890 ms (indicated by arrow) and male #9 (c) a slow singer with an intrinsic chirp period of 2,230 ms. Synchronisation with coupling phases of 0.8–1.0 and 0–0.2 occurred when both males were entrained to a stimulus period similar to their own intrinsic chirp period, whereas stable alternation (phase 0.4–0.7) was found with entrainment to a stimulus period larger than their intrinsic chirp period. In the fast singer quasiperiodicity was found in response to a very large stimulus period (2,400 ms) and in the slow singer in response to a very small stimulus period (1,800 s). When the PRCs of the song oscillators of both males were used in a simulation, there was a high degree of similarity between simulation and experimental data with real males, with respect to the coupling phases and occurrence of synchronisation, alternation and quasi-periodicity (b, d).
Fig. 4.
Coupling phases of real males (a, c) and simulated oscillators (b, d) upon entrainment to different stimulus periods. Male #1 (a) is a fast singer (intrinsic CP 1.89 s indicated by an arrow) and male #9 (c) a slow singer (intrinsic CP 2.23 s). Using the PRC of both oscillators, the coupling phases in response to periodical stimuli were simulated (b, d). Note the high degree of similarity between simulation and experimental data with real males. Synchronisation (coupling phases 0.8–1.0 and 0–0.2) occurs upon entrainment to a stimulus period similar to the intrinsic chirp period; stable alternation (phases 0.4–0.7) was found upon entrainment to a slower stimulus period. In the fast singer quasiperiodicity was found in response to a very large stimulus period (2.4 s) and in the slow singer in response to a very small stimulus period (1.8 s)
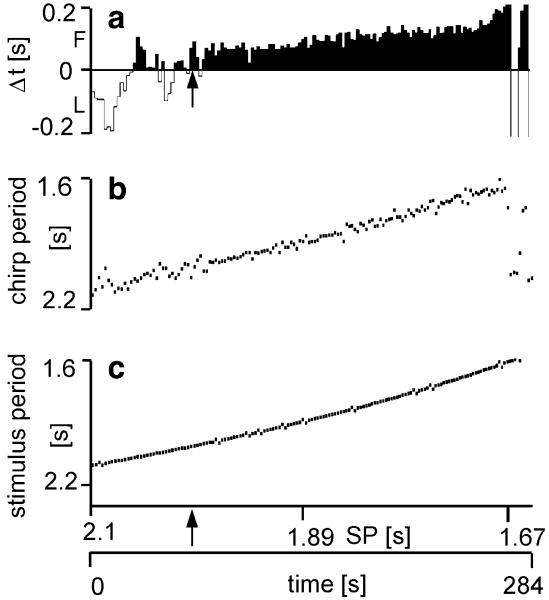
We also entrained males with a gradually increasing chirp rate, by shortening the CP by 3 ms after each chirp. A typical result from one male with an intrinsic CP of 2 s (see arrow) is shown in Fig. 5. As predicted from the results of modelling the interactions of two oscillators (Fig. 3d-f), 1:1 phase locking was found over a broad range of SPs (Fig. 5b). Also, both the probability for leader and follower chirps as well as Δt depends on the relative CP, in the same way as in the model. At a stimulus period of 2.09 s, which is about 100 ms longer compared to the intrinsic CP, the male produced leader chirps with a Δt up to −200 ms. With decreasing periods of the periodical stimulus shorter than the individual’s own CP (arrow), the male consistently locked in as a follower with increasing Δt up to about 170 ms at a SP of 1.7 s. Chirp timing showed a higher variability for leader chirps compared to follower chirps (Fig. 5a, upper trace). When the periodical stimulus decreased further in its CP (<1.7 s), this elicited quasi-periodical chirping, again as predicted from oscillator coupling shown in Fig. 3d.
Fig. 5.
Entrainment of a male over a time of 284 s to a periodical stimulus presented at 70 dB SPL with gradually increasing rate. The stimulus interval was decreased by 3 ms after each stimulus (c). The chirp period of the male (b) follows the stimulus period in a synchronised fashion from stimulus periods of 2.1–1.6 s; still smaller stimulus periods resulted in quasi-periodicity. Synchronisation to a faster stimulus rate compared to the males’ intrinsic CP (arrows) resulted in follower chirps with gradually increasing Δt values (black area in a). In contrast, synchronisation to slower rates resulted in leader chirps with a Δt of up to −200 ms
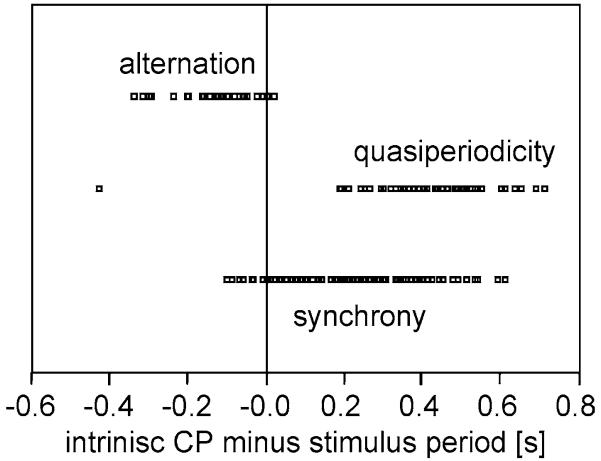
Further entrainment experiments were performed to identify the range of time differences between stimulus period and the intrinsic CP which results in synchrony, alternation, or quasi-periodicity. Results from 15 males, tested for a total of 208 entrainment experiments are presented in Fig. 6. Synchrony occurs over a broad range of relative CPs, predominantly when the male has an intrinsic chirp rate faster than the entraining stimulus. Alternation is elicited when males sing at a lower rate than the stimulus rate (intrinsic CPs up to 400 ms shorter than SP), whereas quasi-periodicity was observed at relative CPs between 200 and 700 ms. These results are in accordance with the predictions made from the rate-phase plot (Fig. 3d). Quasi-periodic dynamics are characterised by a recurrent irregular CP and stimulus phase. This type of oscillator response is also observed in a mathematical model of periodically driven oscillators (Guevara and Glass 1982). The type of phase coupling has important consequences for the leader to follower ratio: whereas about the same number of leader and follower chirps are produced during quasi-periodic dynamics, five times more leader chirps are found during 1:1 synchronisation. The L/F ratio observed during 1:1 synchronisation depends on the relative SP (Pearson correlation=0.519; P=0.001, n=41). Synchronising males exhibit a significantly higher L/F ratio when the stimulus period was within 0.2 s of their intrinsic CP (P<0.05, t test).
Fig. 6.
Results of experiments with males entrained to different stimulus rates. In order to compensate for different intrinsic CPs between males a relative stimulus period was calculated by subtracting the intrinsic CP from the stimulus period. Entrainment to similar or shorter stimulus periods compared to the intrinsic CP of individuals resulted in synchronisation, entrainment to longer stimulus periods always resulted in alternation. Quasi-periodicity was mainly found upon entrainment to faster stimuli
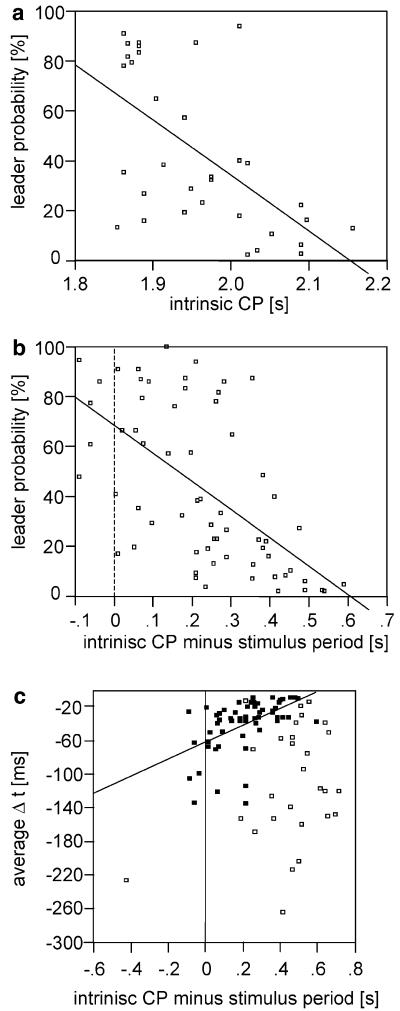
Therefore, a male’s intrinsic chirp period acts as a reliable predictor for the probability of producing leader chirps when entrained to fast periodical stimuli (Fig. 7a). Each dot in the figure refers to a single male entrained to a periodical stimulus (SP between 1.6 and 1.8 s). Those males with a shorter intrinsic CP have a higher probability for becoming a leader than males with longer intrinsic CPs. Further, the probability for leader chirps depends on the difference between intrinsic CP and the stimulus period (Fig. 7b). A difference of 0.0 s makes leader chirps more likely (R2=0.390; F=40.2; P<0.001; linear regression). Further, Δt depends on the relative CP: higher Δt values are found with smaller differences between the intrinsic CP and the stimulus period (R2=0.270; F=20.7; P<0.001; n=58; linear regression; Fig. 7c; filled squares). Such a correlation was not found in quasi-periodic interactions (Fig. 7c; open squares).
Fig. 7.
a The intrinsic chirp period of males determines the probability to become the leader upon entrainment to periodical stimuli. Each dot in a refers to a single male entrained to a periodical stimulus (SP between 1.6 and 1.8 s). Those males with a shorter intrinsic CP have a higher probability to become a leader than males with longer intrinsic CPs. Regression analysis showed a significant negative correlation of the intrinsic chirp period of different males and the probability for leader chirps (R2 = 0.366; F = 17.877; P<0.0001; β = −0.605; n = 33; y= −223.05x+480.07). A similar correlation was found between the relative stimulus period and the probability for leader chirps (b) (R2 = 0.390; F = 40.24; P<0.0001; β = −0.624; y = −112.854x+68.523). The average Δt of synchronised chirps (filled squares) was found to correlate positively with the time difference between intrinsic CP minus stimulus period (c) (R2 = 0.270; F = 20.69; P<0.0001; β = 0.519; n = 58; y = 101.308x–61.014). No such correlation exists in quasi-periodical interactions (open squares)
Individual PRCs and the effect of intensity
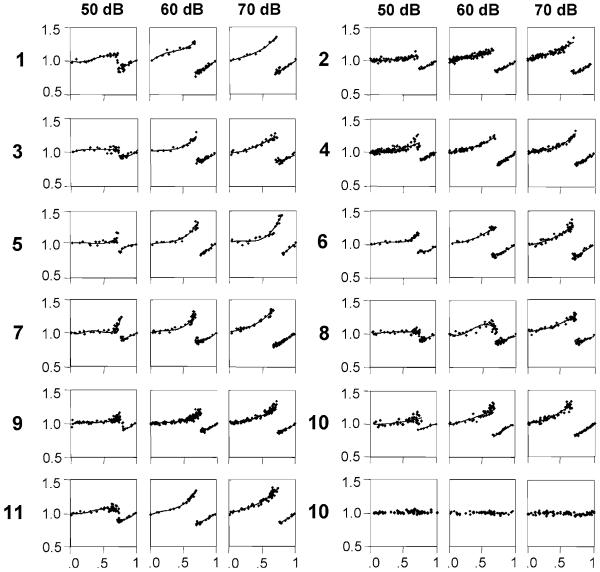
We have shown before that males within the population vary in their calling with respect to their intrinsic CP, and that this parameter largely determines the probability for a leadership upon entrainment to periodical stimuli. However, the particular shape of the PRC may vary between males as well, which might also influence chirp timing in an interaction. We thus characterised the PRCs of 11 different males at three different stimulus intensities (Fig. 8). In Fig. 8, males are arranged according to their intrinsic CP, where male #1 has the shortest intrinsic CP (1.89 s) and male #11 has the longest intrinsic CP (2.32 s). Despite the variation in the intrinsic CP, there is no systematic difference in the PRCs of slow and fast chirping males. However, the transition phase and the slopes of both branches were found to be intensity dependent. At 50 dB SPL the transition phase is quite well expressed in some males, but barely visible in others (compare, e.g. males #3 and #6). At this SPL, the transition phase is significantly higher when compared to 60 (P<0.01, paired t-test) and 70 dB SPL (P<0.05, paired t -test). As a representative example for all males tested, the PRC of the cycle following the disturbed cycle is shown for one male (male #10) in the lowest line. It demonstrates that there is no effect of a stimulus for the cycle following the disturbed cycle.
Fig. 8.
PRCs of 11 males obtained from playbacks at 50, 60 and 70 dB SPL. With increasing stimulus intensity the transition phases are more prominent. Note that for one male (male #10) the normalised cycle length of the cycle following the disturbed cycle is shown (last row) to demonstrate that it remains unaffected by the stimulus. For further explanation see text
Simulations of male duets have shown that the probability for bistable alternation is sensitive to the position of the transition phase of the PRCs, where high transition phases favour bistable alternation (data not shown). For example, male #9 in Fig. 8 exhibits a higher transition phase at 50 dB SPL compared to 70 dB SPL and thus increases the probability for alternation from 33% (70 dB SPL) to 50% (50 dB SPL). On the other hand, overlap of both branches of the PRC reduces the probability for bistable alternation. We found an overlap of 0.02 phase units which could be enough to prevent males from sustained alternation in real duets (data not shown).
On average, the slope of the right branch of the PRCs is significantly steeper at 60 (P<0.05, paired t-test) and 70 dB SPL (P<0.01, paired t-test) compared to 50 dB SPL. Simulations of duetting males sharing the same PRC have shown an increase in the range of 1:1 locking as a result of higher slope values of both branches of the PRC. In the example shown in Fig. 3a, the range of 1:1 locking at 50 dB SPL is limited to 250 ms when compared to 500 ms at 70 dB SPL. Higher slope values obtained for male #1 resulted in a range of 1:1 locking of 850 ms (at 70 dB SPL).
Coupling types obtained from modelled duets
The shape of the left and right branches of PRCs, experimentally determined for 11 different males (Fig. 8), was fitted by polynomials in order to simulate duets between all males. The resulting type of steady-state coupling at 70 dB SPL, as well as the resulting temporal relationship as leader and follower, is summarised in a duet matrix (Table 1). Most evident is the fact that faster males (CPs <2.0 s) were clearly established as leaders in interactions with those males having longer CPs. However, even males with relatively long CP managed to take the leader role when interacting with even slower males. For example, male #6 with an intrinsic CP of 2.11 s is follower when interacting with males with a CP <2.0 s, whereas the same male is leader when interacting with males #9, 10 and 11, which have CPs >2.2 s. Thus, despite the individuality of the PRCs and the fact that the simulation included the realistic noise in the data for the PRCs, a difference between the intrinsic CP of about 150 ms is sufficient to establish the leader and follower role. When a male interacts with an identical oscillator (diagonal in the table), either leads to synchronisation with a Δt of less than 50 ms or bistable alternation. Males #5, 9 and 11 have high transition phases favouring bistable alternation in duets with males of similar intrinsic CP.
Table 1.
Chirp timing in pairs of realistically simulated males differing in their intrinsic CP
| Male no. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intrinsic CP (s) | 1.89 | 1.89 | 1.90 | 1.96 | 1.97 | 2.11 | 2.15 | 2.16 | 2.23 | 2.30 | 2.32 | |
| 1 | 1.89 | S/F | S/F | S/A/F | S/F/A | A/F/S | F/S | F/S | F | F/A/L | F | F/L/S |
| 2 | 1.89 | S/L/F | S/L/F | S/F/A/L | S/F/L | F/S/A | F/S | F/S | F/S | F/A | F | F/L/S |
| 3 | 1.90 | S/A/L | S/A/L/F | A/S/L/F | S/A/F/L | A/F/S | F | F | F/A | F/A/L | F | F/L |
| 4 | 1.96 | S/A | S/F/A | S/A/L/F | A/S | A/S/F | F/S | F/S | F/S | F/A | F | F |
| 5 | 1.97 | A/L/S | A/S/L | L/A/S | A/S/L | A/S/L/F | S/A/F | F/S | A/S/F | A/F | F/S | F |
| 6 | 2.11 | L/S | L/S | L/S | L/S | A/S/L | S/L/F | S/F/L | S/A | F/S/A | F/S | F/S |
| 7 | 2.15 | L | L/S | L/S | L/S | S/L/A | S/L | S | S | A/S/F | S/F | F/S |
| 8 | 2.16 | L/S | L/S | L/A | L/S | A/S/L | S/A | S/F | S/A | S/A/F | F/S | F/S |
| 9 | 2.23 | L/A/F | L/A | L/A | L | A/L | L/S | S/L/A | S/A/L | S/A/L/F | S/F/A | S/F/A |
| 10 | 2.30 | L | L | L/A | L | L | L/S | L/S | S/L | S/L | S/L/F | S/F/L |
| 11 | 2.32 | L/F/A | L/F/A | L/A/F | L/A/F | L | L/S | L/S | L/S | S/L/A/F | S/L/A/F | A/S/F |
Male duets with oscillator properties shown as PRCs in Fig. 8 were realistically simulated at 70 dB SPL. The intrinsic CP is increasing from males #1 −11 and the resulting steady-state couplings observed between male duets are shown in a matrix. The resulting type of coupling is given from the point of view of males listed in the header of each column. Further coupling types are grouped according to their likelihood with the most likely one written on the left side. Bold letters correspond to a likelihood of more than 50%. A dominant leader or follower role is indicated by italic letters. For example, male #4 with an intrinsic CP of 1.96 s is the leader with a high probability when interacting with males #6–11. Similarly, male #7 is follower for most of the time when interacting with males #1–5, but leader in an interaction with males #10 and 11. Note that with a difference of about 150 ms between the intrinsic CPs of two males a dominant leader or follower role is established despite individual differences between their PRCs S Synchronisation (difference between chirp endings ≥−50 and ≤ 50 ms); L leader (≥−300 and < −50 ms); F follower (>50 and ≤ 300 ms); A alternation (< −300 or > 300 ms)
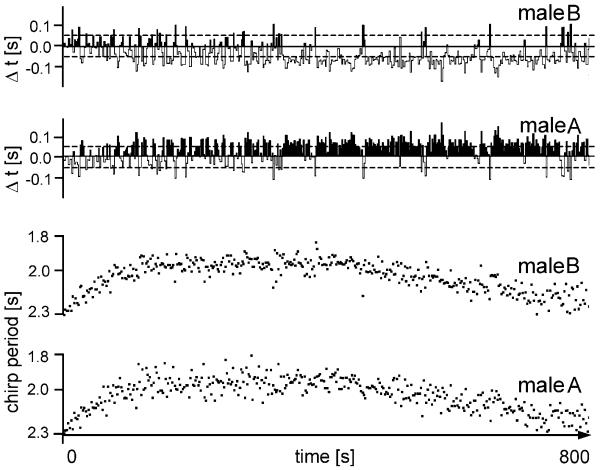
The results of modelling chirp interactions on the basis of individual PRCs were fully confirmed in experiments with real males. Figure 9 gives one example for a chirp interaction between two males over the time of a complete singing bout of 800 s. The intrinsic CP of male A was 2,170 ms and of male B 1,980 ms. Thus, according to the results presented in Table 1, a relative CP of 190 ms should be sufficient for a higher proba-case: after establishment of a higher chirp rate within the 50% of the interactions (107 leader:14 follower in a total of 192) on an average Δt of 70 ms (measured in the period with a high joint CR). For another 34% of chirp interactions, a Δt less than 50 ms was found. It is also evident from the gross pattern of the CR of both males that it is almost identical; male A with the intrinsic slower rate now follows exactly the faster male. This is are quickly followed by the other.
Fig. 9.
Synchronous chirp timing in a song interaction between two males with different intrinsic CPs (male B 1.98 s; male A 2.17 s). The average joint chirp period during the middle part of the interaction is the same (1.99 s) as the intrinsic chirp period of the faster male. Male B was the leader more frequently (107 times compared to only 14 times in male A). Further, only 34% of all chirps in the middle part of the interaction showed precise synchrony (Δt of less than ±50 ms, dashed lines)
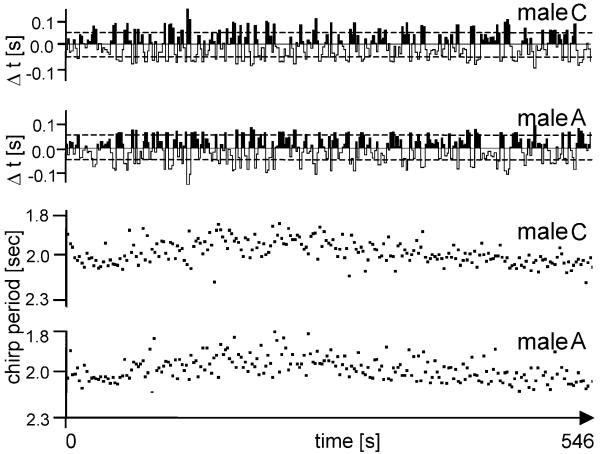
In contrast, song interactions between two males with equal or similar intrinsic CP exhibit a frequent change of the leader and follower role and a high degree of synchrony. Figure 10 shows the results of an interaction of male A with male C, both with a similar intrinsic CP (1,970 and 1,950 ms, respectively), with the consequence of a frequent switch of the leader and follower role after each fourth chirp, more than 43% leader/follower synchronisation and 57% synchronous chirps with a Δt of less than 50 ms (precise synchronisation). The similarity in the intrinsic CP of both males is reflected in the probability of leader and follower roles: male A was leader in 51%, male C in 49% of interactions with a Δt of more than 50 ms.
Fig. 10.
Synchronous chirp timing in a song interaction between two males with identical intrinsic chirp periods (both males 2.17 s). The interaction resulted in a frequent change of the leader and follower role (upper traces). Statistically, after every fourth chirp the leader/follower roles reversed. In the middle part of the singing bout both males were leader and follower at the same frequency. The joint chirp rate in the interaction was faster (2.0 s) than the intrinsic solo chirp rates of both males. 57% of all chirps in the middle part of the interaction showed a Δt of less than ±50 ms (dashed lines; precise synchrony)
Discussion
The current study confirms the hypothesis that individual properties of the song oscillator sufficiently explain the outcome of chirp interactions in duets of male M. elongata. Among all properties tested, the intrinsic CP was found to influence chirp timing most. This was shown both in behavioural experiments by entrainment of males to periodical stimuli which differed in their rate, in real male song interactions, as well as in computer simulations. Individual differences in PRCs (Fig. 8) are important for the establishment of alternation or synchrony as long as the intrinsic CPs of both oscillators are rather similar (Table 1). However, a difference between both intrinsic CPs of about 150 ms was sufficient to override individual differences in the PRCs and clearly allows us to predict the outcome of an interaction with respect to the amount of time singing as leader and follower (Table 1).
There is a shift in the transition phase of the PRC to higher values at lower intensities (50 dB SPL). The most likely explanation for this shift is the fact that a chirp of M. elongata shows a typical triangular shape with syllables at the end increasing in intensity (see Fig. 1a). For a receiver, the initial syllables of a chirp at 50 dB SPL remain subthreshold, which in turn leads to a delayed response. The absolute shift of the transition phase observed at 50 dB compared to 70 dB SPL is in the order of 70–100 ms (at a CP of 2 s), which corresponds quite well to the delayed perception of the first four to five syllables. A similar shift in the transition phase for stimuli differing by 25 dB was reported by Sismondo (1990). One consequence of this shift is a higher probability of alternation of males interacting at greater distances.
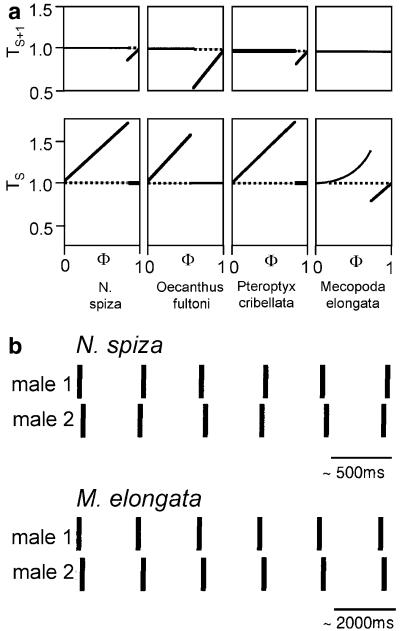
Phase-response curves are known from a number of rhythmically calling insects. They have been presented in varying ways, so that for a comparison it is useful to put all in the same format (Fig. 11a). Here, the period of the intrinsic song is the cycle from one chirp (inclusive) to the next (exclusive). The male’s own chirp appears in phase ϕ = 0, the next chirp in ϕ = 1 (which is at the same time ϕ = 0 of the next cycle). An applied stimulus appears in phase 0 ≤ ϕ < 1 within a cycle, which is the disturbed cycle. The duration of the disturbed cycle divided by the intrinsic cycle length is given as Ts in Fig. 11. In some animals there is also a change in response to a stimulus in the cycle following the disturbed cycle; the PRCs of these cycles are also presented in the figure (y-axis, Ts+1).
Fig. 11.
a PRCs of four insect species with rhythmically calling or flashing oscillators. a PRCs of four rhythmically communicating insect species. Note that the PRCs of the song oscillators of N. spiza, O. fultoni and P. cribellata are fundamentally different from the PRC of M. elongata, with respect to the response at stimulus phases higher than the transition phase, and the response in the cycle following the disturbed cycle, which remains unaffected in M. elongata, but is shortened in the other insects. b Schematic diagram of synchronous chirp interactions of two males in N. spiza and M. elongata, resulting from their PRCs. In both species, male #2 is the one with the longer intrinsic chirp period. Whereas in N. spiza the leading role switches every second interaction, the intrinsically slower singing male in M. elongata is a consistent follower
The PRCs of the song oscillators of N. spiza, Oecanthus fultoni and Pteroptyx cribellata, known as synchronisers, are fundamentally different from the PRC of M. elongata (cf. Fig. 11a). Whereas in all insects of the comparison low-stimulus phases result in an increase in the disturbed cycle (albeit to a different degree), the response at stimulus phases higher than the transition phase is different: in N. spiza, O. fultoni and P. cribellata the disturbed cycle remains unaffected, whereas the following cycle Ts+1 is shortened. In contrast, under the same condition, M. elongata shortens the disturbed cycle; the following one remains unaffected (see also male #10 in Fig. 8). From the viewpoint of the inhibitory resetting model, the left branch in the PRC of M. elongata would correspond to a phase delay and the right branch to a phase-advance mechanism. To our knowledge Pterophylla camellifolia, an alternating species, is the only one with a very similar PRC and hence a similar mechanism responsible for the phase advance and phase delay compared to M. elongata (Shaw 1968). Even the variability of solo CPs and the width of the distribution of individual intrinsic CPs are similar in both species. Further, both species increase their CP in alternating interactions compared to solo singing. The major reason why Pterophylla males mainly alternate and Mecopoda males synchronise can be seen in the late transition phase in the former, together with a strong overlap between the two PRC branches. Indeed, using such a PRC in our coupled oscillator model resulted in stable alternation interrupted by occasional transients of synchrony, very similar to what was found in interacting males (Shaw 1968). Therefore, a similar mechanism underlying the phase shift in response to acoustic stimuli seems to be likely for theses two species. Meixner and Shaw (1986) also reported the synchronous song interactions for N. nebrascensis, where the leader and follower roles are fixed for long periods of time, and faster males take the leader role more often. Interestingly, in N. nebrascensis the leader role is clearly established when the CPs of two males differ by about 180 ms, a value almost identical found in Mecopoda (Table 1). Inhibitory resetting is highly unlikely in N. nebrascensis given the high duration of more than a second of the song elements produced by males, and the fact that complete suppression of song elements in followers was not observed. However, the PRC describing the properties of the underlying oscillator was not studied, so it remains to be tested whether the song oscillators in Mecopoda and N. nebrascensis have the same properties.
We can only speculate on why such strong differences exist between the mechanisms leading to synchrony within the Tettigoniidae. One argument may be that synchronising species differ strongly in their call rate. For example, compared with N. spiza, M. elongata exhibits a call rate which is four to five times lower. An inhibitory resetting mechanism in Mecopoda would result in many missing chirps if they fall in the “forbidden interval”, and thus the duty cycle of the follower would be drastically reduced. Using a computer program that runs the inhibitory resetting model (M. Tourtellot; http://www.ukans.edu/~eeb/faculty/greenfie.html), we managed to simulate synchronous interactions with Mecopoda song parameters (albeit unknown durations of oscillator return intervals and unrealistically long effector delays). However, of 250 simulated chirp interactions about 70% of chirps were suppressed, and only the remaining exhibited synchrony. Thus, inhibitory resetting may produce a dramatic loss in signalling “ontime” in species calling at low rates. The much faster chirping N. spiza is similarly affected by inhibitory resetting, but the much higher call rate would still guarantee a duty cycle high enough for reliable signalling. This is also important from the viewpoint of females choosing between synchronising males. In Mecopoda, females can only assess the timing of leader and follower chirps, and these roles are relatively fixed for long periods of time when males differ in their intrinsic CPs by more than 150 ms (Table 1, Fig.9). N. spiza males also exhibit leader and follower chirps in synchrony but, in addition, due to repeated inhibition of follower chirps relative to leader chirps, the task of the choosing female is even easier. The call duty cycle of the intrinsically slower chirping male can be strongly reduced in a male duet. Thus, in addition to the precedence effect females can assess this obvious difference as well.
Two models have been suggested in order to explain alternation and synchrony in acoustic insects and fireflies: the integrate and fire model (Hanson et al. 1971) and the inhibitory resetting model (Greenfield and Roizen 1993). Both models assume that there is an underlying oscillator which, in order to trigger sound production, needs to reach an excitatory threshold. In the inhibitory resetting model, the time required to reach the basal level of the oscillator after triggering is the oscillator-return interval. There is also a short effector delay between the time of reaching threshold and the onset of sound production, which includes the time required by any neuronal and muscular elements to activate the song apparatus. A disturbance (stimulus) results in a tonic inhibition to the basal level of the oscillator for the duration of the disturbance (thus the name “ inhibitory resetting”). Such inhibition of the oscillator due to stimuli has been confirmed for N. spiza (Greenfield and Roizen 1993), and was also reported for fireflies (Hanson 1978).
There are at least three aspects in the inhibitory resetting model which makes it inappropriate to explain the PRC and chorusing of M. elongata: (1) Dependent on the phase of the stimulus only the disturbed cycle is prolonged or shortened by M. elongata males. In contrast, N. spiza males shorten the next cycle following a stimulus applied at a later phase in their cycle. (2) The effector delay is a basic requirement of the inhibitory resetting model. This delay is approximately of the same duration as the oscillator return interval for oscillators corresponding to the model. Greenfield (1994a) estimated about 50–200 ms for the time required from oscillator triggering to sound production. Sismondo (1990) estimated this delay for M. elongata at 75 ms. Our own estimates are based on the following assumption: because the insects shorten the disturbed cycle with late stimulus phases, the effector delay must be shorter than the time between stimulus and the following chirp. Thus for M. elongata the maximal value for the effector delay ranges between 50 and 100 ms, which is in good agreement with Sismondo’s estimate. Since this time is small compared to the intrinsic CP of about 2,000 ms, the effector delay can be ignored in models describing the song interactions in M. elongata. The effector delay is much shorter than the part of the cycle where stimuli result in a shortening of the disturbed cycle, which is about 600–800 ms (see Figs. 2, 8). In the inhibitory resetting model the effector delay should be similar to this time of the cycle. (3) Finally, the tonic inhibitory action of a stimulus in the IR model is not compatible with the song oscillator in Mecopoda. At stimulus phases larger than the transition phase, the time difference between stimulus and the next chirp of the male is much smaller (50–150 ms) when compared to a chirp duration of 250–300 ms. Such a strong stimulus-chirp overlap would be incompatible with a tonic inhibitory resetting in the IR model. Further arguments stem from observations, where we tested the influence of an abrupt change of the stimulus duration on the cycle length of alternating males (stimulus period 2 s). Neither a stimulus 100 ms longer or shorter in duration was effective in changing the entrained cycle lengths. Such a change would be expected in a song oscillator model including tonic inhibition. Based on their intrinsic chirp periods and their PRCs, two males of Mecopoda synchronise their chirps, if their intrinsic chirp periods do not differ too much. In these interactions, the intrinsically faster male is the leader in a stable 1:1 phase coupling (Fig. 11b). This is different in N. spiza: “the leading role within synchronising pairs usually alternates during successive chirp periods” (Greenfield and Roizen 1993; see Fig. 11b). Thus there is a kind of stable 2:2 coupling in synchronous interactions of N. spiza, which never happens in M. elongata.
Further differences concern the responses of the underlying oscillators to entrainment stimuli with varying periods. In M. elongata, males synchronise in a 1:1 manner with external stimuli when the repetition rate differs in either direction from the target individual (Fig. 5). Males with intrinsic periods of 2.1 s have been observed phase coupling to stimuli with periods as low as 1.43 s, which represents an increase of 30% of the intrinsic rate (Kratzer 2000). On the other hand, males also synchronise to stimuli with periods higher than their intrinsic period, thus reducing their chirp rate (Fig. 5). Such synchronising behaviour is not compatible with a competitive hypothesis of song interaction, where the individual with a faster intrinsic rate should not adopt to a slower stimulus. However, one should also consider the consequences when males synchronise with faster or slower stimuli with respect to the leader and follower roles: if they accommodate a constant stimulus slower than their intrinsic chirp period, they gain the leader role, whereas they become followers when synchronising to faster stimuli (Figs. 5, 10). In N. spiza, however, males basically stop calling when the rate of external stimuli is about 20% higher than their intrinsic rate (Greenfield and Roizen 1993), whereas in the snowy tree cricket, males are either inhibited or synchronise to every other stimulus (Walker 1969); for similar patterns of response in anurans see Moore et al. (1989).
Ultimately, female response patterns will strongly determine the timing interactions of males in a given species. If females prefer signals leading in time, synchrony can be interpreted as ongoing competition between males for the leadership in song interactions. Indeed, the frequent switching of leader and follower roles in song interactions of the snowy tree cricket (Walker 1969) and N. spiza (Greenfield and Roizen 1993) is a strong indication for such a competition, if we consider the strong preference for leading signals that have been reported for N. spiza and several other species of insects and anurans (Klump and Gerhardt 1992; Greenfield 1994b; Grafe 1996, 1999; Snedden and Greenfield 1998). However, even in M. elongata, with no indication for frequent switching between leader and follower roles, there is also a strong preference for leading chirps by females (Römer et al. 1997). As a result, we would expect selection for ever faster chirp rates, since males with faster chirp rates are more often leaders in interactions with males of slower rates.
In order to explain how males with slower chirp rates could still obtain matings with females under selection for leader chirps, we have to consider the conditions in a natural population under which males are able to attract females. First of all, the distribution of intrinsic chirp periods (Fig. 1c) of the male population indicates that the majority of males have intrinsic periods centred around 2 s, and about 50% of males at the population mean differ by less than 150 ms in their intrinsic chirp period. If these males interact with each other, the probability of becoming a leader or follower is close to 0.5 (compare male–male interaction in Fig. 10). Only if the chirp periods differ by 150 ms and more, the leader role is taken by one male more often and can be predicted with high accuracy (see also Table 1).
Römer et al. (2002) have also shown that the temporal advantage in the representation of the leader signal in the CNS of a female can be compensated by increased loudness of the follower signal, or even be reversed with still higher intensities. The value of 9 dB for compensating a leader signal with a temporal advantage of 120 ms can be explained by the ramp-like amplitude modulation of the male signal over 250–300 ms, where the leader signal with a temporal advantage of 120 ms exhibits an amplitude advantage of about 7 dB for the next 180 ms of overlap. The behavioural preference for the leading male call is similarly abolished in females of the frog Hyla cerenea when the SPL of the lagging signal is increased by 6 dB over that of the leading signal (Klump and Gerhardt 1992) and in N. spiza when the SPL of the lagging signal is increased by 4 dB (26-ms signal offset) (Snedden and Greenfield 1998). If we assume that all males within a population call at the same absolute intensity, various environmental parameters may still contribute to a considerable variation in their relative SPL at the position of a receiver. Such factors include distance and geometric spreading of sound, excess attenuation, the position (height) of a signaller in the vegetation, the broadcast directivity pattern of the signaller, and different ambient noise levels at different receiver sites (reviewed in Römer 1998). As a result of a combination of all these variables, a female may be stimulated more strongly by a male producing a follower signal, and orient phonotactically towards this male, despite the general preference for leader signals in females. This could explain, on the ultimate level, why males of M. elongata with the higher intrinsic chirp period, which are followers in an acoustic interaction with faster males most of the time, may still gain some fitness benefits from calling as followers in a population with randomly positioned female receivers.
Nevertheless, those males which take the leader role in an interaction with substantial Δt should attract on average more females than followers even under complex field conditions. However, call rate is also known to be an important energetically demanding song character which could be limited by male condition (Bailey et al. 1994; Hoback and Wagner 1997; Reinhold et al. 1998). This hypothesis is subject of a current ongoing study with the investigation of male calling energetics. Preference of the leader may therefore be a selection of a male of better condition.
Abbreviations
- CP
Chirp period
- PRC
Phase-response curve
- SP
Stimulus period
- SPL
Sound pressure level
References
- Alexander RD. Natural selection, specialized chorusing behavior in acoustical insects. In: Pimentel D, editor. Insects, science and society. Academic; New York: 1975. pp. 35–77. [Google Scholar]
- Bailey WJ, Withers PC, Endreby M, Gaull K. The energetic costs of calling in the bushcricket Requena verticalis (Orthoptera: Tettigoniidae: Listroscelidinae) J Exp Biol. 1993;178:21–37. [Google Scholar]
- Buck J, Buck E, Case F, Hanson FE. Control of flashing in fireflies. V. Pacemaker synchronisation in Pteroptyx cribellata. J Comp Physiol A. 1981;144:287–298. [Google Scholar]
- Gerhardt HC, Huber F. Acoustic communication in insects and anurans. Common problems and diverse solutions. The University of Chicago Press; Chicago: 2002. [Google Scholar]
- Glass L, Graves C, Petrillo GA, Mackey MC. Unstable dynamics of a periodically driven oscillator in the presence of noise. J Theor Biol. 1980;86:455–475. doi: 10.1016/0022-5193(80)90345-8. [DOI] [PubMed] [Google Scholar]
- Grafe TU. The function of call alternation in the African reed frog (Hyperolius marmoratus): precise call timing prevents auditory masking. Behav Ecol Sociobiol. 1996;38:149–158. [Google Scholar]
- Grafe TU. A function of synchronous chorusing and a novel female preference shift in an anuran. Proc R Soc Lond B. 1999;266:2331–2336. [Google Scholar]
- Greenfield MD. Cooperation and conflict in the evolution of signal interactions. Annu Rev Ecol Syst. 1994a;25:97–126. [Google Scholar]
- Greenfield MD. Synchronous and alternating choruses in insects and anurans: common mechanisms and diverse functions. Am Zool. 1994b;34:605–615. [Google Scholar]
- Greenfield MD. Acoustic communication in Orthoptera. In: Gangwere SK, Muralirangan MC, Muralirangan M, editors. The bionomics of grasshoppers. CAB International; Wallingford: 1997. pp. 197–230. [Google Scholar]
- Greenfield MD, Roizen I. Katydid synchronous chorusing is an evolutionary stable outcome of female choice. Nature. 1993;364:618–620. [Google Scholar]
- Greenfield MD, Tourtellot MK, Snedden WA. Precedence effects and the evolution of chorusing. Proc R Soc B. 1997;264:1355–1361. [Google Scholar]
- Guevara MR, Glass L. Phase locking, period doubling bifurcations and chaos in a mathematical model of a periodically driven oscillator: a theory for the entrainment of biological oscillator and the generation of cardiac dysrhythmias. J Math Biol. 1982;14:1–23. doi: 10.1007/BF02154750. [DOI] [PubMed] [Google Scholar]
- Hanson FE. Comparative studies of firefly pacemakers. Fed Proc. 1978;37:2158–2164. [PubMed] [Google Scholar]
- Hanson FE, Case F, Buck E, Buck J. Synchrony and flash entrainment in a New Guinea firefly. Science. 1971;174:161–164. doi: 10.1126/science.174.4005.161. [DOI] [PubMed] [Google Scholar]
- Hoback WW, Wagner WE., Jr The energetic cost of calling in the variable field cricket, Gryllus lineaticeps. Physiol Entomol. 1997;22:286–290. [Google Scholar]
- Klump GM, Gerhardt HC. Mechanisms and function of call-timing in male-male interactions in frogs. In: McGregor PK, editor. Playback and studies of animal communication. Plenum; New York: 1992. pp. 153–174. [Google Scholar]
- Kratzer S. Verhaltensuntersuchungen zu Gesangsinterak-tionen bei der Laubheuschrecke Mecopoda elongata (Orthoptera: Tettigonidae) Karl-Franzens Universität Graz; 2000. Diploma thesis. [Google Scholar]
- Meixner AJ, Shaw KC. Spacing and movement of singing Neoconocephalus nebrascensis males (Tettigoniidae: Copophorinae) Ann Entomol Soc Am. 1979;72:602–606. [Google Scholar]
- Meixner AJ, Shaw KC. Acoustic and associated behavior af the coneheaded katydid, Neoconocephalus nebrascensis (Orthoptera: Tettigoniidae) Ann Entomol Soc Am. 1986;79:554–565. [Google Scholar]
- Moore SW, Lewis ER, Narins PM, Lopez PT. The call-timing algorithm of the white-lipped frog, Leptodactylus albilabris. J Comp Physiol A. 1989;164:309–319. [Google Scholar]
- Otte D. Communication in Orthoptera. In: Sebeok TA, editor. How animals communicate. Indiana University Press; Bloomington: 1977. pp. 334–361. [Google Scholar]
- Prestwich KN. The energetics of acoustic signaling in anurans and insects. Am Zool. 1994;34:625–643. [Google Scholar]
- Reinhold K, Greenfield MD, Jang Y, Broce A. Energetic cost of sexual attractiveness: ultrasonic advertisement in wax moths. Anim Behav. 1998;55:905–913. doi: 10.1006/anbe.1997.0594. [DOI] [PubMed] [Google Scholar]
- Römer H. The sensory ecology of acoustic communication in insects. In: Hoy RR, Popper AN, Fay RR, editors. Comparative hearing: insects. Springer; Berlin Heidelberg New York: 1998. pp. 63–69. [Google Scholar]
- Römer H, Bailey WJ. Insect hearing in the field. II Male sapacing behaviour and correlated acoustic cues in the bushcricket Mygalopsis marki. J Comp Physiol A. 1986;159:627–638. [Google Scholar]
- Römer H, Hedwig B, Ott SR, Elsner N, Wässle H. Proceedings of the 25th Göttingen Neurobiolgy Conference. Thieme Stuttgart; 1997. Proximate mechanism of female preference for the leader male in synchronising bushcrickets (Mecopoda elongata) p. 322. [Google Scholar]
- Römer H, Hedwig B, Ott SR. Contralateral inhibition as a sensory bias: the neural basis for a female preference in a synchronously calling bushcricket, Mecopoda elongata. Eur J Neurosci. 2002;15:1655–1662. doi: 10.1046/j.1460-9568.2002.02003.x. [DOI] [PubMed] [Google Scholar]
- Shaw KC. An analysis of the phonoresponse of males of the true katydid, Pterophylla camellifolia (Fabricius) (Orthoptera: Tettigoniidae) Behaviour. 1968;31:203–260. [Google Scholar]
- Sismondo E. Synchronous, alternating, and phase-locked stridulation by a tropical katydid. Science. 1990;249:55–58. doi: 10.1126/science.249.4964.55. [DOI] [PubMed] [Google Scholar]
- Snedden WA, Greenfield MD. Females prefer leading males: relative call timing and sexual selection in katydid choruses. Anim Behav. 1998;56:1091–1098. doi: 10.1006/anbe.1998.0871. [DOI] [PubMed] [Google Scholar]
- Thiele DR, Bailey WJ. The function of sound in male spacing behaviour in bushcrickets (Tettigoniidae: Orthoptera) Aust J Ecol. 1980;5:275–286. [Google Scholar]
- Thornhill R, Alcock J. The evolution of insect mating systems. Harvard University Press; Cambridge: 1983. [Google Scholar]
- Walker TJ. Acoustic synchrony: two mechanisms in the snowy tree cricket. Science. 1969;166:891–894. doi: 10.1126/science.166.3907.891. [DOI] [PubMed] [Google Scholar]
- Zelick R, Narins PM. Characterization of the advertisement call oscillator in the frog Eleutherodacytylus coqui. J Comp Physiol. 1985;156:223–229. [Google Scholar]