Effect of strain on voltage-controlled magnetism in BiFeO₃-based heterostructures

Abstract

Voltage-modulated magnetism in magnetic/BiFeO₃ heterostructures can be driven by a combination of the intrinsic ferroelectric-antiferromagnetic coupling in BiFeO₃ and the antiferromagnetic-ferromagnetic exchange interaction across the heterointerface. However, ferroelectric BiFeO₃ film is also ferroelastic, thus it is possible to generate voltage-induced strain in BiFeO₃ that could be applied onto the magnetic layer across the heterointerface and modulate magnetism through magnetoelastic coupling. Here, we investigated, using phase-field simulations, the role of strain in voltage-controlled magnetism for these BiFeO₃-based heterostructures. It is predicted, under certain condition, coexistence of strain and exchange interaction will result in a pure voltage-driven 180° magnetization reversal in BiFeO₃-based heterostructures.

It is accepted that voltage-modulated magnetism in magnetic/BiFeO₃ (BFO) layered heterostructures is based on a combination of intrinsic coupling between the coexisted ferroelectric and antiferromagnetic orders in BFO, and the antiferromagnetic-magnetic exchange interaction across the heterointerface¹,²,³,⁴. However, ferroelectric BFO film, if not fully clamped by substrate, would generate voltage-induced strains that could be transferred to the magnetic thin film across the heterointerface and modulate magnetism together with exchange interaction through magnetoelastic coupling. Influence of this strain on voltage-modulated magnetism in BFO-based heterostructures has remained largely unexplored since raised by Mathur⁵, though a giant voltage-induced strain of over 5% has later been observed in BFO thin films with mixed rhombohedral and tetragonal phases⁶,⁷.

In this article, we explore how strain affects the voltage-modulated magnetism in BFO-based heterostructures by taking the Co_0.9Fe_0.1(CoFe)/BFO thin-film heterostructure as an example. (001) BFO thin films were grown on (110) DyScO₃ substrate, exhibiting two-variant ferroelectric domains with 71° wall due to anisotropic film-substrate misfit strains⁸. In particular, the magnetic domain patterns in the top CoFe film almost copy the in-plane projection patterns of the ferroelectric domains at the BFO surface²,⁹. Such magnetic domain pattern is induced by an effective magnetic field from the canted magnetic moment M_c in BFO via Dzyaloshinskii-Moriya (DM) exchange interaction¹⁰,¹¹, namely, H_DM-field. The direction of H_DM-field (also M_c) is perpendicular to the plane of the polarization P and the antiferromagnetic axis L¹²,¹³, i.e., H_DM = P × L, resulting in a non-uniform H_DM-field distribution based on the two-variant 71° ferroelectric domains. In this case, when electrically rearranging ferroelectric domain configuration to switch the in-plane net polarization in BFO by 180°, rotation of H_DM-field within individual ferroelectric domain could lead to an overall 180° switching of the in-plane net magnetization² in CoFe. 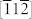Detailed experimental analysis¹⁴ reveals that the H_DM-field (M_c) lies along the and directions corresponding to the 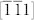and 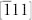polarizations, while along the 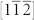and 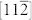directions corresponding to the 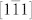and [111] polarizations, respectively (figure 1a).

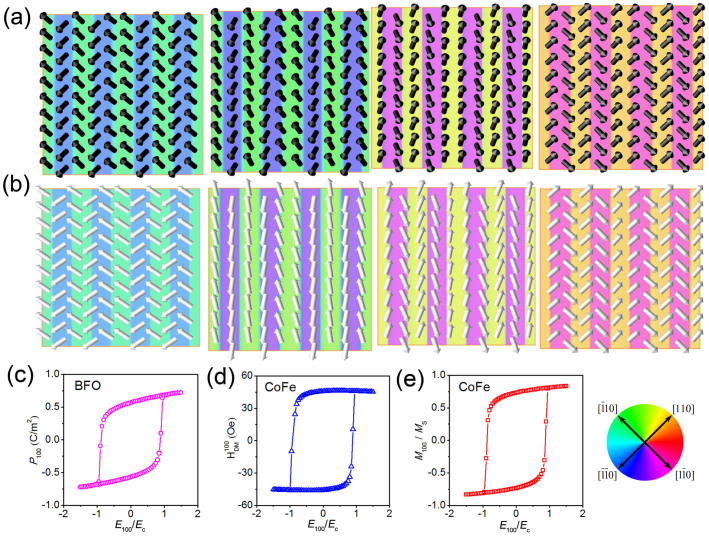
Figure 1. Voltage-controlled magnetism in CoFe/BiFeO₃ heterostructure.

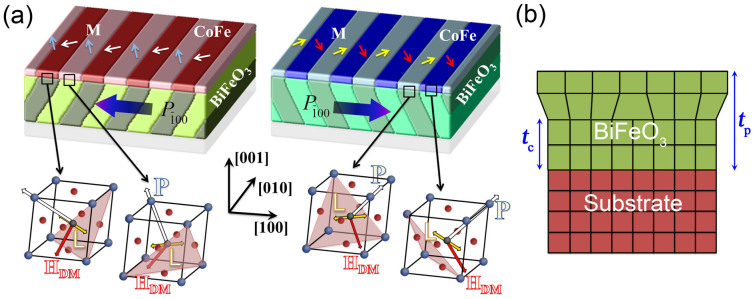
(a) Locally coupled magnetic and ferroelectric domains in the Co_0.9Fe_0.1(CoFe)/BiFeO₃(BFO) heterostructure reproduced by phase-field model (the first row), based on electric-field switching of the interfacial exchange coupling field H_DM which is perpendicular to the plane of electric polarization P and the antiferromagnetic axis L in BFO (the second row). The slim arrows indicate orientations of local magnetization vectors. (b) Schematic of an epitaxial BFO film with partially relaxed substrate clamping when the film thickness t_p exceeds the critical value t_c for the generation of interfacial dislocations.

Furthermore, the first few unit cells at the BFO thin film surface would become stress-free when the thickness of the BFO film was above a certain critical value [t_c ~70 nm for the BFO films grown on DyScO₃(DSO) substrate¹⁵,¹⁶] to allow the presence of lattice defects such as dislocation (figure 1b). In this case, sizable and non-uniform strain can be generated associated with local non-180° ferroelectric polarization (i.e., ferroelastic) switching under an electric-field. The strain can be further transferred to the top magnetic thin film across the interface and modulate the magnetic domain structure locally via magnetoelastic coupling¹⁷. Transfer of such non-uniform strain has recently been demonstrated in BaTiO₃ single crystal-based heterostructues¹⁸,¹⁹,²⁰,²¹, which exhibit a similar one-to-one domain pattern match between magnetic thin film and ferroelectric BaTiO₃ underneath. Particularly, it was proposed that²² such non-uniform ferroelastic strain transfer alone could drive a 180° in-plane net magnetization reversal similarly to the non-uniform H_DM-field driven reversal shown in figure 1a. These similarities thus raise one interesting question for BFO-based heterostructures: what role does the non-uniform strain in BFO play in the electric-field induced magnetization reversal? A phase-field²³,²⁴ model is developed herein (see Method section) to address this question, and illustrate new possibility in electric-field-controlled magnetism under coexistence of non-uniform H_DM-field and non-uniform strain.

Results

In-plane net magnetization reversal purely by H_DM-field

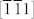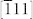We first examine the influence of the interfacial H_DM-field on the electric-field driven magnetization reversal in the CoFe/BFO heterostructure. If the electric-field applied along the [100] direction (E₁₀₀) exceeds the coercive field of BFO (E_c), the initial alternating and ferroelectric domains would switch by 71° to the 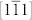and [111] domains, respectively, during which the polarization vectors would always keep a head to tail configuration (see figure 2a) to reduce the electrostatic energy. This leads to a full reversal of the average polarization along the [100] direction (i.e., P₁₀₀), as illustrated by the simulated ferroelectric hysteresis loop in figure 2c. Note that individual ferroelectric domain under a certain E₁₀₀ results in one unique local H_DM-field distribution [Eq. (11)]. Correspondingly, figure 2b presents the in-plane projections of the H_DM-field, e.g., an initial configuration of head to tail in-plane 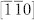and 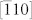orientations. The induced local magnetization distributions (viz. domain structures) in the CoFe film are almost identical to those of in-plane H_DM-field (not shown here for simplicity), while both distributions are essentially the same as the in-plane projections of the ferroelectric domains and thereby accounts for the domain pattern transfer between the CoFe and BFO films². Furthermore, a full reversal of the net [100] magnetization (M₁₀₀) in the CoFe film occurs when reversing the average in-plane H_DM field along the [100] direction (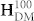) with an electric-field, as shown by their electric-field switching loops in figure 2e and 2d, respectively. The magnitude of the total H_DM field [i.e., 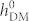, see Eqs. (11) and (12) in the Method section] is taken as 100 Oe based on a relevant experimental measumrent⁹.

Figure 2. In-plane net magnetization reversal via electric-field switchable H_DM-field.

In-plane electric-field (E₁₀₀/E_c = 1) induced dynamic changes in (a) the local distributions of polarization (top view) in the two-domain-variant BFO film, and (b) the in-plane projections of the H_DM-field (the same for the local magnetization). The background color indicates the orientation of the local polarization/H_DM/magnetization field (see the color wheel). Electric-field switching loops of average (c) polarization, (d) in-plane H_DM field, and (e) magnetization along the [100] direction. E_c represents the coercive field of the BFO film.

It is worth noting that such net magnetization reversal may not be triggered if the 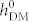was too small, because the striped magnetic domains cannot be stabilized unless 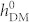exceeds 35 Oe (see figure 3a), where the influence of strains is not incorporated (λ_s = 0). As it can be seen, once the striped domains form at 35 Oe, the net in-plane magnetization can then be reversed, i.e., the normalized magnetization M₁₀₀/M_s changes from −0.7 to about 0.7, by changing the polarity of the net in-plane polarization. Simulated magnetic and ferroelectric domain structures at 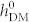= 6 Oe and 100 Oe are illustrated in the inset of figure 3a. We argue that the critical 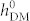value for net magnetization reversal should be strongly dependent on the coercive field of the magnetic thin film, because influence of H_DM-field is equivalent to an external non-uniform magnetic field [Eq. (9)].

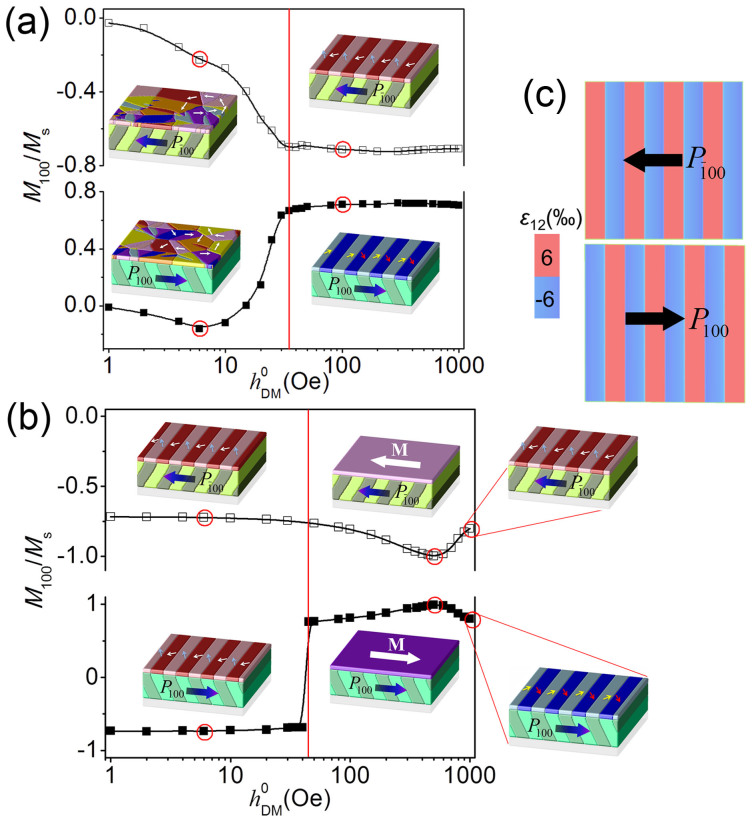
Figure 3. Effects of H_DM-field and strain on voltage-induced magnetic domain switching.

Variations on M₁₀₀/M_s (the normalized magnetization along the [100] direction) as a function of 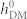(the magnitude of the H_DM-field) before and after reversing the in-plane average polarization from 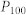to 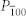in the CoFe/BFO heterostructure, driven by (a) only H_DM-field, and (b) H_DM-field together with ferroelastic strain. The insets are magnetic and ferroelectric domain structures at 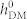= 6 Oe and 100 Oe in (a), and the 6 Oe, 500 Oe, and 1000 Oe in (b). The slim arrows indicate the orientations of local magnetization vectors. (c) Distribution of the non-uniform ferroelastic strain arising from the ferroelectric domains at the BFO surface before and after polarization reversal.

Full magnetization reversal driven by both H_DM-field and strain

Figure 3b shows the M₁₀₀/M_s variations as a function of 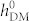before (the upper panel) and after (the lower panel) reversing the net in-plane polarization, driven by both non-uniform H_DM-field and non-uniform ferroelastic strain. Strain distributions before and after polarization reversal are plotted in figure 3c, with an alternating distribution of ±0.6% [also see Eq. (4a)]. Of interest, the magnetic striped domains can be stabilized during the growth of CoFe film by the growth-induced strains [see Eq. 4(b)] imposed by the striped ferroelectric (also ferroelastic) domain pattern at the BFO surface even when 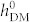= 0 (i.e., no exchange interaction but sole strain effect, see figure 3b). However, these striped domains cannot be switched to achieve an in-plane net magnetization reversal when 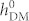is small (weak exchange interaction). For example, at 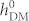= 6 Oe, the striped domains only demonstrate a change in pattern periodicity (see corresponding domain structures in the inset of figure 3b) when reversing in-plane polarization. Thus, although non-uniform ferroelastic strain contributes to the stabilization of the domain stripes, it alone cannot trigger the net magnetization reversal. On the contrary, this strain could even suppress the reversal compared to the case purely driven by H_DM-field (figure 3a), as demonstrated by (i) the enhancement of the critical value of 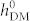from 35 Oe to 45 Oe (see the solid line in figure 3b), and (ii) the different magnetic domain stripes at 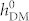= 6 Oe (prevailing strain effect) and 1000 Oe (prevailing exchange interaction) with the same FE domain patterns underneath (i.e., both are before electric-field poling, see the upper panel of figure 3b).

These counteractive non-uniform H_DM-field and non-uniform strain can, however, be exploited to achieve a full rather than net magnetization reversal. As shown in figure 3b, the magnetic striped domains are straightened out to form a uniform single domain when 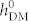is about 500 Oe. We attribute this to the almost equal contributions from the competing strain effect and exchange interaction at this point. Indeed, taking the coupled magnetic and ferroelectric domain structures at 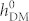= 0 Oe as the reference, the changes in magnetic free energy induced by strain and H_DM-field are 8.26 × 10⁴ J/m³ and −7.95 × 10⁴ J/m³, respectively, at 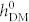= 500 Oe. Furthermore, a full 180° magnetization reversal takes place when reversing the in-plane polarization (see corresponding domain structures in figure 3b), which should promise higher application potential for low-power memory applications²⁵,²⁶ than the average magnetization reversal in striped multi-domain. Further simulations show that the range of 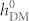required for such voltage-driven 180° magnetization reversal is from 393 Oe to 778 Oe, whereas the rest 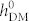values that are over 45 Oe only lead to a net magnetization reversal, in which the contribution form H_DM-field is enough to trigger magnetization reversal but much smaller/larger than contribution from strain. Particularly, the range of 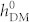for 180° reversal can be tuned by engineering the saturation magnetostriction coefficient λ_s (e.g., by using different magnets) and/or the magnitude of ferroelastic strains [e.g., by tuning polarization, see Eq. (4a)]. Detailed analysis can be found in Supplemental materials S1.

Dynamics of magnetic domain switching

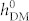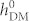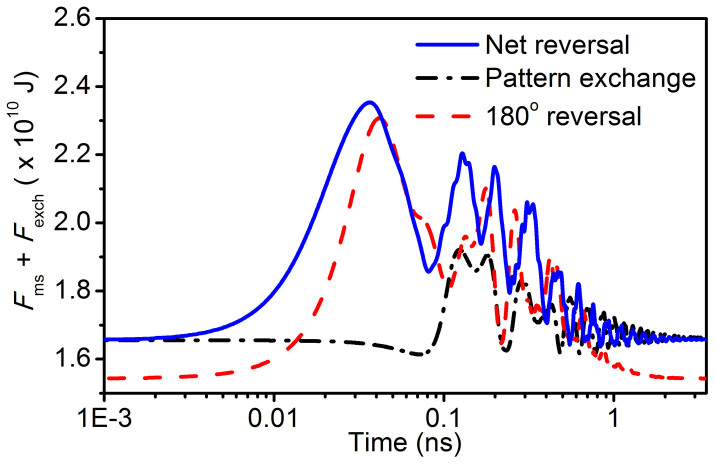
So far three different voltage-induced magnetic domain switching paths has been observed under the coexistence of H_DM-field and strain, including the change in domain pattern periodicity (pattern exchange) when H_DM-field is weak or absent (< 45 Oe), the full magnetization reversal when contributions from H_DM-field and strain are comparable (393 Oe < < 778 Oe), and the net magnetization reversal for the remaining values of 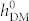. To unravel the underlying physics, we track the time-dependent changes in the sum of the magnetostatic and exchange energy (i.e., F_ms + F_exch) for these different paths (figure 4), and their local magnetic vector distributions at various time stages are shown in Supplemental Materials S2. For the net magnetization reversal at 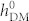= 1000 Oe, an energy barrier is surmounted during its initial stages (<0.04 ns), whereas for the change in domain pattern periodicity at 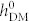= 6 Oe, a lower energy path is present throughout the evolution. Given the almost identical energy states between these striped domains with opposite net magnetization (i.e., pattern exchange and net reversal in figure 4), and also given their similar energy oscillation trends after surmounting the energy barrier, it can be concluded that the energy barrier can only be overcome by the unidirectional H_DM-field rather than the uniaxial strain. In particular, for the full magnetization reversal at 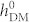= 500 Oe, the counteraction between H_DM-field and strain leads to the lowest energy state before and after switching, however, an energy barrier still needs to be surmounted to complete the reversal.

Figure 4. Free energy analysis for different voltage-induced magnetic domain switching paths.

Time-dependent changes in the sum of magnetostatic and exchange energy for three different voltage-induced magnetic domain switching in CoFe/BFO heterostructures, driven by both non-uniform H_DM-field and non-uniform strain. The magnitudes of H_DM-field (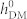) are taken as 6 Oe, 500 Oe, and 1000 Oe for pattern exchange, net magnetization reversal, and 180° full magnetization reversal, respectively.

Discussion

Voltage-controlled magnetism in magnetic/BiFeO₃ heterostructures is a complex process with multiple underlying mechanisms, depending on the size of such heterostructures²⁷. In the present article, our focus has been put on the effects of both ferroelastic strains and DM exchange interaction in the CoFe/BiFeO₃ heterostructures currently investigated. Besides these effects, the modulation of magnetism could also be contributed by the voltage-induced changes in interface charge densities²⁸,²⁹, and/or interface orbital configuration (e.g., via Fe-O hybridization, refs. ^30,31). Such interface effects would become more remarkable as the thickness of the CoFe film (2.5 nm herein) further decreases³². On the other hand, further decrease in the lateral size of the heterostructures may allow us to study the complex interplay among strain, exchange interaction, and possibly the charge/orbital effect in ferroic single-domains. This is not only fundamentally interesting, but also important for the design of high-density magnetoelectric devices²⁵,²⁶. The model established herein could provide a good starting point for the further study of these issues.

In summary, a phase-field model has been developed to understand how strain affects the voltage-modulated magnetism in BFO-based heterostructures. The model is validated by reproducing the experimentally observed voltage-driven in-plane net magnetization reversal in a CoFe/BFO heterostructure² driven by non-uniform H_DM-field. Then we evaluate the stable magnetic and ferroelectric domain structures by adding the influence of the non-uniform ferroelastic strain that arises from the ferroelectric domain patterns at the BFO surface. Under such coexistence of H_DM-field and strain, three different magnetic domain switching paths are discovered depending on the magnitude of the H_DM-field, including a full 180° reversal of uniform magnetization when contributions from H_DM-filed and strain are comparable. Analysis on magnetic domain switching dynamics demonstrates the lowest energy state for such full magnetization reversal, as well as the decisive role of H_DM-field for both full and net magnetization reversals.

Methods

Phase-field model

In phase field approach, the magnetic and ferroelectric domain structures are described by the spatial distributions of the local magnetization vector M = M_S(m₁,m₂,m₃) and local polarization vector P = (P₁,P₂,P₃), respectively, where M_S and m_i (i = 1,2,3) represent the saturation magnetization and the direction cosine³³.

The temporal evolution of the ferroelectric domain structure in (001)-oriented BFO thin films is governed by the time-dependent Landau-Ginzburg (TDGL) equation³⁴, i.e.,

where L is a kinetic coefficient that is related to the domain wall mobility and F_P is the total free energy of the FE layer, which can be expressed as,

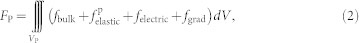here f_bulk, 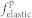, f_electric, and f_grad indicate the densities of bulk free energy, elastic energy, electrostatic energy, and gradient energy of the BFO, respectively, with V_P representing the volume of the ferroelectric layer in the heterostructure. The mathematical expressions for the f_bulk, f_grad, and f_electric of the BFO (001) thin films are described in literature³⁵. Corresponding to the local in-plane electric-fields applied across the CoFe/BFO heterostructure via planar poling electrodes², the electrostatic energy density f_electric is obtained under a short-circuit boundary condition³⁶.

The elastic energy density 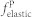is calculated as,

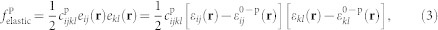where 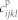is the elastic stiffness tensor of the BFO and e_ij(r) the position-dependent elastic strain; ε_ij(r) is the total strain and 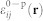is the spontaneous (stress-free) strain of the BFO arising from the electrostrictive effect, i.e., 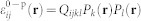(i,j,k,l = 1,2,3,4), where Q_ijkl is the electrostrictive coefficient tensor. Following Khachaturyan's elastic theory³⁷, the total strain ε_ij(r) can be expressed as the sum of homogeneous and heterogeneous strains, i.e. 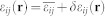. Among them, the heterogeneous strain δε_ij(r) does not cause any macroscopic deformation in a sample, i.e.,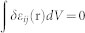, and can be calculated as 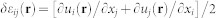, where u_i(r) is the displacement.

The homogeneous strain 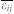represents the macroscopic deformation, whose in-plane components equal the film/substrate mismatch strain 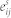if the BFO (001) thin films were fully constrained by the DSO (110) substrate, i.e., 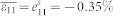, , 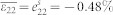and 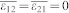. The mechanical equilibrium equation, i.e., 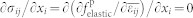, is then solved by taking σ₁₃ = σ₂₃ = σ₃₃ = 0³⁸. It is noteworthy that such anisotropic biaxial in-plane strains can reduce the ferroelectric domain variants of the rhombohedral BFO from eight to two⁸, leading to the unique two-variant striped domains with 71° walls as reconstructed in figure 1a. Particularly, in a partly relaxed BFO thin film (figure 1b), a non-uniform ferroelastic strain 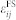could be generated across the first few stress-free unit cells of individual ferroelectric domain, which can be expressed as,

Here t_s( = t_p-t_c) denotes the thickness of the stress-free unit cells at the BFO film surface (see figure 1b), which is approximated to be 40 nm by taking the total thickness t_p of BFO as 110 nm³⁹.

Corresponding to the two-variant FE domains at the BFO surface, a two-variant striped strain distribution with alternating ±0.6% can be derived. Such non-uniform strain 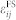would further be transferred, at least partially¹⁸, to the upper CoFe film that has a much smaller thickness (t_m ~2.5 nm, ref. 2) than t_s. Note that the two-variant striped domains in the BFO film should still emerge at the thickness t_p of 110 nm as observed in experiments³⁹, though the possible interfacial dislocations would somewhat release the anisotropic mismatch strains from the orthorhombic DSO substrate. Nevertheless, even the fully constrained BFO thin films with striped domains can impose structural strains on the upper magnetic thin film during its growth,³³ similarly to those observed in magnetic/BaTiO₃ heterostructures.¹⁸,¹⁹ Thus, the average growth-induced strain affects the domain structure of the as-grown magnetic thin film together with the interfacial H_DM field, which can be expressed as,

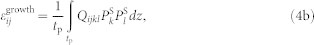where 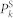is the spontaneous (or remnant) polarizations under zero external electric fields. Accordingly, when applying an electric-field to the BFO film, the resultant polarization switching would change spatial distributions of both the H_DM( = P × L) field and the strain 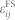[Eq. (4a)] at the interface.

Magnetic domain structures of the CoFe film will then evolve driven by these non-uniform H_DM field and non-uniform 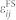(or the 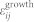for simulating the domain structures of as-grown CoFe film), and can be described by the Landau-Lifshitz-Gilbert (LLG) equation, i.e.,

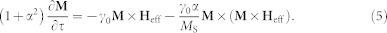Here γ₀ and α are the gyromagnetic ratio (taken as −2.2 × 10⁵ m·A⁻¹·s⁻¹ from ref. 40) and the Gilbert damping constant (~0.01 from ref. 41), respectively, whereby the real time step ΔT (~0.06 ps) for the magnetic domain evolution can be determined by 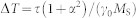with Δτ = 0.02. H_eff is the effective magnetic field, given as 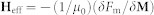, with μ₀ denoting the vacuum permeability and F_m the total free energy of the CoFe layer. The F_m is formulated as,

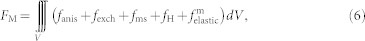where f_anis, f_exch, f_ms, f_H, and 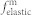are the magnetocrystalline anisotropy energy density, exchange energy density, magnetostatic energy density, the H_DM-field energy density, and elastic energy density, respectively. Among them, the f_anis is neglected for simplicity regarding the isotropic nature of the polycrystalline CoFe film. The isotropic f_exch is determined by the gradient of local magnetization vectors, i.e.,

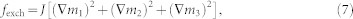where J denotes the exchange stiffness constant. The magnetostatic energy density f_ms can be written as,

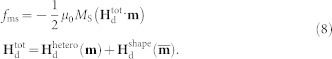Here the stray field 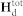consists of a heterogeneous part 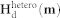from the magnetostatic interaction which depends on local magnetization distributions and is obtained by solving magnetostatic equilibrium equation, i.e., 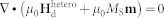, under periodic boundary conditions⁴². 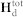also includes an demagnetization part 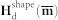that relates to the average magnetization by the sample-size dependent demagnetizing factor matrix N⁴³, i.e., .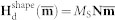

Furthermore, the H_DM-field energy density can be expressed, similarly to the Zeeman energy of an external magnetic field, as,

The 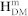indicates the H_DM-field imposed on the CoFe film, and is given as,

where t_i denotes the thickness of the interface creating interfacial magnetic interaction, and the H_DM-field vector in the BFO layer can be expanded as,

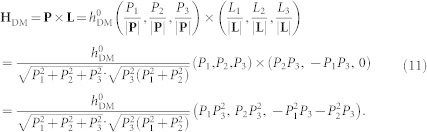The P_i and L_i (i = 1,2,3) are the components of the polarization vectors and the antiferromagnetic axes along the cubic <100> axes, respectively, and the 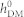represents the magnitude of the H_DM field that depends on the chemical composition and geometric size of a specific BFO-based heterostructure⁹,⁴⁴. Note that the antiferromagnetic axis L is expressed as L = (P₁, P₂, 0) × (0, 0, P₃), which indicates an alignment along either the in-plane 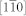or [110] axis depending on polarization orientations (see figure 1a). Equation (11) clearly indicates that non-uniform nature of the H_DM-field related to individual ferroelectric domain at the BFO surface, which can propagate across the heterointerface and act on the CoFe film similarly to the case in non-uniform ferroelastic strains 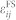[Eqs. (4a) and (4b)]. Combining Eq. (11), Eq. (10) can be rewritten as,

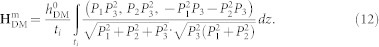Influence of non-uniform 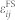on magnetic domain structures is characterized by changes in the elastic energy density of the CoFe, i.e., 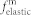, which can be calculated similarly to that in ferroelectric BFO [Eq. (3)] but use the elastic stiff constants of CoFe. Note these non-uniform 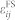are included in the position-dependent stress-free strain 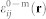of the magnets,

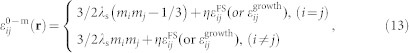with λ_s denoting the saturation magnetostrictive coefficient, taken as −62 ppm herein⁴⁵. The coupling factor η (0 ≤ η ≤ 1) is introduced to describe the possible loss of transferred strain due to imperfect interface contact, and is assumed to be 1 for a full strain transfer.

Temporal evolutions of the ferroelectric and magnetic domain structures are obtained by numerically solving the TDGL and LLG equations using semi-implicit Fourier spectral method⁴⁶ and Gauss-Seidel projection method⁴⁷, respectively. The material parameters used for simulations, including the Landau coefficients, electrostrictive coefficients, elastic constants, gradient energy coefficients of BFO layer, and the saturated magnetization, exchange stiffness constant, elastic constants of CoFe layer, are taken from literatures⁴⁸,⁴⁹,⁵⁰. The discrete grid points of 128Δx × 128Δy × 48Δz with real grid space Δx = Δy = 10 nm, and Δz = 4 nm are employed to describe the BFO film/substrate system, wherein the thickness of BFO t_p is taken as 112 nm by setting t_p = 28Δz, and the thickness of the interface t_i creating the interfacial magnetic interaction is taken as 4 nm by setting t_i = 1Δz. While for CoFe thin film, discrete grid points of 128Δx × 128Δy × 20Δz with Δx = Δy = 10 nm, and Δz = 0.5 nm are used, where the thickness of the CoFe t_m is set to be 2. 5 nm by taking t_m = 5Δz.

Author Contributions

J.J.W., J.M.H. and T.Y. performed the simulations. C.W.N. and L.Q.C. directed the work. J.M.H., J.J.W., L.Q.C. and C.W.N. co-wrote the paper. J.J.W., J.M.H., M.F., J.Z. and C.W.N. analyzed the data. All contributed discussion.

Supplementary Material

Supplementary Information

Supplemental Materials