Abstract
Cells from all kingdoms of life adopt a dizzying array of fascinating shapes that support cellular function. Amoeboid and spherical shapes represent perhaps the simplest of geometries that may minimize the level of growth control required for survival. Slightly more complex are rod-shaped cells, from microscopic bacteria to macroscopic plants, which require additional mechanisms to define a cell’s longitudinal axis, width, and length. Recent evidence suggests that many rod-shaped, walled cells achieve elongated growth through chiral insertion of cell-wall material that may be coupled to a twisting of the cell body. Inspired by these observations, biophysical mechanisms for twisting growth have been proposed that link the mechanics of intracellular proteins to cell shape maintenance. In this review, we highlight experimental and theoretical work that connects molecular-scale organization and structure with the cellular-scale phenomena of rod-shaped growth.
Introduction
Cell shape is dictated physically by the balance of forces on the cell envelope. Turgor pressure due to the high concentration of osmotic solutes inside cells generates an outward pressure on the envelope. To maintain a non-spherical shape, cells must surround themselves with an anisotropic elastic structure that expands to counterbalance this pressure. In animal cells, this is largely achieved through the construction of intracellular cortical networks of actin filaments, although other elastic filaments such as spectrin can also be used. On the other hand, bacteria use a rigid, extracellular cell wall composed of a network of peptidoglycan while plants use a wall composed of cellulose and other polysaccharides [1].
In these walled cells, growth occurs through the spatially regulated insertion of new material into the exoskeletal cell wall. Local insertion of material, performed by a host of proteins, must be coordinated on the cellular scale so that cell shape and the mechanical integrity of the wall are maintained. While molecular experiments have led to the characterization of many of the players in this process, understanding the regulation of shape requires approaches that can bridge the molecular and cellular scales. Two key issues we address in this review are (i) how individual molecules can organize into chiral filaments to generate a spatially coordinated pattern of growth, and (ii) the biophysical interactions required for robust, rod-shaped growth.
Cell-wall growth in bacteria
Cell shape in nearly all bacteria is governed by the peptidoglycan cell wall, a meshwork of glycan strands crosslinked by short peptides [2, 3]. During growth and division, newly synthesized peptidoglycan subunits are incorporated into the wall through the concerted effort of a number of enzymes including the murein (Mur) and penicillin binding proteins (PBPs). These enzymes construct the cell wall through synthesis of new subunits, breakage of existing linkages in the wall, and insertion of new subunits to grow the peptidoglycan network.
While many of these enzymes have been characterized biochemically, several important biophysical questions about their method of action remain unanswered. For example, severing individual linkages will promote the wall to expand under turgor, leading to a weakened state [4]. However, as new units are added, they can also have a rigidifying effect on the wall if they are actively stressed prior to insertion in order to resist expansion [5]. It is not currently known to what extent wall enzymes must coordinate their activities, in either space or time, in order for growth with a maintained shape to proceed. Biochemical measurements of in vitro peptidoglycan polymerization suggest that at least some of the enzymes may be processive [6–9], however how this processivity manifests in vivo [10] and whether it is coupled between enzymes remains under current investigation.
Rod-shaped growth
Perhaps the simplest systems for studying complex cell growth are elongated rods, which must encode, at the molecular level, a three-dimensional coordinate system that defines the longitudinal cell axis and division plane in addition to the cell length and width. Rod-shaped cells are common in both bacteria and plants. Prokaryotic rods are thought to possess several biophysical advantages over non-elongated cells for functions such as motility and in certain environmental niches [11–13]. In plants, rod-shaped cell growth is coupled directly to the elongation of roots, stems, and other tissues.
Because of their small size and the fast speed of diffusion within the cytoplasm, it is difficult for a bacterial cell to establish precise cytoplasmic gradients with which to define a cellular coordinate system [14, 15]. Instead, it has been proposed that geometric cues such as curvature may provide information about orientation within the cell that can be processed through local binding interactions between inherently curved polymers and a curved surface [16–18]. The determination and maintenance of cell shape is governed by the cellular-scale pattern of wall insertion and the balance of forces on the cell wall [19, 20]. To query whether local geometric cues can guide cellular-scale patterning that robustly generates the correct cell shape requires experimental and computational tools to quantify and connect molecular organization to wall patterning.
While some rod-shaped bacteria insert material at the poles or mid-cell, most model bacteria with a rod shape appear to insert material in a roughly uniform distribution along the cylindrical portion of the cell wall. However, computational simulations studying the consequences of random insertion predict a loss of both cell shape and mechanical integrity [5], suggesting that the orchestration of growth is required for rod-shape maintenance. In elongating bacteria, recent evidence suggests that filaments with chiral (left- or right-handed) positioning along the membrane are used to coordinate insertion, producing both a rod-like shape and a robustly cross-linked cell wall that twists as it grows [21].
Protein filaments are inherently chiral
Biopolymer filaments such as actin, microtubules, and bacterial flagellar filaments are linear assemblies of individual monomeric units. The molecular binding interactions between protein monomers define the spatial relationship between adjacent monomers in a filament. In general, three angles that encapsulate the relative orientation of neighboring monomers along the filament define this relationship (Figure 1A). Different combinations of angles between monomer subunits lead to a variety of beautiful and complex filament shapes (Figure 1B) whose geometry has been the subject of study as far back as Euler. A common feature of all of these shapes is their helicity, due to the fact that a constant bend and twist per monomer leads to chiral backbones [22–25]. Indeed, as early as 1950, the helical nature of biological chains was recognized, with a prescient focus on biological growth [25].
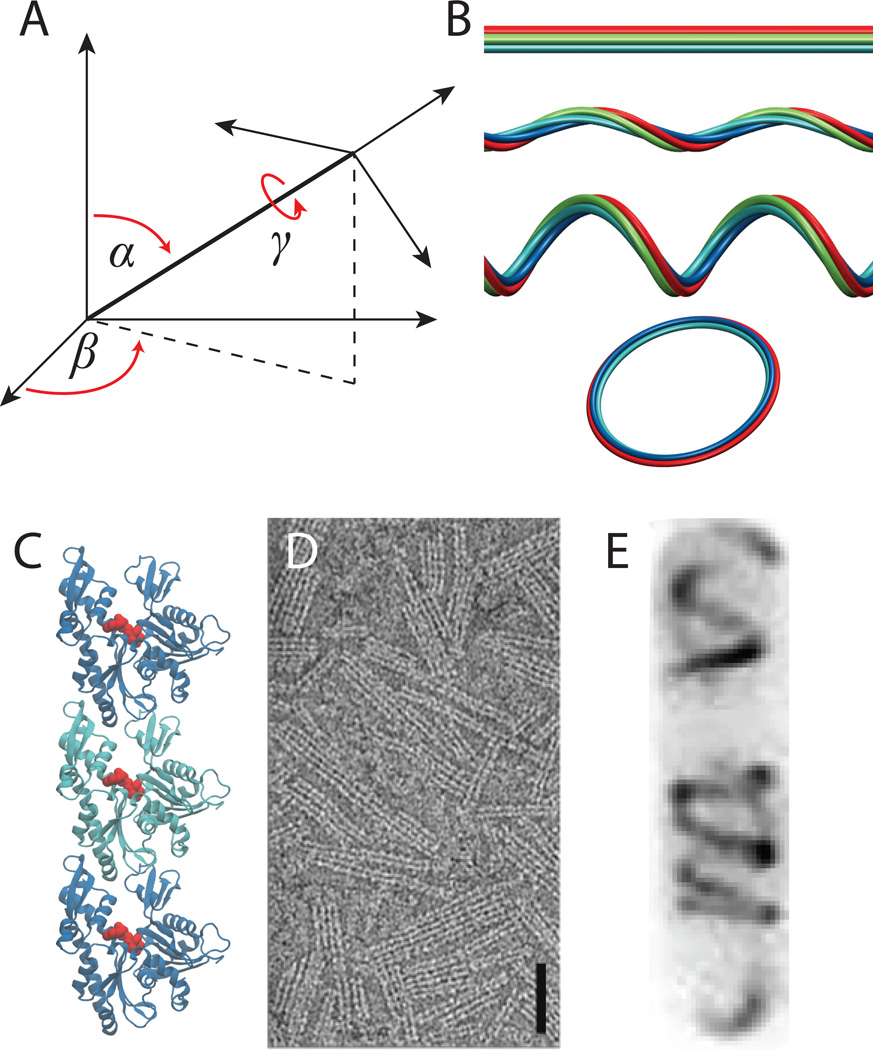
Figure 1.
(A) Three angles, often referred to as Euler angles, are needed to describe an arbitrary rotation between adjacent monomers in a polymer. (B) Different combinations of the Euler angles α, β, and γ yield different filament geometries including straight rods, helices, and rings. (C) X-ray crystallography has revealed that MreB monomers polymerize into linear protofilaments (adapted from [62]). (D) MreB binds directly to lipid membranes in a double-protofilament geometry (adapted from [34]). (E) In live cells, MreB labeled with YFP at the N-terminus forms polymeric structures with a clear left-handed chirality.
Of the observed classes of filaments, simplified shapes such as straight lines and rings are extreme limits in which some of the relative orientation angles are zero. One particularly interesting property of these filaments in a biological context is that resultant shapes can have features on length scales much larger than the size of an individual monomer. Examples of these include the radius of curvature for a ring and the pitch of a helix, both of which can be arbitrarily large compared to the scale of the proteins themselves. These features are independent of the chemical kinetics that affect the length of filaments through assembly and disassembly. Thus, polymerization of filaments can generate cellular-scale “order” independent of the monomer size or chemical kinetics. Outstanding questions surrounding this topic are the extent to which this order is established for filaments in living cells, and the mechanisms through which this order can be maintained and utilized for cellular-scale phenomena such as growth.
In bacteria, a number of cytoskeletal polymers have been described as helical. Filament bundles of the tubulin homolog FtsZ form tightly wound circumferential rings at the division plane in nearly all prokaryotes, and have been observed to form helical structures away from the division plane [26–30]. The actin homolog MreB can form filaments in a preferentially left-handed orientation with a pitch on the order of a few hundred nanometers (Figure 1E) [21, 31, 32] while the intermediate-filament homolog CreS generates a helix with a pitch longer than the typical cell length that is revealed only when cells grows filamentously [33]. Addressing the biological relevance of these polymeric structures for cell shape requires an understanding of how they organize inside a rod-shaped cell and of how in turn they regulate wall growth.
Cell curvature can mediate localization and orientation of filaments
In vitro experiments indicate that E. coli MreB interacts preferentially with curved membranes. Filaments bind directly to the outside lipid vesicles in a double-protofilament configuration and sometimes induce inward indentations of the membrane, suggesting a preference for the more negatively curved (convex) inner membrane surfaces of a rod-shaped cell (Figure 1C, D)[34]. However, in vivo membrane binding appears to be more complicated, involving other factors such as RodZ [35, 36]. The energetically optimal configuration for a filament bound to a membrane is dictated by the balance of energies associated with membrane binding and both filament and membrane bending. The energy cost of bending a filament can be conceptualized as a spring, where the “extension” of the spring is proportional to the difference between the preferred and actual curvatures of the filament. For a membrane with variable curvature, a filament will naturally gravitate toward a location and orientation that most closely matches its preferred geometry, as long as the filament is sufficiently stiff and there is sufficient monomer turnover or filament movement to allow the sampling of many configurations. Interestingly, many bacterial cytoskeletal filaments have rapid dynamics [26, 37], suggesting that they need not be locked into a non-optimal orientation.
For E. coli MreB, the observation that depolymerization of MreB significantly decreases the bending stiffness of living cells [38] and the tendency of MreB filaments to indent vesicles indicate that filaments are stiff and have a strong preference for convex curvatures that would naturally lead to orientation along the circumferential direction of a cylinder. In a similar manner, any underlying helical arrangement of membrane interaction sites on the filaments will require the introduction of torsion about the filament axis for membrane binding to occur, which can lead to the selection of a preferred chirality along the membrane surface determined by the handedness of the path of interactions sites along the filament surface.
Spatial control of cell-wall synthesis
In Gram-negative species such as E. coli and Caulobacter crescentus, MreB is rapidly depolymerized by the small molecule A22. In the presence of A22, approximately rod-shaped growth continues for a short period of time, but subsequently cell width increases and cells become round after ~2-3 divisions [5]. This progression indicates that MreB is not required for wall synthesis, but rather acts indirectly to regulate the process through interactions with proteins such as the PBPs (Figure 2A). While these interactions may serve a purely biochemical purpose, it has been hypothesized that one function of MreB is to regulate the cellular localization of the PBPs, similar to the guidance of cellulose synthase complexes by microtubules in plants [39]. In the presence of the division-inhibiting antibiotic cephalexin, the slow, progressive loss of rod-like shape in A22-treated cells is mimicked in simulations of random, unregulated wall insertion [5], providing further support for MreB’s role as an organizing scaffold on the cellular scale. It is still unknown how the conformation of MreB is transmitted to the periplasm, although it is thought to be mediated by binding to the periplasmic proteins MreC/D.
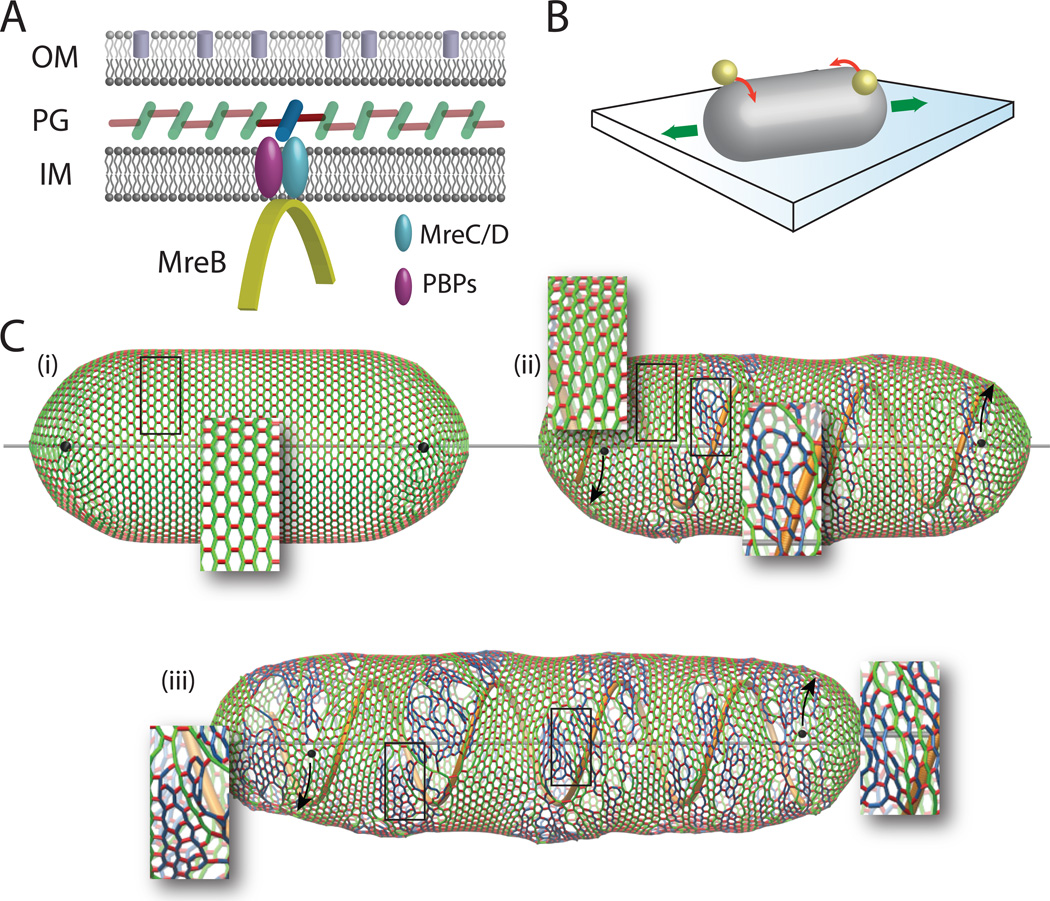
Figure 2.
(A) MreB polymers orchestrate rod-shaped growth via the localization of peptidoglycan synthesis enzymes in the periplasm between the inner (IM) and outer (OM) membranes. (B) Both E. coli and B. subtilis twist as they elongate during rod-shaped growth, revealed by the opposite rotation of the two ends. (C) Computer simulations of bacterial cell growth reveal that a left-handed, helical insertion pattern of glycan strands, guided by MreB (yellow), into an initially achiral wall generates a right-handed peptidoglycan meshwork (old glycan strands in green, newly inserted glycan strands in blue). As more growth takes place, the fraction of right-handed glycan strands increases, and this results in a left-handed twist of the two black spheres at each endcap during elongation.
A longstanding question is the mechanism by which rod-shaped cells elongate only along their longitudinal axis. Although it has been established that MreB is required for this mode of growth, how cells bridge the subcellular scales of MreB filaments and their micron-scale shape has remained unclear. Our recent computational analysis of the consequences of wall insertion from left-handed helical segments revealed that such a pattern could cause a shearing force on the wall that orients the glycan strands in a right-handed fashion (Figure 2) [21]. Much like the opening of a cardboard toilet paper roll along its helical seam, the insertion of new space between this seam results in a twisting of the body that manifests as opposite rotation of the two ends. The handedness of this growth twist is dictated by both the handedness of the insertion pattern and the stiffest direction of the peptidoglycan network. Thus, the orientation of the glycan strands could provide a global template for biasing growth that extends across the entire cell surface.
It is worth noting that some debate exists about the length of MreB polymers in vivo. Biochemical and structural studies indicate that MreB polymerizes, although these studies do not address the length of polymers in live cells [34, 40, 41]. While several in vivo measurements, using either immunolabeling or fluorescent protein fusions, indicate that MreB forms micron-sized filaments [35, 37, 42], other work using different fluorescent fusions has reported a more patchy concentration pattern consistent with short polymers on the order of hundreds of nanometers [43, 44]. Recent electron cryotomography measurements have failed to identify polymers in unlabeled cells, although it is unclear whether this technique has the power to resolve filaments that are very thin or close to the membrane [45]. Interestingly, when overexpressed, chiral filaments of the MreB-YFP N-terminal fusion slightly separated from the membrane can be resolved within tomograms [46], with a left-handedness matching that of a super-resolution study with a similar N-terminal fusion [47] and perhaps revealing that such tagscan stabilize shorter native polymers toelucidate their intrinsic chirality.
Regardless, E. coli cells exhibit twisting during elongation regardless of whether MreB is labeled with a fluorescent protein [21]. Moreover, disruption of MreB by A22 eliminates the growth twisting of E. coli cells and results in walls that lack the cellular-scale right-handed ordering of the glycan strands. Therefore, MreB appears necessary for the cellular-scale phenomenon of chiral growth.
Due to the stochasticity of insertion and heterogeneity in the connectivity of the wall network, the formation of pores during growth is likely unavoidable. While large pores may increase protein import and export across the surface, pores can also represent a significant danger to the cell. During antibiotic treatment, cell lysis typically results from the formation of large pores that permit the cytoplasmic membrane to bleb into the extra cellular environment [4]. A consideration of the competition between the tendency of the membrane to expand through pores due to turgor and the cost of bending a membrane in order to bleb leads to an estimate of a critical pore diameter of ~40 nm [48], the formation of which could result from the unregulated insertion of material leading to heterogeneities in wall density. To establish the minimal requirements for maintenance of rod shape, computational simulations have identified that cells must maintain a uniform distribution of wall insertion along the circumferential direction to avoid the runaway growth of pore sizes in the wall [5]. Spatial patterning by MreB achieves this goal as long as the MreB is sufficiently stiff that it does not passively follow the deformation generated by new wall insertion. In addition, the right-handed glycan ordering generated by a left-handed insertion pattern serves to produce a cell wall with reduced numbers of defects and pores in the peptidoglycan lattice relative to a random pattern. Computational simulations demonstrated that a wide range of distributions of helical fragment insertion patterns coordinating PBPs, including those in which MreB filament length is below the diffraction limit of conventional microscopy, could establish long-range chiral order in the cell wall and effect robust elongation [5, 21, 49]. Thus, the connection between helical MreB filaments and chiral growth is consistent with all imaging data from MreB, including those experiments that find very short filaments.
Recent observations in E. coli and B. subtilis indicate that cell-wall insertion causes the circumferential rotation of MreB relative to the cell wall. This rotation may act to distribute wall insertion across the surface of the cell, ensuring that a relatively small number of MreB polymers can nevertheless produce a robust shape insensitive to fluctuations in insertion pattern or environmental perturbations such as osmotic shock [49]. One outstanding challenge is to determine which aspects of its growth mechanism E. coli has in common with other rod-shaped organisms such as B. subtilis. The cell body in this Gram-positive bacterium was shown to twist in a right-handed fashion, with a similar magnitude to that of E. colisuggesting an underlying chiral growth mechanism [21]. Although some studies have reported a distribution of right-handed helical filaments of MreB in B. subtilis [50], other recent studies have failed to resolve such structures [43, 44], indicating that many filament structures may be below the diffraction limit of visible light.
Chiral growth in plants
Despite the substantial differences in molecular compositions between the cytoskeletons and cell walls of bacteria and plants, there are intriguing physical parallels between their hypothesized growth mechanisms. The plant cell wall differs from the bacterial cell wall in being composed primarily of cellulose, hemicellulose, and pectin, with cellulose being the major constituent and thought to provide the bulk of the tensile strength. Like the bacterial kingdom, the plant kingdom exhibits an enormous variety of modes of growth. These different modes, such as diffuse growth and tip growth, can manifest in different cells of the same organism. Also like bacteria, all of these modes are thought to revolve around the patterning and mechanical relaxation of the wall due to turgor pressure, although they also involve mechanical coupling among cells in a multicellular tissue.
In diffusely growing cells, including the rod-shaped cells of the stem and root axis epidermis, deposition of new cellulose is guided by apparent interactions between cellulose synthase complexes (CSCs) in the plasma membrane and cortical microtubules (Figure 3A) [39]. Existing evidence indicates that CSCs are propelled through the membrane by synthesis of their product [51, 52] and their microtubule guide rails are repositioned dynamically during growth [53, 54]. Thus, the orientation of the cortical microtubule array appears to provide a scaffold that spatially and dynamically orders wall material. Furthermore, the initial positioning of CSCs at the membrane as they are delivered by secretory vesicles is also determined by cortical microtubule organization [55]. As in bacteria, the role of the cortical cytoskeleton appears to be primarily positional; in wild type cells, neither CSC insertion rates into the plasma membrane [55] nor CSC velocities [52, 53] are significantly affected by microtubule disassembly. Dynamic repositioning of both CSC trafficking to the membrane and paths of cellulose deposition by shifting microtubule array organization may allow the cell to control the distribution and degree of uniformity of wall biosynthesis. Finally, cortical microtubule arrays in cells that undergo primarily axial growth show a distinct helical pitch (Figure 3B-D). A wide range of mutations, exemplified by spr1 [56–59], result in the change of this pitch and can also cause twisted growth with opposite chirality, manifested at the level of the multicellular tissue. It has been suggested that such mutations may cause axial twisting in single cells in tissue culture [60], but it remains to be determined if this single-cell twisting also occurs within multicellular tissues.
Figure 3.
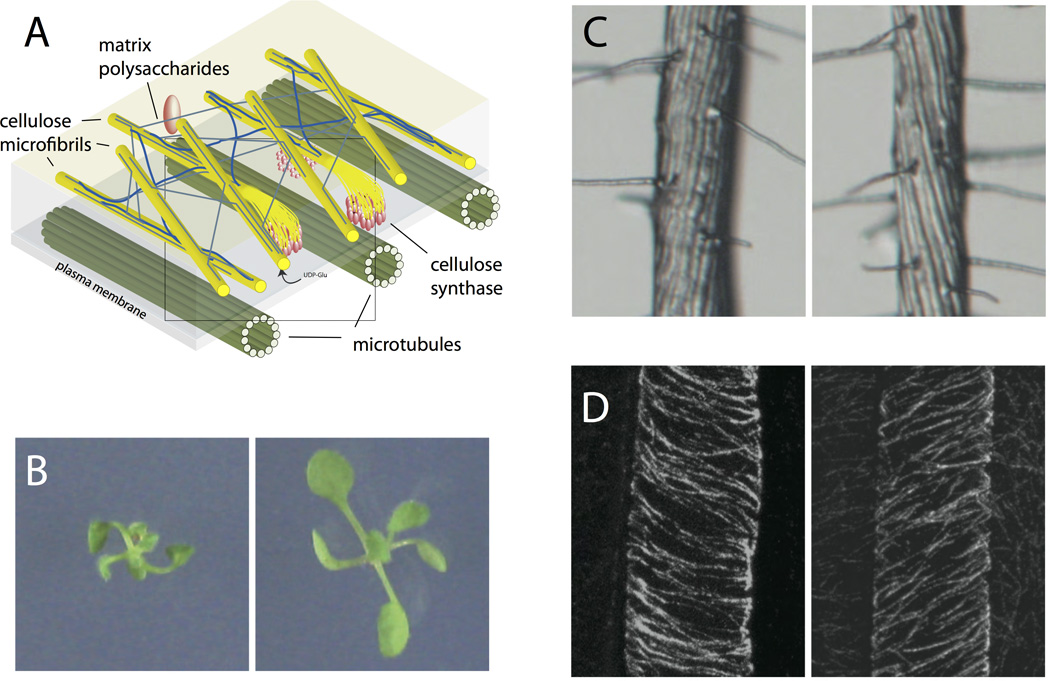
(A) In plant cells, microtubules (green) guide cellulose synthase molecules (red) as they polymerize cellulose microfibrils (yellow). (B) Mutants in the tubulin protein show chiral growth with opposite-handed phenotypes in ten-day-old seedlings. (C) These mutations result in root epidermal cells forming twisted helices. (D) This helical cell morphology is the result of chiral microtubules in the elongating epidermal cells. (B-D adapted from [56])
Discussion
Recent experimental and theoretical work on walled cell growth clearly indicates that spatial patterning of material, perhaps guided by the geometric conformations of polymeric proteins, results in specific cellular shapes. The biological significance of chiral growth with a particular handedness is as yet unclear, though it is intriguing that the genetic sectoring of an expanding E. coli colony adopts a chiral pinwheel pattern at macroscopic scale [61]. However, several intriguing questions are as yet unanswered, largely due to the lack of tools to connect the molecular and cellular scales in living cells. Current implementations of quantitative light microscopy lack the ability to reliably measure and track the locations of multiple proteins in three dimensions relative to a cell’s shape. The development of such 3D tracking systems to measure and correlate the position and motion of proteins such as MreB, the PBPs, and other growth factors will be critical for testing and refining models. Along the same lines, attempts to visualize the organization of the peptidoglycan cell wall at the molecular scale have been largely unsuccessful. New methods that achieve higher resolution, potentially based on averaging of electron microscopy or atomic-force microscopy images, are needed to visualize the structure of walls in cells of different shapes and walls modified either genetically or by drug treatment. Furthermore, significant gaps in our knowledge of how different elements of the growth machinery work together have inhibited our progress in understanding cell shape. New techniques, both in vivo as well as using purified systems in vitro to identify minimal working systems, will also be needed to define a consistent picture of the necessary components of cell shape determination. Finally, wall growth is an incredibly complex problem that incorporates the spatially localized action of many molecular components with concurrent activities, along with the ensuing mechanical effects on the cell envelope. A full understanding of growth will likely require new computational techniques for simulating cellular phenomena using accurate representations of geometry, physics, and chemistry in different cells types.
Acknowledgements
The authors acknowledge assistance from Jen Hsin with graphics, and Carolina Tropini and Russell Monds for careful readings of the manuscript. K.C.H. and J.W.S. acknowledge support from NSF CAREER Awards.
References
- 1.Boal DH. Mechanics of the cell. edn 2nd. Cambridge; New York: Cambridge University Press; 2012. [Google Scholar]
- 2.Holtje JV. Growth of the stress-bearing and shape-maintaining murein sacculus of Escherichia coli. Microbiol Mol Biol Rev. 1998;62:181–203. doi: 10.1128/mmbr.62.1.181-203.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Scheffers DJ, Pinho MG. Bacterial cell wall synthesis: new insights from localization studies. Microbiol Mol Biol Rev. 2005;69:585–607. doi: 10.1128/MMBR.69.4.585-607.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Huang KC, Mukhopadhyay R, Wen B, Gitai Z, Wingreen NS. Cell shape and cell-wall organization in Gram-negative bacteria. Proc Natl Acad Sci U S A. 2008;105:19282–19287. doi: 10.1073/pnas.0805309105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Furchtgott L, Wingreen NS, Huang KC. Mechanisms for maintaining cell shape in rod-shaped Gram-negative bacteria. Mol Microbiol. 2011;81:340–353. doi: 10.1111/j.1365-2958.2011.07616.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Barrett D, Wang TS, Yuan Y, Zhang Y, Kahne D, Walker S. Analysis of glycan polymers produced by peptidoglycan glycosyltransferases. J Biol Chem. 2007;282:31964–31971. doi: 10.1074/jbc.M705440200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Perlstein DL, Wang TS, Doud EH, Kahne D, Walker S. The role of the substrate lipid in processive glycan polymerization by the peptidoglycan glycosyltransferases. J Am Chem Soc. 2010;132:48–49. doi: 10.1021/ja909325m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang TS, Manning SA, Walker S, Kahne D. Isolated peptidoglycan glycosyltransferases from different organisms produce different glycan chain lengths. J Am Chem Soc. 2008;130:14068–14069. doi: 10.1021/ja806016y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Yuan Y, Barrett D, Zhang Y, Kahne D, Sliz P, Walker S. Crystal structure of a peptidoglycan glycosyltransferase suggests a model for processive glycan chain synthesis. Proc Natl Acad Sci U S A. 2007;104:5348–5353. doi: 10.1073/pnas.0701160104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Sliusarenko O, Cabeen MT, Wolgemuth CW, Jacobs-Wagner C, Emonet T. Processivity of peptidoglycan synthesis provides a built-in mechanism for the robustness of straight-rod cell morphology. Proc Natl Acad Sci U S A. 2010;107:10086–10091. doi: 10.1073/pnas.1000737107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cooper S, Denny MW. The relationship of bacterial shape to motility: A conjecture on shape determination in motile, rod-shaped bacteria. FEMS Microbiology Letters. 1997;148:227–231. [Google Scholar]
- 12.Dusenbery DB. Fitness landscapes for effects of shape on chemotaxis and other behaviors of bacteria. Journal of bacteriology. 1998;180:5978–5983. doi: 10.1128/jb.180.22.5978-5983.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cho H, Jonsson H, Campbell K, Melke P, Williams JW, Jedynak B, Stevens AM, Groisman A, Levchenko A. Self-organization in high-density bacterial colonies: efficient crowd control. PLoS biology. 2007;5:e302. doi: 10.1371/journal.pbio.0050302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tropini C, Rabbani N, Huang KC. Physical constraints on the establishment of intracellular spatial gradients in bacteria. BMC Biophys. 2012;5:17. doi: 10.1186/2046-1682-5-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Chen YE, Tropini C, Jonas K, Tsokos CG, Huang KC, Laub MT. Spatial gradient of protein phosphorylation underlies replicative asymmetry in a bacterium. Proc Natl Acad Sci U S A. 2011;108:1052–1057. doi: 10.1073/pnas.1015397108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Huang KC, Ramamurthi KS. Macromolecules that prefer their membranes curvy. Mol Microbiol. 2010;76:822–832. doi: 10.1111/j.1365-2958.2010.07168.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ramamurthi KS, Lecuyer S, Stone HA, Losick R. Geometric cue for protein localization in a bacterium. Science. 2009;323:1354–1357. doi: 10.1126/science.1169218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ramamurthi KS, Losick R. Negative membrane curvature as a cue for subcellular localization of a bacterial protein. Proc Natl Acad Sci U S A. 2009;106:13541–13545. doi: 10.1073/pnas.0906851106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Jiang H, Si F, Margolin W, Sun SX. Mechanical control of bacterial cell shape. Biophysical journal. 2011;101:327–335. doi: 10.1016/j.bpj.2011.06.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Jiang H, Sun SX. Morphology, growth, and size limit of bacterial cells. Physical review letters. 2010;105:028101. doi: 10.1103/PhysRevLett.105.028101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang S, Furchtgott L, Huang KC, Shaevitz JW. Helical insertion of peptidoglycan produces chiral ordering of the bacterial cell wall. Proc Natl Acad Sci U S A. 2012;109:E595–E604. doi: 10.1073/pnas.1117132109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Andrews SS, Arkin AP. A mechanical explanation for cytoskeletal rings and helices in bacteria. Biophys J. 2007;93:1872–1884. doi: 10.1529/biophysj.106.102343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Nizette M, Goriely A. Towards a classification of Euler-Kirchhoff filaments. Journal of Mathematical Physics. 1999;40:2830–2866. [Google Scholar]
- 24.Andrews SS, Arkin AP. A mechanical explanation for cytoskeletal rings and helices in bacteria. Biophysical journal. 2007;93:1872–1884. doi: 10.1529/biophysj.106.102343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Crane HR. Principles and Problems of Biological Growth. The Scientific Monthly. 1950;70:376–389. [Google Scholar]
- 26.Ben-Yehuda S, Losick R. Asymmetric cell division in B. subtilis involves a spiral-like intermediate of the cytokinetic protein FtsZ. Cell. 2002;109:257–266. doi: 10.1016/s0092-8674(02)00698-0. [DOI] [PubMed] [Google Scholar]
- 27.Fu G, Huang T, Buss J, Coltharp C, Hensel Z, Xiao J. In vivo structure of the E. coli FtsZ-ring revealed by photoactivated localization microscopy (PALM) PLoS One. 2010;5:e12682. doi: 10.1371/journal.pone.0012680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Osawa M, Anderson DE, Erickson HP. Curved FtsZ protofilaments generate bending forces on liposome membranes. EMBO J. 2009;28:3476–3484. doi: 10.1038/emboj.2009.277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Sun Q, Margolin W. FtsZ dynamics during the division cycle of live Escherichia coli cells. J Bacteriol. 1998;180:2050–2056. doi: 10.1128/jb.180.8.2050-2056.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Thanedar S, Margolin W. FtsZ exhibits rapid movement and oscillation waves in helix-like patterns in Escherichia coli. Curr Biol. 2004;14:1167–1173. doi: 10.1016/j.cub.2004.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vats P, Rothfield L. Duplication and segregation of the actin (MreB) cytoskeleton during the prokaryotic cell cycle. Proc Natl Acad Sci U S A. 2007;104:17795–17800. doi: 10.1073/pnas.0708739104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Vats P, Shih YL, Rothfield L. Assembly of the MreB-associated cytoskeletal ring of Escherichia coli. Mol Microbiol. 2009;72:170–182. doi: 10.1111/j.1365-2958.2009.06632.x. [DOI] [PubMed] [Google Scholar]
- 33.Cabeen MT, Charbon G, Vollmer W, Born P, Ausmees N, Weibel DB, Jacobs-Wagner C. Bacterial cell curvature through mechanical control of cell growth. EMBO J. 2009;28:1208–1219. doi: 10.1038/emboj.2009.61. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Salje J, van den Ent F, de Boer P, Lowe J. Direct Membrane Binding by Bacterial Actin MreB. Mol Cell. 2011;43:478–487. doi: 10.1016/j.molcel.2011.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bendezu FO, Hale CA, Bernhardt TG, de Boer PA. RodZ (YfgA) is required for proper assembly of the MreB actin cytoskeleton and cell shape in E. coli. EMBO J. 2009;28:193–204. doi: 10.1038/emboj.2008.264. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Shiomi D, Sakai M, Niki H. Determination of bacterial rod shape by a novel cytoskeletal membrane protein. EMBO J. 2008;27:3081–3091. doi: 10.1038/emboj.2008.234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Defeu Soufo HJ, Graumann PL. Dynamic movement of actin-like proteins within bacterial cells. EMBO Rep. 2004;5:789–794. doi: 10.1038/sj.embor.7400209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wang S, Arellano-Santoyo H, Combs PA, Shaevitz JW. Actin-like cytoskeleton filaments contribute to cell mechanics in bacteria. Proc Natl Acad Sci U S A. 2010;107:9182–9185. doi: 10.1073/pnas.0911517107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Paradez A, Wright A, Ehrhardt DW. Microtubule cortical array organization and plant cell morphogenesis. Curr Opin Plant Biol. 2006;9:571–578. doi: 10.1016/j.pbi.2006.09.005. [DOI] [PubMed] [Google Scholar]
- 40.Bean GJ, Amann KJ. Polymerization properties of the Thermotoga maritima actin MreB: roles of temperature, nucleotides, and ions. Biochemistry. 2008;47:826–835. doi: 10.1021/bi701538e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Bean GJ, Flickinger ST, Westler WM, McCully ME, Sept D, Weibel DB, Amann KJ. A22 disrupts the bacterial actin cytoskeleton by directly binding and inducing a low-affinity state in MreB. Biochemistry. 2009;48:4852–4857. doi: 10.1021/bi900014d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kruse T, Bork-Jensen J, Gerdes K. The morphogenetic MreBCD proteins of Escherichia coli form an essential membrane-bound complex. Mol Microbiol. 2005;55:78–89. doi: 10.1111/j.1365-2958.2004.04367.x. [DOI] [PubMed] [Google Scholar]
- 43.Dominguez-Escobar J, Chastanet A, Crevenna AH, Fromion V, Wedlich-Soldner R, Carballido-Lopez R. Processive movement of MreB-associated cell wall biosynthetic complexes in bacteria. Science. 2011;333:225–228. doi: 10.1126/science.1203466. [DOI] [PubMed] [Google Scholar]
- 44.Garner EC, Bernard R, Wang W, Zhuang X, Rudner DZ, Mitchison T. Coupled, circumferential motions of the cell wall synthesis machinery and MreB filaments in B. subtilis. Science. 2011;333:222–225. doi: 10.1126/science.1203285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Swulius MT, Chen S, Jane Ding H, Li Z, Briegel A, Pilhofer M, Tocheva EI, Lybarger SR, Johnson TL, Sandkvist M, et al. Long helical filaments are not seen encircling cells in electron cryotomograms of rod-shaped bacteria. Biochem Biophys Res Commun. 2011;407:650–655. doi: 10.1016/j.bbrc.2011.03.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Swulius MT, Jensen GJ. The helical MreB cytoskeleton in E. coli MC1000/pLE7 is an artifact of the N-terminal YFP tag. J Bacteriol. 2012 doi: 10.1128/JB.00505-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Grotjohann T, Testa I, Leutenegger M, Bock H, Urban NT, Lavoie-Cardinal F, Willig KI, Eggeling C, Jakobs S, Hell SW. Diffraction-unlimited all-optical imaging and writing with a photochromic GFP. Nature. 2011;478:204–208. doi: 10.1038/nature10497. [DOI] [PubMed] [Google Scholar]
- 48.Daly KE, Huang KC, Wingreen NS, Mukhopadhyay R. Mechanics of membrane bulging during cell-wall disruption in gram-negative bacteria. Phys Rev E Stat Nonlin Soft Matter Phys. 2011;83:041922. doi: 10.1103/PhysRevE.83.041922. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Teeffelen Sv, Wang S, Furchtgott L, Huang KC, Wingreen NS, Shaevitz JW, Gitai Z. The bacterial actin MreB rotates and rotation depends on cell-wall assembly. Proc Natl Acad Sci U S A. 2011;108:15822–15827. doi: 10.1073/pnas.1108999108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Daniel RA, Errington J. Control of cell morphogenesis in bacteria: two distinct ways to make a rod-shaped cell. Cell. 2003;113:767–776. doi: 10.1016/s0092-8674(03)00421-5. [DOI] [PubMed] [Google Scholar]
- 51.DeBolt S, Gutierrez R, Ehrhardt DW, Melo CV, Ross L, Cutler SR, Somerville C, Bonetta D. Morlin, an inhibitor of cortical microtubule dynamics and cellulose synthase movement. Proc Natl Acad Sci U S A. 2007;104:5854–5859. doi: 10.1073/pnas.0700789104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.DeBolt S, Gutierrez R, Ehrhardt DW, Somerville C. Nonmotile cellulose synthase subunits repeatedly accumulate within localized regions at the plasma membrane in Arabidopsis hypocotyl cells following 2,6-dichlorobenzonitrile treatment. Plant Physiol. 2007;145:334–338. doi: 10.1104/pp.107.104703. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Chan J, Calder G, Fox S, Lloyd C. Cortical microtubule arrays undergo rotary movements in Arabidopsis hypocotyl epidermal cells. Nat Cell Biol. 2007;9:171–175. doi: 10.1038/ncb1533. [DOI] [PubMed] [Google Scholar]
- 54.Shaw S, Kamyar R, Ehrhardt D. Sustained microtubule treadmilling in Arabidopsis cortical arrays. Science. 2003;300:1715–1718. doi: 10.1126/science.1083529. [DOI] [PubMed] [Google Scholar]
- 55.Gutierrez R, Lindeboom JJ, Paredez AR, Emons AMC, Ehrhardt DW. Arabidopsis cortical microtubules position cellulose synthase delivery to the plasma membrane and interact with cellulose synthase trafficking compartments. Nat Cell Biol. 2009;11:797–806. doi: 10.1038/ncb1886. [DOI] [PubMed] [Google Scholar]
- 56.Ishida T, Kaneko Y, Iwano M, Hashimoto T. Helical microtubule arrays in a collection of twisting tubulin mutants of Arabidopsis thaliana. Proc Natl Acad Sci U S A. 2007;104:8544–8549. doi: 10.1073/pnas.0701224104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Nakajima K, Furutani I, Tachimoto H, Matsubara H, Hashimoto T. SPIRAL1 encodes a plant-specific microtubule-localized protein required for directional control of rapidly expanding Arabidopsis cells. Plant Cell. 2004;16:1178–1190. doi: 10.1105/tpc.017830. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Thitamadee S, Tuchihara K, Hashimoto T. Microtubule basis for left-handed helical growth in Arabidopsis. Nature. 2002;417:193–196. doi: 10.1038/417193a. [DOI] [PubMed] [Google Scholar]
- 59.Sedbrook JC, Ehrhardt DW, Fisher SE, Scheible W-R, Somerville CR. The Arabidopsis sku6/spiral1 gene encodes a plus end-localized microtubule-interacting protein involved in directional cell expansion. Plant Cell. 2004;16:1506–1520. doi: 10.1105/tpc.020644. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Lloyd C, Chan J. Helical microtubule arrays and spiral growth. Plant Cell. 2002;14:2319–2324. doi: 10.1105/tpc.141030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Hallatschek O, Hersen P, Ramanathan S, Nelson DR. Genetic drift at expanding frontiers promotes gene segregation. Proc Natl Acad Sci U S A. 2007;104:19926–19930. doi: 10.1073/pnas.0710150104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.van den Ent F, Amos LA, Lowe J. Prokaryotic origin of the actin cytoskeleton. Nature. 2001;413:39–44. doi: 10.1038/35092500. [DOI] [PubMed] [Google Scholar]