A Finite Element Approach for Modeling Micro-structural Discontinuities in the Heart

Abstract

The presence of connective tissue as well as interstitial clefts forms a natural barrier to the electrical propagation in the heart. At a microscopic scale, such uncoupling structures change the pattern of the electrical conduction from uniform towards complex and may play a role in the genesis of cardiac arrhythmias. The anatomical diversity of conduction structures and their topology at a microscopic size scale is overwhelming for experimental techniques. Mathematical models have been often employed to study the behavior of the electrical propagation at a sub-cellular level. However, very fine and computationally expensive meshes are required to capture all microscopic details found in the cardiac tissue. In this work, we present a numerical technique based on the finite element method which allows to reproduce the effects of microscopic conduction barriers caused by the presence of uncoupling structures without actually resolving these structures in a high resolution mesh, thereby reducing the computational costs significantly.

I. INTRODUCTION

Although cardiac tissue is often considered to be a functional syncytium at a macroscopic size scale, this is not the case at a microscopic size scale, where tissue is made up of discrete cells. Cells are interconnected via gap junctions to facilitate current flow among adjacent cells where coupling is a function of direction, with significantly more gap junctions at the intercalated discs, i.e. the terminal endings of a myocyte along the long axis of the cell, than along the lateral border of a myocyte. The discreteness of the intracellular matrix is reflected in the discontinuous nature of impulse propagation at the microscopic size scale which was demonstrated in numerous studies, both with experimental [1], [2] as well as modeling work [3], [4], [5]. Discontinuous propagation is omnipresent in the heart, even in perfectly healthy tissue, however, at the organ scale discontinuous effects secondary to gap junction coupling are likely to be of lesser relevance, when considering the global dynamics of phenomena such as activation and repolarization sequences or the formation of arrhythmias. However, pathological remodeling processes may lead to a reduction in the number of viable gap junctions or in their phosphorylation state, or to an expansion of interstitial cleft spaces which prevents gap junctions from maintaining functional links with adjacent cells. Such an increase in cleft spaces manifests itself in more pronounced discontinuities in propagation. While cell-to-cell propagation mediated via gap junctions leads to very small delays of some tens of μs and zig-zag propagation patterns at the size scale of some tens of μm, conduction delays due to increased cleft spaces, depending on the severity of remodeling, may be orders of magnitude longer, at the size scale of a few milliseconds, with zig-zag pathways at the order of a few millimeters [5].

In agreement with the syncytial idea, computational models of cardiac electrophysiology at the tissue and organ scale represent the myocardium as a continuum where discontinuities at the microscopic size scale are fully ignored. Most modeling approaches rely on a homogenization procedure [6] where tissue properties are averaged over an ensemble of cells. Spatial discretization is then governed purely by accuracy constraints imposed by the biophysics of a propagating depolarization wavefront, but not by the discrete geometries of myocytes. Such macros-scale continuum approaches are employed to simulate tissue and organ scale phenomena where rather coarse discretizations are preferred to keep the computational load manageable. Therefore any structural discontinuities which are below the chosen spatial resolution of a model remain unaccounted for. Although it is feasible to discretize a whole heart at a paracellular resolution which would allow to explicitly account for fine-scale discontinuities, computational costs may be prohibitive, even when using the most powerful high performance computing facilities available today.

In this study we propose a novel finite element (FE) approach which allows to account for fine-scale structural discontinuities without increasing the spatial resolution to explicitly resolve these structures. Instead, coarser discretizations are used to resolve the macro-structure of the tissue, and finer uncoupling structures which are below the chosen spatial discretization, are projected conformally onto the mesh. Infinitely thin layers of electrical isolation are then enforced along the conformal projections, thus reproducing the barrier effect caused by the structural discontinuities. The feasibility of the approach is demonstrated in simulations of impulse propagation in two-dimensional sheets of cardiac tissue which were derived from high resolution images of histological images.

II. METHODS

In this study we developed a computationally efficient FE formulation for solving the monodomain equations, which is suited for studying discontinuities in impulse propagation at a microscopic size scale. The general idea of the method is to represent microscopic barriers found in the cardiac tissue by infinitely thin insulating lines in the FE mesh. These insulating lines are computed based on high resolution histological images of cardiac tissue, like shown in Fig. 1, and projected onto a coarse mesh by decoupling some of its elements. The decoupling is done via renumbering of nodes shared among adjacent elements along an insulating line, i.e. a node has unique spatial coordinates, but its numbering may differ among neighboring elements. An important aspect of this approach is that the no-flux conditions assumed at the tissue boundaries is implicitly satisfied by the FE formulation. The propagation delay due to the presence of such infinitely thin insulating lines is very similar to the barrier effect caused by the presence of microscopic discontinuous structures, such as interstitial clefts and connective tissue in the cardiac tissue.

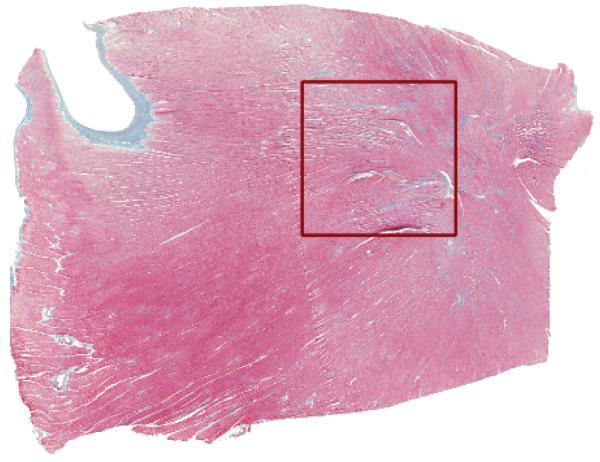
Fig. 1.

High resolution histological image of a tissue slice from the rabbit ventricle. The staining (Masson’s trichrome) resulted in a coloring of cardiac cells (red), connective tissue (blue) and interstitial cleft spaces (white). The region marked by a red square was used for mesh generation.

A. Governing Equations

The dynamics of the processes that underlie the action potential (AP) in a cardiac cell are typically described by a set of ordinary differential equations describing the transmembrane current I_m:

$$I_m=C_m\frac{\partial V_m}{\partial t}+I_{ion}(V_m,\eta )-I_{stim}$$ (1)

$$\frac{d\eta }{dt}=f(t,\eta )$$ (2)

where C_m is the membrane capacitance, V_m is the potential across the cell membrane, I_ion is the density of the total ionic current flowing through the membrane channels, pumps and exchangers, which in turn depends on V_m and on a set of state variables, η, and I_stim is a stimulus current. In this study the cell model presented in [7] is used to simulate the AP of mammalian ventricular myocytes.

In cardiac tissue, the spread of excitation wave can be described by the monodomain formulation:

$$\nabla \cdot (\sigma \nabla V_m)=\beta I_m$$ (3)

where σ is the conductivity tensor with the eigenaxis σ_l and σ_t along and transverse to the preferred axes of the tissue, respectively, and β is the homogenized membrane surface-to-volume ratio.

B. Image Processing

A histological slice from the rabbit ventricle was taken post-experimentum, colored using Masson’s trichrome staining (see Fig. 1) and imaged at high resolution (1000 by 1000 pixels, where each pixel has 12.7μm).

The digitized image was segmented using color clustering and thresholding techniques to distinguish myocardium (red) from connective tissue (blue) and intercellular clefts (white). In order to keep the simulations tractable, only a portion of the histological image, the squared region delineated in Fig. 1, was used to construct the FE meshes in this work (See Fig. 2-A).

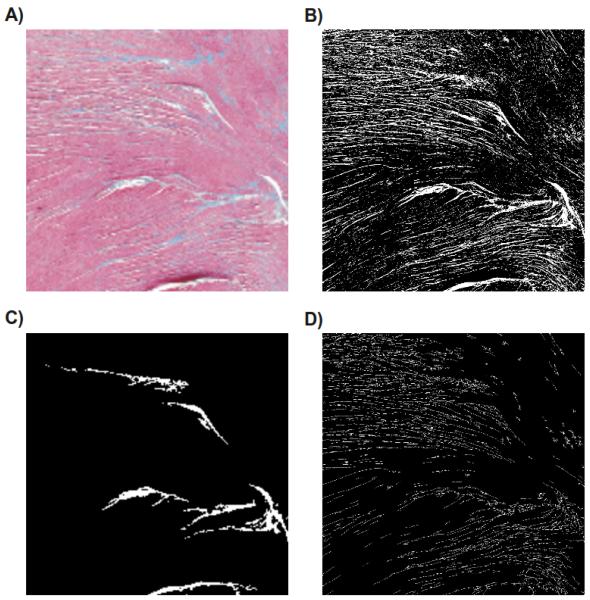
Fig. 2.

(A) Selected section of the high resolution histological image used to built the FE meshes. (B) Results obtained after segmentation of the high resolution image. (C) Segmented image obtained with a reduced resolution. (D) Skeleton computed according to the high resolution segmented image.

The high resolution segmented image shown in Fig. 2-B was subsequently downsampled to (200 by 200 pixels) as can be seen in Fig. 2-C. Note that this reduction in resolution caused a significant loss of information, where all smaller isolating structures present in the high resolution image disappeared. To recover information on morphology and topology of the microstructure, a skeletonization algorithm [8] was applied to the high resolution segmented image to extract the lost information and store it as a skeleton of thin lines. Fig. 2-D presents the results obtained with skeletonization process. Note that the microstructures visible in the high resolution image are now represented as thin lines, except for very small ones which were not accounted for during the skeletonization process (their morphometric features were below a predefined threshold of the number of connected pixels).

C. Mesh Generation

The FE meshes used in this work were generated directly from the segmented histological images [9]. In the process, each pixel segmented as a myocyte was meshed as a two-dimensional quadrilateral element whereas pixels segmented as uncoupling structures (clefts or connective tissue) were not represented in the mesh. In total, three FE meshes of equal size but different resolutions were generated: a reference fine mesh based on the segmentation of the high resolution image (Fig. 2-B), where all microstructural details were retained; and other two coarser meshes based on the lower resolution segmented image shown in Fig. 2-C, where only major uncoupling structures were kept.

The fine and one of the coarse meshes were used as they are to simulate excitation spread in the tissue, whereas an additional processing step was required for the remaining coarse mesh. First, the skeleton extracted at the image processing stage (See Fig. 2-D) was projected onto the coarse mesh. For this sake, the skeleton, defined as a set of edges where each edge is spanned by two nodes, was translated into coordinates which map onto the same space as the coarse FE mesh. Then, the coordinate points describing the skeleton served as input to the algorithm described in Fig. 3. The goal of the algorithm is to decide which nodes of the coarse mesh should be renumbered in order to reproduce the barrier effect caused by the presence of clefts and connective tissue in the cardiac tissue.

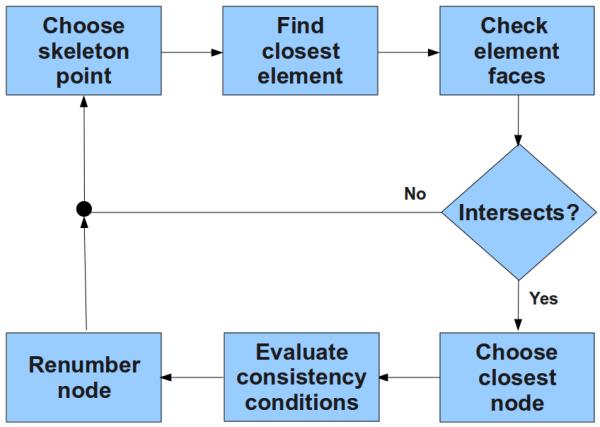
Fig. 3.

Schematic representation of the renumbering algorithm to disconnect nodes of a FE mesh.

The first step of the algorithm consists of selecting a coordinate point of the skeleton and map it onto the coarse mesh in order to find in which element this point is located. The next step is to verify if this point represents a barrier between this element and the neighboring elements. To do so, the algorithm checks if this point intersects one of the faces of this element. If there is an intersection, the closest node to this point is selected to be renumbered in the mesh according to a few conditions that have to be met to guarantee the consistency of the mesh. The output of the algorithm is a list of nodes to be renumbered in the mesh. This list is used then either to directly renumber a mesh, or more elegantly, to be fed into the simulator where nodes are renumbered on the fly, leaving the original mesh untouched.

D. Computer Simulation Protocols

Computer simulations of the excitation spread in a 2D sheet of tissue were performed using the Cardiac Arrhythmia Research Package (CARP) [10] using a single core of an AMD Opteron(tm) 2.2 GHz dual-core processor and 8,GB of RAM running a 64-bit openSUSE Linux system. The orientation of myocyte axes in the intracellular domain, as identified in the segmentation procedure, were considered aligned with the x-axis. Wavefront propagation was initiated by delivering a transmembrane stimulus at the top right corner of the sheet. Three different setups were used: a fine mesh, consisting of 1000 × 1000 quadrilateral elements with an edge length of 10 μm capturing all microstructural details found in the histological image; a coarser mesh, consisting of 200 × 200 quadrilateral elements with an edge length of 50 μm, where only major structures resolved at a lower resolution (see Fig. 2-B); and finally, the same coarse grid was used, but employing the renumbering technique to enforce no-flux boundaries along the infinitely thin insulating lines obtained by the skeletonization process.

III. RESULTS

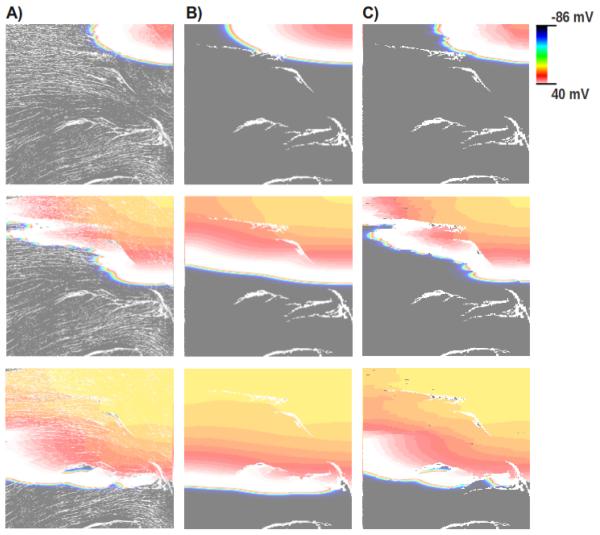
Fig. 4 shows the simulation results obtained with the three different FE meshes at three different time instants. Fig. 4-A shows simulations based on the fine mesh, particularly in the middle panel, significant wavefront fractionation appears as a consequence of the presence of microstructural discontinuities. In contrast, much smoother wavefronts are observed with the coarse mesh due to the absence of the fine structural discontinuities. Only around larger structures some fractionation appeared (Fig. 4-B). Finally, using the same coarse mesh, but using the discontinuous FE technique, both the global activation sequence as well as details of the wavefront morphology appear to be very similar to the results obtained with the fine mesh (see Fig. 4-C).

Fig. 4.

Spatial distribution of the transmembrane potential V_m in all three models at three different time instants (from top to bottom) after the stimulus onset. Results obtained with (A) the fine mesh, (B) the coarse mesh, and (C) applying the discontinuous FE formulation to the coarse mesh.

Moreover, the computational load is significantly reduced. The simulation using the coarse mesh shown in Fig. 4-C lasted about 4 min, while the simulation using the fine mesh took about 290 min to complete. Thus, the proposed technique could reduce the overall execution time by a factor of ~ 70 over the fine setup while capturing all subtle effects of small discontinuous structures on wavefront fractionation.

IV. CONCLUSIONS AND FUTURE WORKS

A. Conclusions

In this work we proposed a new numerical technique based on the FE method which allows to represent the discontinuous effects of uncoupling structures on wavefront propagation in cardiac tissue on a coarse mesh, without the need to use high resolution meshes to explicitly resolve these structures. The presented results clearly demonstrate the potential of the proposed technique. Using this technique, both the overall activation sequence as well as subtle details of wavefront fractionation matched very well with results obtained with the high resolution grid. In addition to that, execution times were reduced significantly, by about a factor of 70, as compared to simulations performed with full spatial resolution.

B. Future Works

In this study the basic principle of the FE approach was shown to represent the effects of fine-scale discontinuous structures on wavefront propagation. In the future this basic concept has to be extended in three ways to be of more general utility: first, in the context of bidomain simulations an additional complexity arises, stemming from the fact that discontinuities exist only in the intracellular space, but not the interstitial space. Consequently, the nodal renumbering approach has to be employed only to the intracellular grid, but not the extracellular/interstitial grid. Therefore, around renumbered nodes there is no one to one relationship between nodal points belonging to intracellular and extracellular grid, requiring a more elaborate procedure when assembling the right hand side of the elliptic portion of the bidomain equations. Secondly, although results were demonstrated in a two-dimensional tissue sheet, the basic concept extends straight forwardly to three dimensions, albeit the preprocessing stages, mainly skeletonization, projections of the skeleton onto a 3D grid, and identifying the nodes for renumbering is more challenging. Further, to allow smoother representations of structural discontinuities, the information on skeleton topology may be used for generating unstructured meshes where meshes are spatially refined in the vicinity of the uncoupling structures. Finally, nodal pairs which arose in the process of renumbering may be reconnected to simulate the effect of non-myocytes such as fibroblasts [11] which may be expressed in cleft regions which are filled with connective tissue. This is equivalent to modeling the effect of very thin layers of fibroblast in a three dimensional myocardium.