Three-dimensional flow contrast imaging of deep tissue using noncontact diffuse correlation tomography

Abstract

This study extended our recently developed noncontact diffuse correlation spectroscopy flowmetry system into noncontact diffuse correlation tomography (ncDCT) for three-dimensional (3-D) flow imaging of deep tissue. A linear array of 15 photodetectors and two laser sources connected to a mobile lens-focusing system enabled automatic and noncontact scanning of flow in a region of interest. These boundary measurements were combined with a finite element framework for DCT image reconstruction implemented into an existing software package. This technique was tested in computer simulations and using a tissue-like phantom with anomaly flow contrast design. The cylindrical tube-shaped anomaly was clearly reconstructed in both simulation and phantom. Recovered and assigned flow contrast changes in anomaly were found to be highly correlated: regression slope = 1.00, R² = 1.00, and p < 10⁻⁵ in simulation and regression slope ≥ 0.97, R² ≥ 0.96, and p < 10⁻³ in phantom. These results exhibit promise of our ncDCT technique for 3-D imaging of deep tissue blood flow heterogeneities.

Blood flow distribution in tissues can provide vital information to healthcare professionals including clinicians and research investigators. Alterations in blood flow may result, for example, in regions of tissue presenting with ischemia and hypoxia. These abnormalities are associated with and help characterize many diseases including pressure ulcers, stroke, and cancer. Furthermore, blood flow contrast imaging can assist in applications such as cancer diagnosis and therapy monitoring.¹ Near-infrared diffuse correlation spectroscopy (DCS) has emerged as a highly advantageous blood flow monitoring modality through inherent noninvasiveness, safe application, portability, deep tissue probing (up to several cm), and relative affordability.^{1, 2, 3, 4} Most DCS systems employ contact-based interaction with the sample. However, in tissues, contact measurements can promote hemodynamic variations induced by compression or disturb sensitive areas. We have recently developed a noncontact DCS system that uses a lens-focusing technique to circumvent these influences.^{2, 4}

Despite advances in DCS applicability there have been limited tomographical imaging realizations. A few studies involving three-dimensional (3-D) diffuse correlation tomography (DCT) have been performed with tissue-like phantoms, computer simulations, and in vivo rat brain.^{5, 6, 7} An early contact-based approach was applied to phantoms,⁵ but is disadvantaged in vivo as described previously. Very few noncontact-based DCT examinations have been conducted as well. In these, lenses were positioned between a sample and optical fiber grid connected to light and detection elements.^{6, 7} These arrangements, however, were only tested on small animals with limited source-detector (S-D) separations ranging from ∼2 to 10 mm. Flexibility is minimal and expense increases with the scaling of the region of interest (ROI). Another limitation of these studies is reliance on analytical solutions assuming a simple semi-infinite geometry and strict heterogeneities (e.g., spherical) of tissue which precludes the transition to complex boundaries and imperfect heterogeneities. Complications would also become apparent in accommodating complex boundaries with numerous S-D fibers. Furthermore, in testing these types of systems, the imitation of flow contrast changes often relies on solid phantoms (no flow) embedded in liquid phantoms (Intralipid; Brownian particle motion) or the converse case. This method lacks elegance due to the restrictively static nature of the components once prepared, specifically the solid phantom material. The current study seeks to remedy many of these concerns. First, we extended our noncontact DCS system^{2, 4} to noncontact DCT (ncDCT) using a motorized stage for automated and customizable ROI scanning capabilities. Next, a finite-element-method (FEM) based facilitation of DCT image reconstruction was accomplished through integration into an open software package for diffuse optical spectroscopy/tomography (DOS/DOT) termed NIRFAST.⁸ Finally, validation efforts included computer simulations and a phantom testing design allowing flow variations.

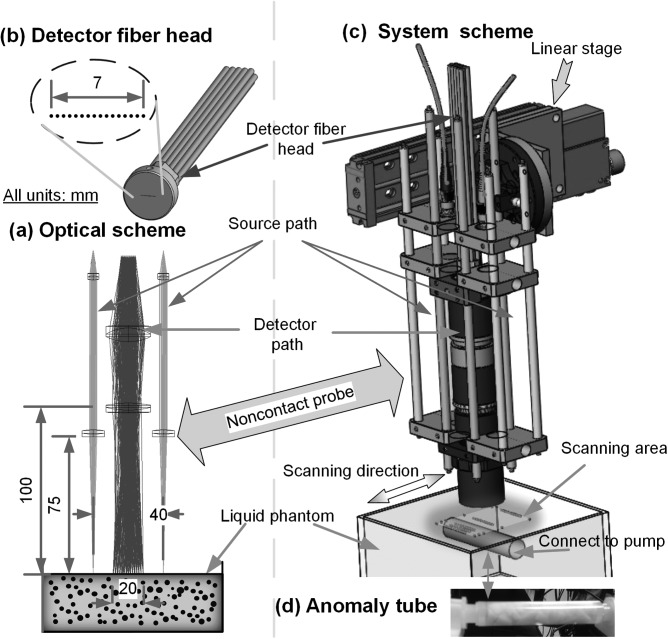
Extending DCS into DCT attaches the burden of collecting many boundary measurements. As such, our noncontact probe was upgraded to have two identical laser source paths and one detector path (Fig. 1a) doubling our previous number of available S-D pairs. In each source path, output from a multimode fiber (WF200/220/245, CeramOptec, MA, USA) connected to a laser was projected onto the tissue phantom surface through lenses.^{2, 4} The detector fiber head (Fig. 1b) in the detector path contained 15 single-mode fibers (SM800-5.6-125, Fibercore, CA, USA) equally arranged in a 7 mm line covering a 20 mm range through lenses at 100 mm working distance. The resulting S-D separations were in the span of 10 to 30 mm, thus allowing up to ∼15 mm penetration depth.¹ Instrument operation involves two 825 nm long coherence lasers (coherence length > 5 m, CrystaLaser, NV, USA) emitting photons to tissue through individual source paths alternatively. The photons traveling through the sample are collected by a detector array of 15 avalanche photodiodes (APD, Perkin Elmer, Canada) through the detector path. A multiple channel autocorrelator (Correlator.com, NJ, USA) takes the APD outputs and simultaneously calculates the correlation functions for the 15 S-D pairs per source.³ Another significant improvement was the integration of a motorized stage for automatic and precise ROI scanning (Fig. 1c) through probe translation. Either rotational or linear motion staging is available to maximally fit the subject geometry (e.g., breast shape or slab shape). This design feature enables large ROI coverage and flexible S-D arrangements without greatly increasing hardware requirements and costs (e.g., fibers, APDs, and correlators). In this study, the ncDCT modality was motivated by the linear stage (T-LSM200A, Zaber, Canada).

Figure 1.

Illustration of (a) the ncDCT focusing apparatus with photon projections to and from a sample, (b) linear array of single-mode detector fibers, (c) motorized staging over a representative ROI, and (d) the pump-connected cylindrical tube-shaped anomaly.

In DOS theory, the detected photon fluence rate $\Phi \left(\mathit{r},\omega \right)$ in highly scattering media such as biological tissue obeys the frequency-domain (FD) diffusion equation⁸

$$\nabla \cdot \left(\left(\frac{D\left(\mathit{r}\right)}{\mathrm{v}}\right)\nabla \Phi \left(\mathit{r},\omega \right)\right)-\left({\mu }_a\left(\mathit{r}\right)+\frac{i\omega }{v}\right)\Phi \left(\mathit{r},\omega \right)=-S\left(\mathit{r},\omega \right),$$ (1)

where r is the position vector and v is the light speed in the medium. ${\mu }_a\left(\mathit{r}\right)$ is the medium absorption coefficient, and $D(\mathit{r})\approx v/3{\mu }_s^{\prime }\left(\mathit{r}\right)$ is the medium photon diffusion coefficient where ${\mu }_s^{\prime }\left(\mathit{r}\right)$ is the medium reduced scattering coefficient. $S\left(\mathit{r},\omega \right)$ is the isotropic source term modulated at angular frequency ω. Our measurements use a point source continuous-wave (CW) approach ($\omega =0$). In DCS theory, focus is on the unnormalized electric field autocorrelation function, $G_1\left(\mathit{r},\tau \right)=\mathit{E}\left(\mathit{r},t\right){\mathit{E}}^{*}\left(\mathit{r},t+\tau \right)$, obeying a formally similar diffusion equation (CW) to DOS⁵

$$\nabla \cdot \left(\left(\frac{D\left(\mathit{r}\right)}{\mathrm{v}}\right)\nabla G_1\left(\mathit{r},\tau \right)\right)-\left({\mu }_a\left(\mathit{r}\right)+\frac{1}{3}{\mu }_s^{\prime }\left(\mathit{r}\right)k_0^2\alpha ⟨\Delta r^2\left(\tau \right)⟩\right)G_1\left(\mathit{r},\tau \right)=-S\left(\mathit{r}\right)e^{i\left(2\pi \tau c/\lambda \right)},$$ (2)

where τ is the autocorrelation delay time, c is the speed of light in vacuum, and λ is the wavelength. In practice, only the modulus is considered with the right-hand side then resembling Eq. 1 in CW form (i.e.,$-S\left(\mathit{r}\right)$). We propose to next write ${\mu }_a^d\left(\mathit{r},\tau \right)=\frac{1}{3}{\mu }_s^{\prime }\left(\mathit{r}\right)k_0^2\alpha ⟨\Delta r^2\left(\tau \right)⟩$, having the same unit as ${\mu }_a\left(\mathit{r}\right)$ and stemming from the common referral to $\frac{1}{3}{\mu }_s^{\prime }\left(\mathit{r}\right)k_0^2\alpha ⟨\Delta r^2\left(\tau \right)⟩$ as the “dynamic absorption” of correlation with delay time τ due to dynamic processes.⁵$k_0$ is the wave number of the incident light field. α is the unitless ratio of dynamic scatterers to total (dynamic and static) scatterers. $⟨\Delta r^2\left(\tau \right)⟩$ is the mean-square displacement in time τ of the moving scattering particles (e.g., red blood cells); for the case of diffuse motion, $⟨\Delta r^2\left(\tau \right)⟩=6D_B\left(\mathit{r}\right)\tau$ where $D_B\left(\mathit{r}\right)$ (unit: ${\text{cm}}^2/\mathrm{s}$) is an effective diffusion coefficient of the moving scatterers. Thus, we redefine the dynamic absorption to ${\mu }_a^d\left(\mathit{r},\tau \right)=2{\mu }_s^{\prime }\left(\mathit{r}\right)k_0^2\alpha D_B\left(\mathit{r}\right)\tau$. The combined term $\alpha D_B\left(\mathit{r}\right)$ is referred to as the blood flow index in tissues and can be extracted by fitting the analytical solution of Eq. 2.^{1, 3}

The extension of DCS to DCT is comparable to that of DOS to DOT which images optical property contrast based on Eq. 1 and its inverse solution (i.e., image reconstruction).⁷ Proper algorithms for the forward/inverse solutions to Eq. 2 can therefore be employed to reconstruct flow index contrast. The FEM framework has been applied to model light transportation in comprehensive diffuse media to resolve the geometry and heterogeneity limitations for DOS/DOT.⁸ Exploiting the high mathematical similarity of the forward and inverse problems (e.g., boundary condition and mathematical assumptions) between DOS (Eq. 1) with CW source and DCS (Eq. 2), we report the application of FEM in DCS/DCT. We introduced this concept into the FEM based light transport and image reconstruction modules from NIRFAST⁸ as a shortcut for FEM implementation. DCT then can be conceptualized as a formulation of DOT which with CW computes $G_1\left(\mathit{r},\tau \right)$ instead of $\Phi \left(\mathit{r},\omega \right)$, by updating ${\mu }_a\left(\mathit{r}\right)$ to ${\mu }_a\left(\mathit{r}\right)+{\mu }_a^d\left(\mathit{r},\tau \right)$, and reconstructs ${\mu }_a\left(\mathit{r}\right)+{\mu }_a^d\left(\mathit{r},\tau \right)$ instead of ${\mu }_a\left(\mathit{r}\right)$ only. The correlation function can be simulated using multiple delay times and combining all $G_1(\mathit{r},\tau )$ along the time sequence τ. Reconstructed ${\mu }_a\left(\mathit{r}\right)+{\mu }_a^d\left(\mathit{r},\tau \right)$ then enables extracting the flow index $\alpha D_B\left(\mathit{r}\right)$ through the definition of ${\mu }_a^d\left(\mathit{r},\tau \right)$. As a result, the realm of DCT becomes available for comprehensive imaging under arbitrary geometries and optical properties. For brevity, the position vector r is implied hereafter.

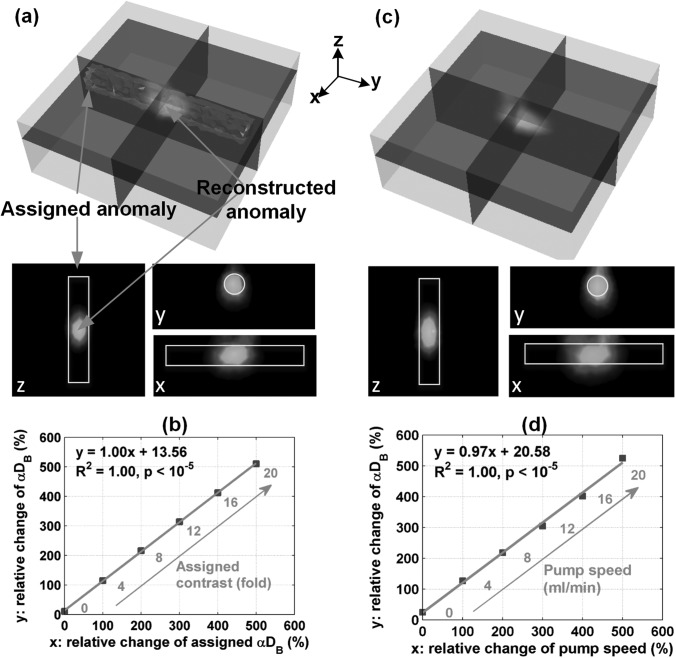
To test our theoretical DCT technique through computer simulations, we first evaluated forward solution accuracy in a homogeneous situation (i.e., no anomaly). A slab mesh [dimension (mm): 90 (H) × 90 (W) × 35 (D)] was generated with total node number 73 949 simulating liquid phantom solution in a slab shaped container (e.g., aquarium). Optical properties were set throughout at ${\mu }_s^{\prime }=$  8.00 cm⁻¹ and ${\mu }_a=$  0.045 cm⁻¹ close to breast tissue values.⁹ The slab flow indices $\left(\alpha D_B\right)$ were set close to Intralipid phantom values^{5, 10} at 1 × 10⁻⁸ cm²/s and correspond to the background tissue. As shown in Fig. 1c, the noncontact probe was scanned linearly (mimicked in simulation) across the ROI in 15 steps with an increment of 4 mm/step generating a scanning area of 40 mm × 56 mm and 450 (15 steps × 15 APDs × 2 sources) effective S-D pairs. The forward solution (i.e.,$\hspace{0.17em}{G}_1(\hspace{0.17em}\tau )$) was calculated by the modified NIRFAST with τ from 0 to 8 × 10⁻⁶ s. Minimal simulation aberrations over the measured ROI (1% mean discrepancy and 1.45% standard deviation) were observed between $\alpha D_B$ extracted using the established semi-infinite analytical solution² of Eq. 2 and the assigned$\hspace{0.17em}\alpha D_B$. With the forward solution verified, the next simulation embodied recovery of an anomalous presence and subsequent contrasts. A cylindrical tube-shaped anomaly [dimension (mm): 13 (Dia.) × 80 (L)] was inserted beneath the middle of the ROI with a depth of 12.5 mm from the tube center to the ROI surface. The anomaly optical properties (i.e., ${\mu }_a\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}{\mu }_s^{\prime })$ were matched to the background tissue. The attributed anomaly $\alpha D_B$ was varied with contrast ranging from 0, 4, 8, 12, 16, and 20 times of the background (1 × 10⁻⁸ cm²/s). Reconstruction was conducted on a second mesh with coarse finite element division (node number: 11 025) and the same optical properties. The delay time $\tau =3.2$× 10⁻⁶ s was used to calculate ${\mu }_a^d\left(\tau \right)$. Due to limited ROI dimensions along the tube, only partial anomaly reconstruction was possible (Fig. 2a). For percentage flow change comparison, the reconstructed anomaly peak flow value was normalized to the averaged step differences of $\alpha D_B$. Both the shape (Fig. 2a) and relative anomaly flow contrast changes (Fig. 2b) were well reconstructed (regression slope = 1.00, R² = 1.00, and p < 10⁻⁵). We also used a half maximum threshold to segment the anomaly and then calculated its mean flow value. An excellent linear relationship was also observed between the reconstructed and assigned percentage flow changes (data are not shown; regression slope = 1.00, R² = 1.00, and p < 10⁻⁵). To evaluate the errors in depth reconstruction (localization) of the anomaly and their dependence on the size of anomaly, we performed supplementary simulations using the existing tube and a smaller tube [6 (Dia.) mm × 80 (L) mm]. The anomaly central depth was varied up to ∼16.5 mm beneath the surface. The reconstructed central depths of the tube anomalies and the relative changes of flow index contrasts were accurate when the assigned anomaly was localized in the sensitive region of light diffusion (i.e., anomaly central depth ≤ 12.5 mm; data are not shown). These simulation results demonstrated the robustness of the proposed FEM-based ncDCT technique.

Figure 2.

Results of computer simulation and phantom experiment utilizing a homogeneous slab background and internally placed tube-shaped anomaly of varied flow contrast. The reconstructed anomaly from the last step with highest flow contrast is shown (a) 3-D overlaid on the assigned anomaly and two-dimensional cross-section views (x, y, z) in the simulation and (c) in the phantom experiment. Both (b) and (d) show a linear relationship between the assigned anomaly and reconstructed flow indices expressed as ratios of relative changes respectively in the simulation and phantom experiment. 3-D data are displayed with open source visualization software ParaView (Kitware, NY, USA).

We next validated the developed system in practical object measurements by phantom experimentation. A background of liquid phantom was placed in an aquarium (Fig. 1c) and a pump-connected cylindrical tube anomaly was filled with liquid and small pieces of solid phantom (Fig. 1d). The tissue-like liquid phantom comprised Intralipid, distilled water, and India ink and has been used extensively for DCS calibrations.⁴ Intralipid particles (Fresenius Kabi, Sweden) provide control of scattering (${\mu }_s^{\prime }$) and Brownian motion ($D_B$; $\alpha \approx$1) while India ink controls absorption (${\mu }_a$). We set ${\mu }_s^{\prime }$ and ${\mu }_a$, respectively, at 8.10 cm⁻¹ and 0.044 cm⁻¹ while quantifying them with a FD tissue-oximeter (Imagent, ISS, IL, USA).¹¹ To create flow index contrasts against the background, a clear plastic tube [dimension (mm): 13.5 (Dia.) × 80 (L)] with a very thin wall (0.35 mm) was placed at ∼12.5 mm (tube center to ROI surface) into the background liquid phantom (Fig. 1). The tube was mostly filled with small pieces of solid phantom (${\mu }_s^{\prime }=10.00$  cm⁻¹ and ${\mu }_a=$ 0.10 cm⁻¹) to randomize pumped particle motions as Brownian motion and generate a diffusive circumstance for photons. Solid phantoms comprised titanium dioxide, silicon, and carbon black. A peristaltic pump (HV-77201-60, Cole Parmer, IL, USA) connected in series with a hydraulic capacitor that damped fluid pulsations was employed to create step increases in steady flow from 0 to 20 ml/min at 4 ml/min increments within the tube. The high percentage of solid components (no particle motion therein) made the flow index in the tube close to 0 when no flow motivation was induced by the pump. The noncontact probe was first calibrated to the homogeneous liquid phantom region to unify ${\alpha D}_B$ measurement for each S-D separation. The scanning procedure was linear as assumed in simulations. Total scanning time was ∼20 min with 60 s sampling time per step at 0.5 Hz DCS sampling rate for each laser. For each S-D pair, the interval average (60$\hspace{0.17em}\times$ 0.5 = 30 points) represents the corresponding boundary measurement for that step. We used identical reconstruction parameters as the simulation including slab mesh and delay time τ with the exception of a median filter application. This latter addition assisted in stabilizing inherent experimental noise not encountered in the ideal simulation.⁸ The relationship between macro pumped flow (unit: ml/min) and micro particle motion ($\alpha D_B$ unit: cm²/s) is complicated, but was confirmed linear.¹² For this case, the assigned flow represents the macro flow (pump speed) rather than DCS indices. In Fig. 2d, relative macro and micro flow changes were presented in the same way used in simulation. A tube-shaped anomaly was clearly recognizable after image reconstruction (Fig. 2c). The reconstructed flow indices accurately captured the flow changes in the tube when quantified with the peak value (Fig. 2d; linear regression slope = 0.97, R² = 1.00, and p < 10⁻⁵) and with the mean of segmented anomaly (data are not shown; linear regression slope = 0.99, R² = 0.96, and p < 10⁻³). The liquid phantom system provided both a circumstance of complex dynamic particles and changes of particle motion and possesses the potential for easily updating tissue properties in both the background and the anomaly.

In the simulations and phantom tests, we note that no optical property mismatch between anomaly and background was induced, i.e., $\Delta {\mu }_s^{\prime }=0$ and $\Delta {\mu }_a=0$. Our previous studies have revealed that the mismatch of ${\mu }_a$ and ${\mu }_s^{\prime }$ resulted in estimation errors of DCS flow index.¹⁰ To evaluate these influences on ncDCT, we carried out supplementary computer simulations and phantom experiments; the optical properties of background or anomaly were changed to create ${\mu }_a$ and ${\mu }_s^{\prime }$ contrasts. We found that inaccurate ${\mu }_s^{\prime }$ assumptions resulted in much greater flow index contrast errors than inaccurate μ_a, which are consistent with our previous findings.¹⁰ Nevertheless, the relative changes of reconstructed flow index contrasts over a large range of property contrast variations (2- to 3-fold) were accurately reconstructed even with the incorrect assumptions of optical properties (data are not shown). The problem of modeling such heterogeneity can be solved by combining DCT with other FD or time-domain DOT imaging instruments. To our advantage, the FEM-based implementation software proposed is fully capable of incorporating such arbitrary heterogeneities.

Previous DCT studies emphasized assigning a selective delay time τ to each S-D pair based on the analytical or approximate solution of Eq. 2 which relies on simple geometry and optical properties as mentioned above.⁶ By contrast, we propose to use a uniform τ. From the view of ${\mu }_a^d\left(\tau \right)$, assigning uniform τ unifies the ${\mu }_a^d\left(\tau \right)$ on the same time scale such that τ does not generate extra ${\mu }_a^d\left(\tau \right)$ contrast. τ (3.2 × 10⁻⁶ s) was selected in this study based on a few simulations and exhaustive sensitivity optimization has not yet been completed. Specifically, we selected several small τ values ($\tau \le 1.9\times {10}^{-5}$s) from the entire range (generally from $1.0\times {10}^{-7}$ to $1.0\times {10}^{-3}$ s) to reconstruct flow contrasts in computer simulations for comparisons. The variations in the mean values and regression slopes of flow index contrasts reconstructed with different τ were found to be $5\pm 10\%$ and <$\hspace{0.17em}5\%$, respectively (data are not shown), indicating the robustness of ncDCT method in this range. Note that large τ (e.g., $>\hspace{0.17em}1.9\times {10}^{-5}$s) may lead to unstable results in reconstructed flow indices. Based on the definition of dynamic absorption ${\mu }_a^d$(τ) in Eq. 2, a large τ may result in an effective absorption (${\mu }_a$+ ${\mu }_a^d$(τ)) greater than the normal range of tissue absorption, thus influencing the stabilities of forward and inverse solutions in NIRFAST. A good τ selection is complicated by considerations such as the occurrence of any weight distinctions or redundancies between equations generated by different$\hspace{0.17em}\tau$. This may be especially true when the flow contrast of the imaging anomaly differs greatly. Furthermore, recruiting multiple τ (assemble more equations at different time scales for each S-D pair) may promote robustness in solving an ill-posed inverse problem. These questions will be investigated in the future.

In conclusion, we reported a ncDCT system for 3-D flow contrast imaging. A FEM framework was introduced to simulate temporal electric field autocorrelation diffusive transport and reconstruct spatially distributed flow contrasts. The imaging capability of flow contrasts was validated through both simulations and phantom experimentation. We tested the ncDCT system on a simple semi-infinite geometry herein, but by incorporating other imaging modalities (e.g., MRI and photogrammetric scanning) arbitrary geometry can be obtained. The noncontact breakthrough design enables potential imaging of deep blood flow contrast in real human tissues (e.g., breast tumor, pressure ulcer) without distorting hemodynamic properties.