Deriving adaptive MRF coefficients from previous normal-dose CT scan for low-dose image reconstruction via penalized weighted least-squares minimization

Abstract

Purpose: Repeated computed tomography (CT) scans are required for some clinical applications such as image-guided interventions. To optimize radiation dose utility, a normal-dose scan is often first performed to set up reference, followed by a series of low-dose scans for intervention. One common strategy to achieve the low-dose scan is to lower the x-ray tube current and exposure time (mAs) or tube voltage (kVp) setting in the scanning protocol, but the resulted image quality by the conventional filtered back-projection (FBP) method may be severely degraded due to the excessive noise. Penalized weighted least-squares (PWLS) image reconstruction has shown the potential to significantly improve the image quality from low-mAs acquisitions, where the penalty plays an important role. In this work, the authors' explore an adaptive Markov random field (MRF)-based penalty term by utilizing previous normal-dose scan to improve the subsequent low-dose scans image reconstruction.

Methods: In this work, the authors employ the widely-used quadratic-form MRF as the penalty model and explore a novel idea of using the previous normal-dose scan to obtain the MRF coefficients for adaptive reconstruction of the low-dose images. In the coefficients determination, the authors further explore another novel idea of using the normal-dose scan to obtain a scale map, which describes an optimal neighborhood for the coefficients determination such that a local uniform region has a small spread of frequency spectrum and, therefore, a small MRF window, and vice versa. The proposed penalty term is incorporated into the PWLS image reconstruction framework, and the low-dose images are reconstructed via the PWLS minimization.

Results: The presented adaptive MRF based PWLS algorithm was validated by physical phantom and patient data. The experimental results demonstrated that the presented algorithm is superior to the PWLS reconstruction using the conventional Gaussian MRF penalty or the edge-preserving Huber penalty and the conventional FBP method, in terms of image noise reduction and edge/detail/contrast preservation.

Conclusions: This study demonstrated the feasibility and efficacy of the proposed scheme in utilizing previous normal-dose CT scan to improve the subsequent low-dose scans.

INTRODUCTION

Low-dose computed tomography (CT) is desirable due to the growing concerns about excessive radiation exposure in clinic,¹ especially for applications in image-guided intervention where repeated scans are required and the subsequent accumulated radiation dose could be significant. For instance, CT is used in a cine mode to guide a needle for lung nodule biopsy, where up to ten scans may be performed on the same regions. One simple and cost-effective way to reduce the radiation dose is to lower the x-ray tube current and/or shortening the exposure time (mAs) or the x-ray tube voltage (kVp) in repeated CT scans, but the resulted image quality from the conventional filtered back-projection (FBP) image reconstruction algorithm may be degraded due to the excessive noise, which makes the repeated low-dose CT scans a less attractive option for image-guided intervention.

Many methods^{2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17} have been proposed to improve the reconstruction of low-mAs scanned data. Although the filter based algorithms^{2, 3, 4} are computationally efficient and can suppress the noise to some extent, they often sacrifice structural details which could be critical, due to a lack of noise modeling in the filtration. Statistical iterative reconstruction (SIR) algorithms,^{5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17} which take into account of statistical properties of the data, have been shown to be superior in suppressing noise and streak artifacts. A typical SIR algorithm formulates a cost function in a statistical sense and then derives a corresponding algorithm, frequently in iterative manner, to minimize the cost function for image reconstruction. The cost function usually consists of two terms: (i) a data-fidelity term, which models the statistics of the acquired data and (ii) a penalty term, which regularizes the data-fidelity term for a desired solution. The penalty term in the cost function plays a critical role for successful image reconstruction.^{10, 11, 12, 13, 14, 15} One established family of the penalties is based on the Markov random field (MRF) model,¹⁸ which describes the statistical distribution of a voxel given its neighbors. The MRF-based penalties generally relay on voxel values within a small fixed neighborhood, e.g., a 3 × 3 window in two-dimensional (2D) case, and usually give equal weighting coefficients for neighbors of equal distances from the central one without considering structure information in the local region. A quadratic functional form, which corresponds to a Gaussian MRF model, has been widely used.^{5, 9, 12} A variation of this established penalty family takes nonquadratic forms, which adjust their functional forms to penalize less on large differences among neighboring voxels while maintaining a similar penalty on small differences, compared to the quadratic form, aiming to achieve a better edge preservation.^{19, 20, 21, 22} But the reconstruction results could be sensitive to the choice of “transition point” (or edge threshold) which controls the shape of the functional form, because the edges in an image are unlikely to be determined by a single value.²¹ In addition, the variation makes the cost function nonquadratic and could result in computational complexity.¹¹ An alternative variation of the established penalty family takes nonequal weighting coefficients for neighbors of equal distances from the central one, e.g., making the coefficients dependent on the image intensity difference.¹¹ While some gains were observed, it is still limited because the intensity difference between two voxels does not reflect the whole picture of the local region. This study aims to take the whole local region into consideration while retaining the computational advantages of the quadratic functional form.

In the applications with repeated CT scans, previous scan can be exploited as prior information due to the similarity among the reconstructed image series of the scans. These scans generally contain the same anatomical structures. While somewhat misalignment and/or deformation may occur among the image series, they can be mitigated through registration of the image series and/or modeling the effects in constructing the cost function. Using the reconstruction from previous normal-dose scan to improve the follow-up low-dose scan reconstructions has become a research interest recently.^{23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33} For instance, Yu et al.²³ proposed a previous scan-regularized reconstruction (PSRR) method for perfusion CT imaging by replacing the unchanged regions of the low-dose CT image with the corresponding embodiments in the previous normal-dose reconstruction and employing a nonlinear noise filtration in the remaining regions. Ma et al.²⁴ and Xu and Muller²⁵ investigated restoration on the low-dose CT images with the help of the previous normal-dose image via the nonlocal means (NLM) noise filtration algorithm. The above efforts also explored the use of the previous scan as a penalty for regularized iterative image reconstructions. For instance, the studies^{27, 28} incorporated a prior image (averaging over FBP reconstructions from different time frames) as a penalty into their prior image-constrained compressed sensing (PICCS) framework for time-resolved sparse-view CT reconstruction. Tian et al.³⁰ presented a temporal NLM regularization for low-dose 4D dynamic CT reconstruction, where the reconstruction of the current frame image utilizes the previous iteration results of the two neighboring frames. Ma et al.³¹ proposed a low-mAs perfusion CT image reconstruction method by incorporating a previous normal-dose unenhanced image into the regularization term for the subsequent reconstruction of the low-dose enhanced CT images. Recently, Wang et al.³⁴ explored the potential of using a high quality image to estimate the MRF weighting coefficients for penalized reconstruction of its corresponding image from noisy (or low-dose) data. They exploited an 11 × 11 MRF window and estimated the MRF weighting coefficients from a high-quality bone-region sample image, and then incorporated the single set of MRF coefficients into an iterative CT reconstruction framework to preserve details in the bone structures. Inspired by this recent work, this study aims to incorporate a previous normal-dose CT scan into the quadratic functional form, while considering adaptively the entire local region for the MRF weighting coefficients, for the purpose of reconstructing the subsequent low-dose CT images. In this way, both the MRF window size and the corresponding coefficients are adaptively estimated for better reflection of the prior information in both space and frequency domains. Thus, it is expected that with the proposed penalty term from the previous normal-dose scan, the reconstruction from the follow-up low-dose scans will be substantially improved.

The remainder of this paper is presented as follows. In Sec. 2, we illustrate our SIR framework and our design of the penalty term based on the previous normal-dose scan. Section 3 validates the performance of our proposed reconstruction method using both physical phantom and patient datasets. After a discussion of existing issues and future research directions, we draw conclusions of this study in Sec. 4.

METHODS

Statistical model

With the assumption of monochromatic x-ray generation, the acquired CT transmission data can be described by a statistically independent Poisson distribution plus a Gaussian distributed system electronic noise^{35, 36, 37, 38}

$$N_i\sim \mathrm{Poisson}\left({\overline{N}}_i\right)+\mathrm{Gaussian}\left(0,{\sigma }_e^2\right),$$ (1)

where ${\overline{N}}_i$ is the expectation value of the number of x-ray photons collected by the detector bin i, ${\sigma }_e^2$ is the variance of the electronic noise. In modern CT systems, in order to reduce the effect of detector dark current, the mean of the electronic noise is often calibrated to be zero.³⁸

According to the Lambert-Beer's law, the line integral along an attenuation path can be calculated as,

$${\overline{\mathrm{y}}}_i=\ln (N_{0i}/{\overline{N}}_i)\mathrm{and}{y}_i\simeq \ln (N_{0i}/N_i),$$ (2)

where N_0i represents the mean number of x-ray photons just before entering the patient and going toward the detector bin i and can be measured by system calibration, e.g., by air scans. The approximation for the second part in Eq. 2 reflects an assumption that the Lambert-Beer's law can be applied to the random values.

Based on the noise model 1 and the use of the Lambert-Beer's law 2, the relationship between the mean and variance of the line integral measurements {y_i} (or log-transformed data) can be described by the following formula:^{36, 37, 38}

$$\begin{array}{ccc}\hfill \mathrm{var}\left(y_i\right)& =& {\sigma }_{y_i}^2=\frac{{\overline{N}}_i+{\sigma }_e^2}{{\overline{N}}_i^2}=\frac{1}{N_{0i}}\exp \left({\overline{y}}_i\right)\hfill \\ & & \times \left(1+\frac{{\sigma }_e^2}{N_{0i}}\exp \left({\overline{y}}_i\right)\right).\hfill \end{array}$$ (3)

PWLS criterion

Given the first and second statistical moments of the line integral measurements {y_i}, a weighted least-squares (WLS) data-fitting can be obtained^{8, 39}

$$\begin{array}{ccc}\hfill \Phi \left(\mathbf{y}\right|\mathit{\mu })& & ={(\mathbf{y}-\overline{\mathbf{y}})}^T{\mathit{\Sigma }}^{-1}(\mathbf{y}-\overline{\mathbf{y}})\hfill \\ & & ={(\mathbf{y}-\mathbf{A}\mathit{\mu })}^T{\mathit{\Sigma }}^{-1}(\mathbf{y}-\mathbf{A}\mathit{\mu }),\hfill \end{array}$$ (4)

where y = (y₁, …, y_I)^T is the vector of measured line integrals as mentioned above, and I is the number of detector bins; μ = (μ₁, …, μ_J)^T is the vector of attenuation coefficients of the object to be reconstructed, and J is the number of image voxels; A is the system or projection matrix with the size I × J, and its element A_ij is typically calculated as the intersection length of projection ray i with voxel j in the object 3D space (in 2D presentation, pixel will be used, instead of voxel); Σ is the covariance matrix, and since the measurement among different detector bins are assumed to be independent, the matrix Σ is diagonal and $\mathit{\Sigma }=\mathrm{diag}\{{\sigma }_{y_i}^2\}$; the symbols T and −1 herein are transpose and inverse operators, respectively.

Mathematically, low-dose CT image reconstruction is an ill-posed problem due to the presence of noise in the line integral measurements. Therefore, the image estimation that directly minimizes the WLS criterion in Eq. 4 can be very noisy and unstable. So researchers reformulate this problem with the maximum a posterior (MAP) estimator by posing a penalty term (or equivalently, prior term) to regularize the solution, that is,

$$\begin{array}{ccc}\hfill \Phi \left(\mathit{\mu }\right|\mathbf{y})& & =\Phi \left(\mathbf{y}\right|\mathit{\mu })+\beta U(\mathit{\mu })\hfill \\ & & ={(\mathbf{y}-\mathbf{A}\mathit{\mu })}^T{\mathit{\Sigma }}^{-1}(\mathbf{y}-\mathbf{A}\mathit{\mu })+\beta U\left(\mathit{\mu }\right),\hfill \end{array}$$ (5)

where U(μ) denotes the penalty term and β is a smoothing parameter which plays a role of controlling the tradeoff between the data fidelity and the penalty term. Equation 5 is the well-known penalized WLS or PWLS criterion in the image domain.

Subsequently, low-dose CT image reconstruction is to estimate the attenuation map by minimizing the PWLS criterion with a positive constraint

$${\mathit{\mu }}^{*}=\underset{\mu \ge 0}{\arg \min }\Phi \left(\mathit{\mu }\right|\mathbf{y}).$$ (6)

Penalty or regularization term

Under the Gaussian MRF model, a quadratic-form regularization is widely used for iterative image reconstruction^{5, 9, 12}

$$U\left(\mathit{\mu }\right)=\sum _j\sum _{m\in W_j}{b}_{jm}{({\mu }_j-{\mu }_m)}^2,$$ (7)

where index j, as defined above, runs over all the pixels in the image domain, W_j denotes a small fixed neighborhood window (typically eight neighbors in a 2D case) of the jth image pixel, and b_jm is the weighting coefficient that indicates the interaction degree between pixel j and pixel m. Usually the weighting coefficient is considered to be inversely proportional to the Euclidean distance between the two pixels. Thus, in 2D case, b_jm = 1 for the four horizontal and vertical neighboring pixels, b_jm = $1/\sqrt{2}$ for the four diagonal neighboring pixels, and b_jm = 0 otherwise. In this study, the normalized form was used to make ${\sum }_{m\in W_j}{b}_{jm}=1$, which is given as

$$\begin{array}{ccc}& & \frac{1}{4+2\sqrt{2}}\left[\begin{array}{ccc}\hfill 1/\sqrt{2}& \hfill 1& \hfill 1/\sqrt{2}\\ \hfill 1& \hfill 0& \hfill 1\\ \hfill 1/\sqrt{2}& \hfill 1& \hfill 1/\sqrt{2}\end{array}\right]\mathrm{or}\hfill \\ & & \left[\begin{array}{ccc}\hfill \frac{1}{4+4\sqrt{2}}& \hfill \frac{1}{4+2\sqrt{2}}& \hfill \frac{1}{4+4\sqrt{2}}\\ \hfill \frac{1}{4+2\sqrt{2}}& \hfill 0& \hfill \frac{1}{4+2\sqrt{2}}\\ \hfill \frac{1}{4+4\sqrt{2}}& \hfill \frac{1}{4+2\sqrt{2}}& \hfill \frac{1}{4+4\sqrt{2}}\end{array}\right].\hfill \end{array}$$ (8)

The major drawback of the quadratic-form regularization is that it fails to take the discontinuities in images into account, thus may lead to over smoothing of edges or fine structures in the reconstructed image.^{11, 12, 14} To mitigate this issue, researchers^{19, 20, 21, 22} replaced the quadratic potential function with nonquadratic functions that increase less rapidly for sufficiently large differences, such as the Huber potential function which is defined as⁴⁰

$$\begin{array}{ccc}& & \varphi \left(\Delta \right)=\left\{\begin{array}{c}{\Delta }^2/2\left|\Delta \right|\le \delta \hfill \\ \delta \left|\Delta \right|-{\delta }^2/2|\Delta |>\delta \hfill \end{array}\right.,\mathrm{or}\hfill \\ & & \varphi \left(\Delta \right)=\left\{\begin{array}{c}{\Delta }^2\left|\Delta \right|\le \delta \hfill \\ 2\delta \left|\Delta \right|-{\delta }^2|\Delta |>\delta \hfill \end{array}\right.,\hfill \end{array}$$ (9)

where δ is a threshold parameter. The Huber potential function penalizes the difference between neighboring pixels quadratically if the absolute difference pixel value |Δ| is smaller than the threshold δ and it will apply a linear penalty to the large difference of |Δ| > δ which usually occurs at edges. By this way, the regularization term in Eq. 7 changes to the edge-preserving Huber penalty. In this study, the second part in Eq. 9 was adopted, and the threshold parameter δ was set to one-tenth of the maximum value, as suggested by some researchers.⁴¹

Inspired by the work of Wang et al.,³⁴ in this work, we investigate the design of an adaptive MRF regularization term which exploits space-variant MRF window size and adaptive weighting coefficients, which are predicted from local sampling window of a normal-dose scan, to help the following low-dose scan CT reconstruction. The proposed adaptive MRF regularization term is defined as

$$U\left(\mathit{\mu }\right)=\sum _j\sum _{m\in A{W}_j}{b}_{jm}^{N{D}_{\_}predict}{({\mu }_j-{\mu }_m)}^2,$$ (10)

where, AW_j is no longer a fixed neighborhood window, but varies depending on the object scale (to be described later). Also, the coefficients $b_{jm}^{N{D}_{\_}predict}$ are no longer constant but adaptively predicted from the previous normal-dose scan. The symbols AW and ND are short for adaptive-window and normal-dose, respectively. AW_j and $b_{jm}^{N{D}_{\_}predict}$are determined through the following three steps.

Computation of object scale

The scale at every pixel j, K(j), is defined as the radius of the largest hyperball (or hypercirle in a 2D case) centered at the pixel j such that all pixels within the ball satisfied a predefined image intensity homogeneity criterion.^{42, 43} For any pixel j in a given image, a digital ball of radius r centered at j is the set of pixels,

$$B_r\left(j\right)=\left\{h\right|‖h-j‖\le r\},$$ (11)

where ‖h − j‖ denotes the Euclidean distance between j and h. Then, a fraction FO_r(j) (“fraction of object”) is defined. It indicates the fraction of the ball boundary occupied by a region which is sufficiently homogeneous with j, and can be described by

$$F{O}_r\left(j\right)=\frac{{\sum }_{h\in B_r\left(j\right)-B_{r-1}\left(j\right)}{H}_{\psi }({\mu }_j-{\mu }_h)}{\left|B_r\left(j\right)-B_{r-1}\left(j\right)\right|},$$ (12)

where |B_r(j) − B_r-1(j)| is the number of pixels in the region B_r(j) − B_r-1(j), and H_ψ is a homogeneity function defined by

$$H_{\psi }\left(x\right)=\exp \left(-\frac{x^2}{2{\sigma }_{\psi }^2}\right),$$ (13)

where σ_ψ is the region-homogeneity parameter and computed following the method as in Ref. 42.

Thus, the scale at pixel j, K(j), is computed as follows: K(j) is initialized as one. Then we iteratively increase the ball radius r by one and check the value of FO_r(j). When the first time this fraction falls below t_s (usually set to be 85%), we consider that the ball contains an object region different from that to which j belongs and set the scale value of K(j) as r–1.⁴³ Table 1 lists the pseudocode for the object scale computation.⁴²

Table 1.

Pseudocode for the object scale computation.

For each pixel j:

begin

r = 1;

while FQr(j) > ts (e.g., 85%)

r = r+1;

end

K(j) = r−1;

end

Figure 1b illustrates an example of the object scale map calculated from one transverse CT slice of the anthropomorphic torso phantom of Fig. 1a. The black/gray dots indicate pixels with low-scale values, while the white regions are relative uniform with high-scale values.

Figure 1.

(a) One transverse slice of the anthropomorphic torso phantom; (b) the corresponding object scale map of the CT image in (a).

Determination of MRF window size and sample window size

For each pixel in the FBP reconstructed image from the normal-dose scan, an explicit MRF window can be modeled with its size determined by the object scale, which is a quantitative measure of local uniformity as described above. In terms of signal processing, when the neighborhood of a specific pixel tends to be homogeneous (i.e., when its object scale is large), there exists a small spread of frequency spectrum, and vice versa. Therefore, a lower-order MRF, penalizing only differences among immediately neighboring pixels, is adequate to model a small spread of frequency spectrum (i.e., when the object scale is large), while a higher-order MRF is required when the spread of frequency spectrum is large (i.e., when the object scale is small). The correspondence between the object scale and MRF window size was empirically set in this study in a 2D presentation, as shown in Table 2.

Table 2.

MRF window size setting based on object scale, and corresponding sample window size required for MRF coefficient prediction.

Object scale	MRF window size	Number of coefficients to be predicted	Sample size needed to reach 90% prediction power	Actual sample window size used
>7	3 × 3	8	136	13 × 13
6–7	5 × 5	24	206	15 × 15
4–5	7 × 7	48	278	17 × 17
2–3	9 × 9	80	355	19 × 19
0–1	11 × 11	120	435	21 × 21

Subsequently, assuming similar frequency spectrums among nearby pixels, the MRF coefficients for each pixel were predicted adaptively from a local sample window. Statistically, to ensure the prediction power of the least-squares linear regression with a certain number of predictors (i.e., the number of MRF coefficients to be predicted), the required sample size needs to be determined. Given a type I error rate of less than 5%, the sample size was calculated using the G*Power software (Ref. ⁴⁴) to achieve a prediction power of at least 90% at a medium effect size (Cohen's f² = 0.15). The actual sample window size utilized in this study was designed to be a bit larger than the required sample size, as summarized in Table 2.

Hence, the prediction of adaptive MRF coefficients depends on an adaptive MRF window size and the corresponding sample window size. Figure 2 shows an example of the MRF window as well as the prediction sample window for a pixel (the central pixel) whose object scale is 4–5. According to Table 2, a 7 × 7 MRF window (labeled with gray marker) and 17 × 17 sample window should be adopted for this pixel. Similar MRF/sample window selection strategy based on Table 2 is performed for pixels in the 2D image one-by-one.

Figure 2.

Example illustration of the MRF/sample window designed for one single pixel (the central pixel). The gray window represents the 7 × 7 MRF window, and the white window is the corresponding 17 × 17 sample window.

Prediction of MRF coefficients

After we have obtained the MRF and sample window sizes for each pixel in the FBP reconstructed image slices of the normal-dose CT scan, we can predict the corresponding MRF coefficients for each pixel via least-squares regression as every pixel can be predicted from a linear combination of its clique-mates. The clique-mates of current pixel here are the neighbors within the MRF window. According to Ref. 34, the least-squares predicted coefficients for the clique-mates can be formulated as

$$\begin{array}{ccc}& & {\mathbf{b}}_j^{ND\_predict}\hfill \\ & & =\underset{{\mathbf{b}}_j}{\arg \min }\sum _{k\in S_j}{\left({\mu }_k^{ND}-{\mathbf{b}}_j^T{\mu }_{A{W}_k}^{ND}\right)}^2\hfill \\ & & ={\left[\sum _{k\in S_j}\left({\mu }_{A{W}_k}^{ND}{\left({\mu }_{A{W}_k}^{ND}\right)}^T\right)\right]}^{-1}\left[\sum _{k\in S_j}\left({\mu }_{A{W}_k}^{ND}{\mu }_k^{ND}\right)\right],\hfill \end{array}$$ (14)

where b_j is the vector of MRF coefficients for the neighbors of pixel j within the MRF window, S_j is the sample window of pixel j, AW_k represents the set of neighbors for pixel k within the MRF window, and ${\mu }_{A{W}_k}$is the vector of corresponding attenuation value for them. Herein, the expression ${\sum }_{k\in S_j}\left({\mathit{\mu }}_{A{W}_k}^{ND}{\left({\mathit{\mu }}_{A{W}_k}^{ND}\right)}^T\right)$ is the sample autocorrelation matrix, while${\sum }_{k\in S_j}\left({\mathit{\mu }}_{A{W}_k}^{ND}{\mathit{\mu }}_k^{ND}\right)$ is the sample cross-correlation vector. The symbol ND was defined before as the short for normal-dose.

In order to solve Eq. 14, the sample autocorrelation matrix is required to be of full rank and reversible. This condition is met for all the pixels except for some whose object scale is relatively large, where the intensity homogeneity leads to the multicollinearity of the sample space. In our experiments, we empirically set a robust threshold on the object scale to be 7. For those pixels with scale above this threshold, their MRF window size should be 3 × 3 according to Table 2, and therefore, we set their weighting coefficients the same as that for the conventional GMRF in Eq. 8. For the pixels with object scale under the preset threshold, the MRF coefficients were estimated directly using Eq. 14. And it is worth noting that the sum of predicted MRF coefficients ${\mathbf{b}}_j^{N{D}_{\_}predict}$ for the pixel j using Eq. 14 is close to 1 (e.g., 0.95–1.05).

Selection of smoothing parameter β

The smoothing parameter β controls the tradeoff between the data fidelity term and the regularization term. A larger β value produces a more smoothed reconstructed image with lower noise but also lower resolution, and vice versa. Determining the optimal β value for SIR algorithms is still an open question.

In this study, to ensure the fairness of the comparison among the PWLS iterative reconstruction using the conventional GMRF regularization (referred to as PWLS-isotropic), the PWLS iterative reconstruction using the edge-preserving Huber regularization (referred to as PWLS-Huber), and the presented PWLS iterative reconstruction using the proposed adaptive MRF regularization (referred to as PWLS-adaptive), the parameter β is first adjusted manually through two widely-used quantitative metrics so that the best image quality can be obtained for the PWLS-isotropic algorithm.

One metric is the traditional root mean squared error (RMSE), which indicates the difference between the reconstructed image and the ground truth image and also characterizes the reconstruction accuracy. The other metric is the universal quality index (UQI) (Ref. ⁴⁵) which measures the similarity between the reconstructed image and the ground truth image. The UQI quantifies the noise, spatial resolution, and texture correlation between two images, and has been widely used in CT image quality evaluation during past years. Let μ_r denote the vector of the reconstructed image and μ₀ be the vector of the ground truth image or reference image, the two metrics are defined as (Q is the number of image pixels),

$$\begin{array}{ccc}\hfill \mathrm{RMSE}& & =\sqrt{\frac{{({\mathit{\mu }}_{\mathbf{r}}-{\mathit{\mu }}_{\mathbf{0}})}^T({\mathit{\mu }}_{\mathbf{r}}-{\mathit{\mu }}_{\mathbf{0}})}{Q}}\hfill \\ & & =\sqrt{\frac{1}{Q}\sum _{n=1}^Q{({\mu }_{r,n}-{\mu }_{0,n})}^2},\hfill \end{array}$$ (15)

$$\mathrm{UQI}=\frac{4Cov\{{\mathit{\mu }}_{\mathbf{r}},{\mathit{\mu }}_{\mathbf{0}}\}}{\mathrm{var}\left\{{\mathit{\mu }}_{\mathbf{r}}\right\}+\mathrm{var}\left\{{\mathit{\mu }}_{\mathbf{0}}\right\}}•\frac{{\overline{\mu }}_r{\overline{\mu }}_0}{{\overline{\mu }}_r^2+{\overline{\mu }}_0^2},$$ (16)

where ${\overline{\mu }}_r=\frac{1}{Q}{\sum }_{n=1}^Q{\mu }_{r,n},{\overline{\mu }}_0=\frac{1}{Q}{\sum }_{n=1}^Q{\mu }_{0,n},\mathrm{var}\left\{{\mathit{\mu }}_{\mathbf{r}}\right\}=\frac{1}{Q-1}{\sum }_{n=1}^Q{({\mu }_{r,n}-{\overline{\mu }}_r)}^2,\mathrm{var}\left\{{\mathit{\mu }}_{\mathbf{0}}\right\}=\frac{1}{Q-1}{\sum }_{n=1}^Q{({\mu }_{0,n}-{\overline{\mu }}_0)}^2$, $cov\{{\mathit{\mu }}_{\mathbf{r}},{\mathit{\mu }}_{\mathbf{0}}\}=\frac{1}{Q-1}{\sum }_{n=1}^Q({\mu }_{r,n}-{\overline{\mu }}_r)({\mu }_{0,n}-{\overline{\mu }}_0).$

The β value that offered the lowest RMSE and also the highest UQI is regarded as the optimal β and used in the following evaluations. The presented procedure of choosing optimal β value is similar to that in Ref. 12, but much easier to implement.

Then, for the PWLS-Huber and PWLS-adaptive algorithms, an identical β value can be adopted so that they have matched noise level in the uniform regions as the PWLS-isotropic algorithm. The reason for this is that, in the relative uniform regions, both the PWLS-Huber algorithm and the PWLS-adaptive algorithm actually use the same quadratic penalty as Eq. 7 according to Eq. 9 and Sec 2.C.3. Therefore, an identical β value ensures all the three SIR algorithms have matched noise level in the uniform regions, and a fair comparison can thus be performed on edge, detail and contrast preservation.

Summary of presented PWLS reconstruction method

With the WLS criterion and the newly designed quadratic-form MRF regularization presented above, our PWLS iterative reconstruction scheme for low-dose CT reconstruction can be summarized as follows:

$$\begin{array}{ccc}\hfill {\mathit{\mu }}^{*}& =& \underset{\mu \ge 0}{\arg \min \{}{(\mathbf{y}-\mathbf{A}\mathit{\mu })}^T{\mathit{\Sigma }}^{-1}(\mathbf{y}-\mathbf{A}\mathit{\mu })\hfill \\ & & +\beta \sum _j\sum _{m\in A{W}_j}{b}_{jm}^{N{D}_{\_}predict}{({\mu }_j-{\mu }_m)}^2\}.\hfill \end{array}$$ (17)

Minimization of this cost function can be achieved with many algorithms, and in this study, the Gauss-Seidel (GS) updating strategy was exploited due to its rapid convergence.^{5, 6, 22} It updates each pixel sequentially, and the values for all pixels are updated in each iteration. The use of the GS strategy for the minimization solution of Eq. 17 is given in the Appendix. The flowchart of deriving the MRF weighting coefficients and PWLS minimization for image reconstruction is shown by Fig. 3.

Figure 3.

Flow chart of the proposed PWLS iterative reconstruction with adaptive MRF regularization for low-dose CT.

EXPERIMENTS AND RESULTS

In this study, experimental physical phantom and patient data were utilized to validate the presented PWLS iterative reconstruction scheme using the proposed adaptive MRF regularization (referred to as PWLS-adaptive) with comparison to the PWLS-Huber algorithm, the PWLS-isotropic algorithm and the classical FBP algorithm.

Anthropomorphic torso phantom study

Data acquisition

An anthropomorphic torso phantom (Radiology Support Devices, Inc., Long Beach, CA) was used for experimental data acquisition. The phantom was scanned by a Siemens SOMATOM Sensation16 CT scanner (Siemens Healthcare, Forchheim, Germany) in a cine mode at a fixed bed position. The x-ray tube voltage was set to be 120 kVp, while the mAs level was set to be 40 mAs. Each scan included 1160 projection views evenly spanned on a 360° circular orbit, and each view included 672 detector bins. The distance from the x-ray source to the detector arrays was 1040 mm and the distance from the x-ray source to the rotation center was 570 mm. The CT scanner was rotated 150 times around the phantom.

The central slice sinogram data (672 bins × 1160 views) of one scan was extracted for this feasibility study, which is regarded as low-dose scan. The averaged sinogram data from those 150 repeated scans of that slice were reconstructed by the FBP method to serve as the ground truth image for evaluation purpose and also as the previous normal-dose scan for MRF coefficients prediction. The size of reconstructed image is 512 × 512 with pixel size of 1.0 × 1.0 mm².

Visualization-based evaluation

As illustrated in Sec 2.D, the β value that offered the lowest RMSE and the highest UQI for the PWLS-isotropic algorithm with the anthropomorphic torso phantom was 3 × 10⁵. Therefore, this β value was adopted for all the three SIR algorithms in the following evaluations.

The reconstructed images by FBP, the PWLS-isotropic with β = 3 × 10⁵, the PWLS-Huber with β = 3 × 10⁵, and the PWLS-adaptive with β = 3 × 10⁵ from the noisy 40 mAs sinogram are shown in Fig. 4. It can be observed that all the SIR algorithms outperformed the FBP in terms of noise and streak artifact suppression. As for the three SIR algorithms, the PWLS-adaptive is superior to the PWLS-isotropic and the PWLS-Huber in terms of edge/detail preservation, which will be quantified in Sec. 3.A.3.

Figure 4.

A reconstructed slice of the anthropomorphic torso phantom: (a) The FBP reconstruction from the averaged sinogram; (b) The FBP reconstruction from 40 mAs sinogram; (c) The PWLS-isotropic reconstruction from 40 mAs sinogram, β = 3 × 10⁵; (d) The PWLS-Huber reconstruction from 40 mAs sinogram, β = 3 × 10⁵, δ = 0.004; (e) The PWLS-adaptive reconstruction from 40 mAs sinogram, β = 3 × 10⁵. All the images are displayed with the same window.

Quantitative evaluation

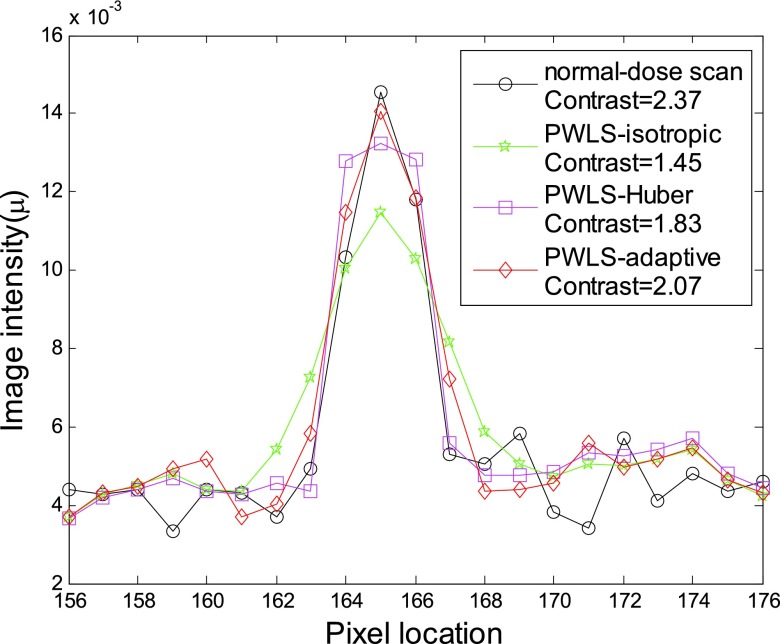
To quantitatively demonstrate the benefits of our proposed scheme, we compared the performance of the four algorithms on the reconstruction of ROIs with detailed structures, which were labeled with dotted rectangles in Fig. 4b. Besides the RMSE and UQI defined in Eqs. 15, 16, two more metrics were employed to quantitatively evaluate the image quality of the detailed ROIs. They are correlation coefficient (CC) and signal-to-noise ratio (SNR), which are defined as

$$\mathrm{CC}=\frac{{\sum }_{n=1}^Q({\mu }_{r,n}-{\overline{\mu }}_r)({\mu }_{0,n}-{\overline{\mu }}_0)}{\sqrt{{\sum }_{n=1}^Q{({\mu }_{r,n}-{\overline{\mu }}_r)}^2{\sum }_{n=1}^Q{({\mu }_{0,n}-{\overline{\mu }}_0)}^2}},$$ (18)

$$\mathrm{SNR}=10{\log }_{10}\left(\frac{{\sum }_{n=1}^Q{({\mu }_{r,n}-{\overline{\mu }}_r)}^2}{{\sum }_{n=1}^Q{({\mu }_{r,n}-{\mu }_{0,n})}^2}\right).$$ (19)

The corresponding quantitative results are shown in Fig. 5. As we can see, the proposed PWLS-adaptive algorithm offered the lowest RMSE and the highest UQI/CC/SNR for all the five detailed ROIs.

Figure 5.

Performance comparison of four algorithms on the reconstruction of detailed ROIs labeled in Fig. 4b with four different metrics. The corresponding algorithms are illustrated in figure legend.

Profile-based evaluation

To further visualize the difference among the four reconstruction algorithms, a horizontal profile of the resulting images were drawn across the line labeled in Fig. 4b. The profile comparison further demonstrated the advantage of three SIR algorithms over the FBP on noise suppression, as well as the advantage of the PWLS-adaptive over the PWLS-isotropic and the PWLS-Huber on edge/contrast preservation at the matched noise level (see Fig. 6).

Figure 6.

Comparison of the profiles along the horizontal line labeled in Fig. 4b between the four algorithms with 40 mAs sinogram and ground truth image. The corresponding algorithms are illustrated in figure legend.

Patient data study

Data acquisition

To evaluate the algorithms in a more realistic situation, the raw sinogram data were acquired using the same Siemens scanner as in Sec. 3A from a patient who was scheduled for CT scan for medical reasons under the approval of the Institutional Review Board (IRB) of the Stony Brook University. The scanning geometry is the same as that for the anthropomorphic torso phantom. The tube voltage was set to be 120 kVp, and the mAs level was 100 mAs. We regarded this acquisition as the normal-dose scan, and instead of scanning the patient twice, we simulated the corresponding low-dose sinogram data by adding noise to the normal-dose sinogram data using the simulation method in Ref. 35. The noisy measurement N_i at detector bin i was generated according to the statistical model

$$N_i\sim \mathrm{Poisson}\left(N_{0i}\exp (-{\overline{y}}_i)\right)+\mathrm{Gaussian}\left(\mathbf{0},{\sigma }_{\mathbf{e}}^{\mathbf{2}}\right),$$ (20)

where N_0i was set to be 5 × 10⁴ and ${\sigma }_e^2$ was set to be 10 (Ref. ³⁵) for low-dose scan simulation in this study. Then the corresponding noisy line integral y_i was calculated by the logarithm transform.

Visualization-based evaluation

The reconstructed images from the normal-dose sinogram data with the FBP algorithm serve as the ground truth image for this patient data study. Then, with the method illustrated in Sec. 2D, the optimal β value for the PWLS-isotropic algorithm with the simulated low-dose patient sinogram data are 2 × 10⁵. Again, the identical β value was adopted for the PWLS-Huber and the PWLS-adaptive so that the noise level in the uniform background region is equivalent for all the three PWLS algorithms.

One slice of the reconstructed images are shown in Fig. 7, where (a) and (b) are the FBP reconstructed images from the acquired normal-dose and simulated low-dose sinogram data, respectively, and (c), (d), (e) are the reconstructed images from the simulated low-dose sinogram by the PWLS-isotropic, the PWLS-Huber, and the PWLS-adaptive algorithms with β = 2 × 10⁵. It is evident that all the three SIR algorithms outperformed the FBP in terms of noise suppression, and the PWLS-adaptive algorithm was superior to the PWLS-isotropic and the PWLS-Huber in terms of edge and detail preservation.

Figure 7.

Reconstructed transverse slice of the patient data: (a) The FBP reconstruction from the normal-dose sinogram; (b) The FBP reconstruction from the simulated low-dose sinogram; (c) The PWLS-isotropic reconstruction from the simulated low-dose sinogram, β = 2 × 10⁵; (d) The PWLS-Huber reconstruction from the simulated low-dose sinogram, β = 2 × 10⁵, δ = 0.004; (e) The PWLS-adaptive reconstruction from the simulated low-dose sinogram, β = 2 × 10⁵. All the images are displayed with the same window.

Quantitative evaluation

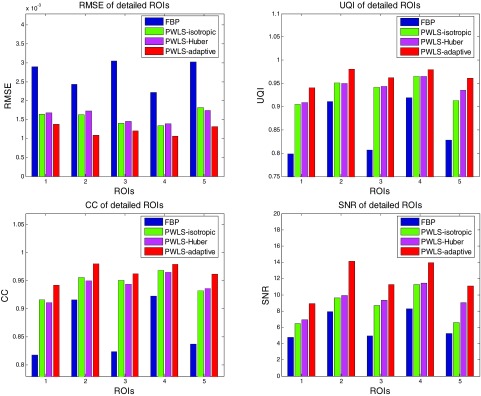
To quantitatively demonstrate the benefits of our proposed scheme, we compare the performance of the four algorithms on the reconstruction of ROIs with detailed structures, which were labeled with red rectangles in Fig. 7b. The corresponding quantitative results based on the four different metrics were shown in Fig. 8. Again, the PWLS-adaptive algorithm yielded the lowest RMSE and the highest UQI/CC/SNR for all the five detailed ROIs.

Figure 8.

Performance comparison of four algorithms on the reconstruction of detailed ROIs labeled in Fig. 7b with four different metrics. The corresponding algorithms are illustrated in figure legend.

Profile-based evaluation

Figure 9 shows the targeted horizontal profiles [labeled with line in Fig. 7b] of the reconstructed images by the four reconstruction algorithms in Fig. 7 as compared to that of the FBP reconstruction with normal-dose sinogram. The profile comparison quantitatively demonstrated the advantage of the three SIR algorithms over the FBP on noise suppression, as well as the advantage of the PWLS-adaptive over the PWLS-isotropic and the PWLS-Huber on edge and contrast preservation at the matched noise level.

Figure 9.

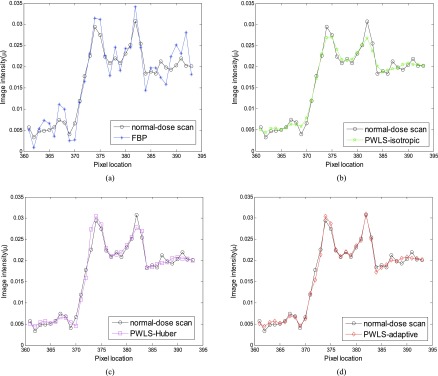
Comparison of the profiles along the horizontal line labeled in Fig. 7b between the four algorithms with simulated low-dose sinogram and the FBP reconstruction with the normal-dose sinogram. The corresponding algorithms are illustrated in figure legend.

Contrast preservation evaluation

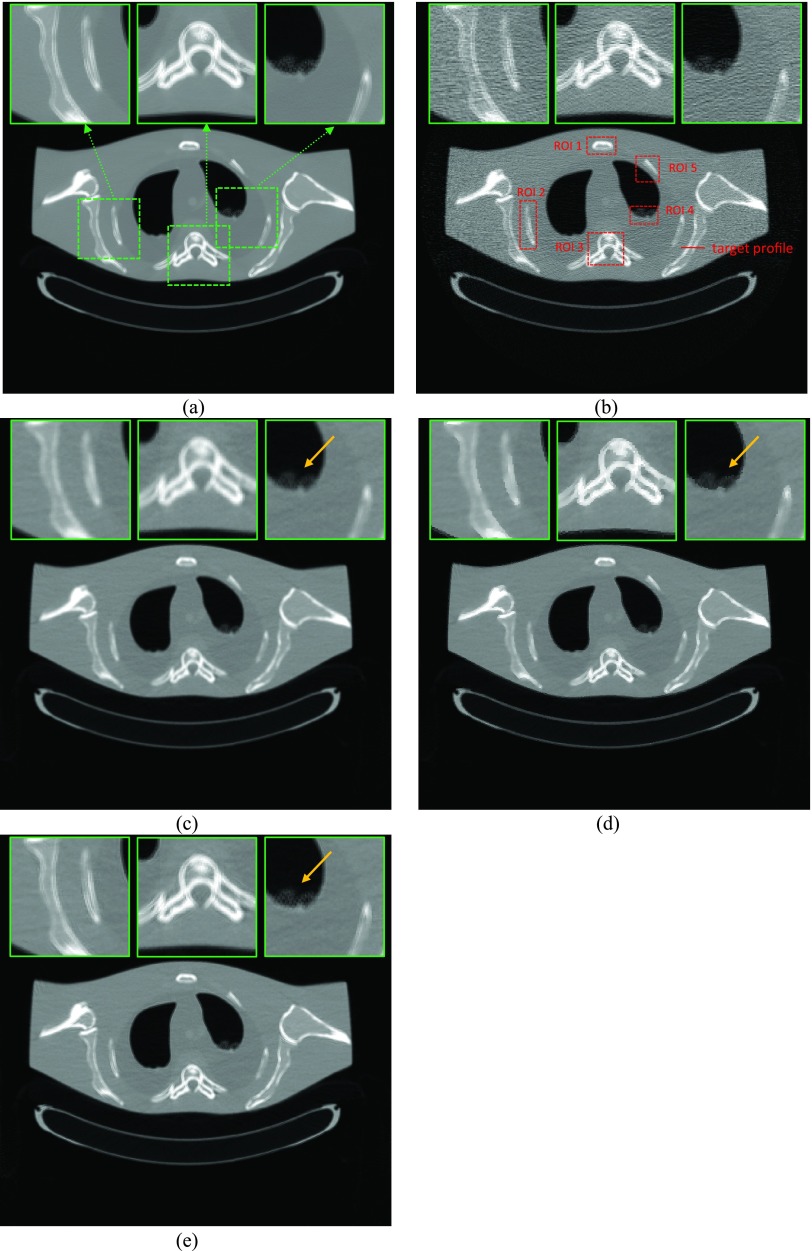
Figure 10 shows the vertical profiles [labeled in Fig. 7b] through a small object for the three SIR algorithms with comparison to the FBP reconstruction from the normal-dose sinogram. The contrasts shown in the figure legend were computed with²⁶

$$\mathrm{Contrast}=\frac{{\mu }_{\max }-{\mu }_{\mathrm{base}}}{{\mu }_{\mathrm{base}}},$$ (21)

where μ_max is the maximum value of a profile through the object, while μ_base is the mean value of the profile baseline.

Figure 10.

Comparison of the profiles along the vertical line labeled in Fig. 7b between the three SIR algorithms with simulated low-dose sinogram and the FBP reconstruction with the normal-dose sinogram. The contrast of the small object and the corresponding algorithms are illustrated in figure legend.

The reconstructed small object by the PWLS-adaptive algorithm has higher contrast (2.07) than that of the PWLS-isotropic algorithm (1.45) and the PWLS-Huber algorithm (1.83), and is closer to that of the FBP reconstruction from the normal-dose sinogram (2.37).

DISCUSSION AND CONCLUSION

The penalty/regularization term which reflects prior information is very important for the SIR algorithms.^{10, 11, 12, 13, 14, 15} In the applications with repeated CT scans, previous scan can be utilized as prior information for current scan because of the rich similar information existing among the reconstructed image series of the scans. Strategies using the image reconstructed from previous scan/scans to improve the current scan reconstruction have been explored in several studies.^{23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33} Different from these works, we proposed to utilize the frequency information in the FBP reconstructed image from the previous normal-dose scan to improve the follow-up low-dose (mAs) scans by incorporating a quadratic-form MRF regularization with adaptive MRF window and adaptive coefficients predicted from the previous normal-dose scan into the established PWLS iterative reconstruction scheme (PWLS-adaptive). The experimental results with both physical phantom and patient data demonstrated the feasibility and efficacy of the proposed scheme. We further compared the reconstruction results using the PWLS-adaptive to that using the conventional Gaussian MRF penalty (PWLS-isotropic) and the edge-preserving Huber penalty (PWLS-Huber). The results consistently showed that the presented PWLS-adaptive algorithm is superior on edge, detail, and contrast preservation at the matched noise level. In turn, this study showed us again how critical the penalty term is for the SIR algorithms.

It may seem counterintuitive to employ a small MRF window for uniform regions and a large MRF window for nonuniform regions in this study. Therefore, we emphasize again that this kind of MRF window size selection is operated in the frequency domain. The rationale behind this approach is that the more uniform the local structure is, the smaller the frequency spectrum spread is, so a smaller MRF window should be adopted, and vice versa. Traditional penalties generally utilize a small fixed MRF window size (e.g., 3 × 3 in the 2D case), which limit the spectral description to a crude low-pass model. By increasing MRF window size, the penalty term raises the number of degrees of freedom in spectral description, and can include the high frequency information.³⁴ In this way, the high frequency components, such as the edges and details, could be better preserved. In our another work⁴⁶ which also utilizes the object scale map, we employed a large MRF window for uniform regions while a small MRF window for edge regions, but the weighting coefficients were adopted inversely proportional to the Euclidean distance between the central and neighboring pixels. The consideration was based on the reasons that the neighbors cupping is strong for uniform regions and a large MRF window should be employed while the neighbors cupping is weak for edge regions thus a small MRF window may be more reasonable. Generally, these are two different ways of utilizing the object scale map, one in the frequency domain as in this study, while the other in the spatial domain as in Ref. 46.

In this proof-of-concept study, the image misalignment issue between the low-dose scan and the corresponding normal-dose scan was not considered explicitly. In some applications where the normal-dose scan and low-dose scan is perfectly aligned, the proposed PWLS-adaptive algorithm can be used directly. For example, in the image-guided needle biopsy for lung nodule analysis, the motion among different scans can be ignored when CT is used in a cine mode and the patient holds the breath during each single scan. In the applications where misalignment between the low-dose and normal-dose scans cannot be ignored, registration can be first employed to align the scans. We plan to investigate the influence of image registration accuracy on our proposed method in a future study.

While improving scanner hardware and optimizing scanning protocols can improve the dose utility, software approaches such as SIR algorithms provide an alternative and a more cost-effective means for further dose reduction while retaining satisfactory image quality. One major drawback of the SIR algorithms is their computational burden due to multiple reprojection and back-projection operation cycles in the projection and image domains. However, with the constant computational improvements of fast computers, the SIR algorithms including the presented scheme are moving closer to clinical use and can play a dominate role there.

APPENDIX: OPTIMIZATION APPROACH AND IMPLEMENTATION ISSUE

The pseudocode for the cost function minimization in Eq.17 is listed as follows (where A_j denotes the jth column of the projection matrix A):

Initialization:

$$\begin{array}{c}\widehat{\mathit{\mu }}=\mathrm{FBP}\left\{\mathbf{y}\right\};\mathbf{q}=\mathbf{A}\widehat{\mathit{\mu }}\widehat{\mathbf{r}}=\mathbf{y}-\mathbf{q};\mathit{\Sigma }=\mathrm{diag}\left\{{\sigma }_{y_i}^2\right\};\hfill \\ {\lambda }_j={\mathbf{A}}_j^T{\mathit{\Sigma }}^{-1}{\mathbf{A}}_j,\forall j\hfill \end{array}$$

For each iteration:

begin

For each pixel j:

begin $$\begin{array}{c}\hfill {\widehat{\mu }}_j^{\mathrm{old}}:={\widehat{\mu }}_j;\\ \hfill {\widehat{\mu }}_j^{\mathrm{new}}:=\frac{{\mathbf{A}}_j^T{\Sigma }^{-1}\widehat{\mathbf{r}}+{\lambda }_j{\widehat{\mu }}_j^{\mathrm{old}}+\beta \sum _{m\in A{W}_j}{b}_{jm}^{N{D}_{\_}predict}{\mu }_m}{{\lambda }_j+\beta \sum _{m\in A{W}_j}{b}_{jm}^{N{D}_{\_}predict}};\\ \hfill {\widehat{\mu }}_j:=\max \{0,{\widehat{\mu }}_j^{\mathrm{new}}\};\\ \hfill \widehat{\mathbf{r}}:=\widehat{\mathbf{r}}+{\mathbf{A}}_j\left({\widehat{\mu }}_j^{\mathrm{old}}-{\widehat{\mu }}_j\right);\end{array}$$

end

end

In our implementations, we stop the reconstruction process after a number of iterations when the estimated images between two successive iterations become very small. This kind of stopping rule has been widely used in the iterative image reconstruction community.⁹, ¹⁵ For the datasets presented in this study, 20 iterations were seen to be large enough for good convergence.