Abstract
Purpose: To investigate the feasibility of a new two-dimensional (2D) multichannel response (MCR) analysis approach for the detection of clustered microcalcifications (MCs) in digital breast tomosynthesis (DBT).
Methods: With IRB approval and informed consent, a data set of two-view DBTs from 42 breasts containing biopsy-proven MC clusters was collected in this study. The authors developed a 2D approach for MC detection using projection view (PV) images rather than the reconstructed three-dimensional (3D) DBT volume. Signal-to-noise ratio (SNR) enhancement processing was first applied to each PV to enhance the potential MCs. The locations of MC candidates were then identified with iterative thresholding. The individual MCs were decomposed with Hermite–Gaussian (HG) and Laguerre–Gaussian (LG) basis functions and the channelized Hotelling model was trained to produce the MCRs for each MC on the 2D images. The MCRs from the PVs were fused in 3D by a coincidence counting method that backprojects the MC candidates on the PVs and traces the coincidence of their ray paths in 3D. The 3D MCR was used to differentiate the true MCs from false positives (FPs). Finally a dynamic clustering method was used to identify the potential MC clusters in the DBT volume based on the fact that true MCs of clinical significance appear in clusters. Using two-fold cross validation, the performance of the 3D MCR for classification of true and false MCs was estimated by the area under the receiver operating characteristic (ROC) curve and the overall performance of the MCR approach for detection of clustered MCs was assessed by free response receiver operating characteristic (FROC) analysis.
Results: When the HG basis function was used for MCR analysis, the detection of MC cluster achieved case-based test sensitivities of 80% and 90% at the average FP rates of 0.65 and 1.55 FPs per DBT volume, respectively. With LG basis function, the average FP rates were 0.62 and 1.57 per DBT volume at the same sensitivity levels. The difference in the two sets of basis functions for detection of MCs did not show statistical significance.
Conclusions: The authors' experimental results indicate that the MCR approach is promising for the detection of MCs on PV images. The HG or LG basis functions are both effective in characterizing the signal response of MCs using the channelized Hotelling model. The coincidence counting method for fusion of the 2D MCR in 3D is an important step for FP reduction. Further study is underway to improve the MCR approach for microcalcification detection in DBT.
Keywords: computer-aided detection (CADe), digital breast tomosynthesis (DBT), multichannel response (MCR) analysis, Hermite–Gaussian (HG), Laguerre–Gaussian (LG)
INTRODUCTION
Breast cancer remains one of the leading causes of cancer mortality among women. Mammography can detect small cancers, when they are at an early stage and most responsive to treatment. However, the performance of mammography is limited by the overlapping fibroglandular tissues that can cause both false negative diagnosis and false positive recalls. Digital breast tomosynthesis (DBT) (Ref. 1) is a new imaging modality that builds on the full-field digital mammography (FFDM) technology. In DBT, a series of projection view (PV) images is acquired as the x-ray source is moved over a limited range of angles. The total dose required for DBT is kept at nearly the same or only slightly higher than that of a regular mammogram. Tomosynthesized slices of the imaged volume are reconstructed from the series of PV images. Although DBT can only provide quasi three-dimensional (3D) information with limited resolution along the depth (Z) direction, the reduced overlap of breast tissue provides superior conspicuity and detectability of subtle lesions in comparison with conventional projection mammograms.2, 3, 4, 5, 6
Despite its success in improving the detection of soft tissue lesions, the ability of DBT in microcalcification (MC) detection is still under investigation.7, 8 Detection of MC in DBT is more challenging because of the large search space, the separation of a cluster into a number of DBT slices, and the potential blurring of MCs from the image acquisition and reconstruction processes. The synthesis of an FFDM-like two-dimensional (2D) image from the DBT scan is one of the potential solutions to help visualization of MCs in DBT. Alternatively, computer-aided detection (CADe) has been shown to improve radiologists’ accuracy for MC detection in mammography. It can be expected that CADe will also play an important role in DBT interpretation.
Development of CADe system for breast cancer on DBT is still at an early stage because the availability of patient DBT cases is still limited for this new modality. One of the common approaches for CADe on DBT, referred to as 3D approach, is to use the reconstructed DBT slices, or the DBT volume, as input. The multiple-PV information is combined by image reconstruction techniques before computerized analysis. Bernard et al.9 developed an algorithm for the detection of MC clusters on filtered backprojection reconstructed slices. On a data set of 13 DBT volumes containing MC clusters and 37 normal DBT volumes, their method had a sensitivity of 85% at an average of 1.4 FP marks per breast volume. Sahiner et al.10 developed a CADe scheme for MC clusters by using an enhancement-modulated 3D calcification response function in combination with iterative thresholding and 3D region growing techniques. This approach achieved a sensitivity of 85% at an average of 3.8 FPs per DBT volume on a data set of 144 two-view DBT volumes from 72 breasts. The strength of 3D approaches is that it takes advantage of the image reconstruction that accurately combines the information from the low dose PVs and increases the signal-to-noise ratio (SNR). The SNR of MCs in the reconstructed DBT is affected by the reconstruction methods and parameters used. Therefore, the performance of the CADe system may depend on the reconstruction algorithm used for the tomosynthesis.
Alternatively, a 2D approach may be used for lesion detection in DBT in which the individual PVs are used as input and then the information from all PVs is merged by using the geometrical information of the DBT system. This approach offers the potential advantage of being independent of reconstruction techniques although it may not be practical for human readers. In addition, current CADe algorithms developed for regular mammograms can be applied to the PVs since each of the individual PVs can be treated as a regular mammogram with proper image preprocessing. However, due to the low SNR of the input PVs, it is challenging to design effective CADe methods for breast cancer detection. Reiser et al.11 investigated a 2D approach for MC detection. On a data set of 30 image sets with MC clusters and 30 image sets without visible findings, their detection method achieved a sensitivity of 86% with 1.3 FP clusters per DBT volume.
We are developing methods and evaluating the usefulness of CADe for MCs in DBT. In this study, our purpose is to investigate the feasibility of a 2D multichannel response (MCR) analysis approach to clustered MC detection in DBT.
MATERIALS
DBT acquisition
A GE second generation prototype DBT system at the University of Michigan was used to acquire DBT scans. The system has a CsI phosphor/a:Si active matrix flat panel digital detector with dimensions of 19.20 × 23.04 cm and a pixel pitch of 0.1 × 0.1 mm. The detector is stationary during image acquisition. The system uses a step-and-shoot design and acquires PV images from a total of 21 angles in 3° increments over a ±30° range in less than 8 s. The distance from the x-ray focal spot to the center of the rotation is 64 cm and the focal spot to the detector distance is 66 cm. The x-ray source rotation plane is parallel to the chest wall edge of the detector. For visualization of the MC clusters in the data set, the DBT was reconstructed with in-house developed software based on the simultaneous algebraic reconstruction technique (SART).12 The reconstructed image volumes were only used to mark the locations of MC clusters and individual MCs for generating reference standard and training purposes. The voxel resolution of the reconstructed DBT volume in the X–Y plane was chosen to be the same as the pixel pitch of the detector (0.1 × 0.1 mm) while the slice spacing in the Z direction was chosen to be 1 mm. The same voxel size was used for the ray-tracing operations in the coincidence counting method, to be described later.
Image set
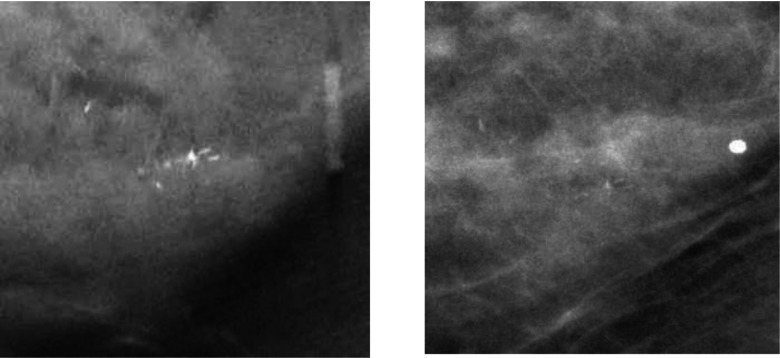
This study was IRB approved and HIPAA compliant. Human subjects who were recommended for biopsy of clustered MCs (Breast Imaging Reporting and Data System, BI-RADS 4 and 5) in our Breast Imaging Division were recruited with written informed consent. Two-view, craniocaudal (CC) and mediolateral (MLO), DBTs of the affected breast were acquired. The dose per DBT view was set to be about 1.5 times of that of a single-view conventional mammogram. A data set of 82 DBT views from 41 breasts was collected from 40 patients including one patient with MC clusters in both breasts. An experienced Mammography Quality Standards Act (MQSA) radiologist marked the location of the biopsied MC cluster with a 3D bounding box in each DBT volume based on all available clinical and imaging information and provided a subtlety rating on a scale of 1–10 (10 = most subtle). A total of 32 malignant and 10 benign biopsy-proven MC clusters were included in the data set. The radiologist also provided an estimate of breast density based on the four BI-RADS categories by reading the corresponding mammograms of the breasts since there is not yet BI-RADS density categories designed for DBT. Figure 1 shows an example of a region of interest (ROI) containing clustered MCs. The distributions of the breast density and cluster subtlety in DBT volume are shown in Fig. 2.
Figure 1.
Image example. Left: ROI on the central slice of the reconstructed DBT volume. Right: the same ROI on the projection view at 0°.
Figure 2.
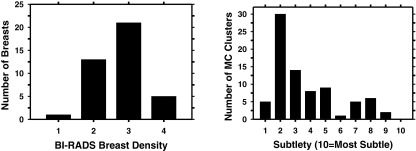
Characteristics of our data set. Left: distribution of breast density in terms of BI-RADS category estimated by a MQSA radiologist. Right: distribution of the subtlety ratings of the MC clusters in DBT volume judged by the same radiologist. The subtlety rating was estimated for the CC and MLO views of each cluster independently.
CADe SYSTEM
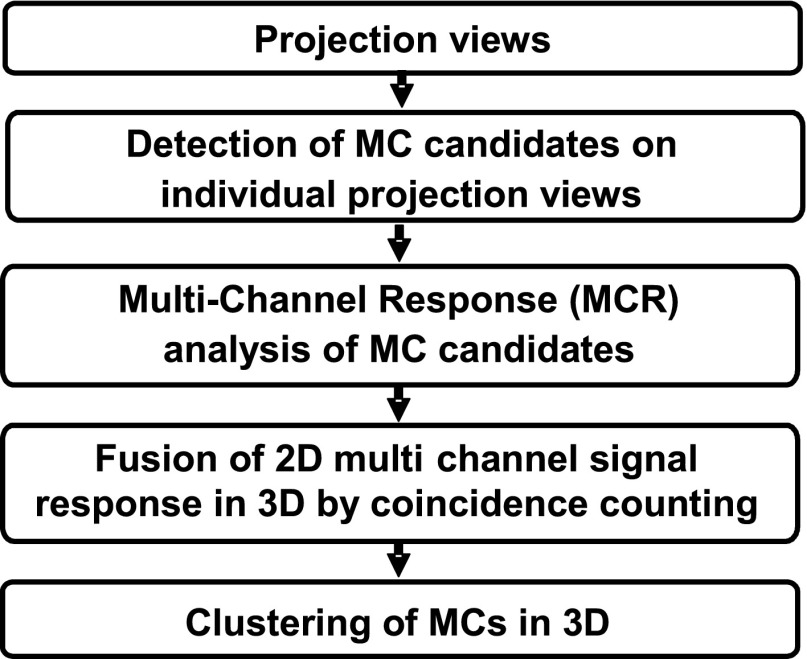
We developed a CADe system for MC detection using the 2D PV images as input rather than the reconstructed DBT volume. The 3D information is utilized by the coincidence counting method that backprojects the detected MC candidates on the PVs and traces the coincidence of the ray paths in 3D. A schematic diagram of our CADe system is shown in Fig. 3. The pixel value in each PV has a linear relationship with the x-ray intensity incident on the detector over a wide exposure range. Assuming that the x-ray spectrum has an effective monoenergetic energy and the effects of beam hardening and scatter can be ignored in the design of computerized image processing methods, a logarithmic transformation was applied to the raw pixel intensities of the PV which was then input to the CADe system. The MC cluster detection processes are described below.
Figure 3.
Schematic diagram of our CADe system for MC detection in DBT using a 2D approach.
Prescreening of MC candidates
We previously developed a difference-image technique based on a box-rim filter to reduce the structured background and improve the SNR of the MC candidates in FFDM.13 In this study, we used the same technique for prescreening of MC candidates in PVs of DBTs. Briefly, in the difference-image technique, a signal-enhancement filter is used to enhance the signal and smooth the random noise and a signal-suppression filter is used to remove the signal and again smooth the random noise. The two filtered images are then subtracted to produce a difference image in which the low-frequency structured background is removed and the high-frequency noise is suppressed. If the two filters are linear, the two processes can be combined into one which is effectively a bandpass filter. An 8 × 8 pixel box-rim filter was selected for MC enhancement in FFDMs of 0.1 × 0.1 mm pixel size. With an iterative global thresholding technique, a variable threshold that will extract about 160–180 individual MC candidates having top ranking of filter response on each PV is automatically chosen. The MC candidates are segmented and their size and shape are refined with a region growing method adaptive to the local contrast-to-noise ratio (CNR). In this method, the local mean pixel value and root-mean-square (RMS) noise within a 51 × 51-pixel kernel centered at the MC candidate centroid is estimated. The central pixels of the kernel that contain the signal candidate are excluded from the estimation. With the eight-connectivity criterion, the candidate is grown to the neighboring pixels. A connected pixel is retained as a part of the candidate if its CNR value is larger than a predefined CNR threshold of 1.9 chosen for segmentation in the noisy PV images. The shape, size, CNR, and a refined centroid location of each candidate are determined after the local segmentation.
Multichannel response analysis of MC candidates
The MC candidates detected in the PVs are subjected to the MCR analysis that will be used to discriminate MCs from FPs by analyzing the channelized image components at potential MC locations within the breast region. Theoretically, one can describe the signal detection problem with an ideal observer model.14 In the ideal observer model, an image is represented as an M × 1 vector g. The likelihood ratio between two class distributions is defined by
| (1) |
where is the probability density of g given by class k (= 1 or 2). Under the assumption that the task is a signal known exactly and background known exactly (SKE/BKE) problem, the logarithm of likelihood ratio or test statistic λ can be defined as
| (2) |
where the weighting vector Wideal is defined as
| (3) |
is the mean vector for class k (= 1 or 2) and Σideal is the covariance matrix for both classes.
A caveat of an ideal observer model is the high dimensionality that may lead to the rank-deficient problem. The channelized Hotelling observer (CHO) (Ref. 14) that has been used to model signal detection tasks alleviates the dimensionality problem. Note that we do not intend to model a human observer in this study, but we made use of the idea to extract signal response from the MC candidates. With the CHO model, a region of interest (ROI) centered at an MC on a PV image can be represented by a multichannel filter bank using a set of orthonormal basis functions {b1, … bN}. The channelized basis functions are a set of optimal templates each of which can characterize an image in specific frequency bands. A given ROI image can be decomposed into a linear combination of multiple channels:
The ROI is therefore characterized by a set of channelized responses {f1, …, fN} that can be treated as a vector f = {f1, …, fN} in the space spanned by the set of orthonormal basis functions {b1, …, bN}. With this representation, the task of differentiating the true and false MC candidates can be formulated as a linear classification model to classify a given vector f into one of the two classes:
where is the mean vector for class k, k = 1,2 and Σ is an N × N covariance matrix for both classes. Therefore, the multichannel response, MCR(f), is a weighted sum of the individual channel response {f1, …, fN} that can be used as a decision variable for receiver operating characteristic (ROC) analysis.
From the analysis of the channel responses of a set of training ROI samples containing true MCs and FPs, the type of multichannel basis functions, the number of channels N that are effective for characterizing MCs can be determined by maximizing the separation between the two classes.
In this study, we investigated two types of basis functions: the Hermite–Gaussian (HG) polynomials, and the Laguerre–Gaussian (LG) polynomials, for MC representation, as described below. These two particular basis functions were chosen because, as the product of Hermite or Laguerre polynomials and a Gaussian function, they correspond to perturbations around a circular Gaussian. They also have many remarkable properties; they form an orthogonal (orthonormal if properly normalized) set of basis functions, are invariant under Fourier transforms which leads to an analytical form for convolution,15, 16 and can be derived from a generating function or a recursion relation. The LG and HG functions have been used in many areas, for example, the HG and LG functions describe the eigenstates of 2D quantum harmonic oscillator,15, 17 while the LG functions are commonly used in the CHO model for image quality assessment and simple signal detection tasks.
Hermite–Gaussian polynomials
The HG basis functions can be written as
| (4) |
where n ⩾ 0 (n = 0 yields a Gaussian distribution), Hn(x) is a Hermite polynomial of order n, r is the distance between a pixel in the ROI image and the center of the ROI, and s is a scaling factor. These functions are orthonormal in the sense that (δnm: Kronecker delta). In this study, we used the “physicists’ Hermite polynomials” defined by
| (5) |
The HG basis functions form a complete basis for smooth and integrable functions. Thus, an object profile f(x) can be expanded as
| (6) |
From the orthonormality condition, the coefficients are given by
| (7) |
In practice, the HG basis functions in the 2D domain can be constructed by taking the tensor product of any two 1D basis functions. In this study, a MC is centered at the center of the ROI image and, since MCs are small objects, they are assumed to be rotationally symmetric in all directions. We therefore constructed an isotropic 2D basis function by using the same 1D basis function for both dimensions.
Laguerre–Gaussian polynomials
The LG functions can be expressed as
| (8) |
where r is the distance between pixels in the image and the center of the ROI, s is a scaling factor, and Ln is the nth Laguerre polynomial. The Laguerre polynomials are defined by
| (9) |
where n ⩾ 0 (n = 0 yields a Gaussian distribution). An object profile can be expressed as a linear combination of the LG basis functions in a similar way as the HG functions, as shown in Eqs. 6, 7.
Coincidence counting method for fusion of 2D multichannel signal response in 3D
The coincidence counting method based on two-stage ray-tracing is designed to fuse the 2D MCR into a 3D response by using the known geometry of the DBT system. The object location in the 3D breast volume is estimated as a cone-shaped path connecting the focal spot location and the segmented object image on the PV plane. If the same MC candidate is detected in many PVs, the backprojected paths will intersect in the breast volume that can be considered the most likely location of the MC. In contrast, those without or with very few coincidence counts in the breast volume will be more likely to be noise and may be excluded for further processing. The two-stage ray-tracing consists of a backprojection process to identify all possible locations (voxels) where the MC candidates detected on the PVs may originate from, and a forward-projection process to eliminate redundant locations by using the counts accumulated in the voxels as a guide. Two volumes are generated to keep track of the coincidence counts and the accumulated 3D MCR values at a given voxel in the 3D space, as detailed below.
In the first-stage ray tracing, the x-ray path is backtraced from the locations of MC candidates to the x-ray source and the voxels intersecting with the x-ray path are recorded. Consider the backprojection process in matrix form as
| (10) |
where An is the projection matrix for the nth PV with aij as its (i, j)th element, n = 1, …, N; x is a vector containing all J voxels in the DBT volume with xj as itsjth element, j = 1, …, J; and is a vector containing all I pixels in the nth PV image with yi as its ith element, i = 1, …, I. The value of a targeted element xj in the DBT volume can be estimated by tracing all x rays traveling through this voxel. The voxel values of a backprojection volume can be written as
| (11) |
where is the (j,i)th element of the inverse of matrix An.
Our coincidence counting method is different from backprojection reconstruction in that the goal is not to estimate the linear attenuation coefficients in the volume so that the x-ray intensity values on the PV images are not used. For the generation of the volume of coincidence counts, the pixel values on the nth PV are taken as
| (12) |
| (13) |
For the generation of the volume of 3D MCR values, the pixel values on the nth PV are
| (14) |
| (15) |
where li is the actual path-length of the ith ray from the x-ray source to the ith pixel on the nth PV that intersects with the jth voxel calculated from the DBT system geometry.
Each MC candidate from a PV should only contribute to a single detection in the 3D space, but the traced ray of a MC candidate can intersect multiple voxels and contribute to many initial MC candidate voxels in the 3D MCR volume along the x-ray path. Therefore, the first-stage ray tracing process may cause an overestimation in the number of initial 3D candidate MCs. A second-stage ray tracing is designed to identify the most likely MC locations in the 3D volume. Initial MC candidate voxels are first located as those with coincidence counts greater than 2. All of the initial 3D MC candidates are then put into a priority queue where the one with the larger coincidence counts is assigned a higher priority. A forward ray tracing (from the x-ray source to the detector) and volumetric updating process will be performed sequentially following the priority from high to low for each initial 3D MC candidate in the priority queue. The forward ray tracing tracks all rays contributing to the candidate. The updating process updates the two volumetric data obtained in the first stage along the ray paths by eliminating the potentially redundant counts contributed to the 3D MC candidates as follows. For the coincidence counting volume, the candidate with the highest count and thus the highest priority along the ray path is kept while the counts for other candidates with lower priority along the same ray path are deducted. For the 3D MCR volume, the 3D MCR score of the candidate with the highest count is kept while the MCR scores for other candidates with lower counts along the same ray path are reduced by the amount contributed by the deducted rays. After the two volumes are updated, the set of 3D MC candidates are updated by excluding the 3D MC candidates that have updated coincidence counts less than 3. The set of remaining 3D MC candidates is then finalized by merging the connected components based on 26-connectivity in the coincidence counting volume. The MCR value of each voxel is obtained from the 3D MCR volume. The maximum MCR value among all connected voxels of a MC candidate is taken as the 3D MCR value of the candidate.
Dynamic clustering of MCs in 3D
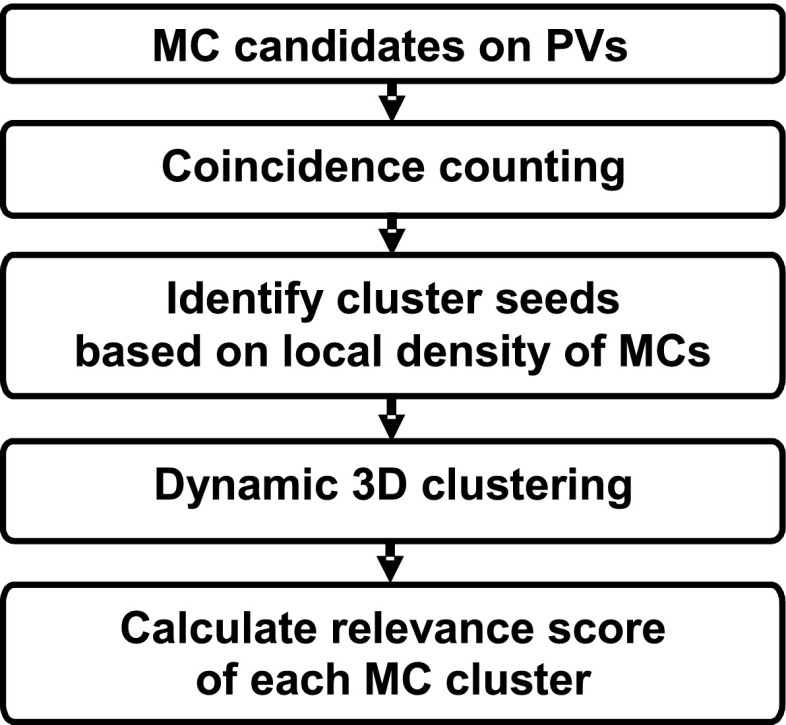
With the detected individual MC candidates (signals) in the 3D volume after coincidence counting, potential MC clusters are formed by a dynamic clustering procedure based on the fact that clinically significant MCs generally appear in clusters. In this process, a location associated with a higher density of potential signals, which is defined as the number of signals in a 20 × 20 × 20 mm volume of interest (VOI) centered at each of the potential signals, is given a higher priority as a starting region to grow a cluster. The dynamic clustering will search for new members in the neighborhood of the starting location and updates the cluster centroid after each new member is added. The inclusion criterion of a potential signal to the current cluster is that its distance from the cluster centroid is less than 5 mm. The cluster will stop growing if no more potential signals in the neighborhood can satisfy the inclusion criterion. Once a signal is included in a given cluster, it will be marked and excluded from being a candidate member of other clusters. The process continues until no more clusters can be grown in the breast region. The remaining signals that are not found to be members of any potential clusters will be considered as isolated noise objects and excluded in further analyses. The cluster relevance score of each identified MC cluster is defined as the sum of the 3D MCR values of all its members. Figure 4 summarizes the process of the identification of 3D MC clusters.
Figure 4.
Schematic diagram of the identification of 3D MC clusters.
Performance evaluation
In order to evaluate our 2D approach to MC detection in DBT, two-fold cross validation was employed for training and testing. We divided the collected 40 patients with two-view DBTs into two equal sized independent subsets by case, i.e., all views of the same case were grouped into the same subset. The focus of the training was to select the multichannel basis functions for MCR analysis and the formulation of the linear classification model.
To select the basis functions to describe MCs on the PVs, a set of ROI images with and without MCs were used as training samples. A 2D PV is basically a low-dose FFDM but the CNR of individual MCs on the PVs is very low. To obtain more reliable true MCs, a trained researcher used a graphical user interface to mark the locations of individual MCs in the reconstructed DBT volume within the bounding box of the clusters drawn by the experienced radiologist. Each marked MC was then ray-traced to the 21 PVs using the known imaging geometry of the DBT system to find the corresponding locations of the MC on the PVs. A 31 × 31-pixel ROI was extracted from each of these locations as training samples. The ROI size was chosen to be large enough to cover an individual MC and its surrounding background. In our data set, a total of 1135 individual 3D MCs were marked in the 82 DBT volumes. Forward projection of these MCs resulted in 23 835 2D MC candidates on the PVs.
FP training samples were obtained from the MC candidates in the DBT volume after the prescreening stage of the CADe system (described above). In this study, the radiologists drew a 3D VOI around each true MC cluster. To find the corresponding 2D bounding box on the PVs, we projected an extended VOIs of the MC cluster (10 extra pixels on each side) onto the 21 PVs in order to allow spaces around the true MCs for estimation of the background noise during the training. The location of a prescreening detected MC candidate on a given PV was compared to the bounding box of the true MC cluster projected to the PV. The MC candidates outside the bounding box were considered FPs. A 31 × 31-pixel ROI was also extracted from each of the FP locations as training samples. There were a total of 211 344 2D-FPs on the PVs (i.e., an average of 122.7 FPs/PV at prescreening). For the twofold cross validation subsets, one contained 10 902 true MCs and 100 820 FPs and the other contained 12 933 true MCs and 110 524 FPs.
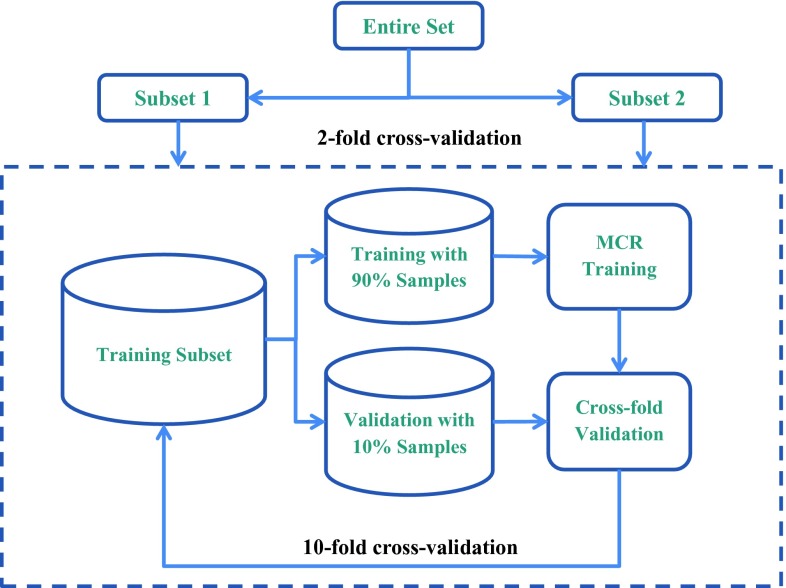
Figure 5 showed the training and testing schemes in this study. Within each of the two cross validation cycles, the best set of parameters of the multichannel basis functions (HG and LG), including the number of channels and the best scaling parameter for the differentiation of true and false MC candidates, was selected using the training subset with tenfold cross validation resampling. For each of the tenfold cross validation cycles, the filter bank of selected parameters was applied to the MC candidates in the PVs of the training subset (90% of the samples in the training subset) to generate the channelized responses {f1, …, fN} and formulate the CHO model. The 2D MCR for each MC candidate in the validation subset (remaining 10% of the samples in the training subset) was then obtained from the trained CHO model and the area under the ROC curve (AUC) was estimated for the validation subset in this tenfold cross validation cycle. The average AUC obtained from averaging the AUCs of the ten validation subsets was used as the figure-of-merit to guide the selection of the filter bank parameters within the training subset.
Figure 5.
Illustration of training and testing schemes in this study. A twofold cross validation method was used for training and testing of the overall detection performance of the CADe system. When one subset was used for training, tenfold cross validation was performed within the training subset to select the parameters of the channelized basis functions. The trained CADe system was applied to the other subset for testing and a FROC curve was obtained from each of the twofold cross validation cycle.
Using the selected parameters from the training subset, the multichannel filter bank was used in the CHO model to calculate the 2D MCR of each MC candidate in the respective test subset in the twofold cross validation process. The 3D MCRs were then generated from the 2D MCRs by the coincidence counting method described above and used as the decision variable for classification of the true and false MCs in 3D. The AUC was calculated from ROC analysis of the classification performance for each test subset.
After FP reduction and dynamic clustering in 3D, the overall cluster detection performance of the CADe system was evaluated with a free response ROC (FROC) analysis by varying a decision threshold applied to the cluster relevance score. At a given relevance threshold, a cluster was classified as a true positive (TP) cluster if the center of its bounding box was located within the box marked by radiologist as a true cluster; otherwise, it was a FP cluster. FROC curves were obtained on both a per-view and a per-cluster basis. For view-based FROC analysis, the MC cluster in each DBT volume was considered an independent target. While for cluster-based FROC analysis, the MC cluster imaged on the two-view DBT was considered to be the same target and detection of the cluster on either one or both views was considered to be a TP detection. The clusters in the left and the right breasts of the subject with bilateral MCs were counted as different targets in the cluster-based FROC analysis.
RESULTS
Figure 6 showed the average test AUCs as a function of the number of channels for different scaling factors when the 2D MCR was used for classification of true and false MCs detected on the PVs at prescreening. The results for each training subset and for the LG and HG basis functions were plotted separately. With the HG basis functions [Figs. 6a, 6b], the average validation AUCs ranged from 0.644 to 0.686 for training subset 1 and from 0.732 to 0.754 for training subset 2. The maximum AUCs were observed at the parameter setting of n = 3 and s = 7 for both subsets. With the LG basis functions [Figs. 6c, 6d], the average validation AUCs ranged from 0.643 to 0.684 for training subset 1 and from 0.731 to 0.753 for training subset 2. The maximum AUCs were observed at the parameter setting of n = 17 and s = 7 for subset 1 and n = 14 and s = 8 for subset 2. The parameters with the maximum validation AUCs were selected for the two filter banks in the subsequent performance evaluation.
Figure 6.
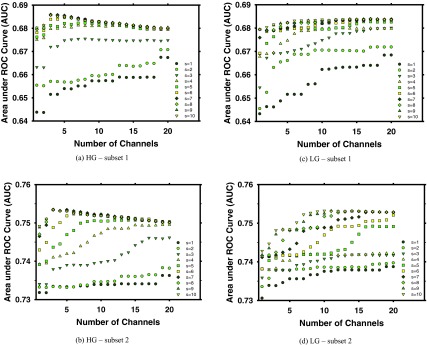
Dependence of the average validation AUCs obtained from tenfold cross validation within each training subset. (a) and (b) HG basis functions. (c) and (d) LG basis functions. (a) and (c) Subset 1. (b) and (d) Subset 2.
After fusion of the 2D MCR into 3D MCR, the AUCs in classifying individual true MCs from FPs in the two test subsets were evaluated. With the HG basis functions, the AUCs were 0.872 ± 0.013 and 0.874 ± 0.012, respectively. With the LG basis functions, the corresponding AUCs were 0.872 ± 0.013 and 0.872 ± 0.012, respectively. No statistically significant differences (p > 0.05 with ROC analysis) between the HG and LG filter banks were observed for either of the test subsets.
After 3D clustering, the cluster relevance score was used as decision threshold to generate FROC curves. The view-based FROC curves for the two test subsets are shown in Fig. 7a for the HG basis functions and Fig. 7c for the LG basis functions. The cluster-based FROC curves were shown in Fig. 7b for the HG basis functions and Fig. 7d for the LG basis functions. An average FROC curve was also estimated from the curves of the two test subsets by averaging the FP rates at the corresponding sensitivity levels.
Figure 7.
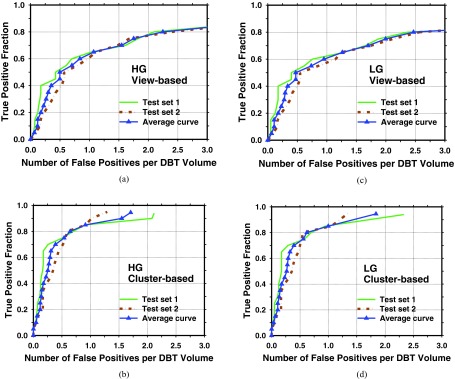
FROC curves for detection of clustered MCs in DBT volumes. The average curves were derived from the curves for the two test subsets by averaging the FPs rates at the corresponding sensitivity level. (a) and (c) View-based FROC curves; (b) and (d) cluster-based FROC curves; (a) and (b) HG basis functions; and (c) and (d) LG basis functions.
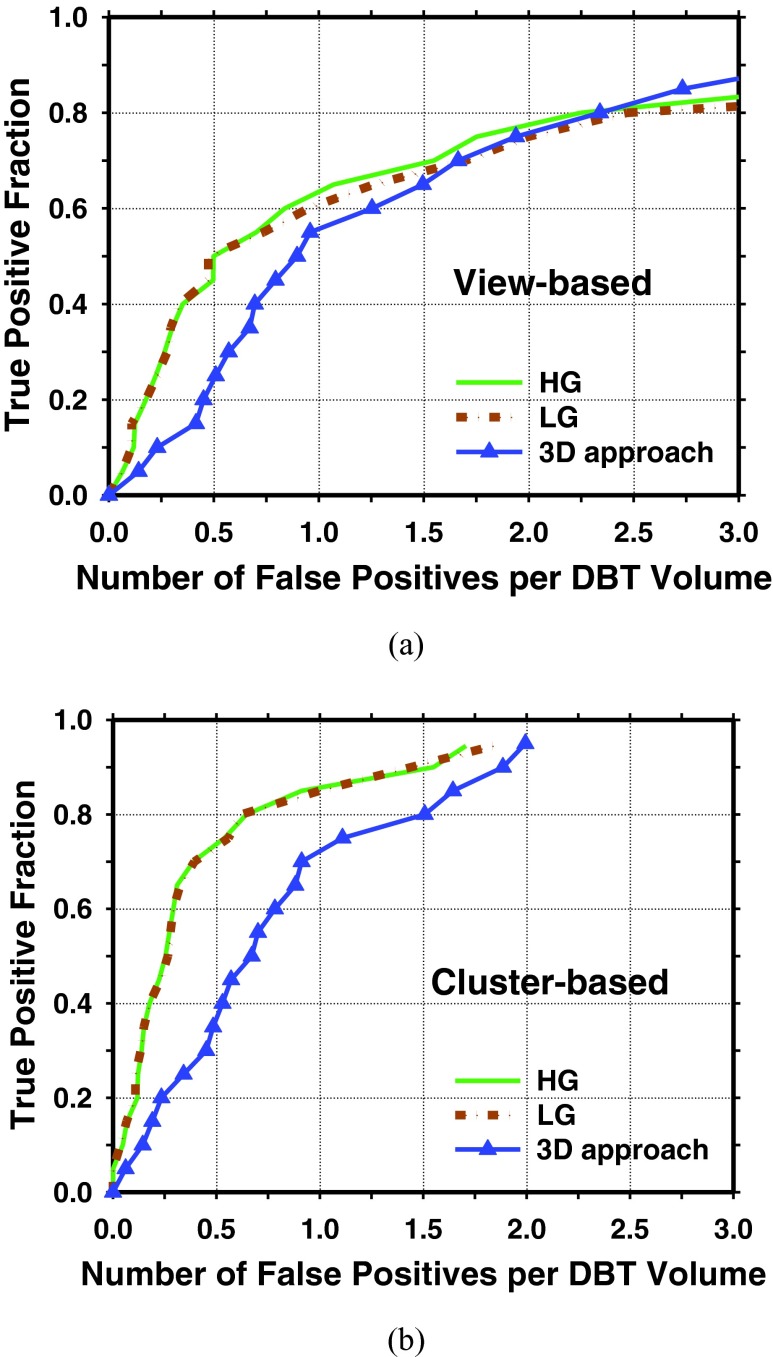
We have previously developed a prototype CADe system for detection of clustered MCs in DBT using a 3D approach.10 Figure 8 showed a comparison of the FROC curves from the current and the previous approaches for the same data set used in this study. Table 1 showed a comparison of the FP rates of the current and previous approaches at three sensitivity levels.
Figure 8.
FROC curves for detection of clustered MCs in DBT volumes with our previously developed prototype CADe system using a 3D approach (Ref. 10). For the HG and LG basis functions, the average curves were derived from the curves for the two test subsets by averaging the FPs rates at the corresponding sensitivity level. For the 3D approach, the FROC curve was obtained directly from the entire data set. (a) View-based FROC curves; (b) cluster-based FROC curves.
Table 1.
Cluster-based FROC detection performance of the CADe systems in test subset 1, test subset 2, and the average over the two test subsets using the HG and the LG basis functions. The detection performance of our prototype CADe system using the 3D approach by Sahiner et al. (Ref. 10) on the entire data set is also shown in the last column for comparison.
| FPs per DBT volume |
|||||||
|---|---|---|---|---|---|---|---|
| Cluster-based | Test subset 1 |
Test subset 2 |
Average |
3D approach | |||
| sensitivity | HG | LG | HG | LG | HG | LG | (Ref. 10) |
| 70% | 0.26 | 0.29 | 0.52 | 0.50 | 0.39 | 0.40 | 0.91 |
| 80% | 0.70 | 0.70 | 0.59 | 0.55 | 0.65 | 0.63 | 1.51 |
| 90% | 2.08 | 1.95 | 1.02 | 1.19 | 1.55 | 1.57 | 1.89 |
DISCUSSION
In this study, we developed a 2D channelized approach in combination with a coincidence counting method for detection of clustered MCs in DBTs. The results indicated the effectiveness of our detection approach and demonstrated the feasibility of 2D-based computerized MC detection that made use of PVs as input and the geometric information of the DBT imaging system to combine the detection on PVs for FP reduction. The channelized approach decomposes the ROI image of each candidate object into a linear combination of localized basis functions of different shapes. The information about the object is therefore encoded in the channelized responses, which are then fused in 3D and used for classification. In a conventional approach, a set of feature descriptors is usually extracted from the candidate objects and the true and false lesions are differentiated by a trained classifier in the multidimensional feature space.
We compared two multichannel filter banks, the HG and the LG basis functions, for characterization of MC signals. The LG basis functions have been found to be useful for the channelized Hotelling Observer model for relatively large and low contrast signals. In this study, we investigated if the LG and HG functions may be used as basis representation for small, higher contrast signals such as microcalcifications in computerized detection without the human observer. The Hermite and Laguerre polynomials are both related to the confluent hypergeometric function.18 From ROC analysis, we found that these two basis functions performed similarly on the classification of MCs from FPs but a smaller size of filter bank could be used for the HG basis functions. Since the use of high frequency components may include more noise and computation time will increase with the number of filter channels, a smaller size of filter bank is usually preferred.
To further understand if the detection performance would be affected by breast density and the subtlety of the MC clusters, we analyzed the breast density and the subtlety ratings of the false negative (FN) clusters. Table 2 summarized the number of FNs at two decision threshold levels on the FROC curves for the HG and LG filter banks and the number of FNs that were common to both. Table 3 shows the mean and standard deviation of the breast density and subtlety ratings of the FN clusters by a MQSA radiologist. In comparison, the mean and standard deviation of the breast density and subtlety ratings by the same radiologist for the entire data set were 2.76 ± 0.71 and 3.74 ± 2.23, respectively.
Table 2.
Comparison of the numbers of FP clusters and false negative clusters for detection of MC in DBT volume between the LG and HG basis functions. Cluster-based FROC analysis was used in this comparison.
| FPs per | Number of false negatives |
||
|---|---|---|---|
| DBT volume | HG (M and B) | LG (M and B) | Common |
| 1.0 | 5 (5 and 0) | 6 (6 and 0) | 4 |
| 0.5 | 12 (11 and 1) | 12 (11 and 1) | 11 |
Note: M = malignant; B = benign.
Table 3.
The mean and standard deviation of breast density and cluster subtlety ratings by a MQSA radiologist for the FN clusters missed by using the LG and HG basis functions for detection of MC clusters in DBT volume.
| HG basis functions |
LG basis functions |
|||||
|---|---|---|---|---|---|---|
| FPs per | Number | Breast | Number | Breast | ||
| DBT volume | of FNs | density | Subtlety | of FNs | density | Subtlety |
| 1.0 | 5 | 3.20 ± 0.84 | 6.80 ± 1.68 | 6 | 3.00 ± 0.89 | 6.25 ± 2.14 |
| 0.5 | 12 | 3.08 ± 0.79 | 6.50 ± 1.94 | 12 | 3.08 ± 0.79 | 6.83 ± 1.71 |
These analyses do not reveal noticeable relationship between breast density and the detection performance of MC clusters. On the other hand, it appeared that the visual appearance of FNs was subtler than that of TPs for MC detection with our 2D approach. The difference in the mean subtlety ratings between the TPs and FNs at 0.5 FPs per DBT volume was statistically significant (p = 0.03) with two-tailed unpaired t test at 95% confidence level. In our data set, we have 32 malignant and 10 benign MC clusters. The numbers of FNs for benign clusters were 1 and 0 at 0.5 and 1.0 FPs per DBT volume, respectively. The average subtlety rating of the 10 benign MC clusters was 3.77 ± 2.23, while the subtlety rating of the single benign FN cluster was 6.0. The reason of miss may more likely be related to the visibility than to the malignant or benign status of the MC clusters. Note that due to the limited sample size these stratified analyses may not be reliable and need to be verified with a larger data set in the future.
For both the HG or LG filter banks, we constructed isotropic 2D basis functions by using the same 1D basis functions in the horizontal and vertical directions while other studies used anisotropic basis functions for different purposes.19, 20 One reason to choose isotropic function is because most of the MCs are punctate or too small to show a well-defined shape. In addition, even there are linear or branching MCs, their orientations are quite random in an image. If anisotropic filters are used, MCRs at all orientations will need to be extracted and analyzed. Although we had 23 835 2D MCs projected from 1135 manually marked 3D MCs in the current data set, subsets of MCs of specific shape and orientation would be too small for training. Further study of anisotropic basis functions may be pursued if large sets of MCs of various shapes and orientations with manually marked locations become available in the future. A major drawback of using the channelized filter bank approach is that it requires individually identified MCs for training of the parameters. Manually marking the MC locations is a very tedious process and it is difficult to collect a very large training set.
In principle, the set of PVs together with the geometry of the DBT system should contain the same information as the reconstructed DBT volume because the latter is derived from the former. The reconstruction process that combines the information from the PVs generally can enhance the signal and reduce noise. However, the performance of a CADe system using the reconstructed volume as input may depend on the reconstruction technique and parameters used because they affect the resulting image quality. On the other hand, detection of signals on the individual PVs may be more difficult because of the low exposure and thus noisy images, but the CADe system will be independent of reconstruction. Fusion of the detected candidates on PVs in 3D using the DBT system geometry is a crucial step to differentiate true and false signals. Our coincidence counting method was found to increase the classification accuracy substantially. However, both our 2D-PV and 3D approaches are still at the early stage of development and further improvement and assessment with large data sets are needed for a more reliable comparison. Furthermore, the choice between the two approaches would depend on the expected application of the CADe system.
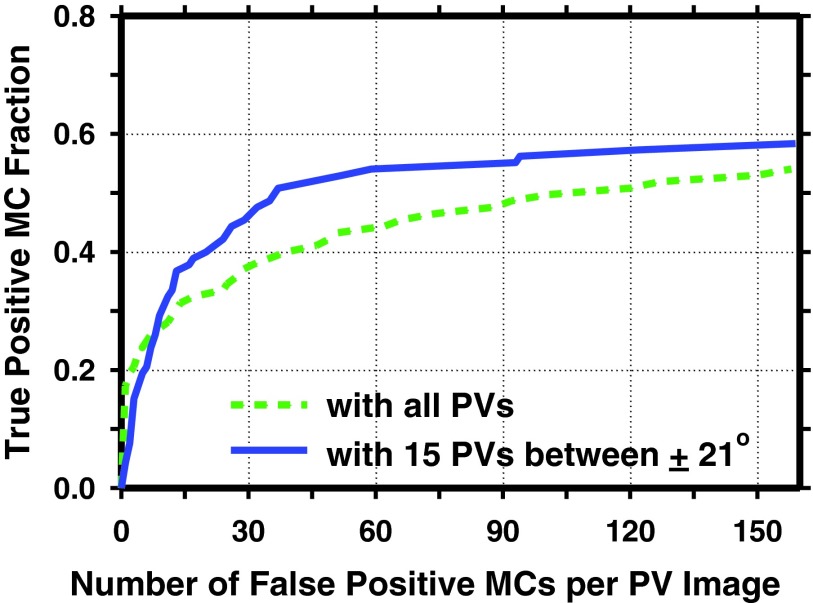
An important issue with the detection of MCs on PVs is that, for a DBT system with a large tomographic scan angle and uniformly distributed exposure over the PVs, the exposure for PVs at large angles decreases rapidly because of the increasing x-ray path-length through the breast tissue, leading to increased image noise. The large oblique incidence angle to the detector also increases image unsharpness. In this study, we observed that the detection of MCs in the PVs at large angles was poorer than those at small angles. Figure 9 compared the prescreening of individual MCs in the PVs with and without the PVs at large angles (i.e., using only the 15 PVs between ±21°). The sensitivity was calculated as the fraction of MC candidates detected at prescreening that were at the locations where the manually marked individual MCs were projected to the PVs. The curve was generated by varying the CNR threshold chosen for prescreening. It can be observed that the sensitivity at a given FP rate was substantially higher on the PVs at small angles. After the 2D MCRs on PVs were combined into 3D MCRs by coincidence counting, the classification performance was greatly improved as indicated by the AUCs. This suggested that the fusion of the 2D MCRs from the PVs using the coincidence counting technique did strengthen the signals and help distinguish them from noise.
Figure 9.
Comparison of prescreening sensitivities of individual MCs with and without PVs at large angles (>21°). Solid curve: prescreening on all PVs (21 PVs centered at 0° and between ±30°); dashed curve: prescreening on PVs with narrow angles (using only 15 PVs centered at 0° and between ±21°).
Our CADe system included many stages, each of which is composed with several image processing and machine learning techniques. The choice of parameters in each stage may affect the performance of the CADe as a whole. In this study, we focused on selection of the multichannel filter bank and their parameters to characterize the individual MCs and the fusion method to merge the 2D information in 3D. We made use of the previously developed techniques for microcalcification detection on FFDMs for the other stages. Further optimization of the techniques may improve the detection accuracy of the 2D CADe system for DBT. For example, in the prescreening stage, the current strategy only achieved a sensitivity ranging from about 49% to 59% on different PVs for the individual MCs. Retraining the SNR enhancement stage and other parameters for the detection on PVs may improve the sensitivity while controlling the FP rate. We refrained from further tuning of the parameters to avoid overtraining because of the limited data set in this study.
CONCLUSION
We developed a 2D approach for detection of clustered MCs in DBT that made use of PVs as input. A channelized approach using a multichannel filter bank for extracting signal response from individual MCs on the PVs was adapted from the channelized Hotelling observer model. A coincidence counting method using two-stage ray tracing technique and the geometric information of the DBT imaging system was designed to fuse the information from the PVs and to reduce noise. Our experimental results indicated the feasibility of this 2D-based CADe system for MC detection in DBT.
ACKNOWLEDGMENTS
This work is supported by USPHS Grant No. R01 CA151443. The content of this paper does not necessarily reflect the position of the funding agencies and no official endorsement of any equipment and product of any companies mentioned should be inferred.
References
- Niklason L. T. et al. , “Digital tomosynthesis in breast imaging,” Radiology 205, 399–406 (1997). 10.1148/radiology.205.2.9356620 [DOI] [PubMed] [Google Scholar]
- Poplack S. P., Tosteson T. D., Kogel C. A., and Nagy H. M., “Digital breast tomosynthesis: Initial experience in 98 women with abnormal digital screening mammography,” Am. J. Roentgenol. 189, 616–623 (2007). 10.2214/AJR.07.2231 [DOI] [PubMed] [Google Scholar]
- Andersson I., Ikeda D., Zackrisson S., Ruschin M., Svahn T., Timberg P., and Tingberg A., “Breast tomosynthesis and digital mammography: A comparison of breast cancer visibility and BIRADS classification in a population of cancers with subtle mammographic findings,” Eur. Radiol. 18, 2817–2825 (2008). 10.1007/s00330-008-1076-9 [DOI] [PubMed] [Google Scholar]
- Hakim C. M., Chough D. M., Ganott M. A., Sumkin J. H., Zuley M. L., and Gur D., “Digital breast tomosynthesis in the diagnostic environment: A subjective side-by-side review,” Am. J. Roentgenol. 195, W172–W176 (2010). 10.2214/AJR.09.3244 [DOI] [PubMed] [Google Scholar]
- Skaane P. et al. , “Prospective trial comparing full-field digital mammography (FFDM) versus combined FFDM and tomosynthesis in a population-based screening programme using independent double reading with arbitration,” Eur. Radiol. 23, 2061–2071 (2013). 10.1007/s00330-013-2820-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rose S. L., Tidwell A. L., Bujnoch L. J., Kushwaha A. C., Nordmann A. S., and Sexton R., “Implementation of breast tomosynthesis in a routine screening practice: An observational study,” Am. J. Roentgenol. 200, 1401–1408 (2013). 10.2214/AJR.12.9672 [DOI] [PubMed] [Google Scholar]
- Spangler M. L., Zuley M. L., Sumkin J. H., Abrams G., Ganott M. A., Hakim C., Perrin R., Chough D. M., Shah R., and Gur D., “Detection and classification of calcifications on digital breast tomosynthesis and 2D digital mammography: A comparison,” Am. J. Roentgenol. 196, 320–324 (2011). 10.2214/AJR.10.4656 [DOI] [PubMed] [Google Scholar]
- Wallis M. G., Moa E., Zanca F., Leifland K., and Danielsson M., “Two-view and single-view tomosynthesis versus full-field digital mammography: High-resolution X-ray imaging observer study,” Radiology 262, 788–796 (2012). 10.1148/radiol.11103514 [DOI] [PubMed] [Google Scholar]
- Bernard S., Muller S., and Onativia J., “Computer-aided microcalcification detection on digital breast tomosynthesis data: A preliminary evaluation,” Digital Mammography, Lecture Notes in Computer Science Vol. 5116 (Springer, Berlin, 2008), pp. 151–157. [Google Scholar]
- Sahiner B., Chan H.-P., Hadjiiski L. M., Helvie M. A., Wei J., Zhou C., and Lu Y., “Computer-aided detection of clustered microcalcification in digital breast tomosynthesis: A 3D approach,” Med. Phys. 39, 28–39 (2012). 10.1118/1.3662072 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiser I., Nishikawa R. M., Edwards A. V., Kopans D. B., Schmidt R. A., Papaioannou J., and Moore R. H., “Automated detection of microcalcification clusters for digital breast tomosynthesis using projection data only: A preliminary study,” Med. Phys. 35, 1486–1493 (2008). 10.1118/1.2885366 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y., Chan H.-P., Wei J., and Hadjiiski L. M., “Selective-diffusion regularization for enhancement of microcalcifications in digital breast tomosynthesis reconstruction,” Med. Phys. 37, 6003–6014 (2010). 10.1118/1.3505851 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ge J., Sahiner B., Hadjiiski L. M., Chan H.-P., Wei J., Helvie M. A., and Zhou C., “Computer aided detection of clusters of microcalcifications on full field digital mammograms,” Med. Phys. 33, 2975–2988 (2006). 10.1118/1.2211710 [DOI] [PubMed] [Google Scholar]
- Barrett H. H., Yao J., Rolland J. P., and Myers K. J., “Model observers for assessment of image quality,” Proc. Natl. Acad. Sci. U.S.A. 90, 9758–9765 (1993). 10.1073/pnas.90.21.9758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Refregier A., “Shapelets: I. A method for image analysis,” Mon. Not. R. Astron. Soc. 338, 35–47 (2003). 10.1046/j.1365-8711.2003.05901.x [DOI] [Google Scholar]
- Refregier A. and Bacon D., “Shapelets: II. A method for weak lensing measurements,” Mon. Not. R. Astron. Soc. 338, 48–56 (2003). 10.1046/j.1365-8711.2003.05902.x [DOI] [Google Scholar]
- Wunsche A., “Laguerre 2D-functions and their application in quantum optics,” J. Phys. A: Math. Gen. 31, 8267–8287 (1998). 10.1088/0305-4470/31/40/017 [DOI] [Google Scholar]
- Coffey M. W., “Properties and possibilities of quantum shapelets,” J. Phys. A: Math. Gen. 39, 877–887 (2006). 10.1088/0305-4470/39/4/009 [DOI] [Google Scholar]
- Kelly B. C. and McKay T. A., “Morphological classification of galaxies by shapelet decomposition in the Sloan digital sky survey. II. Multiwavelength classification,” Astron. J. 129, 1287–1310 (2005). 10.1086/427999 [DOI] [Google Scholar]
- Victor J. D., Mechler F., Ohiorhenuan I., Schmid A. M., and Purpura K. P., “Laminar and orientation-dependent characteristics of spatial nonlinearities: Implications for the computational architecture of visual cortex,” J. Neurophysiol. 102, 3414–3432 (2009). 10.1152/jn.00086.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]