Abstract
Characterization of the complex branching architecture of cerebral arteries across a representative sample of the human population is important for diagnosing, analyzing, and predicting pathological states. Brain arterial vasculature can be visualized by magnetic resonance angiography (MRA). However, most MRA studies are limited to qualitative assessments, partial morphometric analyses, individual (or small numbers of) subjects, proprietary datasets, or combinations of the above limitations. Neuroinformatics tools, developed for neuronal arbor analysis, were used to quantify vascular morphology from 3 T time-of-flight MRA high-resolution (620 μm isotropic) images collected in 61 healthy volunteers (36/25 F/M, average age = 31.2 ± 10.7, range = 19–64 years). We present in-depth morphometric analyses of the global and local anatomical features of these arbors. The overall structure and size of the vasculature did not significantly differ across genders, ages, or hemispheres. The total length of the three major arterial trees stemming from the circle of Willis (from smallest to largest: the posterior, anterior, and middle cerebral arteries; or PCAs, ACAs, and MCAs, respectively) followed an approximate 1:2:4 proportion. Arterial size co-varied across individuals: subjects with one artery longer than average tended to have all other arteries also longer than average. There was no net right–left difference across the population in any of the individual arteries, but ACAs were more lateralized than MCAs. MCAs, ACAs, and PCAs had similar branch-level properties such as bifurcation angles. Throughout the arterial vasculature, there were considerable differences between branch types: bifurcating branches were significantly shorter and straighter than terminating branches. Furthermore, the length and meandering of bifurcating branches increased with age and with path distance from the circle of Willis. All reconstructions are freely distributed through a public database to enable additional analyses and modeling (cng.gmu.edu/brava).
Introduction
Cerebrovascular disorders are the leading cause of death, devastating morbidity, and long-term disabilities in humans, worldwide. Individual and group variations in the neurovascular structure–function relationship have not yet been comprehensively investigated. Quantitative characterization of cerebrovascular architecture from modern magnetic resonance angiography (MRA) may lead to a better understanding of physiological function and pathological dysfunction of the cerebrovascular system. MRA is a non-invasive technique for three-dimensional visualization of cerebral arteries. It is based on the contrast between rapidly moving arterial blood and stationary tissues that surround the vessel. To date, most MRA studies have been limited to qualitative or semi-quantitative assessments (El-Barhoun et al., 2009), partial morphometric analyses (Bullitt et al., 2009; Chen et al., 2011), small numbers of subjects (Canham and Finlay, 2004), and proprietary datasets (Nowinski et al., 2009a). A more comprehensive structural characterization of the cerebral arterial tree can be achieved by reconstructing the vascular arborization into an explicit 3D representation (Bullitt et al., 2005; Passat et al., 2006). In addition to enabling extensive morphometric analysis, these reconstructions can be used for subject-specific assessment of individual risks of vascular malformation using fluid dynamics modeling (Cebral et al., 2003; Oshima et al., 2001). These approaches require specification of appropriate boundary conditions and constraints related to arterial branch geometry and bifurcation characteristics (Onate et al., 2000; Olufsen, 1999). However, the difficulties of manually reconstructing extensive vascular structure limited numerical simulations to synthetic arterial tree models (Bui et al., 2010; Dokoumetzidis and Macheras, 2003; Karch et al., 1999; Olufsen et al., 2000).
Here, we show that 3D reconstruction of the cerebral arterial vasculature can be achieved using existing methods originally developed for digital tracing and quantitative analysis of neuronal trees (Brown et al., 2005; Halavi et al., 2012; Scorcioni et al., 2008). Further, we demonstrate how the existing analysis methods can be used to study individual and population differences in cerebral vasculature at the level of the entire vasculature, specific arteries or single branches. Age-related changes, hemispheric lateralization, and gender-related difference in cerebral circulation may all be important risk factors in cerebrovascular disorders (Zanatta et al., 2012; Zurada et al., 2011). For instance, increase in tortuosity of right arterial trees during normal aging may have clinical implications (Zurada et al., 2010, 2011), while higher rate of subarachnoid hemorrhages in women may be caused by hormonal differences (Ghods et al., 2012).
This report provides the most extensive quantification to date of the global and local anatomical features of arterial vasculature, including size, symmetry, branching characteristics, bifurcation angles, and path meandering, for a representative sample of the normal human population. We reconstructed the entire cerebral arterial trees visible in the MRA images, including basilar and the internal carotid arteries that feed the circle of Willis (CoW) and the six major arteries stemming from CoW, including the middle, anterior, and posterior cerebral arteries (MCAs, ACAs, and PCAs, respectively). These six arteries were followed and reconstructed for ~300 mm from the CoW, through ~15 bifurcation points along the paths. We focused on morphological measures most relevant to common pathological conditions and least affected by potential imaging limitations. In addition to characterizing normative statistics for this representative population sample, we systematically compared arterial geometry between hemispheres, genders, and branch types; and among arteries, along the path, and across subject ages. Our analysis reproduced and extended previous knowledge of the human cerebrovascular architecture. In addition to the tools to reconstruct, visualize, and analyze the vascular arbors, the entire dataset is freely shared with the greater research community (http://cng.gmu.edu/brava).
Methods
Subjects and data acquisition
Imaging data were collected at the Research Imaging Institute, University of Texas Health Science Center at San Antonio, using a Siemens TRIO, 3 T scanner and 12-channel head coil. 61 healthy, right-handed participants (36/25 F/M, average age = 31.2 ± 10.7, range = 19–64 years) recruited as part of the International Consortium for Brain Mapping (ICBM: Mazziotta et al., 1995, 2001). Exclusion criteria included endocrinal, neurological (stroke, TIA and history of aneurysms), and psychiatric illnesses, and MRI counter-indications as detailed elsewhere (Kochunov et al., 2009a,b).
Magnetic resonance angiography
MRA data were collected using a 3D, spoiled, gradient echo time-of-flight (TOF) sequence (Huettel et al., 2004) with 620 μm isotropic resolution and the following control parameters: TE/TR/flip angle = 4.4 ms/24.0 ms/18°. 3D-TOF sequence collects spatially contiguous data by performing 3D encoding of the entire imaging volume (Bernstein et al., 2004). To reduce saturation of TOF effects, the data were collected as two overlapping 200 mm thick slabs aligned with AC–PC and full brain coverage. Head motion was suppressed using expandable foam and mechanical head-holder. Slab thickness and excitation angles were varied in two healthy volunteers to optimize digital reconstruction reliability. A file with the final parameters used in this study can be downloaded from the reconstruction database. The study design was evaluated and approved by the Institutional Review Board at the University of Texas Health Science Center in San Antonio and all subjects signed an informed consent form.
Digital reconstructions
Digital reconstructions of arterial trees from 3D, TOF MRA images were carried out by the same person using the freeware Neuron_ Morpho plugin (personal.soton.ac.uk/dales/morpho; Brown et al., 2005) for ImageJ (imagej.nih.gov; Collins, 2007). The Neuron_Morpho functionality provides for tracing the spatial course of the six major cerebral arteries starting at the circle of Willis. The arterial tree was quantified as a series of interconnected tapering cylinders characterized by their 3D coordinates, diameter, and link to the previous node. The results were saved as ASCII files in the SWC format (Ascoli et al., 2001). The SWC format fully describes branching structures as a parsimonious series of interconnected tapering cylinders characterized by their x, y, and z positions, radius, the identity of the parent cylinder, and an arbitrary numeric tag to label structures of interest. The application of a neuronal tree reconstruction and analysis method to 3D TOF scans is non-trivial, given the different nature and scale of data. However, such extension is not entirely original. Another recent method developed for neuronal tracing was deemed to be highly generalizable (Wang et al., 2011). That method was also successfully customized for digital tracing of MRA image stacks (Wang, 2011). These previous reports discuss the similarities and differences between neuronal and angio-graphic segmentation.
The arterial vasculature was reconstructed in each subject as a single arbor stemming from the basilar artery (BA). The first visible point along the BA was chosen as the origin for the vascular tree in every subject. The internal carotid arteries (ICAs) and all visible connecting vessels of the CoW were also reconstructed, with the exclusion of the anterior communicating arteries so as to unambiguously maintain a binary tree structure of the resulting reconstructions in all subjects, greatly aiding consistent comparisons within and across the population sample. All six major arteries stemming from the CoW (right and left MCAs, ACAs, and PCAs) were completely reconstructed through each visible ending. The vascular reconstructions were systematically validated by detecting defects such as intersecting branches, zero-diameter branches, spatially overlapping branches, disconnected branches, etc. (Halavi et al., 2008) followed by thorough visual inspection. Reconstructions for each subject were visually validated by overlaying the reconstructed arborization onto the original MRA image stack and 3D volume renderings.
Morphological analysis
Morphometric parameters were extracted from the digital reconstructions using L-Measure (http://krasnow1.gmu.edu/cn3), an open source tool originally developed to quantify axonal and dendritic morphology (Scorcioni et al., 2008). An expansive battery of variables was selected to yield a comprehensive statistical characterization of angio-graphic anatomy at both global and local levels, including measurements of size, distances, angles, and branching structure. In order to explain the definitions of the trivial metrics, we adopt the following standard terminological notation (e.g. Brown et al., 2008). Additional details, as well as diagrams accompanying each morphometric definition, are documented online on the L-Measure help page.
We refer to a branch as a sequence of reconstruction points starting from a bifurcation (or from the root) and ending at the next bifurcation (bifurcating branch) or at a termination (terminating branch). The branch order is the number of bifurcations between a given point in the arborization and the root. The branch path length or simply branch length is the geodesic distance between the beginning and ending of a branch (i.e., the sum length along the branch). Branch tortuosity is the ratio between branch length and the Euclidean (straight) distance between its beginning and ending (Diedrich et al., 2011). The fractal dimension is the slope of the linear regression obtained from the log– log scatter plot of path vs. Euclidean length moving from the second to the last reconstruction point along a branch.
The total length of an arborization is the sum of all of its branch lengths. Its maximum path and Euclidean distances are respectively the geodesic and straight distances from the root to the farthest termination points (the farthest geodesic and Euclidean points do not necessarily coincide). The height of an arborization is the minimum vertical span of a box encompassing the brain in the horizontal plane that contains 95% of the reconstruction points. Width and depth are similarly defined for the spans perpendicular to the sagittal and coronal planes, respectively.
Two types of amplitude angles were measured at bifurcations. The remote bifurcation amplitude is the angle between the bifurcation point and the last reconstruction points of each of the two branches away from the root. The local bifurcation amplitude is the angle between the bifurcation point and the first reconstruction points of each of the two branches away from the root. The (remote) tilt is the smaller of the two angles between the bifurcation point, the previous bifurcation towards the root, and each of the last reconstruction points of the two branches away from the root. The torque is the angle between the plane of the current bifurcation and the plane of the previous bifurcation towards the root. The bifurcation partition measures the imbalance between the numbers of terminations in the two sub-trees, and is de-fined as the ratio of the difference between these two numbers over their sum minus two (Van Pelt et al., 1992). This formulation yields a unitary partition for fully asymmetric bifurcations (giving rise to one terminating and one bifurcating branch) and a nil partition for fully symmetric bifurcations (with identical numbers of terminations in the two sub-trees).
Statistical analysis
Effects of gender and hemispheric lateralization were assessed by Student's t test (for normally distributed variables) and Wilcoxon–Mann–Whitney nonparametric test (otherwise). Significance was determined by two-tailed exact p values after Bonferroni correction for multiple testing. Pairwise correlations were determined with Pearson's coefficient, with the p values indicating the probability of independent distributions. The age difference between males (31.48 ± 10.12) and females (30.97 ± 10.23) was not significant (p > 0.1). In selected analyses the sample was also divided by median age (28 years) into an older (38.2 ± 9.2, N = 32) and a younger (23.4 ± 2.4, N = 29) group.
Data availability
All reconstructions presented in this study along with extracted morphological measurements and metadata are freely accessible (http://cng.gmu.edu/brava). The graphical user interface was designed for browsing, searching, visualizing, organizing, and downloading data, metadata, and morphometric statistics.
Results
Visual aspect and inter-subject variation of reconstructed arterial vasculature
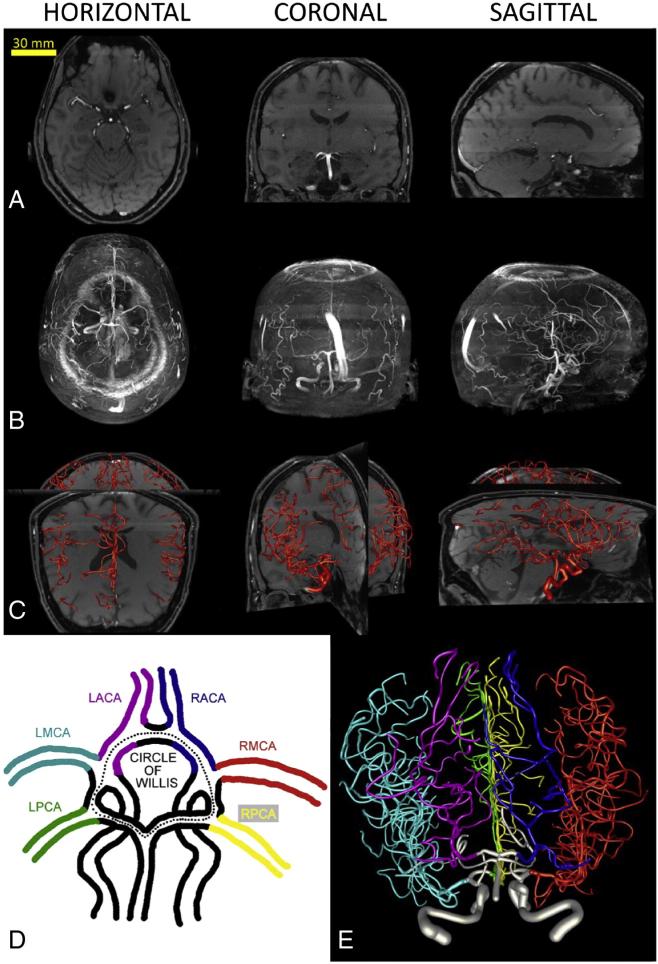
Brain arterial arbors for all subjects are shown in Fig. 1. Although vessels were always reconstructed from individual sections (Fig. 1A), occasional toggling to maximum intensity projections was useful to assess the full extent of the structure (Fig. 1B). Throughout the tracing process, the (partial or complete) reconstructed structure was periodically embedded in the data to verify its accuracy and facilitate correction of reconstruction errors using perpendicular views (Fig. 1C) or pseudo-3D rotational volume rendering. The quality of all reconstructions was independently verified by a second investigator.
Fig. 1.
Digital reconstructions of human brain vasculature from MRA imaging. A. Arterial arbors are semi-manually traced from single planar sections of each image stack in horizontal, coronal or sagittal views. B. Maximum intensity projections in the same orientations reveal a fuller extent of the imaged structure. C. Embedding of the final reconstructed arborization within the original image stack enables tracing validation by facilitating critical inspection of branch correspondence and identification of incomplete sub-trees. D. Color-coded schematic of the circle of Willis and the six major arteries stemming from it. E. Complete reconstruction of the brain vasculature corresponding to panels A–C (from a 59 year-old male) and color-coded by artery according to panel D.
The reconstruction pipeline yielded complete reconstructions (down to the image resolution) for all subjects. Two reconstructions from the same subject, imaged on different scanners, confirmed high reproducibility both by visual assessment and morphometric comparison. The six major arteries stemming from the CoW (Fig. 1D) were present in every subject and the same color scheme (Fig. 1E) was used consistently across the entire sample. High-resolution rendering of complete individual reconstructions provided visual information about the detailed vascular patterns within and across hemispheres, subjects, genders, and ages (Fig. 2). Qualitative comparison among the entire sample revealed noteworthy inter-subject variability of the size and shape of the six major arteries and entire arbors (Fig. 3), prompting further investigation by morphometric analysis.
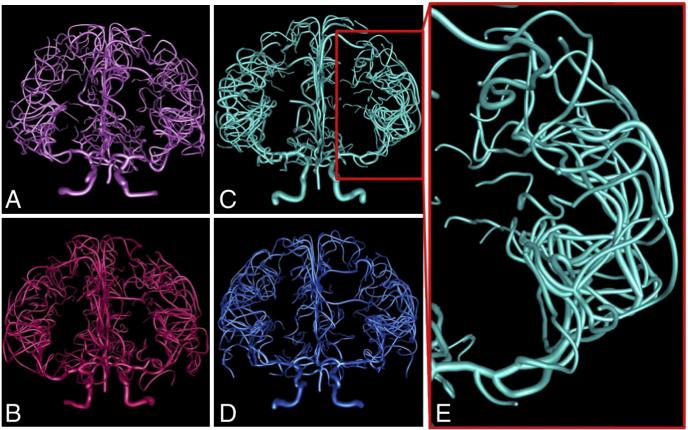
Fig. 2.
Representative arterial reconstructions color-coded by age and gender. A. Female, age 19 (light pink). B. Female, age 47 (dark pink). C. Male, age 21 (light blue). D. Male, age 46 (dark blue). E. Zoom-in on the left MCA, the largest of the arteries stemming from the circle of Willis, from panel C.
Fig. 3.
Visual variability of arterial structure across the population sample. All complete reconstructions (except those displayed in Figs. 1 and 2) are ordered in this montage by age and gender and color-coded by artery. Ages of females and males are shown in pink and blue, respectively.
Quantitative anatomy of cerebral arteries
As a simple initial normative quantification of arterial morphology and variability within our dataset, we extracted summary statistics for several scalar parameters characterizing the entire vascular structure in terms of overall size, bifurcation angles and symmetry, and branch features (Table 1). The sensitivity of the apparent diameter on blood flow in TOF MRA (Lell et al., 2007), especially at higher branch order, renders a purely structural interpretation ambiguous. Thus, we focused our analysis on diameter-independent parameters. However, we checked whether diameter differed by gender or changed by age in the first few branch orders, and found no significant differences in either case (data not shown).
Table 1.
Whole arterial metrics.
| Metric | Overall (N = 61) μ ± σ (min-max) | |
|---|---|---|
| Overall size | Total # branches | 208.6 ± 39.6 (138–330) |
| Total length (mm) | 7002.8 ± 945.8 (4752–9171) | |
| Max branch order | 15.46 ± 1.34 (13–19) | |
| Max path distance (mm) | 289.0 ± 23.5 (250–362) | |
| Max Euclidean distance (mm) | 108.9 ± 4.8 (98–123) | |
| Width (mm) | 118.3 ± 5.0 (109–129) | |
| Height (mm) | 84.6 ± 3.6 (76–93) | |
| Depth (mm) | 130.0 ± 9.1 (102–146) | |
| Bifurcation | Mean bifurcation tilt (°) | 45.69 ± 4.35 (37.13–56.60) |
| Mean bifurcation torque (°) | 54.31 ± 2.29 (48.61–60.28) | |
| Mean bifurcation amplitude (°) | 60.83 ± 2.97 (53.49–69.21) | |
| Mean local bifurcation amplitude (°) | 89.43 ± 3.19 ( 83.21–98.62) | |
| Mean partition | 0.51 ± 0.04 (0.41–0.59) | |
| Branch | Mean bifurcating tortuosity | 1.28 ± 0.05 (1.17–1.40) |
| Mean terminating tortuosity | 1.64 ± 0.09 (1.47–1.84) | |
| Mean bifurcating fractal dimension | 1.09 ± 0.01 (1.06–1.13) | |
| Mean terminating fractal dimension | 1.15 ± 0.02 (1.11–1.19) | |
| Mean bifurcating branch length (mm) | 25.02 ± 2.71 (19.35–30.14) | |
| Mean terminating branch length (mm) | 43.25 ± 5.35 (32.72–60.42) |
The variability of overall size was similar to that reported for other measures of human body size (e.g. ISO, 2010). For example, the coefficients of variation (CVs) for total length and number of branches were between 0.1 and 0.2, and the corresponding ranges went from 65% to 160% of the respective means. The various metrics of size were highly cross-correlated (e.g. between total length and number of branches: R = 0.83, p < 0.05). We also compared each of these metrics between right and left hemispheres, males and females, and as a function of age. None of the differences was statistically significant, with the only exception of height, which was greater in males than in females (85.66 ± 4.14 mm vs. 83.81 ± 2.94 mm, p < 0.001), again possibly reflecting the same trend in body size (ISO, 2010). A previously reported measurement of total arterial length from a single (51 year old male) subject, 8704 mm (Nowinski et al., 2011b) fell approximately half a standard deviation from our sample mean and within our sample range (Table 1) by a comfortable margin.
Bifurcation characteristics are important as the prevalence of aneurysms is higher at or near bifurcations (Lindekleiv et al., 2010). These metrics represent sample means of averages within arbors, and therefore display a substantially lower variability (e.g. CV < 0.05 for mean amplitude and range from 88% to 114% of the mean). Interestingly, the local amplitude angle was nearly one and a half times larger than the remote amplitude angle (p < 10−6). Bifurcations started at nearly orthogonal angles, but branches tended to grow towards each other before bifurcating again or terminating. The distribution of partition values indicates that arterial bifurcations display an intermediate arbor balance between perfectly symmetric and fully asymmetric trees. As for overall size, there were no statistical differences in measured bifurcation characteristics between hemispheres, genders, and across age, suggesting that these summary scalar metrics alone cannot explain group or bilateral differences of aneurysm prevalence.
Branch features are also relevant to cerebrovascular disease. For example, branch meandering, as measured by tortuosity (Bullitt et al., 2003) is altered in pathologies as different as stroke (Alazzaz et al., 2000), diabetes (Liem et al., 1996; Moritani et al., 2001), anemia (Vicari et al., 2011), and hypertension (Diedrich et al., 2011; Spangler et al., 1994). Earlier morphological investigations on neuronal dendrites described substantially longer terminating branches than bifurcating branches (Claiborne et al., 1990). These studies, however, did not extend to other branch characteristics, such as tortuosity, or multiple neuron types. When separately analyzing bifurcating and terminating branches (Table 1), we found surprisingly large and highly signifi-cant differences in branch length, tortuosity, and fractal dimension (p < 10−4 in all three cases). Specifically, terminating branches were on average 73% longer, 28% more tortuous, and 6% more fractal than bifurcating branches.
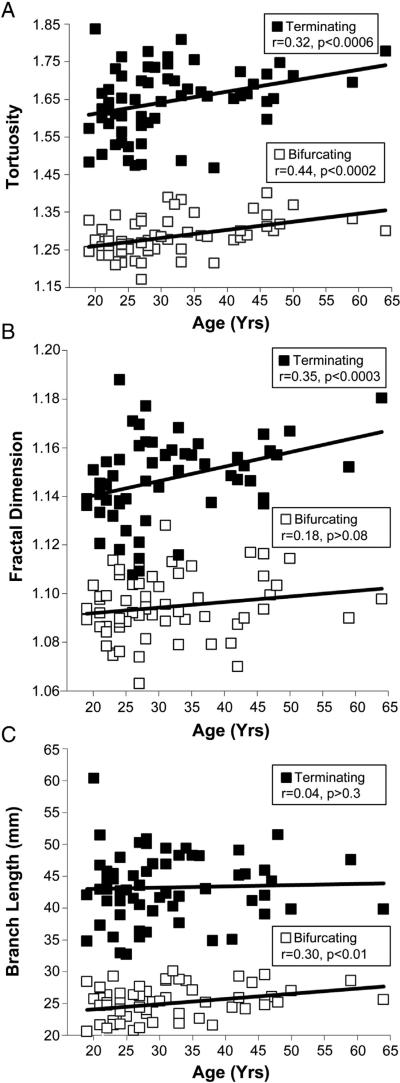
Although these branch properties, similar to size and bifurcation features, did not change between hemispheres and genders, we found significant changes with the age of the subjects (Fig. 4). Tortuosity increased with age in both bifurcating and terminating branches (Fig. 4A). Fractal dimension increased with age in terminating, but not bifurcating branches (Fig. 4B). In contrast, branch length increased in bifurcating, but not terminating branches (Fig. 4C). Further investigation will be necessary to determine the source and functional implication of these distinctions.
Fig. 4.
Change of bifurcating and terminating branch metrics with age. A. Branch tortuosity statistically tends to increase with the age of subjects. B. Fractal dimension significantly increases with age in terminating, but not bifurcating, branches. C. Branch length significantly increases with age in bifurcating, but not terminating, branches.
Size differences and proportional scaling among cerebral arteries
Next we examined the scalar morphometric characteristics of individual cerebral arteries (Table 2). As expected, MCAs were significantly larger than ACAs, and ACAs were significantly larger than PCAs. For example, MCAs had twice as many branches and twice as much total length as ACAs, and ACAs had 50% more branches and 50% greater total length than PCAs (p < 10−4 for each of these comparisons). While these trends tended to be generally true across the sample, the size distribution of ACAs overlapped with those of both the MCA and PCA, and there were occasional exceptions of individuals with larger PCAs than MCAs. Moreover, the height, width, and depth of individual arteries did not systematically follow the same trends even at the level of sample means, because of the different orientations of the cerebral arteries relative to the canonical (horizontal, coronal, and sagittal) planes of the brain.
Table 2.
Individual artery metrics.
| Metric | ACA (N = 122) μ ± σ (min–max) | MCA (N = 122) μ ± σ (min–max) | PCA (N = 122) μ ± σ (min–max) |
|---|---|---|---|
| Total number of branches | 26.0 ± 8.5 (4–52) | 52.7 ± 11.2 (30–94) | 18.9 ± 5.9 (6–34) |
| Total length (mm) | 877.4 ± 201.3 (234–1344) | 1878.2 ± 297.4 (967–2636) | 500.8 ± 124.1 (228–770) |
| Max branch order | 6.15 ± 1.53 (1–10) | 8.80 ± 1.40 (6–13) | 5.93 ± 1.66 (2–10) |
| Max path distance (mm) | 187.1 ± 18.7 (143–268) | 224.7 ± 22.1 (182–298) | 150.5 ± 16.6 (111–194) |
| Max Euclidean distance (mm) | 96.3 ± 9.1 (66–113) | 98.7 ± 6.2 (80–112) | 90.7 ± 7.1 (70–102) |
| Width (mm) | 26.0 ± 5.4 (10–48) | 38.5 ± 3.0 (33–48) | 30.5 ± 6.9 (16–49) |
| Height (mm) | 72.5 ± 7.5 (50–98) | 69.4 ± 5.6 (52–85) | 52.4 ± 10.2 (21–74) |
| Depth (mm) | 109.1 ± 14.3 (52–149) | 105.6 ± 10.0 (77–127) | 66.3 ± 6.7 (52–86) |
We also extracted all bifurcation and branch scalar morphometrics for the individual cerebral arteries (data not shown), and they were all statistically indistinguishable from the distributions reported in Table 1 (p > 0.1 in all cases). All the above measurements were also compared between males and females, right and left hemispheres, and across subject age (not shown), and no additional significant differences were found relative to the analysis of whole vasculature. The previously reported length values from an individual subject (Nowinski et al., 2009b), while larger than our means (MCA: 2198.7 mm; ACA: 1229.9 mm; PCA: 528.1 mm) fell within statistical expectation and the observed range of our sample.
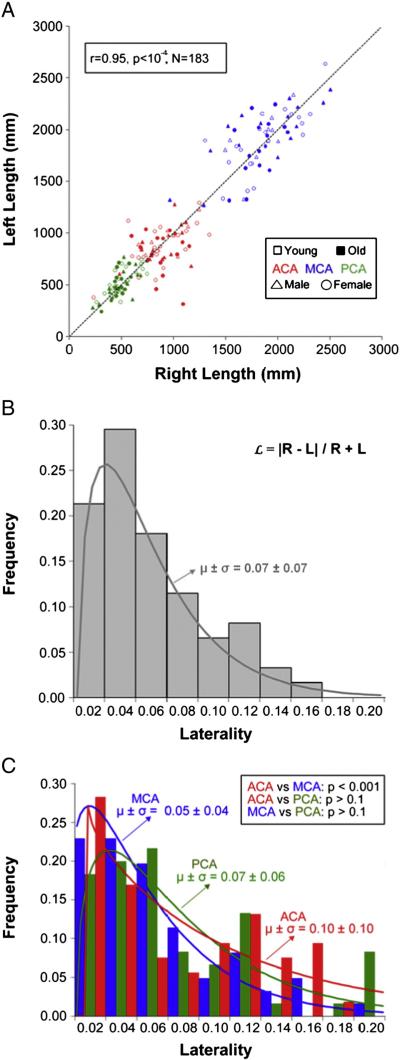
While summary statistics are useful by providing normative population baselines and a simple overview of vascular morphology, a more in-depth analysis is necessary to characterize the detailed arterial architecture within and among individual brains. We first focused on individual hemispheric dominance, or laterality (Fig. 5). There was a strong linear correlation between right and left lengths across the sample (Fig. 5A) and within genders, age groups, and artery types (R > 0.65, p < 0.001 in all cases). Although there was no overall hemispheric dominance across the sample, we investigated individual lateralization by defining laterality () as the absolute inter-hemispheric length difference normalized by total length:
where R and L are the right and left lengths, respectively. The distribution of laterality was statistically equivalent between genders and age groups, and whether calculated from 183 artery pairs (Fig. 5B) or the complete hemispheric vasculatures of 61 individuals. ACAs were significantly more lateralized than MCAs (Fig. 5C), but there were no other differences between cerebral arteries.
Fig. 5.
Hemispheric laterality of reconstructed vasculature length. A. The length differences between left and right artery pairs tend to vary in both directions and proportionally across trees. The dashed line indicates where left and right artery pairs would be of identical length. B. Laterality is the normalized absolute inter-hemisphere length difference within artery pairs (in the formula, R and L represent right and left lengths, respectively). C. ACA is significantly more lateralized than MCA, but there are no other differences between arteries, gender, and age.
The within-subject composition of arterial length was further considered to determine whether cerebral arteries might compensate for each other (Fig. 6). Specifically, we have recently discovered a form of morphological homeostasis in cortical dendrites (Samsonovich and Ascoli, 2006), whereas if a neuron is found to have a dendritic (sub-) tree smaller than expected based on population expectation, it would also tend to possess another (sub-)tree larger than average. It is unknown whether the same phenomenon might apply to brain arterial vasculature. The (bilateral) length of each cerebral artery visually appears to scale proportionally with overall size (Fig. 6A). Indeed, a significantly positive length cross-correlation was found between each artery and the rest of the vascular arborization (R values for MCA, ACA, and PCA: 0.68, 0.56, and 0.53, respectively, p < 10−4 in all cases), as well as between each pair of arteries (not shown). These data do not support the compensatory hypothesis. On the contrary, they suggest proportional scaling of brain arteries: if the vasculature is big, every artery is big, and vice versa.
Fig. 6.
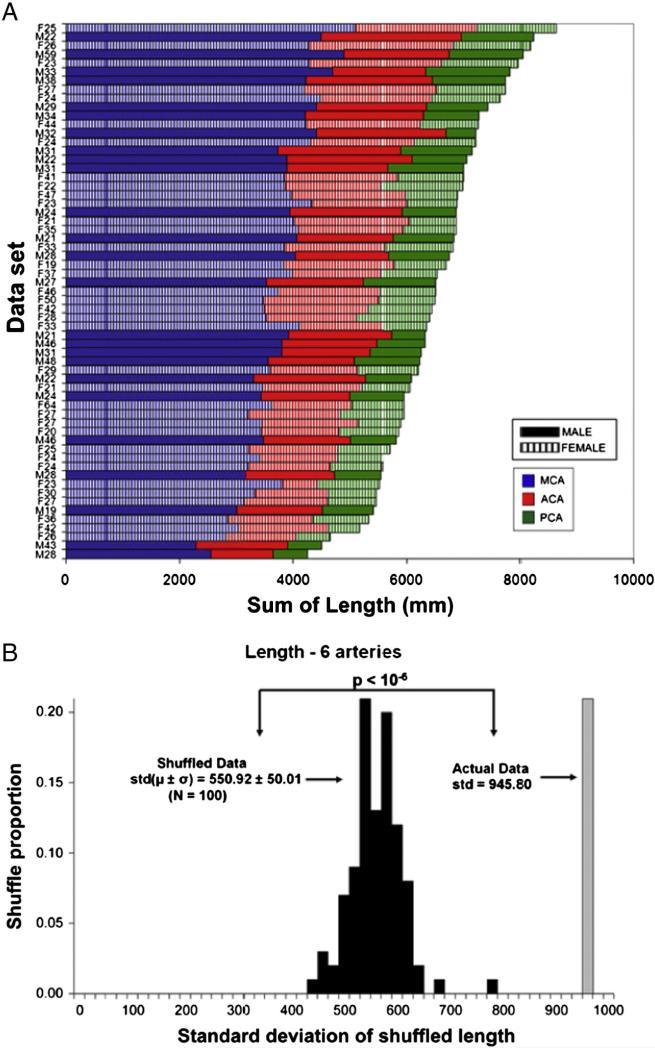
Individual artery length co-varies with total vasculature extent. A. Combined left/right arterial composition of all individual subjects ranked by total length reveals similar distributions across ages and genders. B. The observed population variance of the total arterial length is nearly 8 standard deviations greater than the mean length obtained by stochastically shuffling each of the corresponding 6 arteries within the sample. This indicates that subjects with longer-than-average vasculature also tend to have longer-than-average individual arteries.
To further test this possibility, we generated one hundred surrogate datasets by stochastically (but exclusively, i.e. non-repetitively) picking one of the six cerebral arteries from our sample. Then we measured the standard deviation of their total length and compared it to the observed value of the (single) real distribution. Morphological homeostasis and proportional scaling produce opposite predictions that the surrogate variance should be respectively greater and smaller than the real one. The result (Fig. 6B) provides uncontroversial support for proportional scaling, falsifying the compensation hypothesis. The same analyses (Figs. 5 and 6) repeated with other size metrics (e.g. number of branches) supported the same conclusions.
Systematic variation of selected morphometric properties along the vascular path
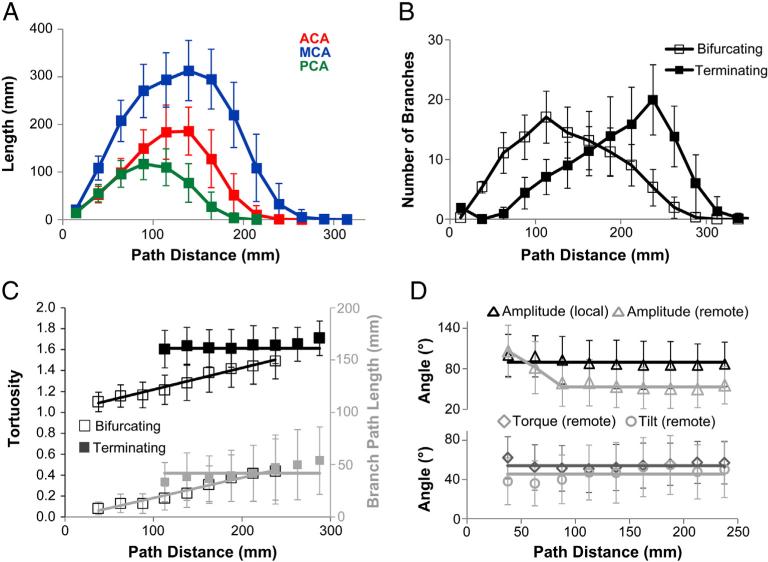
Lastly, we tested whether vascular morphology varied systematically along the arterial path or was uniform from the CoW to the distal branches (Fig. 7). The lengths of the major cerebral arteries were normally distributed across path distance (Fig. 7A): best fitting means and standard deviations of the sample distributions were 1878.2 ± 297.4, 877.4 ± 201.3, and 500.8 ± 124.1 mm for MCAs, ACAs, and PCAs, respectively. Bifurcating and terminating branch distributions had opposite skews (Fig. 7B): bifurcating branches arborize densely near the CoW and gently drop off; terminating branches increase slowly to peak farther out and decrease suddenly shortly thereafter. The length and tortuosity of bifurcating branches increase linearly along the path from the CoW (Fig. 7C), whereas terminating branches remain constant throughout the tree. Due to these contrasting behaviors, the values of the two branch types become similar around the distance at which terminating branches are densest (cf. Fig. 7B).
Fig. 7.
Vasculature extent, branching, and selected local metrics vary along the arterial path. A. Arterial length is normally distributed across the path distance from the circle of Willis and scales across MCAs, ACAs, and PCAs. B. Bifurcating and terminating branch distributions have opposite skews: the number of bifurcating branches peaks near the circle of Willis and gradually decreases thereafter; the number of terminating branches increases slowly and drops off suddenly at farther path distances. C. Branch length and tortuosity increase with path distance for bifurcating, but not terminating branches. D. Branching angles are largely constant along the arterial path: local amplitude is always larger than the (“remote”) angle measured at the end of the branch, except near the CoW.
Branching angles are independent of path distance (R2 < 0.04, p > 0.3 in all cases), except near the CoW, where remote amplitude is similar to local amplitude (Fig. 7D), decreasing to a constant mean angle after ~90 mm. This may be explained by the shorter branch lengths near the CoW (cf. Fig. 7C), reducing the opportunity for branches to meander closer towards each other. Indeed, remote amplitude is significantly different between branches shorter and longer than 20 mm (66 ± 4°, N = 3333 vs. 54 ± 32°, N = 2965, respectively, p < 10−4). Additionally, remote amplitude is negatively correlated with branch length, but only in shorter (<20 mm) branches, suggesting a length threshold to provide branches with enough freedom to reach their optimal angular spread. All individual cerebral arteries had similar trends when analyzed separately (not shown).
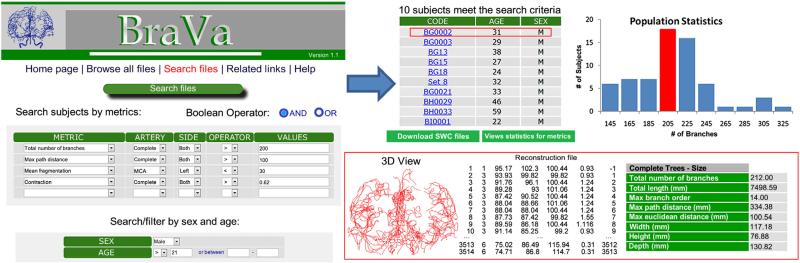
Public online availability of reconstructions
The normative dataset of 61 vascular reconstructions is freely downloadable at cng.gmu.edu/brava (Fig. 8). Boolean searches allow fast data retrieval filtered by any combination of the described morphometric features as well as subject age and gender. The reconstructions can be viewed as raw coordinate files or pseudo-3D visualized as rotating growth animations with color-coded individual arteries. The data include diameter information, analysis of which may be challenging to interpret. Similar to neuronal reconstructions at NeuroMorpho.Org, users can also render and manipulate the reconstructions within their browser in a built-in virtual reality online display. The morphometric results are also stored in the database and can be queried for complete trees or each of the six major arteries.
Fig. 8.
Accessibility and function of the BraVa database. The complete digital arterial reconstructions from all 61 MRA-imaged subjects described in this study, as well as the individual arteries, can be searched, downloaded, analyzed, and visualized by morphometric features and metadata.
Discussion
We adapted existing neuronal morphology methods for quantification of arterial arborization from high-resolution MRA data. We performed these analyses on a large sample of healthy human subjects and tested effects of age, gender and hemispheric lateralization on the main arterial tree. Earlier imaging data based upon hemodynamic response of blood vessels provided useful information on vascular anatomy, including arterial bifurcations (Fanucci et al., 1988, 1990; Rossitti and Lofgren, 1993b; Karch et al., 2000; Zurada et al., 2010, 2011) and branch tapering (MacLean et al., 1992; Roach and MacLean, 1993). However, these studies were limited in the number of subjects, completeness of the reconstruction, or detail of the quantitative analysis. This study replicated previous findings and expanded upon them by performing the analysis of arterial morphology across the entire cerebrum. Our findings include vascular quantification by size, bifurcation, and branch metrics. We found no significant differences in overall size and structure by gender, age or hemispheres. The three major arteries differ in size (PCA:ACA:MCA ~ 1:2:4), confirming on a larger population previous small-sample findings (Nowinski et al., 2013), and co-vary within subjects. There is no hemispheric dominance across the population in any of the individual arteries, but ACAs are individually more lateralized than MCAs. ACAs, MCAs, and PCAs have similar branch level properties, but throughout the arterial vasculature, bifurcating branches are significantly shorter and straighter than terminating branches. Moreover, the length and tortuosity of the bifurcating branches increased with age and path distance from the CoW.
Precise characterization of vascular anatomy is important for understanding cerebrovascular diseases (O'Flynn et al., 2007) and formation of intracranial aneurysms in particular (Bor et al., 2008; Canham and Finlay, 2004; Ingebrigtsen et al., 2004). For example, aneurysm prevalence varies between genders and hemispheres (Horiuchi et al., 2006), and sharply increases after the age of 50 (Wardlaw and White, 2000). We measured an extensive battery of global and local morphological properties, from the entire vascular arbors to individual arterial branches, including but not limited to size, distances, and angles. None of these geometric features explains gender or hemispheric differences in aneurysm prevalence. Nevertheless, several differences across age emerged when separately examining bifurcating and terminating branches.
It should be noted, however, that of the 61 subjects used in this study only two females and one male were over the age of 50. Therefore, more data from older individuals is needed to study morphological characteristics that might predict age prevalence of aneurysms. The most dramatic morphological differences were found between bifurcating and terminating branches, and between bifurcating branches farther and closer to the CoW. These findings raise the intriguing possibility of a structural underpinning of the prevalence of aneurysms near bifurcations (Norman and Powell, 2010) and closer to the CoW (Kayembe et al., 1984), where almost all branches are bifurcating rather than terminating. Interestingly, tortuosity, usually associated with greater hemorrhagic prevalence, increased with distance from the CoW and was higher in terminating than bifurcating branches.
Strong functional and structural hemispheric dominance is present in the human brain (Chiron et al., 1997; Geschwind and Galaburda, 1985; Good et al., 2001; Hugdahl, 2005; Lancaster et al., 2003; Serrien et al., 2006; Watkins et al., 2001). Inter-hemispheric differences in arterial size were present in all individuals, but without a net right or left prevalence. Laterality was most pronounced for ACA, with no gender or age effects. The variability of whole arterial arbor size was also similar between genders, and was consistent across individual arteries (i.e. larger right MCA was predictive of larger left ACA), indicating that vascular trees do not compete with or compensate for each other. Both local and remote branching angles remained remarkably constant throughout the arterial vasculature. Arterial bifurcations started at near-orthogonal angles and systematically closed in to significantly narrower remote amplitude. These observations are consistent with optimal design principles proposed to explain other aspects of arterial geometry and function, such as the “principle of minimum work” (Rossitti and Lofgren, 1993a), Murray's law of dissipation (Liu and Kassab, 2007; Painter et al., 2006; Sherman, 1981), and fractal scaling (Kassab, 2006; Zamir, 2001) similar to other biological systems (Kamiya and Takahashi, 2007). In contrast, the lack of branch-level differences between hemispheres or among MCAs, ACAs, and PCAs suggests surprising absence of vascular differentiation among functional regions (e.g. visual vs. motor areas).
While 3 T TOF MRA remains the preferred routine technique for detailed morphological analysis of brain arteries (Ahmed and Masaryk, 2004; Bammer et al., 2005; Insko and Carpenter, 2004; Parmar et al., 2005), it is important to recognize its limits. These include saturation of the signal in the direction that is parallel to slab orientation and reduced visibility in the branches with slower flow velocity and near the top of the imaging slab (Wilms et al., 2001). Thus, the spatial resolution of our data may not have been sufficient to resolve full arterial trees (Nowinski et al., 2011a,b). The number of missed branches can be reduced by collecting data at finer scale with a 7 T scanner, which allows resolving smaller arteries such as the medial, intermediate and lateral lenticulostriate branches of MCA (Nowinski et al., 2013).
We did not fully report arterial diameter information because use of TOF MRA may lead to its underestimation (Vaphiades and Horton, 2005) due to the signal dependence on flow velocity. Our limited evaluation of arterial diameter in the first few branch orders from the CoW, however, revealed no significant difference by age or gender. The availability of all reconstructions in our database enables future investigation of additional aspects of arterial morphology with due interpretative care. It would be particularly interesting to compare the diameter measures of these reconstructions with physical “ground truth” measures to facilitate better estimates from non-invasive imaging. Interestingly, diameter determination is a limiting factor in the morphometry of neuronal dendrites as well (Scorcioni et al., 2004), although the source of the problem is obviously different.
Despite these limitations, this study and the accompanying database provide an unprecedented normative collection of quantitative morphometric parameters measured from in vivo 3D imaging of the arterial vasculature of the human brain. Technological developments in the field allow for high-resolution mapping of both arterial and venous circulation by using ultra-high-resolution (isotropic-500 μm) MRI and CT angiography data (Nowinski et al., 2013). The dataset presented here can be extended in future studies to a broader range of ages, integrated with other imaging modalities, augmented with vein information, and compared with different experimental conditions including pathological states. Moreover, the reconstructions can be used to implement complex computational models of fluid dynamics that may aid understanding of physiological function and cerebrovascular diseases.
Acknowledgments
This work was supported by the NIH grants NS39600, EB001955, EB015611, EB006395, and NS061770 and by the Human Brain Mapping Project, which was jointly funded by the NIMH and NIDA (P20 MH/DA52176). We thank Drs. Duncan Donohue, Ruggero Scorcioni, Stephen Senft, Maryam Halavi, Ms. Sridevi Polavaram, and other members of CN3, for helpful discussion throughout the course of this project.
Footnotes
Conflict of interest
Authors declared no Conflict of Interest.
References
- Ahmed M, Masaryk TJ. Imaging of acute stroke: state of the art. Semin. Vasc. Surg. 2004;17(2):181–205. doi: 10.1053/j.semvascsurg.2004.03.013. [DOI] [PubMed] [Google Scholar]
- Alazzaz A, Thornton J, Aletich VA, Debrun GM, Ausman JI, Charbel F. Intracranial percutaneous transluminal angioplasty for arteriosclerotic stenosis. Arch. Neurol. 2000;57(11):1625–1630. doi: 10.1001/archneur.57.11.1625. [DOI] [PubMed] [Google Scholar]
- Ascoli GA, Krichmar JL, Nasuto SJ, Senft SL. Generation, description and storage of dendritic morphology data. Philos. Trans. R. Soc. B-Biol. Sci. 2001;356(1412):1131–1145. doi: 10.1098/rstb.2001.0905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bammer R, Skare S, Newbould R, Liu C, Thijs V, Ropele S, Clayton DB, Krueger G, Moseley ME, Glover GH. Foundations of advanced magnetic resonance imaging. NeuroRx. 2005;2(2):167–196. doi: 10.1602/neurorx.2.2.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein MA, King KF, Zhou J. Handbook of MRI Pulse Sequences. Elsevier Academic Press; Burlington, Vermont: 2004. [Google Scholar]
- Bor AS, Velthuis BK, Majoie CB, Rinkel GJ. Configuration of intracranial arteries and development of aneurysms: a follow-up study. Neurology. 2008;70(9):700–705. doi: 10.1212/01.wnl.0000302176.03551.35. [DOI] [PubMed] [Google Scholar]
- Brown KM, Donohue DE, D'Alessandro G, Ascoli GA. A cross-platform free-ware tool for digital reconstruction of neuronal arborizations from image stacks. Neuroinformatics. 2005;3:343–359. doi: 10.1385/NI:3:4:343. [DOI] [PubMed] [Google Scholar]
- Brown KM, Gillette TA, Ascoli GA. Quantifying neuronal size: summing up trees and splitting the branch difference. Semin. Cell Dev. Biol. 2008;19(6):485–493. doi: 10.1016/j.semcdb.2008.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bui AV, Manasseh R, Liffman K, Sutalo ID. Development of optimized vascular fractal tree models using level set distance function. Med. Eng. Phys. 2010;32(7):790–794. doi: 10.1016/j.medengphy.2010.04.014. [DOI] [PubMed] [Google Scholar]
- Bullitt E, Guido G, Pizer SM, Lin W, Aylward SR. Measuring tortuosity of the intracerebral vasculature from MRA images. IEEE Trans. Med. Imaging. 2003;22(9):1163–1171. doi: 10.1109/TMI.2003.816964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullitt E, Muller KE, Jung I, Lin W, Aylward S. Analyzing attributes of vessel populations. Med. Image Anal. 2005;9(1):39–49. doi: 10.1016/j.media.2004.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullitt E, Rahman FN, Smith JK, Kim E, Zeng D, Katz LM, Marks BL. The effect of exercise on the cerebral vasculature of healthy aged subjects as visualized by MR angiography. AJNR Am. J. Neuroradiol. 2009;30(10):1857–1863. doi: 10.3174/ajnr.A1695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Canham PB, Finlay HM. Morphometry of medial gaps of human brain artery branches. Stroke. 2004;35:1153–1157. doi: 10.1161/01.STR.0000124926.76836.df. [DOI] [PubMed] [Google Scholar]
- Cebral JR, Castro MA, Soto O, Lohner R, Alperin N. Blood flow models of the circle of Willis from magnetic resonance data. J. Eng. Math. 2003;47(3–4):369–386. [Google Scholar]
- Chen YC, Li MH, Qiao RH. Analysis of correlation between the number of lenticulostriate arteries and hypertension based on high-resolution MR angiography findings. AJNR Am. J. Neuroradiol. 2011;32(10):1899–1903. doi: 10.3174/ajnr.A2667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chiron C, Jambaque I, Nabbout R, Lounes R, Syrota A, Dulac O. The right brain hemisphere is dominant in human infants. Brain. 1997;120:1057–1065. doi: 10.1093/brain/120.6.1057. [DOI] [PubMed] [Google Scholar]
- Claiborne BJ, Amaral DG, Cowan WM. Quantitative, three-dimensional analysis of granule cell dendrites in the rat dentate gyrus. J. Comp. Neurol. 1990;302(2):206–219. doi: 10.1002/cne.903020203. [DOI] [PubMed] [Google Scholar]
- Collins TJ. ImageJ for microscopy. Biotechniques. 2007;43(1 Suppl.):25–30. doi: 10.2144/000112517. [DOI] [PubMed] [Google Scholar]
- Diedrich KT, Roberts JA, Schmidt RH, Kang CK, Cho ZH, Parker DL. Validation of an arterial tortuosity measure with application to hypertension collection of clinical hypertensive patients. BMC Bioinforma. 2011;18(12 Suppl.):S15. doi: 10.1186/1471-2105-12-S10-S15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dokoumetzidis A, Macheras P. A model for transport and dispersion in the circulatory system based on the vascular fractal tree. Ann. Biomed. Eng. 2003;31(3):284–293. doi: 10.1114/1.1555627. [DOI] [PubMed] [Google Scholar]
- El-Barhoun EN, Gledhill SR, Pitman AG. Circle of Willis artery diameters on MR angiography: an Australian reference database. J. Med. Imaging Radiat. Oncol. 2009;53(3):248–260. doi: 10.1111/j.1754-9485.2009.02056.x. [DOI] [PubMed] [Google Scholar]
- Fanucci E, Oriacchio A, Pocek M. The vascular geometry of human arterial bifurcations. Investig. Radiol. 1988;1:713–718. doi: 10.1097/00004424-198810000-00002. [DOI] [PubMed] [Google Scholar]
- Fanucci E, Oriacchio A, Pocek M, Magrini A, Salomoni E. Optimal branching of human arterial bifurcations. Invest. Radiol. 1990;25(1):62–66. doi: 10.1097/00004424-199001000-00016. https://www.ncbi.nlm.nih.gov/m/pubmed/2298553/?i=6&from=/7458985/related. [DOI] [PubMed] [Google Scholar]
- Geschwind N, Galaburda AM. Cerebral lateralization. Biological mechanisms, associations, and pathology: I. A hypothesis and a program for research. Arch. Neurol. 1985;42:428–459. doi: 10.1001/archneur.1985.04060050026008. [DOI] [PubMed] [Google Scholar]
- Ghods AJ, Lopes D, Chen M. Gender differences in cerebral aneurysm location. Front. Neurol. 2012;3:78. doi: 10.3389/fneur.2012.00078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good CD, Johnsrude I, Ashburner J, Henson RNA, Friston KJ, Frackowiak RSH. Cerebral asymmetry and the effects of sex and handedness on brain structure: a voxel-based morphometric analysis of 465 normal adult human brains. NeuroImage. 2001;14:685–700. doi: 10.1006/nimg.2001.0857. [DOI] [PubMed] [Google Scholar]
- Halavi M, Polavaram S, Donohue DE, Hamilton G, Hoyt J, Smith KP, Ascoli GA. NeuroMorpho.Org implementation of digital neuroscience: dense coverage and integration with the NIF. Neuroinformatics. 2008;6(3):241–252. doi: 10.1007/s12021-008-9030-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Halavi M, Hamilton KA, Parekh R, Ascoli GA. Digital reconstructions of neuronal morphology: three decades of research trends. Front. Neurosci. 2012;6:49. doi: 10.3389/fnins.2012.00049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horiuchi T, Tanaka Y, Hongo K. Sex-related differences in patients treated surgically for aneurysmal subarachnoid hemorrhage. Neurol. Med. Chir. (Tokyo) 2006;46:328–332. doi: 10.2176/nmc.46.328. [DOI] [PubMed] [Google Scholar]
- Huettel SA, Song AW, McCarthy G. Functional Magnetic Resonance Imaging. Sinauer Associates, Inc.; Sunderland, Massachusetts: 2004. [Google Scholar]
- Hugdahl K. Symmetry and asymmetry in the human brain. Eur. Rev. 2005;13(2):119–133. [Google Scholar]
- Ingebrigtsen T, Morgan MK, Faulder K, Ingebrigtsen L, Sparr T, Schrimer H. Bifurcation geometry and the presence of cerebral artery aneurysms. J. Neurosurg. 2004;101:108–113. doi: 10.3171/jns.2004.101.1.0108. [DOI] [PubMed] [Google Scholar]
- Insko EK, Carpenter JP. Magnetic resonance angiography. Semin. Vasc. Surg. 2004;17(2):83–101. doi: 10.1053/j.semvascsurg.2004.03.010. [DOI] [PubMed] [Google Scholar]
- ISO (International Organization for Standardization) Basic Human Body Measurements for Technological Design — Part 2: Statistical Summaries of Body Measurements From Individual ISO Populations (TR 7250-2) 2010 [Google Scholar]
- Kamiya A, Takahashi T. Quantitative assessments of morphological and functional properties of biological trees based on their fractal nature. J. Appl. Physiol. 2007;102:2315–2323. doi: 10.1152/japplphysiol.00856.2006. [DOI] [PubMed] [Google Scholar]
- Karch R, Neumann F, Neumann M, Schreiner W. A tree-dimensional model for arterial tree representation, generated by constrained constructive optimization. Comput. Biol. Med. 1999;29(1):19–38. doi: 10.1016/s0010-4825(98)00045-6. [DOI] [PubMed] [Google Scholar]
- Karch R, Neumann F, Neumann M, Schreiner W. Staged growth of optimized arterial model trees. Ann. Biomed. Eng. 2000;28:495–511. doi: 10.1114/1.290. [DOI] [PubMed] [Google Scholar]
- Kassab GS. Scaling laws of vascular trees: of form and function. Am. J. Physiol. Heart Circ. Physiol. 2006;290:H894–H903. doi: 10.1152/ajpheart.00579.2005. [DOI] [PubMed] [Google Scholar]
- Kayembe KN, Sasahara M, Hazama F. Cerebral aneurysms and variations in the circle of Willis. Stroke. 1984;15:846–850. doi: 10.1161/01.str.15.5.846. [DOI] [PubMed] [Google Scholar]
- Kochunov P, Coyle T, Lancaster J, Robin DA, Hardies J, Kochunov V, Bartzokis G, Stanley J, Royall D, Schlosser AE, Null M, Fox PT. Processing speed is correlated with cerebral health markers in the frontal lobes as quantified by neuroimaging. NeuroImage. 2009a;49:1190–1199. doi: 10.1016/j.neuroimage.2009.09.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kochunov P, Robin D, Royall D, Lancaster J, Kochunov V, Coyle T, Schlosser A, Fox P. Can structural MRI cerebral health markers track cognitive trends in executive control function during normal maturation and adulthood? Hum. Brain Mapp. 2009b;30:2581–2594. doi: 10.1002/hbm.20689. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster JL, Kochunov PV, Thompson PM, Toga AW, Fox PT. Asymmetry of the brain surface from deformation field analysis. Hum. Brain Mapp. 2003;19:79–89. doi: 10.1002/hbm.10105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lell M, Fellner C, Baum U, Hothorn T, Steiner R, Lang W, Bautz W, Fellner FA. Evaluation of carotid artery stenosis with multisection CT and MR imaging: in-fluence of imaging modality and postprocessing. AJNR Am. J. Neuroradiol. 2007;28(1):104–110. [PMC free article] [PubMed] [Google Scholar]
- Liem MD, Gzesh DJ, Flanders AE. MRI and angiographic diagnosis of lupus cerebral vasculitis. Diagn. Neuroradiol. 1996;38:134–136. doi: 10.1007/BF00604798. [DOI] [PubMed] [Google Scholar]
- Lindekleiv HM, Valen-Sendstad K, Morgan MK, Mardal KA, Faulder K, Magnus JH, Waterloo K, Romner B, Ingebrigtsen T. Sex differences in intracranial arterial bifurcations. Gend. Med. 2010;7(2):149–155. doi: 10.1016/j.genm.2010.03.003. [DOI] [PubMed] [Google Scholar]
- Liu Y, Kassab GS. Vascular metabolic dissipation in Murray's law. Am. J. Physiol. Heart Circ. Physiol. 2007;292:H1336–H1339. doi: 10.1152/ajpheart.00906.2006. [DOI] [PubMed] [Google Scholar]
- MacLean NF, Kratky RG, Macfarlane TWR, Roach MR. Taper: an important feature of y-bifurcations in porcine renal arteries and human cerebral arteries. J. Biomech. 1992;25(9):1047–1052. doi: 10.1016/0021-9290(92)90039-4. [DOI] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox P, Lancaster J. A probabilistic atlas of the human brain: theory and rationale for its development. The International Consortium for Brain Mapping (ICBM). NeuroImage. 1995;2:89–101. doi: 10.1006/nimg.1995.1012. [DOI] [PubMed] [Google Scholar]
- Mazziotta JC, Toga AW, Evans A, Fox PT, Lancaster JL, Zilles K, Woods R, Paus T, Simpson G, Pike B, Holmes C, Collins L, Thompson P, MacDonald D, Iacoboni M, Schormann T, Amunts K, Palomero-Gallagher N, Geyer S, Parsons L, Narr K, Kabani N, Le Goualherg Boomsma, D., Cannon T, Kawashima R, Mazoyer B. A probabilistic atlas and reference system for the human brain: International Consortium for Brain Mapping (ICBM). Philos. Trans. R. Soc. B-Biol. Sci. 2001;356:1293–1322. doi: 10.1098/rstb.2001.0915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moritani T, Shrier DA, Numaguchi Y, Takahasi C, Yano T, Nakai K, Zhong J, Wang HZ, Shibata DK, Naselli SM. Diffusion-weighted echo-planar MR imaging of CNS involvement in systemic lupus erythematosus. Acad. Radiol. 2001;8(8):741–753. doi: 10.1016/S1076-6332(03)80581-0. [DOI] [PubMed] [Google Scholar]
- Norman PE, Powell JT. Basic science for clinicians. Site specificity of aneurysmal disease. Circulation. 2010;121:560–568. doi: 10.1161/CIRCULATIONAHA.109.880724. [DOI] [PubMed] [Google Scholar]
- Nowinski WL, Thirunavuukarasuu A, Volkau I, Marchenko Y, Aminah B, Puspitasari F, Runge VM. A three-dimensional interactive atlas of cerebral arterial variants. Neuroinformatics. 2009a;7(4):255–264. doi: 10.1007/s12021-009-9055-0. [DOI] [PubMed] [Google Scholar]
- Nowinski WL, Volkau I, Marchenko Y, Thirunavuukarasuu A, Ng TT, Runge VM. A 3D model of human cerebrovasculature derived from 3 T magnetic resonance angiography. Neuroinformatics. 2009b;7(1):23–36. doi: 10.1007/s12021-008-9028-8. [DOI] [PubMed] [Google Scholar]
- Nowinski WL, Chua BC, Marchenko Y, Puspitsari F, Volkau I, Knopp MV. Three-dimensional reference and stereotactic atlas of human cerebrovasculature from 7 Tesla. NeuroImage. 2011a;55(3):986–998. doi: 10.1016/j.neuroimage.2010.12.079. [DOI] [PubMed] [Google Scholar]
- Nowinski WL, Puspitasaari F, Volkau I, Marchenko Y, Knopp MV. Comparison of magnetic resonance angiography scans on 1.5, 3, and 7 Tesla units: a quantitative study of 3-dimensional cerebrovasculature. J. Neuroimaging. 2011b doi: 10.1111/j.1552-6569.2011.00597.x. http://dx.doi.org/ 10.1111/j.1552-6569.2011.00597.x (Mar 29. [Epub ahead of print]) [DOI] [PubMed]
- Nowinski WL, Puspitasari F, Volkau I, Orrison WW, Jr., Knopp MV. Quanti-fication of the human cerebrovasculature: a 7 Tesla and 320-row CT in vivo study. J. Comput. Assist. Tomogr. 2013;37:117–122. doi: 10.1097/RCT.0b013e3182765906. [DOI] [PubMed] [Google Scholar]
- O'Flynn PM, O'Sullivan G, Pandit AS. Methods for three-dimensional geometric characterization of the arterial vasculature. Ann. Biomed. Eng. 2007;35(8):1368–1381. doi: 10.1007/s10439-007-9307-9. [DOI] [PubMed] [Google Scholar]
- Olufsen MS. Structured tree outflow condition for blood flow in larger systemic arteries. Am. J. Physiol. Heart Circ. Physiol. 1999;276:257–268. doi: 10.1152/ajpheart.1999.276.1.H257. [DOI] [PubMed] [Google Scholar]
- Olufsen MS, Peskin CS, Kim WY, Pedersen EM, Nadim I, Larsen J. Numerical simulation and experimental validation of blood flow in arteries with structured-tree outflow conditions. Ann. Biomed. Eng. 2000;28(11):1281–1299. doi: 10.1114/1.1326031. [DOI] [PubMed] [Google Scholar]
- Onate E, Bugeda G, Suarez B. International Center for Numerical Methods in Engineering. Barcelona, Spain: 2000. Proceedings European Congress on Computational Methods in Applied Sciences and Engineering. ECCOMAS 2000. p. 20. ISBN: 84-89925-70-4. [Google Scholar]
- Oshima M, Ryo T, Toshio K, Nobuyuki T, Kiyoshi T. Finite element simulation of blood flow in the cerebral artery. Comput. Methods Biomech. Biomed. Eng. 2001;191(6–7):661–671. [Google Scholar]
- Painter PR, Eden P, Bengtsson HU. Pulsatile blood flow, shear force, energy dissipation and Murray's law. Theor. Biol. Med. Model. 2006;3:31. doi: 10.1186/1742-4682-3-31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parmar H, Sitoh YY, Hui F. Normal variants of the intracranial circulation demonstrated by MR angiography at 3 T. Eur. J. Radiol. 2005;56:220–228. doi: 10.1016/j.ejrad.2005.05.005. [DOI] [PubMed] [Google Scholar]
- Passat N, Ronse C, Baruthio J, Armspach JP, Maillot C. Magnetic resonance angiography: from anatomical knowledge modeling to vessel segmentation. Med. Image Anal. 2006;10(2):259–274. doi: 10.1016/j.media.2005.11.002. [DOI] [PubMed] [Google Scholar]
- Roach MR, MacLean NF. The importance of taper proximal and distal to Y-bifurcations in arteries. Front. Med. Biol. Eng. 1993;5(2):127–133. [PubMed] [Google Scholar]
- Rossitti S, Lofgren J. Vascular dimensions of the cerebral arteries follow the principle of minimum work. Stroke. 1993a;24(3):371–377. doi: 10.1161/01.str.24.3.371. [DOI] [PubMed] [Google Scholar]
- Rossitti S, Lofgren J. Optimality principles and flow orderliness at the branching points of cerebral arteries. Stroke. 1993b;24(7):1029–1032. doi: 10.1161/01.str.24.7.1029. [DOI] [PubMed] [Google Scholar]
- Samsonovich A, Ascoli G. Morphological homeostasis in cortical dendrites. Proc. Natl. Acad. Sci. U. S. A. 2006;103:1569–1574. doi: 10.1073/pnas.0510057103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scorcioni R, Lazarewicz M, Ascoli G. Quantitative morphometry of hippocampal pyramidal cells: differences between anatomical classes and reconstructing laboratories. J. Comp. Neurol. 2004;273:177–193. doi: 10.1002/cne.20067. [DOI] [PubMed] [Google Scholar]
- Scorcioni R, Polavaram S, Ascoli GA. L-Measure: a web-accessible tool for the analysis, comparison and search of digital reconstructions of neuronal morphologies. Nat. Protoc. 2008;3(5):866–876. doi: 10.1038/nprot.2008.51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serrien DJ, Ivry RB, Swinnen SP. Dynamics of hemispheric specialization and integration in the context of motor control. Nat. Rev. Neurosci. 2006;7:160–166. doi: 10.1038/nrn1849. [DOI] [PubMed] [Google Scholar]
- Sherman TF. On connecting large vessels to small: the meaning of Murray's law. J. Gen. Physiol. 1981;78:431–453. doi: 10.1085/jgp.78.4.431. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spangler KM, Challa VR, Moody DM, Bell MA. Arteriolar tortuosity of the white matter in aging and hypertension. A microradiographic study. J. Neuropathol. Exp. Neurol. 1994;53(1):22–26. doi: 10.1097/00005072-199401000-00003. [DOI] [PubMed] [Google Scholar]
- Van Pelt J, Uylings HB, Verwer RW, Pentney RJ, Woldenberg MJ. Tree asymmetry—a sensitive and practical measure for binary topological trees. Bull. Math. Biol. 1992;54(5):759–784. doi: 10.1007/BF02459929. [DOI] [PubMed] [Google Scholar]
- Vaphiades MS, Horton JA. MRA or CTA, that's the question. Surv. Ophthalmol. 2005;50(4):406–410. doi: 10.1016/j.survophthal.2005.04.002. [DOI] [PubMed] [Google Scholar]
- Vicari P, Silva GS, Nogutti MA, Neto FM, dos Santos NJ, Massaro AR, Figueiredo MS. Absence of association between TNF-α polymorphism and cerebral large-vessel abnormalities in adults with sickle cell anemia. Acta Haematol. 2011;125(3):141–144. doi: 10.1159/000321935. [DOI] [PubMed] [Google Scholar]
- Wang Y. A Broadly Applicable Three-Dimensional Neuron Reconstruction Framework Based on Deformable Models and Software System With Parallel GPU Implementation ((Doctoral Dissertation). Retrieved from Proquest Dissertations and Theses. 2011 Accession Order No. AAT 3496420. [Google Scholar]
- Wang Y, Narayanaswamy A, Tsai CL, Roysam B. A broadly applicable 3-D neuron tracing method based on open-curve snake. Neuroinformatics. 2011;9(2–3):193–217. doi: 10.1007/s12021-011-9110-5. [DOI] [PubMed] [Google Scholar]
- Wardlaw JM, White PM. The detection and management of unruptured intracranial aneurysms. Brain. 2000;123(2):205–221. doi: 10.1093/brain/123.2.205. [DOI] [PubMed] [Google Scholar]
- Watkins KE, Paus T, Lerch JP, Zijdenbos A, Collins DL, Neelin P, Taylor J, Worsley KJ, Evans AC. Structural asymmetries in the human brain: a voxel-based statistical analysis of 142 MRI scans. Cereb. Cortex. 2001;11(9):868–877. doi: 10.1093/cercor/11.9.868. [DOI] [PubMed] [Google Scholar]
- Wilms G, Bosmans H, Demaerel PH, Marchal G. Magnetic resonance angiography of the intracranial vessels. Eur. J. Radiol. 2001;38:10–18. doi: 10.1016/s0720-048x(01)00285-6. [DOI] [PubMed] [Google Scholar]
- Zamir M. Fractal dimensions and multifractality in vascular branching. J. Theor. Biol. 2001;212:183–190. doi: 10.1006/jtbi.2001.2367. [DOI] [PubMed] [Google Scholar]
- Zanatta P, Messerotti Benvenuti S, Valfre C, Baldanzi F, Palomba D. The role of asymmetry and the nature of microembolization in cognitive decline after heart valve surgery: a pilot study. 2012;27:199–206. doi: 10.1177/0267659112437776. [DOI] [PubMed] [Google Scholar]
- Zurada A, Gielecki J, Tubbs RS, Loukas M, Maksymowicz W, Cohen-Gadol AA, Michalak M, Chlebiej M, Zurada-Zielinska A. Three-dimensional morpho-metrical analysis of the M1 segment of the middle cerebral artery: potential clinical and neurosurgical implications. Clin. Anat. 2010;24:34–46. doi: 10.1002/ca.21051. [DOI] [PubMed] [Google Scholar]
- Zurada A, St Gielecki J, Tubbs RS, Loukas M, Zurada-Zielinska A, Maksymowicz W, Nowak D, Cohen-Gadol AA. Three-dimensional morphometry of the A1 segment of the anterior cerebral artery with neurosurgical relevance. Neurosurgery. 2011;67:1768–1782. doi: 10.1227/NEU.0b013e3181fa7fcb. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All reconstructions presented in this study along with extracted morphological measurements and metadata are freely accessible (http://cng.gmu.edu/brava). The graphical user interface was designed for browsing, searching, visualizing, organizing, and downloading data, metadata, and morphometric statistics.