Fabrication, Characterization, and Functionalization of Dual Carbon Electrodes as Probes for Scanning Electrochemical Microscopy (SECM)

Abstract

Dual carbon electrodes (DCEs) are quickly, easily, and cheaply fabricated by depositing pyrolytic carbon into a quartz theta nanopipet. The size of DCEs can be controlled by adjusting the pulling parameters used to make the nanopipet. When operated in generation/collection (G/C) mode, the small separation between the electrodes leads to reasonable collection efficiencies of ca. 30%. A three-dimensional finite element method (FEM) simulation is developed to predict the current response of these electrodes as a means of estimating the probe geometry. Voltammetric measurements at individual electrodes combined with generation/collection measurements provide a reasonable guide to the electrode size. DCEs are employed in a scanning electrochemical microscopy (SECM) configuration, and their use for both approach curves and imaging is considered. G/C approach curve measurements are shown to be particularly sensitive to the nature of the substrate, with insulating surfaces leading to enhanced collection efficiencies, whereas conducting surfaces lead to a decrease of collection efficiency. As a proof-of-concept, DCEs are further used to locally generate an artificial electron acceptor and to follow the flux of this species and its reduced form during photosynthesis at isolated thylakoid membranes. In addition, 2-dimensional images of a single thylakoid membrane are reported and analyzed to demonstrate the high sensitivity of G/C measurements to localized surface processes. It is finally shown that individual nanometer-size electrodes can be functionalized through the selective deposition of platinum on one of the two electrodes in a DCE while leaving the other one unmodified. This provides an indication of the future versatility of this type of probe for nanoscale measurements and imaging.

Ultramicroelectrodes (UMEs) offer high mass transport rates, low ohmic (IR) effects, low double layer charging,¹⁻³ and, as such, are optimal for many applications from kinetic measurements to electrochemical imaging. UMEs serve as imaging probes in scanning electrochemical microscopy (SECM), which has been used widely to study the interfacial process at the microscale and nanoscale, especially electrocatalysis⁴⁻⁶ and biological systems.⁷⁻¹² However, the overwhelming majority of these systems use single electrode probes and SECM can be productively extended to increasingly complex and challenging systems through the use of dual-electrode probes. In principle, such probes would allow two redox-active species to be detected concurrently or would permit redox-active species to be generated at one electrode and collected at the other electrode.^13,14

Dual-electrode systems are widely used to study the kinetics of redox reactions.^15,16 Usually, but not exclusively,^17,32 such devices operate in an amperometric/voltammetric mode, where each electrode is held at a potential to oxidize or reduce a target species of interest, and the current measured at each electrode relates to the flux of that active species, arriving at the electrode. In generation/collection (G/C) mode, one electrode generates the species of interest (oxidizes or reduces the analyte (A) to produce an active species (S1)) that is then collected at the other electrode [via oxidation or reduction to produce the starting material or another species (S2)]:

The flux of active species generated and collected depends on the geometry of the dual-electrode system and the mass transport between the electrodes. The G/C mode is often characterized by the collection efficiency, which is defined as the ratio of the current measured at the collector electrode to that measured at the generator electrode, usually under steady-state conditions.

Dual electrode systems that are constructed in a probe-type configuration include ring-disk,^18,19 dual-ring,²⁰ and dual-disk²¹⁻²⁴ geometries. Probe-based dual electrode systems have been constructed using single and dual barrel (theta) borosilicate and quartz pipets as a scaffold.^21,25 However, collection efficiencies for the majority of these systems have been low because the interelectrode distance has often been large with respect to the electrode size. A range of electrode sizes from 50 μm²¹ to nm²³ have been reported, but the wider adoption of these systems has been limited due to difficulties in fabricating and characterizing the probes.

Herein, we present a quick and simple method for the fabrication of probe-based dual carbon electrodes (DCEs). This method allows the reproducible fabrication of a wide range of DCE sizes (from nanoscale to microscale). DCEs are prepared from a laser-pulled quartz theta pipet followed by pyrolytic carbon deposition. This is a development of a recent method reported for making scanning ion conductance–scanning electrochemical microscopy (SICM–SECM) probes.²⁵ Pyrolytic deposition of carbon to form electrodes is a popular method, employed to form several different SECM probes.^20,26−28

Nanoscale DCEs are rather challenging to characterize geometrically.²⁹⁻³¹ As part of this study, we therefore developed a finite element method (FEM) simulation that allowed the effective geometry of individual nanoscale probes to be estimated from single-barrel voltammetry and G/C measurements. Furthermore, to demonstrate the suitability of these probes for SECM and to provide further insight into the probe geometry, approach curves, to insulating (inert) and conductive (active) surfaces, were recorded in the probe G/C mode using intermittent contact-SECM (IC-SECM).³²⁻³⁵

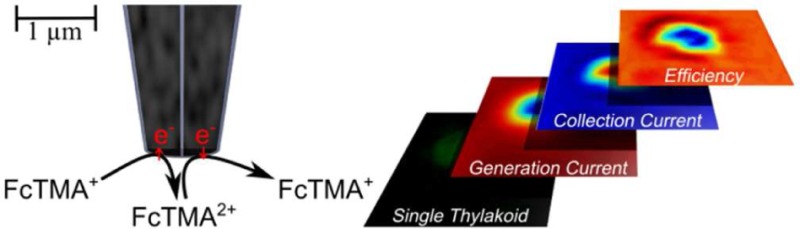
As a proof-of-concept, we used DCEs to study photosynthesis, at a film of isolated thylakoid membranes. In higher plants, thylakoid membranes contain the light-dependent components of photosynthesis, where light is absorbed and used to split water (at photosystem II).³⁶ Electrons, produced from the splitting of water, are transferred through the linear electron transport pathway before being used to produce the energy-rich molecule, NADPH.³⁶ Interestingly, a number of artificial electron acceptors can intercept the electrons and be reduced by various components of this thylakoid membrane-bound electron transport pathway.^36,37 We use a DCE to locally generate an artificial electron acceptor (oxidizing ferrocenylmethyl trimethylammonium, FcTMA⁺, to produce FcTMA²⁺) and to monitor the local flux of both species. The SECM platform also allowed us to construct two-dimensional (2D) current images of a single thylakoid membrane, highlighting the subtle interactions of a locally generated electron acceptor with a dynamic biological membrane.

Finally, we show that individual electrodes within a single probe can be functionalized, through the selective deposition of platinum. This demonstrates that DCEs could be used as a platform for a range of chemical sensing applications in the future.

Experimental Section

Materials and reagents, together with details of the protocols used to prepare thylakoid membranes, are detailed in sections S1–S3 of the Supporting Information.

Electrode Fabrication

DCEs were fabricated by adapting the method previously described by Takahashi et al.²⁵ Quartz theta pipets (o.d., 1.2 mm, i.d., 0.9 mm, Intracell) were pulled using a laser puller (P-2000, Sutter Instruments); see section S4 of the Supporting Information for pulling parameters. Butane was passed through the pulled pipet, via tubing, under an argon atmosphere. The tip of the probe was heated with a butane torch for 35 s, to pyrolytically deposit carbon from the butane, as illustrated in Figure 1A. Electrical contact to each electrode was established by inserting a copper wire through the top end of the pipet barrel to make contact with the carbon layers. A field-emission scanning electron micrograph (SEM) (Supra 55-VP, Zeiss) of a typical nanoscale DCE is shown in Figure 1B, and an optical image of a larger DCE is shown in Figure 1C.

Figure 1.

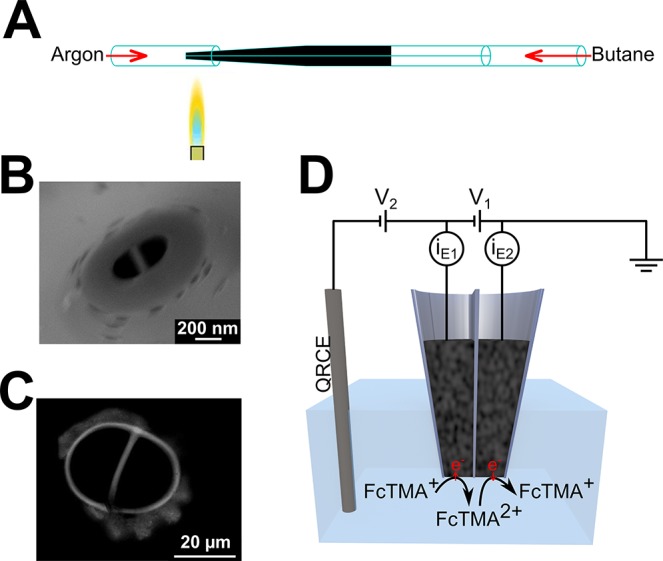
(A) Schematic of the carbon deposition step of dual-electrode fabrication, in which butane is passed through the pulled quartz theta pipet and pyrolyzed using a hand-held butane torch under an argon atmosphere. (B) SEM of a typical nanoscale DCE. (C) Optical image of a micrometer-scale DCE. (D) Schematic of dual-electrode configuration, with two working electrodes in the barrels of the probe and an Ag/AgCl QRCE in solution. The current is measured at each working electrode (i_E1 and i_E2), while the potential of the working electrodes, with respect to the QRCE, is controlled by V₁ and V₂. In the G/C mode, FcTMA⁺ is oxidized at one electrode to produce FcTMA²⁺ that is reduced at the other electrode.

Electrochemical Measurements

A three-electrode configuration was used, with two working electrodes (the two electrodes of the probe) and a single Ag/AgCl (silver chloride-coated silver wire) quasi reference/counter electrode (QRCE) in the bulk of the solution, as illustrated in Figure 1D. In the G/C mode, the potential of one electrode was set to 0.5 V with respect to the QRCE for the diffusion-limited one-electron oxidation of FcTMA⁺ to FcTMA²⁺, and the other electrode was at 0 V with respect to the QRCE for the diffusion-limited one-electron reduction of FcTMA²⁺. This was achieved in our electrochemical configuration by setting V₁ = 0.5 V and V₂ = −0.5 V (Figure 1D). The current at each working electrode was measured using a custom-built high sensitivity bipotentiostat (see the section S5 of the Supporting Information for a description of the SECM instrument).

Simulations and Theory

Electrochemical measurements provide a quick estimation of the apparent size of an electrode.²⁹ We developed a steady-state three-dimensional (3D) FEM simulation of nanoscale (100–1000 nm) DCEs based on the probe geometry observed in SEM images of typical nanoscale DCEs (e.g., Figure 1B) to estimate the probe geometry from steady-state diffusion-limited currents. A full description of the FEM simulation, including Figure S1 of the Supporting Information showing the probe geometry and example diffusion profiles, is given in section S6 of the Supporting Information.

The electrodes in the probe are semielliptical in shape, and the model is configured so that there are only two independent variables, the major axis size for each of the electrodes. Thus, in principle, only two current measurements are needed to determine the geometry of the probe.

Platinization of Carbon Nanoelectrodes

Carbon nanoelectrodes were platinized in a solution of chloroplatinic acid H₂PtCl₆ (2 mM) in 0.1 M sulfuric acid. The reduction of Pt at the carbon nanoelectrode was induced by cycling the potential twice from −1 to +0.5 V, at a scan rate of 750 mV s^–1.

Results and Discussion

DCEs were fabricated with a high success rate (ca. 85%, based on more than 100 made) on the day of use, with approximately 3 min required per tip. A typical DCE (see Figure 1, panels B and C) consists of two planar semielliptical electrodes separated by a septum and surrounded by glass. The septum size and small surround of glass are typical for probes constructed from theta nanopipets by the laser pulling technique.^24,25,38

Each electrode of a DCE was individually characterized using the steady-state currents for the one-electron oxidation of FcTMA⁺ obtained from linear sweep voltammograms. Typical examples for each of the two electrodes of a single probe are shown in Figure 2A. As expected, the LSVs show a sigmoidal response. When coplanar electrodes are assumed, the different magnitude of the limiting currents for each electrode, within an individual probe, indicates that the electrodes are not the same size. Generally, the individual electrodes in a single probe may have slightly different sizes due to asymmetry in the individual barrel sizes in the pulled theta pipet.

Figure 2.

(A) LSVs (20 mV s^–1) for the oxidation of FcTMA⁺ to FcTMA²⁺ at each individual electrode in a nanoscale DCE, while the other electrode was unconnected. (B) LSV for generation (electrode 1) and corresponding collection current (electrode 2) for FcTMA⁺/FcTMA²⁺, as the potential of the generator electrode (x-ordinate value) was swept and the collector electrode potential was held at 0 V. (C) The geometry sets, for electrode 1 in blue and electrode 2 in red, calculated from a FEM model that can generate the single barrel currents. The two geometry sets are consistent with electrode 1 major axis radius 500 ± 50 nm and electrode 2 major axis radius 400 ± 25 nm. (D) The set of geometries, for electrode 1 in blue and electrode 2 in red, calculated from the FEM model that is consistent with the generation and collection currents. The two are self-consistent at electrode 1 major axis radius 450 ± 50 nm and electrode 2 major axis radius 400 ± 50 nm. (E) Collection efficiencies, from simulations, for a range of probe sizes.

This DCE was then used in the G/C mode, with the FcTMA^+/2+ redox couple. The potential of the generation electrode was swept for the oxidation of FcTMA⁺ to FcTMA²⁺, while the potential of the collection electrode was held constant at 0 V for the reduction of any FcTMA²⁺ back to FcTMA⁺. The resulting generation and collection currents are shown in Figure 2B. The generation current shows the typical sigmoidal shape; however, the magnitude of the limiting current is slightly larger than observed for the single-electrode response above, as the second electrode regenerates FcTMA⁺, so providing positive redox feedback to the generator electrode. The collection current shows a similar sigmoidal shape, resulting from the change in local FcTMA²⁺ concentration induced by the generator electrode. The ratio of collection current to generation current defines the collection efficiency, and this probe had a diffusion-limited collection efficiency of ca. 30%. This reasonable collection efficiency is achieved because the small distance between the two electrodes minimizes diffusional losses.

Nanoscale DCE Characterization

While nanoscale electrodes can be routinely fabricated,^39,40 the resulting probe geometry is often difficult to determine precisely.²⁹ In principle, it is possible to determine the individual probe geometry for a DCE by SEM after experiments; however, this was found to be problematic due to crystallization of the redox species and supporting electrolyte on the probe. Practically, the estimation of probe geometry is usually achieved by using analytical expressions, or simulations, to relate the experimental current responses to electrode dimension, taking care to avoid pit falls due to nonplanar geometrical affects (especially recessed electrodes).⁴¹⁻⁴³ More complex geometries, such as the probes used herein, need custom FEM simulations to determine probe geometries from current measurements. A FEM model of the DCE was formulated so that the geometry only depended on the size of the electrode major axes and this allowed the geometry to be determined from only two current measurements.

We calculated the sizes of the nanoscale electrodes in the DCE used to record the data in Figure 2 (panels A and B), using the FEM model. First, the geometry was calculated from the diffusion-limited currents at the individual electrodes (Figure 2A). The probe size (defined by the size of the major axes) consistent with the diffusion-limited current measured at electrode 1 is shown in blue in Figure 2C, while the probe size consistent with the measured limiting current for electrode 2 is shown in red. Note that for this model, the size of a particular electrode, as determined from its current, shows a weak dependence on the size of the other (unconnected) electrode because changing the size of the latter electrode changes the minor axis size (and also the septum and glass surround width). For example, a smaller unconnected electrode promotes more back diffusion and a slightly higher current at the active electrode. The point at which the two curves in Figure 2C intersect, 500 ± 50 nm for electrode 1 and 400 ± 25 nm for electrode 2, is the only possible probe geometry, constrained by the model assumptions, which could produce the two individual electrode currents.

The geometry of the probe can also be calculated from the diffusion-limited generation/collection currents, shown in Figure 2 B. With electrode 1 generating FcTMA²⁺ and electrode 2 collecting FcTMA²⁺ (i.e., both electrodes active), the calculated probe size consistent with the measured generation current is shown in blue in Figure 2D, while the probe size consistent with the measured collection current is shown in red. Again, the point at which these two sets of electrode sizes intersect, the electrode 1 major axis of 450 ± 50 nm and electrode 2 major axis of 400 ± 50 nm was the geometry of the probe, constrained by the model assumptions, calculated from the generation/collection currents. It is evident that the size of electrode 1, from the two geometry calculations 500 ± 50 nm versus 450 ± 50 nm, is reasonably consistent, as is the size of electrode 2, 400 ± 25 nm versus 400 ± 50 nm.

Working surfaces, from which electrode sizes for different currents can be determined, were constructed from the FEM model, and these are shown in Figure S2 and section S7 of the Supporting Information. This highlights that the G/C experiments are particularly sensitive to the probe size. In addition, the calculated collection efficiency is shown in Figure 2E. This shows that probes with similar-sized electrodes have collection efficiencies of ca. 30%. A relative increase in generation electrode size compared to the collection electrode results in a decrease in collection efficiency, while decreasing the generator electrode size increases the collection efficiency.

SECM Measurements

DCEs were deployed in SECM to investigate their behavior, in G/C mode, close to the surfaces. With FcTMA⁺ oxidation at one (generator) electrode and FcTMA²⁺ reduction at the second (collector) electrode, DCEs were translated toward insulating (glass) and conductive (gold) surfaces using the IC-SECM mode.³² With IC-SECM, the probe is oscillated normal to the surface (in this case with an amplitude of 32 nm at 70 Hz frequency), and damping of the oscillation amplitude is detected when the tip comes into physical intermittent contact with the surface. This mode provides a current-independent means of detecting when the tip and the substrate surface make contact, which is valuable for estimating the distance between the probe tip and the surface during the approach curve measurements.

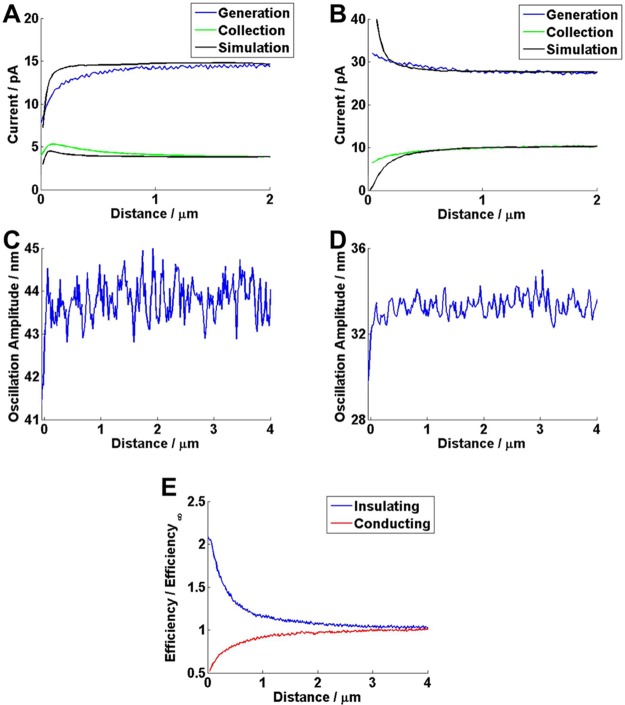
The DCE generation and collection currents for approaches to glass and gold surfaces are shown in Figure 3 (panels A and B), respectively. The position at which the tip comes into contact with the surface is seen as a sharp drop in the tip position oscillation amplitude (Figure 3, panels C and D). For convenience, this point is assigned as a distance of 0 μm between the probe electrode and the surface, although in reality, imperfection in the probe alignment and geometry lead to nonzero distances between the active electrodes and the surface.⁴⁴

Figure 3.

(A) Generation and collection currents during the approach of a DCE probe to an insulating (glass) substrate, with the results for a FEM simulation (generation electrode major axis size of 120 nm and collection electrode major axis size of 95 nm) of the same system. (B) Generation and collection currents, for an approach to a conducting (gold) substrate, with the results for a FEM simulation (generation electrode major axis size of 160 nm and collection electrode major axis size of 440 nm). (C and D) Probe oscillation amplitude, showing a sharp decrease that indicates probe contact with the surface, for (A and B, respectively). (E) Experimental collection efficiencies for (A and B).

When approaching the inert substrate, the generation current decreases, but interestingly, the collection current increases before dropping off when the tip is very close to the substrate. The transient increase in the collection current is because the substrate confines the generated species, FcTMA²⁺, close to the electrodes, limiting diffusional losses, so leading to enhanced diffusional coupling between the two electrodes. However, once the tip gets much closer to the inert surface, the significant decrease in the generation current, due to the blocking effect of the substrate on the diffusion of FcTMA⁺ to the generator, causes the collection current to decrease. On the other hand, Figure 3E clearly shows that the absolute collection efficiency increases as the distance from the substrate surface decreases. In this plot, the collection efficiency at a particular distance is normalized with respect to that measured in bulk solution.

The approach to a conducting substrate shows that the generation current increases with a decrease of the distance to the substrate (positive feedback),⁴⁵ while the collection electrode is in competition with the substrate and thus as the tip gets closer to the substrate, the current at this electrode drops. This competition increases with closer tip/substrate separation and so the collection efficiency decreases monotonically throughout an approach (Figure 3E). The data in Figure 3E highlights that the morphology of an SECM collection efficiency approach curve is hugely sensitive to the nature of the substrate, and this provides a route to functional imaging of surface processes, as we demonstrate below.

We now use the FEM model to assess the approach curves. The sizes of the individual electrodes in the probes used for the approach curve experiments were calculated from the steady-state (bulk) generation and collection currents, as described above. For the approach to the insulating surface, the apparent probe dimensions were defined by 120 nm for the generator electrode major axis and 95 nm for the collector electrode major axis, while for the approach to the conducting surface, the generator electrode major axis was 160 nm, and the collector electrode major axis was 440 nm. Simulation results for approach curves, with the probe perfectly aligned to the surface (which is an approximation as already discussed), to both insulating and conducting substrates were calculated and are shown in black in Figure 3 (panels A and B). These show the same topological features as observed in the experimental results, most obviously the increase in collection current when approaching an insulating substrate. However, quantitative differences are evident between the experimental and simulation results, particularly during the approach to the insulating substrate (Figure 3A). In this case, the decrease in experimental generator current is apparent at a distance which we would not expect based on the simulation. This suggests that the true probe geometry is larger than determined from the model, and that, in turn, the electrode is recessed. Such recessions are not uncommon in nanoscale electrodes,^29,46 and quantitative analysis of approach curves is a powerful way of highlighting nonidealized electrode geometries.⁴¹ While we could develop our model to account for misalignment of the probe with respect to the surface and nonideal geometry, this would introduce a number of extra independent parameters, which are not needed for the initial applications herein, in which we seek to demonstrate attributes of DCE generation-collection measurements in a semiquantitative fashion.

Probing Redox Reactions at Thylakoid Membranes

We demonstrate the use of generation-collection measurements to monitor the reactions of an artificial electron acceptor at thylakoid membranes during photosynthesis. The SECM configuration allowed the DCE to be placed close to, but not touching, a monolayer of thylakoid membranes. The DCE, operated in G/C mode, also allowed a flux of the artificial electron acceptor (FcTMA²⁺) to be generated locally in a controllable manner and permitted the local flux of both FcTMA²⁺ and FcTMA⁺ to be measured concurrently, with good time resolution.

The interaction of electrogenerated FcTMA²⁺ with thylakoid membranes was investigated using the DCE shown in Figure 1C in the G/C mode, as illustrated in Figure 4A. The probe was placed over a sparse monolayer of thylakoid membranes (a typical surface coverage is indicated in the fluorescence image of Figure 4B) and approached in the dark to the point of maximum collection current, as shown in the approach curve in Figure 4C. Note that the morphologies of the generator and collector current approach curves are consistent with the thylakoid membrane presenting an inert surface, as discussed above. The probe was then held stationary while the sample was illuminated using the fluorescence microscope (at a wavelength of 470 nm with an intensity of 3.5 × 10¹⁶ photons s^–1 cm^–2) for a period of 30 s, and the generation and collection currents during this time were measured. Figure 4 (panels D and E) shows the relative change in the generation current and collection current during this period, respectively. Upon illumination, it is apparent that FcTMA²⁺ is reduced to FcTMA⁺ at the thylakoid membranes, as there is an increase in the magnitude of the generation current and a decrease in the magnitude of the collection current. Interestingly, a steady-state response is quickly reached, with a ca. 30 pA increase in the generation current and a corresponding ca. 30 pA decrease in the collection current. FcTMA²⁺ reduction at the thylakoid membranes ceases immediately when the light is turned off, as evidenced by the return to the generation and collection currents to original values. This corresponds to a turnover rate of FcTMA²⁺ to FcTMA⁺ of ca. 2 × 10⁸ s^–1. An advantage of the DCE probe is that the electron acceptor is generated locally and the spatial resolution is correspondingly high, approximating to the tip size.

Figure 4.

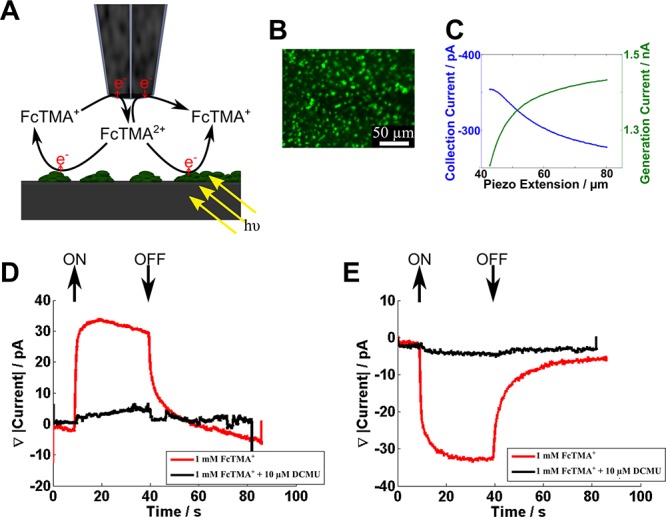
(A) Schematic of the DCE in the generation/collection mode, with the FcTMA^+/2+ couple, above a sparse monolayer of thylakoid membranes. (B) Fluorescence microscopy image of a sparse monolayer of thylakoid membranes, observed as green spots on the surface. (C) Approach curves for placing the DCE above the surface containing thylakoid membranes (probe size defined in text). (D) Generation current response as the monolayer of thylakoid membranes is illuminated with and without DCMU. (E) Collection current response as the monolayer of thylakoid membranes is illuminated with and without DCMU.

To confirm the FcTMA²⁺ reaction with illuminated thylakoid membranes, the herbicide, 3-(3,4-dichlorophenyl)-1,1-dimenthylurea (DCMU), which blocks the linear electron transport pathway³⁶ was added. As observed in Figure 4 (panels D and E), the addition of 10 μM DCMU essentially entirely eliminated the light-mediated response. This confirms that FcTMA²⁺ is reduced by a component of the photosynthetic electron transport pathway. Interestingly, we can exclude the possibility that FcTMA²⁺ accepts electrons directly from PSII, as is the case, for example, with silicomolybdate because DCMU inhibits the electron transport pathway after this point.³⁶

Thylakoid Membrane Imaging

A DCE in G/C mode was used to image a single thylakoid membrane. The probe (generator electrode major axis ca. 1700 nm and collector major axis ca. 700 nm) was placed directly above a single thylakoid membrane at a distance where the maximum collection current was detected (as above) and then scanned laterally across the sample at a constant height in the G/C mode. The sample was illuminated (470 nm, at 3.5 × 10¹⁶ photons s^–1 cm^–2) during the scan to activate the photosynthetic response at the membrane.

A fluorescence image of the thylakoid membrane, due to the autofluorescence of chlorophyll, is shown in Figure 5A. This matches well with the electrochemical images of the thylakoid membrane, one from the generation current (Figure 5B) and one from the collection current (Figure 5C) obtained in a single image scan with a DCE. The decrease in generation current over the thylakoid membrane is predominantly the result of local topography features, which is expected as thylakoid membranes are typically 2–4 μm in height. The collection current also decreases over the thylakoid membrane. However, the collection efficiency (Figure 5D) decreases over the thylakoid membrane. This is only possible over an active surface, as shown in the approach curves in Figure 3 and indicates that the thylakoid membranes are actively consuming the electrogenerated FcTMA²⁺. The effect is very subtle and would be difficult to detect from a single probe SECM feedback measurement, not the least because of the convolution of activity and topography in such measurements and the fact that the activity of a single thylakoid membrane is low. Although the substrate generation/tip collection mode might allow the processes to be probed, this would require FcTMA²⁺ in bulk solution and this mode is characterized generally by a significant loss of spatial resolution.^40,44 In contrast, we see the degree of activity very readily in the collection efficiency image. Although a simple constant height SECM imaging technique was presented here a further important aspect of these probes is that one could use the response of one electrode to sense topography and the other to sense substrate activity.²²

Figure 5.

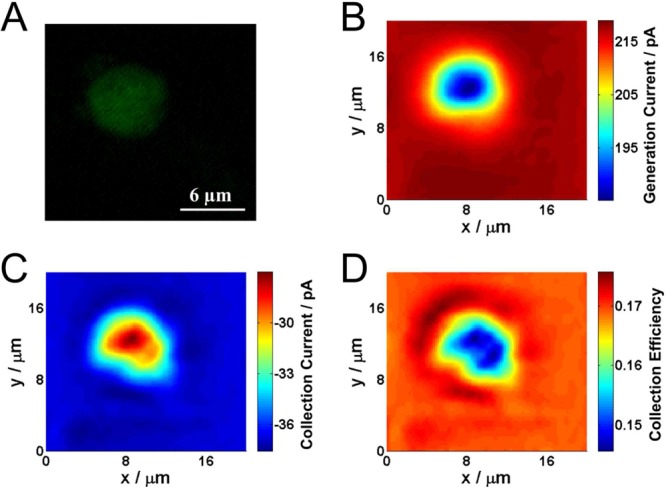
(A) Fluorescence image of a single thylakoid membrane. (B) Generation current (FcTMA⁺ oxidation) image of the thylakoid membrane. (C) Collection current (FcTMA²⁺ reduction) image of the thylakoid membrane. (D) Collection efficiency image of the thylakoid membrane. The electrochemical images were acquired over a period of 400 s.

Platinization of Carbon Nanoelectrodes

Finally, we consider preliminary experiments that show DCEs can be easily and selectively modified, though with the selective deposition of Pt on one electrode while leaving the other one unmodified. Figure S3 in the Supporting Information shows CVs of 1 mM ferrocenemethanol oxidation in aerated solution, for the individual electrodes of a probe, before and after the selective deposition of Pt on one of the electrodes. The deposition of Pt dramatically changes the catalytic properties of the electrode toward oxygen reduction, as can be seen by the additional oxygen reduction current observed in the negative potential region of Figure S3B of the Supporting Information. However, the deposition of Pt does not appreciably change the size of the electrode, as the ferrocenemethanol oxidation limiting current does not change noticeably with the Pt deposition. This highlights the possibility of using DCEs for electrochemical sensing which, with further developments, may allow multicomponent chemical analysis at the nanoscale.

Conclusions

DCEs are simple and quick to fabricate with a wide range of tunable electrode sizes. The probes are well suited to SECM experiments because of the relatively small total size of the end of the probe enabling close positioning to an interface, while the small interelectrode distance leads to high sensitivity.

For nanoscale DCEs, a FEM model was developed to assist in characterizing the probe size based on simple steady-state limiting current measurements. The electrode sizes were calculated from either single barrel FcTMA⁺ oxidation currents or the G/C currents. This allowed us to estimate the apparent probe geometry from two different measurements and compare them. However, as highlighted in the approach curve measurements, the FEM model does not capture subtle geometric imperfections, such as protruding or recessed electrodes or slight misalignment of the probe. Nonetheless, these initial studies highlight that the probes can be used in a semiquantitative fashion and, if required, the morphology of approach curves could be further analyzed to provide additional information on these imperfections.

We have demonstrated that DCEs can be used to interrogate interfaces and surfaces with high sensitivity. DCEs were used to assess local changes in the FcTMA⁺ and FcTMA²⁺ flux during illumination of thylakoid membranes and in 2D imaging of a single thylakoid membrane. In both cases, subtle interactions of electrogenerated electron acceptors with the active surface were determined readily through the G/C response.

Further work to extract the geometry from current-based measurements could expand the quantitative capabilities of these probes. In addition, we have shown that individual probes within the DCE can be functionalized, as exemplified by selective deposition of Pt on one electrode while leaving the other one unmodified. Platinized nanoelectrodes have been shown to be promising probes for intracellular measurements.⁴⁷ DCEs may thus find applications as single-cell chemical sensors and other modifications are evidently realizable.

Supporting Information Available

Thylakoid membrane sample preparation, probe laser pulling parameters, and information on SECM instruments are available. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.