Abstract
The [2,3]- and [1,2]-sigmatropic rearrangements of ammonium ylides are studied by a combination of experimental, standard computational, and dynamic trajectory methods. The mixture of concerted [2,3] rearrangement and bond cleavage observed experimentally is accounted for by the outcome of trajectories passing through the formal [2,3] rearrangement transition state. In this way the bond cleavage is promoted by the pericyclic stabilization of the [2,3] transition state. It is proposed that this dynamic effect is responsible for the pervasive co-occurrence of the two rearrangements.
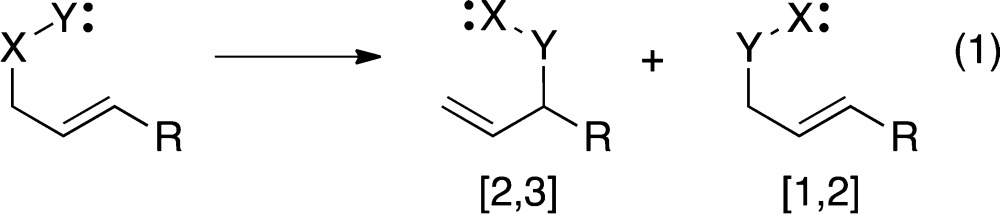
[2,3]-Sigmatropic rearrangements are a large and synthetically valuable class of reactions that are thermally allowed as concerted processes within the Woodward–Hoffmann framework of pericyclic reactions.1 A vexing trait of these reactions is that they are routinely plagued by competitive [1,2]-sigmatropic rearrangements (eq 1).2 Concerted [1,2] rearrangements of this type are not viable in theoretical analyses,3 and the understanding of [1,2] rearrangements has focused on stepwise mechanisms. The generally accepted mechanism for the [1,2] reaction is a two-step bond cleavage/recombination process, and this is supported by diverse evidence, including for example CIDNP observations. Considering the disparate nature of the [2,3] versus [1,2] rearrangements, their pervasive co-occurrence appeared extraordinary, and we sought an underlying reason. The combined experimental, conventional computational, and dynamic trajectory studies described here suggest that the two reactions are commonly competitive because they can occur by the same transition state. The results also show how dynamics can lead the stability of a primary process to foment secondary reaction pathways.
 |
1 |
To better understand the nature of these rearrangements, we
sought
to fully characterize two closely related reactions, one undergoing
solely the [2,3] rearrangement and another undergoing the combination
of [2,3] and [1,2] processes. The simple and well-behaved Sommelet–Hauser
rearrangements of amino acid derived ammonium salts 1 and 4 were chosen for study. The DBU-mediated rearrangement
of the unsubstituted ylide 2 derived from 1 occurs entirely by the [2,3] process, as supported by a consistent
allylic transposition of deuterium when using labeled 1 and the absence of crossover in a mixed labeled/unlabeled reaction
[see the Supporting Information (SI)].
In contrast, the rearrangement of the more substituted 5 affords a mixture of the [2,3] product 6 and the [1,2]
(Stevens rearrangement) product 7 (80:20 at 90 °C,
95:5 at 25 °C). The noninvolvement of the protonated DBU in the
rearrangement was supported by the observation of an identical product
ratio when potassium hydride was employed as the base.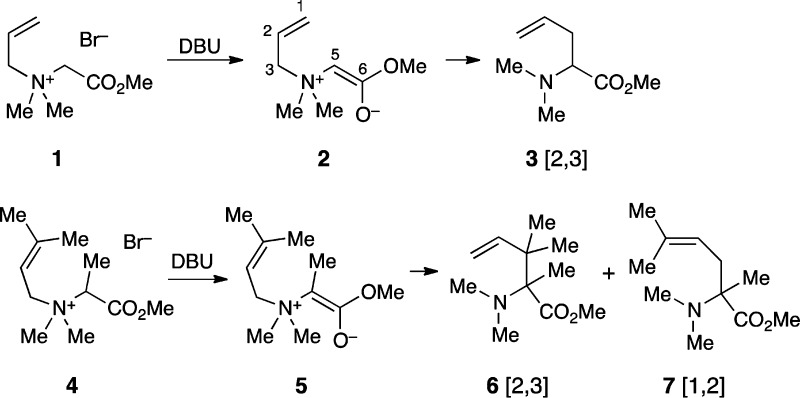
The 13C kinetic isotope effects (KIEs) for the rearrangement of 1 were determined at natural abundance by NMR methodology.4 Reactions of 1 in DMF containing 4-Å powdered molecular sieves at 25 °C were taken to partial conversion by treatment with 15–20 mol % of DBU. The purified product 3 was then analyzed by 13C NMR in comparison with samples of 3 obtained from 100% conversion reactions employing excess DBU. The position-by-position differences in the 13C isotopic composition of the samples were determined using the carbon of the methoxy group as an internal standard, with the assumption that its isotopic composition has changed negligibly. From the changes in the isotopic composition and the reaction conversions, the isotope effects were calculated in a standard way (see the SI).
The results are summarized in Figure 1. The most notable observation is that the 13C KIE at C3 is quite large while those at C1 and C5 are small. Qualitatively, this suggests that C3–N bond breaking is much more important in the transition state than C1–C5 bond making. A more quantitative interpretation of the KIEs will be provided by their comparison with computed KIEs.
Figure 1.
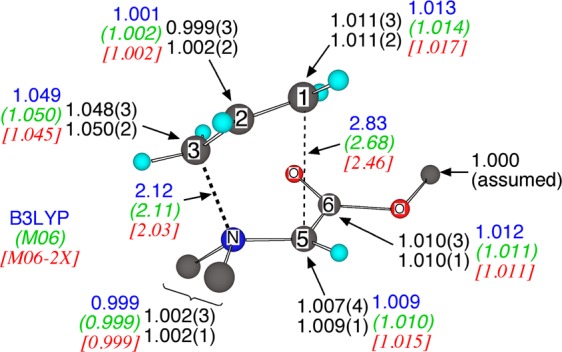
CVT transition structure for the rearrangement of 2, experimental 3C KIEs (black, with 95% confidence limits in parentheses), and predicted (CVT/SCT) 13C KIEs.
Computational transition structures for the rearrangement of 2 vary drastically. In an exploration of 64 combinations of DFT methods, basis sets, and solvent models, the C1–C5 interatomic distance in the rearrangement transition structure varied from 2.28 to 3.14 Å (see the SI). Many of the structures are inconsistent with the experimental KIEs. The 13C KIEs predicted for each transition structure were obtained from transition state theory including corrections for canonical variational transition state theory (CVT) effects and small-curvature tunneling (SCT).5 Transition structures in which the C1–C5 distance was less than 2.6 Å lead to predicted C1 and C5 13C KIEs that are too large versus experiment (>1.014 at C1, >1.012 at C5) and lead to predicted C3 KIEs that are too small versus experiment (<1.046). This is illustrated by the M06-2X6 predictions shown in Figure 1. Transition structures with a C1–C5 distance greater than 2.9 Å lead to predicted C1 KIEs that are too small (<1.008); for example the B97D3/6-31G* structure has a C1–C5 distance of 3.00 Å and a predicted C1 KIE of 1.005. In this way the KIEs provide an experimentally based measurement of the transition state geometry,7 and the 2.6–2.9 Å C1–C5 distance marks a transition state that is decidedly “loose” though not fully dissociative. For comparison, the simplest Claisen rearrangement has a forming C–C bond distance of 2.2 Å.
The rearrangement of 5 is more complex, and its inner
workings were examined by means of a crossover experiment. A mixture
of labeled precursor 4-d8 and unlabeled 4 was reacted at 90 °C, and the isotopic composition
of the [2,3] and [1,2] products 6 and 7 was
analyzed by ESI-MS. Both 6 and 7 exhibit
M+2 and M+6 peaks indicative of crossover. However, the amount of
crossover is low: 17.9% for [1,2] product 7 and only
4.9% for [2,3] product 6. The low proportion of crossover
indicates that most of the reaction occurs by an intramolecular mechanism.
The much lower crossover in 6 than 7 indicates
that the [2,3]-product can be formed by an intramolecular process
that is not available to the [1,2] product, presumably the concerted
rearrangement.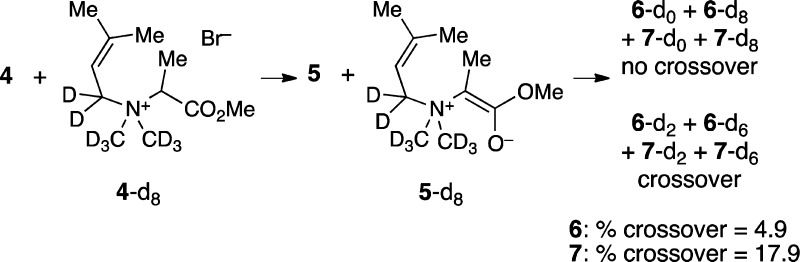
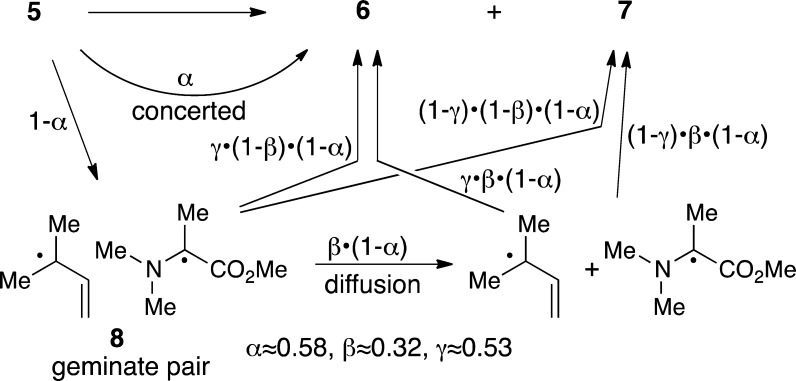
The crossover results were interpreted in more detail with a kinetic model (Scheme 1) and minimal assumptions. A fractional portion of the reaction, α, undergoes a concerted rearrangement, while 1-α undergoes bond cleavage to give the geminate radical pair 8 in a solvent cage. A portion of 8, β, then diffuses apart while 1-β recombines to form 6 or 7. The model then makes the uncertain assumption that a constant portion γ of recombining radicals affords 6, regardless of whether recombination occurs from the initial geminate pair or from diffusion together in solution. The observed ratio of 6:7 and the amount of crossover in each then fully defines α, β, and γ as 0.58, 0.32, and 0.53, respectively. The α value of 0.58 is best considered as an upper limit, since plausible errors tend to decrease α (see the SI for a discussion). There is also significant uncertainty in the values, but the experimental observations can only be accounted for by roughly comparable amounts of concerted rearrangement versus C–N bond cleavage, in-cage reaction versus diffusional separation of 8, and [2,3] versus [1,2] recombination of radical pairs.
Scheme 1. Kinetic Model for the Rearrangement of 5.
A conventional mechanistic analysis would implicitly
assume that
the mixture of concerted [2,3] rearrangement and bond cleavage arises
from a competition between respective transition states for the two
reactions (CVT structures 9‡ and 10‡, respectively). However, this does not
account for the large proportion of bond cleavage observed. In VTST
calculations5 on the UB3LYP-D2, UM06, and
UM06-2X energy surfaces,6 the CVT/SCT rate
constants at 90 °C for cleavage via 10‡ are predicted to be 25–50 times lower than the [2,3] rearrangement
via 9‡. All of the unrestricted DFT
calculations appear to underestimate the relative barrier for the
bond cleavage by 2–7 kcal/mol, based on UBD(T)/cc-pvtz calculations
on model [2,3] rearrangement versus bond-cleavage transition structures
(see the SI). Allowing for this error,
simple bond cleavage would be expected to be negligible. 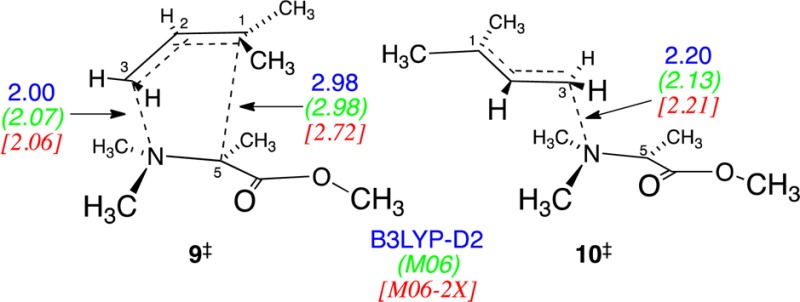
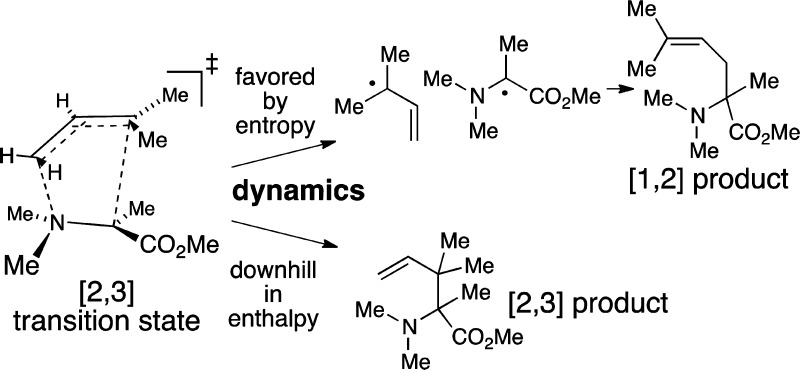
We envisioned that the bond cleavage could arise dynamically from the nominal concerted [2,3]-sigmatropic transition state, and quasiclassical direct-dynamics8 trajectories were employed to explore this possibility. Using a series of energy surfaces, trajectory calculations were initiated from the area of 9‡. Each normal mode in 9‡ was given its zero-point energy (ZPE) plus a Boltzmann sampling of additional energy appropriate for either 25 or 90 °C, with a random phase and sign for its initial velocity. The transition vector was given a Boltzmann sampling of energy. The trajectories were then integrated both forward and backward in time in 1-fs steps until 5, 6, or 8 was formed. The results are summarized in Table 1.
Table 1. Outcome of Trajectories Passing through 9‡.
| method | rearrangement (6):cleavage (8) |
|---|---|
| UB3LYP-D2/6-31G*/PCMa,c | 33:114 (22%:78%) |
| UB3LYP-D2/6-31G*/PCMb,c | 74:111 (40%:60%) |
| UM06-2X/6-31+G**/PCMa,c | 64:22 (74%:26%) |
| UM06-2X/6-31G*/PCMa,c | 319:68 (82%:18%) |
| UM06-2X/6-31G*/PCMa,d | 274:35 (89%:11%) |
| UM06/6-31G*/PCMa,c | 9:79 (11%:89) |
| ONIOM with 24 CH3CNb,c,e | 32:44 (42%:58%) |
| experimental | 58%:42% (upper limit) |
Quasiclassical.
Fully classical.
90 °C.
25 °C.
The ONIOM used UB3LYP-D2/6-31G* for the atoms of 9‡ and PM3 for the CH3CN molecules. The trajectories were started from a transition structure located after a series of cycles of simulated annealing.
The extraordinary observation in Table 1 is that all of the trajectories passing through the “[2,3]-sigmatropic transition state” afford mixtures of the rearrangement product 6 and cleavage to 8. The predicted ratio of rearrangement and cleavage never identically matches the experimental ratio, but the results from the various methods bracket experiment. The M062X calculations predict too little cleavage; this seems related to the prediction of too tight of a transition structure, based on the results above with 1. M06 and B3LYP-D2 trajectories overestimate the amount of cleavage, but the agreement is very reasonable considering the limitations of the energy surfaces and the upper-limit nature of the experimental observation. The energy surfaces themselves are questionable and afflicted by spin contamination as the bond cleavage ensues, but on any of the energy surfaces investigated the fastest process for bond cleavage passes through the [2,3]-sigmatropic transition state!
From a dynamical standpoint, the cleavage can be understood with reference to the overlays of trajectory points in Figure 2. At the transition state the C3–N bond is breaking and this process inevitably continues as the trajectory proceeds. If C1 and C5 are moving toward each other at the transition state, this motion continues and the [2,3] rearrangement consummates. However, the association of C1 with C5 is energetically weak, and motions in orthogonal modes can negate their small approaching motion in the transition vector. When this occurs, cleavage ensues. In trajectories that zeroed out the energy in orthogonal modes, the [2,3] rearrangement occurs regardless of the energy in the transition vector. The use of a fully classical energy distribution in the orthogonal modes led to a modest decrease in the amount of cleavage. The inclusion of explicit solvent molecules had little effect; collisions with solvent are too rare to impact the outcome of the trajectories.
Figure 2.
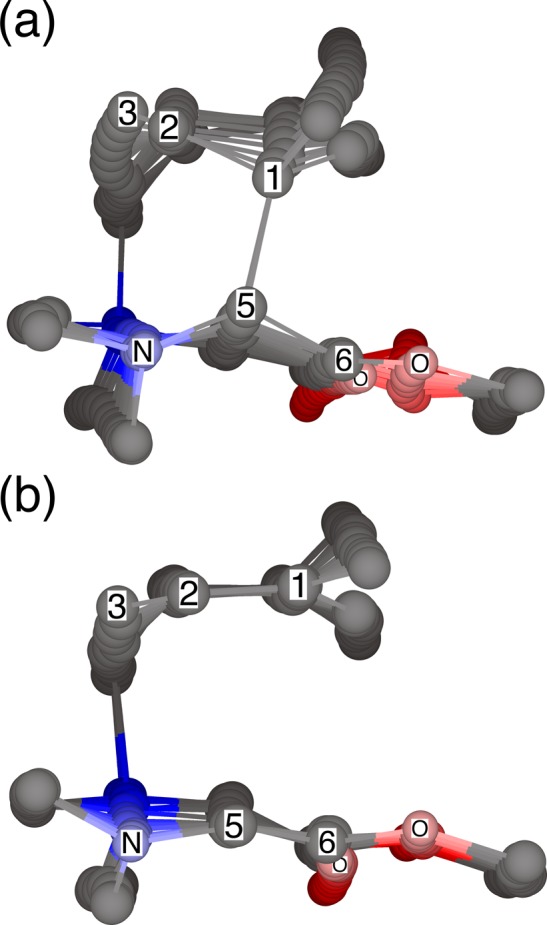
Overlays of trajectory points for (a) a concerted [2,3]-rearrangement and (b) simple cleavage, with both occurring through the same transition state. The points are spaced at 10-fs intervals. Earlier points are darker and in back. The transition state is about one-third from the back.
From a statistical standpoint, the mixture of rearrangement and cleavage processes occurring from a single transition state may be qualitatively viewed as resulting from a bifurcation on the free-energy surface.9 Formation of the [2,3] product is downhill enthalpically from the transition state, but C1–C5 bond formation requires a constriction of motion that is disfavored entropically. In the VTST calculations there were no additional dynamic bottlenecks for formation of 6. From its comparable occurrence in the trajectories, we presume that there is also no free-energy barrier after 9‡ for the cleavage to form 8. Cleavage is disfavored enthalpically, but it frees motions and is favored entropically.
Direct C3–N bond cleavage via 10‡ and bond cleavage via the rearrangement transition state 9‡ have exactly the same overall thermodynamics. Why then should cleavage via 9‡ be favored? To start, structures need not pay the full enthalpic cost of the formation of the separate radical fragments of 8 for cleavage to become favored. Instead, they need merely reach a point where the incremental enthalpy gain on further cleavage is countered by gain in entropy (the slope of H versus −TS in Figure 3). Cleavage can then ensue without any additional free-energy barrier. In harmonic estimates, the entropy gain in going from 9‡ to 8 is ∼18 e.u., enough to fuel an enthalpy gain of over 5 kcal/mol. The enthalpic component of the barrier for cleavage is stabilized in the area of 9‡ by the favorable orbital interactions of the allowed pericyclic rearrangement. Beyond the area of 9‡, the free energy drops as cleavage ensues despite a rise in enthalpy. As a result, the free-energy barrier for cleavage is lowest along the path through 9‡. Intriguingly, then, the stabilization of the pericyclic transition state has the effect of also stabilizing the pathway for the co-occurring nonpericyclic process. In this way the allowed pericyclic reaction promotes the formally forbidden reaction.
Figure 3.
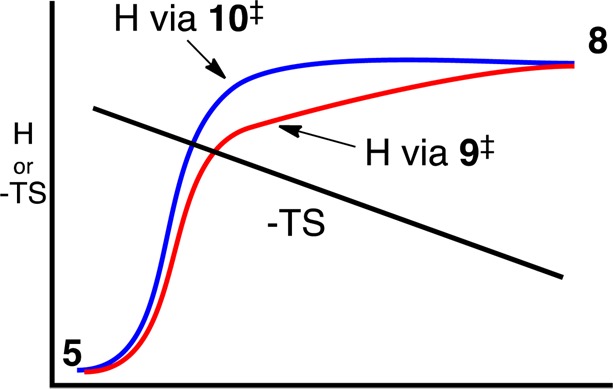
Qualitative reaction coordinate diagram illustrating the advantage of forming 8 via 9‡. Cleavage becomes barrierless in G when the drop in −TS exceeds the rise in H.
The [1,2] rearrangement could certainly occur without any involvement of the [2,3] transition state; in some cases the pericyclic [2,3] transition state is simply sterically infeasible. However, the loose character of transition states for [2,3]-sigmatropic rearrangements is a common feature of calculated transition structures in the literature.3b−3f We would propose that the combination of commonly loose rearrangement transition states and the potential for such transition states to lead dynamically to bond cleavage is the major cause of common co-occurrence of [2,3]- and [1,2]-sigmatropic rearrangements. The generality of the observations here and their role in the formation of mixtures of products in other rearrangement reactions will be the subject of future studies.
Acknowledgments
We thank the NIH (Grant GM-45617) for financial support.
Supporting Information Available
Complete descriptions of experimental procedures, calculations, energies, and structures. This material is available free of charge via the Internet at http://pubs.acs.org.
The authors declare no competing financial interest.
Funding Statement
National Institutes of Health, United States
Supplementary Material
References
- For key mechanistic studies, see:; a Baldwin J. E.; Patrick J. E. J. Am. Chem. Soc. 1971, 93, 3556–3558. [Google Scholar]; b Bickart P.; Carson F. W.; Jacobus J.; Miller E. G.; Mislow K. J. Am. Chem. Soc. 1968, 90, 4869–4876. [Google Scholar]; c Baldwin J. E.; Erickson W. F.; Hackler R. E.; Scott R. M. Chem. Commun. 1970, 576–578. [Google Scholar]; d Baldwin J. E.; Hackler R. E. J. Am. Chem. Soc. 1969, 91, 3646–3647. [Google Scholar]; e Mageswaran S.; Ollis W. D.; Sutherland I. O. Chem. Commun. 1973, 656–657. [Google Scholar]; f Ollis W. D.; Rey M.; Sutherland I. O. J. Chem. Soc., Perkin Trans. 1 1983, 1009–1027. [Google Scholar]
- See the Supporting Information for a list of 100 papers that have observed mixtures of [2,3] and [1,2] rearrangements. For selected examples, see:; a Millard B. J.; Stevens T. S. J. Chem. Soc. 1963, 3397–3403. [Google Scholar]; b Jaber D. M.; Burgin R. N.; Helper M.; Zavalij P. Y.; Doyle M. P. Org. Lett. 2012, 14, 1676. [DOI] [PMC free article] [PubMed] [Google Scholar]; c Maleczka R. E. Jr.; Geng F. Org. Lett. 1999, 1, 1111–1113. [DOI] [PubMed] [Google Scholar]; d Venneri P. C.; Warkentin J. J. Am. Chem. Soc. 1998, 120, 11182–11183. [Google Scholar]; e Gawley R. E.; Moon K. Org. Lett. 2007, 9, 3093–3096. [DOI] [PMC free article] [PubMed] [Google Scholar]; f Tayama E.; Takedachi K.; Iwamoto H.; Hasegawa E. Tetrahedron 2010, 66, 9389–9395. [Google Scholar]
- Selected theoretical or computational studies:; a Grovenstein E. Jr. Angew. Chem., Int. Ed. Engl. 1978, 17, 313. [Google Scholar]; b Wu Y.-D. J. Org. Chem. 1991, 56, 5657–5661. [Google Scholar]; c Heard G. L.; Yates B. F. J. Org. Chem. 1996, 61, 7276–7284. [DOI] [PubMed] [Google Scholar]; d Ghigo G.; Cagnina S.; Maranzana A.; Tonachini G. J. Org. Chem. 2010, 75, 3608–3617. [DOI] [PubMed] [Google Scholar]; e Reid D. L.; Warkentin J. J. Chem. Soc., Perkin Trans. 2 2000, 1980–1983. [Google Scholar]; f Haeffner F.; Houk K. N.; Schulze S. M.; Lee J. K. J. Org. Chem. 2003, 68, 2310–2316. [DOI] [PubMed] [Google Scholar]
- Singleton D. A.; Thomas A. A. J. Am. Chem. Soc. 1995, 117, 9357–9358. [Google Scholar]
- a Zheng J.; Zhang S.; Corchado J. C.; Chuang Y.-Y.; Coitino E. L.; Ellingson B. A.; Truhlar D. G.. GAUSSRATE, version 2009-A; University of Minnesota: Minneapolis, MN, 2010. [Google Scholar]; b Zheng J.; et al. POLYRATE–version 2010; University of Minnesota: Minneapolis, MN, 2010. [Google Scholar]
- A 6-31+G** basis set and PCM solvent model were used in all cases unless otherwise stated.
- Hirschi J. S.; Takeya T.; Hang C.; Singleton D. A. J. Am. Chem. Soc. 2009, 131, 2397–2403. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hase W. L.; Song K. H.; Gordon M. S. Comp. Sci. Eng. 2003, 5, 36–44. [Google Scholar]
- The use of thermodynamic terms (assuming a canonical ensemble) here is imprecise but helpful as a qualitative aid to intuition. For other mechanisms describable as bifurcations on the free-energy surface, see:; a Bekele T.; Lipton M. A.; Singleton D. A.; Christian C. F. J. Am. Chem. Soc. 2005, 127, 9216–9223. [DOI] [PMC free article] [PubMed] [Google Scholar]; b Katori T.; Itoh S.; Sato M.; Yamataka H. J. Am. Chem. Soc. 2010, 132, 3413–3422. [DOI] [PubMed] [Google Scholar]; c Sun L.; Song K.; Hase W. L. Science 2002, 296, 875–878. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.