Effect of Heterogeneity and Noise on Cross Frequency Phase-Phase and Phase-Amplitude Coupling

Abstract

Cross-frequency coupling is hypothesized to play a functional role in neural computation. We apply phase resetting theory to two types of cross-frequency coupling that can occur when a slower oscillator periodically forces one or more oscillators: phase-phase coupling, in which the two oscillations are phase-locked, and phase-amplitude coupling, in which the amplitude of the driven oscillation is modulated. Our first result is that the shape of the phase resetting curve predicts the tightness of locking to a pulsatile forcing periodic input at any ratio of forced to intrinsic period; the tightness of the locking decreases as the ratio increases. Theoretical expressions were obtained for the probability density of the phases for a population of heterogeneous oscillators or a noisy single oscillator. Results were confirmed using two types of simulated networks and experiments on hippocampal CA1 neurons. Theoretical expressions were also obtained and confirmed for the probability density of N spike times within a single cycle of low frequency forcing. The second result is a suggested mechanism for phase-amplitude coupling in which progressive desynchronization leads to decreasing amplitude during a low frequency forcing cycle. Network simulations confirmed the theoretical viability of this mechanism, and that it generalizes to more diffuse input.

Introduction

Cross frequency coupling of a faster rhythm by a slower rhythm is hypothesized to organize the activity of the brain in several different contexts (Canolty and Knight 2010; Jensen and Colgin 2007; Sauseng and Klimesch 2008). In this scheme, slow rhythms are entrained across large brain regions at behaviorally relevant time scales by both external sensory input and internal cognitive processes, and provide a frame of reference for the faster rhythms that are local and reflect faster time scales for internal computations (Canolty and Knight 2010). An additional implication is that the internal cognitive processes are discretized because they can only update once per slow rhythm cycle. For example, visual attentional capture is hypothesized to be regulated by a theta band (5–10Hz) periodicity in occipital cortex (Chakravarthi and VanRullen 2012), whereas conscious updating is thought to be gated by the state of high-alpha/low-beta (12–20 Hz) oscillations in fronto-central areas. In the hippocampus, nested gamma (30–150 Hz) cycles within theta cycles are hypothesized to encode current and predicted locations that are updated on each theta cycle (Jensen and Colgin 2007). In addition, lower frequency brain rhythms like delta (1–4 Hz) can become phase-locked to rhythmic external sensory input (Schroeder and Lakatos 2009), creating windows of maximum sensitivity aligned with the expected arrival of the relevant stimulus. Another postulated function for cross frequency coupling is the chunking of information; for example, theta oscillations, likely entrained by auditory input, are hypothesized to chunk speech signals into syllables with phonemes encoded on nested gamma cycles (Giraud and Poeppel 2012).

We are primarily interested in two types of cross frequency coupling, phase-to-phase coupling and phase-to-amplitude coupling. We consider only 1:N coupling, in which there is a single cycle of the slow oscillation for every N cycles of the fast oscillation. In phase-to-phase coupling, there is a relatively constant phasic relationship between the low and high frequency oscillations. This type of coupling is referred to as phase-locking. In phase-to-amplitude coupling, the amplitude of the faster oscillation varies with the phase of the slower oscillation. This latter type of coupling is sometimes referred to as nesting. Phase locking and nesting are not mutually exclusive but rather can coexist. We use theta/gamma nesting in the hippocampus as one illustrative example (Bragin et al 1995; Colgin 2013). For a first order, simplifying approximation we will neglect feedback coupling from the high frequency oscillator to the low frequency oscillator as well as connections between fast oscillators, and focus on feedforward entrainment of a population of unconnected high frequency oscillators by a low frequency oscillator in order to establish some general principles.

Under the approximation of unidirectional drive, the low frequency oscillator can cause phase locking by altering a single cycle of the driven high frequency oscillator so that one cycle of the slow oscillation becomes equal to N cycles of the fast oscillation: N−1 unperturbed cycles and one cycle whose duration is adjusted so that exactly N cycles in the fast oscillator fit within one cycle of the slow oscillator. We focus on another simplifying case, in which the effect of the slow oscillation on the fast oscillation is pulsatile to some degree, meaning that the spikes or bursts of input in the low frequency oscillator are not spread out equally over the N cycles, but the effect is concentrated in one cycle. We derive some theoretical results for the tightness of phase-phase coupling in this case, validate these results in a biological neural oscillator, show that, in a heterogeneous population of high frequency oscillators, phase-locking can lead to phase-amplitude coupling, or nesting, and finally use simulations to generalize this finding to coupling that is not sharply pulsatile.

Phase resetting theory is often applied to single neuron oscillators, but it is important to note that the theory is equally valid for modular network oscillators, as long as the relevant network oscillator can be characterized by a PRC (as in Akam et al. 2012 or Malerba and Kopell 2013). It is controversial (Bartos et al 2007) the degree to which brain rhythms are mediated by oscillatory neurons or by ensembles of interacting neurons that are not oscillatory in the absence of the network rhythm.

Methods

Phase resetting theory applied to unidirectional cross frequency coupling

The simplest phase-locked solutions occur for periodic forcing of an oscillator (Glass and Mackey 1988; Rinzel and Ermentrout 1998), called a 1:N periodic solution, in which there are N cycles of the forced oscillator for every periodic stimulus. The source of the periodic forcing here is considered as the lower frequency oscillator, so the forcing frequency is P_F and the intrinsic, free-running period of the forced oscillator is P_i. Since the oscillations are periodic, we analyzed them in terms of their phase φ, which we define as varying evenly from 0 to 1 during a single oscillation. For periodically spiking neurons, the timing of the spike determines the beginning (phase zero) as well as the end (phase one) of the cycle. Every cycle is considered to be identical and the phase is modulo one because it is reset to zero each time a phase of one is reached. The response of the free-running oscillator to a single stimulus can be measured as the normalized shortening or lengthening of the cycle containing the perturbation. The normalized change in cycle period is called the phase resetting

$$f(\phi )=\frac{P_{\mathit{perturbed}}-P_i}{P_i}$$

A plot of the normalized change in cycle length versus the phase at which the stimulus is delivered is called the phase response (or phase resetting) curve (PRC). Starting from any initial phase φ[n] at which a stimulus is received, the following equation determines the evolution of the phase on successive stimuli indexed by n:

$$\phi [n+1]=\phi [n]-f(\phi [n])+\frac{P_F}{P_i}-N$$ (1)

There are two steps to updating the phase. First, the resetting f(φ[n]) due to the forcing stimulus received at phase φ[n] is subtracted from φ[n] to reflect the phase immediately after the input is received, then the phase must updated during the interval until the next periodic input is received. After an elapsed time equal to an integral number of intrinsic periods NP_i, φ[n] would be unchanged. However, in general the forcing period is not an integral multiple of the intrinsic period, so the second step is to add a detuning term $\frac{P_F}{P_i}-N$ that reflects the normalized difference between the forcing period and an integral number of intrinsic periods. A phase locked mode can only occur if the phasic relationships are constant, requiring that in the limit φ[n + 1] = φ[n]. From Eq. (1), it follows that the forcing period is exactly equal to the N cycles of the forced oscillator plus the phase resetting due to the single input per N cycles: P_F = P_iN + P_if(φ^*), where φ^* is the phase of the forced oscillator at the time it receives each input in a phase-locked mode. A phase locked mode exists if the following is satisfied.

$$\exists {\phi }^{\ast }\in [0,1]\mid f({\phi }^{\ast })=\frac{P_F}{P_i}-N$$ (2)

If we define f_min and f_max as the respective minimum and maximum of the phase resetting curve, the required phase resetting falls within the range of phase resetting measured for that input if

$$f_{\mathit{min}}\le \frac{P_F}{P_i}-N\le f_{\mathit{max}}$$ (3)

The derivative of the right hand side of Eq. 1 must have an absolute value less than one for stability (Rinzel and Ermentrout 1998), so the criterion for a stable locking is −1 < 1 − f(φ^*) < 1. We will refer to regions of the PRC that satisfy the stability criterion as stable branches.

Network Structure

A simple two layer feedforward architecture was used, with the homogeneous low frequency population of neuronal models or phase oscillators unidirectionally projecting to each neuronal model or phase oscillator in the higher frequency populations, and with no coupling within a population.

Simulations using Morris Lecar model

The Morris Lecar (1981) model was used with parameters as in Rinzel and Ermentrout (1998) in the parameter regimes given for type 1 PRCs (single stable branch) and type 2 PRCs (two stable branches). The synaptic currents were modeled as I_syn =g_syns(V−E_syn), where g_syn is the maximum synaptic conductance and E_syn is equal to −75 mV for inhibitory synaptic connections and equal to 0 mV for excitatory synaptic connections. The rate of change of the gating variable s is given by:

$$\frac{ds}{dt}=\frac{\alpha (1-s)}{1+e^{-\frac{V_{\mathit{pre}}}{2}}}-\frac{s}{{\tau }_{\mathit{syn}}}$$

where V_pre is the voltage of the presynaptic cell, α=6.25ms⁻¹ is the rate constant of the synaptic activation, and τ_syn is the synaptic decay time constant and was set to 1.0 ms for excitation and 7.5 ms for inhibition (Compte et al. 2003).

Simulations of pulse-couple phase oscillators

The pulse-coupled simulator (http://nisms.krinc.ru/rth/uniPRCsim) developed in our lab for this study and based on our previous work (Achuthan and Canavier 2009, Canavier and Achuthan 2010) reduces each component oscillator to a phase oscillator that is completely described by its phase response curve and its instantaneous period. As described above, the phase is defined as 1 at the time of a spike, and reset to 0 immediately after. The phase of each oscillator is randomly initialized. When an input from neuron j is received, the phase of neuron i is first updated to reflect the change in phase due to its instantaneous frequency (1/P_i) during the interval since the last update, and then it is updated by the phase resetting f_ij(φ_i) produced by input j in neuron i.

$$\frac{d\phi }{dt}=\frac{1}{P_i}+{\sum }_j{f}_{ij}({\phi }_j)\delta ({\phi }_j-1)$$ (4)

The delta function indicates that updates were performed at the time of each spike in neuron j. If spikes were received simultaneously, the resetting due to multiple inputs was summed under the constraint that a cycle cannot be shortened by more than the time remaining until the oscillator would have spiked in the absence of an input (causality). The phase resetting curves for the pulse-coupled simulator were measured using the Morris Lecar model described above for simulations corresponding to ML networks. For simulations exploring phase amplitude coupling for a single pulsatile input, we used a linear PRC with a slope of one (Maex and DeSchutter 2003, Malerba and Kopell 2013), because this PRC shape is maximally synchronizing across a population of identical oscillators. This type of PRC arises when there is a constant delay from the onset of the synaptic input until the next spike. When the input was more distributed we approximated the response to weaker inputs as also linear, but with a small slope, such that the response to a large number of such inputs would approach a linear PRC with a slope of one.

The variability in oscillatory microstructure (Siapas et al 2005), when included in the phase oscillator network simulations, was simulated by modeling the instantaneous cycle period as an Ornstein Uhlenbeck (O-U) process. The O-U process for the instantaneous period P_i in differential form is:

$${dP}_i=(\mu -P_i)\frac{dt}{\tau }+\sigma {dW}_t$$ (5)

The term containing the mean period μ is the mean reverting term, and the term containing σ is the diffusion term, where W_t is a Wiener process. We discretize (5) as follows (Gillespie 1996) using an exponential integrator that assumes the derivative is constant over the time step and uses an explicit exponential solution during the time step Δt

$$P_i[n+1]=P_i[n]+(\mu -P_i[n])\left(1-e^{-\frac{\mathrm{\Delta }t}{\tau }}\right)+\sigma \mathcal{N}(0,1)\sqrt{\frac{\tau }{2}\left(1-e^{-\frac{2\mathrm{\Delta }t}{\tau }}\right)}$$ (6)

where 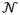(0,1) is Gaussian random process with zero mean and unit standard deviation; σ is a parameter that scales the noise term in the O-U process, and τ is the time constant for mean reversion. Unfortunately, precise solution of this equation requires knowledge of the quantity we are trying to calculate, because the elapsed time Δt = P_i[n + 1], so use the instantaneous intrinsic period on the previous cycle as an approximation of the time step in order to obtain an estimate of the intrinsic period after the mean reversion $P_i^{\ast }[n+1]$

$$P_i^{\ast }[n+1]=(\mu -P_i[n])\left(1-e^{-\frac{P_i[n]}{\tau }}\right)+P_i[n]$$ (7)

Then we use the quantity $P_i^{\ast }[n+1]$ to estimate the time step for the diffusion term:

$$P_i[n+1]=P_i^{\ast }[n+1]+\sigma \mathcal{N}(0,1)\sqrt{\frac{\tau }{2}\left(1-e^{-\frac{2P_i^{\ast }[n+1]}{\tau }}\right)}$$ (8)

This formulation is not precise because the one dimensional Brownian motion ignores the effect of the lengthening or shortening of the cycle due to the phase resetting applied during that cycle. We confirmed using additional simulations that this lack of precision in the effective value of σ across cycles negligibly impacts the results.

LFP approximation and estimation of gamma power

Since the network had no spatial structure, the local field potential was approximated by assuming each spike in the network generated a synaptic current modeled as biexponential with a rise time of 2 ms and a fall time of 5 ms, then summing all currents.

To show how gamma power changes within the theta cycle, we first sampled the approximated LFP signal at 250 Hz, then filtered this signal using a ninth-order Butterworth filter in the 25 – 50Hz range. The signal was filtered in backward and then forward time to minimize phase distortion. We then obtained an analytical signal the using the Hilbert transform and its Gabor representation, and estimated the power of gamma band as sum of the squared real and imaginary parts of the analytical signal. Finally, the gamma power in each theta cycle was averaged across all theta oscillation periods.

Experimental Methods

Acute hippocampal slices (400 μm-thick) were prepared using a vibratome from 7 to 10-week old male Sprague Dawley rats, according to methods approved by the Louisiana State University Health Sciences Center Institutional Animal Care and Use Committees as previously described (Ascoli et al. 2010). Animals were anaesthetized with an intra-peritoneal injection of ketamine and xylazine, perfused through the ascending aorta with an oxygenated solution and decapitated. For the recordings, the slices were placed in a submerged chamber and perfused with an external solution containing (in mM): NaCl 125, KCl 2.5, NaHCO₃ 25, NaH₂PO₄ 1.25, CaCl₂ 2, MgCl₂ 1 and dextrose 25, which was saturated with 95% O₂ and 5% CO₂ at 34–36°C (pH 7.4). CA1 pyramidal neurons were visualized using a Zeiss Axioskop microscope equipped with differential interference contrast (DIC) optics. Somatic whole-cell patch-clamp recordings were obtained using a Dagan BVC-700 amplifier in the active ‘bridge’ mode. The intracellular solution contained (in mM): K-methylsulphonate 130, HEPES 10, NaCl 4, Mg₂ATP 4, Tris₂GTP 0.3, phosphocreatine (di-Tris salt) 14 (pH 7.3); the resistance of the electrodes in the bath was generally 2–3 MΩ and the series resistance was below 20 MΩ. In order to isolate the recorded neuron from the presynaptic afferents, 6-cyano-7-nitroquinoxaline-2,3-dione (CNQX, 20 μM), DL-2-amino-5-phosphonopentanoic acid (DL-APV, 50 μM) and gabazine (12.5 μM) were added to the recording solutions to block AMPA and NMDA glutamatergic receptors and GABA_A receptors, respectively.

Tonic depolarizing current (90–350 pA) was injected in the recorded neurons to evoke repetitive firing at 7–12 Hz. After letting the firing frequency stabilize (> 20 seconds), brief (3 ms) hyperpolarizing or depolarizing current steps (150–250 pA) were injected at various frequencies to mimic a synaptic input (Wang et al 2013).

Data Analysis

We used circular statistics to find the R² vector strength for each experiment to quantify the degree of phase locking observed. The average vector has the mean angle φ_ave of all the data and a length that corresponds to the tightness of the locking (Batschelet E 1981)

R²=X²+Y² where X and Y are calculated according to

$$X=\frac{1}{M}\sum _{k=1}^{M}cos\left(\frac{2\pi ·{tr}_k}{P_F}\right);Y=\frac{1}{M}\sum _{k=1}^{M}sin\left(\frac{2\pi ·{tr}_k}{P_F}\right)$$

where P_F is the forcing period, M is the number of forcing cycles, and tr_k is the k-th interval between the stimulus and the next spike in the biological neuron.

Results

Probability density function for population of heterogeneous oscillators

The phase resetting theory described in the Methods and summarized in Eq. 1–3 considers a low frequency drive to a single high frequency oscillator. Here we extend this theory to consider a low frequency periodic drive to a population of heterogeneous oscillators with frequencies spread over a range within the higher frequency band. Rather than map the distribution of phases on one cycle to the next (Ermentrout and Saunders 2006, Marella and Ermentrout 2008), we solve instead directly for the asymptotic solution. If we assume that the population of high frequency oscillators has a distribution of intrinsic periods rather than a single common period, then we can derive an expression for the probability distribution of the phases at which the individual oscillators receive an input from the common pulsatile low frequency drive. The derivation can be generalized to the case in which the PRC is a function of the intrinsic period: f(φ^*, P_H). However, we will restrict ourselves to the case in which the PRC remains approximately constant as the intrinsic frequency is varied over some range. The dependence of steady state phase-locking at phase φ^* on the intrinsic period of a driven oscillator can be readily found from Eq. 3

$${\phi }^{\ast }=g(P_i)=f^{-1}\left(\frac{P_F}{P_i}-N\right)$$

where the superscript −1 denotes the inverse function. Thus the period of a driven oscillator corresponding to a specific φ^* is:

$$P_i=g^{-1}({\phi }^{\ast })=\frac{P_F}{f({\phi }^{\ast })+N}$$ (9)

Eq. (9) is obtained under the assumption that all periods in the high frequency population satisfy Eq. 3 on a stable branch. The probability density function ρ_φ^* of the phases at the time a low frequency input is received can be calculated in terms of the probability density function of the frequencies ρ_PH using the following formula for a function of a random variable to ensure that the cumulative probability over an interval of phases is the same as the cumulative probability over the corresponding interval of frequencies (Larson and Shubert 1979):

$$\begin{array}{c}{\mathrm{\rho }}_{{\phi }^{\ast }}({\phi }^{\ast })=h(1-\mid 1-f^{\prime }({\phi }^{\ast })\mid )\mid {(g^{-1})}^{\prime }({\phi }^{\ast })\mid {\mathrm{\rho }}_{P_H}\left(g^{-1}({\phi }^{\ast })\right)\\ \text{where}{(g^{-1})}^{\prime }({\phi }^{\ast })=\frac{\partial P_H}{\partial {\phi }^{\ast }}=-\frac{P_F{f}^{\prime }({\phi }^{\ast })}{{(f({\phi }^{\ast })+N)}^2}\end{array}$$

We apply the Heaviside function h(1 − |1 − f′(φ^*)|) to indicate that only phases that satisfy the stability criterion are mapped onto a period within the distribution of the high frequency population. Substituting in the above equation for (g⁻¹)′ and g⁻¹, gives the steady-state phase distribution as follows:

$${\mathrm{\rho }}_{{\phi }^{\ast }}({\phi }^{\ast })=h(1-\mid 1-f^{\prime }({\phi }^{\ast })\mid )\left|\frac{P_F{f}^{\prime }({\phi }^{\ast })}{{(f({\phi }^{\ast })+N)}^2}\right|{\mathrm{\rho }}_{P_i}\left(\frac{P_F}{f({\phi }^{\ast })+N}\right)$$ (10)

Equation (10) can be applied for any PRC (however weak or strong), as long as the variation the period remains within the region where stable solution exists. We confirm the validity of this expression by using simulations of Morris Lecar model neurons and simulations of phase oscillators with a Gaussian distribution of intrinsic periods, so that the following expression for the probability density of the phases applies:

$${\mathrm{\rho }}_{{\phi }^{\ast }}({\phi }^{\ast })=h(1-\mid 1-f^{\prime }({\phi }^{\ast })\mid )\left|\frac{P_F{f}^{\prime }({\phi }^{\ast })}{\sqrt{2\pi {\sigma }_i^2}{(f({\phi }^{\ast })+N)}^2}\right|exp\left(-\frac{{\left({\mu }_i-\frac{P_F}{f({\phi }^{\ast })+N}\right)}^2}{2{\sigma }_i^2}\right)$$ (11)

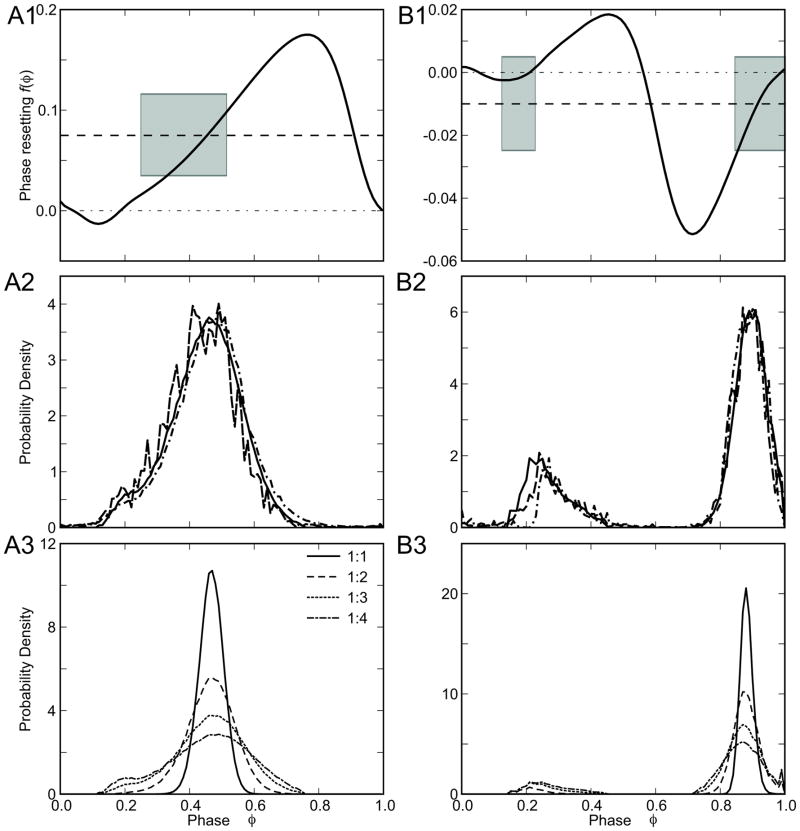
where μ_i and σ_i are the mean and standard deviation of the Gaussian distribution of intrinsic periods. The distribution of periods were not truncated to eliminate points that do not satisfy Eq. 3, but σ_H was small relative to the difference between the mean period and the limits P_min and P_max that support phase locking. Figure 1A1 shows the PRC in response to inhibition for a Morris Lecar model neuron with type 1 parameters as described in Rinzel and Ermentrout 1998, and Figure 1B1 shows the PRC for type 2 in response to excitation. The gray shaded regions show the phases on stable branches that correspond to the mean period plus or minus one standard deviation. The theoretical probability distribution is given by the black curve, the result of the pulse-coupled phase oscillator simulations is given by the dotted curve, and the results of the Morris Lecar model simulations is given by the dashed curve. Note that the probability density is constrained to the stable branches of the PRC, and the number of peaks in the probability density functions corresponds to the number of stable branches in the PRC. The type 2 PRC in Figure 1B1 has two peaks, and a small region of bistability in which both stable branches have overlapping values of the phase resetting and fall within the gray shaded region. However, bistability is not strictly necessary for two peaks since it is the existence of the two stable branches within the range of periods observed that is necessary rather than their overlap.

Figure 1.

Comparison of theoretical and simulated probability density functions for populations of oscillators with a Gaussian distribution in the intrinsic period. A. Type 1 Morris-Lecar model, A1) PRC for single neuron, A2) Phase probability density functions for heterogeneous population. Theoretical prediction (solid curve), and simulations of phase oscillators (dotted curve) were obtained for μ_i= 76.5 ms, σ_i=1.0, P_F=235.62 ms and N=3. The inverse F-I curve was used to select the values of applied currents for conductance-based simulations (dashed line) in order to satisfy a normal distribution with the nominal mean and standard deviation in period. A3) The theoretical prediction of the phase probability density obtained from Eq. 11 for different values of N. B. Type 2 Morris-Lecar model, B1) PRC for single neuron, B2) Phase probability density functions for heterogeneous population with μ_i =82.21ms σ_i=0.4, P_F=242.82 ms and N=3. The thick dashed horizontal line in A1 and B1 corresponds to deterministic value of f(φ^*) with mean period μ computed using Eq. 9. Shaded regions indicate the deterministic solutions on a stable branch as the period varies plus or minus a standard deviation μ_i ± σ_i. C. Dependence of the tightness of phase locking on N, the number of intrinsic cycles that elapse between forcing inputs. B3) Same as A3, but for Type 2 model.

The output of both simulations closely follows the theoretical prediction. Errors in the predictions of the pulse coupled simulator arise from the sampling of the Gaussian deviates whose distribution only approaches Gaussian for very large numbers, and are more prominent in the smaller peak in Figure 1B2 because it is visited less often. Errors in the Morris Lecar network simulations are slightly larger (especially for the smaller peak) because the shape of the phase resetting curve is not strictly invariant to frequency (Fink et al 2011), in contrast to the assumptions made in Eq. 11 and for the pulse-coupled simulator. Overall, however, the agreement is very good. The functional implication of this result is that a PRC with a single stable branch is optimal for synchronization of a population of heterogeneous oscillators.

Figure 1A3 and B3 show that increasing N (and therefore P_F) in a 1:N locking broadens the distribution of the phases described by Eq. 11. This theoretical prediction conforms to our intuition that if you increase the time between forcing pulses, more detuning between oscillators will be observed, resulting in decreased tightness of the locking.

Probability density function for population of oscillators with variable oscillatory microstructure

The Ornstein-Uhlenbeck random process (Uhlenbeck and Ornstein 1930) in intrinsic period is intended to simulate the biological variability in oscillatory period over time (Thounaojam et al, under review). The steady state distribution of the period is Gaussian with effective standard deviation, ${\sigma }_{\mathit{eff}}=\sigma \sqrt{\frac{\tau }{2}}$ where σ and τ are the O-U parameters described in the Methods. This allows a straightforward extension of the results of the previous section simply by substituting σ_eff for σ_i in Eq. 11 from the previous section. The caveat is that certain conditions must be met for convergence to this distribution, namely that the autocorrelation time τ, must be long compared to the mean period μ, (τ/μ ≫ 1), in other words, the period is slowly varying.

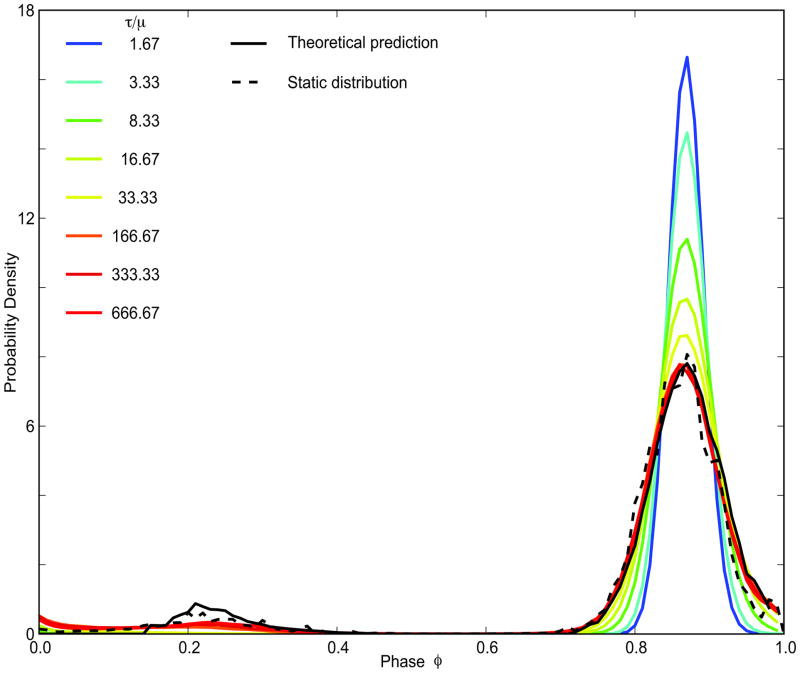
Figure 2 shows pulse coupled phase oscillator simulations for the same PRC as in Figure. 1B and probability density function shown in Figure 1B2. The static distribution refers to the case in which the distribution of the periods across the population is static in time, because different oscillators have different constant periods selected from a Gaussian distribution. The theoretical results are derived for this case, but applied to a distribution of periods that is dynamic. For a population of oscillators with O-U dynamics in the period, the distribution of periods is approximately constant across cycles, but the individual oscillators change their periods slowly and therefore occupy different positions within the distribution on different cycles. Even at low values of the ratio τ/μ, there is a qualitative agreement of the simulations with the theoretical prediction using σ_eff in Eq. 11, and for higher values the agreement is very good. The agreement with the large peak is excellent, and most of the error is in the fit to the smaller peak that is visited less often.

Figure 2.

The probability distribution of the phases for slowly varying random oscillator periods converges to the steady state for τ/μ ratio of two orders of magnitude. Theoretical predictions (black solid line) and simulations for a static distribution of periods across the population (black dashed line) for μ_i =30ms, σ_i =0.10, P_F =119.4ms, N=4. The colored lines are probability densities for O-U processes with same μ, σ_eff=σ_i and different sets of τ and σ. For ratio τ/μ=1.67 τ=50, σ=0.02; for τ/μ=3.33, τ=100, σ=0.0141421; for τ/μ=8.33 τ=200, σ=0.00894427; for τ/μ=16.67 τ=500, σ=0.00632456; for τ/μ=33.33 τ=1000, σ=0.00447214; τ/μ=166.67 τ=5000, σ=0.002; τ/μ=333.33 τ=10000, σ=0.00141421; τ/μ=666.67 τ=20000, σ=0.001.

The intrinsic phase of a neural oscillator at the time that a low frequency stimulus is received is not an observable. Therefore, it is desirable to convert the expression for distribution of phases into a distribution of the intervals from the stimulus onset until the next spike for each oscillator. The time to the next spike tr (see Fig 3A2) is given by

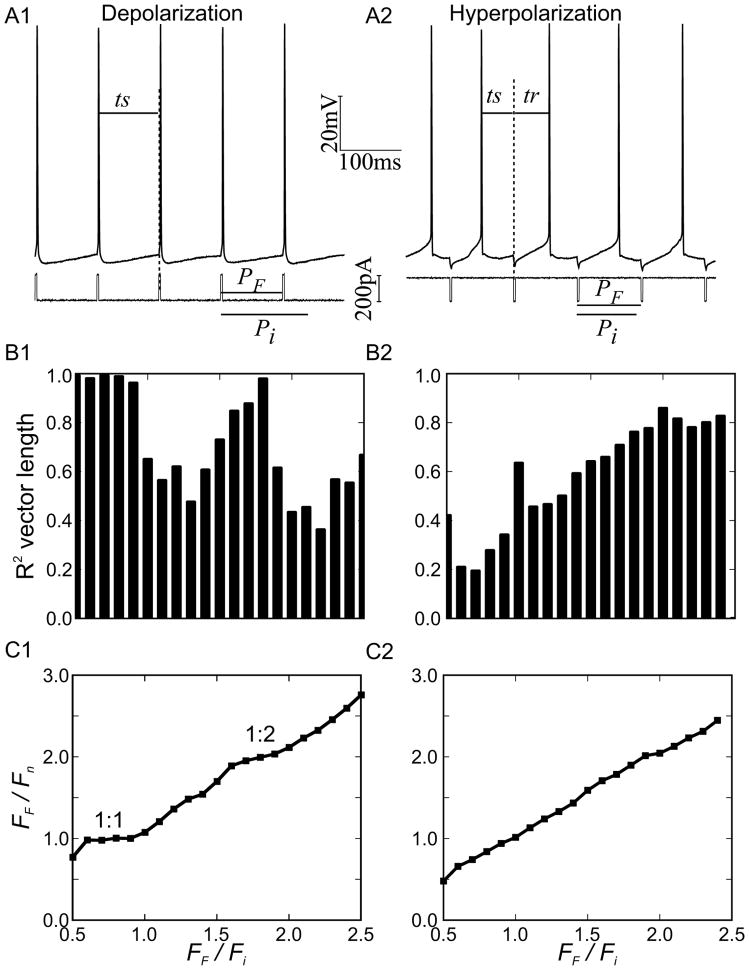
Figure 3.

Periodic forcing of a CA1 pyramidal neuron. A. Experimental procedure for a train of depolarizing (A1) or hyperpolarizing (A2) pulses. B. Vector strength of phase locking for experiments at different ratios of forcing frequency to intrinsic frequency of the neuron at a given level of steady applied current. For depolarizing stimulus trains in B1, there were clear plateaus in vector strength corresponding to 1:1 and 1:2 locking. The vector strength for hyperpolarizing trains in B2 rarely exceeded 0.8 and no plateaus were evident. C. Plots of the ratio of the forcing frequency to the forced frequency for the biological neuron versus the ratio of the forcing frequency versus the free-running frequency immediately before the experiment show plateaus corresponding to 1:1 and 1:2 locking for depolarizing trains (C1) but not hyperpolarizing trains (C2).

$$tr=G(P_H)=P_i(1-{\phi }^{\ast })=P_i\left(1-f\left(\frac{P_F}{P_i}-N\right)\right)$$ (12)

Then the distribution of the next spike time is given by:

$${\mathrm{\rho }}_{tr}(tr)=\mid {G^{-1}}^{\prime }(tr)\mid {\mathrm{\rho }}_{P_H}(G^{-1}(tr))$$ (13)

If the analytical form of the phase resetting curve is known, an analytical form may be obtained. In the following section we obtained the inverse and the probability density for the next spike time numerically.

These results will be applied in two ways in the next two sections: first to the distribution of periods in a single neuron over time, then to a population in which each neuron is pulled toward the same mean but exhibits variability due to different instantaneous values of the period.

Experimental validation of theoretical results in a single neuron with variable oscillatory microstructure

In order to determine the utility of the probability density function predictions in Eq. 11 over and above that of the analysis of Eq. 1–3 that assumes a constant period, we examined phase locking of a biological neuron to a periodic stimulus, shown in Figure 3A. We used both depolarizing pulses (Figure 3A1) and hyperpolarizing pulses (Figure 3A2) as described in the Experimental Methods. CA1 pyramidal neurons have a “N” shaped I–V curve (Yamada-Hanff and Bean 2013) that allows them to fire tonically in response to the application of depolarizing current (Wang et al 2013) or a net increase in depolarizing current produced by the neuromodulatory effects of ACh (Yamada-Hanff and Bean 2013). Here we show the existence of 1:1 and 1:2 locking windows in response to periodic trains of depolarizing or inhibitory pulses. Furthermore, we show that the sharpness of the distribution of the timing of the input relative to the most recent spike in the pyramidal neuron is determined by the shape of the phase response curve.

Figure 3A shows the experimental protocol in a 1:1 locking regime. Figure 3B1 shows that for a train of depolarizing pulses, the vector strength of the locking approached the maximum value of 1 for two frequency regimes, one in which the criterion in Eq. 2 was satisfied for an N =1 (a 1:1 locking) and another in which the criterion was satisfied for N=2 (a 1:2) locking. These regions are manifested as plateaus in the plot of the ratios of forced versus free running frequency of the driven neuron to the forcing frequency. On the other hand, the vector strength (Figure 3B) was weaker in response to trains of hyperpolarizing pulses, and in that case (Figure 3C) the ratio of the forced versus intrinsic frequencies was approximately linear with no obvious plateaus. This indicates that no strong phase to phase coupling was observed in the latter case.

In order to explain these results, we used our previously characterized phase response curves of these neurons to both depolarizing and inhibitory current pulses (Wang et al 2013). The original data from that study was averaged, and then smoothed in Fig 4A to show the difference in the typical shapes of the PRC in response to a single depolarizing or hyperpolarizing input. The theoretical explanations below are intended to be qualitative in nature, and to illustrate how the shape of the PRC influences the probability distribution in the presence of heterogeneity and noise.

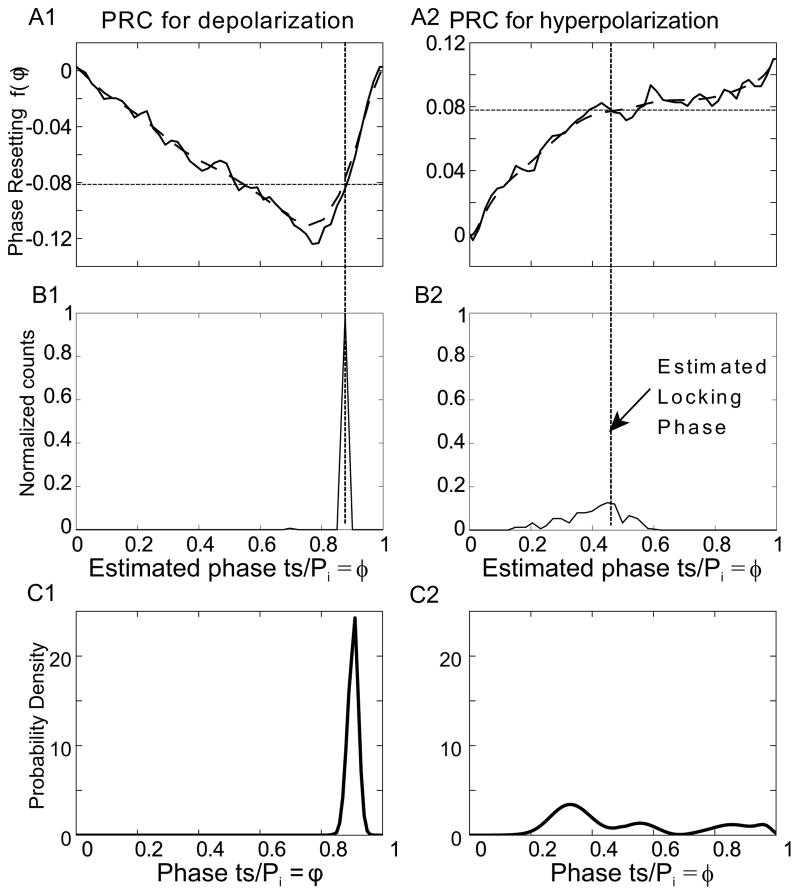
Figure 4.

Comparison of experimental and theoretical distribution of the phase at which the forcing stimulus arrives within the cycle of the forced neuron. A. Averaged PRC (solid line) for CA1 pyramidal neurons (n=14). Data from Wang et al 2013. Data was smoothed by fitting to a Bezier polynomial function (thick dashed curve). A1) PRC for depolarizing pulse, A2) PRC for hyperpolarizing pulse. The thin dashed horizontal line in A1 and A2 corresponds to deterministic value of f(φ^*) for the mean period computed using Eq. 9. B. Phase distribution for one representative example. B1) Depolarizing pulse train: P_F=100ms, P_i=134.12 ± 8.79424 ms, B2) Hyperpolarizing pulse train: P_F=102.6, P_i=99.4±7.6 ms. C. Probability density calculated using Eq. 11. C1) Using the PRC from A1 with parameters : P_F=100 ms and P_i=106±1.5ms and C2) Using the PRC in A2 and parameters P_F=102ms and P_i=95±1.5ms. Since the PRCs in A and the distributions in B are from different studies, the correspondence between theory and experiment is only qualitative.

The PRC for a depolarizing input has two branches (Figure 4A1). The leftmost branch has a negative slope, because the later an input is applied the more it advances the next spike. On the second, rightmost branch there is a positive slope because an input applied late in the cycle evokes a spike with a short, nearly constant, latency, resulting in a positive slope approaching one. Recall that the stability criterion requires the absolute value of the slope at a stable locking point to be between 0 and 2. Therefore the initial branch of the PRC in Figure 4A1 has a negative slope that does not support stable phase-locking, but the second, steep stable branch does. Only a single, less steeply sloping stable branch was observed in the PRC in Fig 4A2 for hyperpolarizing pulses. Firing times for one representative experiment each for a 1:1 locking case (Figure 4B) show that locking occurs on the stable branches as predicted. The phase was estimated simply by dividing the elapsed time between the spike before the stimulus (ts in Fig 3A) and stimulus onset by the free-running intrinsic period measured just prior to the experiment. These examples were chosen to show that for about the same amount of variability in the period, the locking to a depolarizing input is far more precise than to a hyperpolarizing input. The pre-existing theory does not explain the much sharper locking for the case with depolarizing pulses.

Slow variability in the period of these neurons has been observed experimentally (Netoff et al 2005), so assumed that an Ornstein Uhlenbeck process characterizes the variability in the period, and applied the results from the previous section to obtain the expected distribution of the phases at the time a stimulus is received. Eq. 11 for the steady distribution of the phases depends upon both the value of the resetting at each phase and on its slope (see Eq. 10) as well as on σ_eff for the O-U process and the forcing and intrinsic periods. These neurons do not in general remain viable in slice long enough to characterize the PRC in the same neurons used for the periodic forcing experiments, so we cannot obtain an exact parameter match for the representative experiments. However, for the same amount of variability (σ_eff = 1.5 ms), the probability density function calculated using for the shape of a depolarizing PRC was much sharper than that for the hyperpolarizing PRC (Figure 4C), in qualitative agreement with the experimental data in Figure 4B.

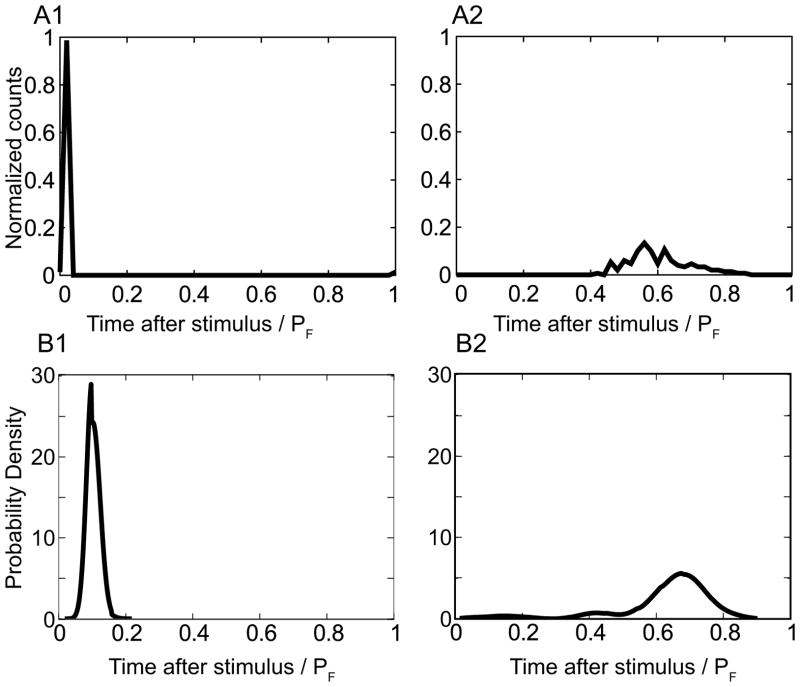
The estimate of the phase in Figure 4B is based on a constant estimate of the period, but we hypothesize that the unobservable intrinsic period actually varies as an O-U process,. Therefore we also compared the distributions of the time until the next spike after the stimulus (tr in Figure 3A2) to account for this source of variability. The distribution of tr for the same representative experiments in Figure 4B is given in Figure 5A. The theoretical distribution of tr (Figure 5B) was calculated as described in Eqs 12 and 13 in the previous section, using the same PRCs and parameters as in Figure 4C and again is in very good qualitative agreement with the observations. Figures 4C and 5B clearly show that for the exact same amount of variability, the theory predicts much more precise locking for PRCs that are shaped like the ones in response to a depolarizing input in contrast to those in response to a hyperpolarizing input.

Figure 5.

Distribution of observable time after the stimulus is also in qualitative agreement with theoretical predictions. A) Normalized experimental distribution for the same examples as in Fig 4 with A1) depolarizing and A2) hyperpolarizing pulses. B. Theoretical predictions for B1) depolarizing and B2) hyperpolarizing pulses with the same model parameters as in Figure 4.

To summarize, we compared two different types of periodic input, namely trains of depolarizing current pulses versus hyperpolarizing current pulses, because the PRC shapes for the two types of pulses were known to be markedly different (Wang et al. 2013). The PRCs in response to a depolarizing pulse have a relatively small stable branch that was also relatively steep, which, when inserted in Eq. 11, correctly predicted a sharp, narrow probability density of stroboscopically sampled phases. The tight locking allowed discernible plateaus corresponding to 1:1 locking and also cross-frequency 1:2 locking. On the other hand, the PRCs in response to hyperpolarizing pulses have a broad single branch with a large relatively flat region, which when inserted in Eq. 11, correctly predicted a broadly distributed low-amplitude probability density of stroboscopically sampled phases that prevented the observation of clear cross-frequency locking.

Desynchronization of spikes during a cycle of low frequency forcing

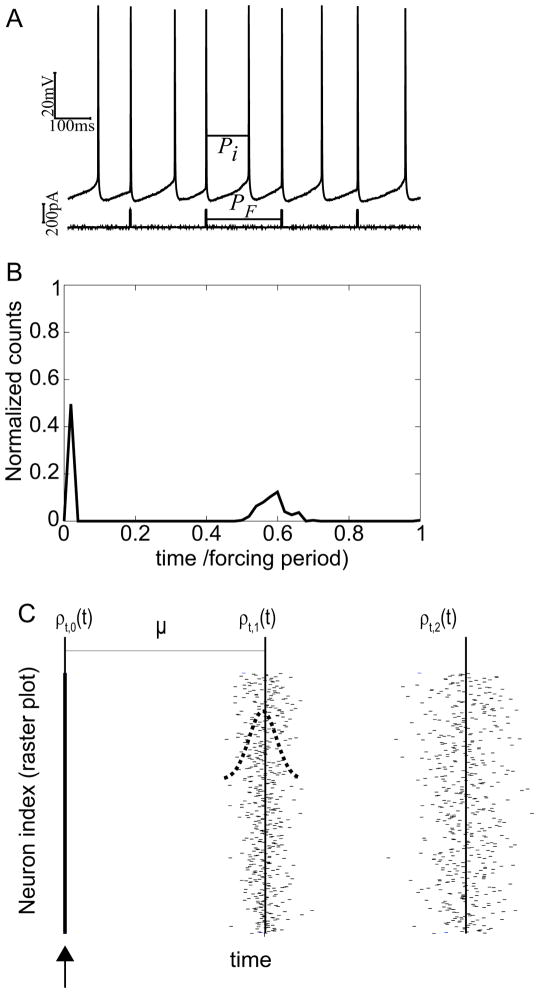
Figure 3B and 5 only analyze the timing of the first spike after the stimulus. In a 1:N locking, there are N spikes between any two low frequency forcing stimuli; Figure 6A shows an example experiment for 1:2 forcing. For the tightly locked 1:2 cases in response to depolarizing pulses, we noted that the distribution of the second spike within a forcing stimulus spike was much broader (Fig 6B). We explain this phenomenon by analogy to a population of oscillators with the period modeled as an intrinsic random process. We consider a special, idealized case in which a strong depolarizing or excitatory input evokes a spike reliably and immediately in every neuron in the population. Of course, this produces exact synchronization and a delta function distribution in spike times ρ_t,0(t) for the first spike across the population. However, subsequent spike times would spread out due to the random fluctuations in the periods of the individual neurons (see Equations below and Figure 6C).

Figure 6.

Spike time spreading in a single neuron over time and in a population. A. Experimental trace for 1:2 locking. B. Single neuron over time. For a single neuron being periodically forced at 1:2 over many cycles, the second spike after the stimulus is much less tightly locked to the stimulus than the first. C. Snapshot of spike times within a population during one cycle of low frequency forcing. In an idealized scenario, the first spike times are perfectly synchronized and the distribution of spike times ρ_t,0 is a delta function. Since the period of each neuron is a random process, on any given cycle, there is a Gaussian distribution of the interval until the next spike. Subsequent spike times become more spread out, as shown by the distribution ρ_t,1 for the first set of spikes times and ρ_t,2 for the second, until the next forcing input is received to reestablish synchrony. The mean period for the population is denoted by μ.

$${\mathrm{\rho }}_{t,0}(t)=\delta (t)$$ (14)

$${\mathrm{\rho }}_{t,1}(t)=\frac{1}{\sigma \sqrt{2\pi \mu }}{e}^{-\frac{1}{2}{\left(\frac{\mu -t}{\sigma \sqrt{\mu }}\right)}^2}$$ (15)

$${\mathrm{\rho }}_{t,n+1}(t)=\frac{1}{\sigma \sqrt{2\pi \mu }}\int {\mathrm{\rho }}_{t,n}(t)e^{-\frac{1}{2}{\left(\frac{x+n\mu -t}{\sigma \sqrt{\mu }}\right)}^2}dx$$ (16)

We can make a connection between the highly idealized case illustrated in Figure 6C with the experimental data in Figure 6A and B by examining the PRC in Figure 4A that is typical of excitatory perturbations to CA1 pyramidal neurons illustrated in Figure 6A and B. The key is that in a steady phase locking, these neurons are receiving an input on the second, stable branch of the PRC in Figure 4A that is approximately linear with a slope of one. The constant latency to the next spike is approximately zero over the region of the PRC which supports phase locking. The constant latency produces a linear PRC with a slope of one that can be represented as f(φ) = φ + b, where the constant latency is P_i(1 − φ + f(φ)) = P_i(1 + b), with b≥−1 so that the latency is nonnegative (Maex and De Schutter 2003). On the second, stable branch of the PRC, b≈−1, so the latency approximately equals zero. This feature allows depolarizing trains to tightly synchronize the first spike after the stimulus.

Network simulations of phase amplitude coupling

In the this section, we suggest that the spike spreading mechanism demonstrated above may provide insight into a specific example of demonstrated cross-frequency phase-amplitude coupling: theta-gamma nesting in the CA1 region of the hippocampus (Bragin et al 1995; Belluscio et al 2012). Inhibitory trains can also synchronize a population with a linear PRC with a slope of one, but the mechanism is slightly different. A conductance-based inhibitory synapse can saturate with strong input, meaning that it hyperpolarizes the target neuron to a nearly constant membrane potential, from which the latency to the next spike is approximately constant regardless of the phase at which an input is received. For this case b≈0 and the latency equals the intrinsic period.

The prediction of spread of the distribution on subsequent low frequency cycles can be applied not only to all the spikes recorded during repeated trials in a single neuron, but also to a snapshot of the distribution of the spike times within a heterogeneous population on different fast cycles within a slow cycle. Since inhibitory drive from the septum and local oriens lacunosum-moleculare interneurons likely plays an important role in theta modulation of gamma oscillations (Colgin 2013), we constructed a network of uncoupled phase oscillators driven by periodic inhibitory input. Our phase oscillators represent modular gamma oscillators that are comprised of reciprocally coupled pyramidal neuron and interneurons, called PING modules (Kopell et al 2010) for pyramidal-interneuronal network gamma. In order to focus on the ability of feedforward input to synchronize a population, we have made the simplifying assumptions to neglect feedback from the gamma oscillator to the theta drive as well as interconnectivity between gamma modules. We start with an example of periodic pulsatile low frequency inputs to a population of oscillators with constant period that is heterogeneous across the population, then look at an example population of oscillators in which the heterogeneity is introduced by O-U variability in the period, and finish with an example in which the assumption of pulsatile forcing is dropped.

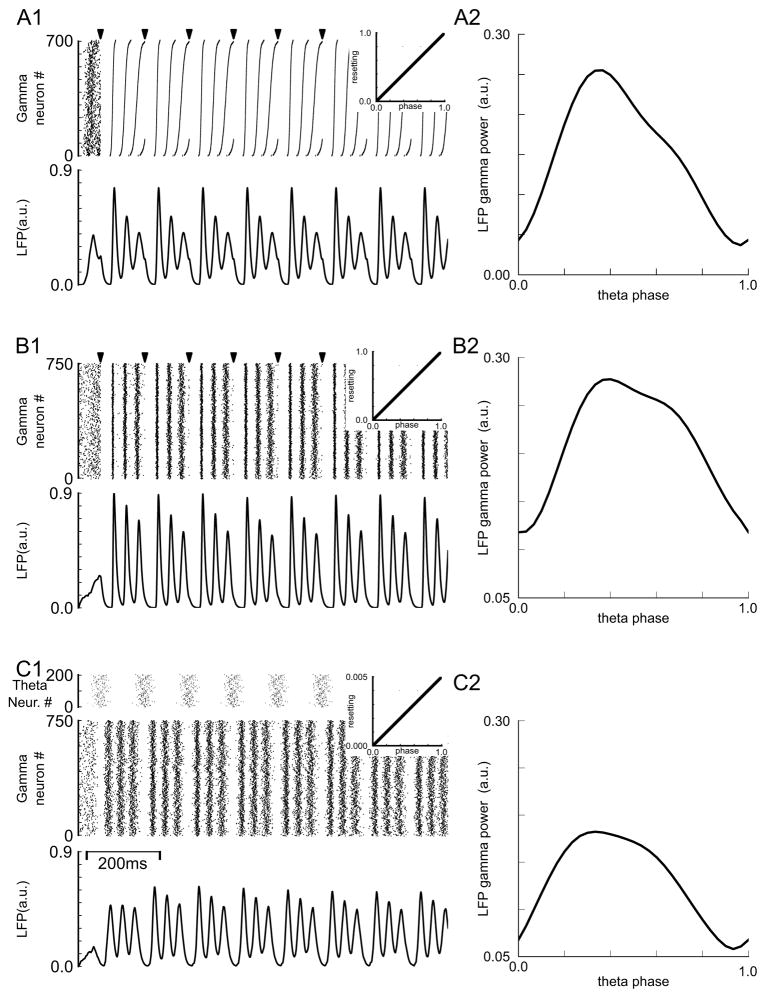
Figure 7A1 shows the response of a population of oscillators with a Gaussian distribution of constant periods to periodic low frequency stimuli (arrows). The PRC is identical for each driven oscillator and is given in the inset at right. The PRC is linear with b=0 and a slope of one, similar to the PRCs measured for computational models of PING modules (Malerba and Kopell 2013). The raster plot at the top of in Figure 7A1 shows the firing time of the gamma modules, which should be interpreted as the synchronized firing time of the interneuron(s) within each module. The raster plot is indexed with the fastest oscillators at the bottom. The population is unsynchronized prior to the first input. The first spike after each input is synchronized and the oscillators become desynchronized in a predictable manner as the faster oscillators fire earlier and earlier on subsequent cycles, in a manner similar to that predicted by Eq. 14–16. However, in contrast to Figures 3A1, the left half of figure 4 and 5, and Fig 6, the synchronization does not occur with short latency, but rather with a latency on the order of an intrinsic period. Since the intrinsic period is different for different neurons, the latency is also different for each neuron, thus the synchronization across the population is only approximate. The simulated local field potential below the raster plot shows phase-phase coupling with the theta oscillation because there are three gamma peaks for each theta cycle between inputs at constant phases (see figure 7 caption). In addition, modulation of gamma power within a theta cycle, shown in Figure 7A2, indicates phase-amplitude coupling. The gamma peaks decay in amplitude, reflecting the progressive loss of synchronization during a stimulus cycle.

Figure 7.

Pulse coupled phase oscillator simulations of theta gamma nesting. A1. Raster diagram (top panel) and LFP (bottom panel) for population of 700 gamma modules. Periods were normally distributed with 33 ms mean and 2.7 ms standard deviation. For the raster diagram modules were sorted from fastest (bottom) to slowest (top). Pulsatile periodic input (arrow marks at top of raster diagram) was applied with a period of 120 ms. The linear PRC is shown in the insets. A2. Dependence of gamma power on theta phase. B. The input was the same as in A but 750 modules with instantaneous intrinsic periods determined by a randomly initialized O-U process were used instead of Gaussian distributed constant periods. The parameters for the O-U process were μ=33 σ=0.1 τ=165. C. Same as in B, but the theta input was arbitrarily divided into 200 proportionally weaker periodic inputs with initial phases distributed normally with mean of 0.5 and standard deviation of 0.0925. The PRC was scaled proportionally (note different scale for inset). Gamma peaks in the LFP occur at the following theta phase within the theta cycle: A1: 0.27(98.8°), 0.45(162.4°), 0.81(291.7°), B1: 0.27(99.1°), 0.55(198.0°), 0.82(297.0°), C1: 0.17(64.1°), 0.45(163.4°), 0.81(293.0°).

Figure 7A is a noiseless, deterministic simulation. In order to simulate the effect of noise and heterogeneity, in Figure 7B the period of each oscillator was modeled as a random O-U process rather than a constant. Although all oscillators were pulled to the same mean value, their random initialization and random time course provides both noise and heterogeneity. The same PRC was utilized as shown in the inset, and the resultant phase-phase (Figure 7B1 bottom) and phase-amplitude coupling (Figure 7B2) is quite similar, although the raster plot (Figure 7B1 top) looks more random.

Obviously, a perfectly pulsatile input is an idealization that allows an analytical description of the probability density functions to be formulated. However, the concept that the low frequency drive is more effective in synchronizing the high frequency population at some times than others is likely to generalize, and we explored this possibility using simulations. We assumed that 200 inputs were required to produce the saturated, constant PRC shown in the insets in Figure 7AB, and made the assumption that the PRC for a single neuron was scaled by 1/200 (note the vastly different vertical scale in inset in Figure 7C1). Simultaneous inputs sum linearly in the pulse coupled simulator, so the slope of the PRC is no longer one in response to fewer than 200 inputs. Then we imposed loose synchronization on the theta inputs by randomizing their initial phases so that the spikes were spread out over about a third of the cycle period, as shown in Figure 7C1 above the top raster plot. A small τ/μ ratio was chosen for simulations in Fig 7 and B and C to allow the LFP solution to quickly converge to a pattern of decreasing amplitude; a larger ratio requires multiple theta cycles for convergence to this pattern. The phase-phase and phase-amplitude coupling are still clearly visible from the raster plot and in the modulation of gamma power by theta phase (Figure 7C1 and C2 respectively), so the hypothesis that phase-amplitude nesting can arise from differential synchronization due to low frequency drive that is not pulsatile is validated. The degree to which this mechanism might contribute to phase-amplitude coupling in theta-gamma nesting in the hippocampus is not known.

Discussion

Summary

The theory for periodic pulsatile forcing of a single limit cycle oscillator is well-developed (Glass and Mackey 1988; Rinzel and Ermentrout 1998). We generalized the theory for phase-locking to a periodic pulsatile drive in a straightforward way to give the steady state probability density of the phases of a population of heterogeneous oscillators stroboscopically sampled at the time a single periodic forcing input is received (Eq. 10 for the general form, Eq. 11 for a Gaussian distribution in period). For the latter case (a Gaussian distribution), we also showed that increasing the ratio N of forced to intrinsic period clearly decrease the tightness of the locking. The same expressions apply to the steady distribution of stroboscopically sampled phases in a single neuron for multiple stimuli, provided the noise in the period takes the form of an Ornstein-Uhlenbeck process. Therefore we were able to successfully test the predictions of Eq. 11 on the tightness of the phase locking observed in a single neuron. We then assumed perfect synchronization evoked by a stimulus and showed in Eq. 14–16 how the probability density broadens for subsequent spikes within a forcing cycle, and generalized this result to predict that synchronization decays similarly for subsequent spike volleys in a heterogeneous population in the absence of stimuli. Finally, we used network simulations to show that this desynchronization causes the amplitude of the driven oscillation to decay during a forcing cycle. A key simulation result is that the mechanism for phase-amplitude coupling persists even when the underlying theoretical assumption is violated by spreading the input out over a forcing cycle so that it is no longer pulsatile.

PRC shapes matter

CA1 pyramidal neurons participate in both theta and gamma LFP oscillations in vivo (Buszaki 1983, 2006). If these neurons function as pacemakers (Yamada-Hanff and Bean 2013) under any in vivo conditions, our results based on PRC shape imply that the most effective input for tight phase-locking of these neurons under those circumstances is a periodic depolarization. However, as stated in the Introduction, PRC analysis should be applied to the minimal oscillatory unit, which may or may not be a single neuron. Typically, in cross frequency modulation, the high frequency oscillations are in the gamma band. For gamma band oscillations, the minimal unit oscillator has been variously hypothesized to be a single interneuron (Wang and Buszaki 1996), an oscillatory module of reciprocally connected interneurons and pyramidal cells (Kopell et al 2010; Malerba and Kopell 2013), or a network oscillator comprised of populations of stochastically firing neurons in which inhibition waxes and wanes, providing tight windows of excitability that occur at gamma frequency (Economo and White 2012).

PRCs are often divided into two types (Hansel et al 1995; Ermentrout 1996). In Type 1, there are mostly changes in cycle length in one direction, either advances or delays. Figure 1A1 shows an example of a Type 1 PRC with mostly delays. For Type 2, there are substantial regions corresponding to both advances and delays. This leads to two prominent stable PRC branches in the Type 2 example in Figure 1B1. We have shown that these two branches lead to two peaks in the probability density function for periodic drive to a population of oscillators with some degree of heterogeneity in period distributed about a center period, which makes Type 1 preferable for tight locking. Since the PRCs in Figure 3A are both type 1, but the PRC in Figure 3A1 leads to tighter locking, we add the caveat that a Type 1 PRC with a steep slope (optimally one) in the stable locking region is optimal for tight locking in situations in which there are multiple simultaneously active high frequency modules with a spread in their intrinsic periods. In contrast, a type 2 PRC has been found to be optimal under the assumption of a population of uncoupled oscillators with a common period receiving a common noisy input (Abouzeid and Ermentrout 2009). Therefore different PRC shapes are optimal for synchronization under different assumptions.

Akam et al 2012 experimentally measured the phase response curve for the entire network generating pharmacologically induced gamma oscillations in the hippocampal CA3 area in a slice preparation. Several different types of inputs, including electrical stimulation of afferent fiber bundles as well as optogenetic stimulation, were utilized in that study. The resultant PRC was always Type 2 with two stable branches regardless of the specifics of how it was measured. A strong pulsatile input appeared to consistently increase the maximum amplitude of the next gamma oscillation in the LFP. This increase in amplitude is consistent with a possible contribution from synchronization of the ongoing activity of distinct gamma modules (see next section), although other interpretations are certainly possible. The observed PRCs are not optimal for feed-forward synchronization by our criteria; however, since the exact nature of the gamma oscillatory module and the theta frequency driving inputs to these modules are not known, the appropriate PRC in response to theta drive has not been characterized.

Phase resetting versus evoked power

There are two fundamental ways in which inputs can affect brain rhythms: 1) by resetting ongoing oscillations versus 2) recruiting additional oscillatory neural ensembles. In this study we have focused on the modulation of synchrony induced by the former as a mechanism for phase-amplitude coupling; however, the contribution of this mechanism is speculative at this time. A more widely held hypothesis is that high-frequency power reflects either a general increase in population synaptic activity or selective activation of a connected neuronal sub-network (Canolty and Knight 2010). Analogously, competing theories were also proposed for the generation of sensory event-related potentials (Shah et al 2004): partial phase resetting of ongoing electroencephalographic oscillations versus stimulus-evoked neural responses, meaning increases in neural activity. In a different context, Schroeder and Lakatos (2008) postulate a role for modulatory inputs in resetting the phase of ongoing activity whereas driving inputs increase activity by recruiting additional neural activity. However, they refer to resetting applied to the entire ongoing rhythm, not to individual oscillators in an ensemble, thus modulatory resetting under their paradigm produces no increase in power, in contrast to Figure 7. Our postulated mechanism for modulation of gamma amplitude is also not consistent with their hypothesis that epochs of nested high gamma amplitude periods are an efficient way of rationing the high metabolic demand of gamma oscillations (Schroeder and Lakatos 2009). Nonetheless, increased gamma synchrony at certain phases of the theta oscillation might partially explain why gamma oscillations in the hippocampus are observed to have their largest amplitude when they co-occur with the theta rhythm (Colgin and Moser 2010).

Implications for neural computation

Significant theta/gamma phase to phase coupling has been observed in hippocampal region CA1 at 1:5 ratios for slow gamma and 1:9 for fast gamma (Belluscio et al 2012). This clear evidence of phase-phase coupling implies either that the gamma oscillations are ongoing in the background at varying levels of synchrony over multiple oscillatory cycles, or that the 1:N locking is re-established very quickly on each theta cycle. Phase to amplitude coupling was also observed with a peak at a theta phase of 200° for fast gamma and 250° for slow gamma. Both phase-phase and phase-amplitude theta-gamma coupling (Bieri et al 2013) are enhanced for fast gamma during coding of future locations and for slow gamma during coding of previous locations. Slow gamma amplitude is more effectively modulated by theta in hippocampal region CA3, whereas fast gamma is more effectively modulated in CA1 (Tort et al 2010). We suggest that some of the theta modulation of gamma power results from resetting heterogeneous gamma modules that optimally synchronize them during certain theta phases. The degree of synchrony within the active gamma ensembles may allow the identification of the proximity of the represented location to the animal’s current location. Regardless of whether the mechanisms proposed in this study are relevant to theta gamma locking or nesting in the hippocampus, there are many other instances of cross frequency coupling in the brain that might involve the alignment of existing oscillations, so this hypothesis should be considered in the design of experiments to probe the nature of cross-frequency phase-phase and phase-amplitude coupling.