Network Meta-analysis of Randomized Clinical Trials: Reporting the Proper Summaries

Abstract

Background

In the absence of sufficient data directly comparing two or more treatments, indirect comparisons using network meta-analyses (NMA) across trials can potentially provide useful information to guide the use of treatments. Under current contrast-based methods for NMA of binary outcomes, which do not model the “baseline” risks and focus on modeling the relative treatment effects, the patient-centered measures including the overall treatment-specific event rates and risk differences are not provided, which may create some unnecessary obstacles for patients to comprehensively understand and trade-off efficacy and safety measures. Many NMAs only report odds ratios which are commonly misinterpreted as risk ratios by many physicians, patients and their care givers.

Purpose

We aim to develop network meta-analysis to accurately estimate the overall treatment-specific event rates.

Methods

A novel Bayesian hierarchical model, developed from a missing data perspective, that borrows information across multiple treatment arms, is used to illustrate how treatment-specific event proportions, risk differences (RD) and relative risks (RR) can be computed in NMAs. We first compare our approach to alternative methods using two hypothetical NMAs assuming either a fixe RR or a fixed RD, and then use two published NMAs on new-generation anti-depressants and antimanic drugs to illustrate the improved reporting of NMAs possible with this new approach.

Results

In the hypothetical NMAs, our approach outperforms current contrast-based NMA methods in terms of bias. In the NMAs on new-generation anti-depressants and on antimanic drugs, the outcomes were common with proportions ranging from 0.21 to 0.62. As expected, the RR estimates differ from ORs. In addition, differences in the magnitude of relative treatment effects and the statistical significance of several pairwise comparisons from previous report could lead to different treatment recommendations.

Limitations

First, to facilitate the estimation of overall treatment-specific event proportions, we assume that each study hypothetically compares all treatments, with unstudied arms being missing at random conditional on the observed arms. However, it is plausible that investigators may have selected treatment arms on purpose based on the results of previous trials, which may lead to “nonignorable missingness” and potentially bias our event rate estimation. Second, we have not considered methods to identify and account for potential inconsistency in our missing data network meta-analysis framework. Both methods await further development.

Conclusions

The proposed NMA method can accurately estimate treatment-specific event rates or proportions, RDs, and RRs, and is recommended in practice. Application of this approach can lead to different conclusions, as illustrated here, from current NMA models that only estimate ORs.

1. Introduction

Comparative effectiveness research (CER) relies on accurate assessment of treatment efficacy and safety to provide evidence to inform health-care decisions that then may need to be tailored to a specific patient. The growth of interest in evidence-based medicine has led to a dramatic increase in attention paid to systematic reviews and meta-analyses.^{1, 2} In order to account for the growing number of treatment comparisons of interest for a given condition, methods for network meta-analysis (NMA) (also called mixed or multiple treatment comparisons) which expand the scope of conventional pairwise meta-analyses have been developed. NMA simultaneously synthesizes both direct comparisons of interventions within randomized controlled trials (RCTs) and indirect comparisons across trials. In the simplest case, one may be interested in comparing two treatments A and C. Direct evidence can only be obtained from RCTs of A versus C, while indirect evidence can be obtained from RCTs of either A or C versus a common comparator B.³ When both direct and indirect evidence are available, the two sources of information can be combined as a weighted average using appropriate statistical methods. With appropriate assumptions, borrowing strength from indirect evidence allows more precise estimates of treatment differences than can be obtained from pairwise meta-analysis.⁴

A limitation of reporting for many current NMA methods for binary outcomes is that the only summary statistic usually reported is the OR^5-13. Though it is well-known that RRs and ORs diverge when events are common (i.e., event rates are higher than 10%)^14-17, ORs are often mistakenly thought as RRs by physicians, patients and their care givers. Absolute measures including treatment-specific event rates and RDs contain important information that cannot be expressed by ORs¹⁸. Thus both relative measures and absolute measures should be reported and reporting only OR is not proper. However, to the best of our knowledge, only a few published NMAs^{19, 20} have reported RR, but none have reported the treatment-specific event rates and RDs. This limitation in reporting arises because many current statistical approaches and software^21-29 are not capable of estimating treatment-specific response proportions and summary statistics such as the risk difference (RD) and risk ratio (RR). They focus on treatment contrasts where one of the arms of each study is chosen as “baseline”. Since many NMAs do not have a common “control” arm such as a “placebo” or “standard” intervention and different trials may have different “baselines”, specifying a common distribution for “baseline” groups is generally not interpretable. Thus, many current NMA methods treat the underlying “baseline” risks as nuisance parameters and therefore fail to estimate the treatment-specific response proportions. Although a few^{25, 30-33} discussed the transformation from the ORs to RRs and RDs, they depend on a strong assumption that either the event rate in a “reference” treatment group can be accurately estimated from some external data, or by summarizing only trials with the “reference” arm with a separate (random effects) model. In many cases, such external data are not available limiting the applicability of the former approach. Furthermore, even if some external data are available, it may come from a different population than what the NMA may represent. From the theory of missing data analysis³⁴, these current NMA methods are unbiased only under a strong assumption of missing completely at random (i.e., all trials randomly choose to include or not include the “reference” arm). Furthermore, it is less statistically efficient and the back transformed RRs and RDs can be noticeably different if a different treatment arm is chosen as the “reference” group even with exactly the same model and priors.

To address this issue, we developed a novel multivariate Bayesian hierarchical model from the perspective of missing data analysis. We compare our approach to other alternative methods using two hypothetical NMA data sets and then re-analyze two network meta-analyses in which the ORs are the only effect measures reported to illustrate potential differences. We showed how more relevant and proper summary statistics can be summarized.

2. Methods

Let us consider a network meta-analysis with a collection of studies i = 1, 2,…, I, and each of the studies only reports on a subset of the complete collection of K treatments. Let k_i be the number of treatments and S_i be the set of treatments that are compared in study i. Studies with k_i >2 are called “multi-arm” studies, in contrast to k_i= 2 for “two-arm” studies. Let D_i= {(y_ik,n_ik), k ∈ S_i} denote the available data from the i^th trial, where n_ik is the total number of subjects and is the total number of successes for the k^th treatment in the i^th study. We then denote the corresponding probability of success by p_ik. In this section, we first briefly review the most commonly used contrast-based approach, then present our novel arm-based approach illustrating how to accurately estimate the overall treatment-specific event rates from the perspective of missing data analysis. At last, we evaluate the performance of a few alternative methods using two hypothetical examples.

2.1 The Contrast-Based (CB) approach

Let b_i be the specified “baseline” treatment for the i^th trial, commonly denoted as b for simplicity. Let X_ik =1 if k≠b and X_ik = 0 if k = b. The most commonly used CB models use the following Bayesian hierarchical model^{25, 35},

$$y_{ik}\sim \mathit{\text{Bin}}(n_{ik},p_{ik}),k\in S_i,i=1,\dots ,I$$ (2.1)

$$logit(p_{ik})={\mu }_i+X_{ik}{\delta }_{ibk},{\delta }_{ibk}\sim N(d_{bk},{\sigma }_{bk}^2),d_{hk}=d_{bk}-d_{bh},b\ne h\ne k\in S_i,\mathit{\text{Corr}}({\delta }_{ibh},{\delta }_{ibk})={\gamma }_{hk}^{(b)},b\ne h\ne k\in S_i.$$

Some prior distributions are then chosen for μ_i, d_bk, ${\sigma }_{bk}^2$ and ${\gamma }_{hk}^{(b)}$. As many NMAs do not have a common “baseline” and different “baselines” are needed for different trials, the “baseline” effect μ_i is treated as nuisance parameter and specifying a common distribution for μ_i is generally not interpretable. As a consequence, unless a strong assumption that either the overall event rate of a “reference” group is available based on some external data or can be unbiasedly estimated by summarizing only trials with the “reference” arm by a separate (random effects) model, current CB based approach is not able to estimate the overall treatment-specific event rates, RRs and RDs.

2.2 The Arm-Based (AB) approach

We view the analytic challenges associated with NMA from the perspective of missing data analysis^{34, 36-39}. The basic idea of this “arm-based” approaches to NMA (which focus on modeling the event proportions for each treatment arm), in contrast to the “contrast-based” approaches (which focus on modeling the relative treatment effects, e.g., ORs, comparing treatments), has been briefly discussed by Salanti et al.^{40, 41}, but thoroughly not from the missing data perspective. When viewed from this perspective, the proportion of patients responding to each treatment and associated summary statistics such as the RD, RR and OR can be estimated. Specifically, we assume that each study hypothetically compares all treatments, many of which are missing by design and thus can be considered as missing at random³⁶.

Specifically, we consider the multivariate Bayesian hierarchical mixed model (MBHMM), which extend the bivariate generalized linear mixed model for the meta-analysis of comparative studies of two arms⁴². First, we assume conditional on P_i={p_ik} the elements y_ik of Y_i={y_ik} are independently binomially distributed with probability mass function

$$P(Y_i=y_i)\propto {\prod _{k\in S_i}(p_{ik})}^{y_{ik}}{(1-p_{ik})}^{n_{ik}-y_{ik}}.$$ (2.2)

Second, we assume a multivariate normal distribution (MVN) for {p_ik} on a probit transformed scale. In the absence of any individual level covariates, the model is specified as

$${\mathrm{\Phi }}^{-1}(p_{ik})={\mu }_k+{\sigma }_k{\nu }_{ik},{({\nu }_{i1},\dots ,{\nu }_{iK})}^T\sim MVN(0,R_K),$$ (2.3)

where Φ() is the standard normal cumulative distribution function, (μ₁,…, μ_K) are treatment-specific fixed effects, R_K is a positive definite correlation matrix, and σ_k is the standard deviation for the random effects ν_ik. Let diag(σ₁,…,σ_K) be a diagonal matrix with elements σ_i, the covariance matrix is thus Σ_K =diag(σ₁,…,σ_K)× R_K × diag(σ₁,…,σ_K), Here, σ_k captures trial-level heterogeneity in response to treatment k, and R_K captures the within-study dependence among treatments. Based on the model in equation (2), the population-averaged (or marginal) treatment-specific event rate can be estimated as

$${\pi }_k=E(p_{ik}|{\mu }_k,{\sigma }_k)={\int }_{-\infty }^{+\infty }\mathrm{\Phi }({\mu }_k+{\sigma }_{k}z)\phi (z)dz=\mathrm{\Phi }({\mu }_k/\sqrt{1+{\sigma }_k^2}),k=1,\dots ,K,$$ (2.4)

where ϕ() is the standard normal density function. In addition to the marginal event rate π_k, we focus on the marginal relative treatment effects of RR and RD. The marginal OR, RR and RD are defined as OR_kl= [π_k/(1−π_k)]/[π_l/(1−π_l)], RR_kl= π_k/π_l and RD_kl= π_k−π_l for a pairwise comparison between treatments k and l(k ≠l).

Since improper prior distributions may lead to an improper posterior in some complex models^43-46, we selected minimally informative but proper priors. Specifically, we chose a weakly informative prior $N(0,{\tau }_{\mu }^2)$ for μ_k with ${\tau }_{\mu }^2=1000$, and a Wishart prior for the precision matrix, i.e., ${\sum }_K^{-1}\sim W(V,n)$, where the degrees of freedom n=K, V is a known K×K matrix with diagonal elements equal 1.0, and off-diagonal elements equal 0.005. It turned out that the above prior corresponded to a 95% CI of 0.45 to 32.10 for the standard deviation parameters and a 95% CI of −1.00 to 1.00 for the correlation parameters, which is computed via simulations using the R function rWishart(). The Washart distribution is the conjugate prior of the precision matrix of a multivariate-normal random vector in Bayesian statistics, which facilitates the computation of the unstructured posterior covariance matrix.

We implemented our method within a fully Bayesian framework using Markov chain Monte Carlo (MCMC) methods with the WinBUGS software^{47, 48}. Weakly informative priors were used and posterior samples were drawn using Gibbs and Metropolis-Hastings algorithms^{49, 50} with convergence assessed using trace plots, sample autocorrelations, and other standard convergence diagnostics^{51, 52}. A generous burn-in period of 1,000,000 iterations was used, with 1,000,000 subsequent iterations retained for accurate posterior treatment effect estimates.

By borrowing information across multiple treatments, the multivariate Bayesian hierarchical mixed model that we utilize reduces potential bias when missing is not completely at random, compared to a naive approach of estimating population-averaged treatment-specific event proportions or rates based solely on studies that used a particular treatment. With this Bayesian approach, we used the 95% posterior credible intervals to assess statistical significance (according to whether the CI included the null value) instead of p-values⁵³. The corresponding WinBUGS code is presented in the appendix.

2.3 Evaluation of different approaches

To investigate the performance of the proposed “arm-based” multivariate Bayesian hierarchical mixed model, we create two hypothetical network meta-analysis data sets under either a homogenous relative risk (RR) or a homogenous rate difference (RD) assumption. Each network meta-analysis includes 11 trials and 3 treatment arms. Because in a typical network meta-analysis, most trials only compare a subset of all treatments of interest, we let two trials compare all three treatments, and three trials each comparing A and B, B and C, A and C, respectively. The total numbers of patients are equal to 1000 for arm A, 2000 for arm B, and 500 for arm C in all trials. The response rates for arm A are assigned from a uniform distribution ranging from 0.10 to 0.40 in ascending order for the 11 trials. The corresponding numbers of responses for arm B and C in each trial are assigned based on a fixed RR or a fixed RD assumption. Specifically, the RR of B vs. A is 1.50 and C vs. A is 2.00 under the fixed RR assumption, and the RD of B vs. A is 15% and C vs. A is 25% under the fixed RD assumption. To simplify illustration, we ignore the random sampling error and assume the number of events is equal to the response rates multiplied by the total number of patients.

We analyzed the above two hypothetical data using four methods. The first is based on Cochran-Mantel-Haenszel procedure with estimates of the log OR and variance as discussed in Yusuf et al. (we refer to this as Peto’s method)⁵⁴. With this fixed effect method, inferences are based on the direct head-to-head pairwise comparisons. The second and third methods are the Lu & Ades' “contrast-based” network meta-analysis method under either a homogeneous variance (i.e., the HOM model) or an unstructured heterogeneous variance assumption (i.e., the ID model)³⁵. It combines the direct and indirect evidence, but it is not able to estimate the population-averaged treatment-specific event rates. The fourth is the “arm-based” network meta-analysis method that we have proposed. By borrowing information across treatment arms, it is able to estimate the treatment-specific event rates. The hypothetical data and the assumptions underlying these four methods are given in the web appendix wTable 1 and wTable 2, respectively.

3. Results

3.1 Comparison of Four Methods for Hypothetical Data

Table 1 presents the ORs based on the pairwise head-to-head comparisons for each hypothetical trial. The difference between the mean ORs from the observed data versus the mean ORs from the full data illustrates the potential bias of summarizing treatment effects based only on trials with particular treatment arms, i.e., the direct head-to-head comparisons. As evidenced by these two examples, the direction of bias can be either toward the null or away from the null, depending on the underlying data generating and missing data generating mechanisms, which limits the application and generalizability of methods based on direct head-to-head comparisons. For example, the true mean OR of B vs. A under a fixed RR assumption is 1.85, as compared to the mean OR of 1.66 based on the available direct head-to-head comparisons. The true mean OR of B vs. A under a fixed RD assumption is 2.15, as compared to the mean OR of 2.45 based on the available direct head-to-head comparisons.

Table 1. The odds ratios based on pairwise head-to-head comparisons.

	I. Fixed RR			II. Fixed RD
	B vs. A	C vs. A	C vs. B	B vs. A	C vs. A	C vs. B
Trial 1	1.59	2.25	1.42	3.00	4.85	1.62
Trial 2	1.62	2.35	1.45	2.60	4.10	1.58
Trial 3	1.66	2.47	1.49	2.36	3.65	1.55
Trial 4	1.70	2.61	1.54	2.20	3.35	1.53
Trial 5	1.75	2.79	1.60	2.08	3.14	1.51
Trial 6	1.80	3.00	1.67	2.00	3.00	1.50
Trial 7	1.86	3.27	1.76	1.94	2.90	1.49
Trial 8	1.93	3.63	1.88	1.90	2.83	1.49
Trial 9	2.02	4.12	2.04	1.87	2.79	1.50
Trial 10	2.12	4.85	2.28	1.84	2.78	1.51
Trial 11	2.25	6.00	2.67	1.83	2.79	1.52
Mean OR1	1.66	2.90	1.97	2.45	3.54	1.54
Mean OR2	1.85	3.40	1.80	2.15	3.29	1.53

OR = Odds Ratio; RR = Relative Risk; RD = Rate Difference; Mean OR₁ is the mean of ORs from the observed data assuming the greyed cells are not available as in many NMAs; Mean OR₂ is the mean of ORs from the full data assuming all the greyed cells are observed and available.

Table 2 compares the population-averaged treatment-specific event rate estimates from the observed data vs. that from the full data based on the new method. It shows that with this approach, estimates of the population-averaged treatment-specific event rates are nearly unbiased. In addition, the information loss due to missing data is mostly recovered as evidenced by the similarity of the length of the posterior credible intervals.

Table 2. Population Averaged Event Rate Estimates under Fixed RR and RD Assumptions.

	Event Rates	Treatment A	Treatment B	Treatment C
I. Fixed RR	True	0.25	0.375	0.50
	Observed data	0.25(0.19,0.34)	0.37(0.28,0.46)	0.50(0.38,0.61)
	Full data	0.25(0.19,0.31)	0.37(0.29,0.45)	0.50(0.38,0.59)
II. Fixed RD	True	0.25	0.40	0.50
	Observed data	0.24(0.18,0.33)	0.40(0.33,0.48)	0.50(0.43,0.57)
	Full data	0.25(0.19,0.32)	0.40(0.34,0.46)	0.50(0.43,0.56)

Results based on the proposed method; OR = Odds Ratio; RR = Relative Risk; RD = Rate Difference.

Table 3 compares the relative treatment effect estimates for the four methods using the observed data (which assume that the greyed cells in web appendix wTable 1 are not available as in many NMAs) and the full data (which assume that each trial has three arms and there is no missing arms), respectively. Under the hypothetical data generating mechanisms, all 4 model assumptions are incorrect, and the “true” ORs are not well defined. Thus, we choose the estimates from the full data as the “true” ORs under each model assumption. The closer the estimates from the observed data are to that from the full data, the less bias of the method. Under both fixed RR and fixed RD assumptions, Peto's method is potentially biased since it incorporates only the direct information (the available head-to-head comparisons of two treatments). For example, under the fixed RR assumption, the estimated OR from Peto's method is 1.63 comparing treatment B vs. A using the observed data set, while the corresponding OR from the full data set is 1.83 illustrating some biases. Lu & Ades' contrast-based method shows potential biases, which is consistent with the results from simulation studies⁵⁵. For example, under the fixed RR assumption, the estimated ORs of B vs. A from the observed data are 1.60 (95% CI 1.39, 1.81) and 1.66 (1.44, 1.85) under the Lu and Ades' HOM and ID model assumptions, while the corresponding estimated ORs from the full data is 1.87 (1.66, 2.09) and 1.88 (1.75, 2.00), respectively. In contrast, using our proposed arm-based method, estimates for the ORs, RRs and RDs under both fixed RR and RD assumptions are nearly unbiased.

Table 3. Relative Treatment Effects Estimates under Fixed RR and RD.

		Observed Data			Full Data
		B vs. A	C vs. A	C vs. B	B vs. A	C vs. A	C vs. B
I. Fixed RR
OR	Peto	1.63 (1.50,1.77)	3.06 (2.74,3.41)	1.93 (1.75,2.13)	1.83 (1.74,1.93)	3.36 (3.13,3.61)	1.78 (1.67,1.90)
	HOM*	1.60 (1.39,1.81)	3.18 (2.75,3.64)	1.99 (1.73,2.31)	1.87 (1.66,2.09)	3.29 (2.89,3.71)	1.76 (1.50,2.06)
	ID#	1.66 (1.44,1.85)	3.23 (2.66,4.07)	1.98 (1.56,2.44)	1.88 (1.75,2.00)	3.30 (2.78,3.90)	1.76 (1.48,2.09)
	New§	1.72 (1.29,2.30)	2.97 (2.20,4.12)	1.74 (1.34,2.24)	1.78 (1.52,2.09)	2.96 (2.38,3.63)	1.66 (1.40,1.96)
RR	True	1.50	2.00	1.33	1.50	2.00	1.33
	New§	1.45 (1.18,1.78)	1.98 (1.63,2.41)	1.36 (1.19,1.57)	1.49 (1.34,1.66)	1.98 (1.77,2.21)	1.33 (1.22,1.45)
II. Fixed RD
OR	Peto	2.20 (2.03,2.37)	3.45 (3.10,3.83)	1.54 (1.41,1.69)	1.99 (1.89,2.09)	3.23 (3.01,3.46)	1.53 (1.44,1.63)
	HOM*	2.28 (2.08,2.54)	3.36 (3.03,3.76)	1.47 (1.32,1.63)	2.06 (1.94,2.20)	3.15 (2.92,3.41)	1.53 (1.42,1.65)
	ID#	2.31 (2.07,2.59)	3.40 (3.00,3.93)	1.47 (1.30,1.66)	2.07 (1.94,2.21)	3.16 (2.91,3.42)	1.53 (1.41,1.66)
	New§	2.09 (1.48,2.85)	3.17 (2.28,4.31)	1.52 (1.19,1.95)	1.99 (1.66,2.36)	2.98 (2.44,3.59)	1.50 (1.28,1.75)
RD	True	0.15	0.25	0.10	0.15	0.25	0.10
	New§	0.16 (0.09,0.22)	0.26 (0.19,0.32)	0.10 (0.04,0.16)	0.15 (0.11,0.18)	0.25 (0.21,0.28)	0.10 (0.06,0.14)

^*The contrast-based NMA with a homogeneous variance assumption

^#The contrast-based NMA with an unstructured heterogeneous variance assumption

^§The proposed arm-based NMA with an unstructured heterogeneous variance assumption

OR = Odds Ratio; RR = Relative Risk; RD = Rate Difference;

3.2 Re-analyses of two network meta-analyses recently published in The Lancet

3.2.1 Comparative efficacy and acceptability of 12 antidepressants

Cipriani et al.⁶ Comprehensively summarized results of 117 randomized controlled trials (25,928 participants) from 1991 to 2007, and compared 12 new-generation antidepressants in terms of efficacy and acceptability in acute-phase treatment of major depression. The main outcomes were the proportions of patients who responded to a treatment or discontinued the allocated treatment (dropped out). Response was defined as the total number of patients who had a reduction of at least 50% from baseline score at 8 weeks on the Hamilton depression rating scale (HDRS).

Table 4 presents a summary of the efficacy results using the proposed method. A similar table that only cited ORs and 95% CIs was reported by Cipriani et al⁶. The population-averaged treatment-specific response proportions are given in the diagonal entries in the table. These proportions range from 0.48 (95% CI 0.41 to 0.55) to 0.62 (95% CI 0.57 to 0.67) for mirtazapine (MIR). The upper and lower triangular panels report the RRs and RDs of all pairwise comparisons. Table 5 summarizes the treatment discontinuation proportions using the proposed method in the same format as the efficacy results. The population-averaged treatment-specific dropout rates (diagonal entries in the table) range from 0.21 for citalopram (CIS) (95% CI 0.17 to 0.26) and escitalopram (ESC) (95% CI 0.17 to 0.26) to 0.29 (95% CI 0.23 to 0.37) for reboxetine (REB).

Table 4. Population averaged responses (proportions), relative risks, and risk differences of the 12 antidepressants.

	BUP	CIT	DUL	ESC	FLU	FVX	MIL	MIR	PAR	REB	SER	VEN
BUP	0.57 (0.52,0.62)	1.02 (0.90,1.16)	1.09 (0.94,1.27)	0.95 (0.85,1.05)	1.07 (0.97,1.18)	1.09 (0.94,1.26)	1.10 (0.90,1.36)	0.92 (0.82,1.03)	1.04 (0.94,1.15)	1.19 (1.02,1.42)	0.97 (0.88,1.07)	0.95 (0.87,1.05)
CIT	0.01 (-0.06,0.08)	0.56 (0.50,0.62)	1.07 (0.91,1.25)	0.93 (0.83,1.03)	1.05 (0.94,1.16)	1.07 (0.92,1.24)	1.08 (0.87,1.34)	0.90 (0.80,1.02)	1.02 (0.91,1.14)	1.17* (0.99,1.38)	0.95 (0.84,1.06)	0.94 (0.83,1.04)
DUL	0.05 (-0.04,0.13)	0.03 (-0.05,0.12)	0.52 (0.46,0.60)	0.87 (0.76,0.99)	0.98 (0.86,1.12)	1.00 (0.84,1.20)	1.01 (0.80,1.28)	0.85 (0.73,0.98)	0.96 (0.83,1.09)	1.09* (0.91,1.34)	0.89* (0.77,1.03)	0.88* (0.76,1.01)
ESC	-0.03 (-0.09,0.03)	-0.04 (-0.11,0.02)	-0.08 (-0.15,-0.01)	0.60 (0.56,0.65)	1.13 (1.04,1.23)	1.15 (1.01,1.33)	1.16 (0.95,1.43)	0.97 (0.88,1.08)	1.10 (1.01,1.20)	1.26 (1.08,1.49)	1.03 (0.94,1.13)	1.01 (0.92,1.10)
FLU	0.04 (-0.02,0.09)	0.03 (-0.03,0.08)	-0.01 (-0.08,0.07)	0.07 (0.02,0.12)	0.53 (0.50,0.56)	1.02 (0.90,1.16)	1.03 (0.85,1.25)	0.86 (0.79,0.94)	0.97 (0.90,1.05)	1.11* (0.96,1.30)	0.91 (0.84,0.98)	0.89 (0.83,0.96)
FVX	0.05 (-0.03,0.12)	0.03 (-0.05,0.11)	0.00 (-0.09,0.09)	0.08 (0.00,0.15)	0.01 (-0.06,0.08)	0.52 (0.46,0.59)	1.01 (0.82,1.26)	0.85 (0.74,0.97)	0.96 (0.83,1.08)	1.09* (0.91,1.33)	0.89* (0.78,1.02)	0.88 (0.76,1.00)
MIL	0.05 (-0.06,0.16)	0.04 (-0.08,0.15)	0.01 (-0.12,0.12)	0.08 (-0.03,0.19)	0.01 (-0.09,0.11)	0.01 (-0.11,0.11)	0.52 (0.43,0.63)	0.84 (0.68,1.02)	0.95 (0.78,1.14)	1.08* (0.85,1.38)	0.88 (0.72,1.07)	0.87 (0.71,1.05)
MIR	-0.05 (-0.12,0.02)	-0.06 (-0.13,0.01)	-0.09 (-0.18,-0.01)	-0.02 (-0.08,0.05)	-0.09 (-0.14,-0.03)	-0.09 (-0.17,-0.02)	-0.10 (-0.20,0.02)	0.62 (0.57,0.67)	1.13 (1.03,1.24)	1.29 (1.10,1.54)	1.05 (0.95,1.16)	1.04 (0.94,1.14)
PAR	0.02 (-0.03,0.08)	0.01 (-0.05,0.07)	-0.02 (-0.09,0.05)	0.06 (0.00,0.11)	-0.02 (-0.05,0.02)	-0.02 (-0.09,0.05)	-0.03 (-0.13,0.08)	0.07 (0.02,0.13)	0.55 (0.51,0.58)	1.14* (0.99,1.35)	0.93* (0.86,1.02)	0.92 (0.84,1.00)
REB	0.09 (0.01,0.17)	0.08* (-0.01,0.16)	0.05* (-0.05,0.14)	0.12 (0.04,0.20)	0.05* (-0.02,0.13)	0.05* (-0.05,0.14)	0.04* (-0.08,0.17)	0.14 (0.06,0.22)	0.07* (-0.01,0.15)	0.48 (0.41,0.55)	0.82 (0.69,0.95)	0.80 (0.68,0.93)
SER	-0.02 (-0.08,0.04)	-0.03 (-0.10,0.04)	-0.06* (-0.14,0.02)	0.02 (-0.04,0.07)	-0.06 (-0.10,-0.01)	-0.06* (-0.14,0.01)	-0.07 (-0.17,0.04)	0.03 (-0.03,0.09)	-0.04* (-0.09,0.01)	-0.11 (-0.19,-0.03)	0.59 (0.54,0.63)	0.98 (0.90,1.07)
VEN	-0.03 (-0.08,0.03)	-0.04 (-0.11,0.03)	-0.07* (-0.15,0.01)	0.01 (-0.05,0.06)	-0.07 (-0.11,-0.02)	-0.07 (-0.15,-0.00)	-0.08 (-0.18,0.03)	0.02 (-0.04,0.08)	-0.05 (-0.10,-0.00)	-0.12 (-0.20,-0.04)	-0.01 (-0.06,0.04)	0.60 (0.56,0.64)

Drugs are reported in alphabetical order. Diagonal panels are the population averaged response rates (i.e., proportion of patients who had at least 50% reduction from the baseline score on HDRS); upper triangular and lower triangular panels are the relative risks (RRs) and risk differences (RDs) of the first drug in alphabetical order compared with the second drug in alphabetical order, respectively. Drugs with higher response rate are more effective; RRs larger than 1.0 or positive RDs favor the first drug in alphabetical order. To obtain comparisons in the opposite direction, reciprocals should be taken for RR and opposite sign should be used for RD. Statistically significant results are in bold and underlined. Comparisons statistically significant here but not in Cipriani et al⁶. or vice versa are noted with *. For all summaries, we report both the Bayesian posterior medians and the 95% credible intervals. BUR=bupropion, CIT=citalopram, DUL=duloxetine, ESC=escitalopram, FLU=fluoxetine, FVX=fluvoxamine (FVX), MIL=milnacipran, MIR=mirtazapine, PAR=paroxetine, REB=reboxetine, SER=sertraline, and VEN=venlafaxine.

Table 5. Population averaged dropout proportions, relative risks, and risk differences of the 12 antidepressants.

	BUP	CIT	DUL	ESC	FLU	FVX	MIL	MIR	PAR	REB	SER	VEN
BUP	0.25 (0.21,0.30)	1.20 (0.93,1.54)	0.92 (0.70,1.22)	1.20 (0.94,1.52)	0.98 (0.81,1.17)	0.88 (0.65,1.17)	0.87 (0.65,1.22)	1.00 (0.78,1.28)	0.95 (0.78,1.15)	0.87* (0.65,1.17)	1.17 (0.94,1.45)	0.96 (0.79,1.16)
CIT	0.04 (-0.02,0.10)	0.21 (0.17,0.26)	0.77 (0.58,1.03)	1.00 (0.78,1.27)	0.82 (0.66,1.01)	0.73 (0.54,0.99)	0.73 (0.53,1.04)	0.83 (0.65,1.09)	0.79* (0.64,0.99)	0.73 (0.54,0.98)	0.97 (0.78,1.23)	0.80 (0.64,1.01)
DUL	-0.02 (-0.10,0.05)	-0.06 (-0.14,0.01)	0.27 (0.22,0.34)	1.30* (0.99,1.69)	1.07 (0.83,1.35)	0.95 (0.68,1.32)	0.95 (0.67,1.37)	1.09 (0.81,1.45)	1.03 (0.81,1.30)	0.94 (0.68,1.32)	1.27* (0.97,1.66)	1.04 (0.80,1.34)
ESC	0.04 (-0.02,0.10)	0.00 (-0.05,0.05)	0.06* (-0.00,0.13)	0.21 (0.17,0.26)	0.82 (0.67,1.00)	0.73 (0.54,0.99)	0.73 (0.53,1.03)	0.83 (0.65,1.09)	0.79 (0.65,0.98)	0.73 (0.54,0.99)	0.97 (0.78,1.23)	0.80 (0.64,1.00)
FLU	-0.01 (-0.05,0.04)	-0.05 (-0.09,0.00)	0.02 (-0.05,0.09)	-0.05 (-0.09,0.00)	0.26 (0.23,0.28)	0.90 (0.70,1.15)	0.89 (0.69,1.21)	1.02 (0.84,1.25)	0.97 (0.86,1.10)	0.89* (0.70,1.15)	1.19* (1.02,1.41)	0.98 (0.85,1.12)
FVX	-0.04 (-0.12,0.04)	-0.08 (-0.16,-0.00)	-0.01 (-0.11,0.08)	-0.08 (-0.16,-0.00)	-0.03 (-0.11,0.03)	0.29 (0.23,0.37)	1.00 (0.71,1.43)	1.14 (0.86,1.52)	1.08 (0.84,1.40)	0.99 (0.71,1.39)	1.33 (1.01,1.76)	1.09 (0.84,1.42)
MIL	-0.04 (-0.13,0.05)	-0.08 (-0.17,0.01)	-0.01 (-0.12,0.09)	-0.08 (-0.17,0.01)	-0.03 (-0.12,0.04)	-0.00 (-0.10,0.10)	0.29 (0.21,0.37)	1.15 (0.82,1.57)	1.09 (0.80,1.42)	0.99 (0.68,1.42)	1.34 (0.97,1.79)	1.10 (0.79,1.45)
MIR	0.00 (-0.06,0.06)	-0.04 (-0.10,0.02)	0.02 (-0.05,0.10)	-0.04 (-0.10,0.02)	0.01 (-0.05,0.05)	0.04 (-0.04,0.12)	0.04 (-0.05,0.13)	0.25 (0.21,0.30)	0.95 (0.77,1.16)	0.87 (0.65,1.18)	1.17 (0.93,1.46)	0.96 (0.77,1.18)
PAR	-0.01 (-0.06,0.04)	-0.06* (-0.10,-0.00)	0.01 (-0.05,0.08)	-0.06 (-0.10,-0.01)	-0.01 (-0.04,0.02)	0.02 (-0.04,0.10)	0.02 (-0.05,0.11)	-0.01 (-0.06,0.04)	0.27 (0.24,0.30)	0.92 (0.71,1.20)	1.23 (1.04,1.47)	1.01 (0.86,1.19)
REB	-0.04* (-0.12,0.04)	-0.08 (-0.16,-0.01)	-0.02 (-0.11,0.08)	-0.08 (-0.16,-0.00)	-0.03* (-0.11,0.03)	-0.00 (-0.10,0.10)	-0.00 (-0.11,0.10)	-0.04 (-0.12,0.04)	-0.03 (-0.10,0.05)	0.29 (0.23,0.37)	1.35 (1.01,1.76)	1.10 (0.84,1.43)
SER	0.04 (-0.01,0.09)	-0.01 (-0.05,0.05)	0.06* (-0.01,0.13)	-0.01 (-0.05,0.05)	0.04* (0.00,0.08)	0.07 (0.00,0.15)	0.07 (-0.01,0.16)	0.04 (-0.02,0.09)	0.05 (0.01,0.09)	0.07 (0.00,0.15)	0.22 (0.18,0.25)	0.82* (0.68,0.98)
VEN	-0.01 (-0.06,0.04)	-0.05 (-0.11,0.00)	0.01 (-0.06,0.09)	-0.05 (-0.10,-0.00)	-0.01 (-0.04,0.03)	0.02 (-0.05,0.11)	0.03 (-0.06,0.11)	-0.01 (-0.07,0.04)	0.00 (-0.04,0.04)	0.03 (-0.05,0.11)	-0.05* (-0.09,-0.00)	0.26 (0.23,0.30)

Drugs are reported in alphabetical order. Diagonal panels are the population averaged dropout rate, upper triangular and lower triangular panels are the relative risks (RRs) and risk differences (RDs) of the first drug in alphabetical order compared with the second drug in alphabetical order, respectively. Drugs with lower dropout rate are more acceptable; RRs smaller than 1.0 or negative RDs favor the first drug in alphabetical order. To obtain comparisons in the opposite direction, reciprocals should be taken for RR and opposite sign should be used for RD. Statistically significant results are in bold and underlined. Comparisons statistically significant here but not in Cipriani et al⁶. or vice versa are noted with *. For all summaries, we report both the Bayesian posterior medians and the 95% credible intervals. BUR=bupropion, CIT=citalopram, DUL=duloxetine, ESC=escitalopram, FLU=fluoxetine, FVX=fluvoxamine (FVX), MIL=milnacipran, MIR=mirtazapine, PAR=paroxetine, REB=reboxetine, SER=sertraline, and VEN=venlafaxine.

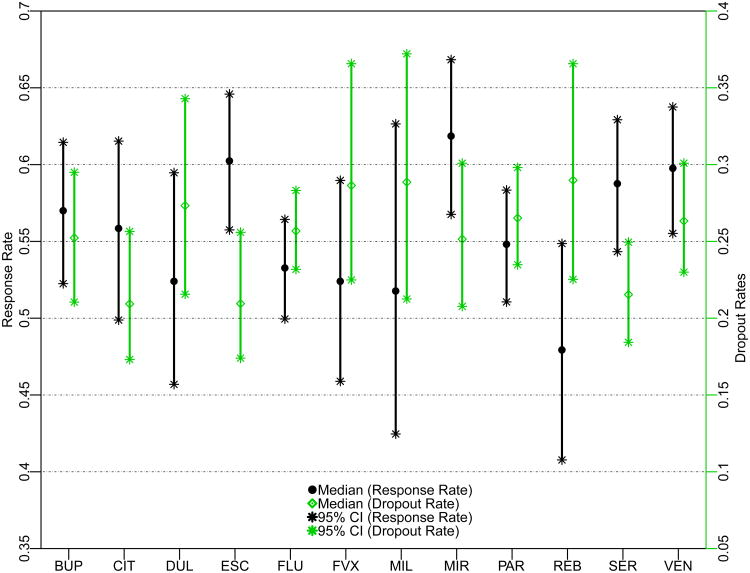
ESC and SER were more effective and more acceptable as measured by the proportion responding and discontinuing treatment. MIR and VEN had good efficacy but low acceptability as measured by the proportion discontinuing treatment. Citalopram (CIT) had high acceptability but low efficacy. To visually compare the efficacy and acceptability of the 12 antidepressant drugs, Figure 1 presents the treatment-specific posterior medians of response and dropout proportions, with their 95% posterior credible intervals.

Figure 1.

Response and Dropout Proportion Estimates of the 12 Antidepressants Using the Proposed Method⁶. BUR = bupropion, CIT = citalopram, DUL = duloxetine, ESC = escitalopram, FLU = fluoxetine, FVX = fluvoxamine (FVX), MIL = milnacipran, MIR = mirtazapine, PAR = paroxetine, REB = reboxetine, SER = sertraline, and VEN = venlafaxine.

As compared to the results of Cipriani et al.⁶, for efficacy, we did not find significant differences between SER and DUL, FVX, and PAR, nor between VEN and DUL. REB was only less effective than BUP, ESC, MIR, SER, and VEN, but not other treatments. In terms of acceptability, both ESC and SER are better-tolerated than FVX, PAR, REB, and VEN. In addition, SER is better-tolerated than FLU. CIT is better-tolerated than not only FVX and REB, but also PAR. Lastly, we did not find significant differences comparing BUP versus REB, and DUL versus ESC and SER.

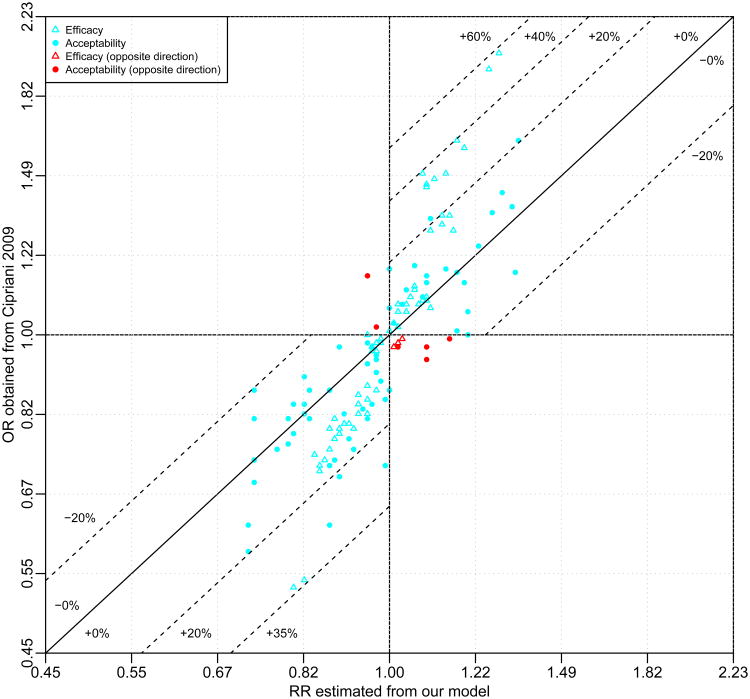
Figure 2 compares the ORs reported in Cipriani et al⁶ (y-axis) against the RRs estimated from our model (x-axis) of the 66 head-to-head comparisons of efficacy and treatment discontinuation. As expected, given how common the outcomes are, 81.1% (107/132) of the treatment effects are overestimated using the OR instead of the RR; only 18.9% (25/132) were underestimated. For efficacy, the overestimation can be as high as 57.4% (OR = 2.03 vs. RR = 1.29 comparing MIR vs. REB) while the underestimation is as high as 5.3% (OR = 1.00 vs. RR = 0.95 comparing MIL and PAR); for acceptability, the overestimation goes up to 28.7% (OR = 0.62 vs. RR = 0.87 comparing BUP vs. REB) while the underestimation can be as large as 19.2% (OR = 0.87 vs. RR = 0.73 comparing CIT and MIL). In addition, 7.6% (10/132) of the comparisons between ORs and RRs have opposite signs, for which both estimates are very close to the null (see red symbols in Figure 2). A direct comparison between the reported ORs in Cipriani et al⁶ and our marginal ORs is presented in the web appendix, and similar conclusions are shown.

Figure 2.

Comparison of the ORs versus the RRs for the 12 Antidepressants. The dotted lines present the percentages of overestimation (bias away from the null) or underestimation (bias toward the null) of the treatment efficacy or acceptability if the ORs reported in Cipriani et al⁶ were misinterpreted as the RRs. The negative percentages denote underestimation and positive percentage denote overestimation.

3.2.2 Comparative efficacy and acceptability of antimanic drugs in acute mania

Cipriani et al.⁷ comprehensively reviewed 68 randomized controlled trials (16,073 participants) from Jan 1, 1980 to Nov 25, 2010, which compared antimanic drugs at therapeutic dose range for the treatment of acute mania in adults. The main outcomes were the mean change on mania rating scales and the proportion of patients who discontinued the assigned treatment at 3 weeks (dichotomous outcome for acceptability). The secondary outcome was response rate (response rate was defined as the proportion of the total number of patients who had a reduction of at least 50% on the total score between baseline and endpoint on a standardized rating scale for mania). Here, we only focus on the binary response for efficacy and the treatment discontinuation or dropout rate. Two treatments, gabapentin and asenapine that were only included in one or two trials were excluded.

Table 6 summarizes the efficacy results. The population-averaged treatment-specific response rates ranged from 0.22 (95% CI 0.08 to 0.48) for topiramate (TOP) to 0.56 (95% CI 0.49 to 0.63) for olanzapine (OLA). Compared to placebo, RRs and RDs were significant for all antimanic treatments, except LAM and TOP. In addition, all active treatments except lamotrigine (LAM) and ziprasidone (ZIP) are significantly more effective than TOP. Table 7 shows the results for acceptability (dropout). The population-averaged treatment-specific dropout proportions range from risperidone (RIS) at 0.30 (95% CI 0.24 to 0.37) to TOP at 0.48 (95% CI 0.32 to 0.65). The upper and lower triangular panels report the RRs and RDs of all pairwise comparisons.

Table 6. Population-averaged responses (proportions), relative risks, and risk differences of the 12 Antimanic drugs.

	ARI	CAR	HAL	LAM	LIT	OLA	PLA	QUE	RIS	TOP	VAL	ZIP
ARI	0.50 (0.44,0.57)	0.96 (0.72,1.37)	0.90* (0.75,1.08)	0.95 (0.61,2.24)	0.92 (0.75,1.13)	0.90 (0.75,1.07)	1.37 (1.17,1.59)	0.93 (0.77,1.12)	0.92 (0.76,1.11)	2.33 (1.05,6.54)	0.96 (0.78,1.17)	1.06 (0.86,1.33)
CAR	-0.02 (-0.18,0.15)	0.53 (0.38,0.68)	0.94* (0.66,1.26)	0.99 (0.58,2.38)	0.96 (0.67,1.30)	0.94 (0.66,1.24)	1.43 (1.01,1.86)	0.97 (0.68,1.29)	0.96 (0.67,1.27)	2.43 (1.03,6.90)	1.00 (0.70,1.34)	1.11 (0.76,1.51)
HAL	-0.05* (-0.15,0.04)	-0.03* (-0.20,0.13)	0.56 (0.48,0.64)	1.05* (0.67,2.49)	1.02* (0.82,1.25)	1.00 (0.83,1.18)	1.52 (1.29,1.77)	1.03* (0.85,1.24)	1.02 (0.84,1.22)	2.59 (1.16,7.26)	1.06* (0.86,1.30)	1.17* (0.95,1.46)
LAM	-0.03 (-0.31,0.29)	-0.00 (-0.32,0.33)	0.03* (-0.26,0.34)	0.53 (0.23,0.81)	0.96 (0.41,1.53)	0.94* (0.40,1.48)	1.44 (0.61,2.24)	0.97 (0.41,1.53)	0.97* (0.41,1.52)	2.41 (0.76,7.37)	1.00 (0.42,1.59)	1.11 (0.47,1.78)
LIT	-0.05 (-0.15,0.06)	-0.02 (-0.20,0.15)	0.01* (-0.11,0.12)	-0.02 (-0.33,0.27)	0.55 (0.46,0.64)	0.98 (0.80,1.19)	1.49 (1.24,1.78)	1.01 (0.83,1.24)	1.00 (0.81,1.23)	2.54 (1.13,7.14)	1.04 (0.84,1.29)	1.15 (0.92,1.47)
OLA	-0.06 (-0.15,0.04)	-0.03 (-0.20,0.13)	-0.00 (-0.10,0.09)	-0.03* (-0.34,0.26)	-0.01 (-0.12,0.10)	0.56 (0.49,0.63)	1.52 (1.33,1.75)	1.03 (0.86,1.24)	1.02 (0.86,1.22)	2.60 (1.17,7.30)	1.07* (0.89,1.28)	1.18* (0.96,1.46)
PLA	0.14 (0.06,0.21)	0.16 (0.00,0.31)	0.19 (0.11,0.27)	0.16 (-0.14,0.45)	0.18 (0.09,0.27)	0.19 (0.12,0.26)	0.37 (0.33,0.41)	0.68 (0.58,0.80)	0.67 (0.57,0.79)	1.70 (0.77,4.80)	0.70 (0.59,0.83)	0.77 (0.65,0.94)
QUE	-0.04 (-0.14,0.06)	-0.02 (-0.18,0.15)	0.01* (-0.09,0.12)	-0.01 (-0.33,0.28)	0.00 (-0.10,0.12)	0.02 (-0.08,0.12)	-0.18 (-0.26,-0.10)	0.55 (0.47,0.62)	0.99 (0.82,1.20)	2.53 (1.13,7.06)	1.03 (0.84,1.27)	1.14 (0.93,1.43)
RIS	-0.05 (-0.15,0.05)	-0.02 (-0.19,0.14)	0.01 (-0.10,0.11)	-0.02* (-0.33,0.27)	-0.00 (-0.12,0.12)	0.01 (-0.09,0.11)	-0.18 (-0.26,-0.10)	-0.01 (-0.11,0.10)	0.55 (0.48,0.63)	2.55 (1.14,7.16)	1.04* (0.85,1.28)	1.15* (0.93,1.44)
TOP	0.29 (0.02,0.45)	0.31 (0.02,0.51)	0.34 (0.07,0.51)	0.31 (-0.09,0.63)	0.33 (0.06,0.50)	0.34 (0.08,0.50)	0.15 (-0.11,0.30)	0.33 (0.06,0.49)	0.33 (0.06,0.50)	0.22 (0.08,0.48)	0.41 (0.15,0.91)	0.45* (0.16,1.02)
VAL	-0.02 (-0.13,0.08)	-0.00 (-0.17,0.17)	0.03* (-0.08,0.14)	0.00 (-0.31,0.29)	0.02 (-0.09,0.14)	0.03* (-0.07,0.13)	-0.16 (-0.25,-0.08)	0.02 (-0.10,0.13)	0.02* (-0.09,0.13)	-0.31 (-0.48,-0.05)	0.53 (0.45,0.62)	1.11 (0.89,1.40)
ZIP	0.03 (-0.08,0.13)	0.05 (-0.12,0.22)	0.08* (-0.03,0.19)	0.05 (-0.26,0.35)	0.07 (-0.04,0.20)	0.09* (-0.02,0.19)	-0.11 (-0.19,-0.03)	0.07 (-0.04,0.18)	0.07* (-0.04,0.18)	-0.26* (-0.42,0.01)	0.05 (-0.06,0.17)	0.48 (0.39,0.56)

Drugs are reported in alphabetical order. Diagonal panels are the population-averaged response rate; upper triangular and lower triangular panels are the relative risks (RRs) and risk differences (RDs) of the first drug in alphabetical order compared with the second drug in alphabetical order, respectively. Drugs with higher response rate are more effective; RRs larger than 1.0 or positive RDs favor the first drug in alphabetical order. To obtain comparisons in the opposite direction, reciprocals should be taken for RR and opposite sign should be used for RD. Statistically significant results are in bold and underlined. Comparisons statistically significant here but not in Cipriani et al7. or vice versa are noted with *. For all summaries, we report both the Bayesian posterior medians and the 95% credible intervals. ARI=aripiprazole, CAR=carbamazepine, HAL=haloperidol, LAM=lamotrigine, LIT=lithium, OLA=olanzapine, PLA=placebo, QUE=quetiapine, RIS=risperidone, TOP=topiramate, VAL=valproate, and ZIP=ziprasidone.

Table 7. Population-averaged dropout proportions, relative risks, and risk differences of the 12 Antimanic drugs.

	ARI	CAR	HAL	LAM	LIT	OLA	PLA	QUE	RIS	TOP	VAL	ZIP
ARI	0.37 (0.30,0.44)	1.01 (0.71,1.51)	0.96 (0.75,1.25)	0.88 (0.62,1.34)	1.01 (0.79,1.30)	1.22 (0.95,1.56)	0.90 (0.74,1.08)	1.15 (0.81,1.69)	1.22 (0.93,1.61)	0.76* (0.54,1.18)	1.07 (0.81,1.42)	0.91 (0.70,1.18)
CAR	0.01 (-0.13,0.13)	0.36 (0.25,0.49)	0.95 (0.64,1.34)	0.87 (0.55,1.41)	1.00 (0.68,1.40)	1.20 (0.82,1.70)	0.89 (0.62,1.20)	1.13 (0.73,1.78)	1.21 (0.80,1.75)	0.75* (0.48,1.22)	1.05 (0.71,1.51)	0.90 (0.60,1.27)
HAL	-0.02 (-0.11,0.08)	-0.02 (-0.15,0.12)	0.38 (0.31,0.47)	0.92 (0.64,1.40)	1.05 (0.81,1.37)	1.27* (1.00,1.62)	0.93 (0.77,1.14)	1.19 (0.86,1.77)	1.27 (0.98,1.68)	0.79* (0.56,1.23)	1.11 (0.84,1.47)	0.95 (0.73,1.23)
LAM	-0.05 (-0.21,0.10)	-0.05 (-0.23,0.13)	-0.03 (-0.20,0.12)	0.42 (0.28,0.56)	1.15 (0.77,1.62)	1.38* (0.91,1.96)	1.02 (0.70,1.39)	1.30 (0.82,2.04)	1.38* (0.91,2.00)	0.86 (0.54,1.40)	1.21 (0.79,1.76)	1.03 (0.68,1.47)
LIT	0.00 (-0.09,0.10)	-0.00 (-0.12,0.13)	0.02 (-0.08,0.12)	0.05 (-0.09,0.21)	0.36 (0.30,0.44)	1.21* (0.94,1.53)	0.89 (0.73,1.07)	1.14* (0.81,1.64)	1.21* (0.92,1.59)	0.75 (0.53,1.15)	1.05 (0.80,1.39)	0.90 (0.70,1.16)
OLA	0.07 (-0.02,0.15)	0.06 (-0.06,0.19)	0.08* (-0.00,0.17)	0.12* (-0.03,0.27)	0.06* (-0.02,0.14)	0.30 (0.25,0.36)	0.74 (0.62,0.87)	0.94 (0.68,1.37)	1.00 (0.78,1.30)	0.62 (0.45,0.96)	0.88 (0.69,1.11)	0.75* (0.59,0.99)
PLA	-0.04 (-0.11,0.03)	-0.05 (-0.16,0.08)	-0.03 (-0.10,0.06)	0.01 (-0.13,0.16)	-0.04 (-0.11,0.03)	-0.11 (-0.16,-0.05)	0.41 (0.36,0.45)	1.28* (0.97,1.79)	1.36 (1.11,1.68)	0.84 (0.63,1.26)	1.18 (0.97,1.47)	1.01 (0.85,1.22)
QUE	0.05 (-0.08,0.17)	0.04 (-0.11,0.20)	0.06 (-0.06,0.19)	0.10 (-0.07,0.27)	0.05* (-0.08,0.15)	-0.02 (-0.13,0.09)	0.09* (-0.01,0.18)	0.32 (0.23,0.43)	1.06 (0.73,1.48)	0.66* (0.43,1.06)	0.93 (0.63,1.32)	0.79 (0.54,1.11)
RIS	0.07 (-0.03,0.16)	0.06 (-0.07,0.20)	0.08 (-0.01,0.18)	0.12* (-0.03,0.27)	0.06* (-0.03,0.15)	0.00 (-0.08,0.08)	0.11 (0.04,0.17)	0.02 (-0.09,0.13)	0.30 (0.24,0.37)	0.62 (0.44,0.97)	0.87 (0.66,1.16)	0.74* (0.57,0.98)
TOP	-0.12* (-0.2910.06)	-0.12* (-0.32,0.08)	-0.10* (-0.28,0.08)	-0.07 (-0.28,0.14)	-0.12 (-0.30,0.05)	-0.18 (-0.35,-0.01)	-0.08 (-0.24,0.08)	-0.16* (-0.34,0.02)	-0.18 (-0.36,-0.01)	0.48 (0.32,0.65)	1.40* (0.90,2.01)	1.19 (0.78,1.70)
VAL	0.02 (-0.08,0.12)	0.02 (-0.11,0.16)	0.04 (-0.06,0.14)	0.07 (-0.08,0.23)	0.02 (-0.08,0.11)	-0.04 (-0.13,0.03)	0.06 (-0.01,0.13)	-0.03 (-0.15,0.10)	-0.04 (-0.14,0.05)	0.14* (-0.04,0.31)	0.35 (0.27,0.43)	0.85 (0.65,1.12)
ZIP	-0.04 (-0.13,0.06)	-0.04 (-0.17,0.10)	-0.02 (-0.12,0.08)	0.01 (-0.14,0.17)	-0.04 (-0.14,0.06)	-0.10* (-0.19,-0.02)	0.00 (-0.07,0.08)	-0.08 (-0.20,0.04)	-0.10* (-0.20,-0.01)	0.08 (-0.10,0.26)	-0.06 (-0.16,0.04)	0.40 (0.33,0.48)

Drugs are reported in alphabetical order. Diagonal panels are the population-averaged dropout rate; upper triangular and lower triangular panels are the relative risks (RRs) and risk differences (RDs) of the first drug in alphabetical order compared with the second drug in alphabetical order, respectively. Drugs with lower dropout rate are more acceptable; RRs lower than 1.0 or negative RDs favor the first drug in alphabetical order. To obtain comparisons in the opposite direction, reciprocals should be taken for RR and opposite sign should be used for RD. Statistically significant results are in bold and underlined. Comparisons statistically significant here but not in Cipriani et al⁷. or vice versa are noted with *. For all summaries, we report both the Bayesian posterior medians and the 95% credible intervals. ARI=aripiprazole, CAR=carbamazepine, HAL=haloperidol, LAM=lamotrigine, LIT=lithium, OLA=olanzapine, PLA=placebo, QUE=quetiapine, RIS=risperidone, TOP=topiramate, VAL=valproate, and ZIP=ziprasidone.

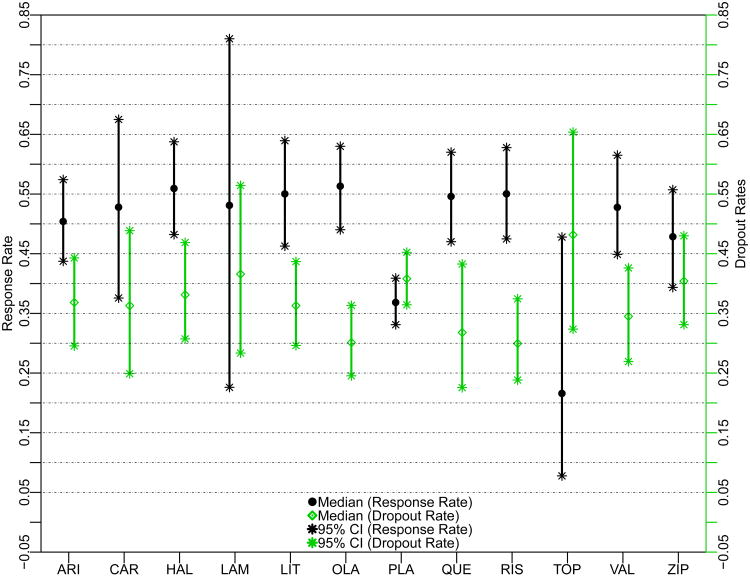
To visually compare the efficacy and acceptability of the 12 antimanic drugs, Figure 3 plots the treatment-specific posterior medians of the response and dropout proportions, with their 95% posterior credible intervals. The 95% credible intervals of LAM and TOP are extremely wide because they are studied in only 3 and 5 trials respectively, much fewer than the others. TOP is less effective and less well tolerated than placebo.

Figure 3.

Response and Dropout Proportion Estimates of the 12 Antimanic Drugs Using the Proposed Method⁷. ARI = aripiprazole, CAR = carbamazepine, HAL = haloperidol, LAM = lamotrigine, LIT = lithium, OLA = olanzapine, PLA = placebo, QUE = quetiapine, RIS = risperidone, TOP = topiramate, VAL = valproate, and ZIP = ziprasidone.

Our results differ from Cipriani et al.⁷ in some aspects. For efficacy, we do not find significant differences between haloperidol (HAL), RIS, and OLA with the other treatments, while in Cipriani et al's paper.⁷, HAL, RIS, and OLA showed significant efficacy compared with some other treatments. For acceptability, except that OLA and RIS have significantly lower proportions of discontinuation compared to placebo, TOP, and ZIP, we do not find any other statistically significant head-to-head comparisons. In contrast, Cipriani et al.⁷ found that OLA, RIS, and quetiapine (QUE) led to significantly fewer discontinuations than did lithium (LIT), LAM, placebo, and TOP.

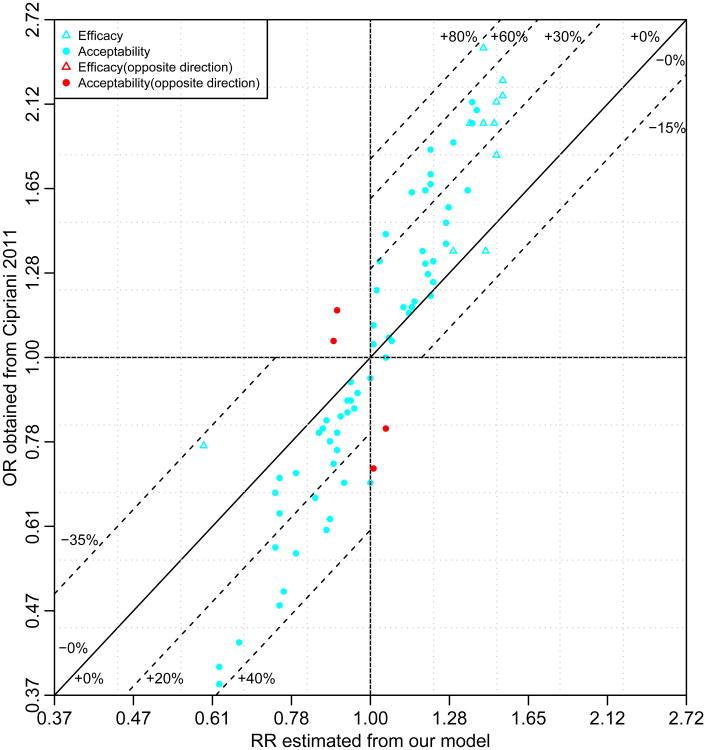
Figure 4 compares the ORs reported in Cipriani et al⁷ (y-axis) against the RRs estimated from our model (x-axis) of the 66 head-to-head comparisons for treatment discontinuation (acceptability) and the 11 comparisons with placebo for efficacy. Overall, 90.9% (70/77) of the treatment effects are overestimated, and 9.1% (7/77) of them are underestimated. Specifically, for efficacy, the overestimation is as high as 74.8% (OR = 1/0.40 = 2.50 vs. RR = 1.43 comparing CAR vs. placebo) while the underestimation is as high as 30.5% (OR = 1/1.30 = 0.77 vs. RR =1/1.702 = 0.59 comparing TOP and placebo). For acceptability, the overestimation is as large as 54.3% (OR = 1/0.47 = 2.13 vs. RR = 1.38 comparing LAM vs. OLA), while the underestimation is as large as 18.0% (OR=1.05 vs. RR=0.89 comparing LIT and placebo). In addition, 6.1% (4/66) of the comparisons between the RRs and the ORs for acceptability are in the opposite direction of the null (red plotting symbols in Figure 4). A direct comparison between the reported ORs in Cipriani et al⁷ and our marginal ORs is presented in the web appendix, and similar conclusions are shown.

Figure 4.

Comparison of the ORs versus the RRs for the 12 Antimanic Drugs. The dotted lines present the percentages of overestimation (bias away from the null) or underestimation (bias toward the null) of treatment efficacy or acceptability if the ORs reported in Cipriani et al⁷ were misinterpreted as the RRs. The negative percentages denote underestimation and positive percentage denote overestimation.

4. Discussion

Network meta-analysis is increasingly utilized to synthesize direct and indirect evidence for different treatments. However, many current network meta-analyses focus on treatment contrasts, in which one of the arms of each study is chosen as “baseline”. Since different studies may have different “baselines”, as a consequence of changing standards of care or changes in the underlying risks of study populations (e.g., initial trial may include more severely ill patients), specifying a common distribution for “baseline” groups is generally not interpretable. Although one may prefer to leave the “baseline” treatment as a fixed, study-specific parameter with the argument that they are fundamentally different from each other. However, while we make a relatively strong assumption on exchangeability of the probability of events within each treatment group across studies, our model is valid under the missing at random (MAR) assumption. The contrast-based Lu and Ades approach is valid only under a missing completely at random (MCAR) assumption, as shown in a recent AHRQ report (http://www.ncbi.nlm.nih.gov/books/NBK116689/pdf/TOC.pdf) and a corresponding technical report⁵⁵. In addition, many current NMA methods only report the relative treatment effect on an OR scale^21-29. Although they do offer valid statistical significance testing concerning the OR and can incorporate data from studies that only report relative treatment effects, without making strong assumptions on the event rate in a “reference” group, they fail to report treatment-specific event rates, risk differences and relative risks, which should be considered in making treatment recommendations. Although in some cases, it is unfortunate that some people tend to misspecify the distribution for the “reference” group and sometimes can lead to incorrect inference and interpretation, it should not construed to against our effort to estimate and report treatment-specific event rates. With the two comprehensive overviews, we illustrate how this novel arm-based Bayesian hierarchical model can be used to estimate these key statistics, and in some circumstances lead to different conclusions.

For the two NMAs^{6, 7} considered, relatively high response proportions (up to 0.62) were observed. The differences between ORs and RRs that we illustrate can be explained in large part by the theoretical difference between the OR and the RR for common events⁵⁶. The limitation of only reporting the ORs is discussed in detail in the web appendix. There is also a theoretical difference between the marginal treatment effects averaged over all studies by our approach, and the conditional treatment effects reported for a typical NWA by the contrast-based approaches such as used by Cipriani et al^{6, 7}. Marginal treatment effects are generally smaller than the conditional treatment effects estimated from random effects models⁵⁷. Finally, our differing ORs and RRs may partially be the result of the potential difference between model assumptions (e.g., the assumed variance and correlation structure) and the potential bias using current contrast-based models as illustrated in the hypothetical data analyses.

To compare the performance of the proposed arm-based versus current contrast-based Bayesian hierarchical models, we create two hypothetical network meta-analysis data sets including 11 trials and 3 treatment arms under either a homogenous RR or a homogenous RD assumption, in which the full data sets (i.e., assuming each trial compares all treatment arms) are available to estimate the true parameters (see details in the Web appendix). We found that the proposed arm-based NMA method outperformed the current contrast-based NMA methods.

In addition to some common concerns of network meta-analysis^{5, 10, 40}, there are some additional limitations for the proposed network meta-analysis approaches. First, to facilitate the estimation of treatment-specific population-averaged event proportions, we assume that each study hypothetically compares all treatments, with unstudied arms being missing at random conditional on the observed arms. Such models allow us to borrow information across multiple treatments within studies to reduce potential bias. However, it is plausible that investigators may have selected treatment arms on purpose based on the results of previous trials, which may lead to “nonignorable missingness” and potentially bias our event rate estimation. In addition, to robustly estimate event rates for each treatment, it is very important to have adequate number of trials with adequate samples for each treatment in a network meta-analysis. Different model assumptions may lead to different results in poorly connected networks. Second, in this article, we only considered a saturated multivariate Bayesian hierarchical mixed model with unstructured variance-covariance matrix. Although various model simplifications gave similar results (not presented), we did not perform analysis over all possible reduced models (e.g. models with equal variances, and/or equal correlations among all treatments), a number of which may further improve statistical efficiency. Arguably, the unstructured variance-covariance matrix allows us to better summarize the evidence contained in the data without enforcing an artificial structure, such as equal variances or equal correlations. Third, in addition to the evaluation of heterogeneity of treatment effects, inconsistency is a major concern in network meta-analysis. Much ongoing debate over the value of network meta-analysis concerns the agreement between the direct and indirect evidence. In addition, inconsistency and its tradeoff with heterogeneity can be very important when selecting the scale for NMA⁶¹. Achana et al⁶². has proposed an important method to adjust for baseline imbalance in order to possibly reduce heterogeneity and inconsistency for the CB methods. Some statistical methods have been proposed for identifying this disagreement when using contrast-based approaches with the odds ratio as the main effect measure^{25, 41, 58-60}, statistical methods for identifying and accounting for potential inconsistency based on our proposed models, formulated from the missing data perspective, await further development. Finally, in this paper, we do not consider individual-level or study-level covariates, which has already been briefly discussed elsewhere^{63, 64}.

In summary, we have proposed and implemented a novel arm-based multiple-treatments meta-analysis in a Bayesian framework, which is different than the methods used by Cipriani in two NMAs^{6, 7}. With this arm-based approach, estimates of treatment-specific event rates or proportions, RDs and RRs are provided. Using two hypothetical data sets, we show that our method provides more accurate estimates than the methods used by Cipriani et al^{6, 7}. Such differences could lead to different treatment recommendations.

Supplementary Material

wTable 1. The Number of Events and Total Sample Sizes of Two hypothetical Network Meta-analyses

RR = Rate Ratio; RD = Rate difference. Greyed cells are assumed to be unobserved.

wTable 2. Summary of different model specifications and their assumptions

Notation: S_i is the set of treatments that are compared in study i (i = 1, 2, …, I), S_kl is the set of studies that directly compared treatments k and l. For each treatment k ∈;S_i(k = 1,…,K), n_ik is the total number of subjects, Y_ik is the total number of responses, and p_ik is the corresponding probability of response. O=observed, E=expected, V = variance for the difference between O and E. Let b represents “baseline” treatment, Φ be the cumulative density function (cdf) of the standard normal distribution. The hyperparameters ${\gamma }_{kl}^b$ describes the correlation between 2 treatment contrasts within a trial, which are only needed in a MTC model when there are multi-arm trials on treatment triples (b, k, l).

Figure 2a. Comparison of the reported ORs in Cipriani et al⁶ versus the ORs from our model for the 12 Antidepressants. The dotted lines present the percentages of overestimation (bias away from the null) or underestimation (bias toward the null) of the treatment efficacy or acceptability. The negative percentages denote underestimation and positive percentage denote overestimation.

Figure 4a. Comparison of the ORs reported in Cipriani et al⁷ versus the ORs from our model for the 12 Antimanic Drugs. The dotted lines present the percentages of overestimation (bias away from the null) or underestimation (bias toward the null) of treatment efficacy or acceptability. The negative percentages denote underestimation and positive percentage denote overestimation.

Glossary for abbreviations

NMA

network meta-analysis

MCAR

missing completely at random

MAR

missing at random

MNAR

missing not at random

RD

risk difference

RR

risk ratio

OR

odds ratio

CER

comparative effectiveness research

RCT

randomized controlled trial

CB

contrast-based

AB

arm-based

MBHMM

multivariate Bayesian hierarchical mixed model

Appendix. Detailed WinBUGS code for the proposed network meta-analysis

We only include the main WinBUGS code here, the actual code for the case studies and hypothetical examples with corresponding data and initial values is posted at http://www.biostat.umn.edu/∼brad/software.html.

model {

for(i in 1:sN) {

p[i]<-phi(mu[t[i]]+ vi[s[i], t[i]]) # model

r[i]∼dbin(p[i], totaln[i]) # binomial likelihood

}

for(j in 1:tS){

vi[j, 1:tN]∼dmnorm(mn[1:tN], T[1:tN,1:tN]) # multivariate normal distribution

}

invT[1:tN, 1:tN]<-inverse(T[ , ])

for (j in 1:tN){

mu[j]∼dnorm(0, 0.001)

sigma[j]<-sqrt(invT[j, j])

probt[j]<-phi(mu[j]/sqrt(1+invT[j, j]))

# population-averaged treatment specific event rate

}

T[1:tN,1:tN] ∼ dwish(R[1:tN, 1:tN], tN) # Wishart prior

for (k in 1:tN) {

rk[k]<- tN + 1 - rank(probt[],k) # ranking

best[k]<-equals(rk[k],1) # prob {treatment k is best}

}

for (j in 1:tN){ # calculation of RR, RD and OR

for (k in (j+1):tN){

RR[j, k] <- probt[j]/probt[k]

RD[j, k] <- probt[j]-probt[k]

OR[j, k] <- probt[j]/(1-probt[j])/probt[k]*(1-probt[k])

}

}

}