Technical Note: The Use of Z-Scores in Probabilistic Sensitivity Analyses

Traditional sensitivity analyses vary only one to three model parameters at a time making it difficult to evaluate the overall uncertainty in the results of a decision model, especially when the model has a large number of variables. Probabilistic sensitivity analyses using second order Monte Carlo simulations capture the overall uncertainty in a model's parameter values and present results as distributions around a mean value for expected utility rather than a point value.

In a probabilistic sensitivity analysis, parameter values are characterized as distributions rather than as discrete values¹. For each iteration of the Monte Carlo simulation, new values are randomly picked from each distribution. However, circumstances may arise in which distributions must be repeatedly accessed during sequential cycles within the Markov simulation. In particular, if regression models are being used to calculate parameter values in the Markov simulation and covariates of such regression models change over time, patient age being the most obvious example, these parameter values will need to be recalculated. One approach is to use an independent pick from the distribution in each subsequent Markov cycle. However, there are likely important dependencies that must be maintained in these future picks from parameter distributions. An extensive literature review did not identify any methods for dealing with repeated picks across Markov cycles during the performance of a probabilistic sensitivity analysis. In this technical note, we describe such a problem that can occur with probabilistic sensitivity analyses and propose a solution.

We developed a decision-analytic Markov state transition model to evaluate the use of bariatric surgery or not for severely obese patients with diabetes. The details of the model, including model structure and model results are reported elsewhere². The decision model was constructed using Decision Maker® and all other analyses were conducted using SAS version 9.3 (Cary, NC).

The probability of death in each monthly cycle of the model was calculated from Cox proportional hazards models that were derived from a large dataset of surgically treated and untreated patients. During repetitive cycles of the Markov simulation the mortality rate in untreated patients was recalculated from the Cox proportional hazards models to account for the increased risk of death as the simulated patient aged. Against this mortality rate, the hazard ratio associated with treatment was applied and the mortality rate for treated patients was obtained.

Since the decision model was calculating the life expectancy of patients with and without treatment, the baseline mortality rate in untreated patients and the hazard ratio for treatment were the most important parameters in the model. However, since they were recalculated with every monthly cycle, standard traditional sensitivity analyses could not capture the uncertainty in these parameters beyond varying them by a standard fixed value which could be accomplished through an additional hazard ratio applied to the mortality rate. Using such traditional methods did not provide useful information regarding the uncertainty associated with the Cox proportional hazards model and the hazard ratios.

Therefore, we performed probabilistic sensitivity analyses by developing distributions for each parameter in the model. To calculate the confidence intervals for the Cox proportional hazards models, we specified a set of covariates in untreated patients and outputted the probability of survival with upper and lower confidence intervals at each model time event using SAS. These were transformed into odds of death with upper and lower confidence intervals for each time frame using the equations in table 1. This process was performed for a range of ages to calculate the odds of death with confidence limits across the age spectrum in the same cohort of patients. We performed a similar process for patients who had bariatric surgery using the same covariate inputs across the same age spectrum.

Table 1.

Equations for converting proportion surviving to log odds

Mortality Rate = (-ln(% surviving at time t))/(time t)

Probability of Death = 1-exp(-(Mortality Rate) × (time))

Odds of Death = (Probability of Death)/(1-Probability of Death)

Log Odds = ln(Odds of Death)

Once the odds and their associated confidence intervals were obtained, the mean and standard deviation of the log-normal distribution were calculated assuming the log-odds are normally distributed³. This was done across a range of ages to generate tables of means and standard deviations for both treated and untreated patients. The tables were then inputted into Decision Maker® and the probability of death was calculated using the log-normal mean and standard deviation during the probabilistic sensitivity analysis. In Decision Maker® the @LOGNORM function was used for this. TreeAge® has a similar function. The probability of death could then be calculated during each cycle as a separate pick from these distributions for treated and untreated patients.

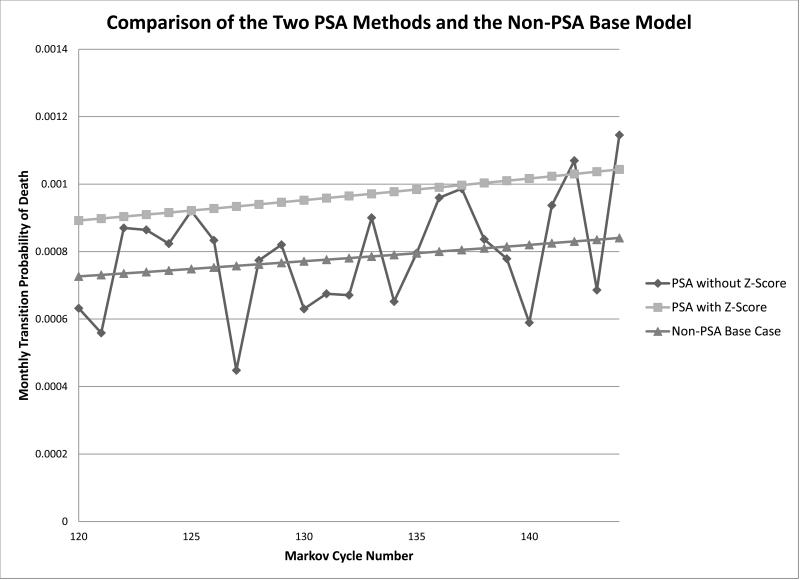
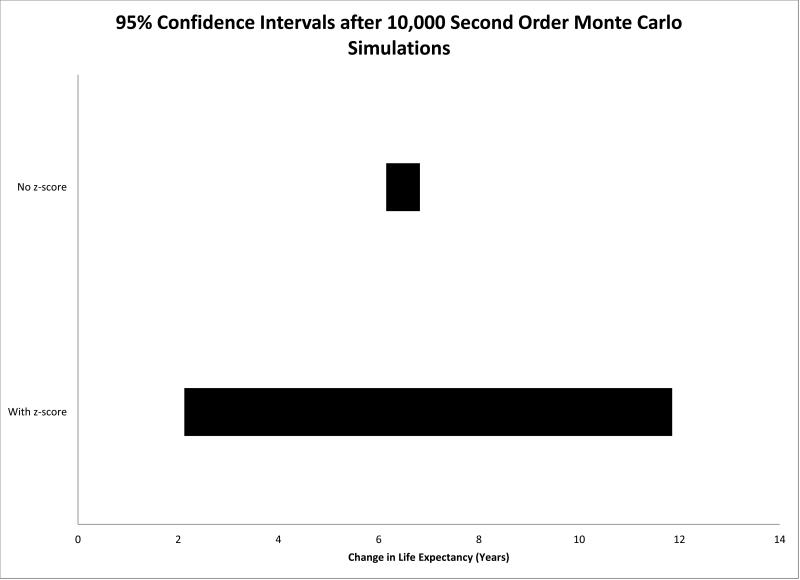
The model was then run as a second order Monte Carlo simulation for 10,000 simulations. During each cycle, a pick was made from the log normal-distributions to calculate the probability of dying for both the treated and the untreated group. The Markov model terminated after approximately 1,600 picks were made from these distributions during each of the 10,000 simulations of the model. The variability of the picks across each cycle is shown in Figure 1 for a representative sample of Markov cycles. The difference between the treated and untreated patients was an average of 6.5 years with a range of 5.9 to 7.1 years (see Figure 2). The 95% confidence interval was 6.2 years to 6.8 years. By randomly picking parameter values from these two distributions for each cycle, the cycles are treated as independent of each other. For example, a random pick from the low end of the distribution in cycle 1 would have no influence on the pick from this distribution in the second cycle. Over the course of 1,600 picks in each simulation, the picks will average out to the mean of the distributions resulting in an optimistic measure of the overall uncertainty in the model.

Figure 1.

Comparison of the two probabilistic sensitivity analysis (PSA) methods and the non-PSA base model. The figure shows the monthly transition probability of death across a sample of Markov cycles. The PSA without using a z-score line demonstrates the variability in picks during each cycle of the Markov simulation. By using the z-score method, there is variability in each Monte Carlo iteration but not between each Markov cycle within a Monte Carlo iteration. Presented is an example where the initial pick is higher than the mean using the z-score method. In practice, this would be balanced by similar examples on the opposite side of the base case.

Figure 2.

Comparison of results of second order Monte Carlo simulations using and not using the z-score method. The figure shows life expectancy gained when bariatric surgery is pursued versus no surgery. 95% confidence intervals are misleadingly narrow when the z-score is not used to maintain a constant variance in picks from parameter distributions across Markov cycles in each Monte Carlo iteration.

Ideally, in each Monte Carlo iteration, only one random pick would be made from each distribution. However, when the probability of death is being updated continually from Cox proportional hazards models, this is not possible. Therefore, we propose the use of a z-score to maintain continuity from one Markov cycle to the next.

A z-score, or standard score, indicates how many standard deviations a value is above or below the mean. During the simulation, a random pick is made from the log-normal distribution in the first cycle as described above. The z-score representing how far this pick falls from the mean is calculated as (pick-mean)/(s.d.). In the next cycle, the z-score is used to pick a non-random value from the distribution calculated from the Cox proportional hazards models as mean + (z-score X s.d.). The z-score does not vary from cycle to cycle but the distribution to which it is applied does. In this way, a random pick from the low end of the distribution in cycle 1 results in a pick from the low end of the distribution in cycle 2 and there is no regression to the mean over the course of the Markov simulation.

A representative example of this is shown in Figure 1 where the initial pick is from the higher end of the distribution. When the z-score is applied to the subsequent Markov cycles as illustrated in the figure, the values used remain the same number of standard deviations above the mean. Across Monte Carlo iterations, the picks will be balanced around the base case.

Using the z-score method, after 10,000 Monte Carlo simulations, the mean difference between the treated and untreated strategies was 6.7 years with a range of -3.4 to 17.3 years. The 95% confidence interval was 2.1 years to 11.9 years (see Figure 2). For each simulation, only two random picks are made from the distributions. If we allow a new and independent pick from each subsequent cycle of the Markov to be made, the apparent variance in the life expectancy gained from bariatric surgery versus no surgery is diminished resulting in an underestimate of the true variance.

Probabilistic sensitivity analyses that make repeated picks from distributions in each Markov cycle will underestimate the true uncertainty in probabilistic sensitivity analyses. By using a fixed z-score for all future Markov cycles based on the distributional pick from the first cycle, the model provides a realistic estimate of the true uncertainty around the decision.