A Hybrid Oscillatory Interference/Continuous Attractor Network Model of Grid Cell Firing

Abstract

Grid cells in the rodent medial entorhinal cortex exhibit remarkably regular spatial firing patterns that tessellate all environments visited by the animal. Two theoretical mechanisms that could generate this spatially periodic activity pattern have been proposed: oscillatory interference and continuous attractor dynamics. Although a variety of evidence has been cited in support of each, some aspects of the two mechanisms are complementary, suggesting that a combined model may best account for experimental data. The oscillatory interference model proposes that the grid pattern is formed from linear interference patterns or “periodic bands” in which velocity-controlled oscillators integrate self-motion to code displacement along preferred directions. However, it also allows the use of symmetric recurrent connectivity between grid cells to provide relative stability and continuous attractor dynamics. Here, we present simulations of this type of hybrid model, demonstrate that it generates intracellular membrane potential profiles that closely match those observed in vivo, addresses several criticisms aimed at pure oscillatory interference and continuous attractor models, and provides testable predictions for future empirical studies.

Introduction

Grid cells recorded in freely moving rodents fire whenever the animal enters a regular triangular array of locations arranged across its environment (Hafting et al., 2005). Grid cells were initially discovered in rat medial entorhinal cortex (mEC), but have since been reported in mice (Fyhn et al., 2008), bats (Yartsev et al., 2011) and humans (Jacobs et al., 2013) and in presubiculum and parasubiculum (Boccara et al., 2010). The scale, orientation, and relative offset of each cell's grid-like firing pattern is conserved across environments (Hafting et al., 2005; Fyhn et al., 2007), aside from expansion in novel environments (Barry et al., 2012a) and responses to the reshaping of a familiar environment (Barry et al., 2007; Derdikman et al., 2009). These properties suggest that grid cells perform path integration, maintaining their spatial firing patterns on the basis of self-motion input (Hafting et al., 2005; McNaughton et al., 2006).

Two main classes of mechanism have been proposed to account for the formation of grid-like firing patterns: oscillatory interference (OI) and continuous attractor network (CAN) dynamics. OI models, following theoretical accounts of place cell theta-phase precession (O'Keefe and Recce, 1993; Lengyel et al., 2003), posit velocity-controlled oscillators (VCOs) whose burst-firing frequency varies with movement direction and speed such that their firing phase tracks displacement along specific preferred directions. The spatial firing pattern of grid cells then results from interference between VCO inputs, firing whenever they are in phase (Burgess et al., 2005; Burgess et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008). In CAN models, following similar accounts of place and head direction cells (Redish et al., 1996; Tsodyks et al., 1996; Zhang, 1996; Samsonovich and McNaughton, 1997; Conklin and Eliasmith, 2005), grid firing patterns represent an attractor state generated by symmetrical recurrent interactions between grid cells whose strength reflects the relative offset of their firing fields (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Guanella et al., 2007; Burak and Fiete, 2009; Pastoll et al., 2013). To perform path integration, activity is shifted by asymmetric interactions with strength that reflects the animal's movement velocity, possibly mediated by conjunctive cells in deeper layers of mEC (Sargolini et al., 2006).

Although these two models hypothesize different mechanisms for path integration, they provide potentially complementary accounts of other properties of grid cell firing (Burgess et al., 2007; Hasselmo and Brandon, 2012; Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013). Therefore, we simulated a hybrid OI/CAN model in which grid cell activity is supported as a stable network state by recurrent inhibitory connectivity and feedforward input from VCOs that shift firing patterns according to movement velocity. In addition, VCOs are arranged in ring attractor circuits (Blair et al., 2008) and grid cell firing is stabilized by environmental information, assumed to come from learned associations with place cells (Redish and Touretzky, 1997; O'Keefe and Burgess, 2005; Burgess et al., 2007). Here, we demonstrate that this model accounts for a range of intracellularly and extracellularly recorded data, addresses several criticisms aimed at pure OI or CAN models, and offers testable predictions for future empirical studies.

Materials and Methods

The main component of the model is a module of grid cells with firing patterns that share a common orientation and scale, but differ in their spatial phase. There are N_offset spatially offset grid-like firing patterns that are each manifested by N_copy cells (all network parameter values are listed in Table 1). Grid cells are modeled as leaky integrate and fire neurons with membrane capacitance (C_m) and conductance (g_m), giving a membrane time constant of ${\tau }_{\text{m}}=\frac{c_{\text{m}}}{g_{\text{m}}}$ according to Equation 1 (all neuron model parameter values are listed in Table 2). Spikes are fired whenever the membrane potential (V_m) reaches a threshold (V_t), after which it is reset to (V_reset).

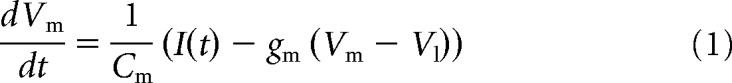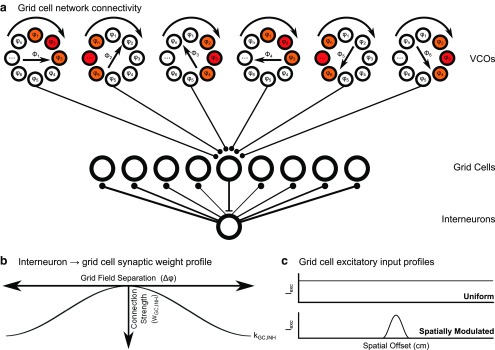
Grid cells receive synaptic input with fixed strength w_GC,VCO from velocity controlled oscillator (VCO) cells that are assumed to be arranged in ring attractor circuits (Blair et al., 2008; Welday et al., 2011; Fig. 1A), following models of head-direction cells (Redish et al., 1996; Zhang, 1996; Song and Wang, 2005). VCO cells in each ring attractor circuit share a single preferred direction (ϕ_VCO), but differ in their phase offset (φ_VCO). To generate grid-like firing patterns, we simulated VCO ring attractor circuit inputs with six preferred directions separated by 60°. We discuss how this specific connectivity may have developed and examine the effects of perturbing VCO-preferred directions on grid-cell-firing patterns (see Fig. 5). To produce evenly spaced grid firing fields, VCO initial phases within each ring attractor circuit have N_VCO,offset evenly distributed offsets. To increase the total number of input cells and so produce more realistic membrane dynamics in the simulated grid cell population, we simulated N_VCO,copy copies of each VCO ring attractor circuit.

Table 1.

Network variables

Parameter	Description	Value
Noffset, 1D track	Total number of distinct grid patterns on the 1D track	40
Noffset, 2D arena	Total number of distinct grid patterns in the 2D arena	36
NVCO, offset, 1D track	Total number of VCO cells in each ring attractor circuit on the 1D track	40
NVCO, offset, 2D arena	Total number of VCO cells in each ring attractor circuit in the 2D arena	6
Ncopy	Total number of grid cells that receive input from a common set of VCOs	48
NINH,copy	Total number of interneurons that receive input from a common set of grid cells	12
NVCO,copy	Total number of VCO ring attractor circuits for each preferred direction	30
⊘VCO	VCO preferred directions	π/3, 2π/3, π 4π/3, 5π/3, 2π rad
σ⊘	SD of VCO preferred direction noise	$0/\frac{\pi }{36}$ rad
rVCO	Mean VCO firing rate	50 Hz
fLFP	Baseline oscillation frequency	8 Hz
β	VCO velocity/oscillation frequency gradient	0.209 cm−1
	Simulation time step	1 ms
σVCO	SD of VCO phase noise	0/0.015 rad
αVCO	VCO phase reset increment	0.5
wGC,VCO	Synaptic weight of VCO to grid cell connections	0.0045
kGC,INH	Mean synaptic weight of interneuron to grid cell connections	0.04 cos (Δφ)
kINH,GC	Mean synaptic weight of grid cell to interneuron connections	0.2
σGC,INH	SD of interneuron to grid cell connection strengths	0.1
σINH,GC	SD of grid cell to interneuron connection strengths	0.2
pGC,INH	Interneuron to grid cell connection probability	0.7
pINH,GC	Grid cell to interneuron connection probability	0.5
treset	Time for which VCO phase reset proceeds before movement onset	5 s

Table 2.

Neuron model variables

Parameter	Description	Value
Cm	Membrane capacitance	0.5 μF
gm	Membrane conductance	25 nS
Vl	Leak reversal potential	−70 mV
Vt	Firing threshold	−50 mV
Vreset	Reset potential	−65 mV
τAMPA	AMPA time constant	5.26 ms
τNMDA,f	Fast NMDA time constant	1.485 ms
τNMDA,s	Slow NMDA time constant	152 ms
τGABA,f	Fast GABA time constant	2.83 ms
τGABA,s	Slow GABA time constant	50 ms
EAMPA	AMPA reversal potential	0 mV
ENMDA	NMDA reversal potential	0 mV
EGABA	GABA reversal potential	−80 mV
gAMPA	AMPA conductance	21.5 nS
gNMDA	NMDA conductance	0.47 nS
gGABA	GABA conductance	14 nS
[Mg2+]	Extracellular Magnesium concentration	1 mM
Iexc	Mean uniform constant excitatory input to grid cells in the absence of recurrent inhibition	0.825 μA
Iexc	Mean uniform constant excitatory input to grid cells in the presence of recurrent inhibition	0.85 μA
Iexc	Mean peak spatially modulated excitatory input to grid cells	0.88 μA
Ilhh	Mean uniform constant excitatory input to interneurons	0.125 μA
σexc	SD of excitatory input to grid cells	0.125 μA
σinh	SD of excitatory input to interneurons	0.25 μA
σPF	SD of spatially modulated excitatory input	30 cm

Figure 1.

Grid cell network connectivity, recurrent inhibitory weight profile, and excitatory input profiles. a, Grid cell network connectivity. Grid cells receive inhibitory input from VCOs and recurrently connected interneurons. VCO cells are arranged in ring attractor circuits, with cells in each circuit sharing a common preferred movement direction Φ but differing in their temporal phase (colored VCOs illustrate the bump of activity in each ring attractor network, warm colors representing higher firing rates). All N_copy grid cells that share a firing pattern, as dictated by the phases of their VCO inputs, project to a unique population of interneurons that send recurrent projections back to the entire grid cell population. b, Recurrent inhibitory weight profile. The strength of connections between the unique population of interneurons associated with each grid firing pattern and all other grid cells in the network is proportional to the cosine of the spatial offset of their grid firing patterns, w_GC,INH ≈ k_GC,INH cos(Δφ). c, Excitatory input profiles. Grid cells receive an excitatory input current I_exc that is either uniform across the environment or spatially modulated to approximate input from hippocampal place cells.

Figure 5.

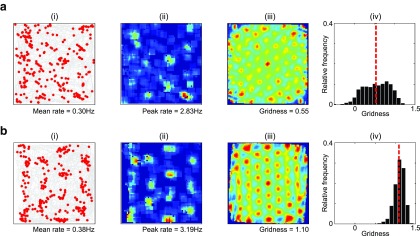
Sensitivity of the grid firing pattern to VCO preferred directions. a, Typical simulation of the OI model in the 2D arena when VCO preferred directions are randomly perturbed (with Gaussian noise of standard deviation: ${\sigma }_{\theta }=\frac{\pi }{36}$. ai, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). aii, Smoothed firing rate map. aiii, Smoothed spatial autocorrelation. aiv, Distribution of gridness scores for all grid cells in this simulation, with mean gridness indicated by the red dashed line. b, Simulation of the hybrid model in the 2D arena with the same VCO preferred directions as a illustrating that recurrent inhibitory connectivity makes the regularity of grid-cell-firing patterns more robust to noise in VCO preferred directions. bi, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). bii, Smoothed firing rate map. biii, Smoothed spatial autocorrelation. biv, Distribution of gridness scores for all grid cells in this simulation, with mean gridness indicated by the red dashed line. Over 10 simulations of the OI and hybrid models, each with its own perturbed VCO preferred direction values, gridness scores were significantly higher in the presence of recurrent inhibitory connectivity (paired t test, p < 0.005, mean gridness values: OI only = 0.36, hybrid model = 0.62).

The burst-firing frequency of cells in each VCO ring attractor circuit (f_VCO) deviates linearly from the baseline frequency (f_base) according to the component of movement velocity along the VCO's preferred direction (v_VCO) dictated by the absolute speed (s) and direction (φ) of the animal's movement (Eq. 2; Burgess, 2008). The scale of the grid field is dictated by the slope of the linear relationship between velocity and burst-firing frequency (β) as follows:

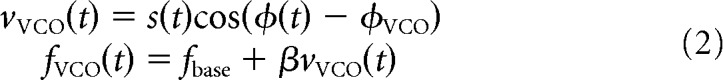Experimental data indicate that inhibitory interneurons (“theta cells”) can function as VCOs, having a burst-firing frequency that obeys Equation 2 (Welday et al., 2011). Accordingly, in our simulations, each VCO produces an inhibitory, inhomogeneous Poissonian spike train (Welday et al., 2011). To model theta phase precession of firing, following (Burgess, 2008), VCOs only fire when movement velocity in the preferred direction (v_VCO) is positive. The probability p(n, t) of firing n spikes in the time step at time t is dictated by the rate function λ_VCO, which is determined by the mean firing rate r_VCO, burst-firing frequency f_VCO and length of the time step Δt (Eq. 3, in which H[] indicates the Heaviside function):

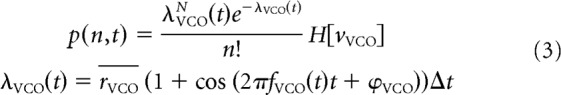Grid cells are reciprocally connected to a population of N_{offset ×} N_INH,copy inhibitory interneurons, also modeled as leaky integrate and fire neurons according to Equation 1. All N_copy grid cells that receive input from VCOs with the same set of phase offsets, and therefore share a grid firing pattern, project to a unique subpopulation of N_INH,copy interneurons with connection probability p_INH,GC and synaptic weights W_INH,GC. This interneuron subpopulation sends reciprocal projections with connection probability p_GC,INH and synaptic weights w_GC,INH back to the entire grid cell population (Fig. 1a). In each case, individual synaptic weights are sampled from a Gaussian distribution with mean amplitude k, multiplied by the normalized cosine of firing field offset Δφ for recurrent inhibitory projections (Fig. 1b), and SD σ. Any synaptic weights that are assigned negative values are set to zero.

The total input current to grid cells and interneurons is a combination of inhibitory and excitatory synaptic conductances and a noisy tonic excitatory current I_x (Eq. 4). Inhibitory synaptic inputs to grid cells from VCOs and interneurons are modeled as a single GABA conductance with an intermediate time constant to match the time course of IPSPs recorded in recent experimental studies (Eq. 5; Couey et al., 2013). Excitatory synaptic inputs to interneurons from grid cells are a combination of AMPA and NMDA conductances (Eqs. 6, 7). In each case, the total synaptic current I is a product of the maximum conductance g; the difference between membrane potential and reversal potential E; and the open channel probability P, which is a function of the time t_j elapsed since each of the j spikes fired in the simulation up to that time step t, either as a single exponential or difference of exponentials with time constant(s) σ (Destexhe et al., 1994). Where the open channel probability is a difference of exponentials, a factor B is used to ensure that the peak conductance is equal to the maximum conductance g. Uniquely, the NMDA conductance G_NMDA is a function of both the membrane potential and extracellular magnesium concentration [Mg²⁺] (Eq. 7; Jahr and Stevens, 1990).

Finally, grid cells receive a noisy tonic excitatory current I_x,exc, drawn from a Gaussian distribution with mean I_exc and SD σ_exc, at each time step. This excitatory input is either uniform across the environment or spatially tuned according to Equation 8, in which x represents the distance between the current position and the grid cell's nearest firing field center, and σ_PF sets the width of the input's spatial tuning (Fig. 1c). The locations of grid cell firing field centers are determined by the weighted centroids of firing fields in smoothed firing rate maps averaged over five 20 min trials without phase noise (see Phase noise and phase reset, below). This spatially tuned input represents a putative projection from hippocampal place cells, the firing locations of which are assumed to be determined by environmental sensory inputs (e.g., boundary vector cells; Hartley et al., 2000; Lever et al., 2009; Burgess and O'Keefe, 2011; Bush et al., 2014). This spatially tuned input is only present in a familiar environment, representing synaptic connections that have been formed by unsupervised Hebbian learning during exploration of that environment. The mean amplitude of this current I_exc is adjusted across simulations to match grid cell firing rates (Table 2). Interneurons also receive a constant feedforward excitatory current I_x,inh that is drawn from a Gaussian distribution with mean I_lnh and SD σ_inh and is uniform across the environment in all simulations. Some simulations were repeated with colored noise (i.e., where I_x is filtered by a synaptic time constant equal to that used here for AMPA conductances) without any qualitative effect on the results described (data not presented).

where:

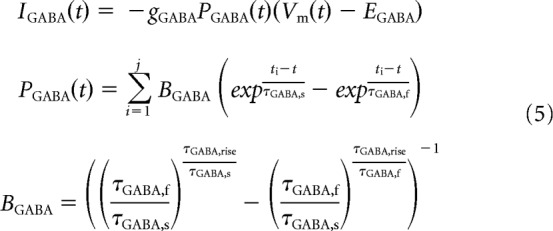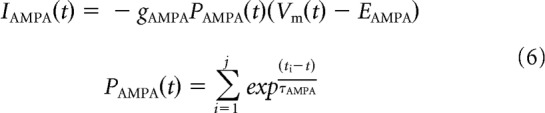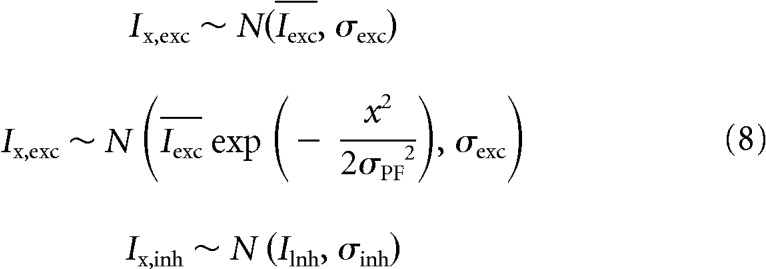Phase noise and phase reset. In each time step, phase noise with zero mean and SD σ_VCO is added to each VCO ring attractor circuit, and population activity in the grid cell network is used to perform phase resetting of the VCO ring attractor circuits to reduce accumulating noise (Song and Wang, 2005; Monaco et al., 2011; Sreenivasan and Fiete, 2011; Blair et al., 2014). This is implemented by calculating the grid cell population activity at the end of each theta cycle and then shifting activity bumps in the VCO ring attractor circuits toward the locations consistent with that grid cell population activity.

VCO phase resetting is implemented heuristically by associating grid-cell-firing patterns with their corresponding VCO phases. First, the phases of the six VCO rings (i.e., the angular positions of the activity bumps in each ring) that best correspond to firing in each grid cell (i.e., the circular mean of the VCO phases when spikes were fired by that grid cell) are computed in the absence of phase noise. This produces a vector of six VCO ring attractor phases $\overrightarrow{{\phi }_j^{*}}$ corresponding to peak firing in each grid cell j. Phase resetting, in simulations with phase noise, occurs at the end of each theta cycle by calculating the VCO phases corresponding to the grid cell activity in that theta cycle ($\overrightarrow{{\phi }_{\text{R}}}$) as the circular mean of $\overrightarrow{{\phi }_j^{*}}$ over grid cells, weighted by the number of spikes fired by each grid cell in the theta cycle n_j. The phases of activity bumps in each VCO ring $\overrightarrow{{\phi }_{\text{VCO}}}$ are then shifted toward $\overrightarrow{{\phi }_{\text{R}}}$ (see Eq. 9, in which α_VCO is a constant):

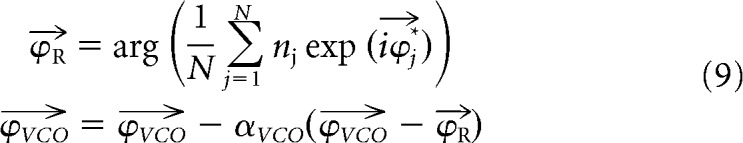In some simulations (Figs. 8, 9), the phase of each VCO ring attractor circuit is assigned randomly upon entry to an environment and phase resetting proceeds for a period of t_reset before movement onset to bring the phase of VCO inputs into alignment with grid cell firing. In a novel environment, uniform excitatory input and recurrent inhibition ensure that the network produces a coherent grid firing pattern in a location determined by the random initial VCO phases and phase resetting then acts to align VCO phases with that grid firing pattern. In a familiar environment, the location represented by grid cell firing is influenced by putative place cell input and phase resetting then acts to align VCO phases with that grid firing pattern (Figs. 8, 9b–e).

Figure 8.

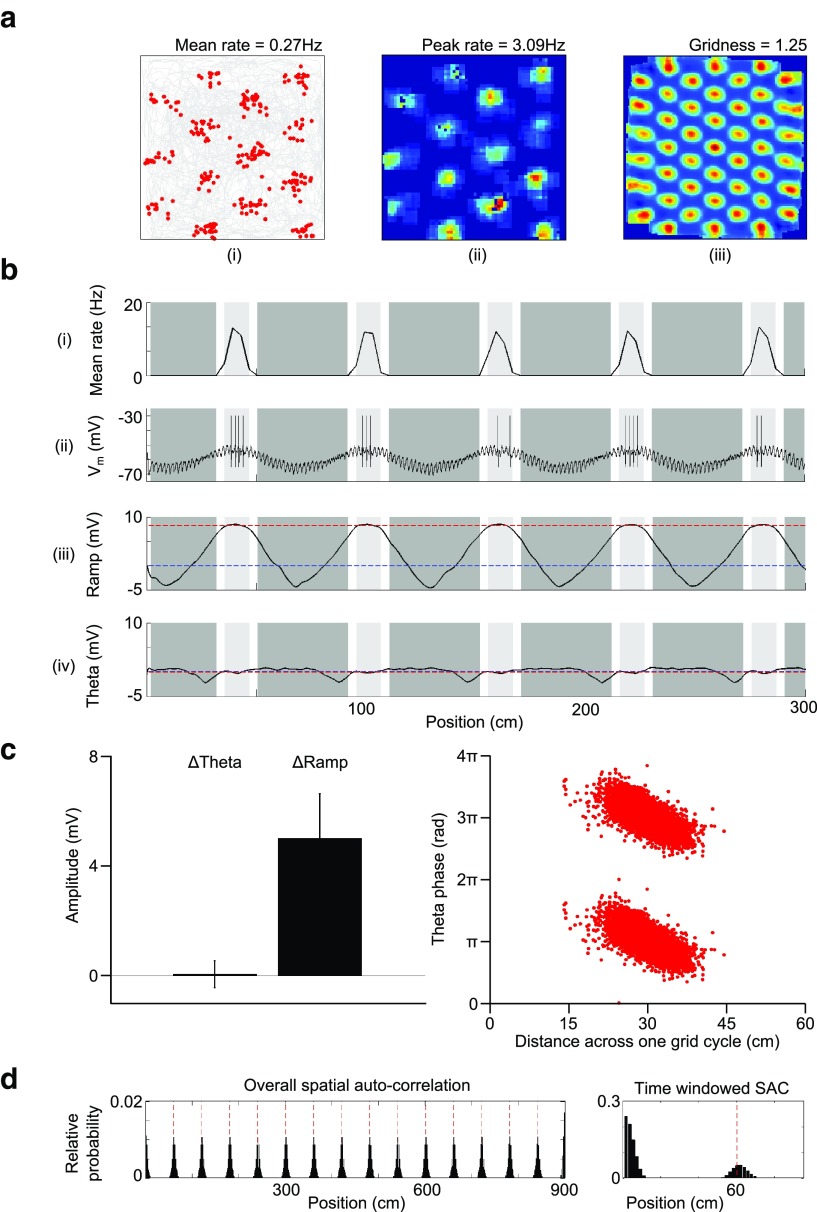
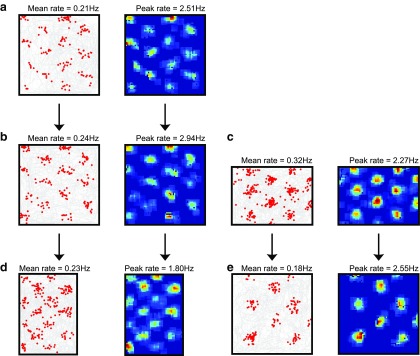
Effects of place cell mediated sensory inputs to the grid cell network in the hybrid model. a, Grid cell firing with place cell inputs in a familiar 2D arena. Grid cells receive spatially modulated excitation corresponding to input from place cells with firing fields centered at the peak of each grid field. ai, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). aii, Smoothed firing rate map. aiii, Smoothed spatial autocorrelation. b, Grid cell firing with place cell inputs on the 1D track. bi, Mean firing rate. bii, Membrane potential of a typical grid cell. biii, Mean low-frequency (<3 Hz) “ramp” amplitude in the membrane potential (note the increase in ramp depolarization compared with Fig. 3c). biv, Mean 5–11 Hz theta amplitude in membrane potential. c, Group data averaged across 50 independent simulations on the 1D track. ci, Mean increase in theta amplitude (ΔTheta) and ramp depolarization (ΔRamp) inside the grid field. cii, Pooled phase of grid cell firing relative to LFP theta. d, Overall and 6 s time-windowed spatial autocorrelations averaged across 10 independent simulations for the hybrid model with phase noise (σ_VCO = 0.015 rad), phase reset, and place cell input.

Figure 9.

Grid firing field intertrial stability and response to deformation of a familiar environment. a, b, Grid cell firing with place cell input, random initial VCO phases, and phase reset in two independent simulations within the same familiar environment. b, c, Grid cell firing with place cell input, random initial VCO phases, and phase reset in two different shaped familiar environments. d, e, Reshaped versions of environments in b and c. Note that the place cell input and phase reset of VCOs by grid firing creates appropriate spatial firing despite initially random VCO phases and also causes deformation of the grid pattern in the reshaped environment (as observed empirically by Barry et al., 2007).

Tracking data.

In simulations of a 1D track, the animal moves at a constant speed of 15 cm/s along a 3 or 9 m linear track. In simulations of a 2D arena, tracking data are taken from Barry et al. (2007), where rats foraged for randomly distributed food reward in a 1 m², 1 m × 0.7 m, or 0.7 m × 1 m arena for periods of 20 min.

Data analysis and presentation.

For data from the 1D track, membrane voltage traces were analyzed in terms of “ramp” depolarization and theta modulation following the methods previously used for experimental data (Domnisoru et al., 2013). Voltage traces for N_copy grid cells with the same firing pattern were mean normalized and spikes removed by linearly interpolating the voltage trace from [−1:25 ms] around the time of each spike fired. Spike-free voltage traces were zero-phase filtered separately in the 0–3 Hz “ramp” band and 5–11 Hz “theta” band using 400^th order finite impulse response filters. Ramp and theta amplitudes at each time point were then extracted from the analytic signal obtained by Hilbert transform and averaged across those N_copy grid cells for periods of movement (i.e., where s >5 cm/s). To determine “in-field” and “out-of-field” locations, mean firing rates in 5 cm bins were averaged across the same set of N_copy grid cells and grid fields were classified as regions where that mean firing rate exceeded 10% of the peak mean firing rate.

Phase precession relative to local field potential (LFP) theta is examined by assuming that the LFP has a constant frequency of f_base = 8 Hz and that the LFP trough (phase ϕ_base = π) corresponds to the time of peak firing in the grid cell population. Phase precession relative to the subthreshold membrane potential oscillation (MPO) is examined by extracting the phase of MPO theta from the analytic signal at the time of each spike.

For data from the 2D arena, firing rate maps were generated by first dividing the total number of spikes fired by each grid cell in 2 cm² spatial bins by the total amount of time spent in those bins during periods of movement (i.e., where s > 5 cm/s) and then smoothing with a 5 bin boxcar kernel. Spatial autocorrelations were used to calculate the gridness metric as described by Hafting et al. (2005); spatial information computed from adaptively smoothed firing rate maps (with a scaling factor of 200) as described by Skaggs et al. (1996); and intertrial stability of grid firing fields computed using the Pearson correlation coefficient between smoothed firing rates maps as described by Barry et al. (2012a).

For convenience, 2D temporal autocorrelation plots and 1D plots of the mean firing rate, ramp depolarization, theta amplitude, and firing phase relative to LFP or MPO (Figs. 2biv, 2ci,ciii–cvi, 3eiv,fi,fiii–fvi, 4bi,biii, 6biv, 8bi,biii–biv) show data that are combined over N_copy grid cells (or N_INH,copy interneurons) with the same grid firing pattern rather than data from the same grid cell combined over many runs. Values given for mean in-field and out-of-field ramp depolarization and theta amplitude and plots of pooled phase precession data (Figs. 2d, 3g, 8c) are averaged over N_copy grid cells in 50 independent simulations on the 1D track. Gridness distributions (Fig. 5aiv,biv) show data that are combined over N_{copy ×} N_offset grid cells from a single simulation and mean gridness values when noise is added to VCO preferred directions are computed across 10 independent simulations, each using different tracking data, in the 2D arena. Similarly, values given for intertrial grid field stability are computed across 10 independent simulations, each using random initial VCO phases and different tracking data, in the 2D arena.

Figure 2.

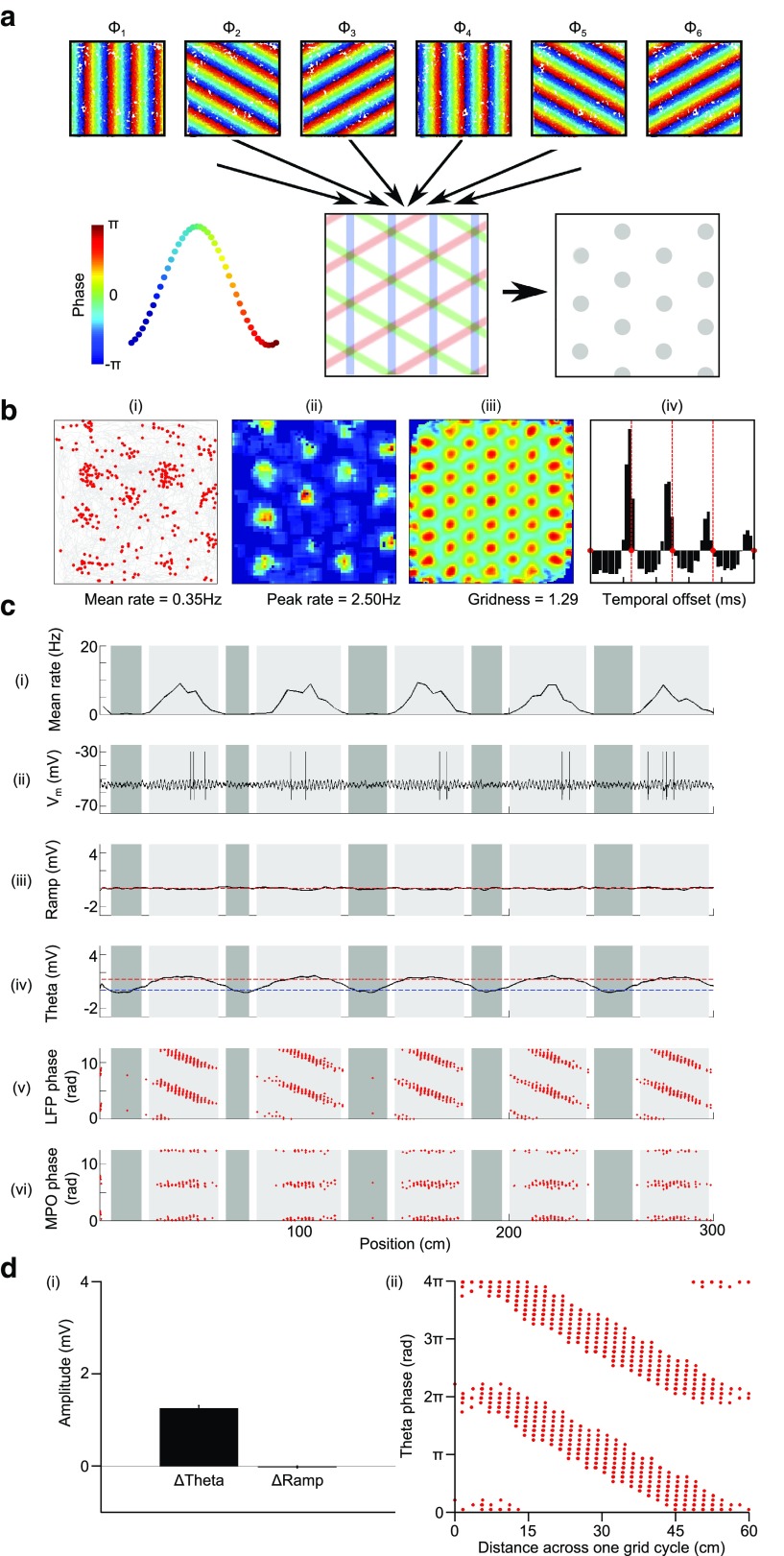
An OI model. a, Schematic illustration of the OI model. VCOs have a burst-firing frequency that deviates linearly from baseline according to movement velocity in a preferred direction Φ, so that displacement in that direction is encoded by their firing phase as band-like patterns across the environment. Combining multiple VCO inputs with preferred orientations that differ by multiples of 60° can then account for the periodic, hexagonal grid firing field. b, Simulations of the OI model in the 2D arena. bi, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). bii, Smoothed firing rate map. biii, Smoothed spatial autocorrelation. biv, Mean temporal autocorrelation, illustrating that burst-firing frequency is higher than baseline theta frequency (marked by red lines), which suggests that phase precession is present in these simulations. c, Simulations of the OI model on a 1D track. ci, Mean grid cell firing rate. cii, Membrane potential of a typical grid cell. ciii, Mean low-frequency (<3 Hz) “ramp” amplitude in the membrane potential. civ, Mean 5–11 Hz theta amplitude in the membrane potential. cv, Phase of firing relative to LFP theta. cvi, Phase of firing relative to theta-band membrane potential oscillations. d, Group data averaged across 50 independent simulations on the 1D track. di, Mean increase in theta amplitude (ΔTheta) and ramp depolarization (ΔRamp) inside the grid field. dii, Pooled phase of grid cell firing relative to LFP theta.

Figure 3.

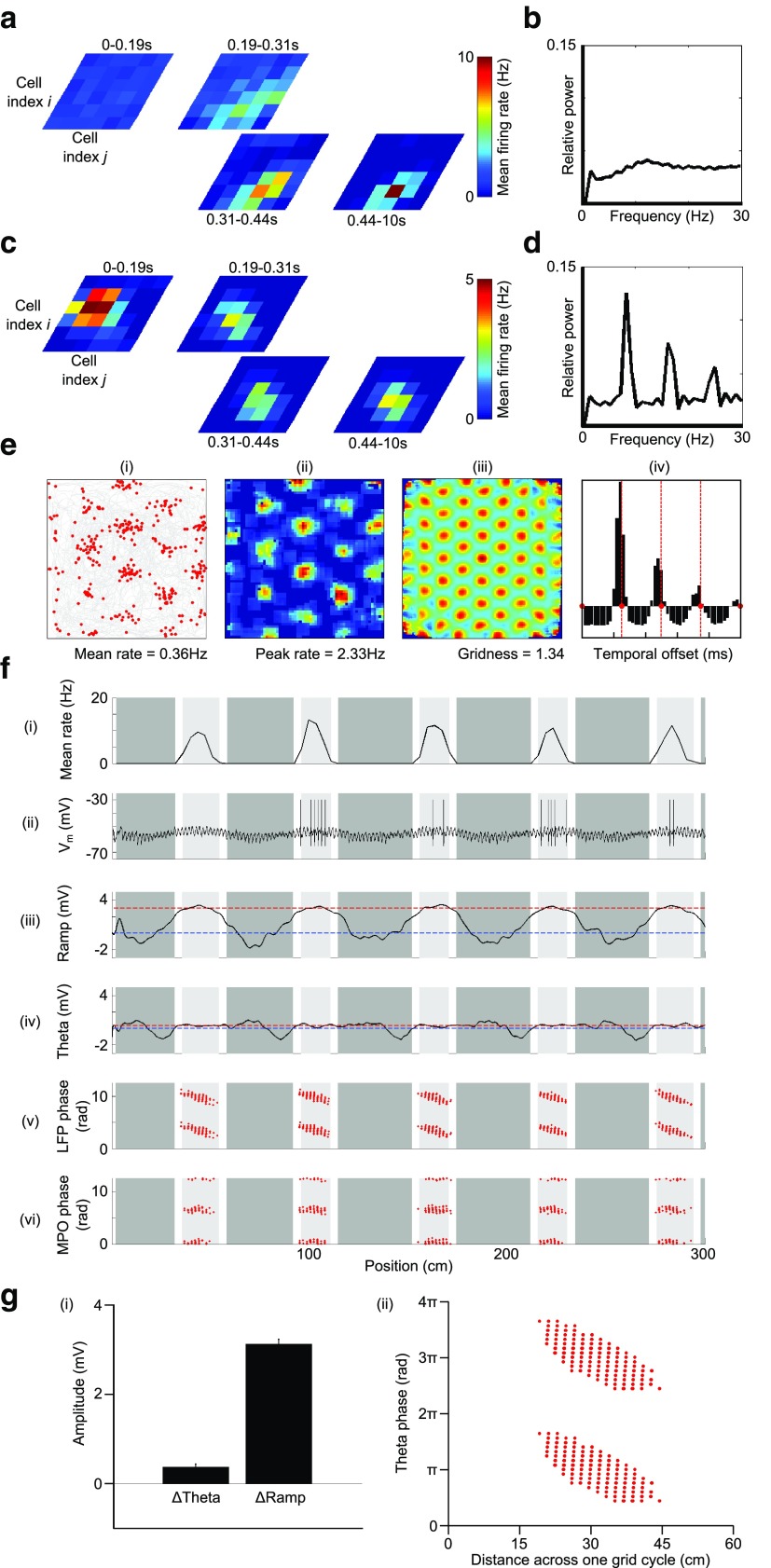
A hybrid OI and CAN model. a, In the absence of rhythmic input from VCOs, uniform feedforward excitatory input to the grid cell network, combined with recurrent inhibitory connectivity, produces a stable network state that is characterized by a single activity bump across the topographically organized sheet of cells. b, The power spectrum of the spike train autocorrelogram averaged across all active cells (i.e., those with mean firing rate >1 Hz over the 10 s simulation) illustrating the lack of rhythmicity in the spike trains during formation and maintenance of the activity bump in the absence of VCO inputs. c, In the hybrid model, spatially tuned rhythmic input from VCOs breaks the input symmetry of uniform feedforward excitation to the grid cell network so that the single, stable activity bump is more rapidly generated in a location dictated by the interference pattern. d, The power spectrum of the spike train autocorrelogram averaged across all active cells illustrating theta rhythmicity in the spike trains during formation and maintenance of the activity bump in the presence of VCO inputs. e, Simulations of the hybrid OI/CAN model in a 2D arena. Input from VCOs determine the location of the activity bump and integrate movement over time, thereby shifting its location according to self-motion. ei, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). eii, Smoothed firing rate map. eiii, Smoothed spatial autocorrelation. eiv, Mean temporal autocorrelation, illustrating that burst-firing frequency is higher than baseline theta frequency (marked by red lines), which suggests that phase precession is present in these simulations. f, Simulations of the hybrid OI/CAN model on a 1D track. fi, Mean grid cell firing rate. fii, Membrane potential of a typical grid cell. fiii, Mean low-frequency (<3 Hz) “ramp” amplitude in the membrane potential. fiv, Mean 5–11 Hz theta amplitude in the membrane potential. fv, Phase of firing relative to LFP theta. fvi, Phase of firing relative to theta-band membrane potential oscillations. g, Group data averaged across 50 independent simulations on the 1D track. gi, Mean increase in theta amplitude (ΔTheta) and ramp depolarization (ΔRamp) inside the grid field. gii, Pooled phase of grid cell firing relative to LFP theta.

Figure 4.

Spatially modulated interneuron activity in the hybrid model. a, Activity of a typical interneuron in the 2D arena. ai, Path taken by the animal (gray) and the location of spikes fired (red). aii, Smoothed firing rate map. aiii, Smoothed spatial autocorrelation. b, Interneuron firing on the 1D track. bi, Mean interneuron firing rate. bii, Membrane potential of a typical interneuron. biii, Phase of firing relative to LFP theta.

Figure 6.

Expansion of grid firing patterns with environmental novelty and generation of grid firing with a lower carrier frequency in the hybrid model. a, Grid scale and field size increase (cf. Fig. 3b) when the slope of the VCO movement velocity–burst-firing frequency relationship is reduced to β = 0.1257, giving a grid scale of 50 cm. All other parameters have the values used in Figures 2 and 3. ai, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). aii, Smoothed firing rate map. aiii, Smoothed spatial autocorrelation. b, Changing the carrier frequency f_base from theta to delta (i.e., f_base = 1.5 Hz) has no effect on grid scale or field size when β is kept constant (cf. Fig. 3b). All other parameters have the values used in Figures 2 and 3, but tonic excitatory current is reduced to I_exc = 0.68 μA to match mean firing rates. bi, Path taken by the animal (gray) and the location of spikes fired by a typical grid cell (red). bii, Smoothed firing rate map. biii, Smoothed spatial autocorrelation. biv, Power spectra of the mean normalized temporal autocorrelation illustrating the strong ∼1.5 Hz modulation of grid cell firing (*) and the absence of a peak in the theta band.

Results

OI model

The OI model posits that path integration is performed by VCOs whose burst-firing frequency varies with the speed and direction of movement such that their firing phase encodes displacement along specific preferred directions (Fig. 2a). The spatial firing pattern of grid cells results from interference between VCO inputs, firing whenever they are in phase (Burgess et al., 2005; Burgess et al., 2007; Blair et al., 2008; Burgess, 2008; Hasselmo, 2008) as an effective superposition of band-like representations of displacement along their preferred directions (Mhatre et al., 2012; see also Krupic et al., 2012; Fig. 2a).

In rodents, grid cell activity is typically observed during translational movement and is accompanied by the movement-related theta rhythm, a 5–11 Hz oscillation in the LFP (Vanderwolf, 1969; O'Keefe and Nadel, 1978; Brandon et al., 2011; Koenig et al., 2011), the frequency of which is modulated by running speed (Rivas et al., 1996; Sławińska and Kasicki, 1998; Jeewajee et al., 2008). Like hippocampal place cells (which typically fire in a single location; O'Keefe and Dostrovsky, 1971), rodent grid cells exhibit theta-phase precession; that is, spikes are fired at successively earlier phases of the LFP theta rhythm as the animal crosses the firing field (O'Keefe and Recce, 1993; Hafting et al., 2008; Reifenstein et al., 2012). Interestingly, theta phase of firing is best correlated with distance traveled through the firing field, even though data are pooled over runs of variable speed (Climer et al., 2013; Jeewajee et al., 2014).

First, we simulated a network of independent grid cells driven by a common population of inhibitory VCOs with a baseline frequency of f_base = 8 Hz and preferred orientations that differ by 60° in both the 1D and 2D environments (see Materials and Methods). Our results demonstrate that oscillatory interference between these inputs is sufficient to generate the grid-field-firing pattern and account for the theta modulation and phase precession of grid cell firing (Fig. 2b,c). Outside of the grid field, inhibitory input from VCOs is phase distributed across each theta cycle, preventing firing. Inside the grid field, the phase alignment of VCO inputs concentrates inhibition within each theta cycle, increasing subthreshold theta amplitude in the grid cell membrane potential and allowing sufficient release from inhibition for constant excitatory input to generate action potentials (Fig. 2c; following Welday et al., 2011 in the use of inhibitory VCOs). Grid cell firing occurs at the peak of these theta band MPOs, which also precess relative to LFP theta. Importantly, the theta-phase precession of grid cell spikes and MPOs matches that observed in intracellular recording studies, but the large increase in theta amplitude (ΔTheta) and absence of ramp depolarization (ΔRamp) inside grid-firing fields (ΔTheta = 1.26 ± 0.48 mV; ΔRamp = −0.02 ± 0.02 mV, averaged over 50 independent simulations; Fig. 2d) is inconsistent with that data (Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013).

CAN dynamics

Empirical data suggest that grid cells function as part of a network with significant local interactions. Extracellular recordings indicate that grid cells occupy modules with similar spatial scales (Barry et al., 2007; Stensola et al., 2012) that exhibit strong relative spatial stability even when unstable with respect to the environment (Yoon et al., 2013). The density of grid cells is highest in mEC layer II, where they appear to be stellate and pyramidal cells (Domnisoru et al., 2013) with relatively few monosynaptic excitatory interactions but significant disynaptic recurrent inhibitory connectivity (Dhillon and Jones, 2000; Beed et al., 2010; Quilichini et al., 2010; Beed et al., 2013; Couey et al., 2013; Pastoll et al., 2013). These properties are consistent with CAN models of grid cell firing (Fuhs and Touretzky, 2006; McNaughton et al., 2006; Guanella et al., 2007; Burak and Fiete, 2009; Pastoll et al., 2013).

Importantly, CAN models differ from OI models in the manner by which they integrate self-motion information. Whereas OI models use velocity-dependent frequency changes in VCO inputs, CAN models use velocity-dependent asymmetric interactions between grid cells, which are thought to be mediated by “conjunctive” directionally modulated grid cells in deeper layers of mEC (Sargolini et al., 2006). Beyond this distinction, the two models account for complementary grid cell properties using independent network mechanisms: the OI model describes the firing of independent grid cells, whereas CAN models describe how recurrent inhibition between grid cells promotes spatial stability. Therefore, as noted previously (Burgess et al., 2007; Burgess, 2008; Hasselmo and Brandon, 2012; Navratilova et al., 2012; Schmidt-Hieber and Häusser, 2013), a combined model might best account for empirical data.

We simulated a hybrid OI/CAN model by incorporating recurrent inhibitory connections into the network of grid cells driven by VCO inputs that is shown in Figure 2, with inhibitory synaptic weights varying as the cosine of firing field separation to create a “twisted torus” topology (Fig. 1b). The grid cell network can then support continuous attractor dynamics such that, in the absence of rhythmic VCO inputs, uniform feedforward excitation is sufficient to generate a single stable “activity bump” at a random location over a period of ∼500 ms, which subsequently moves slowly, smoothly, and stochastically across the flat energy landscape over time (Fig. 3a). There is no rhythmicity in the spike trains generated in these simulations (Fig. 3b). Adding spatially tuned rhythmic inhibition from VCOs breaks the input symmetry of uniform feedforward excitation so that the activity bump is established more rapidly in a specific location dictated by the interference pattern (Fig. 3c). VCO inputs also generate theta frequency oscillations in grid cell spike trains (Fig. 3d) and can subsequently shift the position of the activity bump according to self-motion information (Figs. 3e,f). This represents a departure from existing CAN models, which assume that path integration is performed by rate-coded activity within the grid cell network. Instead, in accordance with OI models, path integration is performed by temporal coding in VCO inputs to the grid cell network.

Simulations of this hybrid model demonstrate that the addition of recurrent inhibitory connectivity has little effect on extracellular grid cell properties, although out-of-field firing is reduced significantly (Figs. 2b, 3b), increasing the amount of spatial information carried by grid cell activity (0.75 ± 0.04 vs 0.61 ± 0.03 bits/spike) and reducing the range of theta-phase precession observed across the (now smaller) firing fields (Figs. 2d, 3g). This reduced phase precession (∼180°) corresponds well to the approximately linear pattern of phase precession seen in grid cells in layer II of mEC, but not the additional early phase spikes that do not align with this pattern (Hafting et al., 2008). However, the combination of rhythmic VCO input and recurrent inhibition in the grid cell network can account for intracellular membrane potential recordings from mice (Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013). First, recurrent inhibition hyperpolarizes grid cells that are out of their firing field, generating a slow, ramped depolarization of the grid cell (ΔRamp = 3.12 ± 0.10 mV, averaged over 50 independent simulations) as recurrent inhibition reduces on entry to the firing field (Fig. 3f,g). Second, recurrent inhibition is theta modulated, as it is driven by active grid cells with theta-modulated firing. Therefore, in contrast to a pure oscillatory interference model, MPO theta amplitude changes little in and out of the firing field (ΔTheta = 0.37 ± 0.06 mV averaged over 50 independent simulations), where it is driven by VCO inputs and recurrent inhibition, respectively (Figs. 2d, 3f,g).

The hybrid model also predicts that the interneuron population which provides recurrent inhibitory input to the grid cell network will exhibit grid-like firing patterns and theta-phase precession, following the active grid cells that drive them (Fig. 4). Previous continuous attractor network models in which interneurons mediate spatially specific recurrent inhibition (Burak and Fiete, 2009; Bonnevie et al., 2013; Couey et al., 2013) make the same prediction, although this has not often been described explicitly (but see Pastoll et al., 2013).

Sensitivity to VCO preferred directions

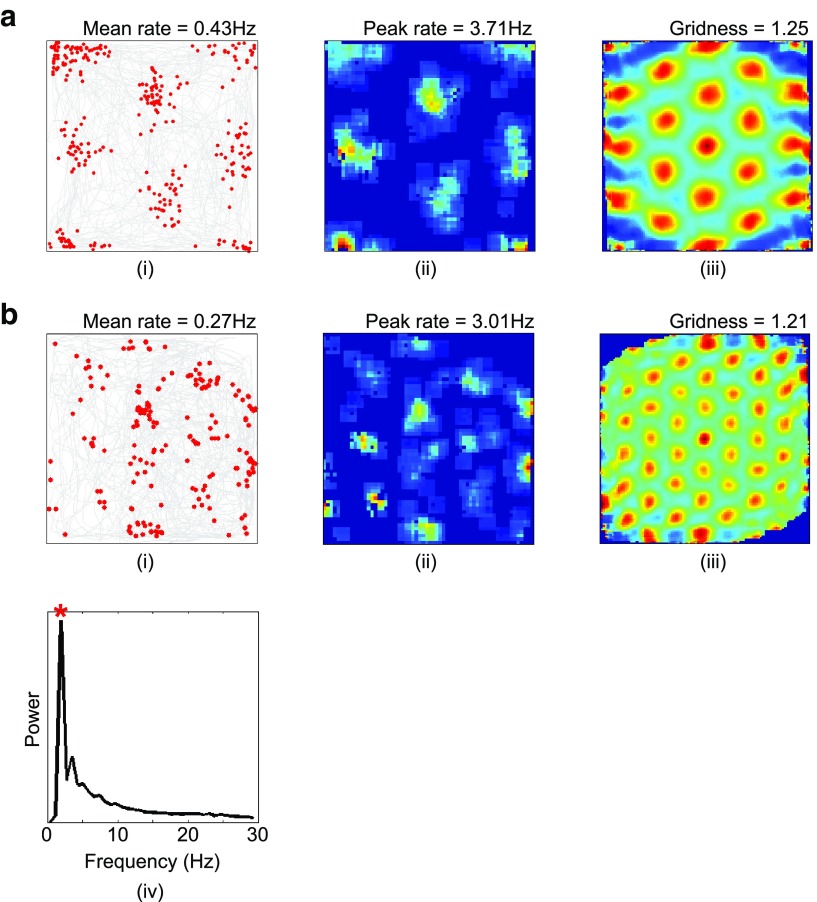
The ability of the OI model to generate regular, triangular, grid-like firing patterns depends on VCO inputs with preferred directions that differ by multiples of 60° (Burgess et al., 2007; Burgess, 2008; Fig. 2a). Adding Gaussian noise to the preferred direction of VCO inputs disrupts grid cell firing patterns, leaving irregular spatial modulation that is reminiscent of firing in the mEC of rat pups before the development of adult-like grid cell activity (Langston et al., 2010; Wills et al., 2010; Fig. 5a). The introduction of recurrent inhibitory connectivity improves the regularity of these firing patterns (Fig. 5b). However, it remains to be established how the “correct” configuration of VCO preferred directions could develop and, similarly, how the precise recurrent connectivity patterns required by CAN models might arise. Previous theoretical studies have demonstrated that this particular distribution of VCO inputs could develop through unsupervised Hebbian learning (Burgess et al., 2007; Mhatre et al., 2012). Other studies have demonstrated that a triangular array of grid firing fields can be generated by VCO inputs with a much wider range of preferred directions (Hasselmo and Brandon, 2012); and we note that the entire distribution of spatially periodic firing patterns in mEC is consistent with VCO inputs with a wider distribution of preferred orientations, not just the grid-like responses produced by differences of 60° (Krupic et al., 2012).

Environmental novelty and grid expansion

The spatial scale, relative orientation, and relative offset of grid-cell-firing patterns are broadly conserved across different environments (Hafting et al., 2005; Fyhn et al., 2007). However, a temporary expansion of the grid firing pattern is observed in a novel environment, which gradually decreases with familiarity, returning the grid pattern to its normal scale (Barry et al., 2012a). This expansion of the grid pattern occurs alongside a reduction in theta frequency (Jeewajee et al., 2008; Barry et al., 2012a) that is potentially related to a reduced rate of increase in theta frequency with running speed, also seen under environmental novelty (Wells et al., 2013). It has been hypothesized that both phenomena are a result of increased cholinergic tone driven by spatial uncertainty (Burgess, 2008; Barry et al., 2012b; Towse et al., 2014).

Both the OI and CAN models can account for expansion of the grid firing pattern by adjusting the gain of self-motion input to grid cells. In the hybrid model, reducing the constant β, which describes the rate of increase in VCO burst-firing frequency with running speed in the preferred direction above the baseline frequency f_base (Eq. 2), leads to a uniform expansion of both grid field size and grid scale (Fig. 6a). A gradual increase in the value of β subsequently returns the grid field to its original scale. Conversely, the other determinant of VCO burst-firing frequency, the baseline frequency f_base, has no effect on the scale of the grid field in these simulations and may reflect nonspatial variables such as anxiolytic drug action (Wells et al., 2013). Accordingly, grid firing patterns of an identical scale can be generated using much lower baseline frequencies, including values in the delta band (e.g., 1.5 Hz; Fig. 6b) that might occur in the hippocampal formation of bats, where theta appears to be absent (Barry and Doeller, 2013; Heys et al., 2013; Yartsev and Ulanovsky, 2013).

Phase noise and phase resetting

Both the OI and CAN models rely on the accurate integration of self-motion inputs to operate without error. In particular, the OI model has been criticized for its reliance on precisely timed oscillations (Giocomo and Hasselmo, 2008; Welinder et al., 2008; Zilli et al., 2009; Fiete, 2010; Dodson et al., 2011) despite evidence for temporally stable, spatially defined membrane potential oscillations in the form of theta-phase precession (O'Keefe and Recce, 1993; Hafting et al., 2008; Harvey et al., 2009; Reifenstein et al., 2012; Climer et al., 2013; Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013; Jeewajee et al., 2014). In the OI model, phase noise can reduce the spatial coherence and temporal stability of the grid firing pattern, as VCO inputs drift independently and may therefore fail to summate sufficiently to drive grid cell firing. It can also reduce spatial stability with respect to the environment, as random correlations in noise will shift the entire grid-firing pattern. Previous theoretical work has demonstrated that coupling VCOs, particularly within ring attractor circuits, can ameliorate the effects of phase noise and reduce path integration error along each preferred direction (Blair et al., 2008; Zilli and Hasselmo, 2010; Orchard et al., 2013; Burgess and Burgess, 2014). Here, we focus on the phase resetting of VCO ring attractor circuits by grid cell population activity and the advantages offered by the presence of continuous attractor dynamics in the grid cell network (Song and Wang, 2005; Blair et al., 2014).

First, we introduce identical random phase noise to all VCO cells in each of the six ring attractor circuits at each time step and examine the effects on grid cell firing. The presence of phase noise rapidly degrades the spatial stability of the grid-firing pattern (Fig. 7a,b). We then incorporate a phase reset mechanism in which grid cell population activity in each theta cycle is used to shift the phase of the activity bump in each VCO ring toward the value that would generate that population activity (see also Song and Wang, 2005; Blair et al., 2014). This mechanism could potentially be implemented by reciprocal projections from grid cells to VCO ring attractor circuits formed by unsupervised Hebbian learning, as grid cells and their VCO inputs are coactive during navigation. The reciprocal coupling of grid cells and VCOs produces additional attractor dynamics in which the grid cell population acts to maintain the current position of the activity bump over time by continually adjusting the phase of VCO inputs to those that would produce an activity bump at that location. The phase reset mechanism therefore stabilizes the grid firing pattern by reducing accumulating phase error both within and between VCO inputs (Fig. 7c).

Figure 7.

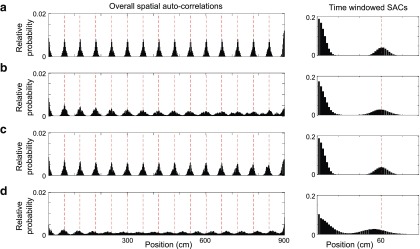
Spatial and relative stability of grid firing patterns with phase noise (from a Gaussian distribution with standard deviation: σ_VCO = 0.015 rad) and phase reset while the simulated animal runs at constant speed on a linear track. The overall spatial autocorrelogram (left) indicates spatial stability across the entire track; the 6 s time-windowed spatial autocorrelogram (right) indicates relative stability. Firing averaged across 10 independent simulations are shown for the hybrid model in the absence of phase noise (a); the hybrid model with phase noise, but without phase reset (b); the hybrid model with phase noise and phase reset (c); and a pure oscillatory interference model with phase noise and phase reset (d). The presence of recurrent inhibition and phase resetting of VCO inputs contributes to relative spatial stability producing sharp, well defined peaks in the autocorrelogram (c) comparable to those seen in the absence of phase noise (a).

In addition, on entry to a novel environment (i.e., before any learned associations from place cells to grid cells, see Environmental familiarity, grid stability and deformation, below) the phase reset mechanism will adjust random initial VCO phases to be coherent both with the grid firing pattern that has arisen and with each other. This phase initialization process provides a potential function for the observation of theta band membrane potential oscillations in grid cells before movement onset in intracellular recordings in virtual environments (Schmidt-Hieber and Häusser, 2013). Importantly, the phase reset mechanism is less effective in the absence of recurrent inhibitory connectivity between grid cells (Fig. 7d). The presence of recurrent inhibition ensures that a coherent grid-like firing pattern is produced by the network even when there are large amounts of accumulated phase noise in the VCO ring attractor circuits. Conversely, the lack of coupling between grid cells in a pure oscillatory interference model means that grid firing patterns become increasingly dispersed and incoherent as phase noise accumulates in each VCO input and degrade completely if discrepancies between the displacements encoded by different VCO inputs become too great.

Environmental familiarity, grid stability and deformation

The observation that grid-cell-firing patterns are stable between visits to an environment (Fyhn et al., 2007), oriented to distal landmarks (Hafting et al., 2005), and parametrically modulated when a familiar environment is reshaped (Barry et al., 2007; Stensola et al., 2012) suggest that grid cell firing becomes coupled to environmental sensory input with experience. Several theoretical models suggest that environmental sensory input to the grid (or VCO) network at familiar locations can correct accumulated path integration error (Redish and Touretzky, 1997; O'Keefe and Burgess, 2005; Fuhs and Touretzky, 2006; Burgess et al., 2007; Monaco et al., 2011; Sreenivasan and Fiete, 2011; Pastoll et al., 2013). Environmental sensory input may reach the grid (or VCO) cell network via projections from hippocampal place cells (O'Keefe and Burgess, 2005; Fuhs and Touretzky, 2006; Burgess et al., 2007; Monaco et al., 2011) and grid cell firing appears to depend on excitatory drive from the hippocampus (Bonnevie et al., 2013).

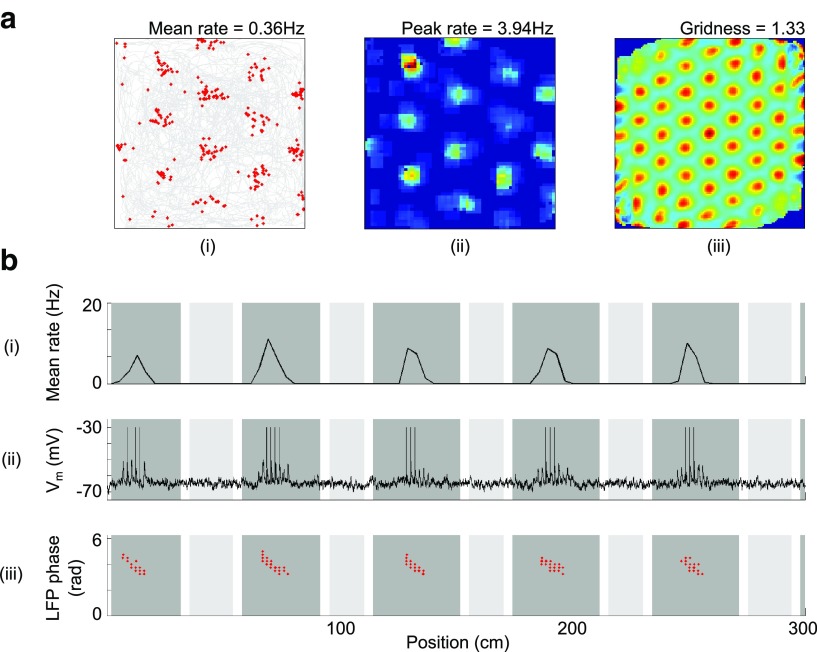
Here, we assume that place cell firing locations are determined by environmental sensory inputs rather than grid cell inputs, for example from boundary vector cells (Hartley et al., 2000; Lever et al., 2009; Burgess and O'Keefe, 2011; Bush et al., 2014). Therefore, given sufficient spatial stability in grid cell activity (Fig. 7c), grid cells could become coupled to the place cells with which they share firing fields via unsupervised Hebbian learning. To examine the effects of such learned associations, we replaced the uniform tonic excitatory input received by grid cells in the simulations above with spatially modulated excitatory input resembling unitary Gaussian place fields centered at the peak of each grid cell's firing field within the environment (Fig. 1c). In the absence of phase noise, this has little effect on the intracellular or extracellular properties of grid cell activity either on the 1D track or in the 2D arena, although out-of-field firing is diminished, further increasing the amount of spatial information carried by grid cell activity (1.07 ± 0.06 vs 0.75 ± 0.04 bits/spike) and ramp depolarization is increased (ΔTheta = 0.05 ± 0.49 mV and ΔRamp = −4.99 ± 1.61 mV, averaged over 50 independent simulations) as excitatory input is restricted to the firing field (Fig. 8a–c). In the presence of phase noise, place cell input helps to drive grid cell firing in the learned firing field locations, which subsequently shifts the phases of VCO inputs toward the values that initially encoded that location, further improving the spatial stability of the grid firing pattern (Fig. 8d).

The coupling between environmental sensory input (via place cells), the firing of grid cells, and the phases of VCOs also account for the stability of grid field firing between visits to an environment and for the temporary deformation of grid firing patterns after the reshaping of a familiar environment. In both cases, putative excitatory input from place cells drives grid cell firing that in turn adjusts the phase of VCO inputs to match incoming environmental sensory information at that location. Therefore, VCO phases that are assigned randomly at the beginning of each simulation (i.e., upon entry to the environment) are subsequently adjusted by place cell driven grid activity at that specific location and rapidly brought into alignment with the phases that initially encoded that location. Grid firing patterns generated in independent simulations that use different movement trajectories, starting locations, and random initial VCO phases but consistent place cell input subsequently exhibit strong spatial stability (r = 0.82 ± 0.02 averaged over all grid cells from 10 independent simulations; Fig. 9a). Moreover, when the shape of a familiar environment is changed, place-cell-firing fields deform to maintain their relative distance to environmental boundaries (O'Keefe and Burgess, 1996), presumably reflecting input from boundary vector cells (Hartley et al., 2000; Lever et al., 2009). Under this same manipulation, grid-cell-firing patterns reshape correspondingly (Barry et al., 2007; Stensola et al., 2012). This effect is replicated by the hybrid model, as path integration information encoded by phase changes in VCO inputs is continually “corrected” by the deformed place cell inputs such that the grid firing pattern is parametrically rescaled (Fig. 9b–e).

Note that the variability between firing rates within each grid field in 2D simulations (Figs. 2b, 3e, 4a, 6a,b) arises from noise in the tonic excitatory current input to grid cells and deviations between the simulated trajectory and the center of each firing field. This does not explain the variability in in-field firing rates that is reliable across experimental trials (Hafting et al., 2005), which would correspond to variations in the strength of place cell mediated environmental sensory inputs in this model.

Discussion

Two main classes of mechanism have been proposed to account for grid cell firing patterns, OI and CAN dynamics, each being supported by different aspects of the experimental data (for review, see Giocomo et al., 2011; Zilli, 2012). Consistent with OI models, grid cell burst-firing frequency shows the predicted effects of running speed, grid scale, and environmental novelty (Jeewajee et al., 2008; Barry et al., 2012a; Wells et al., 2013); VCO cells with the predicted dependence of burst-firing frequency on running direction and speed have been found (Welday et al., 2011); the grid firing pattern correlates with presence of theta rhythm during inhibition of the medial septum (Brandon et al., 2011; Koenig et al., 2011); and spatially periodic firing patterns in mEC appear to be formed from the superposition of spatial bands (Krupic et al., 2012). Consistent with CAN models, conjunctive cells were found (Sargolini et al., 2006); suitable inhibitory connectivity between grid cells in mEC layer II has been identified (Couey et al., 2013); and grid cells exist in discrete modules with similar spatial scales (Barry et al., 2007; Stensola et al., 2012) that exhibit strong relative stability even when unstable with respect to the environment (Yoon et al., 2013). However, the findings supporting each mechanism are largely complementary, suggesting that a combined model may best account for empirical data.

Our model follows previous demonstrations that adding symmetrical recurrent connectivity to single cell OI models benefits spatial stability (Burgess et al., 2007; Burgess, 2008; Hasselmo and Brandon, 2012) and that arranging VCOs in ring attractors benefits phase stability (Blair et al., 2008; Blair et al., 2014). It has also been shown that theta band oscillations can be incorporated into a CAN model (Pastoll et al., 2013); theta-phase precession can occur within a CAN model, although this requires AHP-ADP dynamics that vary with running speed to produce phase coding of location (Navratilova et al., 2012); development of CAN recurrent connectivity would benefit from an initial mechanism for establishing grid-like firing, such as the unsupervised self-organization of band-like VCO firing envisaged by OI models (Burgess et al., 2007; Mhatre et al., 2012); and the stability offered by continuous attractor dynamics is independent of the mechanism used to shift the activity bump. Moreover, intracellular recordings of grid cell membrane potential in head-fixed mice navigating in virtual reality (Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013) show both depolarization within the firing field (consistent with a CAN model) and spike timing that follows a theta-band membrane potential oscillation (consistent with an OI model), suggesting the presence of a hybrid mechanism (Schmidt-Hieber and Häusser, 2013).

Here, we have demonstrated that a simple hybrid model in which grid cells in a continuous attractor network are driven by input from VCOs can account for a wide range of experimental data. Input to grid cells from VCOs accounts for the theta modulation and phase precession of grid cell firing, as well as updating the represented location according to movement (i.e., performing path integration; Fig. 2). Recurrent inhibition between grid cells provides relative stability, increasing the spatial information provided by grid cell responses and accounting for the subthreshold ramp depolarization of grid cell membrane potential observed in intracellular recordings (Fig. 3). Coupling continuous attractor dynamics with a mechanism for correcting the phases of VCO inputs according to grid cell activity mitigates the accumulating phase noise in each VCO ring attractor, maintaining coherent grid firing patterns in the face of VCO phase noise and increasing spatial stability (Fig. 6). Coupling the phase reset mechanism with sensory information, perhaps mediated by unsupervised Hebbian connectivity from place cells, allows the grid field to remain stable between visits to an environment and to be parametrically deformed when that environment is reshaped (Fig. 7).

The principal distinction between the hybrid model presented here and pure CAN models is that path integration is performed by temporal coding in VCO inputs, rather than by rate-coded activity in the grid cell network itself. Therefore, grid firing patterns are updated by oscillatory interference, rather than velocity-modulated firing rate input from conjunctive-like cells (Sargolini et al., 2006). This relaxes the constraints on conjunctive cell properties required by CAN models: that their firing rate and/or directionality must tend to zero at zero running speed to prevent the activity bump drifting in the current heading direction. Similarly, the requirement for precise synaptic connectivity to maintain and smoothly shift the grid field is alleviated because oscillatory interference breaks input symmetry to the attractor network and therefore prevents drift or deterioration of the activity bump over time. Despite these advantages, this hybrid model offers no explanation for the function of conjunctive cells, although it is possible that they provide redundancy in the mechanisms for shifting the grid field according to self-motion information.

We have demonstrated that a simple phase reset mechanism allows the hybrid model to cope with phase noise in VCO inputs that would otherwise rapidly corrupt the grid field (see also Song and Wang, 2005; Blair et al., 2014; Burgess and Burgess, 2014). The existence of phase precession in vivo suggests that phase noise in the hippocampal formation need not preclude robust temporal coding of spatial location (O'Keefe and Recce, 1993); although in vitro studies describe more variable oscillations (Zilli et al., 2009; Dodson et al., 2011). We have also demonstrated that providing environmental sensory input to the grid cell network further ameliorates the effects of phase noise by periodically reducing accumulated path integration error. We therefore propose that the grid cell/place cell network mediates the interaction between environmental sensory inputs, for example, those encoded by boundary vector cells (Lever et al., 2009), and path integration information encoded by VCOs (see also O'Keefe and Burgess, 2005; Burgess and O'Keefe, 2011; Bush et al., 2014). Note however, that our simulations do not include the connectivity from grid cells to place cells that is indicated by the update of place cell responses in the dark.

One issue that faces all continuous attractor network models, including that presented here, is how the requisite synaptic connectivity might be established. Oscillatory interference offers one possible solution, establishing grid like firing in single cells and thereby allowing the tuning of recurrent inhibitory connections to support continuous attractor dynamics by unsupervised learning (Burgess et al., 2007). Importantly, however, the self-organization of band-like firing generated by VCO input to create grid-like firing through OI at the single cell level also likely depends on the presence of lateral inhibition sufficient to generate winner-takes-all dynamics (Mhatre et al., 2012), but without the requirement that it be spatially modulated. This provides an alternative to grid network development through Turing patterns, which depends on the prior existence of center-surround connectivity to create topographically organized activity patterns (McNaughton et al., 2006). The development of inhibitory connectivity within the grid cell network is therefore an important topic for future investigation (Wills et al., 2010; Langston et al., 2010).

The hybrid model described here makes several predictions for empirical studies. First, along with several previous CAN models (Burak and Fiete, 2009; Bonnevie et al., 2013; Couey et al., 2013; Pastoll et al., 2013), it predicts that interneurons in the local grid cell network will exhibit spatially periodic firing fields and phase precession, following the grid cells that drive them. Published intracellular grid cell recordings have focused on stellate and pyramidal cells (Domnisoru et al., 2013; Schmidt-Hieber and Häusser, 2013) and it is not clear whether all grid cells identified by extracellular recordings are excitatory and/or inhibitory neurons, although optogenetic identification of neuronal types could elucidate this issue. Second, in contrast to pure CAN models, self-motion information in the hybrid model is provided by VCO inputs such that selective inactivation of conjunctive cells—perhaps by targeted neurotoxic lesion of the deeper layers of mEC (Wu and Schwarcz, 1998)—could distinguish between CAN models, which require conjunctive cells to update the grid firing field, and hybrid or OI models, which do not. Third, the amplitude of “ramp” depolarization should increase with experience because excitatory input from the hippocampus to grid cells becomes spatially modulated through Hebbian learning, in contrast to suggestions that the hippocampus simply provides tonic excitation (Bonnevie et al., 2013; Couey et al., 2013; but see Kropff and Treves, 2008). Finally, manipulating the strength of VCO and recurrent inhibitory inputs by targeted inactivation of theta rhythmic cells in the septohippocampal circuit or local interneurons in mEC, respectively, should have dissociable effects. In the model, inactivation of VCOs would impair the grid pattern (preventing its updating by movement) and reduce MPO theta amplitude inside firing fields, whereas inactivation of local interneurons would impair the spatial stability and coherence of grid firing and reduce MPO theta amplitude outside of firing fields.

In summary, we have demonstrated that a hybrid oscillatory interference/continuous attractor network model of grid cell firing can account for complementary aspects of existing experimental data. We have shown that a simple phase reset mechanism allows the network to cope with phase noise in the VCO inputs and that grid firing patterns can be coupled to sensory input to further ameliorate path integration error and allow grid rescaling when a familiar environment is reshaped. The model makes several testable predictions for future empirical studies that will further elucidate the mechanisms that account for the remarkable firing pattern exhibited by grid cells.