A computational model of the response of adherent cells to stretch and changes in substrate stiffness

Abstract

Cells in the body exist in a dynamic mechanical environment where they are subject to mechanical stretch as well as changes in composition and stiffness of the underlying extracellular matrix (ECM). However, the underlying mechanisms by which cells sense and adapt to their dynamic mechanical environment, in particular to stretch, are not well understood. In this study, we hypothesized that emergent phenomena at the level of the actin network arising from active structural rearrangements driven by nonmuscle myosin II molecular motors play a major role in the cellular response to both stretch and changes in ECM stiffness. To test this hypothesis, we introduce a simple network model of actin-myosin interactions that links active self-organization of the actin network to the stiffness of the network and the traction forces generated by the network. We demonstrate that such a network replicates not only the effect of changes in substrate stiffness on cellular traction and stiffness and the dependence of rate of force development by a cell on the stiffness of its substrate, but also explains the physical response of adherent cells to transient and cyclic stretch. Our results provide strong indication that network phenomena governed by the active reorganization of the actin-myosin structure plays an important role in cellular mechanosensing and response to both changes in ECM stiffness and externally applied mechanical stretch.

normal functioning of living cells in the human body is intricately tied to the ability of the cell to sense and respond to its mechanical environment, which includes the composition and stiffness of its surrounding tissue and also the stretch patterns that it perceives in vivo. Mechanical stretch, in particular, has been shown to influence many basic cellular processes such as growth, remodeling, apoptosis, and gene expression (3, 22, 32, 40). However, the mechanisms by which intracellular contractile elements of the cell sense and respond to mechanical stretch are not fully understood.

Recent studies have shown that despite considerable diversity in function, the mechanical response of all adherent cells to stretch is universal and independent of their cell type (39, 71). For instance, when subjected to a transient stretch, cells promptly lose their stiffness and traction force followed by a slow recovery back to baseline. While the extent of decline in stiffness and traction is an increasing function of the stretch amplitude, the cell is able to modulate its recovery rate such that the time taken to get back to its baseline mechanical state is the same regardless of the stretch amplitude. Understanding the underlying mechanisms behind this universal response to stretch is key to uncovering the cellular origins of many clinically relevant problems such as the beneficial effect of deep inspirations in healthy subjects (9, 53, 60) and the lack thereof in asthmatics (8, 16, 33, 34) and the role of cyclic stretch in maintaining mechanical homeostasis in multiple cell types (14, 17).

A key element necessary for substrate sensing is the internal indigenous tension or prestress in the actin cytoskeleton generated by myosin II motors that attach to and walk along actin filaments drawing energy from ATP hydrolysis (26, 66, 73). The rate of development of prestress by a living cell is a fast process and reaches equilibrium in time scales of the order of 100 s (39, 50). Within this time frame, it has been experimentally shown that the prestress is borne by a network of randomly polarized actin filaments (2). The active motion of myosin motors within such a network can also result in rearrangement of the actin network (4), and the possibility of self-organized structures emerging in such an active system has been postulated by theoretical models (41, 76) and experimentally observed in actin gels (4, 64) and even in living cells labeled for actin (15, 31, 67). Recently, Borau et al. (6) showed that a network of actin, actin cross-linking proteins, and active molecular motors can replicate response of living cells to changes in substrate stiffness. Since dense networks of actin with nonmuscle myosin II (NM2) motor proteins are present in all adherent cell types, we hypothesized that such active self-organization at the network level is a common pathway that cells employ to sense and respond to both stretch and alterations in the ECM stiffness.

Here, we introduce a simple network model of actin-myosin interactions that links active self-organization of the actin network to the stiffness of the network and the traction forces generated by the network. We demonstrate that such a network replicates not only the effect of changes in substrate stiffness on cellular traction and stiffness and the dependence of rate of force development by a cell on the stiffness of its substrate (50), but also explains the physical response of adherent cells to transient and cyclic stretch (14, 17, 39, 71). Our results provide strong indication that network phenomena governed by the active reorganization of the actin-myosin structure plays an important role in cellular mechanosensing and response to both changes in ECM stiffness and externally applied mechanical stretch.

METHODS

Model setup.

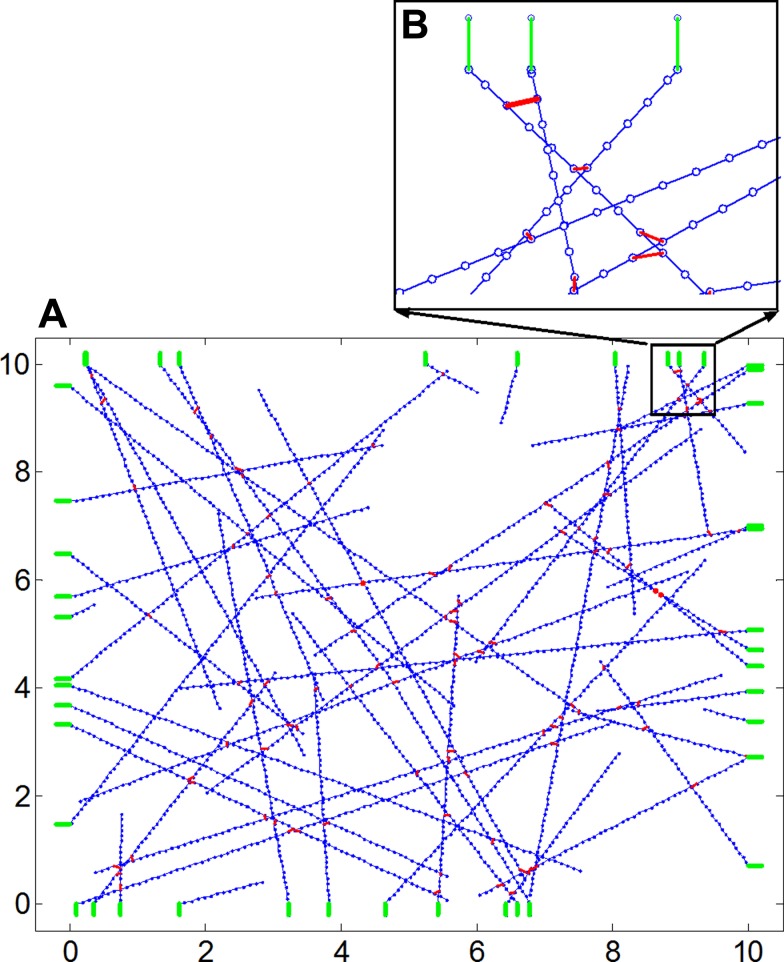
We first consider a randomly oriented 2D network of springs in a square of size L as illustrated in Fig. 1, which represents the subcortical actin network of a cell. Actin filaments are known to carry high tensile forces but can easily buckle under very low compressive loads (76). To model such elastic behavior, each actin filament is discretized as a set of springs of identical length l_0a and spring constant k_a. These springs can exert a force that depends on their length l as f = Θ(l − l_0a)k_a(l − l_0a), where Θ(x) = 0 for x < 0 and 1 for x ≥ 0 is the Heaviside step function. The end points of each spring that makes up an actin filament also serves as discrete binding sites where myosin crosslinks can attach. Each actin filament is modeled as a polarized filament with a positive and a negative end and was created by picking a point at random within the square and moving along a direction φ uniformly distributed in the interval [0,2π) in discrete steps of l_0a until a maximum distance of L was reached or if the boundary of the square was reached, in which case the filament is terminated at the boundary. The start point of each actin filament is assigned a negative polarity and the end point is assigned a positive polarity. To this network of actin, we add N_m linear elastic springs with spring constant k_m and initial length l_0m representing myosin crosslinks (shown in red in Fig. 1), which attach to binding sites along two distinct actin filaments that are separated by a distance less than a specified threshold. At present, there are no experimental measurements of the stiffness of the nonmuscle myosin. Here, we used measurements from striated muscle myosin to specify that k_m was 1.6 times higher than k_a (1, 54, 77). To find binding sites for myosins along the actin filaments, randomly chosen pairs of binding sites along two neighboring actin filaments are checked to see if the distance between them is less than or equal to l_0m. If this condition is satisfied, a myosin crosslink is added to link these two binding sites. The number of actin filaments (N_a) was specified to be approximately equal to the number of myosin crosslinks (N_m). All initial networks were checked for end-to-end connectivity from top to bottom and from left to right.

Fig. 1.

A: to create a prestressed actin network, we start with a set of actin fibers (blue) that are randomly oriented within a square space as shown. B, inset: binding sites for myosin crosslinks are added at regular intervals along each actin filament. Myosin crosslinkers can attach to binding sites on two actin filaments if the binding sites are closer than a specified distance. At points where the actin filaments intersect with the boundary, elastic elements representing the substrate material (green lines) are added to the network and represent the boundary conditions of the actin network. One end of the substrate is attached to the actin and the other end is held fixed.

Boundary conditions.

At every point along the square boundary where an actin filament terminates, a linear elastic spring with spring constant K_ECM is added to the network (shown in green in Fig. 1). These springs represent the combined effective stiffness of the focal adhesion complexes and the substrate material, the elastic boundary for the actin network in adherent cells. All substrate springs connect to an actin filament at one end while the other end is held fixed.

Motor movement.

Within a living cell, nonmuscle myosin II motor proteins use the energy from ATP hydrolysis to repetitively bind to actin and undergo conformational changes that result in the myosin II motor walking along the actin fiber toward its plus (barbed) end. In the model, the walk step for a myosin crosslink is implemented by moving each end of the myosin crosslink (as shown in Fig. 1, inset) to the next binding site on the filament to which it is attached in the direction of the filament's positive end. The rate of ADP release in nonmuscle myosin II has been found to be load dependent and decreases with increasing loads (38). Consequently, the forward velocity of myosin motors decreases with increasing load and when the load on the myosin crosslink approaches the stall force (f_stall), the myosin takes backward and forward steps around the same location (56). For an individual myosin the stall force has been estimated to be ∼2 pN (2, 51). Additionally, direct measurement of the characteristic lifetime of an actin-myosin bond using the optical trap method shows that the bond lifetime τ increases with increasing load up to ∼6 pN, a behavior known as a catch bond. Consistent with these experimental observations, initially, when the network carries no force, the time interval τ between two consecutive walk steps of a myosin crosslink is specified to be the same for all myosin crosslinks. In the model, we specify that once the myosin motor starts walking and the network develops tension, τ increases in proportion to the force (f) that each individual crosslink carries, τ ∝ f for f ≤ f_stall. The exact functional relationship between τ and f is not known for NM2 motors. A linear form is assumed here for simplicity. The dynamic in-place cycling of the myosin motor at stall is not considered here. Instead, we specify that when the load on a myosin crosslink exceeds f_stall, that myosin motor stops (τ → ∞).

Calculating the equilibrium configuration.

After each walk step, the entire network rearranges itself to balance local forces within the network. The new equilibrium configuration is determined by minimizing the total elastic energy of the network given by the sum of the elastic energy of the springs representing actin, myosin, and the substrate. A typical network considered in this study consisted of 55 actin filaments and 50 crosslinks and the corresponding spring network had 3,347 nodes and 3,292 springs. The simulated annealing algorithm (37, 49) was used to minimize the energy of the network. This technique uses a control parameter usually referred to as temperature (T) which is set to a high value initially. The system is perturbed by moving every node by a small amount and the resulting configuration is accepted based on the probability p = e^−(ΔU/T), where ΔU is the change in free energy associated with the perturbation. These steps are repeated until the system reaches thermal equilibrium, at which point the temperature is reduced. The equilibrium criteria for the minimization were set based on the condition that both the magnitude of the maximum resultant force for every node in the network and the magnitude of the mean resultant force for every node in the network decreases below an arbitrarily small value (here 10⁻⁵). After calculating the equilibrium configuration, the clock increment for the entire network was set based on the lowest myosin cross force in the network. An individual motor stops when the force it carries exceeds a f_stall or when both ends of the myosin crosslink have reached the positive end of their respective actin filaments. This process of walking and rearranging the network continues until the traction forces in the network do not change for 150 iterations.

Substrate stiffness and rate of traction force development.

Cells are known to modulate their traction force and the rate of force development in response to changes in substrate stiffness (78). To simulate this behavior using our network model, we vary the stiffness of the substrate springs K_ECM over 6 orders of magnitude (10⁻⁴ to 10²) and measure the maximum traction force that can develop as well as the rate of development of traction force. The rate of force development by the network was quantified using an equivalent velocity calculated as V = dδ/dt, where δ is the average displacement of the substrate springs.

External mechanical stretch and bond rupture.

When the load on an actin-myosin crosslink exceeds its rupture force, the myosin crosslink can detach from the actin filament. The average rupture force of an actin-myosin bond has been found to be 4–6 times higher than its stall force (∼2 pN) and is estimated to be between 9 and 12 pN (12, 55). Preliminary simulations showed that in a prestressed network that has reached equilibrium in traction, the maximum force on a myosin crosslink never exceeded 1.2 f_stall so that when the network develops traction starting from a random network, the bond rupture does not happen. However, when a prestressed network is subjected to external mechanical stretch, actin-myosin bonds can rupture. When an actin-myosin bond ruptures in the network, both ends of the bond detach and the myosin can diffuse through the network and reform at another location in the network where the binding sites on two actin filaments are closer to each other than the specified threshold distance for bond formation.

Measurements.

At each time point, we keep track of the number of myosin motors that walked in that time step, the traction force, the stiffness of the network, and the configuration of the network. The total traction force is measured as the sum of the magnitude of forces carried by the substrate springs. To measure stiffness of the network, we apply a small deformation δr equivalent to 0.01% strain on the network simultaneously in the x and y directions and then measure the resulting change in magnitude of the elastic recoil force of the network, δf. The stiffness of the network is then calculated as the ratio of change in magnitude of the force over change in displacement (δf/δr).

RESULTS

Actin-myosin network self-organizes to achieve equilibrium in traction and stiffness.

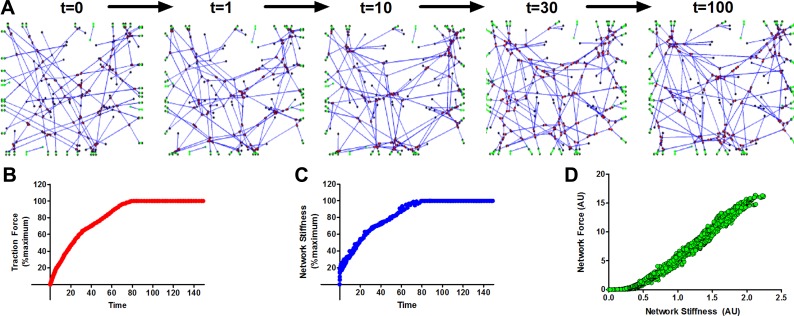
Starting from a network of random filaments as shown in Fig. 1, the myosin motors are allowed to walk along the actin filaments. After each walk step the equilibrium configuration of the network is obtained. Figure 2A shows the resulting changes in structure of the actin network over time. The corresponding traction force generated by the network and the network stiffness are shown in Fig. 2, B and C, respectively. At t ∼ 100, the network reaches equilibrium in both the traction and the stiffness plateaus, and the number of myosin motors that walk in each time step also reduced to an insignificant fraction of the total. The development of traction forces in Fig. 2B is similar to that measured in living cells plated on flexible substrates (50). Further, in Fig. 2D, we plot the changes in network stiffness against the changes in traction force developed by nine different networks with different initial configuration at time t = 0. We find that changes in stiffness are linearly related to changes in traction force during the reorganization of the network by myosin (Fig. 2D). While the model cannot be used to match the absolute stiffness of a living cell as this is not solely a function of actin and myosin, our network model can explain why changes in stiffness and traction force are highly correlated as the cell redevelops tension following a mechanical perturbation (39).

Fig. 2.

A: starting from a random configuration of actin filaments at time t = 0, the myosin II motors walk along the actin filaments, actively rearranging the network and developing traction forces on the boundary springs. B: the total traction force corresponding to the networks shown in A. C: change in stiffness of the network as it develops traction. The ratcheting motion of the myosin crosslinks leads to decrease in length of actin filaments that carry tension; therefore the network also gets stiffer as the network develop tension. D: the change in network stiffness is plotted against the change in traction force developed by nine different networks with different initial configuration at time t = 0. When the network develops internal tension, the changes in stiffness and traction are highly correlated.

Influence of substrate stiffness.

Cells are known to modulate their prestress and traction force in response to changes in substrate stiffness (78). For a given cell type, changes in traction force can be divided into two regimes. In the first regime, the cell develops a traction force in proportion to the change in substrate stiffness for stiffness values below a threshold. Beyond this threshold, however, the traction force exerted by the cell remains largely insensitive to further changes in substrate stiffness (50). While experiments with blebbistatin have revealed that actin-myosin interactions are responsible for the generation of traction (46, 50), why the cell exhibits two regimes of behavior remains unexplained.

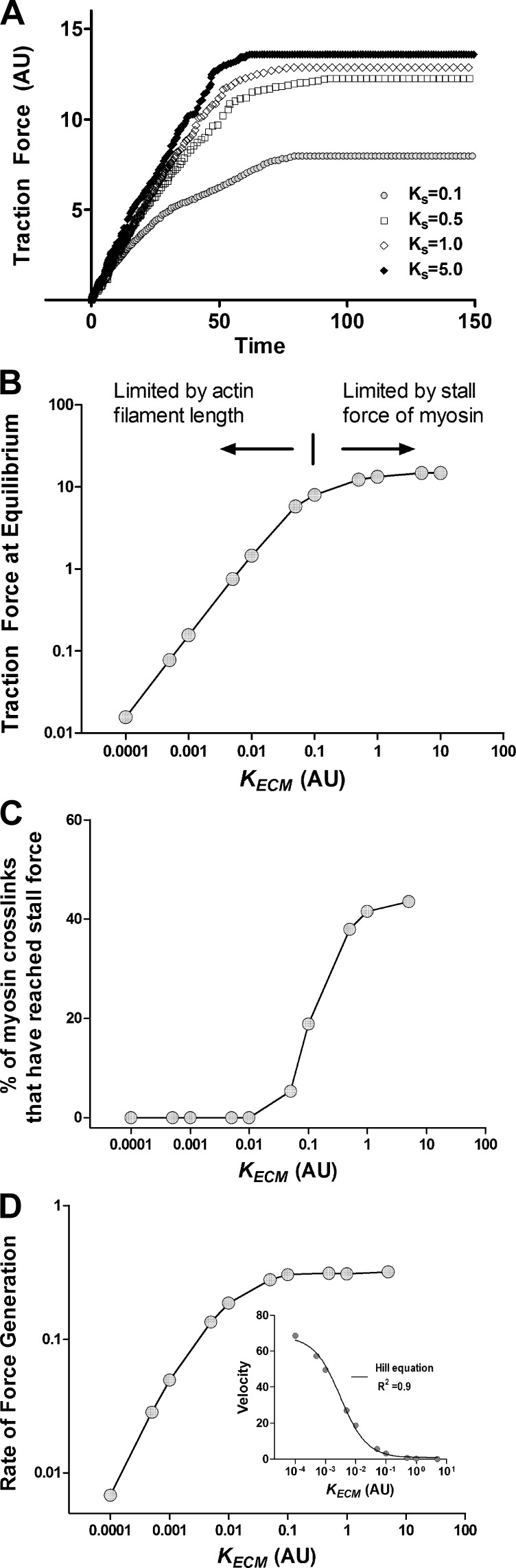
To investigate the response of our actin-myosin network model to changes in substrate stiffness, we vary the stiffness of the boundary springs (K_ECM) and allow the network to reach equilibrium starting from a random configuration. When the substrate stiffness is increased by a factor of 10, the equilibrium traction force increases too; however, the time to achieve equilibrium does not change (Fig. 3A), which is consistent with experimental data reported by Mitrossilis and colleagues (50). In Fig. 3B, we plot the equilibrium traction force achieved by the network for a range of substrate stiffness values spanning six orders of magnitude. We find that, just as in living cells, the response of this active network to changes in substrate stiffness is also characterized by two regimes. For low values of substrate stiffness, the traction force scales almost linearly with substrate stiffness up to a threshold value beyond which further increase in substrate stiffness has no effect on the traction force developed by the network.

Fig. 3.

A: increase in traction force when the substrate stiffness (K_ECM) is increased by 1 order of magnitude. The network develops a higher traction in stiffer substrates, but the time taken to reach equilibrium is almost the same in both cases. B: the maximum traction that a cell can develop scales linearly with substrate stiffness up to a threshold, beyond which the cell cannot generate additional traction. C shows the percentage of myosin crosslinks that carry stall force when the network has reached equilibrium. The two regimes of macroscopic scale behavior of the network traction force in response to changes in substrate stiffness result from different microscopic scale stopping conditions. D: substrate stiffness also modulates the rate at which the network can generate traction force. For low values of substrate stiffness, the rate of force generation also increases in response to an increase in substrate stiffness. In inset, we plot the rate at which the network is able to deform the substrate (velocity), as a function of the substrate stiffness. The solid line is a fit to the nonlinear Hill force-velocity curve empirically observed in muscle tissue strips, which relates the velocity V to the load against with the muscle constricts (in this case, the substrate stiffness, K_ECM) as (K_ECM + a)(V + b) = c, where a, b, and c are constants. Note that the x-axis (K_ECM) is plotted on a logarithmic scale as opposed to a linear scale as commonly plotted in experimental studies.

To understand the origin of this network response, we determine the number of crosslinks with a force larger than the stall force after the network has reached equilibrium for different values of substrate stiffness. We find that around the substrate stiffness that separates the two regimes, there is a sudden increase in the number of myosin crosslinks that have reached stall force. Thus the two regimes correspond to two different ways of the network reaching its equilibrium configuration. In the first regime, as the network develops tension, the substrate, which is very compliant, deforms and releases tension from myosin motors. Since the average distance available for a myosin motor to walk is limited by the size of the network, in the first regime, the myosin crosslinks never achieve stall force and stop only when they reach the positive (barbed) end of the actin filaments. However, in the second regime, the stiffer substrate does not deform as much and the myosin motors are able to reach stall force within the distance available for them to walk. Thus the mechanism by which cells develop tension and sense substrate stiffness is a network phenomenon that cannot be understood solely by considering molecular interactions of actin and myosin in isolation.

As noted in Fig. 3A, not only does the maximum traction force scale with substrate stiffness, but also the rate at which the network can develop traction also depends on the substrate stiffness. Indeed as shown in Fig. 3D, the rate of development of traction force also increases with substrate stiffness to a critical threshold beyond which it does not increase significantly in response to further changes in substrate stiffness. Mitrossilis et al. (50) examined experimentally this behavior in living cells and found that the rate of force development in response to a change in matrix stiffness followed the empirical Hill force-velocity relationship observed in muscle tissue strips (25), where the velocity of constriction was measured as the rate at which the cell deformed the substrate material. This was found to be true not only for muscle cells, but also for nonmuscle cell types, suggesting a common mechanism by which cells develop traction. As described in methods, an equivalent velocity can be calculated as V = dδ/dt, where δ is the average displacement of the substrate springs. The computed force-velocity curve (Fig. 3D, inset) is well described by a fit of the Hill equation: (K_ECM + a)(V + b) = c, where K_ECM is the stiffness of the substrate material and a, b, and c are constants (25). Huxley (29) explained the Hill force-velocity curve in the context of striated muscle. Given the new finding of Mitrossilis that even nonmuscle cells obey the Hill curve, it is not clear if the Huxley model can be applied to understand the behavior of nonmuscle cells. We find that our model of the cortical actin network is able to reproduce dynamics of shortening with no extra constraints or tuning. Thus mechanical interactions in the cortical actin network may be the reason why nonmuscle cells exhibit properties such as the Hill force-velocity curve, which was previously believed to be a unique property of muscle cells and tissues.

Effect of transient stretch.

Since our active network accounts for the dynamics of traction development and shortening velocity, we hypothesized that the model is also able reproduce the response of cells to transient changes in external mechanical environment. Two recent studies uncovered a novel response of living cells, called fluidization: when subjected to transient stretch using a single equibiaxial strain pulse lasting ∼4 s, cells promptly lose their traction and stiffness, followed by an ATP driven recovery phase, with larger stretches leading to larger drops in traction and a faster recovery rate (39, 71). Furthermore, the response to transient stretch was universal and not specific to cell type.

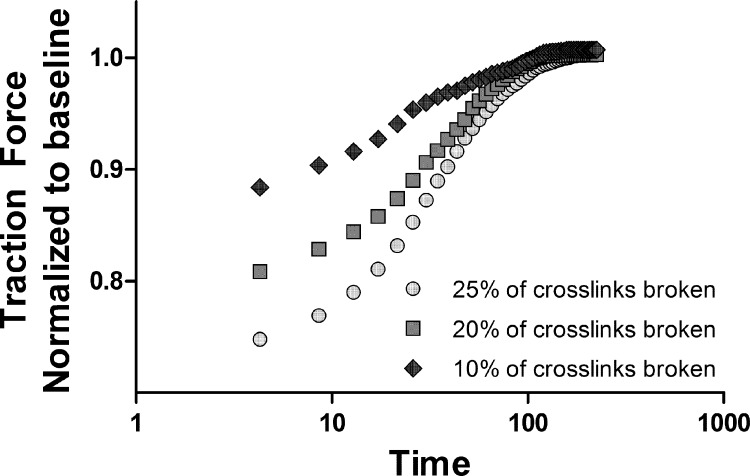
We test this hypothesis by considering a network configuration that has reached equilibrium in traction force. An externally applied stretch causes crosslinks with forces above the rupture threshold to detach (Fig. 4). The crosslinks that detach are then allowed to reattach at locations where the binding sites along two distinct actin filaments are closer than a threshold distance. The sudden drop in internal prestress releases the tension from the bound myosin crosslinks. These crosslinks, as well as the ones that newly attach to actin, can now walk and start rebuilding the traction force. Consistent with observed data in living cells (39), in our network model, the extent of decrease in traction force depends on the magnitude of the applied stretch, and the recovery to the baseline traction takes place in more or less the same time for different stretch magnitudes. Thus the same pre-stress-dependent mechanisms of network rearrangement that drive the recovery in traction following a change in substrate stiffness can also explain the amplitude-dependent decrease and recovery back to baseline following a transient stretch. It should be noted that our present model of force-dependent actomyosin interactions with an elastic network is consistent with the continuous-binding crosslinker model proposed by Donovan et al. (13) and is complementary to other proposed mechanisms such as force-dependent translocation of zyxin from the focal adhesions (11), which depends on the tension generated by the actin-myosin network.

Fig. 4.

Effect of a transient stretch applied at time t = 0 on the traction force exerted by the network. Following the stretch, rupture of crosslinks causes the traction to immediately decrease. The loss of traction is an increasing function of the amplitude of the stretch pulse. The loss of prestress causes the myosin motors to activate; the higher the amplitude of the stretch pulse, the faster the myosin motors walk. The characteristic time of recovery is related to the average distance that a typical myosin motor walks.

Effect of cyclic stretch.

Previous studies have shown that when subjected to cyclic stretch, both muscle and nonmuscle cell types show a substantial decline in traction force (14, 17, 43). The mechanisms that underlie the loss in traction due to cyclic stretch are currently not understood.

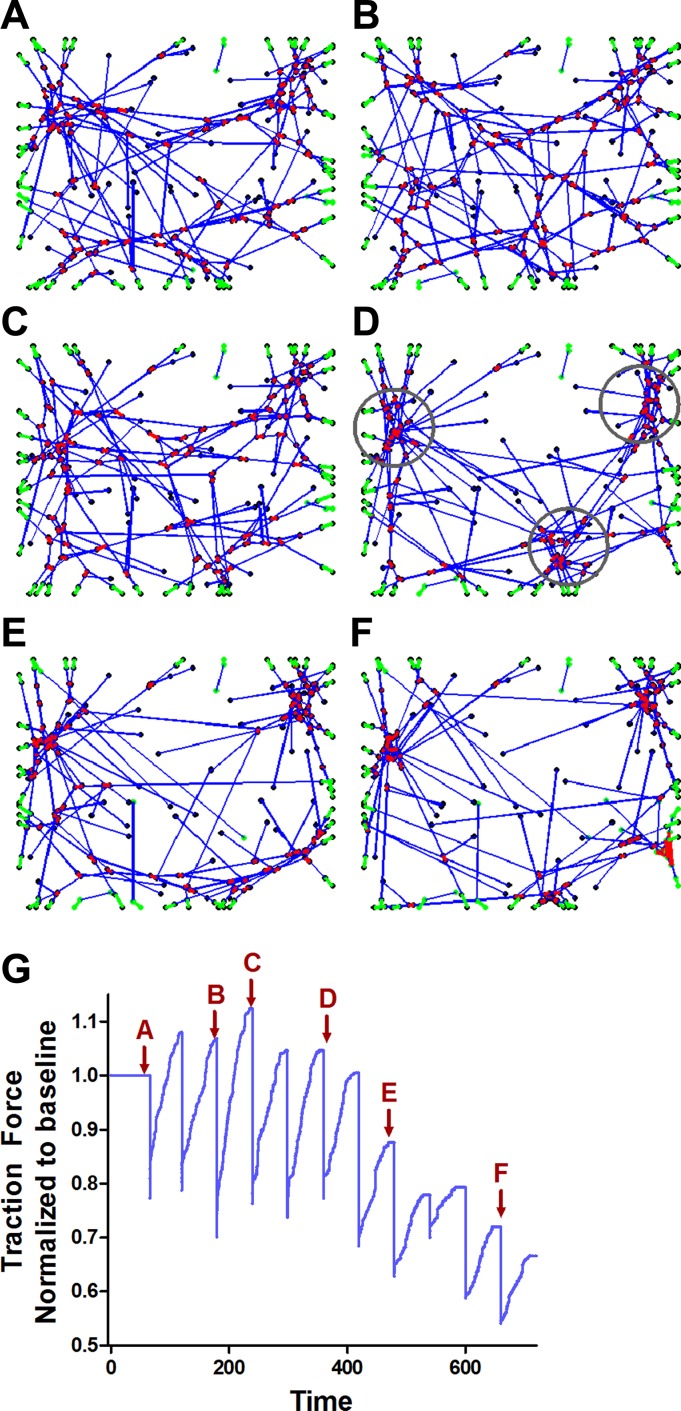
To understand the effect of repeated stretch patterns on our model, we started with a prestressed network (Fig. 5A) and subjected it to repeated equibiaxial strain pulse of the same amplitude every 60 s apart. In between the stretch pulses, the network was allowed to recover its force. The observed changes in the network structure are shown in Fig. 5, A–F, and the concurrent changes in network force are shown in Fig. 5G. The average drop in traction force after 10 stretch cycles (time point F in Fig. 5G) was 24 ± 4%. Concomitant with the changes in traction force, we find that over repeated stretch cycles, stable “star”-like junctions develop that persist through further stretch cycles. These star junctions are created by geometrical configurations in the network where the barbed (+ve) end of different actin filaments are brought together by myosin motors. The formation of star junctions is associated with a decline in network force because force generation depends on the ratcheting motion of myosin crosslinks along actin filaments, and when myosins reattach close to a star junction, the average distance available for a myosin crosslink to ratchet up an actin filament decreases, reducing the network force.

Fig. 5.

Starting from a prestressed network shown in A, the network is subjected to repeated equibiaxial strain pulses of the same amplitude every 60 s apart. In between the stretch pulses, the network was allowed to recover its force. A–F: over repeated stretch cycles, “star”-like junctions (circles in D) develop that persist through further stretch cycles. These star junctions are created by geometrical configurations in the network where the barbed (+ve) end of different actin filaments are brought together by myosin motors. G: the formation of star junctions is associated with a decline in network force. The red arrows correspond to the network configurations shown in A–F.

In a prestressed network at equilibrium, each individual motor can stop either because the force it carries has reached f_stall or because the myosin has walked all the way to the +ve end of the actin filament. In the latter case, the myosin carries lower force and is also under lower strain than a myosin that has reached f_stall. Thus myosins that have reached the +ve end of the actin filaments are less likely to rupture when the network is stretched and junctions persist over repeated stretches. Further, when a myosin crosslink ruptures it will more likely reform close to a junction simply because the star junction has several actin filaments (with binding sites for myosin) in close proximity to each other.

DISCUSSION

Dysfunction in the ability of the cell to sense and respond to mechanical stretch as has been shown to be a common factor in many pulmonary diseases (18, 28), cardiac and vascular diseases (63), renal and bowel disorders (58), as well as cancer cell growth (47), cancer cell invasion (48), and epithelial-to-mesenchymal transitions (23). However, the mechanisms that underlie the ability of the cell to sense and respond to stretch are still unclear. Several previous studies have examined this problem in the context of molecular signaling pathways triggered at the focal adhesions (59, 62). However, recent studies have shown that mechanosensory apparatuses of the cell are not simply localized to the focal adhesions; rather they involve large-scale interactions originating in the actin cytoskeletal network (50, 72).

Several previous studies have used computational modeling to show that myosin crosslinks can actively rearrange actin networks to form self-organized structures (41). Such networks of actin and myosin have been shown to have active contractility and viscoelastic properties consistent with those observed in living cells (35, 36, 76). Recent studies have also shown that actin-myosin networks plays an important role in sensing substrate stiffness (6). In this study, we investigated whether such networks can also explain the physical response of cells to mechanical stretch. To this end, we developed a simple network model of actin-myosin interactions and examined the effect of substrate stiffness and stretch on the ability of the network to modulate its tension and stiffness and compared our modeling results to experimental observations in living cells.

Understanding the mechanisms by which the cell responds to stretch is important especially in organs such as the lung, which is constantly subject to fluctuations in stretch due to tidal breathing. For instance, it has been shown that tidal breathing and especially tidal breathing at elevated minute ventilation antagonizes experimentally induced bronchoconstriction in normal animals and people (10). Disrupting the actin-myosin connectivity and reorganization of the actin-myosin contractile machinery has been proposed by Lavoie and colleagues (44) as a potential novel approach for preventing prolonged bronchoconstriction in asthma. Of particular importance is the fluidization experiment (Fig. 4) which mimics the effect of deep breaths on cell stiffness and traction (39, 57, 71). In this study, we propose a physical mechanism for the response of cells to a single transient stretch (39, 71). When subjected to a transient pulse in stretch, local ruptures occur in the actin-myosin network, thereby reducing the prestress in the network. When the prestress reduces, the myosin II motors activate and start to rearrange the configuration of the network, and this process increases the traction and stiffness of the network. The greater the loss in prestress, the faster the motors will walk. This leads to a faster rate of recovery of stiffness for larger-amplitude transient stretches. All recovery curves converge in the same time, and this is related to the average distance that a motor walks in the network, which is approximately the same for a given network size. In other words, the motors walk approximately the same distance but at velocities that are linked to the prestress in the network.

The active rearrangement of actin by myosin is not the only possible explanation for the experimental observations considered here. An alternative explanation based on dynamic changes in focal adhesion stiffness is feasible. However, while the size of, shape of, and stress on focal adhesions are known to be highly dynamic (68), there are no experimental measurements of the stiffness of focal adhesions (or whether it might vary with stretch or ECM stiffness). For this reason, we have only considered static boundary conditions. Further, given the critical role of actin binding and internal force provided by actin myosin activity in the formation of focal adhesion (45, 80), it is unlikely that these explanations are independent from the mechanisms considered here. It should be also be noted that our present model is consistent with the continuous-binding crosslinker model proposed by Donovan et al. (13) and the force-dependent translocation of zyxin from the focal adhesions (11), which depends on the tension generated by the actin myosin network.

An important mechanism that is not accounted for by the model is the dynamics of actin polymerization in the cell cortex, where actin has been reported to turn over with a half-life of 20–25 s (52). However, it is difficult to translate the observed actin turnover rates into rate of change of stiffness or traction forces using a computational model as the turnover of actin is influenced by a multitude of proteins, which cap, sever, depolymerize, polymerize, or crosslink the cortical actin network(19). At present, there is not enough information on the effect of stretch on all these processes to reliably account for this in our model. Tinevez et al. (70) showed that tension in the cortex of an unstretched cell can be modulated by altering the level of proteins that regulate actin depolymerization such as gelsolin and actin depolymerizing factor (ADF)/cofilin. The same study also reported myosin-inhibitory experiments that showed a very significant, systematic decrease in tension with myosin inhibitor dosage. Clearly, both these processes act in conjunction to regulate tension in the resting cell. However, the relative importance of myosin activity vs. actin polymerization/depolymerization on force and stiffness of the cell is not clear.

Biochemical signaling also plays a critical role in the response of the cell to stretch and substrate stiffness. Integrins have been shown to act as mechanosensors with the cytoplasmic domain of β-integrin, which interacts with focal adhesion kinase, which in turn interacts with other signaling molecules to trigger many downstream signaling cascades (21, 62). Mechanical forces can also directly cause the activation of ion channels and be felt by the nucleus through the cytoskeleton. Thus forces can directly alter gene expression within seconds to minutes following mechanical perturbation (30). Forces transferred via the cytoskeleton can also cause nuclear pores to open and affect the posttranscriptional control of gene expression (75). Indeed, the mechanisms based on the actin-myosin network presented here are only one part of a complex mechanosensing and response machinery in the cell and act in conjunction with these already established molecular signaling pathways that have important mechanosensory roles (21).

Our simple network model is able to replicate the following important experimental observations reported in living cells. 1) The network actively adjusts its tension in response to a change in substrate stiffness K_ECM up to a critical value beyond which the network tension becomes insensitive to further increases in K_ECM (50, 79). 2) The rate of development of traction by the network is dependent on K_ECM and is consistent with the Hill force-velocity equation (50). 3) The development of traction force and development of cell stiffness are highly correlated processes (11, 27). 4) When subjected to a transient stretch, cells promptly lose their traction force and stiffness in a stretch-dependent manner followed by a slow recovery back to their baseline mechanical state. While the loss in traction and stiffness are stretch amplitude dependent, the time of recovery is the same, irrespective of the stretch amplitude. 5) This active network provides a physical basis for the experimental observation that cyclic stretching leads to a decline in traction force and stiffness (14, 17). To verify that our results were not due to the specific choice of parameters, we performed additional simulations in which we separately varied the stiffness of myosin relative to actin (K_M:K_A) by one order of magnitude from 0.4 to 4. The simulations in Figs. 2 and 3 were repeated, and the model showed a strong correlation between network force and stiffness as well as a two-regime traction force behavior identical to that in Fig. 3B. The simulations in Figs. 2 and 3 were also repeated after varying the concentration of actin to myosin (N_A:N_M) from 1:1 to 6:1 as reported in smooth muscle, and our results did not change. Therefore, structural reorganization of the actin cytoskeletal network by active crosslinkers could be a common pathway by which cells respond to both stretch and changes in substrate stiffness.

How is it that a simple mechanical model based purely on movement of myosin crosslinks rearranging an elastic actin network is able to reproduce the response of living cells to both stretch and substrate stiffness? Within a prestressed elastic network, the local force on a myosin crosslink is a function of the total prestress in the network and the configuration of the network. Therefore, the elastic network of actin allows interactions at two different length scales. At the microscale, the myosin motors are able to elastically interact with each other as they move along actin filaments and generate prestress in the network, and the macroscopic scale prestress feeds back to the individual myosin motors and regulates their movement. Thus the strong link between internal prestress associated with mechanical sensing and adaptation to stretch and changes in substrate stiffness are therefore emergent network phenomena that result from microscopic molecular processes attempting to maintain local force balance within a large elastic network in response to an external stimulus such as changes in ECM stiffness or stretch.

Of the many filamentous proteins that form networks within the cytoskeleton, we focused on actin networks because of the experimental observation that the recovery in stiffness of cells and the recovery in traction force are highly correlated (39). Active remodeling of the cytoskeleton was also observed concurrent with these changes (71). While the absolute stiffness is dependent on other filamentous proteins in the cytoskeleton such as microtubules and intermediate filaments as well as a multitude of crosslinking proteins (7, 20, 74), the correlation between the change in stiffness and change in traction force during recovery following a mechanical perturbation indicates that actin is the key contributor to the recovery process. Indeed, our model provides a simple explanation as to why stiffness and traction force should be correlated while the cell develops traction. The ratcheting motion of the myosin crosslinks leads to shorter filaments that carry an increased tension and hence the stiffness also increases as the network generates traction.

It has previously been noted by Bond and Somlyo (5) that polarity reversal of actin filaments occurs at the site of dense bodies in the smooth muscle cell and that this polarity reversal is an essential feature of the basic contractile unit in a vertebrate smooth muscle. Our network model does not present any contradiction with the Bond study. Even in the network, the basic principle is the same: force generation upon myosin movement depends on the polarity of the actin filaments and also how the actin is anchored. The key difference, however, is that the contractile machinery referred to in the Bond study is the parallel contractile array unique to the smooth muscle. The parallel array's structure (the parallel alignment of actin-myosin fibers as well as the polarity of actin referred to by Bond and Somlyo) makes it a perfect arrangement for directed force generation as seen in the smooth muscle. The structure is so set up that all myosin movement translates to force generation. The same is not true for the cortical actin because in this network, the actin can be found oriented randomly (except at the edges of an adherent cell where the actin is found in dendritic network structures). So, the cortical actin network can generate tension, but not as efficiently (not all myosin movement results in force generation) as the parallel contractile arrays found in muscle cell types.

The substrate springs that form the boundary conditions on our network represent the effective stiffness of the substrate material and the focal adhesions. While the size of, shape of, and stress on focal adhesions are known to be highly dynamic (68), there are no experimental measurements of the stiffness of focal adhesions (or whether it might vary with stretch or ECM stiffness). For this reason, we have only considered static boundary conditions. An alternative explanation of the experimental observations considered here based on dynamic changes in focal adhesion stiffness is feasible. However, given the critical role of actin binding and internal force provided by actin-myosin activity in the formation of focal adhesion (45, 80), it is unlikely that these explanations are independent from the mechanisms considered here.

During the initial development of the model, we also considered myofilament formation as this can affect both the distance walked per ATP cycle and the stiffness of the myosin. Implementing this in the model was extremely complicated because the extent to which myosin forms myofilaments is itself a dynamics process and depends on several factors which include intracellular levels of calcium (24), ATP (61), phosphorylation state (69), and also the presence of filament stabilizing proteins (42, 65). Unfortunately, even if we consider multiple studies, there is no conclusive set of experimental data available to reliably incorporate all these phenomena into our network model. Therefore, instead of adding additional complexity, we decided to examine the extent to which a model that does not include duty ratio and myofibril formation can replicate cellular level experiments. Indeed, comparing the present model to previous work by Borau et al. (6), despite significant differences in the details of the implementation at the molecular scale, there is a striking resemblance between the change in network stiffness and network force in response to changes in substrate stiffness shown in Fig. 3 and that reported by Borau et al. Therefore, between these two models, there is clear indication that the network phenomena that both studies replicate are more a function of the molecular interactions set up within the actin cytoskeleton and less dependent on the specific properties of the individual molecular components.

It should be noted that the present model cannot be used to match the absolute value of cell stiffness and traction, which depends on passive crosslinkers such as filamin as well as other cytoskeletal proteins like microtubules and intermediate filaments, which are not considered here (7, 20, 74). In addition, as mentioned above, there is no experimental measurement of focal adhesion stiffness. Therefore, we have not attempted to scale the substrate stiffness or forces in our model to real units. The model can only be used to examine the change in force and stiffness following stretch or change in substrate stiffness, but the absolute value of stiffness or force is difficult to specify without additional experimental details at the molecular level.

There is substantial evidence that cyclic stretch of the underlying matrix leads to a decrease in force and stiffness of adherent cells (14, 17). Upon cyclically stretching our network, we find that the network force also reduces over multiple stretch cycles. In our model, this happens due to the reorganization of the network structure to form clusters or “star” junctions as a consequence of the repeated bond rupture followed by reattachment and recovery in each stretch cycle. These star junctions, which can be seen in the geodesic dome architecture commonly used in tensegrity models (31) and also in the cytoskeletal structure of cells stained for actin (15, 31, 67), form when the barbed end of many actin filaments are brought together by myosin activity. The same phenomenon has been observed in active gels of actin and myosin crosslinks (4) and also predicted in other actin-myosin network models (76). The relative influence of stretch-induced actin polymerization (24, 34) on the formation of actin structures predicted in Fig. 5 is presently unclear. Although there is some evidence of such structures forming in the actin cytoskeleton of epithelial cells subjected to equibiaxial stretch (11), it is not conclusive, and the formation of these star junctions due to repeated stretches remains a prediction of the model.

A commonly reported feature of cytoskeletal remodeling with change in substrate stiffness is the formation of polarized bundles of actin commonly referred to as stress fibers. The absence of stress fibers in our model should not be a limitation for the present study. Here, we focused on the recovery in traction force and cell stiffness following the application of transient stretch or change in substrate stiffness, both of which achieve equilibrium in ∼100 s. In a recent study, Aratyn-Schaus et al. (2) showed that within this time frame, substantial traction is exerted prior to stress fiber formation. Thus the major pre-stress-bearing structure within the time frame we consider here is a network and not stress fibers. Furthermore, while stress fibers do not form on cells plated in soft substrates, cells do develop traction forces within the time frame considered here. Conversely, as we do not consider them, our model cannot explain cellular phenomena that depend on stress fibers such as shape changes in cells with substrate stiffness (81).

Signaling in the cell has traditionally been viewed as solution chemistry. However, our results suggest that mechanosensing and the response of the cell to alterations in its mechanical environment should be considered a network phenomenon. An important application of these ideas could be to study the force-dependent binding kinetics of downstream proteins in mechanotransduction pathways. By being able to predict changes in cytoskeletal geometry in response to stretch, it is possible to study the spatial variability of biochemical reactions whose kinetics are dependent on the local forces on cytoskeletal elements in the cell. Therefore, the principles of actin network reorganization presented here may be able to provide more insight into how mechanotransduction is coordinated spatially and temporally within the cell.

GRANTS

This work was supported by National Heart, Lung, and Blood Institute Grants RO1 HL-098976 and HL-096797.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: H.P. conception and design of research; H.P. designed and implemented the computational model; H.P., K.R.L., and B.S. analyzed data; H.P. interpreted results of experiments; H.P. prepared figures; H.P., K.R.L., and B.S. drafted manuscript; H.P., K.R.L., and B.S. edited and revised manuscript; H.P., K.R.L., and B.S. approved final version of manuscript.