Transductive Neural Decoding for Unsorted Neuronal Spikes of Rat Hippocampus

Abstract

Neural decoding is an important approach for extracting information from population codes. We previously proposed a novel transductive neural decoding paradigm and applied it to reconstruct the rat’s position during navigation based on unsorted rat hippocampal ensemble spiking activity. Here, we investigate several important technical issues of this new paradigm using one data set of one animal. Several extensions of our decoding method are discussed.

I. INTRODUCTION

Neural decoding, as an inverse problem to neural encoding analysis, aims to infer sensory stimuli or motor kinematics based on recorded ensemble neuronal spiking activity. Neural decoding is important not only for understanding neural codes (i.e., neural response features capable of representing all information that neurons carry about the stimuli of interest), but also for extracting maximal information from population neurons in engineering applications, such as brain-machine interfaces [13]. Traditional neural decoding methods based on spiking activity [3], [21], [20], [12] rely on spike sorting, a process that is computationally expensive, time-consuming, and prone to errors [8], [18], [19]. To overcome this drawback, we have proposed a novel transductive neural decoding paradigm and applied it to unsorted rat hippocampal population codes [10].¹ Unlike traditional neural encoding/decoding methods, the proposed paradigm does not require estimating tuning curves (TCs) for individual sorted single units. Our paradigm is also different from other spike-sorting-free decoding methods in the literature [6], [17] in that spike waveform features are used in decoding analysis.

In this paper, we first briefly review the transductive, spike sorting-free decoding method [10], before discussing in greater detail several technical issues related to application of the method to neural data. Next, we discuss extensions to the proposed method. From an information-theoretic perspective, we also propose a practical way to assess the mutual information between sensory stimuli and neural spiking responses, which are mathematically characterized by a spatio-temporal Poisson process (STPP).

II. METHOD: TRANSDUCTIVE NEURAL DECODING

The basic idea of transductive neural decoding described in [10] is to model ensemble neuronal spiking activity as a spatio-temporal point process [15], in which the timing of spike events is defined with a random measure in time, and the “mark” associated with the spike events is defined with another random measure in real space.

A. Spatio-temporal Poisson Process (STPP)

Let us consider a STPP, which is the simplest spatio-temporal point process in which events are independent in time. Let λ(t, a) denote the rate function, and a ∈ S (where S is a vector space). For any subset S_j ∈ S in the space, the number of the events occurring inside the region is also a temporal Poisson process with associate rate function λ_Sj(t):

$${\lambda }_{S_j}\left(t\right)={\int }_{S_j}\lambda (t,\mathbf{a})\mathrm{d}\mathbf{a},\text{and}{\lambda }_S\left(t\right)={\int }_S\lambda (t,\mathbf{a})\mathrm{d}\mathbf{a}.$$ (1)

The expected number of events in any spatio-temporal region is also Poisson distributed with the mean rate given by

$$\mu =\frac{1}{T}{\int }_0^T{\int }_S\lambda (t,\mathbf{a})\mathrm{d}\mathbf{a}\mathrm{d}t={\int }_0^T{\lambda }_S\left(t\right)\mathrm{d}t.$$ (2)

In the special case where the generalized rate function is a separable function of space and time such that

$$\lambda (t,\mathbf{a})={\lambda }_S\left(t\right)p\left(\mathbf{a}\right),$$ (3)

where p(a) represents the spatial probability density function (pdf) of the random variable a, and ${\int }_{S}p\left(\mathbf{a}\right)\mathrm{d}\mathbf{a}=1$. The interpretation of the separable STPP is as follows: To generate random Poisson events in space-time, the first step is to sample a Poisson process with a rate function λ_S(t), and the second step, is to draw a random vector a (associated with each event) from p(a). Therefore, the spatio-temporal point process may be viewed as a purely temporal marked point process, with spatial marks at each time point of event occurrence from the ground process, and the marked space is defined by a random probability measure [15]. Detailed technical backgrounds are referred to [10].

B. Bayesian Decoding

In the context of neural decoding, let random variable a ≡ {a₁, … a_d} ∈ ℝ^d denote the measured d-dimensional feature extracted from the spike waveform (e.g., peak amplitude, waveform derivative, principal components, or any features that are used in spike sorting process), let x ∈ ℝ^q denote the sensory stimulus or motor covariate (such as the animal’s position, head direction, velocity, etc.) that is being decoded. Furthermore, let n denote the number of spike events in the complete d-dimensional space within a time interval [t, t + Δt), and let a_1:n denote the associated n d-dimensional spike waveform features. The d-dimensional feature space is divided evenly into J non-overlapping regions S ≡ (S₁ ∪ S₂ … ∪ S_J), and a_1:n ∈ S.

To infer the probability of the unknown variable of interest x_t at time t, we resort to the Bayes rule

$$P({\mathbf{x}}_t\mid {\mathbf{a}}_{1:n})=\frac{P({\mathbf{a}}_{1:n}\mid {\mathbf{x}}_t)P\left({\mathbf{x}}_t\right)}{P\left({\mathbf{a}}_{1:n}\right)}$$ (4)

where P(x_t) denotes the prior probability, P(a_1:n|x_t) denotes the likelihood, and the denominator denotes a normalizing constant. Provided that a non-informative temporal prior for P(x_t) is used (for this reason, from now on we will drop the subscript t on x_t; the extension of using a temporal prior is discussed later), then Bayesian decoding is aimed to maximize the product of the likelihood and spatial prior P(x):

$$P(\mathbf{x}\mid {\mathbf{a}}_{1:n})\propto P({\mathbf{a}}_{1:n}\mid \mathbf{x})P\left(\mathbf{x}\right)$$ (5)

To compute the likelihood, we assume that the spike events follow a time-homogeneous STPP with a generalized rate function λ(a, x). It follows that the number of events occurring within a time window [t, t + Δt) and subregion S_j in the d-dimensional spike feature space also follows a Poisson distribution with the rate function ${\lambda }_{\Delta t,S_j}\left(\mathbf{x}\right)=\Delta t{\int }_{S_j}\lambda \left(a,x\right)\mathrm{d}\mathbf{a}$, which can be viewed as a spatial TC with respect to the covariate space x. By dividing the spike feature space into J non-overlapping spatial subregions $S\equiv {\cup }_{j=1}^J{S}_j$, we can factorize the likelihood function into a product of Poisson likelihoods of all J subregions

$$P({\mathbf{a}}_{1:n}\mid \mathbf{x})=\prod _{j=1}^{J}Poisson(n\left(S_j\right);{\lambda }_{\Delta t,S_j}\left(\mathbf{x}\right))=\frac{\left[\prod _{j=1}^J{\left(\Delta t{\int }_{S_j}\lambda (\mathbf{a},\mathbf{x})\mathrm{d}\mathbf{a}\right)}^{n\left(S_j\right)}\right]\left[e^{-\Delta t\sum _{j=1}^J{\int }_{S_j}\lambda (\mathbf{a},\mathbf{x})\mathrm{d}\mathbf{a}}\right]}{\prod _{j=1}^{J}n\left(S_j\right)!}$$ (6)

where n(S_j) denotes the number of spike events within the region S_j. In the limiting case when the subregion becomes sufficiently small such that n(S_j) is equal to 0 or 1 within the time interval Δt, simplifying (6) and replacing it into (5) yields the posterior

$$P(\mathbf{x}\mid {\mathbf{a}}_{1:n})\propto \prod _{i=1}^n\lambda ({\mathbf{a}}_i,\mathbf{x})e^{-\Delta t\lambda \left(\mathbf{x}\right)}P\left(\mathbf{x}\right)$$ (7)

where λ(x) denotes the rate of spike events occurring in the covariate space x.

To compute (7), we need to compute or establish a representation for the generalized rate function λ(a, x) and its marginal rate function λ(x). In practice, these rate functions are estimated a priori by recording spike events and their associated features while sampling over the covariate space. Note that the generalized rate function used in (6) can be written as

$$\lambda \left(a,x\right)=\frac{\#spikes\left(a,x\right)}{occupancy\left(\mathbf{x}\right)}=\frac{N}{T}\frac{p\left(a,x\right)}{\pi \left(\mathbf{x}\right)}=\mu \frac{p\left(a,x\right)}{\pi \left(\mathbf{x}\right)}$$ (8)

where N denotes the total number of spike events recorded within time interval (0, T], μ is the mean spiking rate defined in (2), π(x) denotes the occupancy probability of x during the complete time interval, and p(a, x) denotes the joint pdf of a and x. Furthermore, we have $\lambda \left(\mathbf{x}\right)=\mu \frac{p\left(\mathbf{x}\right)}{\pi \left(\mathbf{x}\right)}$, and $\lambda \left(a,x\right)=\lambda \left(\mathbf{x}\right)\frac{p\left(a,x\right)}{p\left(\mathbf{x}\right)}=\lambda \left(\mathbf{x}\right)p(\mathbf{a}\mid \mathbf{x})$, where p(a|x) denotes the conditional pdf.

In the decoding phase, in order to compute the likelihood (6), we would need to evaluate the target point in the functions λ(a, x) and λ(x), or equivalently in p(a, x) and p(x). Finally, to choose the maximum a posteriori (MAP) estimate of x, denoted by x_MAP we simply evaluate the log-posterior (7) among all candidates in the x space, and choose the one that has the highest value.

C. Density Estimation: Parametric vs. Nonparametric Methods

In our decoding paradigm, the essential task is to estimate the joint pdf p(a, x) and its marginal p(x). Multivariate density estimation has been well studied in statistics [14]. Common methods include (i) parametric approaches, which model the data by a finite mixture model (a process similar to spike sorting at the first place); and (ii) nonparametric approaches, such as the histogram or kernel density estimation (KDE). Parametric representation is compact but less flexible; nonparametric approaches are model-free but more computationally expensive.

We investigate two methods here: one is based on an ℓ-mixtures of Gaussians (MoG) model, another based on Gaussian KDE, using a non-isotropic multivariate Gaussian kernel K

$$p(a,x)=\sum _{r=1}^{\ell }{\pi }_{r}K({\mathbf{m}}_r;{\mathbf{H}}_r)$$ (9)

$$p(a,x)=\frac{1}{M{\sigma }_1\dots {\sigma }_m{h}_1\dots h_q}\sum _{m=1}^M\prod _{i=1}^{d}K\left(\frac{a_i-{\tilde{a}}_{i,m}}{{\sigma }_i}\right)\times \prod _{j=1}^{q}K\left(\frac{x_j-{\tilde{x}}_{j,m}}{h_j}\right)$$ (10)

where ${\sum }_{r=1}^{\ell }{\pi }_r=1$, (m_r, H_r) denote the r-th mean vector and diagonal (yet non-isotropic) covariance matrix, respectively, in the mixture model for the augmented vector $\mathbf{Z}=\left(a,x\right);\{{\tilde{\mathbf{a}}}_m,{\tilde{\mathbf{x}}}_m\}$ denotes the m-th source data point from the training set, and σ_i and h_j denote the kernel bandwidth (BW) parameters for the i-th and j-th element in a and x, respectively.

For the MoG model, the unknown parameters ${\{{\pi }_r,{\mathbf{m}}_r,{\mathbf{H}}_r\}}_{r=1}^{\ell }$ are estimated from the expectation-maximization (EM) algorithm. For the KDE, the BW parameters are estimated from [2].

III. MUTUAL INFORMATION BETWEEN STIMULUS AND NEURAL RESPONSES

Let X denote the sensory stimuli, and let R denote the raw neuronal responses (spike waveform). Any feature extraction from raw data (such as spike count, PCA) can be modeled as a generic nonlinear function f. According to the Data Processing Inequality, post-processing of R never increases the mutual information between X and R [13]

$$I(X;f\left(R\right))\le I(X;R)$$ (11)

This inequality is also applicable to spike sorting. In comparison to spike sorting-based decoding, spike sorting-free decoding sidesteps the sorting (clustering) process and reduces information loss, and prevents accumulating sorting error into decoding analysis.

The mutual information between the sensory input x and spike waveform features a is written as [4]

$$I\left(x;a\right)=H\left(\mathbf{x}\right)+H\left(\mathbf{a}\right)-H\left(a,x\right)$$ (12)

where the marginal and joint entropy functions can be estimated from KDE. For instance, given the multivariate kernel density estimator of an unknown pdf p(x), a simple plug-in resubstitution estimator for differential entropy can be written as [1]: $\widehat{H}\left(\mathbf{x}\right)=-\frac{1}{M}{\sum }_{m=1}^M\text{log}{\widehat{p}}_M\left({\mathbf{x}}_m\right)$, where ${\widehat{p}}_M\left(\mathbf{x}\right)$ denotes a kernel density estimator based on M data samples.

In the presence of multi-electrode recording, given the spike waveform feature (a₁, …, a_ℓ) from ℓ electrodes, the mutual information is given by [4]

$$\begin{array}{cc}\hfill I(\mathbf{x};{\mathbf{a}}_1,\dots ,{\mathbf{a}}_{\ell })& =H({\mathbf{a}}_1,\dots ,{\mathbf{a}}_{\ell })-H({\mathbf{a}}_1,\dots ,{\mathbf{a}}_{\ell }\mid \mathbf{x})\hfill \\ \hfill & =H({\mathbf{a}}_1,\dots ,{\mathbf{a}}_{\ell })-\sum _{r=1}^{\ell }H({\mathbf{a}}_r\mid \mathbf{x})\hfill \\ \hfill & =H({\mathbf{a}}_1,\dots ,{\mathbf{a}}_{\ell })+\sum _{r=1}^{\ell }\left[H\left(\mathbf{x}\right)-H({\mathbf{a}}_r,\mathbf{x})\right]\hfill \end{array}$$ (13)

where the second step follows from the conditional independence assumption between the covariate x and the neural response a_r from each electrode. The conditional entropy H(a_r|x) = H(x) − H(a_r, x) can be estimated directly from KDE, and the joint entropy H(a₁, …, a_ℓ) may be estimated with a resampling method.

IV. RESULTS: POSITION RECONSTRUCTION WITH UNSORTED RAT HIPPOCAMPAL ENSEMBLE SPIKING ACTIVITY

A. Experimental Data

For experimental protocol and details, the reader is referred to [10]. Animals were traveling in a 3.1-m linear track environment, which was binned with 0.1-m bin size resulting in 31 position bins. Simultaneous tetrode recordings were collected from the CA1 area of rat hippocampus. In each recording recording session, the waveforms of all unsorted spikes were re-thresholded at 75 μV. Next, for unsorted spike events, the spikes with a peak to trough width of greater than 150 μs are considered as originating from pyramidal cells and are included in the decoding analysis. For each tetrode, the peak amplitudes from 4 channels are used to construct a ∈ ℝ⁴ (see the left panel of Fig. 1 for illustration). In one selected data set studied here, we collect 48 putative pyramidal cells from 18 tetrodes within about 30-min recordings. The first half of the data is used as the training set. The temporal bin size is chosen as Δt = 250 ms, and only run periods (velocity filter 0.15 m/s) are chosen in encoding and decoding analyses. The decoding error is defined as |x_true − x_MAP| (x ∈ ℝ) for each temporal bin.

Fig. 1.

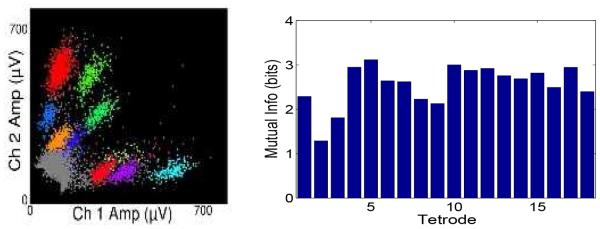
Left: Raw spike amplitudes from one tetrode (shown in 2 channels). Right: Estimated mutual information (bits) between the position (x) and spike amplitude (a) in each tetrode (computed from Eq. 12); note that they are all bounded by the entropy of stimulus (3.36 bits).

B. Experimental Results

1) Transductive Decoding with Sorted vs. All Spikes

For the selected data set, we show the number of spikes per tetrode based on sorted (10664) spikes or all recorded (39383) spikes (Fig. 2, left panel). As seen, nearly 73% recorded spikes are discarded in spike sorting. Potentially, many non-clusterable spikes contain tuning information; and traditional spike sorting-based decoding methods may suffer an information loss by discarding those spikes. The decoding error cumulative distribution function (cdf) curve (Fig. 2, right panel) indicates a statistically significant improvement in decoding accuracy (two-sample KS test: P < 0.001). The median (mean) statistics of decoding error are 0.1111 (0.1920) m for using all spikes, and 0.1172 (0.2051) m for using only sorted spikes. This result also confirms our previous finding [10].

Fig. 2.

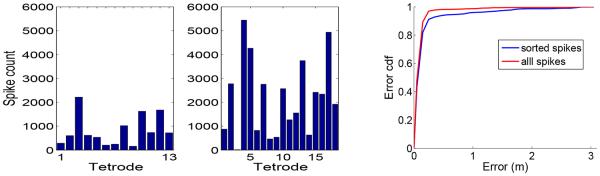
Left: Numbers of spike counts per tetrode for sorted vs. all spikes. Right: Decoding error cdf curves from using sorted and all spikes.

2) Parametric vs. Nonparametric Density Estimation

Next, we compare two density estimators (Eqs. 9 and 10) in our proposed transductive neural decoding paradigm. For the nonparmetric method, we use Gaussian KDE with non-isotropic BW parameters. For the parametric method, we use various numbers (4, 6, 8, 10, 12) of MoG for each tetrode, resulting in a maximum of 216 multivariate Gaussians for 18 tetrodes. Note that using a Gaussian mixture for density estimation is in spirit similar to the clustering process during spike sorting, except that we estimate (a, x) jointly (instead of a alone in spike sorting), and that the spread of the kernels is allowed to be overlapping (without making hard decisions). The decoding results are shown in Fig. 3 (left panel). As seen, the decoding accuracy also improves as the number of the Gaussian mixtures increases. The nonparametric method has a better decoding performance due to its more accurate representation of the density. Besides, for the decoding purpose, a local density representation is more preferable to a global characterization.

Fig. 3.

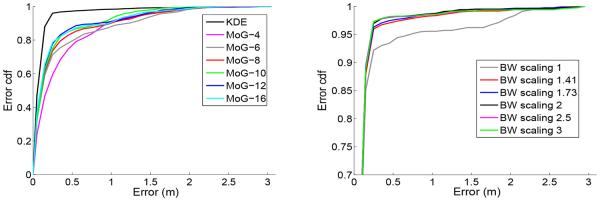
Decoding error cdf curves from both mixtures of Gaussians (MoG) and KDE methods (left), and from using various BW scalings (right).

3) Reduction of Source Samples

In KDE representation, the density is represented by M source data points (at one electrode). Obviously, the storage requirement and computational complexity of decoding is linearly proportional to M. To reduce the computational burden, we attempt to reduce the source samples by two methods. The first method uses a higher threshold (in our case, greater than 75 μV) to exclude low-amplitude spike events. Generally, the low-amplitude spikes have less recoverable information of the stimulus. The second method aims to compress source samples using some computational methods [11], [7], [9]. Here we use a computationally efficient KD-tree method (http://www.ics.uci.edu/~ihler/code/kde.html).

The results of the decoding error statistics are summarized in Table I. As seen from the mean/median error statistics, the decoding accuracy degrades while using a very high threshold; however, better performance can also be expected using a slightly higher threshold (e.g., 100 μV). On the other hand, reducing source sample size using a computational method always degrades decoding accuracy, regardless of the data source (sorted spikes or all spikes).

TABLE I.

STATISTICS OF THE MEAN/MEDIAN DECODING ERROR (UNIT: METER) USING VARIOUS THRESHOLDS OR VARIOUS COMPRESSED SAMPLE SIZE M FOR OUR TRANSDUCTIVE AMPLITUDE-BASED DECODING.

threshold (μV)	sorted spikes	all spikes
100	0.2056/0.1159	0.1928/0.1009
125	0.2174/0.1176	0.2057/0.1116
150	0.2347/0.1197	0.2132/0.1154
M (per tetrode)	sorted spikes	all spikes
500	0.4536/0.1876	N/A
1000	0.3283/0.1307	N/A
2000	0.2444/0.1194	0.5642/0.1598
3000	0.2051/0.1172	0.3960/0.1279
ALL data	0.2051/0.1172	0.1920/0.1111

4) Scaling the BW Parameters

In the presence of noisy spikes (in the low-amplitude space), it is common to use a larger kernel BW to smooth the noise-contaminated samples. To test this idea, we fix the position BW (0.05 m) and scale the initial amplitude BW (estimated from [2]) by different scalars $(\sqrt{2},\sqrt{3},2,2.5,3)$ in all four dimensions. The decoding error cdf curves are shown in Fig. 3 (right panel). For this data set, the optimal scaling parameter is 2, achieving the median (mean) decoding error of 0.1043 (0.1346) m. Note that the mean decoding error is greatly reduced.

V. DISCUSSION

A. Curse of Dimensionality

In a general setting, the dimensionality of the covariate space can be very large: either q is large, or the range for individual univariate dimension is large (with a relatively small bin size). For MAP estimation, a naive even binning of the covariate space can be extremely inefficient, since the occupancy density π(x) may be very sparse. To tackle the “curse of dimensionality” problem, we may use a divide-and-conquer approach by constructing q independent decoders, each one equipped with its own density estimator. Another way is to use informative cues to draw candidate samples from an informative covariate space (an idea similar to importance sampling) [5]. Here we discuss two sampling approaches.

1) Sampling from a Temporal Prior

Within the state-space framework, we can sample the current covariate x from a transition prior of the covariate at the previous discrete time step [3], [21]:

$$P\left({\mathbf{x}}_t\right)=\int p({\mathbf{x}}_t,{\mathbf{x}}_{t-1}){\mathbf{dx}}_{t-1}=\int p({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1})p\left({\mathbf{x}}_{t-1}\right)\mathrm{d}{\mathbf{x}}_{t-1}$$ (14)

where p(x_t|x_t−1) denotes a transition probability density. The posterior can be estimated used a recursive Bayesian filtering rule (for notation simplicity, we have ignored the subscript _1:n for a)

$$\begin{array}{cc}\hfill P({\mathbf{x}}_t\mid {\mathbf{a}}_{1:t})& =\frac{P({\mathbf{x}}_t,{\mathbf{a}}_{1:t})}{P\left({\mathbf{a}}_{1:t}\right)}=\frac{P({\mathbf{x}}_t,{\mathbf{a}}_{1:t}\mid {\mathbf{a}}_{1:t-1})P\left({\mathbf{a}}_{1:t-1}\right)}{P({\mathbf{a}}_t\mid {\mathbf{a}}_{1:t-1})P\left({\mathbf{a}}_{1:t-1}\right)}\hfill \\ \hfill & =\frac{P({\mathbf{x}}_t\mid {\mathbf{a}}_{1:t-1})P({\mathbf{a}}_t\mid {\mathbf{x}}_t,{\mathbf{a}}_{1:t-1})}{P({\mathbf{a}}_t\mid {\mathbf{a}}_{1:t-1})}\hfill \end{array}$$ (15)

where P(a_t|x_t, a_1:t−1) = P(a_t|x_t) (because of the statistical independence between a_t and a_1:t−1 in the spike waveform feature space) denotes the data likelihood at the t-th time step.

2) Kernel Regression

Since at every time step t, we observe the current spike waveform feature a_t; ideally, the candidate sample is drawn from the mode of the posterior P(x|a_t). However, searching for the mode in a high-dimensional covariate space is a very challenging problem. Instead, we can search for the mean in the sample space, which may be computed by a continuous multi-input multi-ouput mapping through nonparametric regression x = g(a), where g(·) is a locally smooth multivariate function

$$\mathbf{g}\left(\mathbf{a}\right)={\mathbb{𝔼}}_{\mathbf{x}\mid \mathbf{a}}\left[\mathbf{x}\right]=\int \mathbf{x}P(\mathbf{x}\mid \mathbf{a})\mathrm{d}\mathbf{x}=\frac{\sum _{m=1}^M{\tilde{\mathbf{x}}}_{m}K\left(\frac{\mathbf{a}-{\tilde{\mathbf{a}}}_m}{\sigma }\right)}{\sum _{m=1}^{M}K\left(\frac{\mathbf{a}-{\tilde{\mathbf{a}}}_m}{\sigma }\right)}$$ (16)

Eq. (16) is known as Nadaraya-Watson kernel regression. However, in the presence of noisy spikes and multi-modes in P(x|a), this scheme might not be effective. Alternatively, we may draw candidate samples from P(a|x) using an auxiliary variable [5].

B. Other Issues

Several remaining issues are worth mentioning. First, region-dependent kernel BW parameters can be considered in KDE. For instance, in the low spike-amplitude space, we may use a small BW for the dense noisy spikes, while a large BW is preferred in the median-to-high amplitude space. In addition, finding a meaningful representation of the feature (e.g., by nonlinear transformation) and selecting an appropriate kernel function (in either parametric or nonparametric density estimation) would help separate different feature clusters and improve the decoding accuracy. Second, we have assumed that each sample point contributes equally in KDE. Alternatively, samples can be merged (according to certain similarity measure) and assigned with unequal weights [22], which also helps reduce the sample size.

All of above-mentioned topics will be the subject of our future decoding analysis investigation, using recordings not only from the rat hippocampus, but also from other brain regions (e.g., primate primary motor cortex). In addition, real-time implementations of our transductive neural decoding paradigm using online (parametric or nonparametric) density estimation is currently under investigation.