Scaling laws of ambush predator ‘waiting’ behaviour are tuned to a common ecology

Abstract

The decisions animals make about how long to wait between activities can determine the success of diverse behaviours such as foraging, group formation or risk avoidance. Remarkably, for diverse animal species, including humans, spontaneous patterns of waiting times show random ‘burstiness’ that appears scale-invariant across a broad set of scales. However, a general theory linking this phenomenon across the animal kingdom currently lacks an ecological basis. Here, we demonstrate from tracking the activities of 15 sympatric predator species (cephalopods, sharks, skates and teleosts) under natural and controlled conditions that bursty waiting times are an intrinsic spontaneous behaviour well approximated by heavy-tailed (power-law) models over data ranges up to four orders of magnitude. Scaling exponents quantifying ratios of frequent short to rare very long waits are species-specific, being determined by traits such as foraging mode (active versus ambush predation), body size and prey preference. A stochastic–deterministic decision model reproduced the empirical waiting time scaling and species-specific exponents, indicating that apparently complex scaling can emerge from simple decisions. Results indicate temporal power-law scaling is a behavioural ‘rule of thumb’ that is tuned to species’ ecological traits, implying a common pattern may have naturally evolved that optimizes move–wait decisions in less predictable natural environments.

1. Introduction

The timing of different activities chosen by an individual animal, such as when to search for resources, to rest or to avoid threats, has a central influence on the success of behaviours that can affect survival and lifetime reproductive output [1,2]. In a foraging context, for example, how long an ambush predator waits in a particular location in the absence of prey encounters before energy is expended in moving to a new location will have an important impact on positive energy balance and hence growth rate [3,4]. The temporal structuring of behaviour may be strongly influenced by natural selection, and so it seems probable that general ‘rules’ of behaviour operate in stochastic biological systems and have naturally evolved to be optimal in specific situations or environments [1,5]. To explore spatial and temporal patterning in behaviour, some recent investigations have used a statistical modelling approach centred on identifying simple features or rules operating in complex biological systems [6,7], which draws on concepts and techniques used in statistical physics to describe stochastic dynamical physical systems [6,8,9]. Results show that behavioural sequences in diverse organisms spanning insects to humans can show spatial and temporal scaling [6,7,10–26], patterns that may embody such general rules. Thus, identifying behavioural scaling laws across diverse species may help to understand how apparently complex behaviours evolved [1,7].

Scaling in organismal behaviour, where behaviour comprises a series of actions such as the consecutive distances moved between turns (step lengths) during searching, or inter-event times (time spent waiting between periods of activity), has been studied in detail only relatively recently [5,6,11,13,15,22]. Classical models of inter-event waiting times used for modelling traffic flow [6] assume that the time interval between two consecutive actions by the same individual is selected randomly following an exponentially decaying Poisson distribution [6], resulting in waiting times with very similar intervals. In contrast to Poisson distributions, power-law scaling describes a frequency distribution of waiting times that lack a characteristic scale, where the ‘bursty’ temporal pattern of actions repeats unchanged across a wide, albeit finite range of time scales, allowing for very long periods of inactivity separating bursts of intense activity [6]. Recent studies demonstrate that waiting time distributions can deviate significantly from the Poisson prediction and are well approximated by power laws [6,11].

Scaling in organism activity or wait patterns such as these are of broad interest because, theoretically, some types of power-law scaling of behaviour can optimize an organism's chances of success during searching (e.g. the Lévy walk patterns seen in animal foraging) [7,24,27,28]. Furthermore, it has been demonstrated that behaviours as diverse as human communication patterns [6,11], currency dispersal [12], animal space use [15,17,21,22,24,26] and times between activity in insects and rodents [10,13,14,18–20,23,25,29] all show scale invariance across relevant scales, suggesting common mechanisms may be present. However, the origins of behavioural scaling phenomena are poorly understood [6,14,25] and direct evidence for its ecological basis is lacking, even though this may clarify whether patterns observed in widely different species have some commonality.

In this study, we investigate the ecology of power-law temporal patterning in animal behaviour. Because power-law scaling in spontaneous behaviour has been observed for animals in simple environments under controlled conditions, it has been hypothesized that the scaling may be an intrinsic process of neural dynamics [10,14,18–20,25] and not driven by environmental structure, such as resource distributions [7,17,24,25]. It is possible that the inverse power-law distributions of intervals between spontaneous neuron firing signals and burst durations observed in vitro [30–32] could provide the timing signals necessary for the execution of temporal scale-invariant behaviours [25]. Nonetheless, very little is known about the presence of power-law scaling in temporal patterns of free-ranging animals in complex, natural environments, and how these patterns compare with those exhibited by the same species under controlled conditions. Here, we use model sympatric predator species spanning ambush to active foraging strategies (i) to test for the presence of scaling in temporal patterning of behaviour among species in both natural and simple environments, (ii) to determine whether they show commonality in scaling exponents within and between species and environments, and (iii) to explore what processes could give rise to the observed patterns.

2. Material and methods

(a). Study animals and tagging

To provide accurate time series of move–wait phases, we recorded the temporal behaviour patterns of 82 individuals from 15 species of bottom-living, marine predatory cephalopod mollusc, elasmobranch (sharks, skates and rays) and teleost fish that comprise a natural assemblage of sympatric species in heterogeneous shelf habitats in the northeast Atlantic Ocean (see electronic supplementary material, table S1 and figure S1). This sedentary predator assemblage exhibits a broad continuum of foraging strategies (hunting modes), from facultative ambush predation—where a predator (e.g. common cuttlefish Sepia officinalis) can actively pursue/overtake certain prey, or instead choose to remain stationary to ambush prey—to obligate ambushing, where predators (e.g. anglerfish Lophius piscatorius) only ambush highly active prey. Individual animals were tracked in the natural environment and in captivity (controlled conditions) for a total of 3204 days using small, pressure-sensitive data-logging tags, which provided 27.5 million data points for analysis of the durations of times spent waiting between activity (figure 1; for details, see electronic supplementary material).

Figure 1.

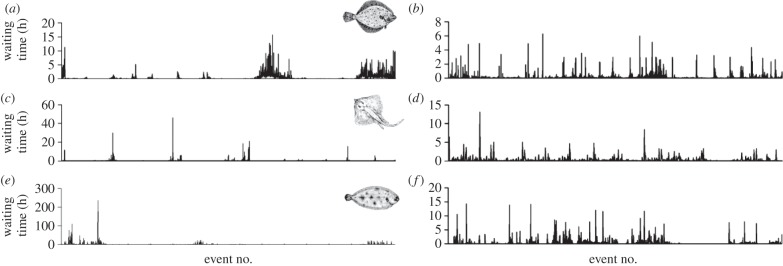
Temporal sequence of waiting times shows an intermittent pattern. Example patterns of waiting times for individual (a,b) European plaice P. platessa, (c,d) thornback ray R. clavata and (e,f) common sole S. solea in natural ((a) over 90 days duration; (c) 90 days; (e) 55.7 days) and in controlled environments ((b) 26.7 days; (d) 23.6 days; (f) 26 days), respectively. Note the burstiness of waiting times is exemplified by many short waits interspersed with some rare but very long waits.

Subadult or adult individual cephalopods, elasmobranchs and teleosts were fitted with one of two types of G5 data-logging storage/archival tag (hereafter abbreviated to DST; Cefas Technology Limited, Lowestoft, UK). Standard DSTs were 31 mm long by 8 mm diameter and weighed 1 g in water, whereas long-life DSTs measured 35.5 mm long × 11.5 mm diameter and weighed 2.1 g in water. DSTs monitor temperature from 2 to 34°C (accuracy 0.1°C, resolution 0.03°C) and pressure to a depth of 100 m (or 200 m for one laboratory and 10 field deployments: accuracy 1%, resolution 0.04%). During laboratory trials, DSTs were programmed to record depth every 5 s for a period of one month, while tags deployed on released animals were programmed to record depth at 20 s, 30 s or 1 min intervals. During experimental trials in the laboratory, animals were held in recirculated seawater aquaria fed directly from the sea. Tagged animals at sea were tracked in the coastal waters of the western English Channel, which comprises a heterogeneous mosaic of habitats when characterized in terms of water depth, substratum type, water column environmental gradients and temporal scales of fluctuations in those gradients (electronic supplementary material, figure S1). Water depth generally increases with distance from the shore, to a maximum depth of 76.5 m. Details of tagging procedures and habitat mapping are given in the electronic supplementary material.

(b). Waiting time analysis

To test for the presence of scaling patterns in waiting behaviour within and between species, the frequency distributions of individual animal waiting times were investigated using maximum-likelihood estimation (MLE). The methods used were those employed by Humphries et al. [24,26] based on Clauset et al. [33]. Details of data pre-processing are given in the electronic supplementary material. We tested power law and truncated Pareto-Lévy (truncated power-law) distributions for each individual animal waiting time series (as a ranked waiting time distribution) and compared each of these with the following alternate distributions: exponential, truncated exponential, lognormal and gamma. Model best fits were assessed using Akaike information criterion (AIC) weight values; see Humphries et al. [24,26] for detailed descriptions. Power spectrum analysis was used to investigate the existence of long-range correlations in the time-series data of individual animals using programming routines in MATLAB [15]. In addition, to investigate the possibility of a particular scale (average waiting time) dominating an entire individual's waiting time series, we used digital signal-processing techniques to identify significant periodic components of the binary time series of activity and waiting for the 16 individuals shown in figure 2. For this purpose, we used programming routines in MATLAB to apply fast Fourier transforms (FFTs) with a ‘Hamming’ window function to the binary time-series data. Further details are given in the electronic supplementary material.

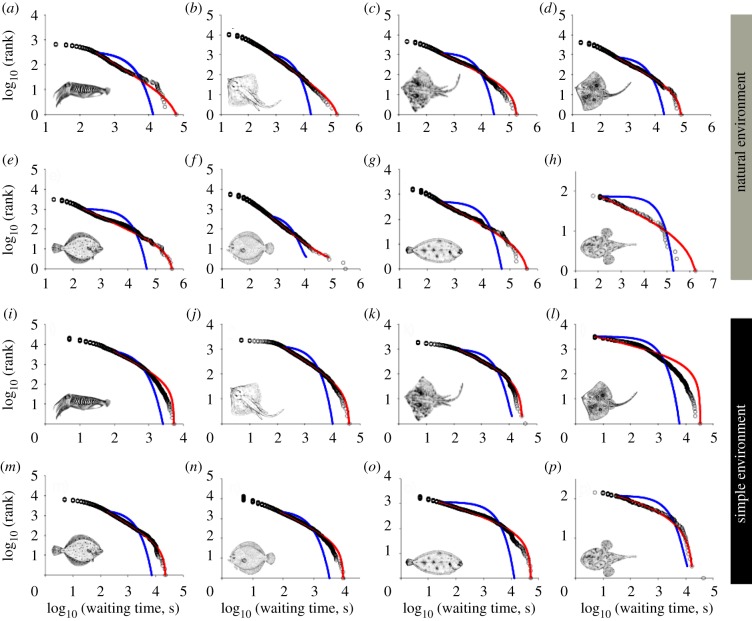
Figure 2.

Power-law scaling of waiting time distributions among individuals of diverse species. Example log–log plots show model best fits to truncated power-law (red lines) and poor fits to an exponential (blue lines) for eight individuals from species tracked both (a–h) in the wild and (i–p) in captivity. (a,i) Common cuttlefish, (b,j) small-eyed ray, (c,k) thornback ray, (d,l) blonde ray, (e,m) European plaice, (f,n) turbot, (g,o) common sole and (h,p) anglerfish.

(c). Trait data

The waiting time patterns of species were compared with species traits (foraging mode, body size and prey preference). Frequency of occurrence data of prey in stomach contents of predators was taken from the published literature for the species we studied and where those investigations analysed stomach samples in the northeast Atlantic region where our tagging work was conducted. Body size data of predators were recorded maximum lengths and masses. Sources and details are given in the electronic supplementary material.

(d). Stochastic priority-list model

A decision-based queuing process model such as a priority-list model [6] prioritizes certain actions over others (e.g. waiting over moving), so it is an appropriate candidate model to examine how simple rules may potentially underlie apparently complex empirical move–wait patterns (figure 1). We extended the stochastic priority-list models introduced by Barabasi [6] and Reynolds [34]. Two competing behaviours (activity 1: waiting; activity 2: moving) are given ‘priorities’ x₁ and x₂ = 1 − x₁ that are randomly selected from some distribution ρ(x). These priorities are treated as probabilities such that activity 1 is chosen as the next activity to perform with probability x₁ and activity 2 is chosen as the activity to perform with probability x₂. If activity 1 is chosen, then the priorities x₁ and x₂ remain unchanged, whereas if activity 2 is chosen, the animal moves and may feed, affecting its ‘state’, and thus new priorities x₁ and x₂ are randomly selected from ρ(x). Following this, a new activity is selected and the cycle repeats. Following the previous approach of Barabasi [6], a degree of determinism was introduced into the model by replacing x₁ with 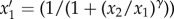and x₂ with 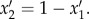This form is chosen because it smoothly interpolates between the aforementioned stochastic protocol (obtained when γ = 1) and a deterministic protocol (obtained as γ → ∞). In the deterministic protocol, the highest-priority activity is the activity that is always performed next (i.e. low-priority activities are no longer occasionally selected). This is because 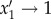if x₁ > x₂ and 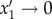if x₂ > x₁. For intermediate cases (γ > 1), the highest-priority activity is executed with probability close to unity while the lower-priority activity is rarely executed.

The priority-list model was implemented numerically with a uniform distribution of priorities: ρ(x) = 1 for 0 ≤ x < 1, otherwise ρ(x) = 0. Simulation data for a given degree of determinism (value of γ) were pooled from 100 independent runs of the model each performed over 10⁵ time-steps. The AIC [33] was used to test whether these data provided more evidence for the distributions of simulated waiting times having inverse power-law

or negative exponential tails

The power-law exponent, μ, and the exponential decay rate, λ, were determined using MLE [33]. The start of the tail of the distributions (a ≈ 10) was ascertained by visual inspection of the survival function (the complement of the cumulative distribution function). To construct the survival function, the simulation data for the waiting times t_i were first ranked from largest to smallest {i = 1, … , n}. The probability that a waiting time is greater than or equal to t_i (the survival function) was then estimated as i/n.

3. Results

(a). Scaling patterns

The temporal sequence of predator waiting times shows an intermittent pattern (figure 1), the greater proportion of waiting events being short but interspersed, with rare very long waits (maximum = 475.4 h) that were up to 4.5 orders of magnitude greater in duration than the shortest wait (5 s; electronic supplementary material, table S2). The intermittent pattern of waiting times was conserved across species and was present in both natural (wild; figure 1a,c,e) and simple (captive; figure 1b,d,f) environments. Statistical modelling (see electronic supplementary material) showed that the frequency distributions of waiting times for all individuals across all species decayed slower than the exponential and were well approximated by a truncated power-law (or in one case a power-law), with straight-line fits on log–log plots over a range between nearly two and four orders of magnitude of the data (mean 2.5 ± 0.6 s.d., n = 82; figure 2; electronic supplementary material, table S2). Best fitting of data to truncated power-laws rather than pure power laws is intuitive because the amount of time a living animal will wait before moving to obtain a resource is finite. Interestingly, the truncation was less pronounced (maximum waiting times were longer) in free-ranging individuals compared with those kept in captivity. For example, the maximum waiting time of common sole Solea solea was on average 17.4 times longer in the wild than in captivity (figures 1e,f and 2g,o). This difference may be due to several factors, but perhaps most important is the likelihood of regular food availability in captivity, which results in the cessation of waiting with the onset of feeding.

We confirmed that individual waiting time patterns were reliably described by truncated power-law models using three sets of additional analyses. First, exponential, truncated exponential, gamma and lognormal distributions were tested as alternative models to the truncated power-law and power-law, but did not provide better fits to any individual (see electronic supplementary material, results, tables S2 and S3, and figure S2). Second, power spectrum analysis of the wait-period time series confirmed that scaling exponents, β, which characterize the frequency dependency of the power spectra, S(f) ∼ f^−β, were approximately 0.6 in the low-frequency regime (wild, mean β = 0.66 (0.08 s.d.), range, 0.48–0.77; controlled, mean β = 0.46 (0.17 s.d.), range 0.27–0.77; electronic supplementary material, figure S3). This supports our result of truncated power-law best fits because β > 0 (‘1/f’ noise) is indicative of scale invariance [15,23,35]; by contrast, β ≈ 0 characterizes ‘white’ noise and describes the pattern expected from a scale-specific or a composite correlated random walk (CCRW; composite Brownian walk, CBW) [23,35]. Therefore, CBWs did not describe the temporal patterns we observed for marine predator behaviours. Lastly, FFTs demonstrated that the waiting time scaling patterns were not dependent on behavioural periodicities in activity/waiting time series (for details see the electronic supplementary material, tables S4 and S5, and figures S4 and S5).

Power-law scaling was ubiquitous among all species studied here, and was present in all individuals of nine species tracked in both natural and simple environments (figure 2). The average scaling exponent (μ) for individual predators was not different in the wild compared with in captivity (mean exponent: wild, μ = 1.58 ± 0.36 s.d., 33 individuals, nine spp.; captivity, μ = 1.59 ± 0.38 s.d., 49 individuals, 15 spp.; F-test, F = 0.91, p = 0.79; t-test on means, t = −0.13, p = 0.90), demonstrating that scaling in waiting time patterns monitored in predators over weeks to months in natural habitats exhibits the same temporal dynamics as found for individuals in captivity. This indicates that environmental complexity (see electronic supplementary material, results) did not alter the principal features of temporal patterning in predator behaviour, lending support to the idea that scaling behaviour is not an emergent property of the environment's structure (e.g. the fractal distribution of food resources [7,26,36]), as has been proposed for foragers in other systems [35,37]. Therefore, it is possible that scaling in waiting times is a general behaviour pattern that improves the chances of foraging success [28] and has naturally evolved.

(b). Species-specific scaling

While we did not find differences in scaling exponents of wait-time frequency distributions between natural and simple environments, exponent values did vary between species, with species' average μ values ranging from 0.96 to 2.07 (electronic supplementary material, figure S6). An exponent of approximately 1 indicates a temporal scaling pattern having a higher proportion of rare but very long waiting times (figure 2h,p), compared with a pattern described by an exponent of approximately 2, where there are proportionately fewer long waits and more shorter waiting times (figure 2a,i). The differences between the mean exponents of species are significant, not only between the highest and lowest μ values (mean exponents: S. officinalis 2.07, L. piscatorius 0.96: variance test, F = 0.53, p = 0.55; t-test, t = −6.36, p < 0.001; each with n = 5), but within the range also (e.g. thornback ray Raja clavata 1.82, n = 8, turbot Scophthalmus maximus 1.38, n = 9: F = 0.63, p = 0.55; t-test, t = 2.41, p = 0.03; electronic supplementary material, figure S6).

This confirms that there are species-specific scaling exponents across the range. An expectation might be that predators from the same taxonomic groups, such as flat-bodied bony fishes (Family Pleuronectidae) or flat-bodied rays (Genus Raja), should each have similar within-taxa exponents on account of species within each taxa sharing a common phylogeny. However, the species-specific scaling exponents are not readily explained by species taxonomic groups: although the two cephalopods S. officinalis and the curled octopus Eledone cirrhosa both have higher mean exponents, 2.07 and 1.84, respectively, the exponents of pleuronectids and rajids vary widely, from 1.22 to 1.83 and 1.36 to 1.82, respectively (electronic supplementary material, figure S6). Of particular interest in this context is that rather than being linked to phylogeny, the scaling exponents appear to correlate to the species’ foraging modes. For example, S. officinalis has the highest scaling exponent and adopts a facultative ambush strategy, while L. piscatorius with the lowest exponent has an obligate ambush strategy.

(c). Scaling exponents and ecological traits

The idea that differences in scaling of temporal behaviour reflect specific types of behavioural strategy raises the question of whether exponent difference is driven by traits linked to an organism's state, because behavioural choices can depend on state [5]. In a foraging context, we reasoned that predators that frequently wait for long periods between prey encounters and subsequent captures should have higher total energy reserves (greater body size and lower relative metabolic rate) than a predator that generally waits for shorter periods. Based on this and previous observations by others [38], we predicted that predators capable of waiting for long periods (e.g. L. piscatorius exponent μ ∼ 1) choose to target active (high-energy density) prey that are encountered less frequently because they are more sparsely distributed, or lower in abundance, but that when captured yield a greater net energy gain than more frequent captures of more numerous but less energy-rich prey. By contrast, predators with higher proportions of shorter waiting times (e.g. S. officinalis μ ∼ 2) are predicted to be smaller (lower total energy reserves and higher relative metabolic rate) and more likely to target generally more abundant but sedentary prey. It is a general trend that highly active prey (e.g. fish), which require a higher energy expenditure by the predator to pursue/overtake them, often have a higher energy content than abundant, sedentary prey (e.g. crabs; electronic supplementary material, figure S7).

To test these possibilities, we related scaling exponents to, first, each predator's length-specific body mass (the maximum body mass/maximum body length), as a proxy for total energy reserves (figure 3a), and, second, to the mean percentage frequency of occurrence of fish found in a predator's diet, a proxy for predator specialization on energy-dense prey (figure 3b; electronic supplementary material, table S6). For both traits, we found negative relationships with scaling exponents, confirming our predictions (figure 3; see legend). Our finding demonstrates that while all predators we studied exhibited scale-invariance in waiting time distributions, the particular scaling exponents of species appear ‘tuned’ to traits associated with a predator's foraging strategy: larger predators specializing on active, energy-dense prey have lower exponents describing a temporal pattern with a higher proportion of very long waits, whereas smaller predators with a more generalist diet including sedentary prey have higher exponents describing fewer longer waits. This introduces a degree of determinism (i.e. which prey to select), associated with the heavy-tailed probabilistic waiting time patterns observed.

Figure 3.

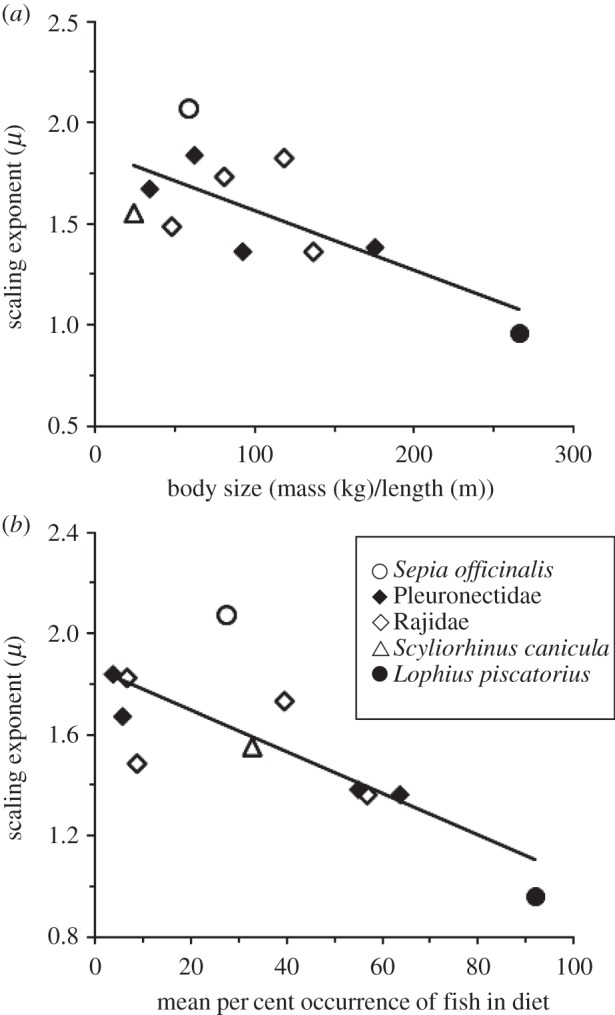
Non-universality in scaling exponents predicted by traits linked to state. Relationships between species mean scaling exponent and (a) predator maximum body mass/maximum body length (a proxy for total energy reserves) and (b) predator's specialization on active prey (mean frequency of occurrence of fish prey in its diet). A multiple linear regression model with exponent as the response variable and predator body mass/body length and percentage fish in diet as predictor variables accounted for 63% of the variation in the response (r² = 0.63; ANOVA, F_2,8 = 6.81, p = 0.019). Considering only fish data improved the model fit, with predictors accounting for 77% of response variation (r² = 0.77; ANOVA, F_2,7 = 11.55, p = 0.006); see the electronic supplementary material.

(d). Simple decision model

Because there are competing behaviours during foraging (e.g. whether to wait for an increasing time versus when to become active and move elsewhere) it has been hypothesized that the ecological advantage of power-law scaling of behaviour may be brought about by constantly updating motor outputs with estimators of state and monitoring effects in a decision-based queuing process [14], which prioritizes certain actions over others. Priority-list models have been shown to account well for some patterns in human [6] and animal [34] behaviour. We extended a stochastic priority-list model [34] by incorporating a deterministic component [6] that reflects differing predator responses to different prey types, to explore whether a set of simple behavioural rules can recover the empirical waiting time patterns and their exponents found here (see Material and methods).

For most distributions ρ(x), the stochastic priority-list model produces power-law-distributed waiting times with an exponent μ = 2 and distributions of moving times with exponential tails [34]. For the purely stochastic model, our results confirm in all cases that inverse power-law tails were convincingly favoured over negative exponential tails, and inverse power-law scaling extended over at least three decades (figure 4a). Although this purely stochastic model produces power-law scaling of waiting times, it did not reproduce the variability of exponents we observed across species (figure 3). Our stochastic–deterministic model produces distributions of waiting times that have inverse power-law tails, and the power-law exponent is dependent upon the degree of determinism (i.e. by the value of γ), and ranges between 2 and 1; here, the distributions of moving times also have exponential tails. However, the characteristic time scale depends on ρ(x), and as a consequence may vary with metabolic state and size. These analytical results were confirmed by numerical simulations and showed that the maximum-likelihood estimates for μ decrease monotonically with increasing γ (figure 4b).

Figure 4.

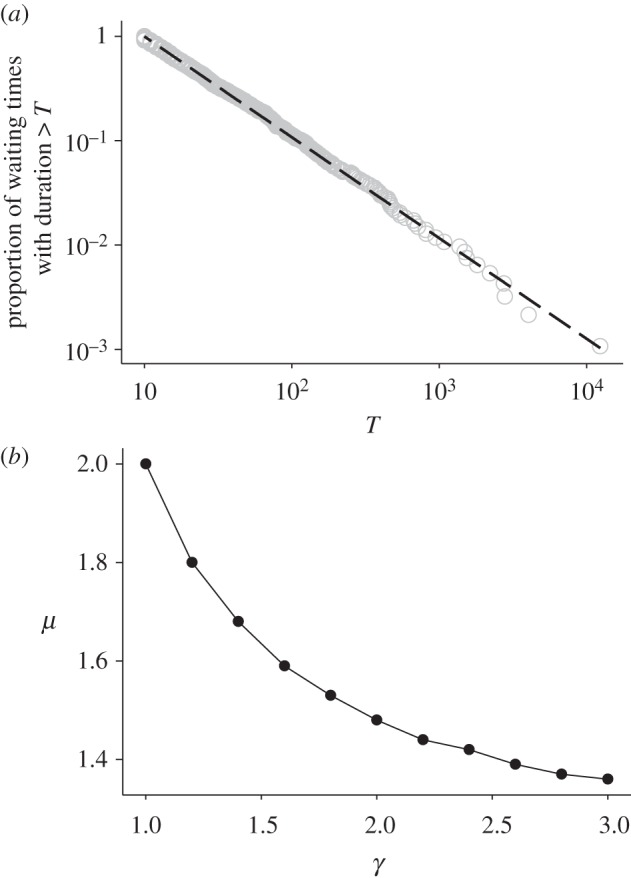
(a) Simulation data for the proportion of waiting times with duration more than T produced by the stochastic priority-list model (γ = 1) (open circles) together with the best fit inverse power-law (black line). The maximum-likelihood estimate for μ = 2.0 and predicts a predator waiting time pattern dominated by short waits. A straight line on this log–log plot is indicative of inverse power-law scaling similar to empirical waiting time distributions (figure 2). (b) The dependency of μ on the degree of determinism (γ) (filled circles), where μ = 2 predicts a waiting time pattern when prey has lower energy content and μ → 1 as the energy content of the prey increases. The line is added to guide the eye.

This model was recast in terms of predation: x₂ is the likelihood of there being prey in the immediate vicinity and x₁ = 1 − x₂. When prey have lower energy content (generally slower moving), the predator often (but not always) moves when the likelihood of there being prey present is high (the stochastic protocol). When prey have high energy content (generally faster moving), the predator always moves to feed when the likelihood of there being prey close by is high (the deterministic protocol). Therefore, we found for our stochastic–deterministic model that predator waiting-times are characterized by the power-law exponent μ = 2 when preferred prey have low-energy content (e.g. lower per cent fish in diet), and μ → 1 as the energy content of the prey increases (e.g. higher per cent fish in diet).

These model results agree well with our empirical results: predators such as L. piscatorius, S. maximus and blonde ray Raja brachyura, which largely specialize on higher-energy-content prey (e.g. active fish), showed scaling exponents of waiting times approaching 1, as predicted by the model, while predators such as S. officinalis, R. clavata and the European plaice Pleuronectes platessa, which are more generalist feeders on mostly lower-energy-content prey, showed exponents approaching 2 (figure 3b; electronic supplementary material, table S6). Furthermore, the model yielded distributions of activity times with exponential tails, with the characteristic time scale being predator-specific, which may vary with metabolic state and size (figure 4). The model's prediction that distributions of activity times have exponential tails was confirmed empirically for all tracked predators: we found typical activity times were predator-rather than prey-specific, and hence varied by body size as expected (see the electronic supplementary material, results and discussion, and figure S8).

The modelling results indicate that a simple set of stochastic/deterministic behavioural rules associated with choice (e.g. how long to wait in response to perceived prey type) can indeed give rise to the waiting time scaling patterns and species-specific scaling exponents we observed for sympatric marine predators. Combined with our observation that differences in scaling exponent change predictably with body size (mass/length; figure 3a), the results suggest that scaling behaviour may have arisen through a complex set of selective forces acting on traits associated with state.

4. Discussion

This study demonstrates the presence of power-law scaling in the temporal dynamics of spontaneous behaviour across sympatric species in both natural (unpredictable) and simple (predictable) environments, and that the different scaling exponents are predicted in part by total energy reserves (body size) and predator specialization (prey type/energy density). The output from a simple behavioural (priority-list) model incorporating a deterministic choice component of predator response to prey type was consistent with empirical results suggesting that the power-law scaling in predator behaviour we observed, which results in apparently complex wait–move patterns, can potentially arise from simple decision-making processes.

An important finding here was the demonstration that the power-law scaling pattern of waiting times was not likely to be an emergent property of environmental structure; instead, our results indicate that it arises from an internally generated, adaptive process, as hypothesized previously [7,35]. While power-law waiting time distributions are evident in the spontaneous behaviour of insects, rodents and humans [6,14,19,20,25,29], there has not previously been a clear demonstration that free-ranging species exhibit the same scaling in waiting times as when they are in captive, controlled conditions. Therefore, our study provides support for a recently proposed mechanism underlying power-law patterns of spontaneous behaviour in animals [14]: namely, a nonlinear signature of spontaneous behaviour under controlled conditions suggests that deterministic endogenous processes are involved in generating behavioural variability such as that described by power-law scaling [14]. Recent research provides further support by showing that power-law-distributed rest-bout durations are modulated, but not perturbed, by dopamine, a neurotransmitter that plays a number of important roles in brain function, including in cognition, voluntary movement and motivation [10,19]. For similar studies with mice and humans, the presence of an underlying neuro- and/or psycho-biological principle governing power-law scaling of behaviour has been suggested [29]. Moreover, the scaling exponents found for Drosophila, desert locusts and rodents were approximately 1.5 [14,19,20,25], which is close to the mean exponent (approx. 1.59) shown here characterizing marine predators. Thus, our findings strongly support the possibility of waiting time scaling as an intrinsic and general behavioural ‘rule of thumb’ in animals by extending it to free-ranging molluscs and lower vertebrates.

It is possible that the temporal (waiting time) scaling laws we identify are the parallel in ambush predators of the spatially scale-invariant Lévy walk (power-law) patterns that seem common among animals that move continually during searching, and which theoretically optimize foraging success, suggesting it to be an adaptive behaviour [15,17,23,24,27]. The proposition that temporal scaling behaviour is intrinsic is supported by empirical evidence showing that the Lévy walk movement patterns observed in mobile marine animals [17,21,24,39] appear independent of resource density or distributions [40]. Theory predicts that Lévy walk movement patterns are optimal in areas with sparsely distributed prey, but in areas where prey is abundant Brownian motion is sufficiently efficient [7]. An adaptive, intrinsic mechanism having power-law scaling predicts this dynamic behaviour: simulations show that if a Lévy forager truncates its move step to consume prey when it is detected in its vicinity (i.e. has simple prey targeting), then a Brownian distribution of move steps will emerge when prey is highly abundant (i.e. closer together) [7,27]. Empirical results for mussels searching for conspecifics (resource targets) to aggregate with showed that part of the mussel movement patterns comprising non-truncated steps only (because no targets were encountered during these move steps) displayed Lévy walks regardless of resource density in the surrounding environment [40]. This suggests that the Lévy walk pattern exhibited by mussels is intrinsic. Taking these studies and the present one together suggests an intrinsic pattern of stochastic (power-law) spontaneous behaviour may apply more generally, from highly mobile pursuit predators such as tunas [17] to the less mobile ambush predators investigated here.

Despite widespread compelling evidence that diverse organisms display movement patterns that can be approximated by scale-invariant Lévy walks [13–15,17,21–26], it was demonstrated recently that the Lévy movement pattern of mussels [39] was marginally better fitted by CBWs, which describe the sum of weighted exponential distributions (e.g. a sum of two, three or four exponentials) [41]. It is not surprising that more complex models such as CBWs will provide marginally better fits to movement data than the simpler Lévy walk model [42]; nonetheless it potentially weakens the arguments for power-law scaling in behaviour. Although it is not unexpected that CBWs are likely to provide slightly better fits than truncated power-law models owing to their greater complexity [42], it is by no means absolute. For example, previous truncated power-law best fits to spatial foraging patterns of albatrosses [24] were confirmed when tested against CBWs with a sum of two, three or four exponential models [26], indicating that CBWs are not always strong alternative models to scale-invariant power-law distributions. Recently, however, it was shown that Lévy walks could be distinguished reliably from CCRWs (CBWs) by applying power spectra [34]. In our study, we used power spectrum analysis [34] to demonstrate that the power spectra of temporal waiting time patterns of marine predators were not consistent with those expected from a CCRW, which supports the view that the possibility of mistakenly selecting a scale-invariant (e.g. truncated power law) model over a scale-dependent (e.g. CCRW) model was minimized by the approach taken. Therefore, we conclude that the scaling in waiting time patterns of benthic predators we found were not likely to be better fitted by scale-dependent models.

Our study also provides the first indication that the frequently observed differences in scaling exponents [17,25] share a common ecology across sympatric species through a continuum of behavioural strategies (foraging modes) correlated with an animal's state (i.e. body mass). It is possible that such a heavy-tailed waiting time behaviour pattern, which has similarities to an intermittent search strategy, may optimize encounter rate with highly active, patchily distributed prey [28]. We hypothesize that power-law scaling of wait times may have naturally evolved as a universal behavioural ‘rule of thumb’ for approximating the optimal encounter rate with prey in different and unpredictable environments. Further, we hypothesize that the species-specific temporal scaling patterns (described quantitatively by exponents) have been selected alongside traits such as body size, as a result of competition for forage resources (see electronic supplementary material, figure S9). Our results are consistent with the hypothesis that competition for valued, energy-dense prey that are unpredictably distributed (e.g. fast-moving fish), where temporal gaps between prey patches can be long, drives selection for predators of increasing body size (electronic supplementary material, figure S9). As such, hunting mode, body size and prey preference predict well the variation in scaling exponents we observed. Theoretical models indicate that broad trends in body size and composition of animals can be understood by considering behaviour such as the starvation–predation trade-off that is fundamental to all predator–prey systems [43]. For example, models show that storage of body fat increases with greater time gaps in food supply [43]. Our results are consistent with this theoretical expectation by showing predators with lower scaling exponents (more frequent very long waits) are larger in body size than predators experiencing fewer interruptions to food supply.

In this study, we have taken a quantitative approach that collapses complex temporal behaviour patterns recorded from free-ranging animals onto a single parameter, the scaling exponent (μ). In doing so, we have identified connectivity between the adaptiveness of temporal scaling dynamics, an organism's traits affecting state and the selective forces shaping behavioural choices, which may provide a basis for a general model unifying scaling phenomena in behaviour patterns [6,7,10–29] with behavioural optimality models [1,2,5]. Perhaps more important, though, the predictable variation of the waiting time scaling exponent with ecological traits (e.g. body size and prey preference) indicates a potential use for predicting animal behaviour waiting time patterns in relation to other traits (such as thermal sensitivity, perhaps). For example, understanding how future climate change will alter animal dispersal patterns is a crucial but often missing component in assessments of species' distributional changes owing to climate [44]. Understanding how animal waiting-time patterns (which in turn affect dispersal likelihood) vary with species thermal sensitivity may provide a means to obtain more realistic estimates of dispersal potential (since long waits arrest dispersal) in response to climate warming, which could inform extrapolations to other species having similar life-history and ecological traits. Furthermore, the common ecology of temporal behavioural dynamics we show here for diverse species with independent evolutionary lineages dating back at least 400 Myr suggests that links between waiting time scaling laws and ecological traits are widespread across taxa. Waiting time scaling exponents could have relevance for comparing behaviour between taxa to test ideas about whether scale-invariant patterns of behaviour are adaptive and have naturally evolved. For instance, the behaviour patterns of marine and terrestrial predators are seldom explored within a single study, yet a comparison of waiting-time patterns in widely separated taxa—such as marine fish and terrestrial snakes that ambush prey—may provide powerful insights into the role of environment in the evolution of foraging behaviour.

Funding statement

Funding was provided by the UK Natural Environment Research Council (NERC) Strategic Research Programme ‘Oceans 2025’ (Theme 6: Science for Sustainable Marine Resources), The Leverhulme Trust and a Marine Biological Association (MBA) Senior Research Fellowship (D.W.S). The work was also supported by the Biotechnology and Biological Sciences Research Council (BBSRC) (A.M.R.).