Commuting fruit bats beneficially modulate their flight in relation to wind

Abstract

When animals move, their tracks may be strongly influenced by the motion of air or water, and this may affect the speed, energetics and prospects of the journey. Flying organisms, such as bats, may thus benefit from modifying their flight in response to the wind vector. Yet, practical difficulties have so far limited the understanding of this response for free-ranging bats. We tracked nine straw-coloured fruit bats (Eidolon helvum) that flew 42.5 ± 17.5 km (mean ± s.d.) to and from their roost near Accra, Ghana. Following detailed atmospheric simulations, we found that bats compensated for wind drift, as predicted under constant winds, and decreased their airspeed in response to tailwind assistance such that their groundspeed remained nearly constant. In addition, bats increased their airspeed with increasing crosswind speed. Overall, bats modulated their airspeed in relation to wind speed at different wind directions in a manner predicted by a two-dimensional optimal movement model. We conclude that sophisticated behavioural mechanisms to minimize the cost of transport under various wind conditions have evolved in bats. The bats’ response to the wind is similar to that reported for migratory birds and insects, suggesting convergent evolution of flight behaviours in volant organisms.

1. Introduction

Owing to the spatial separation of feeding areas from breeding and roosting sites, daily commuting is widespread in various animal taxa. The trajectories of commuting aerial and aquatic animals depend not only on the animals’ own movements but also on the motion of the medium in which they move [1,2]. Hence, the flow vector (i.e. flow speed and direction) of the medium may strongly affect the duration of the journey and energy expenditure during movement. Moreover, a perpendicular component of the flow relative to the animal's heading (e.g. crosswinds) may result in off-course drift, possibly hampering the ability of the animal to reach its goal. In order to arrive at their destination under crosswind conditions, flying animals must therefore overcome induced drift by modifying their behaviour in response to wind. A common solution to this problem is to compensate for lateral drift by changing flight heading [3–5] (electronic supplementary material, figure S1). Because the cost of no compensation and consequent sideways drift may be exceedingly high, fitness-relevant behavioural compensatory mechanisms to minimize wind drift have convergently evolved in both birds and insects [4,6,7].

To estimate the degree of instantaneous wind drift, one must determine the position of individuals at a high frequency throughout their journey. Recent advances in biologging and transmitter technology (reviewed in references [8,9]) have enabled unprecedented long and detailed tracking of increasingly smaller species of animals, and also, in some cases, the simultaneous recording of key behaviours. These developments have provided important insights for different movement phenomena, including long-distance migration, foraging and homing behaviour [10,11]. In addition to determining the animal's position, in the case of flying animals it is essential to concomitantly estimate the wind vector encountered aloft, so that the influence of the ambient flow of air can be separated from the animal's own movement [4,12]. The ability to correctly determine wind direction and speed is critical for inferring animal flight performance, because optimal movement in relation to wind may involve changes in airspeed (speed relative to air), and modulation of this response when the wind is blowing from different directions relative to the heading [13]. Consequently, wind must be estimated at high spatial and temporal resolution to match the relevant scales affecting the flying organisms [14], as has been successfully done in recent studies of bird migration [10,15].

Although crosswind may drift animals off-course, optimal response may involve different behavioural strategies depending on the nature of the encountered winds. Wind drift compensation is predicted when winds are constant during the journey, while changes in wind conditions along the journey are predicted to induce varying behaviour, with expected wind drift and wind drift compensation far away from and close to destination, respectively ([3,16]; see also [2]). Because wind may affect not only the bat's sideways movement but also its forward speed with respect to the destination, bats are also expected to change their behaviour under tail- or headwind conditions. To minimize their cost of transport, airborne animals using flapping flight that encounter tailwinds should reduce their airspeed, and increase it under headwinds [17,18] (electronic supplementary material, figure S2). In addition, a strong effect of crosswind speed on airspeed was suggested [13], such that animals are expected to increase their airspeed with increasing crosswind speed as a way to reduce drift effect. Following the predicted effects of tail- and crosswind on optimal airspeed, specific airspeed responses have been outlined based on the angle between animal heading and wind direction [13]. Bat airspeed is expected to decrease with increasing tailwind assistance (wind direction relative to bat direction 0–20°), but it is predicted to increase, though mildly, under increasing tail- and crosswind speed (wind direction relative to bat direction 20–70°) because of the effects of crosswind (expected increase in airspeed) and tailwind (expected decrease in airspeed). Airspeed is expected to strongly increase under both increasing crosswind speed (wind direction relative to bat direction 70–90°), and increasing cross- and headwind speed (wind direction relative to bat direction 90–180°).

The response of free-ranging birds and insects to wind has been studied so far in the context of foraging trips [5] and long-distance migration [12,19]. Yet, likely owing to the lack of high-resolution information of the flight track and encountered wind, their response during commuting flights remains largely unknown. Moreover, no study has so far investigated flight behaviour in relation to wind in free-ranging bats. Bats travelling long distances during a single night may be subjected to time-related costs involving, for example, the need to allocate time for foraging and exploring new feeding areas. Hence, such time-constrained travel may lead to adaptation to time-minimization of the journey [20]. It has been shown that commuting bats may use the maximum range speed (V_mr) to minimize their cost of transport [21]. We consequently calculate bat airspeed in relation to wind and assume that bats use V_mr during their commuting flights.

To this end, we hypothesized that bats modulate their flight behaviour in relation to wind, and examined the following predictions: (i) to reach their feeding and roosting sites, commuting bats’ compensation for wind drift may depend on wind conditions. Under constant winds, full compensation is expected, and bat lateral speed will not be related to crosswind speed (electronic supplementary material, figure S1). Under variable winds, partial compensation with some degree of lateral drift at the start of the journey and full compensation near the destination is expected [3]. (ii) To minimize their cost of transport, bat airspeed will decrease with tailwind assistance and increase under headwinds ([17,18]; electronic supplementary material, figure S2). (iii) Likewise, bat airspeed will increase with crosswind speed [13,22,23]. Consequently, bat airspeed modulation will follow the pattern suggested by Liechti et al. [13] through a combined response to both tailwind (prediction ii) and crosswinds (prediction iii). Specifically, bat airspeed will decrease with increasing wind speed under wind direction relative to bat direction of 0–20°, slightly increase under increasing wind speed under wind direction relative to bat direction of 20–70°, and strongly increase with wind speed under wind direction relative to bat direction of both 70–90° and 90–180°.

2. Material and methods

(a). Study species and bat tagging procedure

The straw-coloured fruit bat (Eidolon helvum, Kerr, 1792) is widely distributed in sub-Saharan Africa and roosts in colonies of up to 10 million individuals [24]. Using elevated mistnets [25], we captured bats for 8 days, on 2–9 February 2011, at a large colony in the grounds of the 37 Military Hospital in Accra, Ghana (5°35'11’’ N, 0°11'02’’ W). Bats were trapped upon their return from foraging in the morning and kept in cloth bags until further processing. A subset of large adult males (body mass 255–321 g) were selected for logger attachment; all other animals were released at the site of capture. GPS data loggers (e-obs GmbH, Munich, Germany; 24 g, 7–9% of body mass and 21 mm width × 12 mm height frontal area) were attached by trimming the mid-dorsal fur below the shoulder blades and gluing (Sauer-Hautkleber, Manfred Sauer GmbH, Lobbach, Germany) the loggers to their back. Previous experience with other bat species shows that this attachment method ensures that loggers are shed after about 10 days without causing harm to the animals [26,27]. After attaching the tags, all animals were hand fed ad libitum with banana (Musa sp.) and released near their roost trees. Bats were visually observed when released to confirm that they would all depart without any apparent difficulty. The GPS device contained a pinger that operated between 10.00 and 12.00 each day. A radio receiver (Yaesu VR-500, Tokyo, Japan) connected to an H-antenna (Wagener, Germany) was used to locate the pinger's signal while walking through the area of the roosting colony. When getting in close proximity to a data logger, an automatic radio connection to a hand-held base-station was established through a directional high-gain antenna (e-obs) for data downloading.

The GPS data loggers recorded bat horizontal and vertical location at 5 min intervals during commuting flights (figure 1), except for two individuals for which location was determined every 2.5 min. Measurements indicate that 95% of the device's horizontal positions are within 18 m of its actual location (n = 165 measurements at a sampling frequency of 5 min), whereas the corresponding value for vertical positions is 23 m (n = 163 measurements; Orr Spiegel 2013, personal communication). While the logger probably incurred metabolic costs for flying bats [28], we could not detect differences in flight behaviour when bats were directly observed alongside nearby conspecifics in the field. Data were collected during one to six consecutive days until the loggers fell off or the batteries were depleted, and included continuous flights lasting at least 30 min. Our sample includes a total of 37 flights, as follows: two flights (n = 4 bats), three flights (n = 2 bats), five flights (n = 2 bats), 13 flights (n = 1 bat; see figure 1 and the electronic supplementary material, S3). E. helvum tracking data are available through www.MoveBank.org (doi:10.5441/001/1.62s17b4v).

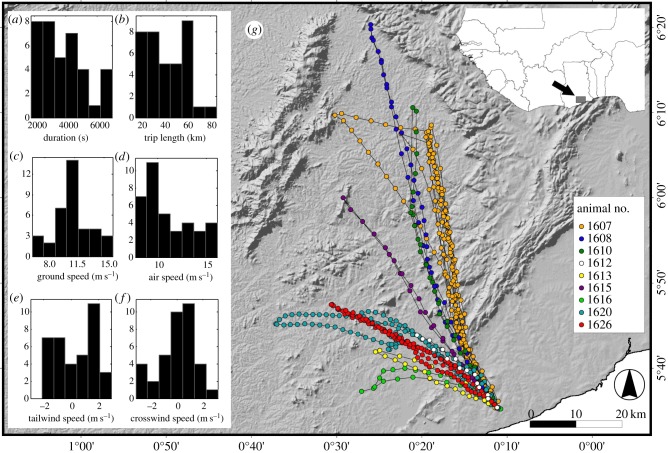
Figure 1.

Map of flight tracks and histograms of main properties of straw-coloured fruit bats’ commuting trips between their roosting colony near Accra, Ghana and feeding sites, recorded between 2 and 9 February 2011. (a) Bat trip duration. (b) Bat trip length. (c) Bat ground speed. (d) Bat air speed. (e) Tailwind speed during flight. (f) Crosswind speed during flight. (g) Bat flight tracks overlaid on a topographic map.

(b). Atmospheric modelling

We simulated the wind encountered by commuting fruit bats using the Regional Atmospheric Modelling System (RAMS). The RAMS consists of non-hydrostatic, compressible dynamic equations, a thermodynamic equation and a set of equations representing the cloud microphysics. It estimates the three-dimensional spatial and temporal distribution of wind fields, temperature, mixing ratios and pressure in a terrain-following coordinate system using a two-way nested grid scheme [29–31]. RAMS input included European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis data, sea temperature, radiation, land-use and topographic data of the study area. Output variables included the u (west–east), and v (south–north) components of wind velocity. The model was applied using three nested grids, with horizontal grid mesh of 1 km × 1 km of the finest grid and vertical mesh size that varied by altitude, starting with a 50 m resolution from the surface and increasing by a factor of 1.1 with altitude (e.g. the second grid cells above surface were 55 m high, from 50 to 105 m above ground). Model steps were calculated every minute, and modelled wind data were spatially and temporally matched to each bat's location and averaged over every 5 min of the bat's commuting flight. Because no wind data were available from the study area, we report error estimates from a different application of RAMS [15]. Based on these error estimates, 95% of the wind data estimates are within 0.7 m s⁻¹ of their actual value, with up to 2.4 m s⁻¹ difference under strong (8 m s⁻¹) but rare winds. In addition, error estimates suggest that RAMS might have simulated wind direction with an average of 25° deviation.

(c). Data analysis

Wind direction was defined as the direction to where the wind was blowing. Bat ground speed was calculated using the speed relative to the straight line between origin and destination of each commuting trip, for the entire trip and for each 5 or 2.5 min flight segments during this trip. Using the projection of u and v (west–east and south–north components of the wind, respectively), wind speeds in the direction of the straight line between origin and destination (tailwind speed) were calculated for the entire trip and for each 5 min during this trip. Bat airspeed was calculated by subtracting the estimated wind speed in the direction of the straight line between origin and destination from the bat's ground speed. Bat sideways speed was calculated from GPS locations using the speed in the perpendicular direction to the straight line between origin and destination of each commuting trip. This calculation was made for each 5 or 2.5 min flight segment; no similar analysis was made for entire commuting trips, because bat sideways speed for an entire trip from origin to destination equals zero. Crosswind speed was calculated using the projection of u and v wind speeds in a direction perpendicular to the trip track direction between the start and endpoints of the flight. To test for wind drift compensation, we regressed bat sideways speed in relation to crosswind speed [32,33]. The regression slope is expected not to differ from zero if a bat compensated for lateral wind drift. This may occur if the bat changed its flight heading towards the incoming wind, as illustrated in the electronic supplementary material, figure S1. When bats fully drift sideways, the regression slope is expected to equal one; intermediate values between zero and one are expected when bats partially compensate for crosswind [12,32,33]. To test for possible changes in flight behaviour along the flight track, we made separate analyses for the first two flight segments of each flight (the first 10 min of flight), and the last two flight segments of each flight (the last 10 min of flight), to test whether wind drift occurred at the beginning of the flight while compensation for crosswind took place close to destination, as has been suggested under changing winds [3]. We additionally tested whether bats adjusted their airspeed in relation to tail- and crosswind speed [22,23] to optimize their cost of transport [17,18]. This was accomplished by regressing bat airspeed relative to the wind component in the direction between the trip's origin and destination. The latter relationship was tested using two different scales of movement: (i) an entire commuting trip between the roost and foraging sites (either from or to the roost), and (ii) a 5 min or 2.5 min interval, determined by the GPS data logger's data acquisition rate. In addition, we calculated the relationship between bat ground speed and the crosswind and tailwind velocities to assess whether strong crosswinds and headwinds incurred slower progress towards the destination. To correct for the unequal sample size from different individuals, the data from each bat were weighted based on the inverse proportion of that bat's sample size from the total data from all the bats [15,34,35]. We additionally report the results of the unweighted regression. E. helvum power curve [18] (electronic supplementary material, figure S2) was calculated using published morphological data [36].

3. Results

Straw-coloured fruit bats made long-distance commuting trips (figure 1 and the electronic supplementary material, S3) to and from their roosting colony or between feeding sites (mean ± s.d. of commuting trips: 42.5 ± 17.5 km, n = 37 trips). The bats’ feeding sites were located north–northwest of the colony (mean ± angular s.d. of the relative direction in relation to the roosting colony: 329.5 ± 8.6°). The feeding sites of the bats that were tracked during multiple nights were very similar on different nights except for one bat that switched to a new feeding site within a single night after visiting its first feeding site. This bat returned from its second feeding site to the roosting site in a straight line without passing through its first feeding site, suggesting either previous knowledge of the route or map-like navigation abilities (figure 1). These findings are in line with those reported for Egyptian fruit bats (Rousettus aegyptiacus) from Israel [37].

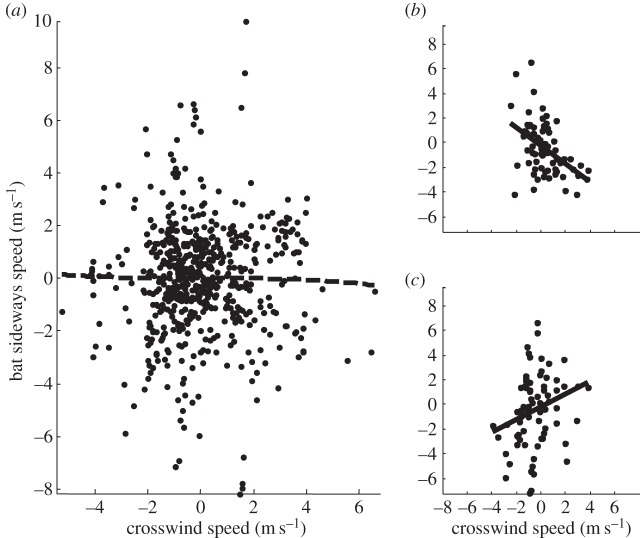
Our analysis suggests that the lateral speed of commuting fruit bats was not related to crosswind speed when the entire flight track is considered (linear regression, Y = 0.031 · X + 0.0001, R² = 0.0005, p = 0.579; figure 2a and electronic supplementary material, tables S1 and S2). The animals seemed to accurately reach their feeding sites and roosting colony, and did not engage in any substantial searching behaviour before landing (figure 1). These findings are in support of our first prediction, suggesting full compensation for lateral wind drift (i.e. bat lateral speed not related to crosswind speed) under constant winds. When considering only the first 10 min of the flight track, our analysis suggests that fruit bats fly in a direction opposite to that of the wind (Y = (−1.01) · X + 0.29, R² = 0.31, p < 0.001), indicating over-compensation of lateral wind (figure 2b and electronic supplementary material, table S1 and S2). When only data from the last 10 min of the flight track are analysed, a significant (p = 0.03), though weak (R² = 0.07), positive relationship between crosswind and bat sideways speed is found (Y = 0.63 · X−0.19), suggesting that the bats may possibly experience a slight wind drift (figure 2c and electronic supplementary material, tables S1 and S2). Bat airspeed decreased under tailwind assistance and increased under headwind (Y = (−0.72) · X + 11.0, R² = 0.201, p = 0.005 and Y = (−0.67) · X + 11.0, R² = 0.155, p < 0.001, for the trip and the 5 min steps scales, respectively; electronic supplementary material, tables S1 and S2). These findings support our second prediction, suggesting that bat airspeed decreases with tailwind assistance and increases under headwinds. In addition, bat airspeed increased with increasing crosswind speed (Y = 1.16 · X + 10.8, R² = 0.397, p < 0.001 and Y = 0.80 · X + 10.7, R² = 0.200, p < 0.001, for the trip and the 5 min steps scales, respectively), and the same was found for bat groundspeed (Y = 1.01 · X + 11.0, R² = 0.378, p < 0.001 and Y = 0.71 · X + 11.0, R² = 0.184, p < 0.001, for the trip and the 5 min steps scales, respectively; electronic supplementary material, table S1), supporting our third prediction, suggesting increase in bat airspeed with crosswind speed. Bat ground speed significantly (p < 0.001) increased under tailwind assistance (Y = 0.32 · X + 10.9) but only for the 5 min timescale (p = 0.256 for the trip scale); however, tailwind assistance explained only 4% of the variation in ground speed (electronic supplementary material, table S1). Hence, bat ground speed was slightly affected by tailwind speed and was overall nearly constant under different tail- and headwind conditions.

Figure 2.

Relationship between bat sideways speed and crosswind speed. (a) All 5 min or 2.5 min timescale flight segments. (b) The first two flight segments (10 min) of each flight. (c) The last two flight segments (10 min) of each flight. The statistical analysis of the relationship using all the data (a) was not significant, suggesting that bats compensate, at least partially, for wind drift. For the first two flight segments (b), we found a negative relationship indicating overcompensation, whereas for the last two flight segments (c), we found a positive relationship indicating wind drift (see details in the electronic supplementary material, table S1).

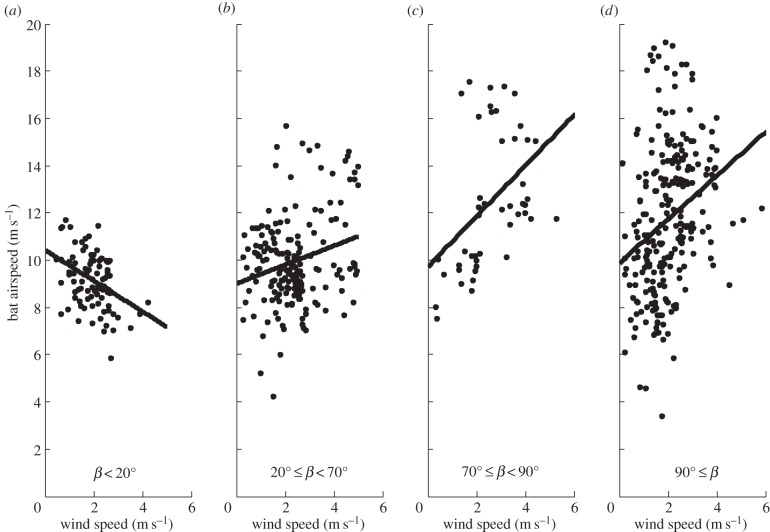
Bats modulated their airspeed in relation to both wind speed and direction (table 1). For wind directions less than 20°, bat airspeed decreased with increasing wind speed (figure 3a). For wind directions between 20° and 70°, bat airspeed moderately increased in relation to bat heading (figure 3b). A steeper slope of this relationship was found for wind directions between 70° and 90° (figure 3c), and between 90° and 180° (figure 3d). Overall, the response of straw-coloured fruit bats to wind (figure 4a) seems to be in general agreement with the predicted response of flying animals to wind (figure 4b). The regression equation is bat airspeed = (−0.57) × tailwind + 0.19 × sidewind² + 10.44 (R² = 0.22). We present the raw data used in this analysis in the electronic supplementary material, figure S4.

Table 1.

Relationships between wind speed (V_w; independent variable) and bat airspeed (V_a; dependent variable) for different sections of wind directions relative to bat heading.

wind direction	model equation	R2	F	p
0–20°	Va = (−0.65) · Vw + 10.43	0.16	17.1	<0.001
20–70°	Va = 0.40 · Vw + 9.00	0.06	11.73	<0.001
70–90°	Va = 1.07 · Vw + 9.71	0.19	10.52	0.002
90–180°	Va = 0.92 · Vw + 9.87	0.10	26.65	<0.001

Figure 3.

Regression analysis of the relationships between bat airspeed and wind speed for different sections of wind directions relative to bat heading. This analysis is based on theoretical calculations outlined in Liechti et al. [13]. Full statistical details of the analysis are reported in table 1. This analysis corresponds well with qualitative predictions as the regressions have a negative slope for wind direction <20° (a), a low positive slope for wind direction between 20° and 70° (b), and a steeper positive slope for wind directions between 70° and 90° (c) and between 90° and 180° (d). See details in table 1.

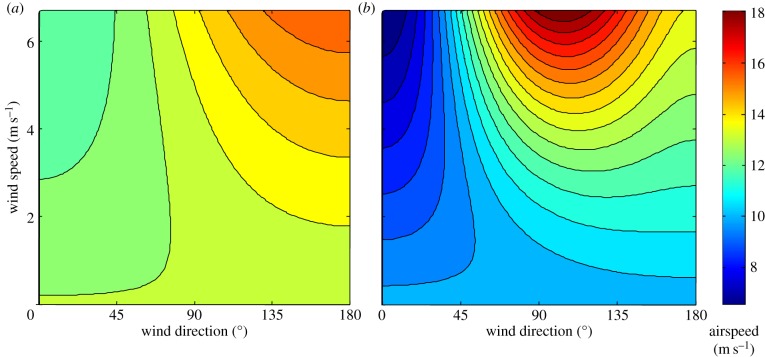
Figure 4.

Calculations of bat airspeed according to the species’ power curve and the wind speed and direction as proposed by Liechti et al. [13]. Bat airspeed is depicted by colour, according to wind direction (x-axis) and wind speed (y-axis). (a) Results of the analysis of tracked Eidolon helvum bats’ data and atmospheric simulations output. (b) Theoretical relationships predicted by Liechti et al. [13], modified for E. helvum using the species’ power curve (see Material and methods).

4. Discussion

Commuting between roosting and feeding sites is a key activity in the daily cycle of many animals, including fruit bats, with consequences for bat metabolism, foraging, navigation and social behaviour. To reach their feeding sites, bats need to compensate for the effects of crosswinds which may necessitate advanced navigational capabilities [37]. Flying directly to the destination site without searching for it is highly advantageous as it may substantially reduce the cost of travel. Nevertheless, such flights may require complicated behavioural responses in relation to wind conditions [13]. By adjusting their heading (electronic supplementary material, figures S1 and S2), bats departing from their roosting colony successfully negotiate their long journeys every night to reach specific feeding sites before returning to their roost. Airspeed modulation in relation to tailwind assistance (figures 3 and 4a, table 1 and electronic supplementary material, S1) is another way by which the bats may reduce their cost of travel [17,18,22]. Moreover, bats adjusted their airspeed under various wind speeds and directions in accordance with the predictions of a two-dimensional optimal flight model (figures 3 and 4 [13]; see below). Hence, our findings suggest that commuting straw-coloured fruit bats move in a highly beneficial manner compared with a naive flyer not adjusting its flight to encountered wind conditions.

Overall, wind conditions during a single journey were rather constant (electronic supplementary material, figure S3), and this may enable the bats to maintain a single behavioural response along the track (wind drift compensation) as opposed to the predicted response under changing winds (drift at the start of the journey and compensation near destination [3]). Indeed, our results suggest that bats did not use the latter behavioural response. Nevertheless, bats overcompensated for wind drift at the start of their flight, which is intriguing. Equally as intriguing was the finding that bats slightly drifted near their destination. Yet, in this case, drift explained only 7% of the variation in bat sideways speed, and thus the magnitude of this effect was subtle, at most. We note that the pattern of overcompensation at the beginning of the flight trajectory and drift near the end of the track is predicted by the solution of Zermelo's navigational problem [2].

The present study has tested the two-dimensional model proposed by Liechti et al. [13], and its findings show a qualitative agreement with optimal flight behaviour under various wind conditions (figure 4). Earlier studies either ignored the predictions of this model, presumably owing to difficulties in estimating wind vectors, or used a unidimensional approach by separately testing the effects of tail- and crosswinds, as we did in the first part of our analysis (electronic supplementary material, table S1). While this approach is highly informative, it cannot answer whether flying animals may adjust their flight to reduce their cost of transport by integrating information on wind direction and speed under a wide range of wind conditions. Moreover, most previous studies that tackled this question found no airspeed adjustments in relation to the wind vector in different species and under a wide range of ecological contexts [38,39]. The study of Hedenström et al. [22] demonstrated airspeed adjustments among migrating arctic birds (not separated by species), and both tailwind and crosswind effects were detected, but with the latter being opposite to the effect predicted by the model (decrease of airspeed with increasing crosswind speed). Crosswind effects on airspeed were also found in a study of migrating swifts [23], but no differences with regard to tail- or headwind were traced in this study. It was consequently concluded that swifts increase their airspeed with wind speed, regardless of its direction. In addition to Hedenström et al. [22], several tens of other studies suggested airspeed adjustments in relation to the predicted relationship between tailwind assistance and airspeed, and it has been consequently concluded that birds generally follow this relationship [40]. For insects, evidence suggests similar response in relation to tailwind assistance for bees [41], dragonflies and butterflies [7]. Specifically, for migrating Pantala dragonflies, airspeed adjustments were detected in relation to tailwind assistance but not in response to crosswinds. The latter study also reported a notable exception of a day-migrating moth that did not adjust its airspeed. Unlike these studies dealing with migrating animals, the present study revealed airspeed modulation in relation to tailwind assistance in mammals engaged in commuting flights.

While airspeed adjustments in relation to tailwind assistance were evident as predicted by theory, an intriguing finding of this study is that groundspeed was nearly constant under very different tailwind conditions, although predicted to increase with tailwind assistance [18]. Maintaining a constant groundspeed during flight may facilitate the buffering of wind effects through airspeed adjustments in migrants that may use different methods of navigation such as landmarks following or optic flow [5,7]. Flight at a constant groundspeed may further facilitate measurement of the total distance travelled [42], which may be important for bats to locate specific feeding sites and their communal roosts.

Overall, the successful arrival of bats to their destination under various wind conditions can be regarded as a convergent movement pattern with migratory noctuid moths and passerine birds that travel over much longer distances [6,19]. Our findings suggest that commuting fruit bats compensate for crosswind effects in a manner similar to that found for flapping birds [6], as both groups seem to rely on their powerful flight to mitigate the effects of wind, as opposed to noctuid moths that attain considerably slower airspeeds. Moreover, bat airspeed adjustments with regard to cross- and tailwind speed show similar patterns to those of birds and insects [7,22,23,40]. We consequently suggest that behavioural adjustments aiming to minimize the cost of transport under various wind conditions have independently evolved in various aerial animal taxa. This demonstrates a wide generalization in responding to external factors during movement (sensu [43]) despite different ecological contexts, taxony and medium (air or water [2]). The specific mechanisms involved may strongly depend on flight performance (the motion capacity sensu [43]), specifically on the airspeeds of the focal groups relative to prevailing wind speeds.

Data on free range flights of bats are limited and, owing to practical challenges in following bats for long durations, were usually measured over limited spatial scale [21]. When no field data are available, one may use a flight model to estimate bat airspeeds [22]. Yet, results of laboratory studies [44] and those of the present study suggest estimated airspeeds using a computer model [45] are considerably higher for E. helvum than measured airspeeds. For example, the minimum power speed was found to be 7 m s⁻¹ [44], whereas it was estimated by the flight model to be 10.4 m s⁻¹ [45]. Similarly, this study measured the bats’ cruising speed and found it to be 11 m s⁻¹, whereas it was estimated to be 13.9 m s⁻¹ by the flight model [45] (under the assumption that bats use the maximum range speed as their cruising speed to minimize their cost of transport during commuting). These differences probably explain why the bats’ measured airspeeds (figure 4a) were lower than predicted airspeeds (figure 4b), albeit similarly varying with wind direction and speed (see also [21]). Other studies [46,47] have additionally reported substantial aerodynamic differences between flapping bats and birds, suggesting that flight models developed for birds should be applied with caution to predict the airspeed of bats.

The technological progress that allows the high-resolution tracking of animals in this study as well as in other studies [37,48] enhances the understanding of different aspects of animal movement ecology [43]. Recently, high-resolution atmospheric simulations have been applied to study how meteorological conditions may shape the soaring behaviour of migrating birds [10,15]. Our study demonstrates the advantages of using detailed atmospheric modelling and rigorously tests predictions related to the effects of external factors (wind vectors) on commuting flyers. The combination of numeric atmospheric simulations and detailed animal tracking is thus critically important for enhancing the understanding of the movement ecology of aerial animals.

Data accessibility

The data used in this study are available on Movebank (http://www.movebank.org, study name ‘Fruit bats in Ghana (data from Sapir et al. 2014)’) and are published in the Movebank Data Repository with doi:10.5441/001/1.62s17b4v.

Funding statement

Funding was provided by the Max Planck Institute for Ornithology and the University of Konstanz.