Auto-aggregation in zoospores of Phytophthora infestans: the cooperative roles of bioconvection and chemotaxis

Abstract

Phytophthora infestans is a highly destructive plant pathogen. It was the cause of the infamous Irish potato famine in the nineteenth century and remains to this day a significant global problem with associated costs estimated at $3 billion annually. Key to the success of this pathogen is the dispersal of free-swimming cells called zoospores. A poorly understood aspect of zoospore behaviour is auto-aggregation—the spontaneous formation of large-scale patterns in cell density. Current competing hypotheses suggest that these patterns are formed by one of two distinct mechanisms: chemotaxis and bioconvection. In this paper, we present mathematical and experimental results that together provide strong evidence that auto-aggregation can only result from a combination of these mechanisms, each having a distinct, time-separated role. A better understanding of the underlying infection mechanisms of P. infestans and potentially other Phytophthora species will in the longer term lead to advances in preventative treatment and thus potentially significant savings in socio-economic costs.

1. Introduction

The oomycetes are a highly destructive group of pathogens responsible for considerable economic losses in both agriculture and aquaculture [1]. Of the over 500 known oomycetes, perhaps the most prominent species is Phytophthora infestans. As early as 1876, it was discovered that P. infestans was the cause of potato late blight disease and, consequently, the devastating Irish potato famine in the nineteenth century [2]. Late blight can spread extremely rapidly and completely destroy entire fields of crops within one to two weeks of the first signs of infection [3]. Billions of dollars are still lost every year to the disease in a combination of crop losses and spending on control measures, hence P. infestans is considered to be an ongoing major global pest [4].

There are numerous similarities between oomycetes and filamentous fungi. However, a closer inspection of morphology as well as genetic studies reveals significant differences between the two. In fact, the oomycetes are now classed as part of the Stramenopile kingdom. Oomycetes have a zoosporic stage in their life cycle, to which the wide and fast spread of late blight can mainly be attributed. Zoospores are single-nucleated, wall-less, non-proliferating cells and are specialized for dispersal in order to infect new hosts. The anatomy of a zoospore is fairly simple: they are bean shaped and have a groove into which two flagella are inserted, which are used for swimming. Given the right environmental conditions, namely cold and wet (below approx. 12°C [3,5]), P. infestans zoospores are released from zoosporangia emerging from infected plant tissue into aqueous environments. They can swim for many hours with the help of internal food reserves (most likely lipids) [6] and exhibit a variety of homing responses. For example, both chemotaxis and electrotaxis have been found to help guide oomycete zoospores towards plant roots [7–9]. After a zoospore arrives at some site on the host, the flagella are shed, the cell becomes immobile and builds a cell wall in a rapid process called encystment [10]. These cysts are adhered to the host by unknown substances, after which they are able to infect host cells directly [11].

1.1. Zoospore auto-aggregation

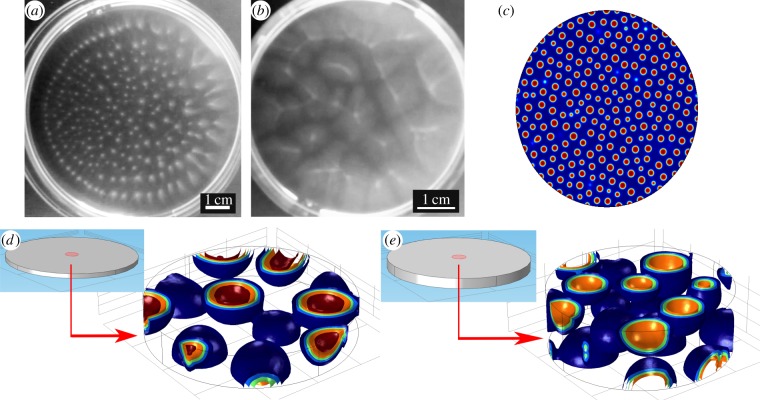
It is known that zoospores of P. infestans (and other species) are able to form micro- and macro-scale patterns in the absence of external signals. It is the macro-scale patterning, which we will refer to as auto-aggregation, that will be the main focus of this paper. We acknowledge that other names for this phenomenon have been used in the past, such as ‘aggregation’ or ‘pattern swimming’ (see [12,13] and [14], respectively). Ko & Chase [13] first described this process for zoospores of Phythophthora palmivora. For low-concentration zoospores, no patterns are generally observed. However, given a sufficiently concentrated suspension of zoospores (10⁵–10⁶ cells ml⁻¹), high-density bands are typically observed, which then break up to form spots with the highest concentration of cells at their centre and a surrounding low-density ‘cloud’. Figure 1a,b displays typical macroscopic patterns. Once established, patterns can be dispersed by gentle shaking of the Petri dish, but soon re-form, suggesting that they are caused by actively swimming cells [15]. In the present literature, two opposing mechanisms have been proposed for this pattern formation process. We discuss these hypotheses below.

Figure 1.

Auto-aggregation patterns in a suspension with varying depths. (a) Three-millimetre-deep suspension showing distinct spot formation (dish diameter 90 mm). (b) Seven-millimetre-deep suspension showing the formation of bands (dish diameter 60 mm). Photographs (a,b) were taken 5 min after the suspension was poured into the dish. (c) Simulation of the chemotaxis-only model in a circular, 9-cm-wide domain. The pattern wavelength is approximately 5–6 mm, which is in agreement with that in (a). (d) Three-dimensional simulation of the chemotaxis-only model in a shallow domain (depth 3 mm, diameter 9 mm). (e) Three-dimensional simulation of the chemotaxis-only model in a deep domain (depth 7 mm, diameter 9 mm). Aggregation is identical in images (d,e), regardless of depth. Colours: blue to red in all simulations represent low to high zoospore density (≈0.5 × 10⁵ to 3 × 10⁶ ml⁻¹). The initial cell density was set at 10⁶ zoospores ml⁻¹ and subjected to small, random perturbations.

Chemotaxis, in this case the directed motion of zoospores up chemical gradients, is known to play a major role in the infection process. For instance, the zoospores of many species of Phythophthora and Pythium have been found to exhibit a chemotactic response to a wide variety of chemicals exuded from plant roots [7,16,17] as well as towards encysted cells, which act to amplify the original signal and recruit more cells once a suitable infection site has been found [18–20]. Based on these observations, it has been speculated that auto-aggregation patterns may also be the result of chemotaxis, but towards an unknown attractant released by swimming zoospores [1,21]. It is thought that this mechanism could help to increase infection potential in the absence of any host stimulus.

Recent experimental evidence reported by Ochiai et al. [14] for P. citricola zoospores led the authors to discount chemotaxis as the main driver of auto-aggregation; as an alternative, they proposed zoospore bioconvection. Bioconvection is a well-studied phenomenon in microorganisms that are slightly denser than their suspending fluid and, owing to one of a number of mechanisms, display a tendency to swim towards the suspension surface. This creates a dense layer of cells at the fluid surface that becomes unstable as a result of gravity, creating so-called convective plumes (figure 2a,b). In the case of zoospores, surface accumulations of Phytophthora megasperma cells were observed by Ho & Hickman [22,23], the reason for which was determined to be cell up-swimming after ruling out other possible factors. Subsequent experiments by Cameron & Carlile [24] produced similar findings for zoospores of other Phytophthora species. The most likely explanation for this behaviour was found upon closer examination of the cell shape. In a study of zoospore morphology, Ho et al. [25] reported that Phytophthora zoospores are larger at the rear than at the front, causing cells to point slightly upwards as they swim, a phenomenon known as gyrotaxis [26]. A comprehensive overview of bioconvection in microorganisms and mathematical modelling approaches can be found in [27] and references therein.

Figure 2.

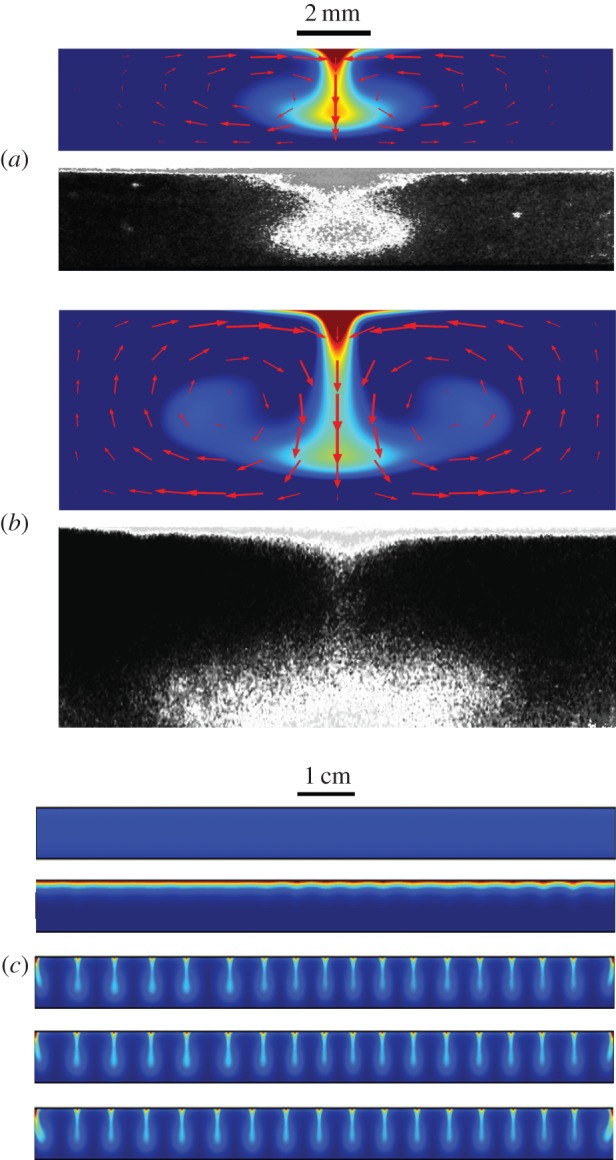
Simulations of the bioconvection-only model show that the structure of zoospore aggregates is consistent with bioconvection. (a,b) Comparison of a single, simulated plume (upper panels) and plume photographs (lower panels) for suspension depths of 3.5 and 7 mm, respectively. Red arrows indicate the direction and magnitude of fluid velocity and show that plumes are produced by convection. The size and structure of simulated plumes are in agreement with our experimental results. (c) Simulation of bioconvection in a 9-cm-wide domain yields an array of plumes with similar size and structure to those shown in figure 1a. The patterns remain steady after long times. Snapshots from top to bottom are at times 0, 4, 7.5, 15 and 450 min (snapshots have been vertically stretched for ease of visualization). In all simulations, the colours blue to red represent low to high zoospore density (≈0–10⁷ ml⁻¹). In (a,b), the initial data were chosen such that the plumes formed in the centre of the domain for computational convenience. In (c), the initial density was set at 10⁶ ml⁻¹ and subjected to small, random perturbations.

In this paper, we present what we believe to be novel experimental observations of the auto-aggregation of P. infestans zoospores over extended time scales. Moreover, we present for the first time a combined bioconvection–chemotaxis mathematical model to describe this process. Our observations and numerical simulations led us to conclude that the current hypotheses for the mechanism of auto-aggregation offer only a partial description of the observable patterns. In fact, we submit that a combination of bioconvection and chemotaxis operating on two different time scales is required to fully explain auto-aggregation behaviour in P. infestans zoospores.

2. Results

2.1. Auto-aggregation patterns form rapidly and are dependent on suspension depth and container geometry

Zoospore auto-aggregation was investigated in varying suspension depths and container geometries. Figure 1a,b shows images of an experiment in which an 8 ml suspension was used in 90 and 60 mm Petri dishes, which resulted in suspension depths of 3 and 7 mm, respectively. In the shallow suspension, a regular arrangement of light (cell dense) spots formed rapidly (within 5 min), with characteristic wavelength of approximately 0.4–0.6 cm (see figure 1a here, and fig. 4 and the related movie in [28]). Each spot marked an aggregate of zoospores, which was approximately radially symmetric, with maximum density at the centre, decreasing towards the detectable edge (radius 0.6–2 mm). A notable feature was the circular boundary of the pattern, which tracked the edge of the container. (The slight blurring on the right-hand side was due to unevenness of the surface on which the dish was placed, causing the suspension to be deeper at this side. This phenomenon is discussed below.) In square dishes, the inner region again displayed the characteristic spot pattern, but the boundary of the patterned area was square (electronic supplementary material, figure S2). The mechanism that controls this component of the pattern formation is not clear and could be the result of meniscus effects or initial flow patterns induced on pouring of the suspension into the dish. In an experiment in which fluid motion was induced manually by shaking the dish from left to right, aggregates distinctly formed at the left and right of the dish (electronic supplementary material, figure S3), suggesting that the initial fluid motion was influencing the initial positions of aggregates.

In suspension depths of 7 mm, different patterns were produced: aggregates were larger in size and had far more irregular shapes, with ridges or bands forming alongside individual spots (figure 1b). The time taken for the formation of these auto-aggregation patterns was again around 5 min. However, the characteristic wavelength of the pattern was increased (to ≈7–12 mm). To investigate the effect of a continuous variation of depth on pattern formation, a tilted Petri dish was used. Band patterns appeared at the deep end and spot patterns at the shallow end, with a gradation of pattern-type occurring between the two (electronic supplementary material, figure S4).

2.2. The mathematical model predicts that chemotaxis alone cannot account for the observed fast-forming auto-aggregation patterns

At present, no auto-attractant for P. infestans has been identified. We therefore considered whether a mathematical model could pinpoint the role, if any, of chemotaxis in the pattern formation detailed above. Given the scale of the observed patterns, we used a population (cell density) model combined with a continuum description of the fluid suspension. The model, given in (4.1), has three main components: the zoospore cell density, the suspension fluid velocity and the level of the chemotactic signal. Two mechanisms for aggregation behaviour were included—chemotaxis and bioconvection. Chemotaxis is the biased random movement of individuals (zoospores) towards an attractive chemical source. In this case, it is assumed that the zoospores themselves release this chemical and thus the process is one of auto-attraction. Bioconvection usually refers to the coordinated motion of large numbers of microscopic swimming organisms through a suspending fluid. In our case, the zoospores are assumed to exhibit gyrotactic bioconvection, i.e. their shape and centre of mass ensures that, on average, the cells swim in an upward direction. Thus, the model comprised a union of the well-known Keller–Segel model for chemotaxis [29,30] with the Navier–Stokes equations for fluid flow including a model for gyrotactic bioconvection, first proposed by Pedley et al. [31]. To the best of the authors’ knowledge, this is the first such dual mechanism model, and a full derivation and analysis is presented in the electronic supplementary material.

On considering chemotactic effects only (setting in (4.1)) qualitative predictions of the model looked extremely promising at first inspection. From an initially uniform distribution of cells, the model predicted the formation of localized aggregations. These were spots with a similar size and formed a pattern with a similar characteristic wavelength to that seen in the experiments (see figure 1a,c). For computational ease, these simulations were conducted in planar geometry, which can be viewed as a reasonable approximation for shallow suspensions. However, other qualitative and quantitative features of the in silico patterns did not match with experimental observations. The time taken for the model pattern to form was several orders of magnitude greater than that for the observed patterns (60 h in simulation time compared with 5 min for the experimental observation). Moreover, the in silico patterns did not contain the characteristic circular outer boundary noted in figure 1a. In fact, the in silico patterns generated by chemotaxis alone were independent of container geometry (see figure 1c and the electronic supplementary material, figures S5 and S6). These qualitative features were essentially insensitive to parameter values in the model. The time taken for the patterns to form and their wavelength could be altered by varying, for example, the strength of the chemotactic response or the degradation rate of the unknown chemoattractant (see [32] for further related discussions). However, parameter sensitivity tests revealed that full agreement with experimental observations could not be achieved: the correct pattern wavelength or the correct time for patterns to form could be obtained, but not simultaneously (see the electronic supplementary material, figures S7 and S8). Moreover, to achieve agreement in either wavelength or formation time required the use of unphysical parameter values.

In order to test the effects of suspension depth on chemotaxis-induced pattern structure, the model was solved in a full three-dimensional spatial geometry. Recall that it was observed that suspension depth had a marked effect on the aggregation pattern (figure 1a,b and the electronic supplementary material, figure S4). On the contrary, the chemotaxis-only model predicted no such dependency. Figure 1d,e illustrates model simulations representing shallow and deep suspensions, respectively, and it is clear that the patterns formed in each case are very similar: there is no marked change in the structure or characteristic wavelength of the pattern. In conclusion, the model simulations provide strong supporting evidence to discount the hypothesis that chemotaxis on its own can be responsible for the fast-forming aggregation patterns reported here and elsewhere.

2.3. Initial pattern formation is consistent with bioconvection

In order to investigate whether bioconvection alone could rapidly generate aggregation patterns, we studied solutions of the mathematical model, this time in the absence of any chemotactic effects (χ set to 0 in (4.1)). Bioconvection simulations in three dimensions are extremely computationally expensive and proved impossible for the large-scale pattern formation processes under consideration here. Therefore, to test a number of hypotheses and for ease of comparison with the experimental data, bioconvection was simulated in a planar geometry representing a vertical section through a diameter of the suspension (the patterns were observed to be either essentially radially symmetric or irregular, so the choice of diameter was unimportant). Restricted three-dimensional simulations of single aggregation plumes were conducted, which displayed very similar properties to those correspondingly predicted by the two-dimensional simulations (electronic supplementary material, figure S9).

2.4. Zoospore aggregates form bioconvective plumes

Figure 2a,b (lower panels) shows examples of zoospore aggregations in shallow and deep suspensions, respectively, viewed from the side. The aggregates clearly form plume-like structures that are typical of structures associated with bioconvection (e.g. [33,34]). The macro-scale patterns shown in figure 1a,b comprise a regular array of these aggregates. Recall that it was observed that these structures formed rapidly (5 min). Numerical simulations of the model further support the hypothesis that bioconvection is responsible for these rapid-forming structures. In the absence of bioconvection, the model predicted that the position of aggregates appeared to be random within the suspension. Moreover, non-bioconvective model aggregates were predicted to be irregular ‘globular’ shapes with the depth of suspension having no effect on the shape or distribution of these structures (figure 1d,e). On the contrary, considering only bioconvection, the model predicted the formation of characteristic plumes that appeared stable, for appropriate suspension depths. Figure 2 shows a comparison of single in silico plumes with photographed plumes for different suspension depths (3.5 and 7 mm), which shows the size and shape of plumes in each case to be in good agreement with model predictions. Red arrows show the direction and magnitude of fluid velocities in each of these cases: at the surface, zoospores are focused towards the centre of the plume, where the density is highest, and pulled downwards into the region of most rapid down-flow. A more complete picture of signal plume formation in this case is shown in the electronic supplementary material, figures S9–S13. These simulations further support the hypothesis that the initial spot formation shown in figure 1a,b is produced by bioconvection.

Figure 2c shows simulated bioconvection in a wide and shallow chamber (90 × 3 mm), representing a vertical cross section of a Petri dish typically used in experiments. Randomly perturbed uniform initial data (equivalent to an initial zoospore concentration of ≈10⁶ zoospores ml⁻¹) were used to simulate the conditions at the beginning of a typical auto-aggregation experiment as shown in figure 1a,b. An array of plumes formed within 5 min; a time scale very close to that seen experimentally. The wavelength of the plume distribution was approximately 5 mm. This is again in close quantitative agreement to our experimental results (see figure 1a). (The distorted plumes at the left- and right-hand edge are most likely a result of a numerical artefact owing to the boundary conditions.) Crucially, the plumes remained stationary after long times (≈8 h simulation time). Numerical experiments with non-uniform initial data were also conducted for shallow depths: plumes shifted to become regularly spaced and then remained stationary (electronic supplementary material, figure S14). In deeper suspensions (7 mm), stability broke down: plumes shifted, merged and split and no steady arrangement was reached (see the electronic supplementary material, figure S15).

2.5. Long-term auto-aggregation patterns require chemotatic attraction between plumes

Previous investigations of auto-aggregation have typically focused on pattern formation in the first few minutes after a suspension has been placed into a Petri dish [12–15]. However, we have found that there are interesting patterning dynamics at work over time scales of many hours that merit attention.

Figure 3a shows images captured every 30 min from a long-running experiment. The first image displays the fast-forming auto-aggregation patterns discussed above. Subsequently, these spots are seen to slowly drift towards one another and combine to form fewer, but larger, aggregates. This drifting appeared not to be random, although, from the experimental results alone, we could not discount the possibility that the movement of aggregates was the result of other credible factors including the intrinsic stochasticity in zoospore swimming patterns, encystment, biocovective entrainment or electrostatic charge. We considered each of these alternatives in turn. The reproducible nature of both the qualitative and quantitative aspects of aggregation, both in vitro and in silico, essentially eliminated the possibility that this is a ‘chance’ phenomenon. Encystment is likely to occur over the long time scale of the experimental observations, but zoospores of P. infestans are denser than the suspension and hence sink on encystment (or indeed cell death). These cells are consequently fixed at the base of the Petri dish and thus cannot play any significant role in the merging of the aggregates, which have their density maxima at the surface of the suspension. However, we did observe slight ‘streaking’ of the plumes at the very final stages of the aggregation process that might be the result of the lower parts of the super-aggregates being attached to the cysts that are attached to the base of the Petri dish (see the electronic supplementary material, figure S16c). We could rule out bioconvective entrainment on a number of grounds. First, the model simulations discussed above predicted that, in the absence of chemotaxis, the swimming behaviour of the zoospores was dominated by gyrotaxis and that steady, fixed aggregation plumes were formed (in appropriately shallow suspension depths). This was true even when the initial cell concentration was much higher in certain parts of the computation domain than others—after a transient period, evenly spaced, stable plumes were formed (electronic supplementary material, figure S15). Finally, in deep domains, where it was observed that stable plumes do not form, the quasi-plume-like structures continually merged and split. So again, even in this case, entrainment could not be viewed as a stable plume-forming mechanism. Electrostatic attraction at the individual cell level could be ruled out immediately. There is no reason to suppose the individual zoospores could exhibit different electrostatic polarities and hence auto-attraction would be very unlikely. To eliminate any possible effects of an electrostatic field being generated by the Petri dish, the experiment was repeated in a glass Petri dish, but there was no change in the observed patterns and so we discounted this possibility (see the electronic supplementary material, figure S16). Finally, it is known that zoospores use chemotaxis to locate suitable infection sites in part by the chemotactic sensing of cysts [19]. So, certainly, they have the ability to alter their swimming patterns in response to chemical gradients. Hence, although not conclusive, we reasonably proposed the auto-attractive mechanism to be chemotaxis. To test this hypothesis, we conducted simulations of the full bioconvection–chemotaxis model, the results of which were in line with many features of experimentally observed long-term behaviour as we now discuss.

Figure 3.

Long-time-scale coarsening of the zoospore distribution pattern. (a) Zoospore aggregates drift towards one another leading to fewer, more dense plumes. Images are of a zoospore auto-aggregation experiment taken every 30 min (top left to bottom right). First image taken approximately 5 min after the suspension was poured into a 90 mm Petri dish. The suspension depth was approximately 3 mm and the initial concentration of zoospores was approximately 7.8 × 10⁵ zoospores ml⁻¹. (b) Simulation of the bioconvection–chemotaxis model predicts the formation, drifting and merging of plumes on an appropriate time scale. Snapshots taken at times equivalent to (top left to bottom right) T = 5.5, 33, 37, 63, 69 and 79 min. The domain shown is 1.2 cm wide. Colours: blue to red represent low to high zoospore densities (≈0–10⁷ zoospores ml⁻¹).

Simulation results for the full bioconvection–chemotaxis model are shown in figure 3b. Plumes formed as in the bioconvection-only simulations, but were subsequently drawn together by chemotaxis. In fact the time scale of this merging was in quantitative agreement with our experimental observations, e.g. the merging of the left and middle plumes in figure 3b took approximately 30 min (see the electronic supplementary material, figure S15). Just before merging took place, the smaller of the two plumes appeared to be distorted as it neared the larger, middle plume (T = 33 min). Otherwise, the overall structure of the plumes remained roughly unaltered. Subsequently, the two remaining plumes started to drift together and finally only one remained near the centre of the domain (T = 75 min). This final plume was steady. The zoospore density and the overall size of the final plume were slightly greater than the corresponding measures in the initial plumes. Similar drifting and merging behaviour was seen in simulations with wider chambers (see the electronic supplementary material, figure S17).

3. Discussion and conclusion

In this study, we provide strong evidence that auto-aggregation of zoospores is driven by a combination of two distinct mechanisms: bioconvection and chemotaxis, and that these mechanisms operate on significantly different time scales. We arrived at this conclusion by using a combination of laboratory experiments and mathematical modelling. The model comprises a union of a Keller–Segel-type system for the chemotactic component with a gyrotatic bioconvection model in the spirit of Pedley. Each component of the model in isolation provides a rich solution structure, and further details are provided in the electronic supplementary material. A more in-depth analysis of the model can be found in [35], and for the chemotactic component in isolation, further analysis is presented in [36]. Full three-dimensional space simulations were constructed for the chemotactic and bioconvective components in isolation (see figure 1d,e and the electronic supplementary material, figure S9). However, simulations of the combined model (4.1) were conducted in two spatial dimensions, either in planar or side aspect geometry. This was dictated by the available computing power. Our system did not have sufficient memory to allow us to compute an accurate time evolution of solutions of the full model in three space dimensions. However, after comparing the three- and two-dimensional simulations, we are confident that the latter are sufficient to capture the important qualitative and quantitative features of the system. A discussion of the model parameters used and how they were estimated is provided in the electronic supplementary material. These were set using a synthesis of information from existing literature, our own experimental observations and by a comparison of model solutions with experimental observations. A parameter sensitivity analysis is presented in the electronic supplementary material. As expected, the model solutions are not in general sensitive to small relative changes in parameter values, but qualitative and quantitative changes do occur as key parameters are pushed through critical values. In line with common procedures, the analysis and numerical simulations were conducted using the non-dimensionalized system (electronic supplementary material, S13–S15). Thus, the non-dimensional parameters represent groups of dimensional parameters. Variations in these non-dimensional parameters therefore represent variation of any one of the group. Thus, the simulations presented in the electronic supplementary material, figures S7 and S8, which display the effects of changing the (non-dimensional) chemotactic sensitivity parameter χ, could represent the consequence of, for example, variations in initial cell density (suspension concentration), the chemotactic sensitivity or the random motility of the cells.

Biconvection and chemotaxis are both concentrative phenomena. Therefore, it is intuitive that each of these processes could potentially lead to zoospore populations in a natural environment becoming more localized, hence increasing infection pressure at spatially distinct sites. We have shown that each of these mechanisms has a specific role to play: bioconvection causes the rapid auto-aggregation of zoospores into plumes that have a maximum density at the surface of the suspension. Only when these aggregates have formed is chemotaxis sufficiently strong to drag these together to form super-aggregates over a much longer time scale. For zoospores of P. infestans, the relevant situation to consider is a population of zoospores confined to a water droplet on the surface of a plant leaf. For example, the usual route for late blight infection of potato leaves is from a water droplet attached underneath a leaf. Potato leaves may be infected on either surface, and although sporangial load may be higher on the upper surface, zoospore-derived infections are more likely to be initiated in the leaf margins and tips of the underside of the leaf where water droplets are retained the longest [37,38]. Hence, the concentration of zoospores at the top of the bioconvective plumes predicted here would act to focus the zoospore close to the leaf surface. For a suspension of zoospores in a droplet on the top surface of a leaf, the implications of the mixed bioconvective–chemotactic processes discussed here are not immediately obvious. However, some recent interesting results regarding auto-aggregation of another microorganism may reveal a possible reason. A bioconvection study by Dombrowski et al. [39] of the Gram-positive bacterium Bacillus subtilis in water droplets showed that when aggregation plumes formed at the surface of the drop, they moved down the curved meniscus. This led to a high accumulation of cells at the narrow contact region at the water–air–solid boundary. If this were also the case for zoospores, accumulation of this type would presumably be advantageous as high concentrations of zoospores would be brought into contact with the plant leaf supporting the water droplet. Moreover, perhaps given the high density in these regions, zoospore–zoospore chemotaxis would amplify this effect, concentrating the zoospores to one site on the contact edge. While we believe the dual mechanism of bioconvection–chemtaxis explains auto-aggregation for zoospores of P. infestans, it remains to be investigated whether this could also explain auto-aggregation processes for root pathogenic oomycetes. Further experimental work and modelling in this area is likely to yield interesting and useful results.

4. Material and methods

Detailed descriptions of all methods are given in the electronic supplementary material.

4.1. Strains and conditions

Phytophthora infestans (strain 88069) plates were grown over 12–14 days on rye agar medium with 2% sucrose added at 18°C [40]. New plates were inoculated by transferring three agar plugs from fully grown plates. Sporangial cleavage and zoospore release was initiated by flooding plates with 10 ml of cold water. The water was ordinary tap water and not autoclaved or de-mineralized as these practices have been known to inhibit zoospore release in past experiments. The flooded plates were left in a cold room at 4°C to release the zoospores over an average 2–3 h period depending on the efficiency of zoospore release.

To harvest zoospores, a sterile glass spreader was used to gently scrape the liquid off the surface of the plate. Suspensions were filtered through a 40 μm cell strainer to remove any empty sporangia, mycelia or other debris. To determine zoospore concentrations, samples from a suspension were placed in a haemocytometer with depth 0.1 mm. Cells were counted from left to right in five grids with an area of 0.04 mm² and this number was scaled appropriately in order to determine the concentration per millilitre. The counting process was repeated three times and an average was used. Photographs of macro-scale patterns (plan view and side aspect) were taken with a Nikon Coolpix 8800 digital camera and the microscopic stills from these experiments were taken using a Leitz Labovert microscope and Infinity Capture software. The contrast and colour of the images were adjusted using Photoshop CS6 in order to make the patterns as clear as possible.

4.2. Mathematical modelling

Our goal was to investigate the validity of each of the hypotheses discussed above in isolation, and finally a combination of both. In order to do this, it was necessary to construct the following bioconvection–chemotaxis model, given in a non-dimensional form below

4.1

The equations are assumed to hold in a spatial domain, with depth, H, measured in the z-direction. This model comprises the Navier–Stokes equations for the velocity of the suspending fluid, combined with mechanisms for chemotaxis (the Keller–Segel model [29,30]) and cell movement via gyrotatic bioconvection [31,41]. The main variables are the fluid velocity, u(x,t), the density of zoospores, n(x,t), and the concentration of chemoattractant, c(x,t).

For a full explanation of the model equations including dimensional and non-dimensional parameter values, see the electronic supplementary material.

PDE (g) and Laminar flow (ns) (incompressible) modules were used in COMSOL (COMSOL Multiphysics webpage: http://www.uk.comsol.com/) to solve the bioconvection–chemotaxis model and Lagrange (Quadratic) shape functions were used in all spatial discretization with the exception of Lagrange (Linear) functions used for excess pressure, p_e. Full details of the COMSOL set-up can be found in the electronic supplementary material.

Funding statement

A.I.M.S. was supported by a Scottish Life Science Alliance Studentship. Our work was supported by the BBSRC and NERC (L.G.B., S.W., P.v.W.) and the University of Aberdeen (P.v.W.).