Dark-field hyperspectral X-ray imaging

Abstract

In recent times, there has been a drive to develop non-destructive X-ray imaging techniques that provide chemical or physical insight. To date, these methods have generally been limited; either requiring raster scanning of pencil beams, using narrow bandwidth radiation and/or limited to small samples. We have developed a novel full-field radiographic imaging technique that enables the entire physio-chemical state of an object to be imaged in a single snapshot. The method is sensitive to emitted and scattered radiation, using a spectral imaging detector and polychromatic hard X-radiation, making it particularly useful for studying large dense samples for materials science and engineering applications. The method and its extension to three-dimensional imaging is validated with a series of test objects and demonstrated to directly image the crystallographic preferred orientation and formed precipitates across an aluminium alloy friction stir weld section.

1. Introduction

X-ray radiography and the subsequent development of computed tomography (CT) has revolutionized modern physical sciences opening up the ability to ‘see’ the three-dimensional internal structure of an object [1]. The most usual contrast mechanism is via X-ray attenuation from interactions with electrons in a material, producing two-dimensional images of the projected electron density on the detector (imaging the bright-field). Electrons also scatter X-rays which, if collected, can add additional contrast and sensitivity to the projected image (imaging the dark-field) [2–4]. By using X-ray diffractometers or spectrometers, the scattered or the emitted radiation can be analysed and exploited to obtain quantitative information about the sample, for example, its crystalline or chemical content [5–7]. In all cases, the images obtained make use of monochromatic ‘pencil’ beams where much of the radiative power of the source X-rays has been discarded by the beam definition process; these images are built by beam scanning and are not directly obtained [8]. Here, we introduce a new method to quantitatively image the dark-field capturing images directly, making use of the full flood field of available beam and importantly, its full spectral output. By recording the information dispersed in X-ray wavelengths, large area two-dimensional images of the entire sample are recorded simultaneously yielding information on the material's physical and chemical state in every pixel. We apply and demonstrate the method to image selected samples relevant to materials science. The novel aspects of this approach enable specific physical and chemical information to be non-destructively imaged in a single radiograph.

X-ray powder diffraction (XRD) is a key structural characterization tool widely used in the identification of single or multi-phase minerals and materials, solving and/or refinement of crystal structures, analysis of solid-state phase transitions and the determination of micro-strain or crystallinity. X-ray fluorescence (XRF), on the other hand, is used as a probe for elemental and chemical analysis. Both methods are non-destructive yielding averaged structural or chemical information from within a scattering volume but unfortunately lack three-dimensional spatial resolution. The combination of these characterization techniques with imaging/tomography was a major scientific advancement, giving researchers a unique ability to see the fundamental three-dimensional crystalline or chemical composition in a variety of complex heterogeneous materials [5,9,10]. To do this, a small cross-sectional X-ray beam (commonly known as a pencil beam) is raster-scanned and/or rotated around a sample, recording diffraction patterns or emission spectra at every point. Data are then reconstructed to yield the two- or three-dimensional crystalline or chemical arrangement of the object. This approach has shown a great deal of success in revealing the complex internal and hitherto unknown structure in a variety of heterogeneous materials, including: biological tissues [11], pigments/paintings [12], cements [13], composite materials [14], nuclear fuels [15] and catalysts [16]. A major drawback of scanning beam tomography is the inherently long acquisition times, generally limiting applications to two dimensions or to studying static systems.

Hyperspectral imaging refers to the collection of data using an imaging spectrometer; a device which gather hundreds of images covering a broad wavelength continuum sampled with a narrow bandwidth, producing hyperspectral ‘data cubes’ (dimensions: spectral domain×spatial domain×spatial domain) [17,18]. The term is traditionally associated with satellite-based remote sensing for military surveillance, mineralogical, geological or environmental applications; typically operating in the optical or infrared regions of the electromagnetic spectrum [19]. This concept can be extended to X-rays. The construction of X-ray imaging spectrometers has only recently been possible owing to the development of efficient photon counting solid-state detectors and advanced integrated circuitry. Systems, currently available, boast only a few hundred or thousand pixels, however applications to imaging are becoming increasingly popular because of the additional information that these devices can provide [20,21]. We combine the benefits of such detectors with a novel data collection strategy and show how the resulting images can be analysed to yield specific material and chemical information in every pixel.

2. Results

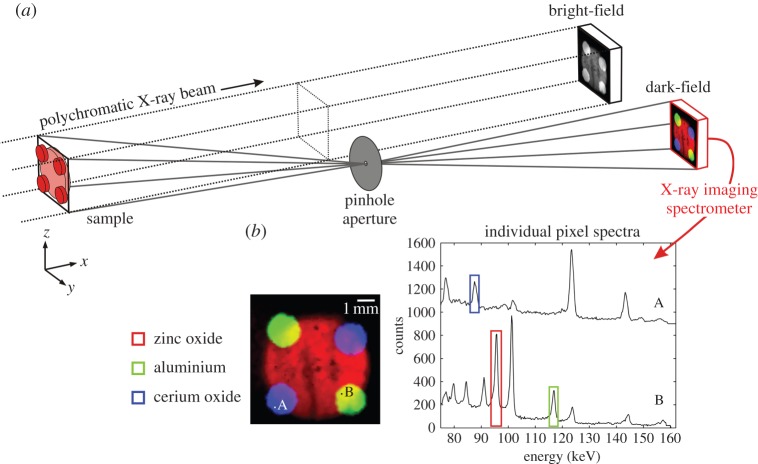
The principle of the experiment is shown in figure 1. A polychromatic X-ray flood-field beam is used to illuminate a sample, which after attenuation produces a bright-field image which is sensitive to the projected electron density within the sample. This traditional imaging method typically yields good contrast but does not give any information on the specific material or chemical content of the object. Such information can be extracted from the scattered or emitted radiation. In order to image the dark-field, we use an off-axis pinhole aperture positioned at low-angle to the direct beam (typically in the range 1^°−5^°). The pinhole defines a set of divergent ray paths producing independent line integrals through the sample and this projects onto an X-ray imaging spectrometer, recording the energy, E, of the scattered radiation on a pixel-by-pixel basis. This yields hyperspectral ‘data cubes’ (dimensions E, y and z) which can be analysed directly. The principal signal source is energy-dispersive XRD, defined by collimation through the pinhole aperture and the areal size of an individual pixel. Bragg peaks appear in the spectra corresponding to the interplanar spacings of the crystalline material. By integrating over specific spectral bands, materials can be identified, imaged and colour-coded to aid interpretation. In this case, three bands were selected and imaged corresponding to diffraction peaks, identifying zinc oxide (red), aluminium (green) and cerium oxide (blue), all in a single projected image. Additional analysis can be subsequently performed by inspecting individual pixel spectra. In this way, structural information, such as lattice parameters, structure refinement, preferred orientation, grain size or strain, can be determined in a user-defined part of the sample.

Figure 1.

Dark-field hyperspectral X-ray imaging. (a) A flood-field polychromatic X-ray beam illuminates a sample, which after attenuation yields a bright-field image. The dark-field is imaged using an off-axis pinhole aperture projecting signals onto an X-ray imaging spectrometer. (b) Individual pixel spectra show distinct diffraction peaks corresponding to different materials within the sample. By integrating over specific spectral bands materials can be mapped accordingly.

A positive feature of this technique is that it simply uses the polychromatic nature of the source X-rays, meaning complicated optics, such as monochromators, focusing mirrors or zone plates, are not required. This is advantageous in reducing the experimental set-up time and cost while increasing the available flux at the sample position, improving sensitivity to weakly scattering materials. A novel aspect of the method is the use of a pinhole aperture. The pinhole not only defines a set of independent divergent ray paths, but also generates a geometric magnification (typically in the range 0.1×−10× magnification), which can be adjusted by altering the focal length. This facilitates studying samples either much larger than the detector or allows the user to ‘zoom-in’ for region-of-interest studies. In addition, pinholes can be easily interchanged enabling compromise between operational flux and spatial resolution.

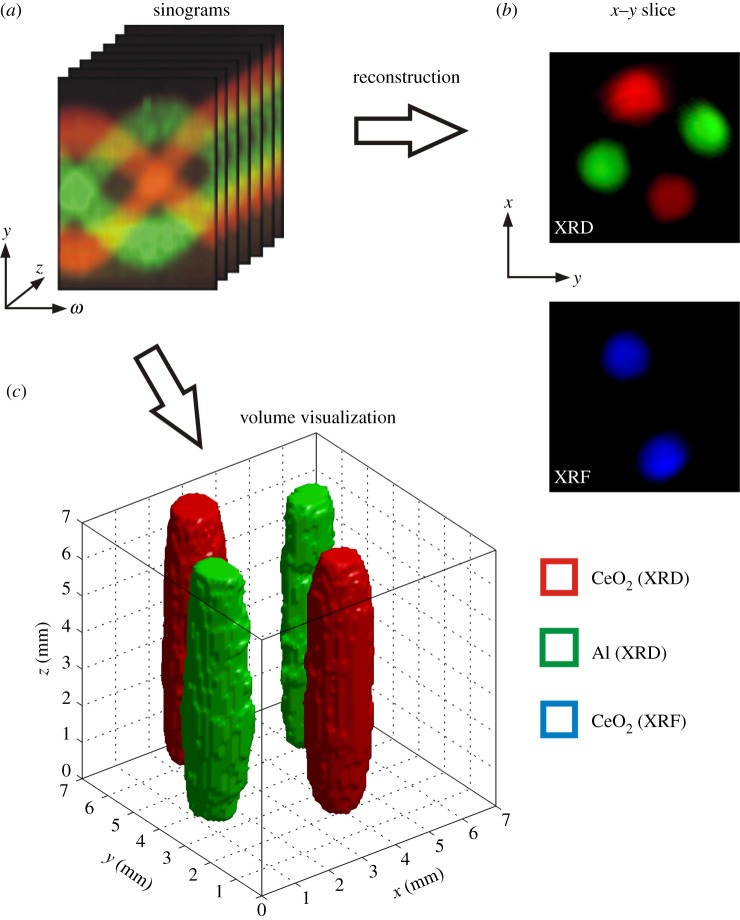
By exploiting the radiographic nature of the imaging method, it is also possible to perform three-dimensional imaging by using standard CT techniques [22]. Figure 2 demonstrates this, where two different materials (aluminium and cerium oxide) have been packed into four tubes in an attempt to resolve the three-dimensional structure. Rotation of the sample around the vertical axis and recording projections at specific angles yields sinograms that show the spatial variation in the image domain (y- and z-directions) as a function of rotation angle (ω) (figure 2a). Three-dimensional image reconstruction can then be performed whereby individual slice planes can be extracted (figure 2b) or full three-dimensional volumes can be visualized (figure 2c). Given the hyperspectral nature of the data, three-dimensional volumes can be segmented using multivariate analysis [23]. Here, we used cluster analysis to group voxels based upon their spectral profiles. This approach is unique; the segmentation is based upon the spectral properties alone rather than thresholding grey levels, as is the case for conventional X-ray CT. We can also segment data based upon the choice of scattering signal. For example, in regions containing cerium oxide we can identify both XRF (Ce Kα @ 34.5 keV and Ce Kβ @ 39.3 keV) and XRD signals, which can be easily separated in the energy domain. In this case, XRD signals are confined to higher energies (typically more than 50 keV) owing to the flux profile of the source, whereas XRF signals are in the lower energy range (typically less than 50 keV). This enables simultaneous chemical and structural imaging; all of which is contained within the same radiograph.

Figure 2.

Tomographic hyperspectral imaging in two and three dimensions. (a) Recording radiograph projections for successive rotation steps of the sample produces sinograms for every row (z-direction) of the detector. (b) Individual slice planes can be reconstructed using standard algorithms using either XRD or XRF signals. Alternatively (c) an entire three-dimensional volume is segmented based upon the spectral profiles in every voxel using cluster analysis (three clusters) and visualized.

By using area detectors, the method is also faster than scanning beam techniques. In this example, exposure times were in the range of 2–5 min per image depending on the desired data quality, yielding hyperspectral images containing 6400 pixels. Current monochromatic XRD scanning beam methods typically have acquisition times in the range of 0.1–1 s per projection, depending on the desired data quality and available experimental equipment [5,16,24]. Based upon these numbers, the hyperspectral method in its current form is at worst two times faster and is potentially up to 50 times faster than scanning beam techniques (see the electronic supplementary material for further calculation details). The speed increases are even better when compared with scanning energy-dispersive XRD methods (typically used for residual stress mapping of thick metallic samples). In this case, exposure times are typically in the range of 30–60 s per projection [25,26], meaning the hyperspectral method in its current form is of the order of 1500 times faster for mapping/imaging. These comparisons are based upon current modestly sized energy-dispersive pixelated detectors; future developments promise faster frame-rates and larger areas with devices already in construction offering four times as many pixels [27]. A major limitation of energy-dispersive XRD methods is their restricted spatial resolution when compared with focused monochromatic X-ray beams which can achieve spatial resolutions down to low micrometre or sub-micrometre levels. These kinds of spatial resolutions are not possible with energy-dispersive methods which cannot be focused evenly throughout the spectral range, however using the described pinhole projection strategy we can easily obtain spatial resolutions of 100 μm, with an estimated lower limit of around 25 μm (see the electronic supplementary material for further calculation details).

Additional benefits of the method include the ability to study specimens housed in special environments (for example, furnaces, loading rigs or other containment vessels) for in situ materials characterization, where unwanted scattering from cell walls/windows are negated. Because we are using high-energy X-rays (more than 50 keV) which have large attenuation distances in dense materials (e.g. metals) sample cell walls or containment vessels essentially become transparent, making the method ideal for studying materials exposed to high temperatures or pressures. Furthermore, there are no sample size limitations associated with this method, which can be a constraint for scanning beam methods [28].

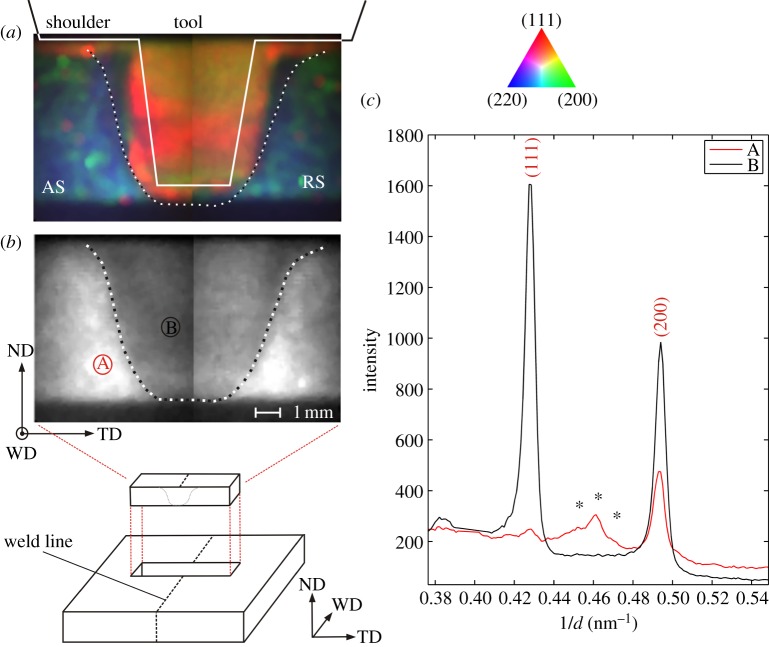
To demonstrate the capabilities for materials science applications, we studied an aluminium alloy friction stir weld. The alloy in question is AA7050-T6, designed for lightweight strength, toughness and resistance to stress-corrosion cracking, commonly used in aircraft and other aerospace structures [29]. Friction stir welding (FSW) is a modern advanced solid-state joining process with several advantages over fusion welding methods, in particular good mechanical properties in the as-welded condition [30]. Understanding the microstructural properties of the welded work-piece as a function of key parameters, such as tool shape, rotation and traverse speed, is critical to improving weld strength and toughness. Here, we examine an FSW using the stationary shoulder technique, a design which reduces the through-thickness temperature gradient, yielding superior mechanical strength across the weld [31]. A sample section (measuring approximately 6×6×40 mm) was cut and removed from the welded plate and placed in the X-ray beam for analysis. We took two radiographs spanning the weld line giving a field of view of approximately 7×13 mm, with the scattering vector parallel to the normal direction (ND). The principal signal was diffraction from (111), (200) and (220) planes of the matrix aluminium which we observed to exhibit a strong preferred orientation. Figure 3a shows the spatial variation of the crystallographic texture across the weld section presented as a composite RGB image depicted as the intensity from the (111) [R], (200) [G] and (220) [B] reflections. Inside the central weld nugget we recorded a strong signal, which is predominantly red in colour, indicating a preferred alignment of (111) planes parallel to the sheet surface (〈111〉//ND), consistent with previous findings [31]. The microstructure of the central weld nugget is dominated by the rotating tool resulting in a very fine-grain structure owing to dynamic recrystallization and strong deformation texture from the extreme thermo-mechanical processing. Outside the weld nugget, the colour is predominantly blue/green, here the (111) peak intensity drops to zero which is indicative of the crystallographic texture of the as-rolled aluminium plate. We also observe red colours directly underneath the shoulder of the tool, again indicating strong scattering from (111) planes in this locality, most probably resultant from a higher heat load underneath the shoulder. Figure 3b shows the scattering intensity of the weld at an equivalent reciprocal d-spacing of 0.46 nm⁻¹. Here, we see high intensity outside the weld region, but inside the intensity falls away. The interface between these regions is highlighted by a black and white dotted line which is also overlaid in figure 3a. The observed higher intensity is attributed to scattering from minority phase precipitates in the base metal. 7xxx series aluminium alloys are known to contain, among others, MgZn₂ precipitates, however, FSW is known to dissolve these precipitates inside both the weld nugget and thermo-mechanically affected zone [32]. Inspection of individual diffraction patterns outside the weld (figure 3c) shows a small broad peak at a reciprocal d-spacing of 0.46 nm⁻¹ which disappears inside the weld. Stars indicate the theoretical positions of the (112), (201) and (004) diffraction reflections from hexagonal MgZn₂. These results have given an unprecedented insight into the complex microstructure of aluminium alloy FSWs, the information of which is all contained within a single radiograph.

Figure 3.

Application of hyperspectral imaging to an aluminium alloy friction stir weld. The normal direction (ND), welding direction (WD) and transverse direction (TD) of the welded plate are shown in the bottom left of the figure. (a) Preferred orientation in the weld section presented as an RGB composite based on the diffraction intensity of the (111) [R], (200) [G] and (220) [B] peaks from the aluminium matrix. The advancing side (AS) and retreating side (RS) of the weld section are shown. The approximate outline of the welding tool and shoulder is drawn as a solid line. (b) Scattering intensity at an equivalent reciprocal d-spacing of 0.46 nm⁻¹; a drop in intensity within the weld is observed. The interface between the two regions is highlighted by a black/white dotted line which is also superimposed on (a). (c) Diffraction patterns from outside (A, red line) and inside (B, black line) the weld. Stars indicate the theoretical positions for hexagonal MgZn₂ diffraction peaks (112), (201) and (004), respectively.

3. Discussion

We have developed a hard X-ray imaging method that is sensitive to the dark-field from both diffraction and fluorescence signals. Using a novel pinhole projection strategy and collecting information dispersed in X-ray wavelengths, we have shown how material and chemical specificity can be obtained in every pixel of a radiograph. Information about the physical state of the sample can be extracted, for example, by using standard XRD powder analysis, quantities such as particle size, crystallographic preferred orientation or strain can be imaged non-destructively. By means of area detectors, the method is also faster than scanning beam techniques, opening up the ability to perform practical full three-dimensional volume imaging or dynamic studies. The method will have application to studying a variety of materials. It should be particularly useful for studying time-resolved processes, such as imaging the formation or transport of material inside large opaque apparatus, or structural rearrangements occurring within objects that result from external applied stimulus (temperature, pressure, etc.) or pre-existing internal drivers such as chemical or electrochemical gradients. Such measurements are not limited to high-flux sources. Indeed, owing the nature of the type of beam used, the method should be easily transferable to the laboratory making use of existing high-power X-ray tubes. In addition, the method is open to further exploitation, for example, using total scattering to obtain characteristic signals from amorphous/semi-crystalline materials (e.g. for medical and security applications [33,34]) and ultimately pair-distribution analysis opening up the potential to image small nanocrystalline and amorphous materials (invisible to standard XRD techniques) allowing identification without a priori knowledge.

4. Methods

Measurements were conducted at beamline I12 of Diamond Light Source Ltd, UK. The beam source is a 4.2 T superconducting multi-pole wiggler offering white beam X-rays which after pre-filtering by 12 mm of copper had a useful energy range between 70 and 200 keV. The beam flux at the sample position is 3×10⁸ ph s⁻¹ mm⁻²/0.1%bw @ 100 keV. The X-ray beam was defined by slits to a size of 8×8 mm². A thick circular tungsten pinhole aperture (diameter 400 μm) was positioned off-axis using motorized stages, defining a mean diffraction angle of 2θ=3^° and geometric magnification of 2.65. The X-ray imaging spectrometer consists of a 1 mm thick CdTe single crystal detector (20×20 mm²) bump-bonded to a large area ASIC packaged with a high performance data acquisition system. The detector is cooled to approximately 8^°C and operated under an applied bias voltage of −500 V at a frame rate of 10 kHz. It has 80×80 pixels on a 250 μm pitch with a sensitivity range of 5–200 keV and resolution of approximately 600 eV @ 59.5 keV and approximately 1400 eV @ 141 keV [21]. During operation, each photon event has its charge and pixel position and the frame in which it occurs recorded. Events are processed and histogrammed according to measured charge, using a total of 800 bins. During this process, a charge-sharing strategy is used to deal with events that may have resulted from the sharing of charge between two or more pixels (these being a subset of neighbouring events in a single frame). Hyperspectral images were energy-calibrated such that each pixel has a common energy axis; the calibrations for each pixel were found from their response to known gamma emission lines from the radioactive decay of ²⁴¹Am. In addition, owing to the spatial variation of the projected scattering angle on the detector, an angular correction is required to bring diffraction peaks onto a common axis. This was calculated and employed using a three-dimensional ray-tracing algorithm based on the known measured positions of the pinhole and detector. The calculated centre pixel energy broadening from collimation is ΔE/E=9.8×10⁻³, with inner and outer pixels varying by ±8% of this value. Image exposure times were in the range of 2–5 min depending on the desired data quality. For CT experiments, the sample was rotated around 180^° in a total of 60 steps, recording a projection image at each step. Tomographic reconstruction was performed using the Simultaneous Algebraic Reconstruction Technique method [22]. Data analysis and volume visualization were performed using custom-written analysis routines in Matlab (v. 7.12, Mathworks, 2011). The aluminium alloy studied was AA7050-T6 with major element weight per cent composition: 5.7–6.7% Zn; 1.9–2.6% Mg; 2.0–2.6 Cu; 0.10–0.15 Zr; balance Al. FSW was conducted at a rotation speed of 1500 r.p.m. and a traverse speed of 100 mm min⁻¹.

The technique at present is not flux limited, that is, we are currently operating at the highest frame rate achievable with our detector system and with large amounts of incident X-ray beam absorption pre-filtering. As such we believe that this experiment could be feasibly performed in the laboratory using high-powered X-ray tubes, as opposed to using synchrotron radiation. All that is required is polychromatic hard X-radiation covering a broad spectral range suitable for energy-dispersive XRD.

Funding statement

This work was undertaken with EPSRC funding granted through EP/H046577/1, EP/F007906/1 and EP/I02249X/1.