Developmental models for estimating ecological responses to environmental variability: structural, parametric, and experimental issues

Abstract

Developmental models that account for the metabolic effect of temperature variability on poikilotherms, such as degree-day models, have been widely used to study organism emergence, range and development, particularly in agricultural and vector-borne disease contexts. Though simple and easy to use, structural and parametric issues can influence the outputs of such models, often substantially. Because the underlying assumptions and limitations of these models have rarely been considered, this paper reviews the structural, parametric, and experimental issues that arise when using degree-day models, including the implications of particular structural or parametric choices, as well as assumptions that underlie commonly used models. Linear and nonlinear developmental functions are compared, as are common methods used to incorporate temperature thresholds and calculate daily degree-days. Substantial differences in predicted emergence time arose when using linear vs. non-linear developmental functions to model the emergence time in a model organism. The optimal method for calculating degree-days depends upon where key temperature threshold parameters fall relative to the daily minimum and maximum temperatures, as well as the shape of the daily temperature curve. No method is shown to be universally superior, though one commonly used method, the daily average method, consistently provides accurate results. The sensitivity of model projections to these methodological issues highlights the need to make structural and parametric selections based on a careful consideration of the specific biological response of the organism under study, and the specific temperature conditions of the geographic regions of interest. When degree-day model limitations are considered and model assumptions met, the models can be a powerful tool for studying temperature-dependent development.

1 Introduction

Developmental models, such as degree-day models, simulate the temperature dependence of developmental processes in order to estimate the timing or range of an ecological process, such as the emergence of a pest, or the establishment of a species in a particular climatic zone. Rather than express development as a progression through time, these models typically describe development as a composite of time and temperature. Degree-day models account for the cumulative sum of degree-time products, with daily time steps resulting in units of “degree-days”. Degree-day models are parsimonious, requiring in their simplest form the estimation of only two parameters; their simplicity and ease of use has led to their broad application across a range of organisms.

Degree-day models were initially developed for agricultural applications and have been used since the 1730s (Reaumur 1735) to estimate optimal timing of fertilization and harvest (Sharratt et al. 1989), to assess the suitability of a given region for specific crops (Ren et al. 2007), to predict the timing and intensity of pest infestation (Dahlsten et al. 1994; Elliott et al. 2009; Nahrung et al. 2008), to anticipate the spread of invasive species (Hartley et al. 2010; Hemerik et al. 2004), and to investigate the impact of biological control (Gutierrez et al. 2011). Because of their widespread use in agriculture, many local agencies make freely available yearly estimates of accumulated degree-days for local crops and pests (University of Illinois 2011; University of California 2011; University of Wisconsin 2011).

One increasingly popular application of degree-day models is in the study of the effects of climate change on populations of organisms whose distribution and development are highly dependent upon temperature, particularly organisms involved in the maintenance of important human diseases. A common method involves determining the annual degree-days that are required to support current populations, and then, using projected temperatures, generating estimates of the spatial distribution of locations where annual degree-day requirements are met under future conditions. Statements are then made regarding the future risk or potential for disease transmission. Some examples include the use of degree-day models to study the effects of climate change on the malarial parasite and malarial mosquito vectors (Lindsay et al. 2010; Yang et al. 2010), the tick vector of Lyme disease (Ogden et al. 2005, 2006), and the intermediate snail host and water-borne life stages of human schistosomes (Yang et al. 2006; Zhou et al. 2008). Many of these studies consider not only the degree-day requirements of the host organism, but also the degree-day requirements of the infectious agent within the host. Analogous analyses have estimated the change in the number of insect generations per year under climate change scenarios (Yamamura and Kiritani 1998).

Though applications of degree-day models are numerous and diverse, the limitations and underlying assumptions of degree-day models are rarely considered or discussed, despite the fact that model output is sensitive to choices regarding model structure, and to uncertainties in model parameters. Previous work has examined degree-day model assumptions and their limitations (Allen 1976; Pruess 1983; Higley et al. 1986; Roltsch et al. 1999; Bonhomme 2000; Bergant and Trdan 2006; Moore et al. 2012), and it is well established that the degree-day model is a simplistic representation of a potentially complex developmental process. Bonhomme (2000) discusses various limits to the degree-day approach in an agricultural context, including the influence of linearizing non-linear development. We extend this line of thought, providing an example of how the linear degree-day model provides substantially different results than non-linear developmental models. Allen (1976), Pruess (1983), and Higley et al. (1986) compare various methods used to estimate accumulated degree-days from temperature data - also in an agricultural context - yet do not examine the various ways upper temperature thresholds are included in such models. We expand on these analyses by comparing the most common methods used to estimate accumulated degree-days, and assessing the dominant ways upper temperature thresholds are incorporated. This analysis is similar to that of Roltsch et al. (1999), but on a shorter time scale and across a broader geographic range.

We begin with a generalized definition of degree-day models, and a description of methods used for estimating model parameters and accumulated degree-days. We next examine the implications of assuming linearity in the developmental response to temperature, and provide an example comparing results from various methods used to calculate degree-days. We conclude with a brief discussion of other important factors that should be considered when applying degree-day models to ecological studies.

2 Methods

2.1 Generalized model of temperature-dependent development

Temperature-dependent development models describe progress towards a developmental target, such as the completion of an instar stage or the onset of reproductive maturation. Let ρ be the rate of development (in units of day⁻¹), where ρ is a function of temperature, T. The gain in development, D, is given by

$$\frac{dD}{dt}=\rho (T).$$ (1)

The total development that occurs in the interval from time t₁ to t₂ is given by the integral of Eqn 1 (Logan and Powell 2001; Powell and Logan 2005). Thus,

$$D={\int }_{t_1}^{t_2}\rho (T(t))dt,$$ (2)

where D is normalized such that D = 0 at the start of development, and D = 1 when the developmental target is reached. Since temperature dependence is not uniform over the full range of environmental temperatures, the rate of development can further be written as

$$\rho (T)=f(T,{\delta }_{min},{\delta }_{\text{opt}},{\delta }_{max}),$$ (3)

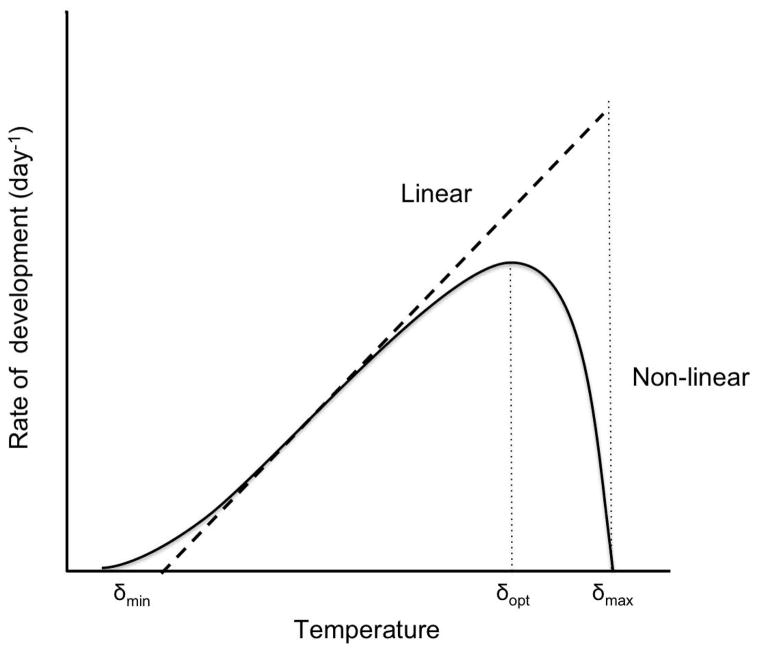
where ρ is expressed as a functional response, f, to temperature given three threshold parameters: δ_min, δ_max, and δ_opt. Development is limited (i.e. goes to zero) below a lower temperature threshold, δ_min, and above an upper temperature threshold, δ_max. Development rate is maximized at an optimum temperature, δ_opt.

Mechanistically, the relationship between temperature and development rate is based on the change in biochemical and enzymatic activity as temperature changes (per “Metabolic Theory (Brown et al. 2004; Molnar et al. 2013)). While there are many structural forms available to represent the functional response, degree-day models generally assume a linear f. The performance of linear versus non-linear functional responses varies depending upon the specific shape of the diurnal temperature curve - and thus on regional climate characteristics - in addition to the modeled organism’s specific threshold requirements, as described next.

2.2 Degree-day model theory

2.2.1 Developmental functional response

Typical degree-day models express the linear rate function as

$$\rho =\{\begin{array}{ll}\frac{T}{K}-\frac{{\delta }_{min}}{K}\hfill & :{\delta }_{min}<T(t)<{\delta }_{max}\hfill \\ 0\hfill & :\text{else}\hfill \end{array},$$ (4)

and thus

$$D(t)=\{\begin{array}{ll}{\int }_{t_1}^{t_2}(\frac{T}{K}-\frac{{\delta }_{min}}{K})dt\hfill & :{\delta }_{min}<T(t)<{\delta }_{max}\hfill \\ 0\hfill & :\text{else}\hfill \end{array},$$ (5)

where the optimal threshold, δ_opt, is excluded (Fig. 1), and parameter K is a species- and developmental target-specific parameter that is interpreted biologically as the total number of degree-day units necessary for development to complete. To see how this interpretation is reached, the linear model can be scaled by multiplying through by K, leading to

Fig. 1.

Relationship between organismal rate of development and temperature. A linear (dashed line) and non-linear (solid line) approximation of the relationship between the rate of development and temperature, and the locations of the three key temperature thresholds, δ_min, δ_opt, and δ_max.

$$k=K·D={\int }_{t_1}^{t_2}(T(t)-{\delta }_{min})dt$$ (6)

for all T where δ_min < T < δ_max. In this expression, k represents the number of degree-day units that are accumulated in the interval from t₁ to t₂, and the developmental target is reached once D = 1, or when k = K. Rescaling the linear model in this way provides a simple expression that relates the degrees above the minimum threshold to the development that results.

The linear model provides a straightforward, accessible method of estimating development rates. However, for many organisms temperature-dependent development is non-linear (Beck 1983), and treating the response as linear leads to an underestimation of development rates at low temperatures, and an overestimation of development rates at high temperatures (Hilbert and Logan 1983) (Fig. 1). The linear model is thus best applied when environmental temperatures fall within intermediate temperature ranges for which the linear approximation is valid (Bonhomme 2000; Bergant and Trdan 2006). Since organisms routinely experience temperature extremes well outside these intermediate ranges, several non-linear models have been developed as alternative functional forms of f (Kontodimas et al. 2004).

2.2.2 Temperature thresholds

Two thresholds, δ_min and δ_max, bound the temperature range in which development occurs in degree-day models. Below δ_min or above δ_max development ceases, while the third threshold, δ_opt, represents the temperature at which the organism has the highest rate of development. Though δ_min and δ_max can easily be specified in the linear model, δ_opt is defined only in non-linear models since linear models have no temperature associated with peak development (except as T → δ_max). To account for the fact that development exhibits diverse behaviors at high temperatures, linear models have been modified with several threshold cutoff methods (Roltsch et al. 1999). One method, the vertical cutoff (Fig. 2a), treats the maximum threshold as previously described, where above δ_max development ceases. In this method, the optimum temperature threshold is undefined. A second method, the horizontal cutoff (Fig. 2b), sets the daily temperature to δ_max when the temperature exceeds the upper threshold. This allows development to continue at a constant rate at all temperatures exceeding the maximum threshold. Finally, using the intermediate cutoff method (Fig. 2c), development proceeds at a decreasing rate as the temperature increases above δ_max, and thus δ_opt = δ_max. Generally, the development that occurs when T > δ_max is set equal to (T ) −2[ρ(T ) − ρ(δ_max)], which is equivalent to subtracting twice the development that occurs above the maximum threshold from the development that would occur if no upper threshold was considered (Roltsch et al. 1999). Other formulations can be used for intermediate cutoffs to incorporate a steeper or more gradual decline in development rates above δ_max, and, though not often done, an additional threshold can be included above which development ceases entirely. Many degree-day applications do not substantiate the choice of thresholds, and thus fail to address conclusions that might have been supported on the basis of alternative threshold types and values. Indeed, including different thresholds can lead to widely differing projections (see Results) and thus the method chosen should most closely mimic the behavior of the studied organism at high temperatures.

Fig. 2.

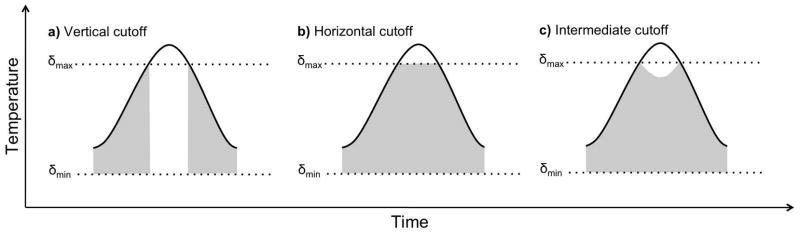
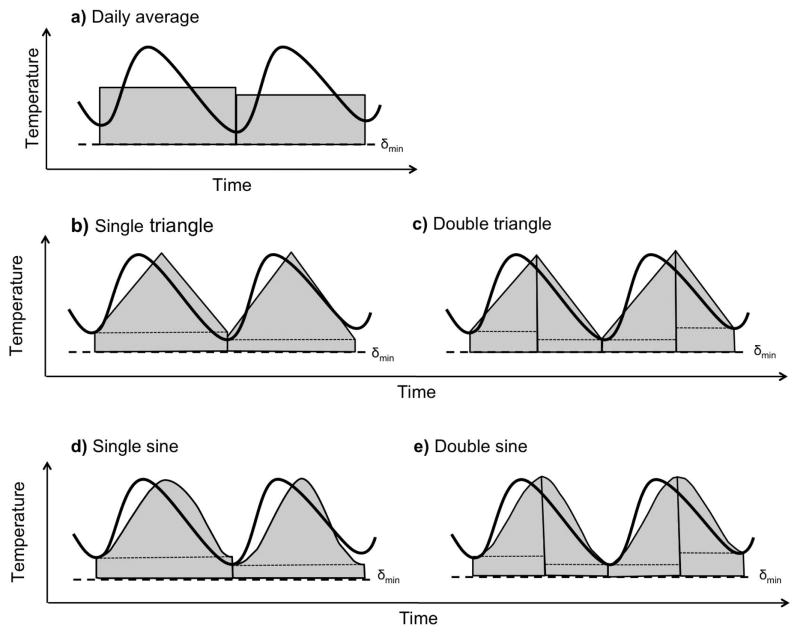
Temperature threshold cutoff methods. Three common cutoff methods used when calculating daily degree-days. a) vertical cutoff; b) horizontal cutoff; c) intermediate cutoff. Each curve represents the temperature over the course of a single day, while the shaded area indicates the timing and degree of development.

In addition to selecting appropriate temperature threshold types, accurate organism-specific parameter values for δ_min, δ_max, and δ_opt are crucial. The most common method used to determine δ_min is to first experimentally derive the temperature-development rate relationship by determining the number of days, d, required for an organism to develop at a range of constant temperatures. Then the development rate, 1/d, is regressed on temperature and the intercept is estimated by solving for the temperature at which the rate is equal to zero (e.g. Campbell et al. (1974); Lardeux and Cheffort (1997); Nahrung et al. (2008); Naves and de Sousa (2009)). Importantly, due to the high mortality or dormancy commonly experienced at low temperatures (Campbell et al. 1974), the intercept always falls outside the range of experimental temperatures, and thus represents an extrapolation of the linear fit (Bergant and Trdan 2006). Additionally, as described above (Fig. 1), the non-linearity of most developmental response functions at low temperatures results in an overestimation of δ_min using linear regression. Extrapolation error and error associated with linearly approximating a non-linear process can lead to significant uncertainties in the estimation of δ_min (Yang et al. 1995; Bergant and Trdan 2006), yet these uncertainties are often disregarded. Importantly, there are also indications that development at constant temperatures differs from development at fluctuating temperatures, and thus care should be taken when applying laboratory-derived estimates to field conditions (Campbell et al. 1974; Beck 1983; Brakefield and Mazzotta 1995).

To estimate δ_max and δ_opt, non-linear developmental models are generally used (Roy et al. 2002; Kontodimas et al. 2004). For many non-linear models, these thresholds appear explicitly within the model equation, and thus can be estimated using non-linear regression (e.g. Briere et al. (1999); Sanchez-Ramos and Castanera (2001); Tobin et al. (2001)) With non-linear models in which one or both of these thresholds cannot be directly estimated, δ_max or δ_opt can often be calculated from other model parameters (Roy et al. 2002).

2.2.3 Degree-days, K and k

Only linear models can provide a direct estimate of K, the total degree-days required for developmental completion. One approach, similar to the intercept method used to estimate δ_min, is to estimate K as the inverse of the slope of the regression of development rates and temperature (e.g. Campbell et al. (1974); Trudgill et al. (2005); Bergant and Trdan (2006)). Another approach to estimating K, assuming δ_min is known, involves a laboratory experiment in which the organism is reared at a constant temperature, T, and the total degree-days required for development is estimated as K = d(T −δ_min), where d is the number of days required for development (Naves and de Sousa 2009). Values of K estimated using this method have been shown to be similar to estimates using the linear regression approach (Naves and de Sousa 2009).

If experimental data are unavailable, K can be calculated from field data - again assuming a known δ_min - using observed development times and daily temperature data (Lopez et al. 2001). Since daily temperature is not constant, the degree-days accumulated per day, k, are calculated using one of the methods presented next, and the summation of k over the observed development period can provide an estimate of K.

The daily degree-days accumulated, k, is generally calculated using daily minimum and maximum temperatures, although temperature fluctuations that occur within the diurnal cycle can strongly influence organism development (Paaijmans et al. 2009). Common methods used include the daily average method, the triangle and double triangle methods, and the sine and double sine methods (Fig. 3), all of which assume a linear functional response.

Fig. 3.

Five common methods used to estimate daily degree-days. a) daily average; b) single triangle; c) double triangle; d) single sine; e) double sine. Each curve represents the temperature cycle over two days, while the area of the shaded region indicates the degree-days that are accumulated (an approximation to the area under the temperature curve).

The daily average method (Fig. 3a) uses daily minimum, T_min, and maximum, T_max, temperatures to estimate accumulated degree-days by applying one of two common calculations (McMaster and Wilhelm 1997). The first method finds the average, T_avg, of T_min and T_max and then compares T_avg to the lower threshold. The accumulated degree-days is then calculated as k = T_avg −δ_min if T_avg > δ_min. The second method compares the daily minimum temperature to the lower temperature threshold before calculating T_avg, with T_min set equal to δ_min if T_max > δ_min and T_min ≤ δ_min. This ensures that so long as the maximum temperature exceeds δ_min, some degree-days will accumulate.

Another approach, the triangle method (Fig. 3b, c), estimates the accumulated degree-days by calculating the area under a triangle, with the base of the triangle spanning the daily minimum temperatures and the peak occurring at the daily maximum (Higley et al. 1986). As implied by the name, the single triangle method forms a single triangle for each diurnal cycle, while the double triangle method fits two triangles to each diurnal cycle. With the double triangle method, the base of the first triangle is set at the minimum temperature of the first half of the day, and the base of the second triangle is set at the minimum of the second half of the day. Given the minor difference between the two triangle methods, it is perhaps not surprising that they produce similar results (Roltsch et al. 1999). In the simplest case, both the single and double triangle methods assume a twelve hour difference between the daily minimum and maximum temperatures (Wilson and Barnett 1983; Allsopp and Butler 1987). This assumption is often modified to better account for the shape of the daily temperature curve by incorporating information on sunrise and sunset, or solar radiation (Reicosky et al. 1989).

Finally, the sine method (Fig. 3d, e) fits a sinusoid to the interval between the minimum and maximum temperatures (Higley et al. 1986). Similar to the triangle methods, the single sine method fits a single sinusoid to the diurnal cycle, while the double sine method forms one sinusoid between the morning minimum temperature and the daily maximum, and a second sinusoid between the daily maximum temperature and the overnight minimum (Allen 1976). Again, similar to the triangle methods, both the single and the double sine waves produce similar results (Wilson and Barnett 1983; Roltsch et al. 1999). The sine methods typically assume a twelve hour difference between the daily minimum and maximum temperatures, though this has been corrected for in several models (Reicosky et al. 1989).

The above methods represent the most common approaches used to estimate degree-days, though no single method has been shown to be superior in all circumstances (Allsopp and Butler 1987; Roltsch et al. 1999). Variations on these approaches have been developed to more accurately estimate k, such as Reicosky et al. (1989), who used a combination of linear equations, sine waves, and exponential decays, and Cesaraccio et al. (2001), who incorporated a square-root function into the double sine method for estimation of early morning temperatures. Though these methods can potentially produce more accurate estimates of k, over the course of several days the results are generally not significantly different from the simpler methods described above (Reicosky et al. 1989; Roltsch et al. 1999).

2.3 Application of degree-day models

Given the many possible degree-day model variants with respect to the form of the developmental functional response, the type of temperature threshold cutoffs and the specific method used to estimate thresholds and accumulated degree-days, we next examine in detail how these factors affect model outcomes.

2.3.1 Linear vs. non-linear development

To examine how differences in choice of f influence predictions of development, the linear degree-day model, as well as four common non-linear functional response models (the Sharpe (Sharpe and DeMichele 1977), Logan (Logan et al. 1976), Holling (Hilbert and Logan 1983), and Lactin (Lactin et al. 1995) models, see Online Resource 1), were used to investigate the emergence times of Nephus bisignatus, a predatory Coleopteran in the Coccinellidae family, widely distributed across a range of climates throughout Europe. The purpose of this analysis was to demonstrate the degree to which emergence times differ between the five models for a well-studied organism for which parameter estimates are available across model diverse types. Thus, despite the fact that limited field emergence time data exist with which to interpret model predictions, we chose N. bisignatus because its developmental response to temperature has been characterized in great detail through laboratory experiments. Model parameters were drawn from previous experimental work (Kontodimas et al. 2004) that fit linear and non-linear models to developmental data from laboratory studies in which N. bisignatus were reared at various constant temperatures. Where previously fit models could not provide estimates of δ_min or δ_max, the lower and upper rearing temperatures at which no development occurred (10 ºC and 35 ºC, respectively) were used. Temperature data were obtained from the European Climate Assessment and Dataset (ECAD 2011) at hourly increments (from 1 January 2003 – 31 December 2003) for 16 weather stations in Europe (Online Resource 2). Stations were chosen to provide a range of yearly temperature profiles, and included two stations each from Finland, Germany, Greece, Italy, Netherlands, Sweden, France, and Denmark.

2.3.2 Temperature cutoff and daily degree-day calculations

Though calculating accumulated degree-days, k, is generally straightforward, the estimate of k will vary considerably depending on the shape of the daily temperature curve (Allsopp and Butler 1987; Roltsch et al. 1999), the type of upper threshold cutoff used (Roltsch et al. 1999), and, due to the linear assumption of the degree-day model, where the maximum and minimum temperatures fall relative to the upper and lower thresholds (Wilson and Barnett 1983; Allsopp and Butler 1987; Roltsch et al. 1999). Thus, it is particularly important to consider how these factors can impact model output when studying ecological responses in regions where differences in the range and distribution of daily temperatures are anticipated. To demonstrate the sensitivity of the daily accumulated degree-days to these factors, a daily estimate, denoted k̂, was estimated across a range of climate zones in the United States by using hourly temperature data (from 1 January 2007 to 31 December 2010) obtained from three US Climate Reference Network (NOAA 2011) weather stations in the eastern United States (Online Resource 3). These stations were chosen to provide a diverse set of diurnal temperature shapes, and included stations in northern Maine, western North Carolina, and southwestern Florida.

At every station, k̂ for each day across the three year period was calculated from daily minimum and maximum temperatures using the daily average method (calculating T_avg prior to comparison with δ_min), the single triangle method, and the single sine method, as well as the horizontal, vertical, and intermediate upper threshold cutoffs. For each day, k̂ was calculated using multiple values for δ_min and δ_max in order to examine how the relative difference between daily temperature extremes and the threshold values affected the estimated degree-days. These estimates were then compared to a benchmark, k_h, estimated using hourly temperatures.

3 Results

3.1 Linear vs non-linear development

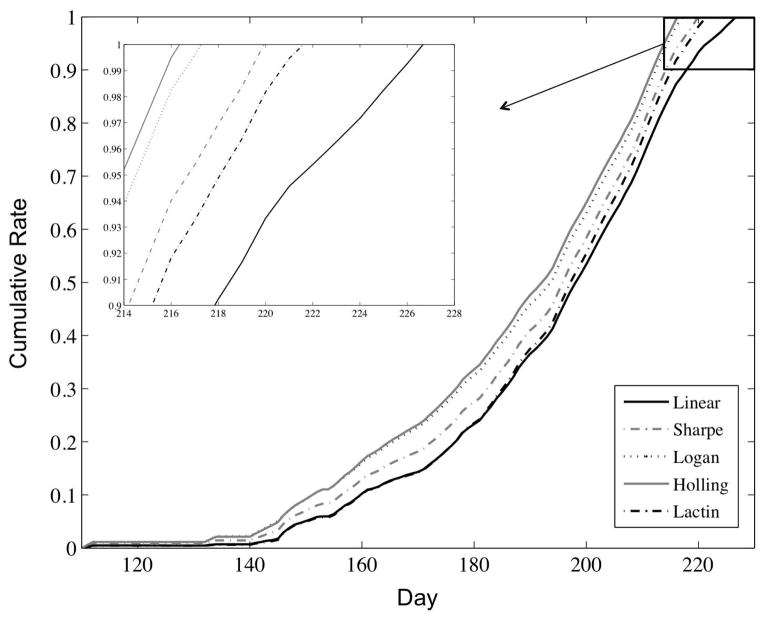
Results across all weather stations were consistent, with the exception that stations in warmer, more southern latitudes, yielded an earlier emergence time than those in cooler, more northern latitudes, as expected (Online Resource 2). A representative plot of development rates for each of the five models from the Finland1 weather station (location: 60.17 ºN, 24.95 ºE) is given in Online Resource 2. When temperatures are near the lower threshold, the predicted rate of development is greatest for the Holling, Sharpe, and Logan models, and lowest for the linear and Lactin models. This is expected given the shape of the developmental curves at low temperatures (Online Resource 1). At high temperatures, the Sharpe, Lactin, and Logan models are essentially equivalent, with all predicting the highest rates of development. At temperatures close to the upper threshold (not shown at this station), the linear model predicts the highest rate of development, while the Holling model decreases drastically. Again, this is expected given the absence of an optimal temperature threshold in the linear model, and the shape of the non-linear models above their optimal thresholds. At intermediate temperatures, all models are approximately equivalent. Over the course of the season, the Holling model predicts emergence on average 8.38 days sooner than predicted by the linear model across all sixteen weather stations (95% CI: (5.71, 11.04); Fig. 4). The Sharpe, Lactin, and Logan models also predict an emergence time significantly different than the linear model, with emergence dates across all weather stations on average 3.88 days (95% CI: (3.05, 4.70)), 3.13 days (95% CI: (2.58, 3.67)), and 6.75 days (95% CI: (4.54, 8.96)) earlier, respectively.

Fig. 4.

Comparison of linear and non-linear functional responses. Comparison of the cumulative developmental rates for the linear functional response and the Sharpe, Logan, Holling, and Lactin non-linear models, using the Finland1 weather station data (Online Resource 2). Inset: differences in predicted emergence time (when the cumulative rate reaches one) for each model.

3.2 Temperature cutoff and daily degree-day calculations

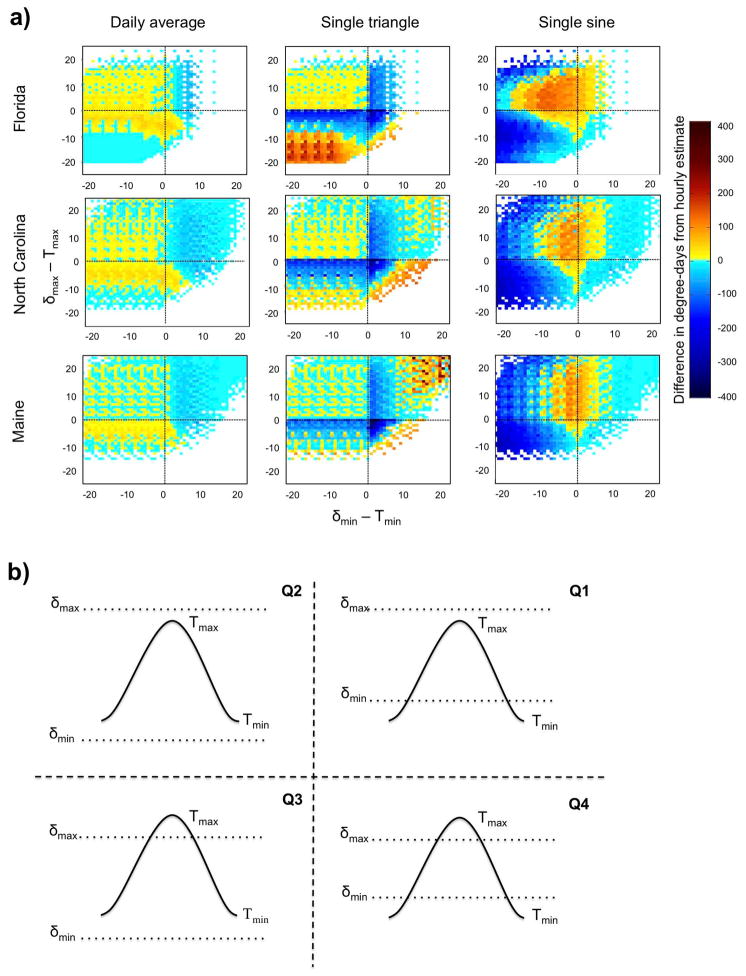
Fig. 5a shows the results using the horizontal cutoff method and assuming a twelve hour difference between the daily minimum and maximum temperatures. The color indicates the difference between k̂ and k_h, with a positive value (reds) indicating an overestimation of the particular method, and a negative value (blues) indicating an underestimation. Each of the four quadrants (Q1–Q4) represents different positions of the thresholds relative to the daily minimum and maximum (Fig. 5b). Cases in which no upper threshold is used are equivalent to the two upper quadrants. Table 1 summarizes the performance of the various methods and indicates the method(s) that agree best with hourly estimates given the relative positions of the thresholds.

Fig. 5.

Comparison of daily degree-day estimation methods. a) Difference between daily degree-days calculated using hourly data, and daily degree-days estimated from the daily average (first column), single triangle (middle column) and single sine (last column) methods, with red colors indicating an overestimation of the particular method, and blue colors indicating an underestimation. For each plot, the color at every point represents the average difference in degree-days for each day of the time series that meets the specified distance between the minimum and maximum daily temperature (T_min and T_max ) and the lower and upper thresholds, respectively, with distances from the lower threshold given along the x-axis, and distances from the upper threshold given along the y-axis. b) Relative positions of the daily minimum and maximum temperatures to the lower and upper thresholds. Each curve represents the temperature cycle for a single day.

Table 1.

Summary of degree-day calculation methods. A summary of the performance of the daily average, single triangle, and single sine methods used to calculate degree-days, given different relative positions of the thresholds and the daily temperature extremes (with table quadrants corresponding to quadrants Q1–Q4 in Figure 5b). Methods shown in bold indicate the best method for the given quadrant.

δmax > Tmaxδmin < Tmin (Q2)	δmax > Tmaxδmin > Tmin(Q1)
Average: generally accurate	Average: slight underestimates
Triangle: generally accurate	Triangle: strong underestimates, strong overestimates
Sine: strong underestimates, strong overestimates	Sine: slight underestimates, (strong δmin close to Tmin)
δmax < Tmaxδmin < Tmin (Q3)	δmax < Tmaxδmin > Tmin (Q4)
Average: generally accurate, (slight δmax close to Tmax)	Average: slight underestimates, slight overestimates
Triangle: strong underestimates, strong overestimates	Triangle: strong underestimates, strong overestimates
Sine: strong underestimates	Sine: slight underestimates

There are distinct differences between the three methods used to calculate k, and these differences are sensitive to the relationship between threshold values and daily temperatures. Both the daily average and the triangle method do well when the daily temperature range falls between the upper and lower thresholds (Q2). The sine method, in contrast, tends to overestimate the degree-days in this region, particularly when δ_min is close to the daily minimum temperature. If a similar plot is made that corrects for the time between the daily minimum and maximum temperatures, rather than assuming a twelve hour difference, this overestimation is greatly reduced (data not shown), indicating that the estimate is sensitive to the shape of the temperature curve. Overestimation when using the sine method also occurs (and can be corrected for) when δ_min is greater than, though still close to, the daily minimum temperature (Q1). Both the daily average and the triangle methods produce an underestimation in this region, with the exception of the triangle method in Maine, which produces overestimations when there are large differences between δ_min and the daily minimum. This underestimation of the daily average method is a result of averaging the daily minimum and maximum temperatures before comparison with δ_min.

When both δ_min and δ_max fall within the daily temperature range (Q4), the sine and daily average method behave similarly, producing slight underestimations in the number of degree-days. The triangle method, in contrast, more severely underestimates the degree-days when δ_min and δ_max are both near the daily minimum and daily maximum temperatures, respectively. However, as the difference between δ_min and δ_max decreases, the triangle method begins to overestimate the degree-days.

Finally, when δ_min is less than the daily minimum temperature and δ_max is less than the daily maximum temperature (Q3), the average method overestimates the degree-days when δ_max is near the maximum temperature. The sine method produces underestimates in this region, while the triangle method produces underestimates when δ_max is near the daily maximum and overestimates as δ_max drops far below the daily maximum. Again, this overestimation with the triangle method is significantly reduced when the time between the daily minimum and maximum temperatures is corrected for, indicating that this overestimation is especially sensitive to the shape of the diurnal temperature cycle.

In summary, the most commonly used method in the literature, the daily average method, generally provides accurate estimates of daily degree-days, with the exception of overestimation when δ_max and δ_min drop below the daily maximum and minimum temperatures, respectively, and underestimation when δ_max and δ_min fall above the daily maximum and minimum temperatures, respectively. The triangle method performs well when the daily temperature range falls within both threshold values. In the other regions, the triangle method tends to either over or underestimate the daily degree-days. Lastly, the sine method tends to underestimate the daily degree-days with the exception of regions where δ_max exceeds the daily maximum temperature and δ_min is close to the daily minimum temperature.

Comparing the different geographic regions indicates that the shape of the diurnal temperature curve, which changes with latitude and elevation, has a pronounced influence on the accuracy of the estimation methods. For instance, when the minimum and maximum thresholds are less than the daily minimum and maximum temperatures, respectively (Q3), the triangle method tends to overestimate the degree-days in Florida, while tending to underestimate the degree-days in Maine. This result is also observed with the sine method when the temperature range falls within both thresholds (Q2). Since in this analysis the relative difference between the daily temperature extremes and the threshold values was held constant between the regions, the shape of the diurnal temperature cycle is clearly responsible for this effect.

If a vertical threshold cutoff is used rather than a horizontal cutoff, the results are similar with only a few differences (data not shown). First, the vertical cutoff improves performance of the triangle and sine methods when both thresholds fall within the daily temperature range (Q4), whereas the daily average method tends to overestimate the degree-days in this region. When δ_min and δ_max are both less than daily minimum and maximum temperatures, respectively (Q3), the performance of the sine method improves, while the triangle method now significantly overestimates the degree-days. Importantly, where the daily average method produced overestimates in Q4 using the horizontal cutoff, the vertical cutoff exacerbates this overestimation. When δ_max exceeds the daily maximum temperature (Q1 and Q2), there is no change in the performance of the methods, as the cutoff is never applied. Similar results are observed using the intermediate threshold cutoff, with the effects of the underestimation more pronounced.

It is apparent that several factors affect the accurate estimation of daily degree-days, and each that degree-day estimation is sensitive to where thresholds fall relative to the daily minimum and maximum temperatures, the type of cutoff used, as well as the shape of the daily temperature curve (as implied by differences between regional zones). Though the results presented here indicate that no one method is universally superior to another, in general the average method produces more accurate estimates over a greater range of temperate profiles. Importantly, this analysis only considers differences on a daily basis; these differences may be amplified or cancelled out over the course of an entire season or year, depending on the frequency with which daily temperature profiles fall in each of the quadrants.

4 Discussion

By assuming a linear response to temperature and relying on a minimal number of parameters that can be estimated through simple growth experiments, degree-day models are straightforward to apply to a diversity of organisms and are accessible to a wide variety of researchers. Although degree-day models have a long history of customized applications to agricultural systems, their increasing use in a variety of contexts has come without a critical examination of degree-day model assumptions, parametric issues, and the interaction of particular model specifications with a range of climatic conditions.

Of obvious importance is the use of a linear function to approximate a non-linear developmental response to temperature. Often, linear degree-day models can generate results that are equivalent to more complicated models. In other cases, the use of a non-linear model is likely to be more appropriate. In short, model choice matters. Our results indicate that, for the prediction of Nephus bisignatus emergence, the difference between linear and non-linear predictions can be up to a week. Such differences between model predictions are not trivial, and have important implications for the use of degree-day models in ecological applications.

One such application is the use of degree-day models to aid in biological control measures. As mentioned, N. bisignatus is a predatory Coccinellidae species. Many species within this family, including N. bisignatus, are used extensively in the biological control of mealybugs, aphids, mites, and other insect pests (Obrycki and Kring 1998). With biological control measures, the synchrony of developmental timing between the control agent and the pest is known to be important (Corley and Bruzzone 2009). For instance, adult Coleoptera are often released seasonally to augment existing populations, and the timing of this release must be matched to pest populations (Obrycki and Kring 1998). Additionally, for the initial selection of biocontrol species, organisms are chosen that are climatically adapted to particular regions, such that the timing of predator emergence coincides with the target life stage of the pest (Samways 1989). Thus, the potential success of a biological control measure depends in part on the accurate prediction of developmental time for both the predator and the pest. This emphasizes the importance of a full exploration of models, and ultimately a careful selection of a final model, for application to a particular system.

Another example of the importance of model choice is found in the infectious disease context. The transmission of malaria is dependent upon the successful development of the parasite within the mosquito host, a temperature-sensitive developmental process (Beier 1998), as well as on the probability of the mosquito surviving long enough for parasite development to complete (Killeen et al. 2000). Thus, one measure of the potential for malaria transmission in a particular region can be estimated by determining the development time of the parasite and seeing if this falls within the survival time of the mosquito (Paaijmans et al. 2009). As parasite development times can fall within days of the average survival of the vector (Charlwood et al. 1997), clearly models producing estimates of development time that differ by several days can strongly determine the outcome of such an analysis. Therefore, the model chosen should be suitable for both the organism and the climatic conditions under study.

Particular attention should be paid to the approach to modeling the organism’s response to high temperatures, as well as to the specific methods used to estimate accumulated degree-days, which can both lead to markedly divergent model projections. This result highlights the need for developmental models that are tailored to the specific system, region, and time scale under study, rather than relying on generic model specifications. One major obstacle to improving degree-day model applications is obtaining suitable temperature data (Higley et al. 1986). Often, mean monthly temperatures are used to calculate degree-days (e.g. Craig et al. (1999); Yang et al. (2006)), despite the fact that even within-day temperature fluctuations can have significant effects on organism development, as well as on disease transmission (Paaijmans et al. 2009, 2010a). Daily, or when possible hourly, temperature data should be used, and careful consideration should be given to the location at which the temperature is measured (Wang 1960; Higley et al. 1986). In some cases, micro-environmental temperature, such as soil temperature (Zhang et al. 2008), or water temperature (Paaijmans et al. 2010b), rather than ambient air temperature, might better represent the conditions experienced by the organism of interest. Finally, the distance between the weather station and the ecological population under study should also be considered (Dabbs 2010). These issues add to other important constraints, such as the limited availability of high spatial and temporal resolution temperature data in developing countries, and the inherent challenges in downscaling projected temperatures to appropriate scales (Bergant and Trdan 2006). These remain major obstacles to effective application of degree-day models to study ecological responses.

Additionally, whether using a linear or a non-linear functional response, establishing that the necessary temperature requirements for development are met may be necessary but not sufficient to establish the viability of an organism in a particular region or climate. Temperature is unquestionably important in governing the development of many organisms, but both linear and nonlinear models generally cannot represent the complete effects of temperature on an organism. Though organisms may continue to develop at the extremes of their temperature range, stress sustained at these temperatures can have important life history implications not captured by these simple models. For example, temperature can influence a multitude of traits, including survival, fecundity, vector biting rate, vector competence, or host immunity (Mordecai et al. 2013; Bensadia et al. 2006; Kilpatrick et al. 2010; Mols and Diederik 1996; Hemerik and van Nes 2008). Additionally, temperature is not the only factor that influences development, as organisms also depend on the availability of sufficient resources (Campbell et al. 1974; Hagstrum and Milliken 1988; Logan et al. 2007), are affected by numerous environmental conditions (e.g. humidity, precipitation) (Wang 1960; Hagstrum and Milliken 1988), and interact in various ways with their surrounding biotic and abiotic environment (Logan et al. 2007). To account for these various factors, many studies incorporate the degree-day framework into detailed population dynamics models (e.g. Hartley et al. (2010); Ogden et al. (2005); Liang et al. (2005); Remais et al. (2007)). Because they account for the interplay of development, mortality, reproduction and other temperature-sensitive processes, such population dynamics models can generate predictions about population viability that differ from models based solely on the degree-day model framework (Moore et al. 2012).

Another important factor to consider is the effect of intra-population developmental variability on degree-day model projections (Hardman 1976; Bolnick et al. 2011). Though there is no question that phenotypic diversity exists, most applications of degree-day models rely on mean estimates of the developmental response to temperature, assuming that all individuals within a population respond equivalently. However, variability within a population can have important consequences for risk analyses. For example, Gould et al. (2005) showed that when intra-population variability was incorporated into a degree-day based risk analysis of an agriculturally important pest, model output changed from a prediction of no risk, to a prediction of limited risk. The incorporation of variability within populations has been formalized in various models of temperature-dependent development (Wagner et al. 1984, 1991) and several population dynamics models (Gilbert et al. 2004; Powell and Bentz 2009). Such approaches increase model complexity considerably, but are important to consider in light of the evidence that relying on mean values can mask important effects.

Finally, as noted in the Introduction, there is an increasing use of linear degree-day models to study species distributions under changing climates, specifically species that are important for infectious disease transmission. It is anticipated that climate change will lead to shifts in regional temperature profiles and differences in the range and distribution of daily temperatures (Lobell et al. 2007; Solomon et al. 2007). Thus, even if model assumptions are met and results validated under current conditions, these same assumptions might not hold when applied to future conditions. This is especially important to consider when degree-day models are used to make projections far into the future, where uncertainties in degree-day model parameter estimates (Bonhomme 2000; Bergant and Trdan 2006; Moore et al. 2012) are compounded with those inherent in climate forecasting (Hawkins and Sutton 2009).

Importantly, degree-day models assume constant threshold values, even when applied to questions posed over broad spatial scales or long time scales inherent in studies of future changes to the global climate system. It is well established, however, that populations can adapt to local conditions, as evidenced by species in more temperate regions, for example, having a lower temperature threshold than those in the tropics (Trudgill et al. 2005). Evolution in traits can occur surprisingly fast, and feedbacks between ecological and evolutionary processes can potentially lead to significant changes in population dynamics (Schoener 2011). Minimum, maximum, and optimum temperatures determined for organismal development today may not be valid under future conditions or when applied to localities different from those in which the data was collected. This is especially important when studying coupled organisms, such as consumer-resource pairs (Logan et al. 2007). Parasites, for instance, often have a higher temperature threshold than their hosts, ensuring that host development is completed before the parasite becomes viable (Campbell et al. 1974). If the temperature thresholds, or the shape of the temperature-development response for either organism changes, it is possible that this synchrony might be disrupted. This has important implications, not only for disease systems, but also for the persistence and distribution of other coupled organisms, such as plants and their pollinators, predators and their prey, and herbivores and their resources (Bale et al. 2002; Visser and Both 2005).

Degree-day models provide a simple and effective means of describing and estimating temperature-dependent development of a diverse set of organisms. Caution, however, is needed when applying degree-day models to questions regarding ecological responses to environmental variation as many of the assumptions of the basic degree-day model framework may not always hold. Attention paid to meeting these assumptions, along with explicit assessment of model limitations such as through detailed sensitivity analyses, can yield models that provide considerable insight.