Modulation of energy-dependent quenching of excitons in antennae of higher plants

Abstract

Energy-dependent exciton quenching, or q_E, protects the higher plant photosynthetic apparatus from photodamage. Initiation of q_E involves protonation of violaxanthin deepoxidase and PsbS, a component of the photosystem II antenna complex, as a result of lumen acidification driven by photosynthetic electron transfer. It has become clear that the response of q_E to linear electron flow, termed “q_E sensitivity,” must be modulated in response to fluctuating environmental conditions. Previously, three mechanisms have been proposed to account for q_E modulation: (i) the sensitivity of q_E to the lumen pH is altered; (ii) elevated cyclic electron flow around photosystem I increases proton translocation into the lumen; and (iii) lowering the conductivity of the thylakoid ATP synthase to protons (g_H+) allows formation of a larger steady-state proton motive force (pmf). Kinetic analysis of the electrochromic shift of intrinsic thylakoid pigments, a linear indicator of transthylakoid electric field component, suggests that, when CO₂ alone was lowered from 350 ppm to 50 ppm CO₂, modulation of q_E sensitivity could be explained solely by changes in conductivity. Lowering both CO₂ (to 50 ppm) and O₂ (to 1%) resulted in an additional increase in q_E sensitivity that could not be explained by changes in conductivity or cyclic electron flow associated with photosystem I. Evidence is presented for a fourth mechanism, in which changes in q_E sensitivity result from variable partitioning of proton motive force into the electric field and pH gradient components. The implications of this mechanism for the storage of proton motive force and the regulation of the light reactions are discussed.

Plant chloroplasts convert light energy into two forms usable by the biochemical processes of the plant (1, 2). Redox free energy is stored by linear electron flow (LEF) through photo-system (PS) II, the cytochrome b₆f complex, PS I, ferredoxin, and finally NADPH. Translocation of protons from the stroma to the lumen is coupled to LEF, resulting in the establishment of transthylakoid proton motive force (pmf), which drives the synthesis of ATP from ADP and P_i at the thylakoid CF_o-CF₁ ATP synthase (3). It has become clear that certain redox carriers and the pmf also play regulatory roles in photosynthesis. The redox status of the electron transfer chain regulates a range of processes by means of the thioredoxin system (4) and the plastoquinone pool (5). Meanwhile, the pH component (ΔpH) of pmf regulates the efficiency of light capture by means of protonation of thylakoid lumen proteins (6). The balancing of these two roles governs the development and efficiency of the photochemical machinery, as well as the avoidance of harmful side reactions.

The Need for Down-Regulation of the Photosynthetic Apparatus

Plants are exposed to widely varying environmental conditions, often resulting in light energy capture that exceeds the capacity of the photosynthetic apparatus (7–10), which in turn can lead to photodamage (11, 12). Plants have evolved a series of mechanisms collectively known as nonphotochemical exciton quenching (NPQ) (9) to harmlessly dissipate excessively absorbed light energy as heat and thereby protect plants from photodamage.

Energy-dependent (i.e., dependent on the energization of the thylakoid membrane) exciton quenching (q_E) is arguably the most important and well characterized component of NPQ in higher terrestrial plants (9, 13, 14), although other processes certainly contribute to photoprotection (e.g., state transitions and long-lived quenching phenomena; see ref. 9 for review). The initiation of q_E depends on light-induced lumen acidification (9, 13, 14), which leads to protonation of two key proteins, violaxanthin deepoxidase (VDE) (15) and PsbS, a component polypeptide of the PS II-associated light-harvesting complex (9, 16, 17). VDE is an integral enzyme of the xanthophyll cycle and catalyzes the conversion of violaxanthin to antheroxanthin and further to zeaxanthin (18–22). The coincident accumulation of antheraxanthin and zeaxanthin with protonation of PsbS activates q_E (16). In the simplest model for q_E activation, photosynthetic proton transfer should increase pmf, acidifying the lumen and increasing q_E, in effect feedback regulating light capture. If the kinetic constraints of such a model were held constant, a continuous relationship between q_E and LEF would be expected (23).

The Need for Flexibility in Antenna Down-Regulation

In contrast, it is generally accepted that antenna down-regulation must be flexible to cope with changing environmental conditions and biochemical demands (22–25), i.e., that the response of q_E to LEF, which we term “q_E sensitivity,” is regulated. In the absence of such flexibility, the photosynthetic apparatus would be prone to catastrophic failures (23, 26). For example, conditions that slow turnover of the Calvin–Benson cycle and restrict the availability of PS I electron acceptors should lower the rate of LEF, attenuating luminal acidification and q_E (23). Subsequently, the increase in excitation pressure (caused by loss of quenching) at the reaction centers, compounded by the accumulation of reduced electron carriers, would result in increased photodamage (9). Thus, a flexible or dynamic relationship between q_E and LEF is essential and indeed has been demonstrated to be substantial (24, 26–31). For example, when CO₂ levels were lowered from ambient to near 0 ppm, the sensitivity of q_E to LEF increased by ≈5-fold (23). From these observations, four models have been proposed to account for q_E modulation.

Model 1: Variable Response of q_E to ΔpH. Changes in the aggregation state of antennae complexes (32) or in pK_a values of key amino acid residues on VDE or PsbS could alter the sensitivity of q_E to the ΔpH component of pmf (i.e., to lumen pH) (15). This could also be achieved by a simple change in the maximum activity of q_E-related enzymes (e.g., VDE) (22).

Model 2: Modulation of the H⁺/e^– Ratio. The stoichiometry of protons per electron translocated through the linear pathway could be increased, thus achieving a higher pmf (and a more acidic lumen) for a given LEF. This effect could result from a change in the proton-to-electron stoichiometry of the linear pathway itself, although this seems unlikely given our current understanding of the mechanisms of these processes (reviewed in ref. 15). Alternatively, increased cyclic electron flow around PS I (CEF1), a process that translocates protons but does not result in net NADPH reduction, could acidify the lumen beyond the capacity of LEF (26). A third possibility is activation of the water–water cycle (WWC) or Mehler peroxidase reaction (33). In the WWC, electrons are extracted from water at PS II and subsequently used to reduce O₂ back to water at the reducing side of PS I. Like CEF1, the WWC produces pmf without net reduction of NADP⁺. Whereas, in principle, the WWC can increase q_E, its activity will appear in our assays as LEF (see below) and thus will not affect q_E sensitivity as we have defined it.

Model 3: Modulating Conductivity of Proton Efflux. Because the extent of pmf in the steady state is determined by the relative flux of protons into and out of the lumen, changing the kinetic properties of the ATP synthase should alter q_E sensitivity (23). In particular, lowering the enzymatic turnover rate of this enzyme, or effectively its conductivity to proton efflux, should increase pmf for a given proton flux (23, 34). This rise in pmf in turn would increase the sensitivity of q_E to LEF (and also to CEF1 or WWC). This group previously developed a noninvasive technique for estimating relative values of proton conductivity, designated g_H+ (ref. 23; see also below). By using this technique, evidence was presented that modification of g_H+ by itself could account for essentially all q_E modulation in intact tobacco plants upon alteration of CO₂ levels from 2,000 to 0 ppm, while maintaining ambient levels of O₂ (23).

Model 4: Variable Partitioning of pmf. Recent work has argued that transthylakoid pmf contains significant contributions from the electric field component (Δψ) (6, 35). It was further argued that varying the relative partitioning of pmf into Δψ and ΔpH would necessarily alter the sensitivity of q_E to total pmf. Yet to be tested, this model states that ΔpH/pmf may change with physiological state.

In this work, we explore q_E modulation under low CO₂ and O₂, where several groups over the past few decades (24, 26–31) have observed enhanced sensitivity of q_E to LEF and attributed this effect to increased activity of CEF1. In contrast, we observed no evidence for enhanced CEF1 and concluded that increased q_E sensitivity under these conditions results mainly from changes in both g_H+ and pmf partitioning.

Materials and Methods

Plant Material. Experiments were conducted at room temperature by using wild-type Nicotiana tabacum xanthi (tobacco) plants grown under greenhouse conditions, as described in ref. 23, and were dark-adapted overnight before being used in spectroscopic assays. Young, fully expanded leaves, gently clamped into the measuring chamber of the spectrophotometer (described below), were allowed to adjust to the chamber conditions for 5 min in the dark before being illuminated for 10 min with actinic light at intensities ranging from 32 to 820 μmol of photons·m^–2·s^–1 photosynthetically active radiation. Steady-state fluorescence and electrochromic shift (ECS) parameters were measured after this actinic period, after which the actinic light was turned off for 10 min to measure the fluorescence amplitude indicative of the quickly recovering component of NPQ, i.e., q_E (see below).

Gas Composition. Room air pumped into the measuring chamber was assumed to represent ambient conditions (≈372 ppm CO₂/21% O₂). Premixed gases balanced with nitrogen were used to alter the gas composition in the measuring chamber and create a pseudomicroclimate of either 50 ppm CO₂/21% O₂ or 50 ppm CO₂/1% O₂. In all cases the stream of air entering the measuring chamber was first bubbled through water to avoid leaf dehydration.

Spectroscopic Assays. The methods for measuring extents of q_E, rates of LEF, and the relative extents of pmf components were as described in ref. 23, except that a newly developed instrument was used. This instrument was based on the nonfocusing optics spectrophotometer (NoFOSpec) (36) but has been modified to allow near-simultaneous measurements of absorbance changes at four different wavelengths. This feat was accomplished by aiming four separate banks of light-emitting diodes (HLMP-CM15, Agilent Technologies, Santa Clara, CA), each filtered through a separate 5-nm bandpass interference filter (Omega Optical, Brattleboro, VT), into the entrance of a compound parabolic concentrator. The photodiode detector was protected from direct actinic light by a Schott BG-18 filter. Current from the photodiode was converted to a voltage by an operational amplifier and the resulting signal was ac-filtered to remove background signals and sampled by a 16-bit analog-to-digital converter on a personal computer data acquisition card (DAS16/16-AO, Measurement Computing, Middleboro, MA). Timing pulses were generated by digital circuitry (PC card D24/CTR 3, Measurement Computing) controlled by software developed in-house. The duration of the probe pulses was set at 10 μs. Actinic illumination was provided by a set of 12 red light-emitting diodes (HLMP-EG08-X1000, Agilent Technologies) and controlled by the timing circuitry. Measuring pulses were typically given at 1- to 10-ms intervals.

Absorbance changes at only one wavelength, 520 nm, were used to estimate rapid (<1 s total trace time) changes in ECS, where its signal predominates on this timescale (36). For longer traces, significant contributions from light scattering have been observed (36). To correct for this, absorbance changes of three wavelengths, 505, 520, and 535 nm, were collected. The three wavelength traces were recorded near-simultaneously, with each light-emitting diode band being pulsed in sequence at 10-ms intervals. Each complete set of three pulses was deconvoluted by using the procedure described in refs. 35–37 to obtain estimates of ECS.

The instrument was also used to measure changes in chlorophyll a fluorescence yield by using the 520-nm light-emitting diode bank as a probe beam, as described in refs. 36 and 37. Saturation pulses (>30,000 μmol of photons·m^–2·s^–1 photosynthetically active radiation) were imposed by using light from an electronically shuttered xenon arc lamp, filtered through heat-absorbing glass. Actinic light was filtered out by using an RG-695 Schott glass filter. Saturation pulse-induced fluorescence yield changes were interpreted as described in refs. 38 and 39. The quantum yield of PS II photochemistry (Φ_II), a measure of the efficiency of PS II electron transfer per quantum absorbed, and estimates of LEF were calculated as described in ref. 38 and 40, respectively. It should be noted that estimates of LEF made this way contain contributions from the WWC but not from CEF1. The q_E component of NPQ was calculated from the saturation-pulse-induced maximum fluorescence yields during steady-state illumination (F_m′) and 10 min (F_m″) after switching off the actinic light (9, 39).

In Vivo Measurements of Proton Flux and pmf Characteristics. This work and analyses are made possible by newly introduced techniques that allow us to noninvasively probe the “proton circuit” of photosynthesis. The theoretical framework for these methods is discussed in refs. 6, 23, 35, 36, and 41 and briefly reviewed here. These techniques take advantage of the ECS (sometimes called ΔA₅₂₀ or ΔA₅₁₈) of certain carotenoid species that naturally occur in the thylakoid membranes. The ECS is a linear indicator of changes in transthylakoid Δψ (42, 43) and is particularly useful for our studies because it responds to the transthylakoid movement of protons, as well as other charged species.

We probed the ECS by using a previously described technique called dark-interval relaxation kinetic analysis (41), in which steady-state photosynthesis is perturbed by short (typically 0.5 s), dark intervals, allowing the photosynthetic apparatus to relax in ways that reveal information about the system in the steady state (41). The amplitude of the light–dark ECS signal (ECS_t) parameter was obtained by taking the total amplitude of the rapid phase of ECS decay from steady state to its quasistable level after ≈300 ms of darkness (23). As previously discussed, ECS_t should reflect total light–dark pmf (i.e., Δψ + ΔpH) (6, 23, 35).

The dark-interval relaxation kinetic analysis technique can also reveal information about the relative conductivity of the ATP synthase to protons, a parameter termed g_H+ (23, 35). Because the ATP synthase is the highest conductance proton efflux pathway, decay of the ECS reflects flux through this enzyme (6, 44). ECS decay kinetics during a dark-interval relaxation kinetic analysis experiment are well fit by first-order decay curves, making it possible to approximate the kinetic behavior as a first-order process, i.e., a process that obeys Ohm's law. In this case, we can use a simple force-flux expression to describe the decay (35):

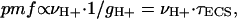[1]

where ν_H+ represents the flux (current) of protons into and out of the lumen† driven by LEF and τ_ECS is the decay time of the ECS upon a light–dark transition and is proportional to the “resistance” (i.e., the inverse of the conductivity) of the ATP synthase to proton efflux (23).

If the proton-to-electron ratio remains constant (41), then the proton flux associated with LEF should be proportional to LEF itself. Taking into account the effective rate constant for proton efflux, or g_H+, we can then estimate the pmf attributable to LEF or pmf_LEF (23) by

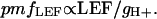[2]

The value of pmf_LEF should be proportional to total pmf if contributions from CEF1 are also constant. Moreover, a continuous relationship between q_E and pmf_LEF would be expected if CEF1, the antenna response to lumen pH, and the relative fraction of pmf stored as ΔpH all remain constant; i.e., a deviation in the relationship between pmf_LEF and q_E would indicate the participation of other factors, notably activation of models 1, 2, or 4 (23).

Dark-interval relaxation kinetic analysis over longer periods of darkness can reveal information regarding the Δψ and ΔpH components of pmf (6, 35). Initially, after the onset of illumination, pmf is stored predominantly as Δψ, because most protons are buffered and the capacitance of the membrane is relatively low (15). Over time, Δψ relaxes because of relatively slow movements of counterions, allowing the accumulation of free protons and subsequent buildup of ΔpH (6). When the actinic light is rapidly shuttered, proton translocation into the lumen is rapidly halted, but proton efflux continues until pmf either completely collapses or comes into equilibrium with the ATP/(ADP + P_i) couple by means of the ATP synthase. Because of luminal proton buffering, Δψ will collapse more rapidly than ΔpH. Even after steady-state Δψ is dissipated, ΔpH will continue to drive proton efflux, establishing an inverse Δψ, positive on the stromal side of the thylakoid membrane. In our measurements, this inverse Δψ phase is measured as an inverted ECS signal. Under appropriate conditions (6, 35), the extent of the inverted Δψ should be proportional to the light-driven ΔpH component of pmf. We thus used the amplitudes of ECS kinetic components as estimates of light-driven Δψ and ΔpH. ECS kinetics in vivo suggest that ≈50% of the pmf is stored as Δψ (35).

Results and Discussion

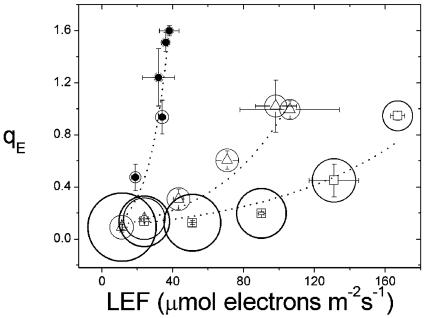
Changing the Levels of CO₂ and O₂ Alters q_E Sensitivity. Fig. 1 shows a plot of q_E against LEF under three atmospheric conditions: (i) ambient (372 ppm CO₂, 21% O₂), (ii) low CO₂ (LC, 50 ppm CO₂ and 21% O₂), and (iii) low electron acceptor (LEA, 50 ppm CO₂ and 1% O₂). Changing from ambient to LC conditions led to a decrease in the LEF required to achieve q_E = 0.8, from ≈160 to 90 μmol of electrons·m^–2·s^–1, representing an ≈2-fold increase in the sensitivity of q_E to LEF, similar to our previous results under these conditions (23). LEA treatment further increased q_E sensitivity, and a q_E = 0.8 was achieved at a LEF of ≈30 μmol of electrons·m^–2·s^–1, an ≈6-fold increase in sensitivity over ambient conditions. The magnitude of this effect was similar to that observed previously on lowering CO₂ to essentially 0 ppm while maintaining O₂ at 21% (23). Our observations are also qualitatively consistent with those of Heber and coworkers (24, 26, 28, 31), who noted that when both CO₂ and O₂ levels were lowered total NPQ increased, even though LEF had decreased.

Fig. 1.

Energy-dependent antenna down-regulation (q_E) as a function of LEF. Measurements of q_E exciton quenching and LEF were performed on intact leaves of tobacco plants over light intensities ranging from 32 to 820 μmol of photons·m^–2·s^–1, as described in the text. Gas compositions were 372 ppm CO₂/21% O₂ (□), 50 ppm CO₂/21% O₂ (▵), and 50 ppm CO₂/1% O₂ (•). The sizes of the circles surrounding the symbols have been set proportional to the conductivity of the ATP synthase to protons (g_H+) as estimated by the inverse of the decay lifetime of the ECS signal, as described in Materials and Methods. The largest diameter symbol was ≈61.3 s^–1, whereas the smallest was ≈15.7 s^–1.

Fig. 1 also shows that g_H+, as estimated from the ECS decay kinetics upon a rapid light–dark transition, decreased by ≈2-fold, which was sufficient to explain the observed increase in q_E sensitivity from ambient to LC conditions (ref. 23 and below). A further, ≈2-fold decrease in g_H+ accompanied the increase in q_E sensitivity upon transition from LC to LEA conditions. These results are consistent with model 3, i.e., that changes in g_H+ alter q_E sensitivity, as previously argued (23).

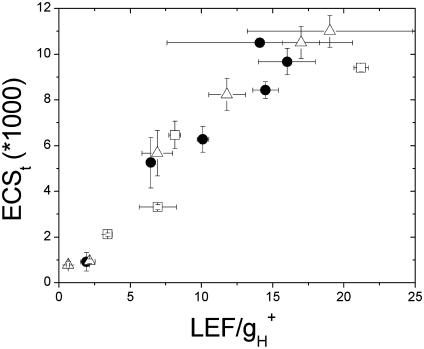
Heber and coworkers hypothesized that increased q_E sensitivity under LEA conditions was best explained by an increase in proton translocation into the lumen as a result of CEF1 (i.e., model 2) (24, 26, 28). Fig. 2 shows that the relationship between light-induced pmf, as estimated from ECS_t and pmf_LEF, i.e., LEF-attributable pmf as estimated by Eq. 2, was, within the noise level, continuous and depended very little on gas composition. The simplest interpretation for these results is that, contrary to model 2, the relative contributions of CEF1 to proton flux did not change appreciably when CO₂ or when both CO₂ and O₂ were lowered.

Fig. 2.

Total light-induced pmf as a function of the pmf attributable to LEF. The ECS_t parameter was taken as a measure of light-induced pmf, whereas the independent measure of pmf or pmf_LEF (LEF/g_H+) was derived from analysis of fluorescence and the kinetics of ECS decay upon a rapid light–dark transition (see Materials and Methods). The symbols and conditions are the same as in Fig. 1. The error bars represent standard deviations for n = 3–5.

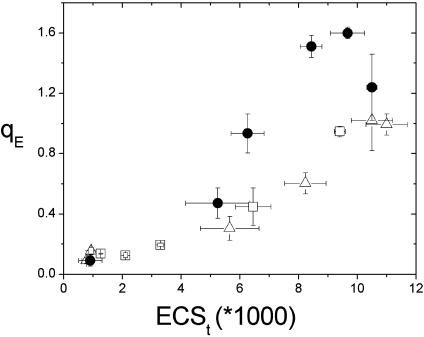
Fig. 3 shows that the q_E responses as a function of steady-state light-induced pmf were very similar (essentially continuous) under ambient and LC conditions, as previously observed (23). This finding strongly suggests that lowering CO₂ alone did not alter the response of the antenna to pmf, consistent with the previous suggestion that changes in g_H+ could solely account for the majority of q_E modulation on altering CO₂ levels (23). These results argue against models 1 and 4 under ambient and LC conditions (23).

Fig. 3.

Energy-dependent antenna down-regulation (q_E) as a function of light-induced pmf, as estimated by the ECS_t parameter. Light-induced pmf (ECS_t) values were derived from analysis of ECS decay kinetics as described in Materials and Methods. The symbols and conditions were as in Fig. 1. The error bars represent standard deviation for n = 3–5.

In contrast, under LEA conditions q_E was notably more sensitive to light-induced pmf (Fig. 3, circles). These data, together with those in Fig. 2, implied that q_E sensitivity changes under LEA conditions could not be attributed solely to changes in g_H+ or CEF1. Instead, the response of q_E to pmf appears to have changed. Overall, these results are consistent with either model 1 or model 4 having a role under LEA conditions.

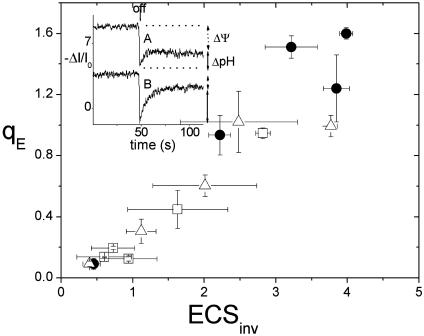
Evidence for Variable Partitioning of pmf. We next used an analysis of the ECS decay kinetics developed in our earlier work to estimate the fractions of light-induced pmf stored as Δψ and ΔpH (refs. 15 and 35; see also Materials and Methods) to distinguish between Models 1 and 4 under LEA conditions. The Inset to Fig. 4 shows ECS kinetic traces upon rapid light–dark transitions at 520 μmol of photons·m^–2·s^–1 under ambient (trace A) and LEA (trace B) conditions. The fraction of pmf attributable to ΔpH was ≈0.3 under ambient and LC (not shown) conditions, reasonably consistent with previous observations (35). On the other hand, the fraction of pmf attributable to ΔpH appeared to increase by ≈2-fold (≈0.69) under LEA conditions. Similar changes were observed at higher and lower light intensities (data not shown). This result is consistent with model 4, where the sensitivity of q_E increases under LEA conditions by altering the balance of transthylakoid Δψ and ΔpH.

Fig. 4.

The relationship between energy-dependent antenna down-regulation (q_E) and the ΔpH component of light-induced pmf, as estimated by the inverted ECS signal parameter. The symbols and conditions are the same as in Fig. 1. The error bars represent SD for n = 3–5. (Inset) Kinetic traces of the ECS signal, deconvoluted as described in Materials and Methods, upon a light–dark transition from steady-state illumination. The extents of the steady-state signal and the inverted region of the signal, which are thought to be proportional to the light-induced Δψ and ΔpH components of pmf, respectively, are indicated by the vertical arrows. The traces were taken at actinic light intensity of 520 μmol of photons·m^–2·s^–1 at ambient (trace A) and LEA (trace B) conditions.

Fig. 4 also shows that the relationship between q_E and our estimate of light-induced ΔpH (inverted ECS signal) remained essentially constant (continuous) under all atmospheric and light conditions. If we assume that the stromal pH remains fairly constant in the light (15, 35), these results strongly suggest that the antenna responses (i.e., at the level of the pK_as for VDE and/or PsbS protonation) to lumen pH and the relative activity of the enzymes controlling the xanthophyll cycle are constant over ambient, LC, and LEA conditions. Taken together, these data argue against model 1 and instead suggest a role for model 4, a mode of modulating q_E sensitivity involving variability in the relative partitioning of pmf into Δψ and ΔpH.

Conclusions

No Evidence for Increases in Steady-State CEF1 Under LEA Conditions. A widely cited mechanism of q_E modulation is that CEF1 is more engaged under LEA conditions (24, 26–31) (i.e., model 2). However, for model 2 to fully account for the observed 5- to 6-fold increase in q_E sensitivity (Fig. 1), the turnover rate of the CEF1 pathway would have to increase to several times that of LEF. In contrast, we found little change in the relationship between our estimates of total pmf based on ECS_t and the pmf calculated from Eq. 2 (Fig. 2). These results imply a constant, fractional turnover of CEF1 (see below) and are therefore inconsistent with a substantial role for changes in CEF1 modulating q_E sensitivity.

Despite the existence of viable models for CEF1, evidence for its involvement in q_E modulation is mixed (45–56). In green algae (e.g., Chlamydomonas) and cyanobacteria (57, 58), as well as in C₄ plant bundle sheath chloroplasts (51), there is strong evidence for participation of CEF1 in ATP synthesis. The situation in C₃ vascular plants is more confusing. The general consensus based on steady-state comparisons of LEF with PS I activity, cytochrome b₆f electron transfer (37), or overall proton translocation (37) is that CEF1 appears to be either negligible or a constant fraction of LEF (41). Our data generally support this view. On the other hand, Joliot and Joliot (59) and Makino et al. (60) presented evidence for high CEF1 rates, approaching those of LEF, during the early stages of photosynthetic induction from dark-adapted states.

One possibility, which could reconcile these two opposing views, is that CEF1 has a high potential capacity but is tightly regulated in the steady state. In fact, we argue that this situation would be expected, because proton efflux from the lumen is tightly coupled to ATP synthesis (61). In the steady state, where consumption of products is matched by their production (62), any increase in proton translocation by CEF1 would require a proportional increase in ATP consumption relative to that of NADPH. This case is the default situation in e.g., C4 bundle sheath cells where production of ATP but not reducing power is needed. In C3 plants, changes in ATP/NADPH output would necessarily require differential engagement of processes that consume disparate ratios of ATP/NADPH, e.g., nitrite reduction, maintenance of ion gradients, etc. Indeed, such processes may impose a requirement on flexibility at the level of the light reactions, in which CEF1 may play an important role (63). However, the overall flux through these alternate processes under most conditions is likely considerably smaller than that through CO₂ fixation in the steady state. During induction, on the other hand, metabolite pools undergo rapid changes, allowing for larger changes in the relative ATP and NADPH sinks, perhaps imposing substantial changes in CEF1:LEF.

It is worth emphasizing that, whereas changes in the fractional turnover of CEF1 do not appear to affect q_E sensitivity under our conditions (Figs. 1 and 2), changes in other modes of q_E modulation will alter the impact of proton translocation, regardless of its source (i.e., LEF or CEF1). Thus, even a low, constant engagement of CEF1 in the steady state will contribute to the triggering of q_E.

Under a Wide Range of Conditions, q_E Sensitivity Changes Are Attributable to Modulation of g_H+. Previously, we have observed substantial changes in g_H+, which could on their own account for the observed changes in q_E sensitivity (23). We concluded that the CF_o-CF₁ ATP synthase plays a central role in transmitting information about the biochemical status of the stroma to the light reactions. We proposed that decreases in electron acceptor availability cause decreases in g_H+, which lead to increases in pmf at a given LEF and ultimately to increases in q_E (23). Our current data support this view, in that the bulk of q_E modulation can be accounted for by changes in g_H+, especially between ambient and LC conditions (Figs. 1 and 2).

A Mechanism of Modulating q_E Sensitivity. In contrast to ambient and LC conditions, q_E appeared more sensitive to light-induced pmf under LEA conditions (Fig. 3, filled circles), suggesting that a factor in addition to changes in g_H+ influences q_E sensitivity. The data in Fig. 4 suggest that this additional factor is not a change in the response of the antennae to lumen pH or a change in the activities of the enzymes controlling the xanthophyll cycle but is most likely a relative increase in the fraction of pmf partitioned into the ΔpH component. Until recently, such variable parsing of pmf would have seemed inconceivable, because the pmf was considered to be composed almost completely of ΔpH; i.e., the Δψ was considered negligible in thylakoids (6, 15, 35). However, a number of lines of evidence suggest that about half of the pmf is stored as Δψ (6, 15, 23, 35). We previously argued that relative changes in the fraction of pmf held as ΔpH would alter q_E sensitivity (15, 35). The data in Figs. 3 and 4 are in vivo evidence for such variable pmf partitioning and its expected consequences for regulation of the light reactions. Moreover, our results support the view that the fraction of pmf stored as Δψ and ΔpH is important in balancing the dual roles of the pmf in allowing sufficient driving force for ATP synthesis while maintaining the pH of the lumen within a range where it can regulate light capture by means of q_E (15, 35).

The Physiological Basis of q_E Modulation. In this work, we chose to study LEA conditions because they have been previously proposed to support large increases in CEF1. There are good arguments that, in terrestrial higher plants, reducing both CO₂ and O₂ to such low levels is unlikely, because consumption of O₂ by respiration will produce CO₂ whereas photosynthesis will liberate O₂, though the conductivity of the stomata to the two gases is very similar (64). Aquatic plants, on the other hand, may routinely experience such conditions (65). Lowering CO₂ levels to nearly 0 while maintaining O₂ at 21% induced a change in g_H+ (23) comparable to that seen under our LEA condition (Fig. 1), while not inducing the apparent change in pmf partitioning seen here (Figs. 3 and 4). One explanation to account for this difference is that g_H+ cannot be decreased below that seen at 0 ppm CO₂, and other mechanisms must be activated to further increase q_E sensitivity. Low O₂ may also have secondary effects, especially at the levels of photorespiration (66) and the WWC (60). Changes in flux through either of these processes would alter the output of ATP/NADPH, and this in turn may effect or trigger changes in pmf partitioning. These arguments suggest that this type of imbalance may be seen under other, more “natural,” conditions. Indeed, in preliminary work, we have noted changes in ΔpH/pmf in intact tobacco and cucumber leaves under wilting conditions (data not shown), hinting at a physiological role.

The mechanism by which thylakoid pmf partitioning is accomplished remains unresolved, although in vitro experiments have indicated that stromal ionic balance and the lumen proton-buffering capacity are major effectors (6, 35). This view is consistent with the role of ion homeostasis in maintaining ΔpH and Δψ across eukaryotic and prokaryotic plasma membranes, and we proposed that similar mechanisms work in chloroplasts in vivo (reviewed in refs. 6 and 35). By extrapolation, any process that affects ionic balance or lumen proton buffering, as a consequence of either regulation or altered metabolism, could change pmf partitioning and thus q_E sensitivity.

The mechanism by which g_H+ is influenced by the stromal status is also unclear, but a reasonable working model involves modulation of stromal P_i (a substrate for the ATP synthase) levels (23). It has been proposed some time ago that sequestration of stromal P_i into metabolic pools plays a critical role in controlling or regulating both the light and dark reactions of photosynthesis under a variety of conditions (67). If our model proves correct, changes in g_H+ (possibly by means of P_i sequestration) would then constitute an important regulatory link between the light and dark reactions of photosynthesis.

Balancing the Two Roles of the pmf. The pmf is a key intermediate in both energy transduction and feedback regulation of the light reactions. Our results strengthen the view that “balancing” these two roles is critical for maintaining the efficiency and productivity of photosynthesis and avoiding harmful side reactions. Under moderately restrictive conditions, e.g., when lowering CO₂ levels alone, modulation of g_H+ appears to alter the balance between light-driven proton flux and the resulting pmf. Under more extreme limitations, i.e., when O₂ levels are also lowered, the balance between pmf and lumen pH appears to be altered. Both mechanisms have the effect of increasing the feedback regulatory effects of limited proton flux.