Automatic Prostate MR Image Segmentation with Sparse Label Propagation and Domain-Specific Manifold Regularization

Abstract

Automatic prostate segmentation in MR images plays an important role in prostate cancer diagnosis. However, there are two main challenges: (1) Large inter-subject prostate shape variations; (2) Inhomogeneous prostate appearance. To address these challenges, we propose a new hierarchical prostate MR segmentation method, with the main contributions lying in the following aspects: First, the most salient features are learnt from atlases based on a subclass discriminant analysis (SDA) method, which aims to find a discriminant feature subspace by simultaneously maximizing the inter-class distance and minimizing the intra-class variations. The projected features, instead of only voxel-wise intensity, will be served as anatomical signature of each voxel. Second, based on the projected features, a new multi-atlases sparse label fusion framework is proposed to estimate the prostate likelihood of each voxel in the target image from the coarse level. Third, a domain-specific semi-supervised manifold regularization method is proposed to incorporate the most reliable patient-specific information identified by the prostate likelihood map to refine the segmentation result from the fine level. Our method is evaluated on a T2 weighted prostate MR image dataset consisting of 66 patients and compared with two state-of-the-art segmentation methods. Experimental results show that our method consistently achieves the highest segmentation accuracies than other methods under comparison.

1 Introduction

Prostate cancer is the second leading cause of cancer death for American males. It is estimated by the American Cancer Society that in year 2012, around 241,740 new cases of of prostate cancer will be diagnosed, and around 28,170 men will die because of prostate cancer. Image guided radiation therapy (IGRT), as a noninvasive approach, is one of the major treatment methods for prostate cancer, and accurate prostate segmentation is a critical step in IGRT.

The T2 weighted magnetic resonance image (MRI) is one of the most commonly used prostate image modalities to perform treatment planning in IGRT due to its superior soft tissue contrast. There are many novel prostate MR image segmentation algorithms proposed in the literature, and they can be broadly classified into two main categories, namely multi-atlases based segmentation methods [1,2] and deformable model based segmentation methods [3,4]. Multi-atlases based segmentation methods generally have two main steps. First, atlases (i.e., training images with segmentation groundtruths) are registered to the target image. Second, label fusion is performed with the registered atlases to obtain the final segmentation result of the target image. The most commonly used label fusion techniques include majority voting (MV), STAPLE based methods [5,6], the SIMPLE algorithm [7], and the non-local mean based label propagation [8,9]. Deformable model based methods first construct a shape prior from available training images. Then, the prostate in the target image is segmented by fitting the deformable model onto the prostate boundary with both shape and appearance constraints. Representative deformable model based methods include the active appearance model (AAM) based methods [3] and probabilistic spatial constrained deformable model based methods [4].

Although many prostate MR image segmentation methods have been proposed, there are still two existing main challenges. The first challenge exists in all prostate image modalities, which is the large inter-subject prostate shape variation. It brings difficulty for multi-atlases based and deformable model based methods to accurately segment the prostate if prostate shape in the target image is significantly different from prostate shapes in the atlases. The second challenge is that the image appearance inside the prostate can have very large variations, which brings difficulty in learning effective image appearance features to capture all the anatomical properties of the prostate. These two challenges are also illustrated by Figure 1.

Fig. 1.

Illustrations of large inter-subject shape and appearance variations of prostate in MR images, where the manual segmentation groundtruths are highlighted by the red contours. Note also the large inhomogeneous image appearances within the prostate region.

Therefore, we are motivated to propose a new prostate MR image segmentation method to address the two main challenges mentioned above. Specifically, the most salient anatomical features to aid segmentation are learnt by subclass discriminant analysis (SDA), which is a discriminant subspace learning method. SDA simultaneously maximizes the inter-class distances and minimizes the intra-class variations of the learnt features. Based on the learnt features, a hierarchical segmentation framework is proposed. In the coarse level, a multi-atlases based sparse label propagation method is proposed to estimate the prostate likelihood of each voxel in the target image, which provides a rough labeling of prostate and non-prostate voxels. Then, voxels with high segmentation confidence can be determined based on the likelihood map. In the fine level, voxels with high segmentation confidence in the target image are served as labeled domain-specific samples, while voxels with low segmentation confidence are served as unlabeled domain-specific samples. These labeled and unlabeled domain-specific samples reflect the prostate anatomical properties in the target image more precisely than those from atlases, and thus they can be used as input for the semi-supervised manifold regularization method to refine the final segmentation result. A prostate MR image dataset consisting of 66 patients is used to evaluate our method, and further compare it with the two state-of-the-art prostate segmentation methods. Experimental results show that our method consistently achieves the highest segmentation accuracies than other methods under comparison.

2 Method

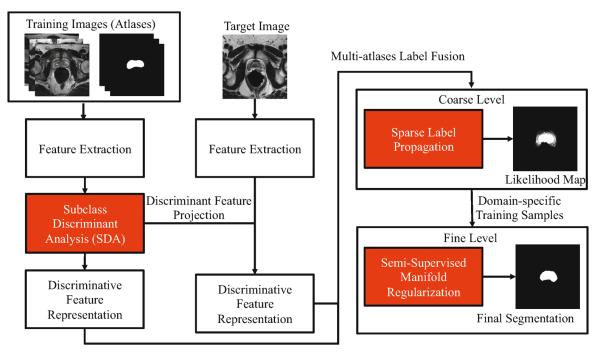
The proposed method can be summarized by Figure 2. Details of each component in Figure 2 is explained below.

Fig. 2.

Flow chart of our method, where all rectangles highlighted in red denote the main contributions of the proposed method

2.1 Discriminant Feature Learning with SDA

As illustrated in Figure 1, using voxel intensity alone is insufficient to distinguish voxels belonging to the prostate and non-prostate regions. Therefore, it is of essential importance for designing highly discriminant voxel signatures. In the ideal case, discriminant voxel signatures should exhibit large inter-class distances and small intra-class variations for different tissue types, which is also known as the linear discriminant analysis (LDA) [10]. LDA aims to project the original signature to a feature subspace such that the projected features can maximize the separation of different classes measured by the Fisher-Rao's separation criterion.

In this paper, the Gabor wavelet function was used to extract the original feature signature. Specifically, given N training images I_i (i = 1, …, N), each image I_i is convolved with 50 Gabor wavelet kernels ψ^j (j = 1, …, 50), to obtain the resulting feature maps $F_i^j$. In each feature map, the multi-resolution patch-based representation [9] with patch sizes K₁ = 5, K₂ = 9, and K₃ = 13 are used as signature for each voxel x, denoted as f(x).

Note that the original signature f(x) may contain many redundant and noisy features. We aim to project the original signature to a discriminant subspace such that the projected features can maximize the inter-class distances and minimize the intra-class variations. Specifically, P voxels are drawn from the training images (e.g., Figure 3 (a)), denoted as x₁,…,x_P. Each voxel x_k (k = 1, …, P) has an anatomical label l_k, with l_k = 1 if x_k belongs to the prostate and l_k = 0 otherwise. We can learn the most discriminant features based on LDA [10] by finding projection vectors w which can maximize the Fisher-Rao's criterion:

$$J\left(\mathit{w}\right)=\frac{{\mathit{w}}^T{\mathbf{S}}_B\mathit{w}}{{\mathit{w}}^T{\mathbf{S}}_W\mathit{w}},$$ (1)

where S_B and S_W denote the between class scatter matrix and the within class scatter matrix defined by Equations 2 and 3, respectively.

$${\mathbf{S}}_B=\sum _{i=1}^C{({\mu }_i-\mu )({\mu }_i-\mu )}^T,$$ (2)

where C denotes the number of classes (i.e., C = 2 in our prostate segmentation problem), μ_i denotes the sample mean of class i, and μ denotes the global mean of all the samples.

$${\mathbf{S}}_W=\sum _{i=1}^C\sum _{{\mathit{x}}_k\in {\zeta }_i}\left(\mathit{f}\right({\mathit{x}}_k)-{\mu }_i){\left(\mathit{f}\right({\mathit{x}}_k)-{\mu }_i)}^T,$$ (3)

where ζ_i denotes the set of voxels belonging to class i, and f(x_k) is the multi-resolution patch signature of voxel x_k.

Fig. 3.

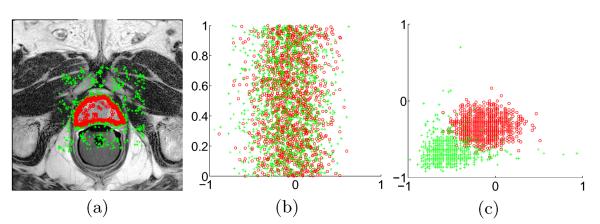
(a) A typical example of sampling voxels drawn from a training image. Samples belonging to the prostate and non-prostate regions are highlighted by small red circles and green crosses, respectively. (b) shows the scatter plot of 1D discriminant feature learnt by LDA, where the horizontal axis represents the projected value of the features. For easy visualization, the projected data points are uniformly distributed along the vertical axis. (c) shows the scatter plot of the top two most discriminant feature learnt by the SDA algorithm.

The most discriminant direction w to project the original features can be obtained by selecting the eigenvectors with the largest eigenvalues of (S_W)⁻¹S_B.

The basic assumption of LDA in defining S_B by Equation 2 is that samples belonging to the same class are generated from a unimodal Gaussian distribution. This assumption generally does not hold for voxels belonging to the prostate and non-prostate regions due to the complex anatomical structure composition in MR images (e.g., in peripheral zones, central zones, rectum, and bladder). In this case, voxels belonging to the same class may exhibit significantly different distributions in the feature space and LDA is no longer applicable. Another limitation of LDA is that it can only project the original feature to a subspace with at most C − 1 dimensions since the rank of S_B can be at most C − 1. In binary medical image segmentation problems (i.e., C = 2 in our problem), LDA can only derive 1-dimensional feature, which is unlikely to well separate voxels belonging to different regions. Figure 3 (b) shows the projected 1D feature with LDA on the drawn samples shown in Figure 3 (a), and it can be observed that samples belonging to the prostate and non-prostate regions cannot be satisfactorily separated.

Therefore, we assume that samples belonging to the same class can belong to different clusters in the feature space. Specifically, for voxels belonging to class i (i.e., only two classes in binary segmentation problem), they can be further partitioned into H_i clusters (i.e., subclasses). Following this assumption, we propose the usage of subclass discriminant analysis (SDA) [12] to learn the most discriminant features. Specifically, we redefine S_B by Equation 4

$${\mathbf{S}}_B=\sum _{i=1}^{C-1}\sum _{j=1}^{H_i}\sum _{k=i+1}^C\sum _{l=1}^{H_k}{p}_{ij}{p}_{kl}({\mu }_{\mathit{ij}}-{\mu }_{\mathit{kl}}){({\mu }_{\mathit{ij}}-{\mu }_{\mathit{kl}})}^T,$$ (4)

where p_ij = P_ij/Q denotes the weight of the jth subclass of class i, with P_ij denoting the number of samples of the jth subclass in class i and Q denoting the total number of samples. μ_ij is the sample mean of the jth subclass in class i. H_i denotes the number of subclasses in class i. Equation 4 aims to maximize the separability of subclasses belonging to different classes. Also, in Equation 4, $\mathit{rank}\left({\mathbf{S}}_B\right)\le \min ({\Sigma }_{i=1}^C{H}_i-1,\mathit{rank}({\mathbf{S}}_W\left)\right)$, which resolves the rank deficiency problem. The number of subclasses H_i of each class i is automatically determined by affinity propagation clustering [13] on samples belonging to each class i.

The SDA discriminant feature extraction procedure can be summarized by Algorithm 1. The dimension of the final features extracted by SDA is determined as the least subset of eigenvectors which occupy more than 95% of the variance similar to [10]. Figure 3 (c) shows the scatter plot of the first two dimensions of the projected features with respect to the drawn voxel samples shown in Figure 3 (a)

Algorithm 1. Discriminant Feature Extraction by SDA

Input: Drawn training voxel samples x1, …, xP, with their multi-resolution patch

signature f(xi) (i = 1, …, P) and anatomical label li.

Output: Projected signature $\widehat{\mathit{f}}\left({\mathit{x}}_i\right)(i=1,\dots ,P)$, and projection matrix M.

1. Compute the within class scatter matrix SW by Equation 3.

2. Perform affinity propagation to cluster voxel samples belonging to the prostate region into H1 subclasses and voxel samples belonging to the non-prostate region into H2 subclasses.

3. Compute the between class scatter matrix SB by Equation 4.

4. Perform eigen-analysis on (SW)−1SB to obtain its most significant eigenvectors forming matrix V, and diagonal matrix Λ containing the largest eigenvalues.

5. Let M = Λ−1/2VT.

6. Calculate the projected feature signature $\widehat{\mathit{f}}\left({\mathit{x}}_i\right)=\mathbf{M}\mathit{f}\left({\mathit{x}}_i\right)(i=1,\dots ,P)$.

7. Return $\widehat{\mathit{f}}\left({\mathit{x}}_i\right)(i=1,\dots ,P)$, and M.

by SDA. It can be visually observed that SDA can separate voxels belonging to the prostate and non-prostate regions more effectively than LDA.

2.2 Coarse Level: Multi-atlases Based Sparse Label Propagation

After learning the feature projection matrix M by Algorithm 1, we can calculate the signature $\widehat{\mathit{f}}\left(\mathit{x}\right)$ of each voxel x in the target image I_new as $\widehat{\mathit{f}}\left(\mathit{x}\right)=\mathbf{M}\mathit{f}\left(\mathit{x}\right)$, where f(x) is the original feature signature of x. The extracted features are then integrated with a multi-atlases based sparse label propagation framework to roughly estimate the prostate likelihood map in the target image.

Given N aligned training images (i.e., atlases) ${\check{I}}_i(i=1,\dots ,N)$ with I_new and their segmentation groundtruths ${\check{S}}_i$, the principle of label propagation [8,9] can be illustrated by Figure 4. For each voxel $\mathit{x}\in I_{\mathit{new}}$, its prostate likelihood is estimated by the voxels $\mathit{y}\in {\check{I}}_i$ around the neighborhood of x, namely the candidate voxels. The contribution of each $\mathit{y}\in {\check{I}}_i$ is represented by a graph weight w_i(x, y), and its corresponding label ${\check{S}}_i\left(\mathit{y}\right)$ in ${\check{S}}_i$ can be propagated to voxel x with weight w_i(x, y). In this paper, the multi-resolution fast free-form deformation (FFD) with the localized mutual information (LMI) registration algorithm [2] was used. Then, the prostate likelihood S_new(x) in I_new can be estimated by label propagation [9] as defined in Equation 5:

$$S_{\mathit{new}}\left(\mathit{x}\right)=\frac{{\Sigma }_{i=1}^N{\Sigma }_{\mathit{y}\in {\mathcal{N}}_i\left(\mathit{x}\right)}{w}_i(\mathit{x},\mathit{y}){\widehat{S}}_i\left(\mathit{y}\right)}{{\Sigma }_{i=1}^N{\Sigma }_{\mathit{y}\in {\mathcal{N}}_i\left(\mathit{x}\right)}{w}_i(\mathit{x},\mathit{y})},$$ (5)

where N_i(x) denotes the set of neighboring voxels of x in image ${\check{I}}_i$, and it is defined as a W × W × W window centered at voxel x. ${\check{S}}_i\left(\mathit{y}\right)=1$ if voxel y belongs to the prostate region in ${\check{I}}_i$, and ${\check{S}}_i\left(\mathit{y}\right)=0$ otherwise.

Fig. 4.

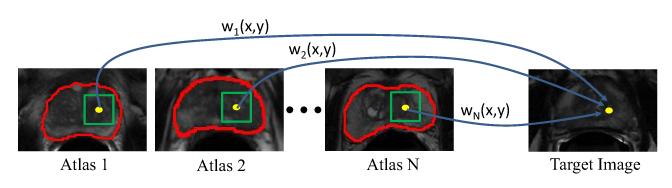
The schematic illustration of multi-atlases label propagation. In this example, N atlases with their segmentation groundtruths highlighted by red contours are available. For the reference voxel highlighted by the yellow dot in the target image, its prostate likelihood can be estimated by comparing its feature signature with those of the neighboring candidate voxels within the green squares in the atlases. The contribution of each candidate voxel y in the ith atlas during label propagation is determined by the graph weight w_i(x, y).

The most straightforward way to determine w_i(x, y) is to directly compute the Euclidean distance between the feature signatures of x and y as similar to [9]. However, the graph weight w_i(x, y) determined in this way may be sensitive to outliers and may not be able to effectively identify the most appropriate candidate voxels for label propagation. Therefore, we are motivated to estimate the graph weight w_i(x, y) based on a group sparse representation framework. Specifically, signatures $\widehat{\mathit{f}}\left(\mathit{y}\right)$ of voxels $\mathit{y}\in {\mathcal{N}}_i$ are reshaped into column vectors and organized into a matrix $\mathbf{A}=[{\mathbf{A}}_1^1,{\mathbf{A}}_1^2,\dots ,{\mathbf{A}}_i^1,{\mathbf{A}}_i^2,\dots ,{\mathbf{A}}_N^1,{\mathbf{A}}_N^2],$ where ${\mathbf{A}}_i^1$ and ${\mathbf{A}}_i^2(i=1,\dots ,N)$ are matrices with candidate voxels belonging to the prostate and non-prostate regions in the ith training image, respectively. We aim to reconstruct the signature $\widehat{\mathit{f}}\left(\mathit{x}\right)$ of each voxel $\mathit{x}\in I_{\mathit{new}}$ by the group sparse representation of columns of A. The sparse coefficient vector β_x associated with x is organized as ${\beta }_{\mathit{x}}={[{\left({\beta }_{\mathit{x}}^{1,1}\right)}^T,{\left({\beta }_{\mathit{x}}^{1,2}\right)}^T,\dots ,{\left({\beta }_{\mathit{x}}^{i,1}\right)}^T,{\left({\beta }_{\mathit{x}}^{i,2}\right)}^T,\dots ,{\left({\beta }_{\mathit{x}}^{N,1}\right)}^T,{\left({\beta }_{\mathit{x}}^{N,2}\right)}^T]}^T,$ where ${\left({\beta }_{\mathit{x}}^{i,1}\right)}^T,{\left({\beta }_{\mathit{x}}^{i,2}\right)}^T$ is the coefficient vector corresponding to ${\mathbf{A}}_i^1,{\mathbf{A}}_i^2$. The graph weight w_i(x, y) is set to the corresponding element in ${\beta }_{\mathit{x}}^{\mathit{opt}}$ for voxel $\mathit{y}\in {\check{I}}_i,$ where ${\beta }_{\mathit{x}}^{\mathit{opt}}$ denotes the optimal solution for minimizing Equation 6:

$$E\left({\beta }_{\mathit{x}}\right)=\frac{1}{2}\Vert \widehat{\mathit{f}}\left(\mathit{x}\right)-\mathbf{A}{\beta }_{\mathit{x}}{\Vert }_2^2+\lambda \Vert {\beta }_{\mathit{x}}{\Vert }_1+\sum _{i=1}^N\sum _{k=1}^2\Vert {\beta }_{\mathit{x}}^{i,k}{\Vert }_2,{\beta }_{\mathit{x}}\ge 0,$$ (6)

where ∥ · ∥₁ denotes the L₁ norm, and λ is the parameter controlling the global sparsity. Equation 6 can be optimized by using Nesterov's method [14].

The group sparsity constraint (third term) enforced in Equation 6 plays the role of atlas selection, as it tends to give more emphasis to candidate voxels from atlases similar to the target image, and effectively excludes outlier candidate voxels from atlases which are significantly different from the target image. On the other hand, the sparsity constraint (second term) further assigns more weights to the candidate voxels from atlases with similar feature signatures to the reference voxel in the target image.

Note that the estimated prostate likelihood map may still not be able to accurately delineate the prostate boundary as illustrated by a challenging example shown in Figure 5. The main reason is that the population information alone cannot fully reflect the anatomical details of the underlying patient. On the other hand, voxels with the highest segmentation confidence (i.e,. with high or low prostate likelihood values) can generally be classified correctly as shown in Figure 5 (c), which can be actually served as additional training samples to reflect the domain-specific knowledge of the target image. In this paper, voxels with prostate likelihood value S_new(x) ≥ 0.85 are determined as domain-specific prostate samples, while voxels with prostate likelihood value 0 < S_new(x) ≤ 0.15 are used as domain-specific non-prostate samples. Other voxels in the target image can be used to serve as unlabeled domain-specific samples.

Fig. 5.

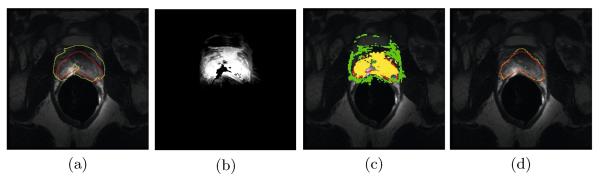
Demonstration on how our method works on a challenging example. (a) shows the estimated prostate boundary (yellow contour) by using sparse label propagation in the coarse level, with the groundtruth prostate boundary overlayed (red contour), and (b) is the corresponding prostate likelihood map. Voxels highlighted with yellow in (c) are determined as domain-specific prostate samples, and voxels highlighted with green in (c) are determined as domain-specific non-prostate samples. (d) shows the estimated prostate boundary (yellow contour) by applying the fine level domain-specific manifold regularization, with the groundtruth prostate boundary overlayed (red contour).

2.3 Fine Level: Semi-supervised Manifold Regularization

As described in Section 2.2, if the prostate shape and appearance information in the target image is significantly different from those in atlases, the segmentation result can be inaccurate. The origin of this problem is that population information from atlases alone is insufficient to represent the anatomical properties in the target image. Figure 5 (a) shows an example of the poor segmentation result obtained by the coarse level sparse label propagation.

Although the likelihood map estimated in the coarse level may not be able to accurately locate the prostate boundary, voxels with the highest segmentation confidences can be reliably identified and served as labeled domain-specific samples as described in Section 2.2 and shown in Figure 5 (c). Other voxels in the target image can be served as unlabeled domain-specific samples to encode the manifold configuration information in the feature space. These voxels provide more relevant and direct anatomical information to guide the segmentation process than voxels from atlases. In this paper, semi-supervised manifold regularization method based on the Laplacian Regularized Least Squares (LapRLS) [15] is used to integrate such information.

Specifically, given t labeled domain-specific training voxels $z_i^L$ (i = 1, …, t), with anatomical label v_i = 1 if $z_i^L$ is determined as prostate samples and v_i = 0 otherwise, and also h unlabeled domain-specific training voxels $z_j^U$ (j = 1, …, h), LapRLS can be formulated as the optimization problem in Equation 7:

$$\underset{\Phi \in {\mathcal{H}}_K}{\min }\frac{1}{t}\sum _{i=1}^t(v_i-\Phi (\widehat{\mathit{f}}{\left(z_i^L\right)\left)\right)}^2+{\gamma }_A\Vert \Phi {\Vert }_K^2+\frac{{\gamma }_I}{{(t+h)}^2}{\mathit{q}}^T\mathbf{L}\mathit{q},$$ (7)

where $\widehat{\mathit{f}}\left(z_i^L\right)$ denotes the discriminant feature representation of voxel $z_i^L$. ${\mathcal{H}}_K$ denotes the reproducing kernel Hilbert spaces (RKHS), and Φ is a mapping function in ${\mathcal{H}}_K$ to map a discriminant feature representation to a prostate likelihood value. $\mathit{q}={\left[\Phi \left(\widehat{\mathit{f}}\right(z_1^L\left)\right),\dots ,\Phi \left(\widehat{\mathit{f}}\right(z_t^L\left)\right),\Phi \left(\widehat{\mathit{f}}\right(z_1^U\left)\right),\dots ,\Phi \left(\widehat{\mathit{f}}\right(z_h^U\left)\right)\right]}^T$, and L is the graph Laplacian of all the training samples computed based on the heat kernel [15]. γ_A and γ_I are weighting parameters of the second and third terms.

Based on the Representer Theorem [15], Φ can be represented as an expansion of kernel functions over both the labeled and unlabeled samples:

$$\Phi \left(\widehat{\mathit{f}}\right(\mathit{z}\left)\right)=\sum _{i=1}^t{\alpha }_{i}K\left(\widehat{\mathit{f}}\right(\mathit{z}),\widehat{\mathit{f}}({\mathit{z}}_i^L\left)\right)+\sum _{j=1}^h{\alpha }_{t+j}K\left(\widehat{\mathit{f}}\right(\mathit{z}),\widehat{\mathit{f}}({\mathit{z}}_j^U\left)\right).$$ (8)

Once the kernel function K is determined, the optimal parameters α_i (i = 1, …, t + h) in Equation 8 which yield the optimal mapping function Φ^opt to minimize Equation 7 can be obtained by Equation 9:

$${\alpha }^{\ast }={(\mathbf{JK}+{\gamma }_{A}t\mathbf{I}+\frac{{\gamma }_{I}t}{{(t+h)}^2}\mathbf{LK})}^{-1}\mathit{Y},$$ (9)

where J = diag(1, …, 1, 0, …, 0) is a (t + h) × (t + h) diagonal matrix with the first t diagonal entries as 1 and the rest as 0. K is the (t + h) × (t + h) Gram matrix with ${\mathbf{K}}_{ij}=K\left(\widehat{\mathit{f}}\right(z_i),\widehat{\mathit{f}}(z_{ij}\left)\right)$. Y is a (t+h) dimensional label vector with Y = [v₁, …, v_t, 0, …, 0], and α* = [α₁, …, α_t+h].

After estimating α*, the optimal mapping function Φ^opt can be obtained by Equation 8. The final segmentation result can be obtained by applying Φ^opt to the feature signature $\widehat{\mathit{f}}\left(\mathit{z}\right)$ of each voxel z in the target image, and classified it to the prostate region if $\Phi \left(\widehat{\mathit{f}}\right(\mathit{z}\left)\right)\ge 0.5$, and classified to the non-prostate region otherwise. Figure 5 (d) shows the estimated prostate boundary refined by the fine level semi-supervised manifold regularization, and it can be observed that the prostate boundary has been accurately located, which implies the importance of incorporating domain-specific appearance information for classification.

3 Experimental Results

Our method was evaluated on a prostate T2 weighted MR image dataset consisting of 66 images taken from 66 different patients in the University of Chicago Hospital, and 9 prostate MR images taken from 9 different patients other than those 66 patients were used as atlases. All MR images were also taken from different MR scanners. For each image, its manual segmentation groundtruth is provided by a clinical expert. The parameters of our method were set as follows by cross validation: W = 15, λ = 10⁻⁴, γ_A = 10⁻⁶, and γ_I = 10⁻⁷. The Gaussian RBF kernel $K\left(\widehat{\mathit{f}}\right({\mathit{z}}_1),\widehat{\mathit{f}}({\mathit{z}}_2\left)\right)=\exp (-\tau \Vert \widehat{\mathit{f}}({\mathit{z}}_1)-\widehat{\mathit{f}}({\mathit{z}}_2)\Vert {}^2)$ was used in the fine level, with kernel parameter $\tau =\frac{1}{128}$.

The following preprocessing procedure was performed: The N3 bias correction algorithm [16] was first performed, followed by the histogram equalization procedure. Three different evaluation measures are used: Dice ratio, Hausdorff distance, and the average surface distance (ASD). Our method was also compared with the two state-of-the-art multi-atlases based segmentation methods proposed by Klein et al. [2] and Coupe et al. [9].

Table 1 lists the average Dice ratio, minimum Dice ratio, mean Hausdorff distance, and mean ASD, along with respective standard deviations (SD), across all the patients for different approaches.

Table 1.

The comparison of different methods with different evaluation metrics. The last three rows show the segmentation accuracy of our method with coarse level (CL) sparse label propagation only, CL based on the features derived by SDA, and finally integrated with domain-specific manifold regularization in the fine level (FL), respectively. The best results are bolded.

Method	Mean Dice + SD (in %)	Min Dice (in %)	Mean Hausdorff + SD (in mm)	Mean ASD + SD (in mm)
Klein et al. [2]	81.8 ± 4.3	47.3	11.7 ± 3.2	2.8 ± 1.2
Coupe et al. [9]	78.4 ± 3.6	34.2	15.8 ± 3.6	4.1 ± 1.5
CL	82.6 ± 4.8	51.4	10.6 ± 3.3	2.6 ± 1.4
SDA+CL	85.1 ± 4.1	63.2	9.6 ± 2.7	2.4 ± 1.2
SDA+CL+FL	88.3 ± 2.6	84.6	7.7 ± 2.1	1.8 ± 0.9

It can be observed from Table 1 that by using the coarse level (CL) only, the segmentation accuracy of our method is slightly higher than Klein's method. By integrating CL with the salient features extracted by SDA, the segmentation accuracy can be further improved, which reflects the contribution of SDA. Finally, by incorporating the fine level (FL) semi-supervised manifold regularization framework, the segmentation accuracy can be significantly boosted up, which is particularly reflected by the minimum Dice ratio.

Figures 6 and 7 show the Dice ratio between the estimated prostate volume and the segmentation groundtruth of each patient with our method by using the CL only, SDA derived features with CL, and further integrated with FL. It can be observed that the segmentation accuracies consistently and progressively increase for all the patients, which illustrates the contribution of each component.

Fig. 6.

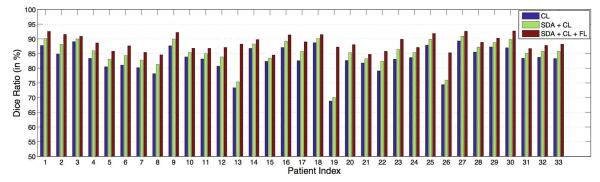
Dice ratio between the estimated prostate volume and the groundtruth of the first 33 patients by using coarse level (CL) segmentation only, SDA derived feature with CL, and finally integrated with the fine level (FL) segmentation.

Fig. 7.

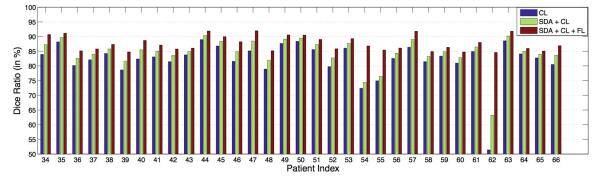
Dice ratio between the estimated prostate volume and the groundtruth of the rest of the 33 patients by using coarse level (CL) segmentation only, SDA derived feature with CL, and finally integrated with the fine level (FL) segmentation

Figure 8 shows some typical segmentation results by our method, and it can be observed that the estimated prostate boundaries by the proposed method are very close to the groundtruth, which implies the effectiveness of our method.

Fig. 8.

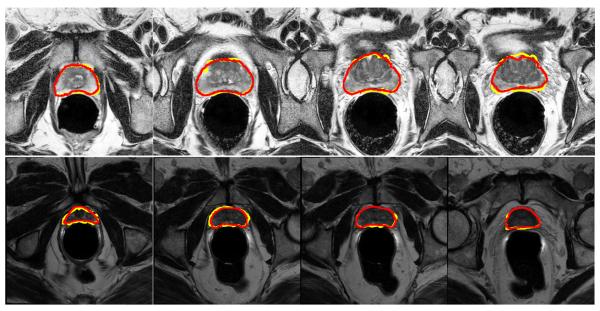
Exemplar segmentation results obtained by the proposed method, where each row represents the segmentation results of a particular patient. Here, the estimated prostate boundary is highlighted in yellow, and the groundtruth prostate boundary is highlighted in red.

The proposed method takes around 2.9 mins on average to segment a 3D prostate MR image. All the experiments were conducted on an Intel Xeon 2.66-GHz CPU computer with MATLAB implementation.

4 Conclusion

In this paper, we propose a new prostate MR image segmentation method. The most discriminant feature signatures for each voxel are learnt by the subclass discriminant analysis (SDA) to aid segmentation. SDA aims to find a discriminant feature subspace which simultaneously maximizes the inter-class distance and minimizes the intra-class variations. The learnt features are integrated with a hierarchical segmentation framework. In the coarse level, a sparse label propagation method is proposed to propagate the population information from atlases to the target image. The estimated prostate likelihood map can reliably identify voxels with the highest segmentation confidences to serve as labeled domain-specific samples of the target image, and voxels with low segmentation confidences are served as unlabeled domain-specific samples to describe the underlying manifold configuration in the feature space. A semi-supervised manifold regularization method is proposed to construct the domain-specific classifier, and it is used to refine the final segmentation result in the fine level. Our method has been evaluated on a prostate MR image dataset consisting of 66 patients and compared with two state-of-the-art multi-atlases based segmentation methods. Experimental results demonstrate that our method consistently achieves the highest segmentation accuracy among the methods under comparison.