Multinomial Probabilistic Fiber Representation for Connectivity Driven Clustering

Abstract

The clustering of fibers into bundles is an important task in studying the structure and function of white matter. Existing technology mostly relies on geometrical features, such as the shape of fibers, and thus only provides very limited information about the neuroanatomical function of the brain. We advance this issue by proposing a multinomial representation of fibers decoding their connectivity to gray matter regions. We then simplify the clustering task by first deriving a compact encoding of our representation via the logit transformation. Furthermore, we define a distance between fibers that is in theory invariant to parcellation biases and is equivalent to a family of Riemannian metrics on the simplex of multinomial probabilities. We apply our method to longitudinal scans of two healthy subjects showing high reproducibility of the resulting fiber bundles without needing to register the corresponding scans to a common coordinate system. We confirm these qualitative findings via a simple statistical analyse of the fiber bundles.

1 Introduction

Research in the area of fiber clustering has resulted in subject- as well as population-specific characterization of the white matter brain structures[1,2]. Clustering algorithm group fibers into feature-based bundles. The resulting fiber bundles delineate different characteristics of white matter regions depending on which features are described by the underlying fiber representation. Existing fiber representations and clustering techniques mostly rely on geometrical features, such as their shape and placement in the 3D space [3]. Groupings based on these features give a brief picture of the structure of the white matter but largely fail to provide information for the further analyses of their neuroanatomical functions, i.e connectivity between brain regions [4]. In this work, we address this issue by proposing a multinomial representation of fibers based on brain connectivity.

We first introduce multinomial feature vectors, called connectivity vectors, which capture the posterior probabilities of a voxel being connected to a set of ROIs. A fiber is encoded by the voxels it passes through as well as the corresponding connectivity vectors at those voxels. We then create a compact multinomial representation for the whole fiber by fusing the corresponding connectivity vectors via the logit transformation. The logit transform enables us to map the connectivity vectors, which are members of the M dimensional simplex , to the Euclidean space ℝ^M, where norm and inner product are defined naturally. In other words, we can perform all calculations in ℝ^M without needing to pay attention to the geometric properties of the manifold spanned by connectivity vectors in .

We complete our representation with the definition of a distance measure, which is essential for clustering. The Hausdorff distance is one of the most popular distances for fibers represented by their geometrical features [5]. However, such a distance does not account for the neuroanatomical functions of fibers neither allow any statistical inference. In [6], authors use kernel density estimation to transform such distances into probabilities and apply it to statistical decision modelling. An alternative was recently proposed by [7], who measure the possible diffusion pathways between predefined ROIs and fibers via the Mahalanobis distance. We also propose the use of the Mahalanobis distance for fibers represented by the connectivity vectors in ℝ^M. We show that the distance is invariant to the parcellation biases over ROIs by proving that this metric is a specific instance of the family of prior invariant distances on . This property is important for clustering as it allows us to ignore implementations issues related to the calculation of the probabilities, e.g. representing fibers by likelihoods or posteriors.

One of the most important characteristic of the proposed representation is the fact that individual fibers and fiber bundles are treated as statistical objects invariant to the image coordinate system. Although it is possible to perform longitudinal or population based studies by analyzing fibers via 3D coordinates [6], an important novelty of the proposed work is the use of informative posteriors related to the connection of fibers to ROIs. In addition, our representation enables the analysis for these type of studies without needing to register the fibers to a common coordinate system. Finally, it allows hypothesis driven statistical analysis over fiber bundles, and can be thought as a first step in creating a probabilistic fiber atlases. This type of analysis requires the bundles to be comparable across the scans to be studied. We evaluate the reproducibility over our approach by applying our representation to the base line and follow up scans of two different subjects. The results are consistent allowing us to visually pinpoint the same fiber bundle across scans as well as perform statistical analyses on the bundles for quantitatively comparison.

2 Fiber Representation

We now describe our representation whose encoding of fibers is based on their connections to ROIs. These connections are captured at each voxel of the fiber by multinomial vectors, called connectivity vectors. We derive a compact representation of fibers, called connectivity signature, by fusing these connectivity vectors via the logit function. We complete the description of our representation by deriving a metric naturally inferred from the space spanned by the connectivity signatures.

2.1 Multinomial Fiber Representation

We view fibers as a collection of voxels and their corresponding probabilistic connectivity vectors. Specifically, let ℝ^M denote M-dimensional real space and

$${\mathbb{S}}^M\equiv \{\mathbf{u}=(u_0,\dots ,u_M)\in {\mathbb{R}}^M:u_0+\dots +u_M=1;u_i>0\text{for}i\in \{0,\dots ,M\}\},$$

is the M-dimensional simplex. u₀ is usually defined as $u_0=1-{\sum }_{i=1}^M{u}_i$ so that the vector u ≡ (u₀, u₁, …, u_M) ∈ has M degrees of freedom. In the remainder, we therefore represent u only by its independent components, i.e. u ≡ (u₁, …, u_M), and mention u₀ where necessary. With respect to our representation, the multinomial vector u(x) ∈ captures the posterior probability of a given voxel x being connected to the ROIs (for instance gray matter regions) {G₁, …, G_M} in the image I. We compute the posteriors based on the outcome of probabilistic tractography (see Section 3 for further details). We call u(x) the connectivity vector and formally define it as

$$\mathbf{u}(x)\equiv \left(p(G_1\mid I,x),\dots ,p(G_M\mid I,x)\right).$$ (1)

We note that the probability $p(G_0\mid I,x)=1-{\sum }_{i=1}^{M}p(G_i\mid I,x)$ is the posterior probability that a given voxel x is not connect to any ROI. Furthermore, we could have u(x) represent likelihoods instead of posteriors. The reason we prefer using posterior probabilities is their superiority in terms of connectivity interpretations. The multinomial vector itself simply explains all possible connections of a voxel. We also assume that the connectivity vectors u(x) are independently drawn from a logistic normal distributions [8] for each voxel x. A popular alternative would have been the Dirichlet distribution [9,10]. However, any Dirichlet distribution can be approximated with a suitable logistic normal distribution [11]. In addition, the logistic normal distribution better fits into the modelling performed in the remainder of this article.

The main intuition behind this probabilistic representation is to enhance the results of deterministic tractography with the notion of uncertainty. This uncertainty is especially helpful in fiber clustering as it provides additional information for separating fibers with respect to just the two regions marking the fiber’s ends. This observation leads us to the following definition: A fiber f in the image I is a collection of voxels x and corresponding connectivity vectors u(x) ∈ . For sake of clarity, connectivity vectors, u(x), will from now on be denoted as u.

One way to represent a fiber is now as a matrix composed of the connectivity vectors u. Figure 1(a) shows a red fiber inside a bundle of the Corpus Callosum together with its matrix representation in Figure 1(b). As expected, the matrix clearly favours two regions, which are the ones touched by the ends of the fiber. Furthermore, the matrix also implicitly encodes geometric properties of the fiber by the changes in the multinomial distribution when moving along the path.

Fig. 1.

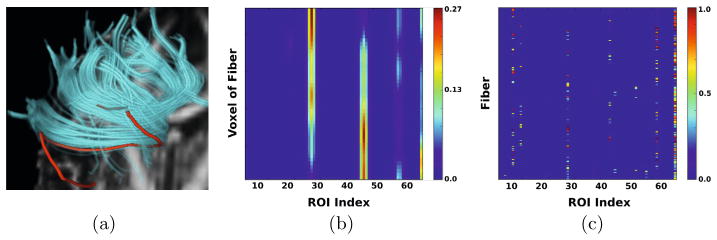
(a) A fiber bundle from Corpus Callosum together with the (b) set of connectivity vectors u of the fiber in red and (c) connectivity signatures 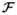of all individual fibers in the bundle. The x-axis of both matrices represents the ROI index. Blue indicates low and red high probabilities being connected to a specific ROIs. Note, how the connectivity vectors implicitly represent the geometry of the fiber in red. The connectivity signature on the other side summarizes the favoured regions by the whole bundle, which seem to be six.

2.2 Log Odds Representation of Fibers

Representing fibers as collections of multinomial vectors enables in-depth analyses over individual fibers. However one may want a more compact representation that can be used for immediate reasoning such as “which regions does the fiber connect with the highest probabilities ?”. To derive such a compact representation, we now map the multinomial random vectors u from the simplex to the Euclidean space ℝ^M. By doing so, we can compress the set of connectivity vectors representing a fiber without the constraints of the simplex.

Given that u is drawn from a logistic normal distribution, the most suitable homeomorphism between and ℝ^M is the logit transform [8]. The log odds vector v(x) ∈ ℝ^M is then defined as the logit transform of the connectivity vector u(x):

$$\mathbf{v}(x)\equiv \mathit{logit}(\mathbf{u}(x))=ln(\mathbf{u}(x)/u_0).$$ (2)

The inverse is called the logistic function σ(·) mapping v ∈ ℝ^M to u ∈

$$\mathbf{u}\equiv \sigma (\mathbf{v})=\frac{e^{\mathbf{v}}}{1+{\sum }_{j=1}^M{e}^{v_j}}.$$ (3)

Similar to the definition of a fiber f, a log odds fiber l is then defined as a collection of voxels x and corresponding log odds vectors v(x).

To define a compact representation of the log odds fiber l, we parametrize it with respect to the discrete arc length s ∈ [0, 1], where l(s) ≡ v(x). Furthermore, we introduce the weight function w(s) ∈ [0, 1] enabling us to emphasize specific parts of the fiber. Our compact representation is motivated by the assumption that the connectivity vectors u(x) are independently drawn for each voxel x as well as the fact that the normalized multiplication between u(x) translates to the sum of v(x) [12]. A natural definition for a compact log odds fiber representation, F ∈ ℝ^M, is thus by the weighted sum of the log odds vectors across the fiber

$$\mathbf{F}\equiv \sum _{s}w(s)·\mathbf{l}(s).$$ (4)

Now, the compact multinomial representation for a fiber is the sigmoid function applied to F:

$$\mathcal{F}\equiv \sigma (\mathbf{F}),$$ (5)

We call 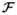, the connectivity signature of fiber f as this multinomial vector summarizes the connectivity of f to the ROIs. One of the most useful properties of the logit transformation is that v ∈ ℝ^M is drawn from a multivariate Gaussian defined by 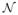(μ, Σ) as u ∈ is drawn from a logistic normal distribution [8] (see Section 2.1). Thus, the log odds representation F of a fiber is again drawn from a Gaussian distribution since the summation of independent normally distributed random variables is also another normally distributed random variable. Furthermore, the connectivity signature 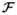must then also be drawn from the logistic normal distribution.

An important property of the proposed log odds fiber representation is the fact that the mean and covariance have real statistical meanings unlike in other representations, such as in [7]. For instance, if we apply the inverse logit function to μ, we get a multinomial vector in which summarizes the average connection probabilities of fiber bundles. Similarly, Σ gives the covariances among connection probabilities of different ROIs.

We end this discussion by pointing out that all the fibers extracted from an image I can be represented by a matrix composed of their connectivity signatures. Figure 1(c) shows an example of such a matrix representing fibers seeded from Corpus Callosum. Note, that the matrix represents all fibers independent of the image orientation. Assuming the generation of fibers is stable across scans, this matrix thus provides a mechanism for performing statistics on fibers among a set of scans without needing to register them beforehand. These assumptions will be justified by the experiments of Section 3.

2.3 Metrics in and ℝ^M

Applications such as fiber clustering rely on metrics that properly measure the distance between fibers. We now define such a metric for our proposed fiber representation. Specifically, let F₁ and F₂ be the compact log odds representations of two fibers with 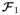and 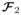being their corresponding multivariate counter-parts. As in our model log odds fibers F are normally distributed, a natural metric is the Mahalanobis distance

$$d({\mathbf{F}}_1,{\mathbf{F}}_2)=\sqrt{{({\mathbf{F}}_1-{\mathbf{F}}_2)}^T{\mathit{\sum }}^{-1}({\mathbf{F}}_1-{\mathbf{F}}_2)},$$ (6)

where Σ is the covariance matrix of their distribution. An alternative motivation behind the Mahalanobis distance is its independence to the prior. In the remainder of this section, we will derive this property by first constructing Riemanian manifolds of the commutative Abelian group as defined in [12], whose metrics are independent of the prior. We then show the equivalence of the Mahalanobis distances to a specific subset of these metrics. Finally, we discuss the importance of the prior invariance for the implementation of our representation.

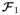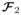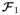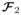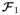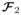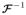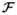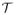
In [12], the addition operation, ⊗, between connection signatures and ∈ is defined as ⊗ ≡ σ(logit( ) + logit( )) = σ (F₁ + F₂) while the inverse is ≡ σ(−logit( )). Now, let 1^T ≡ (1, …, 1) then the corresponding tangent space is ≡ {w ∈ ℝ^M+1 |1^T w = 0} as the inner product of 1 with any curve on the Simplex u^ε = u+ε · w+O(ε²) ∈ has to be one, i.e. 1^T u^ε = 1. 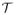Thus, the logarithm function, LOG : → , projecting the simplex to the tangent space, is

$$\mathit{LOG}(\mathcal{F})=\frac{1}{M^2}(M\mathbf{I}-{\mathbf{11}}^T)ln(\mathcal{F}),$$

where I is the identity matrix. Finally, the family of prior invariant metrics on the commutative Abelian group is defined by

$$d_R({\mathcal{F}}_1,{\mathcal{F}}_2)=\sqrt{\mathit{LOG}{({\mathcal{F}}_1^{-1}\oplus {\mathcal{F}}_2)}^T{G}_R\mathit{LOG}({\mathcal{F}}_1^{-1}\oplus {\mathcal{F}}_2)},$$ (7)

where the concentration matrix G_R is positive definite. We show the prior invariance of d_R(·, ·) by denoting the posterior as u^pst ≡ (p(G₁|I, x), …, p(G_M |I, x)), the normalized likelihood as u^lkh ≡ (p(x|I, G₁), …, p(x|I, G_M)) and the prior as u^pri ≡ (p(G₁), …, p(G_M)). According to [12], adding the prior to the likelihood via ⊗ is equivalent to Bayes’ rule as u^pst = u^lkh ⊗ u^pri and the identity ${({\mathbf{u}}_1\oplus \mathbf{p})}^{-1}\oplus ({\mathbf{u}}_2\oplus \mathbf{p})={\mathbf{u}}_1^{-1}\oplus {\mathbf{u}}_2$ holds for any u₁, u₂, p ∈ . Then, the distance $d_R({\mathbf{u}}_1^{\mathit{lkh}},{\mathbf{u}}_2^{\mathit{lkh}})$ defined on is invariant to priors as

$$\begin{array}{l}{d}_R^2({\mathbf{u}}_1\oplus \mathbf{p},{\mathbf{u}}_2\oplus \mathbf{p})=\mathit{LOG}{\left({({\mathbf{u}}_1\oplus \mathbf{p})}^{-1}\oplus ({\mathbf{u}}_2\oplus \mathbf{p})\right)}^T{G}_R\mathit{LOG}\left({({\mathbf{u}}_1\oplus \mathbf{p})}^{-1}\oplus ({\mathbf{u}}_2\oplus \mathbf{p})\right)\\ =\mathit{LOG}{({\mathbf{u}}_1^{-1}\oplus {\mathbf{u}}_2)}^T{G}_R\mathit{LOG}({\mathbf{u}}_1^{-1}\oplus {\mathbf{u}}_2)=d_R^2({\mathbf{u}}_1,{\mathbf{u}}_2)\end{array}$$

so that

$$d_R({\mathbf{u}}_1^{\mathit{lkh}},{\mathbf{u}}_2^{\mathit{lkh}})=d_R({\mathbf{u}}_1^{\mathit{lkh}}\oplus {\mathbf{u}}^{\mathit{pri}},{\mathbf{u}}_2^{\mathit{lkh}}\oplus {\mathbf{u}}^{\mathit{pri}})=d_R({\mathbf{u}}_1^{\mathit{pri}},{\mathbf{u}}_2^{\mathit{pri}}).$$ (8)

If we now define α ≡ (1, 0, …, 0) and specify the concentration matrix as G_R ≡ M²(I − α1^T) Σ⁻¹(I − 1α^T) then the resulting Riemannian metric is equivalent to the Mahalnobis distance of Equation (6): $d^2({\mathbf{F}}_1,{\mathbf{F}}_2)=d_R^2({\mathcal{F}}_1,{\mathcal{F}}_2)$. Thus, the Mahalanobis distance is invariant to any prior, i.e. bias shared among fibers. One of these factors are the priors of ROIs corresponding to their size and shapes. The probabilities in connectivity vectors u (and therefore in 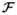) are highly correlated with the partitioning of ROIs since shapes and size of these regions will change the fraction of fibers reaching them. Another important conclusion from the prior invariance is that distances between fibers are not impacted by ones choice of calculating posterior probabilities or normalized likelihoods for the definition of the multinomial vectors u. In summary, choosing the Mahalanobis distance as a metric for fibers greatly simplifies the implementation of our representation due to its invariance to priors.

We end this section by revisiting one more time the multivariate logistic-normal (MLN) distribution that is assumed as a prior over vector u ∈ . One important property is that MLN distribution has more flexibility than the popular Dirichlet distribution, which is the conjugate of the multinomial. The Dirich-let distribution has a single concentration parameter, while MLN has a covariance matrix. This relation corresponds to the distinction between Mahalanobis distance, which is parameterized by a covariance matrix, and KL divergence or the Fisher metric, which have no such parameter. The invariance properties that we have described above may be of some interest to the community that uses MLN for modeling and analysis.

3 Fiber Clustering

We now apply the proposed representation for the clustering of fibers. Our goal is to test the consistency of the corresponding fiber bundles on longitudinal scans as well as across subjects. Consistency across scans is important for the reliability of studies analyzing the changes in the bundles.

3.1 Clustering Algorithm

Our experiment is based on T1 and DTI images of 2 female subjects. Each subject was scanned twice two weeks apart. The scans were acquired on a Siemens 3T VerioTM scanner using a single-shot, spin-echo, echo-planar sequence (TR/TE=11400/78ms, b-value 1000 s/mm2, and 64 gradient directions). We separately created a gray matter parcellation for each DTI scan by applying FreeSurfer to the corresponding T1 image, which was affinely aligned to the DTI [13]. Note, the deformation map created by FreeSurfer is only defined for the gray matter. Inverting the map thus does not accurately register the DTI scan to the atlas of FreeSurfer. Analyses based on our fiber representation has no use for such registrations as our statistical model is invariant to the image coordinate system.

The log odds representations of fibers are created by first extracting the fibers using a streamline tractography [14] and then computing the corresponding connectivity vectors via probabilistic tractography [15]. Specifically, we perform the following steps: (1) create fibers via streamline tractography seeded from the Corpus Collosum, (2) for each fiber, run the probabilistic tractography seeded at each voxel defining the fiber, (3) for each voxel x of the fiber, compute the multinomial vector u(x) of Equation 1 by defining the posterior probability p(G_i|I, x) as the fraction of fibers seeded at this voxel and reaching ROI G_i, (5) calculate the log odds vector v(x) by Equation 2, (6) generate the final log odds representation, F, via Equation 4. Finally, we compute the connectivity signatures, 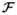, of Equation 5 for visualization and interpretation purposes.

Based on this protocol, we expect our clustering approach to produce very similar fiber bundles for the two time points of each subject.

To cluster the fibers, one could make the simplifying assumption that all fibers are drawn from a common Gaussian distribution. While this model is simple to implement, the resulting fiber bundles of our data set were very inconsistent as the assumption of all fibers being drawn from a single Gaussian distribution is not realistic. We discovered that the multinomial representations of fibers seeded at different white matter (WM) regions greatly vary due to the drastic differences in the connectivity of different WM regions.

We thus instead assume that the fibers are drawn from a mixture of logistic normal distributions in , which is a mixture of Gaussians in ℝ^M. We estimate the mixture of Gaussians via the Expectation-Maximization (EM) procedure [16]. By doing so, we implicitly make use of the Mahalanobis distance between fibers and mixture components’ mean vectors for assigning fibers to mixture components. Hence, the mixture assignment is driven by the Mahalanobis distance thus still inheriting the proposed invariance to the common priors.

The clustering was solely performed on the connectivity signatures, such as the one shown in Figure 2. While the numbers of fibers and their orderings are different across the matrices, the matrices themselves are independent of the image coordinate system. They thus do not need to be registered for evaluating the reproducibility of our method.

Fig. 2.

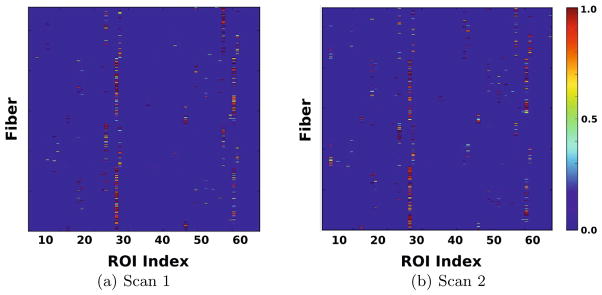
Connectivity signatures of Corpus Callosum corresponding to different scans of a subject. The x-axis represents ROI index. Each row corresponds to connectivity signature 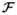of a fiber. Colors indicate the connection probabilities to ROIs. Note, the common patterns of connections even though the scans are not registered or fibers are not ordered.

3.2 Clustering Results

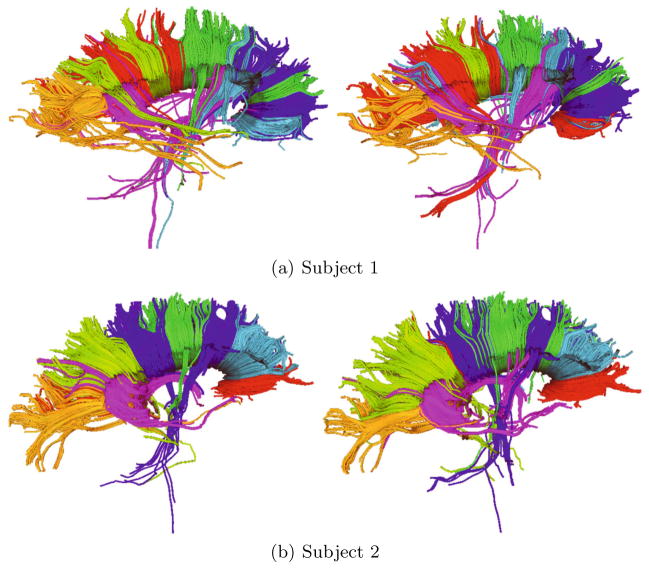
Finally, we review the fiber bundles extracted by our approach for the two subjects with two time points. Figure 3 shows the outcome of our approach for assigning the tracts to 7 fiber bundles. The consistency between the results of baseline and follow up is evident for both subjects. Similarly, there is a high consistency between subjects. We further challenge the repeatability of the algorithm by increasing the number of clusters. Figure 4 shows the outcome with 25 fiber bundles for a single subject. Even with such a fine grain clustering, intra-person consistency is excellent making it possible to pinpoint corresponding fiber bundles across these scans. This qualitative assessment seem to indicate that the proposed clustering algorithm exhibits a strong repeatability in terms of fiber groupings. The results in Figure 3,4 were generated without registering the DTI images. Thus, the consistency in clustering justifies the invariance of our proposed metric to priors over ROIs since individual registrations tend to have minor changes in shapes and sizes of ROIs.

Fig. 3.

Results showing reproducibility of fiber bundles with the proposed representation. Images show clustering of Corpus Callosum with 7 clusters for two subjects. Left and right images correspond to different scans of a subject. Note, the intra-subject consistency for both subjects.

Fig. 4.

Results showing reproducibility of fiber bundles with the proposed representation. Images show clustering of Corpus Callosum of Subject 1, with 25 clusters. Left and right images correspond two different time point scans of the subject. Intra-person consistency is excellent even with a fine grain clustering.

We complement this qualitative interpretations with a quantitative assessment, which also provides an example on doing statistical analysis based on our representation. Fiber bundles generated by the clustering can be treated as statistical objects as each fiber is represented by a multinomial vector. One may assume each bundle as a distribution of such multinomial vectors and then can compare these distributions across scans. We do by representing each fiber bundle via its mean connectivity signature and then comparing signatures across scans via the symmetric KullbackLeibler (KL) divergence which is defined by

$$KL({\overline{\mathcal{F}}}_1,{\overline{\mathcal{F}}}_2)=\frac{1}{2}\sum _{i=1}^M\left(ln\left(\frac{{\overline{\mathcal{F}}}_1(i)}{{\overline{\mathcal{F}}}_2(i)}\right){\overline{\mathcal{F}}}_1(i)+ln\left(\frac{{\overline{\mathcal{F}}}_2(i)}{{\overline{\mathcal{F}}}_1(i)}\right){\overline{\mathcal{F}}}_2(i)\right)$$ (9)

where 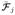(i) is the i^th element of the mean connectivity signature 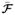of a fiber bundle in scan j.

Our comparison of bundles across scans specifically focus on those pairs that match, i.e. have the lowest divergence score. Figure 5 shows the matched fiber bundle from four different scans and their corresponding symmetric KL-Divergence scores with respect to the first scan. First, we note that the score seems to reflect the geometrical properties of the bundle. The more similar the bundles look, the lower the score. Second, as expected, the bundle of the follow up scan of the same subject received the lowest score.

Fig. 5.

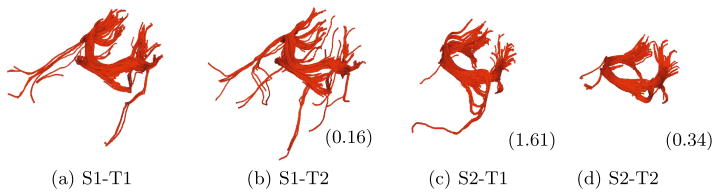
Same fiber bundle in four different scans of two subjects (S1, S2) and two time points (T1, T2). Matching of bundles is performed by KL divergence measure. The values in parentheses are the distances from the first bundle. Thank to our multinomial representation, corresponding fiber bundles across scans can be matched by using probabilistic measures like KL divergence.

Table 1 lists the average symmetric KL divergence of the four different scans clustered into 7 bundles (see Figure 3). The average symmetric KL divergence was computed across the 7 bundles that best matched between scans. Note, the values of intra-subject pairs are always lower than values of inter-subject pairs. These quantitative results seem to echo the qualitative assessment that the bundles generated via our representation are highly consistent.

Table 1.

The average symmetric KL divergence between the mean signature values of matching bundles of two subjects (S1, S2) and two time points (T1, T2). The intra-person distances are always lower than that of inter-person.

	S1-T1	S1-T2	S2-T1	S2-T2
S1-T1	0	1.68	1.92	3.01
S1-T2	1.68	0	3.05	3.63
S2-T1	1.92	3.05	0	1.24
S2-T2	3.01	3.63	1.24	0

4 Conclusion

We developed a multinomial representation of fibers decoding their connectivity to gray matter regions. We simplified clustering these fibers into bundles by deriving a compact encoding of that representation via the logit transformation. Furthermore, we created a distance measure that is invariant to parcellation biases by deriving the family of prior invariant metrics on the simplex of multinomial probabilities. We applied our method on longitudinal scans of two healthy subjects showing high reproducibility of the resulting fiber bundles without needing to register the corresponding scans to a common coordinate system. We confirmed these qualitative findings by measuring the symmetric KL-Divergence of bundles across scans.