Abstract
We propose a new approach for statistical shape analysis of 3D anatomical objects based on features extracted from skeletons. Like prior work on medial representations [7,15,9], the approach involves deforming a template to target shapes in a way that preserves the branching structure of the skeleton and provides intersubject correspondence. However, unlike medial representations, which parameterize the skeleton surfaces explicitly, our representation is boundary-centric, and the skeleton is implicit. Similar to prior constrained modeling methods developed 2D objects [8] or tube-like 3D objects [13], we impose symmetry constraints on tuples of boundary points in a way that guarantees the preservation of the skeleton’s topology under deformation. Once discretized, the problem of deforming a template to a target shape is formulated as a quadratically constrained quadratic programming problem. The new technique is evaluated in terms of its ability to capture the shape of the corpus callosum tract extracted from diffusion-weighted MRI.
1 Introduction
The Blum skeleton [2] is a geometrical construct that provides a powerful set of features for quantifying the symmetric properties of geometric objects, particularly those derived from biomedical imaging. Although the skeleton, or medial axis, was originally described by Blum [2] in the plane (defined as the set of connected curves formed by the centers of maximal inscribed disks a 2D object), the concept and the definition of the skeleton naturally extend to 3D. The skeleton of a 3D object, also called the medial scaffold, consists of surfaces, which are formed by the centers of all maximal inscribed balls (MIBs) in the object. We give a more formal definition in Sec. 2.1, and Fig. 1 provides an illustration.
Fig. 1.

Left: the medial axis of a 2D object, with examples of MIBs tangent to the boundary at one, two and three points. Right: an illustration of a 3D object, half of which has been cut away to reveal the medial scaffold. The medial scaffold consists of surface patches that join along crease curves and terminate at free edge curves.
The Blum skeleton is used frequently in image and shape analysis because it captures important salient properties of natural objects [9]. For instance, the curvature of the skeleton can be used to characterize how an object bends locally, particularly for tube-like or sheet-like objects. Each point on the skeleton is associated with the radius of the corresponding MIB, and the radius function provides a way to measure the local thickness of tube and sheet-like objects. Since many of the commonly studied organs in the human body are sheet-like or tube-like (cerebral cortex, many white matter tracts, myocardium, heart valves, etc.), such measures of thickness and bending are commonly sought in biomedical applications, e.g., to characterize the effects of disease on organs and tissues. Even objects that are not sheet-like (e.g., the hippocampus) have been analyzed using features derived from skeletons [10,3].
The use of skeleton-derived geometric features in statistical shape analysis is complicated by the fact that the composition of the medial axis/scaffold into curves and surfaces, known as branching structure, is almost always different for multiple instances of a given class of geometric objects (e.g., the hippocampi of different individuals). A very small deformation to the boundary of an object, such as adding a bump on the surface, can change the medial branching structure. This variability in branching makes it challenging to find correspondences between medial axes/scaffolds of different instances and to apply the standard tools of statistical shape analysis. In some cases, this challenge can be overcome by pruning smaller branches heuristically until, for each instance, the medial axis/scaffold is reduced to a common branching structure [3]. An alternative approach that allows features derived from skeletons to be used for statistical shape analysis is based on the deformable modeling framework. A template is deformed to optimally match each instance in a class of objects, with deformations constrained to preserve the medial branching structure of the template. The match between each deformed template and the instance it is approximating is not perfect, but in many problems, the mismatch is on the order of the other errors involved in imaging-based morphometry, and thus an acceptable price to pay for preserving homology between skeleton-derived features. Such medially-constrained deformable modeling methods can be divided into two rough groups: (1) methods that model the medial axis/scaffold of the deformable template explicitly, and (2) methods that impose geometric constraints on the boundary of the deformable template. In the first class are the the Pizer et al. m-rep method [7], and derivative techniques such as continuous m-rep [15,12]. These methods explicitly describe the medial scaffold of the deformable template, and derive the boundary of the model algorithmically. Examples from the second class of methods include symmetry-seeking tubular models by Terzopoulos et al. [13], skeleton-constrained 2D level set methods [8], and linked-surface deformable modeling techniques (e.g., [16]).
Among these medially-constrained deformable modeling methods, few have sought to adhere strictly to “true” 3D Blum medial geometry, which, we would argue, takes away from the interpretability of the skeleton-derived features in shape analysis applications. For instance, the original m-rep approach does not model medial scaffolds with multiple branches as such; instead, it models complex objects using subfigures attached to the boundaries of parent figures [7]. Coupled surface methods frequently model surfaces as parallel or constrained to be a certain minimal distance apart [16], constraints that are not directly related to how skeletons are defined. Continuous m-rep methods [15,12], which describe the medial scaffold parametrically and derive the boundary by inverting the skeletonization process, have been successful at creating 3D deformable models that adhere to Blum geometry. However, they suffer from the inherent challenges that arise from trying to explicitly parameterize medial scaffolds, which are, essentially, singularities. For instance, near the free edges of the medial scaffold (see Fig. 1), inverse skeletonization is asymptotic: an infinitesimal step along the medial scaffold maps to a big step on the boundary. Behavior along creases (curves along which medial surfaces join) is also asymptotic and challenging to model. Most difficult of all is to model endpoints of creases parametrically. In fact, just one paper by Terriberry et al. [12] has claimed this capability, and has only demonstrated it with a static example. To our knowledge, the ability to deform templates adhering to 3D Blum geometry to target data has not been demonstrated for templates with multiple branches.1
The main contribution of this paper is to propose a new paradigm for Blum-adherent 3D deformable medial modeling, which bridges these two classes of deformable modeling techniques. Our goals are closest to those of m-rep methods (to allow statistical analysis of skeleton-derived features across populations of objects), but our approach is closer to symmetry-seeking models by Terzopoulos et al. [13] and skeletally coupled level sets by Sebastian et al. [8]. It is the boundary of the deformable template that is modeled parametrically, while the medial scaffold is defined implicitly. Similar to [13,8], constraints are imposed on the boundary parameterization to ensure that deformation does not change the medial branching structure of the template. Unlike [8], which is 2D, and [13], which imposes tubular symmetries, our approach is used to model arbitrary 3D shapes, including those with branching medial scaffolds. An additional contribution of this paper is to formulate the problem deformable modeling with medial constraints as a quadratically constrained quadratic programing (QCQP) problem, leading to efficient, albeit non-convex, optimization.
2 Methods
2.1 3D Medial Geometry Background
We use the term object to refer to a set
 ⊂ ℝn that is homologous to a closed ball and has a smooth boundary, denoted ∂
⊂ ℝn that is homologous to a closed ball and has a smooth boundary, denoted ∂
 . A ball B is a maximal inscribed ball (MIB) in
. A ball B is a maximal inscribed ball (MIB) in
 if B ⊂
if B ⊂
 and there exists no other ball B′ ⊂
and there exists no other ball B′ ⊂
 such that B ⊂ B′. Every point on ∂
such that B ⊂ B′. Every point on ∂
 belongs to exactly one MIB. The Blum [2] medial axis transform (MAT) of
belongs to exactly one MIB. The Blum [2] medial axis transform (MAT) of
 is the transformation that maps each point x ∈ ∂
is the transformation that maps each point x ∈ ∂
 to the center of the MIB containing x. The terms medial scaffold, medial axis or skeleton are used to describe the range of this mapping, i.e., the set of centers of all MIBs in
to the center of the MIB containing x. The terms medial scaffold, medial axis or skeleton are used to describe the range of this mapping, i.e., the set of centers of all MIBs in
 . Generically, the medial scaffold consists of one or more surface patches. Curves that are shared by multiple surface patches in the medial scaffold are called creases. The remaining boundaries of these surface patches are called free edges (see Figure 1).
. Generically, the medial scaffold consists of one or more surface patches. Curves that are shared by multiple surface patches in the medial scaffold are called creases. The remaining boundaries of these surface patches are called free edges (see Figure 1).
Each MIB in
 is tangent to ∂
is tangent to ∂
 at one or more points. Thus, the MAT is a many-to-one mapping. In fact, most MIBs in
at one or more points. Thus, the MAT is a many-to-one mapping. In fact, most MIBs in
 are tangent to ∂
are tangent to ∂
 at two points. Centers of these bitangent MIBs lie on the interiors of the surface patches that form the medial scaffold of
at two points. Centers of these bitangent MIBs lie on the interiors of the surface patches that form the medial scaffold of
 . Centers of MIBs tangent to ∂
. Centers of MIBs tangent to ∂
 at three points form the creases of the medial scaffold. Centers of MIBs that are tangent to ∂
at three points form the creases of the medial scaffold. Centers of MIBs that are tangent to ∂
 at only one point form the free edges of the medial scaffold. These MIBs have a higher order of tangency with ∂
at only one point form the free edges of the medial scaffold. These MIBs have a higher order of tangency with ∂
 , i.e., the radius of such MIB is the reciprocal the larger of the principal curvatures to ∂
, i.e., the radius of such MIB is the reciprocal the larger of the principal curvatures to ∂
 at the point of tangency. As shown by Giblin [4], two more types of MIB tangency occur generically, corresponding to junctions of creases and free edges, and to crease-crease intersections.
at the point of tangency. As shown by Giblin [4], two more types of MIB tangency occur generically, corresponding to junctions of creases and free edges, and to crease-crease intersections.
2.2 Derivation of Medial Constraints on the Boundary
We begin by deriving a constraint on the boundary of a deformable template that ensures that the branching structure of the template’s medial axis is preserved under deformation. We say that two points x1, x2 ∈ ∂
 are medially linked if they belong to the same MIB in
are medially linked if they belong to the same MIB in
 , or, equivalently, MAT(x1) = MAT(x2). Our method is based on the fact that transformations of
, or, equivalently, MAT(x1) = MAT(x2). Our method is based on the fact that transformations of
 that preserve medial links also preserve the branching structure of the medial scaffold. More formally,
that preserve medial links also preserve the branching structure of the medial scaffold. More formally,
Theorem 1
Let
 be an object in ℝ3. Let Φ : ℝ3 → ℝ3 be a bijective and differentiable transformation. Let
be an object in ℝ3. Let Φ : ℝ3 → ℝ3 be a bijective and differentiable transformation. Let
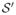 = {x ∈ ℝ3 : Φ−1(x) ∈
= {x ∈ ℝ3 : Φ−1(x) ∈
 }. Suppose that Φ “preserves medial links”, i.e., for any two points x1, x2 ∈ ∂
}. Suppose that Φ “preserves medial links”, i.e., for any two points x1, x2 ∈ ∂
 , the points Φ(x1) and Φ(x2) are medially linked in
, the points Φ(x1) and Φ(x2) are medially linked in
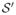 if and only if x1 and x2 are medially linked in
if and only if x1 and x2 are medially linked in
 . Then the MAT of
. Then the MAT of
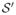 is homeomorphic to the MAT of
is homeomorphic to the MAT of
 .
.
Proof
We outline the proof due to limited space. The proof involves constructing a mapping Ψ between the MAT of
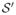 and the MAT of
and the MAT of
 , as follows. Let m be a point on the MAT of
, as follows. Let m be a point on the MAT of
 , then let X ∈ ∂
, then let X ∈ ∂
 be the non-empty set of points where the MIB centered at m is tangent to ∂
be the non-empty set of points where the MIB centered at m is tangent to ∂
 . Let X′ = {x ∈ ℝ3 : Φ−1(x) ∈ X}. If X has only one element, let Ψ(m) be the center of the MIB containing the sole point in X′. If X has multiple elements, any two of them are medially linked, and thus any two elements in X′ are medially linked. Thus, there exists an MIB that is tangent to ∂
. Let X′ = {x ∈ ℝ3 : Φ−1(x) ∈ X}. If X has only one element, let Ψ(m) be the center of the MIB containing the sole point in X′. If X has multiple elements, any two of them are medially linked, and thus any two elements in X′ are medially linked. Thus, there exists an MIB that is tangent to ∂
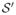 at all points in X′. Let Ψ(m) be the center of that MIB. Proof by contradiction can be used to show that Ψ is bijective and continuous.
at all points in X′. Let Ψ(m) be the center of that MIB. Proof by contradiction can be used to show that Ψ is bijective and continuous.
Next, we write down the sufficient conditions for transformation Φ to preserve medial links. It is a trivial fact that a ball with center m ∈
 and radius R is tangent to ∂
and radius R is tangent to ∂
 at the point x if and only if m = x − R
N, where N is the unit outward normal to ∂
at the point x if and only if m = x − R
N, where N is the unit outward normal to ∂
 at x. It is also simple to show that such a ball is a MIB in
at x. It is also simple to show that such a ball is a MIB in
 if ∀y ∈ ∂
if ∀y ∈ ∂
 , ||y − m|| ≥ R. From these observations, we conclude that two points x1,
x2 ∈ ∂
, ||y − m|| ≥ R. From these observations, we conclude that two points x1,
x2 ∈ ∂
 are medially linked if and only if there exists R > 0 such that x1
– R
N1 = x2
– R
N2 and ||y
– (x1
– RN1)|| ≥ R for all y ∈ ∂
are medially linked if and only if there exists R > 0 such that x1
– R
N1 = x2
– R
N2 and ||y
– (x1
– RN1)|| ≥ R for all y ∈ ∂
 .
.
2.3 Medially-Constrained Model Fitting – Continuous Formulation
We first formulate the problem of fitting a medially-constrained template to a target object in the continuous case. In the following section, the continuous problem is discretized and solved numerically. Let the object
 be a template, whose MAT has the desired branching structure, and let
be a template, whose MAT has the desired branching structure, and let
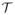 be a target object. The goal is to deform
be a target object. The goal is to deform
 , making it as similar as possible to
, making it as similar as possible to
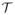 , while maintaining the branching structure of the MAT of
, while maintaining the branching structure of the MAT of
 after deformation.
after deformation.
Let U be some parametric domain (e.g., the unit sphere), and x : U → ∂
 be a smooth bijective map that provides a global parameterization of ∂
be a smooth bijective map that provides a global parameterization of ∂
 . Let
. Let
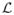 ⊂ U × U be the set of all parameter value pairs (u,
v), such that u ≠ v and x(u) and x(v) are medially linked in
⊂ U × U be the set of all parameter value pairs (u,
v), such that u ≠ v and x(u) and x(v) are medially linked in
 . Let
. Let
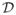 be the set of diffeomorphic transformations of ℝ3 and let
be the set of all bounded continuous positive real-valued functions on
be the set of diffeomorphic transformations of ℝ3 and let
be the set of all bounded continuous positive real-valued functions on
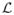 . For any Φ ∈
. For any Φ ∈
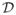 , let
, let
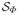 = {x ∈ ℝ3 : Φ−1(x) ∈
= {x ∈ ℝ3 : Φ−1(x) ∈
 }, let xΦ(u) = Φ(x(u)), and let NΦ(u) be the unit outward normal vector to ∂
}, let xΦ(u) = Φ(x(u)), and let NΦ(u) be the unit outward normal vector to ∂
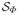 at xΦ(u). Let μ be some measure of dissimilarity between two objects in ℝ3 (e.g., mean closest-point distance) and let ρ be some measure of irregularity of a transformation (e.g., bending energy). The continuous medially-constrained deformable modeling problem seeks to find a transformation Φ* ∈
at xΦ(u). Let μ be some measure of dissimilarity between two objects in ℝ3 (e.g., mean closest-point distance) and let ρ be some measure of irregularity of a transformation (e.g., bending energy). The continuous medially-constrained deformable modeling problem seeks to find a transformation Φ* ∈
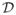 that satisfies
that satisfies
| (1) |
subject to the following two conditions:
| (2) |
| (3) |
The constraints (2,3) guarantee that xΦ(u) and xΦ(v) are medially linked, and hence the that Φ preserves the branching structure of the MAT of
 under deformation. Conversely, any Φ ∈
under deformation. Conversely, any Φ ∈
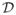 that preserves the branching structure of the MAT of
that preserves the branching structure of the MAT of
 under deformation must satisfy (2,3). Since transformations that preserve MAT branching do exist, we conclude that the minimization problem above is not over-constrained and solutions can be found, in theory. In practice, however, we must discretize and simplify the problem to find solutions.
under deformation must satisfy (2,3). Since transformations that preserve MAT branching do exist, we conclude that the minimization problem above is not over-constrained and solutions can be found, in theory. In practice, however, we must discretize and simplify the problem to find solutions.
2.4 Medially-Constrained Model Fitting – Discrete Formulation
In the discrete implementation, we model the boundary of the deforming template as a triangular mesh, i.e., a piecewise linear surface with triangular elements. We consider this mesh to be an approximation of a continuous boundary surface, and impose medial linkage constraints (2,3) on tuples of mesh vertices, along with additional constraints on mesh quality. We then deform the mesh to maximize similarity with a target object as well as mesh regularity.
Encoding Medial Links
Let Nb be the number of vertices in the mesh describing the boundary of the deforming template, and let xi denote the position of each vertex i ∈ [1, Nb]. Medial links between vertices are encoded by assigning a medial link index Mi ∈ ℕ to each vertex. Any two vertices i, j such that Mi = Mj are considered medially linked. Some of the vertices are not medially linked to any other vertex (corresponding to free edges of medial scaffolds) and some vertices are medially linked to more than one vertex (corresponding to creases on the medial scaffold). Furthermore, the mesh is constructed in such a way that each triangle on the mesh is linked to exactly one other triangle as follows: if vertices (i, j, k) form a triangle, then there exists exactly one other triangle (i′, j′, k′) in the mesh for which Mi = Mi′, Mj = Mj′ and Mk = Mk′.
How can such meshes be constructed? The approach we use is to take a reference object whose medial scaffold has the desired branching structure. We then define a coarse triangle mesh on the medial scaffold, with vertices sampled along creases and free edges (Fig. 2a). Each triple of connected points is included as a triangular face twice, facing in different directions. The result is a mesh of spherical topology that is infinitely thin, as if shrink-wrapped around the medial scaffold. We then “inflate” the resulting mesh onto the boundary of the reference object (Fig. 2b). The medial link index of each vertex on the coarse inflated mesh is just the index of the vertex on the coarse medial mesh from which it originated. Lastly, we apply Loop subdivision [6] to the inflated coarse mesh, resulting in a finer mesh (blue object in Fig. 2b). It is simple to adjust the Loop subdivision scheme to generate medial link indices consistent with the encoding above.
Fig. 2.
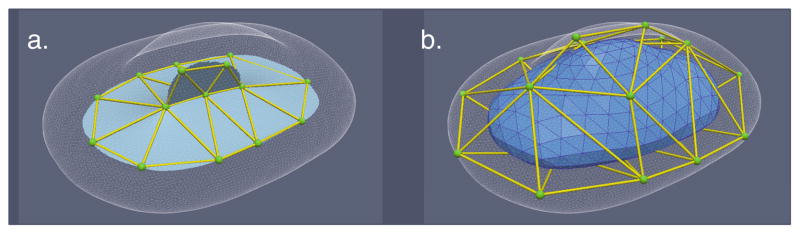
Illustration of the template building process. a. The boundary of a reference object (transparent white surface), its medial scaffold (opaque cyan surfaces), and the coarse mesh formed by points sampled from the creases and free edges of the medial scaffold (green points and yellow tubes). b. The coarse mesh inflated onto the boundary of the reference object (green points and yellow tubes) and a fine mesh obtained by applying Loop subdivision [6] to the coarse mesh.
General Problem Formulation
Once a mesh conforming to the above requirements is created, the problem of deforming it to target objects is defined as a constrained optimization problem. The general form of the problem is
| (4) |
where f is the objective being minimized, and gc are constraint functions, Nv is the number of variables and Nc is the number of constraints. The objective function captures the dissimilarity between the deforming mesh and the target object, as well as the irregularity of the deforming template. The constraints incorporate conditions derived from (2) and (3) that ensure that vertices with the same medial link index are medially linked, and well as additional conditions that ensure mesh quality. The vector of variables ξ includes the vertex coordinates xi, as well as a large number of additional “helper” variables introduced in order to make all constraints quadratic. The terms forming the objective and the constraints are described in the next few paragraphs.
Medial Linkage Constraints
We impose constraints to ensure that any two vertices (i, j) for which Mi = Mj satisfy discrete versions of the conditions of medial linkage (2) and (3). Let k = Mi = Mj. The first condition has the form xi – RkNi = xj – RkNj, where Rk is included as an additional variable in the optimization (analogous to R in the continuous case), and Ni is the approximation of the unit normal vector to the boundary at xi. The computation of Ni requires taking a square root, which would make the constraint non-quadratic. Instead of computing Ni directly, we add it as an additional variable in the optimization, and impose additional constraints on Ni that are quadratic:
where (x,1)i and (x,2)i are a pair of non-parallel vectors in the tangent plane to the boundary at xi. Such a pair of vectors can be approximated as weighted sums of vertices in the one-ring neighborhood of i using a scheme described by Loop [6], with the weights dependent only on the valence of the vertex i.
Note that we have not yet defined any constraint on Rk for vertices that are not medially linked to any other vertex. In the continuous case, we did not have to deal with such points, since MIBs that have a single point of tangency with the boundary are limit cases of MIBs with double tangency [2,4]. In the discrete case, we need to deal with these vertices explicitly. Recall from Sec. 2.1 that the radius of a singly tangent MIB is the reciprocal of the larger principal curvature of the boundary at the point of tangency. This leads to the constraint Rk · κi,2 = 1, where κi,2 is the approximation of the larger principal curvature at xi, and k = Mi. The approximation of κi,2 is not quadratic but, as we did above for the normal vector, we introduce additional variables and constraints to the optimization problem to keep all constraints quadratic. The added variables are the elements of the first fundamental form, the elements of the shape operator, and the principal curvatures. We omit the details due to space limitations.
The condition that mirrors (3) has the form , where k = Mi, for all pairs of vertices i and j. These constraints are quadratic in the variables x, N and R. However, there are constraints, which does not scale well for larger meshes. Fortunately, in practice, if often suffices to relax this constraint just to the vertices j that are in the one-ring neighborhood of i. Analogous relaxation of a global non self-intersection condition is used in continuous m-reps (i.e., positive medial-boundary Jacobian condition) [15].
Mesh quality constraints
For the approximations of the unit normal and principal curvature on a triangular mesh to be accurate, the triangular elements must not be degenerate. We introduce additional constraints on the minimal angle of each boundary triangle, and on the minimum dihedral angle between adjacent triangles. As before, we introduce additional variables into the optimization problem, such as the area of each triangle, the unit normal to each triangle, and the length of each edge, and relate these variables to each other and the vertex coordinates using quadratic constraints.
Similarity to Target Shape
The objective function f consists of a similarity and regularization terms. The similarity term is based on the iterative closest point (ICP) algorithm. At the beginning of optimization, we match each vertex in the template mesh to the closest point on ∂
 , the boundary of the target object
, the boundary of the target object
 . We also match points on ∂
. We also match points on ∂
 to the closest locations on the template. We then minimize the sum of squared distances between the matched points. Specifically, for each vertex i, let yi be the point on
to the closest locations on the template. We then minimize the sum of squared distances between the matched points. Specifically, for each vertex i, let yi be the point on
 that is closest to xi at the start of the optimization. Likewise, for a set of Ns regularly sampled points zj on ∂
that is closest to xi at the start of the optimization. Likewise, for a set of Ns regularly sampled points zj on ∂
 , let
be the closest point on the template mesh, not necessarily a vertex. Let {xij,1, xij,2, xij,3} be the triangle containing
, and let wj,1, wj,2, wj,3 be the barycentric coordinates of
in it. We formulate the objective function as
, let
be the closest point on the template mesh, not necessarily a vertex. Let {xij,1, xij,2, xij,3} be the triangle containing
, and let wj,1, wj,2, wj,3 be the barycentric coordinates of
in it. We formulate the objective function as
| (5) |
where ρ is the regularization term, discussed below. As in ICP, the matching and optimization are alternated for several iterations until convergence.
Regularization
Regularization is implemented using Loop subdivision surfaces. Recall that the template mesh is initially generated by Loop subdivision from a coarse mesh. We define the regularization penalty to be the residual between the deforming template mesh and the best approximation of the deforming mesh by a Loop subdivision surface. Specifically, let x̂q be the vertices in the coarse mesh, for j ∈ [1, Nq]. Applying Loop subdivision creates a new set of vertices, with the coordinate of the i-th vertex in the subdivided surface given by Σq∈Q(i) Wiq x̂q, where Q(i) is the set of vertices in the coarse mesh that contribute to the coordinates of the i-th vertex, and Wiq are the coefficients from the subdivision scheme, which depend only on the structure of the coarse mesh. We add the vertices x̂q as additional variables to the optimization problem. We then define the regularization penalty as the total squared residual , where λρ is the weight given to the regularization term (set to 1 in our experiments). Since Loop subdivision surfaces are smooth, penalizing the residual to the closest fitting Loop subdivision surface imposes smoothness on the template.
Numerical Solution
The optimization problem for deformable modeling with preservation of medial links involves a large number of variables (xi, Ni, Rk, κi,2, x̂j and several others) and a large number of constraints. However, the constraints and the objective function are quadratic in the variables, i.e., have the form and , where the matrices A0 and Ak are sparse. Although the matrices Aq are not positive definite, and thus a global solution can not be guaranteed, the optimization problem can be solved efficiently using interior point methods. Our implementation uses the Ipopt method [14].
3 Experiments and Results
Corpus Callosum Tract Shape Analysis
The goal of this experiment is to demonstrate that the proposed deformable model can accurately capture the shape of the corpus callosum (CC) across a cohort of subjects. To demonstrate this, we first automatically label the CC using atlas-based segmentation, and then fit a deformable medial model to each segmentation, allowing subsequent shape analysis using skeleton-derived features. We focus on the CC because its shape in 3D is non-trivial, and because skeleton-derived features have proved useful for joint analysis of microscopic and macroscopic properties of sheet-like white matter tracts extracted from diffusion MRI [17]. We use diffusion tensor imaging (DTI) data from 51 subjects (ages 29–82, mean 70.0±7.1, 30 females and 21 males) in the IXI brain MRI database (http://biomedic.doc.ic.ac.uk/brain-development). We label the CC in each subject using atlas-based segmentation, with the IXI aging DTI template [17] serving as the atlas. Specifically, we register each subject to the template using the DTI-TK deformable registration algorithm [18], then use the resulting deformation field to map the binary segmentation of the CC from the atlas into the subject space.
Deformable medial modeling proceeds as follows. We manually construct an initial CC mesh that encodes medial links between boundary vertices. We then fit this mesh to the boundary of the CC segmentation in the IXI atlas using our ICP algorithm, creating a template that satisfies medial linkage conditions. Fitting this template to each subject is performed in three steps. First, the template is initialized close to the subject’s CC by applying the deformation computed by DTI-TK to its vertices. This deformation does not preserve medial linkage conditions. Second, we apply the ICP algorithm to fit the deformed template to the subject’s CC segmentation, obtaining a mesh that closely fits the CC shape and satisfies medial linkage conditions. Finally, we refine the fitted mesh using one level of Loop subdivision, and perform one more stage of ICP-style fitting, obtaining a dense mesh satisfying the medial linkage conditions and closely matching the subjects’ CC segmentations. The meshes have the same number of vertices and triangles, which enables point-wise statistical analysis of MAT-derived features. We use the radius values Rk at the vertices of the fitted meshes as a thickness feature, and use a general linear model to test the cross-sectional hypothesis that the thickness of the CC decreases as age increases. To control for multiple comparisons, we use cluster-level permutation testing [5].
Results
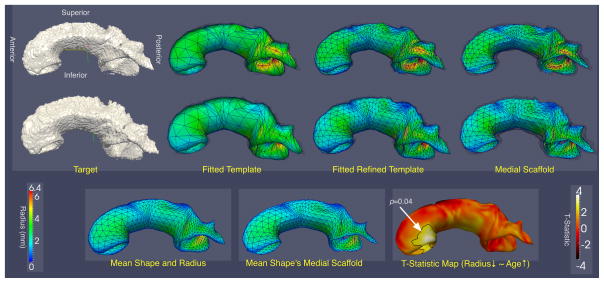
The results of the fitting are illustrated in Fig. 3. The template meshes initially fitted to subject CC segmentations have 410 vertices and 816 triangles. The corresponding constrained optimization problem has 11320 variables, 10116 equality constraints and 3744 inequality constraints. The Jacobian of the constraints is 99.91% sparse, and the Hessian of the Lagrangian is 99.95% sparse. Optimization was successful in 50 of the 51 subjects, converging to a local minimum of f and satisfying all the constraints within the tolerance of 10−8. In one subject, it failed to satisfy the constraints in the 200 steps allowed. For the rest of the subjects, each ICP iteration required an average of 16.5 optimization steps to converge, taking an average of 42 s on a single 2.2GHz Intel CPU core. The number of ICP iterations was fixed at 5 for each subject. After fitting, the root mean squared (RMS) distance from the fitted template boundary to the boundary of the subject’s CC segmentation was 0.89 ± 0.04 mm on average, and the average distance from the segmentation to the template boundary was 1.16 ± 0.05 mm. The subdivided meshes fitted at the last stage have 1634 vertices, 3264 triangles, 42712 variables, 38988/14832 equality/inequality constraints, 99.98% Jacobian and 99.99% Hessian sparsity. ICP required an average of 21.5 optimization steps and 297 s to converge. 2 The RMS template-to-segmentation and segmentation-to-template distances were 0.70 ± 0.04 mm and 0.92 ± 0.05 mm, respectively. Statistical analysis using an a priori cluster T-score threshold of t = 2.0 and 10000 permutations revealed one significant cluster (p = 0.04) where age correlated negatively with thickness, located in the anterior of the CC (the genu). Such a finding is consistent with the literature, e.g., [1].
Fig. 3.
Results from CC fitting experiment. The top two rows show two examples (third-worst and third-best fitting quality) of templates fitted to atlas-based CC segmentations. The columns show the target surface, the template fitted using ICP, the last-stage fitted subdivided template, and the medial scaffold of the latter. The bottom row shows the Procrustes mean of the fitted models, its medial scaffold (computed by applying ICP-style fitting to the Procrustes mean), and the t-statistic map for the age-related thinning hypothesis. The significant cluster (p = 0.04) is outlined.
Proof of Concept for Branching Medial Scaffolds
While the medial scaffold in the CC template has only one surface, the strength of the method is that it is as easily applied to scaffolds with branches. In this pilot experiment, we fit a “fin-like” medial scaffold illustrated in Fig. 2 to a target shape. The target shape is produced by warping the reference shape in Fig. 2 based on a landmark transformation. The ICP algorithm is then used to fit the template to the target shape. Fig. 4 shows the template in relation to the target object before and after the fitting. The medial scaffold of the fitted model is also shown.
Fig. 4.
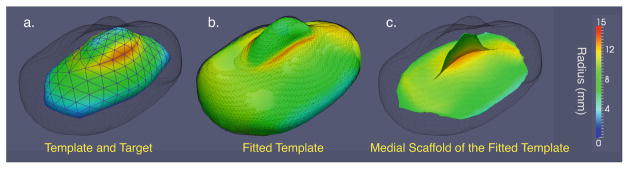
Fitting a medially constrained template with a fin-like medial scaffold to a target object. The boundary of the target object is rendered as a dark gray wireframe in all three views. a. The template before the fitting, colored by the radius value Rk. b. The template after fitting. c. The medial scaffold of the fitted template.
4 Discussion and Conclusions
We presented a new way to fit deformable models to surface and image data with preservation of medial branching structure. The method shows promise for modeling objects whose medial scaffolds have multiple branches, although additional experiments are needed to establish its utility for modeling complex branching shapes in medical imaging data, e.g., the myocardium. The scalability of the method is limited by the need to solve very large sparse linear systems, but for many anatomical structures, meshes having on the order of 1000 vertices should be sufficient to meet modeling needs. The number of empirical parameters in the method is small and performance on real-data is robust, making the method practical for shape analysis applications.
Footnotes
Sun et al. [11] developed a myocardium model with three surfaces joining along a crease, but they did not model the myocardium as a closed surface, which simplified Blum geometry at crease endpoints.
Computation time is dominated by solving sparse systems, and in theory, time should scale with the number of non-zero elements in the sparse matrices, which is less than 4× for the refined mesh. The 9× increase in time may be due to memory limitations.
References
- 1.Bastin ME, Maniega SM, Ferguson KJ, Brown LJ, Wardlaw JM, MacLullich AMJ, Clayden JD. Quantifying the effects of normal ageing on white matter structure using unsupervised tract shape modelling. Neuroimage. 2010;51(1):1–10. doi: 10.1016/j.neuroimage.2010.02.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Blum H. Models for the Perception of Speech and Visual Form. MIT Press; 1967. A transformation for extracting new descriptors of shape. [Google Scholar]
- 3.Bouix S, Pruessner JC, Louis Collins D, Siddiqi K. Hippocampal shape analysis using medial surfaces. Neuroimage. 2005;25(4):1077–1089. doi: 10.1016/j.neuroimage.2004.12.051. [DOI] [PubMed] [Google Scholar]
- 4.Giblin PJ, Kimia BB. On the intrinsic reconstruction of shape from its symmetries. IEEE T Pattern Anal. 2003;25(7):895–911. [Google Scholar]
- 5.Hayasaka S, Nichols TE. Combining voxel intensity and cluster extent with permutation test framework. Neuroimage. 2004;23(1):54–63. doi: 10.1016/j.neuroimage.2004.04.035. [DOI] [PubMed] [Google Scholar]
- 6.Loop CT. Master’s thesis. Department of Mathematics, University of Utah; Salt Lake City: 1987. Smooth subdivision surfaces based on triangles. [Google Scholar]
- 7.Pizer SM, Fletcher PT, Joshi S, Thall A, Chen JZ, Fridman Y, Fritsch DS, Gash AG, Glotzer JM, Jiroutek MR, Lu C, Muller KE, Tracton G, Yushkevich P, Chaney EL. Deformable m-reps for 3D medical image segmentation. Int J Comput Vision. 2003;55(2):85–106. doi: 10.1023/a:1026313132218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sebastian TB, Tek H, Crisco JJ, Kimia BB. Segmentation of carpal bones from CT images using skeletally coupled deformable models. Med Image Anal. 2003;7(1):21–45. doi: 10.1016/s1361-8415(02)00065-8. [DOI] [PubMed] [Google Scholar]
- 9.Siddiqi K, Pizer S. Medial representations: mathematics, algorithms and applications. Vol. 37. Springer; 2008. [Google Scholar]
- 10.Styner M, Gerig G, Lieberman J, Jones D, Weinberger D. Statistical shape analysis of neuroanatomical structures based on medial models. Med Image Anal. 2003;7(3):207–220. doi: 10.1016/s1361-8415(02)00110-x. [DOI] [PubMed] [Google Scholar]
- 11.Sun H, Frangi AF, Wang H, Sukno FM, Tobon-Gomez C, Yushkevich PA. Automatic Cardiac MRI Segmentation Using a Biventricular Deformable Medial Model. In: Jiang T, Navab N, Pluim JPW, Viergever MA, editors. MICCAI 2010, Part I LNCS. Vol. 6361. Springer; Heidelberg: 2010. pp. 468–475. [DOI] [PubMed] [Google Scholar]
- 12.Terriberry TB, Gerig G. A Continuous 3-D Medial Shape Model With Branching. International Workshop on Mathematical Foundations of Computational Anatomy MFCA 2006, in Conjunction with MICCAI; 2006; 2006. [Google Scholar]
- 13.Terzopoulos D, Witkin A, Kass M. Symmetry-seeking models and 3D object reconstruction. Int J Comput Vision. 1988;1(3):211–221. [Google Scholar]
- 14.Wächter A, Biegler LT. On the implementation of an interior-point filter line-search algorithm for large-scale nonlinear programming. Mathematical Programming. 2006;106:25–57. [Google Scholar]
- 15.Yushkevich PA, Zhang H, Gee J. Continuous medial representation for anatomical structures. IEEE Trans Med Imaging. 2006;25(2):1547–1564. doi: 10.1109/tmi.2006.884634. [DOI] [PubMed] [Google Scholar]
- 16.Zeng X, Staib LH, Schultz RT, Duncan JS. Segmentation and measurement of the cortex from 3-D MR images using coupled-surfaces propagation. IEEE Trans Med Imaging. 1999;18(10):927–937. doi: 10.1109/42.811276. [DOI] [PubMed] [Google Scholar]
- 17.Zhang H, Awate SP, Das SR, Woo JH, Melhem ER, Gee JC, Yushkevich PA. A tract-specific framework for white matter morphometry combining macroscopic and microscopic tract features. Med Image Anal. 2010 May; doi: 10.1016/j.media.2010.05.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Zhang H, Yushkevich PA, Alexander DC, Gee JC. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Med Image Anal. 2006;10(5):764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]