Large capacity temporary visual memory

Abstract

Visual working memory (WM) capacity is thought to be limited to three or four items. However, many cognitive activities seem to require larger temporary memory stores. Here, we provide evidence for a temporary memory store with much larger capacity than past WM capacity estimates. Further, based on previous WM research, we show that a single factor — proactive interference — is sufficient to bring capacity estimates down to the range of previous WM capacity estimates. Participants saw a rapid serial visual presentation (RSVP) of 5 to 21 pictures of familiar objects or words presented at rates of 4/s or 8/s, respectively, and thus too fast for strategies such as rehearsal. Recognition memory was tested with a single probe item. When new items were used on all trials, no fixed memory capacities were observed, with estimates of up to 9.1 retained pictures for 21-item lists, and up to 30.0 retained pictures for 100-item lists, and no clear upper bound to how many items could be retained. Further, memory items were not stored in a temporally stable form of memory, but decayed almost completely after a few minutes. In contrast, when, as in most WM experiments, a small set of items was reused across all trials, thus creating proactive interference among items, capacity remained in the range reported in previous WM experiments. These results show that humans have a large-capacity temporary memory store in the absence of proactive interference, and raise the question of whether temporary memory in everyday cognitive processing is severely limited as in WM experiments, or has the much larger capacity found in the present experiments.

Introduction

Working memory (WM), that is, the ability to keep relevant information in mind over short periods of time while performing cognitive manipulations, is crucial to virtually all cognitive activities. Measures of WM correlate with many important measures of intelligence, language comprehension, reasoning, and educational achievement (e.g., Barrouillet, 1996; Daneman & Carpenter, 1980; Daneman & Green, 1986; Engle, Tuholski, Laughlin, & Conway, 1999; Engle, Carullo, & Collins, 1991; Engle, Cantor, & Carullo, 1992; Fukuda, Vogel, Mayr, & Awh, 2010; King & Just, 1991; Kyllonen & Christal, 1990), suggesting that WM is an important determinant of our cognitive abilities.

A wealth of experiments has revealed that there are stringent constraints on WM, such that people can remember only up to four items simultaneously (for reviews, see e.g. Conway et al., 2005; Cowan, 1995, 2001, 2005). Such WM limitations are observed not only in laboratory tasks, but also in everyday life. For example, when trying to remember a telephone number, we are keenly aware that WM capacity is not as large as we might wish it to be. These limitations contribute to the difficulty of doing mental arithmetic (e.g., Hitch, 1978), and might plausibly be one of the root causes of the difficulty of many other cognitive activities such as manipulating algebraic expressions or reasoning about abstract problems.

In other situations, however, there do not appear to be such stringent limitations on what we can temporarily remember. For example, when driving, we can operate the vehicle and monitor the traffic while keeping in mind where we want to go, that we have to go to a gas station, that we have to pick up some food on the way, all while keeping in mind speed limits, while following a conversation, interrupting the conversation to listen to the weather forecast, resuming the conversation, and so on. In such situations, cognitive operations seem to be supported by a temporary memory store that does not rely on active maintenance and has a much larger capacity than three or four items. In line with this view, when objects are embedded in meaningful scenes and when observers can at least partially rely on LTM, previous research has shown that memory capacity for objects is much larger than in typical WM experiments (e.g., Hollingworth, 2004, 2005; Hollingworth & Henderson, 2002).

While there have been important debates on the question of whether a WM capacity of 3 or 4 items is an overestimate, or whether people can really retain only a single item (e.g., Oberauer, 2002; Oztekin, Davachi, & McElree, 2010), here we ask whether people are equipped with a temporary memory mechanism with a much larger capacity, an ability that seems crucial for many practical purposes in everyday cognition. Further, we investigate the robustness of this memory store in the face of a factor that might play an important role in WM as well: proactive interference from previous trials.

Proactive interference in working memory

Proactive interference seems to be a prevalent feature of past WM experiments, to the extent that some authors have specifically argued that a crucial function of WM is to counteract the effects of such interference (Engle, 2002). This can be illustrated by one of the dominant paradigms used for investigating WM memory limitations: the change-detection paradigm pioneered by Luck and Vogel (1997). In such experiments, participants see an array of items (e.g., colored geometric figures), and have to detect whether a second array contains a changed item.

In these and other experiments, investigators attempted to rule out contributions of long-term memory (LTM) by using relatively small sets of materials and reusing the same items in many trials. This, in turn, forces participants to distinguish memory for the current trial from that of previous trials. For example, in Luck and Vogel’s (1997) Experiment 1, stimuli were drawn from just seven different colors; these stimuli were then reused throughout the experiment. Therefore, to avoid contamination from previous trials, participants must try to remember that a given test item was presented in the current trial rather than a prior trial. In other words, reusing the same limited set of items and features might lead to PI across trials.¹

While such experimental paradigms seem to suggest that PI might be important for establishing WM limitations (Engle, 2002), the role of PI for WM is controversial, with some authors proposing that PI has only a limited effect on WM capacity estimates (Hartshorne, 2008; see also Lin & Luck, 2012; Makovski & Jiang, 2008). Those authors found little PI from items in immediately preceding trials, and concluded that PI made only a limited contribution to WM capacity limitations. However, except in some of Hartshorne’s (2008) analyses, those experiments reused small sets of items in many trials, which might have resulted in a substantial level of background PI. Hence, the experiments compared high interference (from items in the immediately preceding trial) to slightly lower interference (from items appearing in earlier trials). In addition, in the studies cited, capacity estimates were mathematically limited to 4 or 5, as only 4 or 5 items were presented. These other constraints on performance may have limited the observable size of the interference effect.

While the studies just cited did not find effects of proactive interference, there is a rich literature showing that proactive interference does constrain how many items can be retained. For example, Keppel and Underwood (1962) studied the retention of consonant trigrams. They showed that, after a 3 s retention interval, recall performance dropped from about 80% for the first triplet to about 55% for the second one, with little change afterwards. This drop in performance was presumably due to proactive interference from having recalled a previous triplet (see also D. D. Wickens, Born, & Allen, 1963).^2;3

Most relevant to the current purposes, Cowan, Johnson, and Saults (2005) presented participants with lists of words, followed by a recognition test. Each list comprised 3, 4, 6 or 8 words, and items were presented for 1.5 s each. Crucially, there were 12 blocks of 12 trials. The first four blocks had words drawn from different categories; the next 8 blocks had words drawn from the same category, thereby producing PI.Cowan et al. (2005) compared performance in the first 4 trials, serving as a low-interference condition, to performance in the last 4 trials, serving as a high-interference condition. They found that performance was markedly better in the low-interference condition.

While these results show that PI has a marked effect on working memory performance, they raise two critical questions. First, if, as we will suggest below, temporary memory capacity is large in the absence of PI, the limited set-sizes in Cowan et al.’s (2005) would not reveal such large capacities; in the experiments below, we will address this issue by using set-sizes of up to 100. Second,Cowan et al. (2005) used relatively long presentation durations of 1.5 s. This raises the question of whether items were encoded in a temporary form of memory, or rather in a stable form of memory such as long-term memory. Further, this relatively long presentation duration might have allowed participants to rehearse items. In fact, Keppel and Underwood (1962) showed that allowing participants to rehearse items for just 2 s before a retention interval had a protective effect on memory, rising the question of what kind of memory storage was utilized by Cowan et al.’s (2005) participants. We will address this question in the experiments below as well.

The capacity of memory

To discuss the nature of memory limitations, it is useful to briefly introduce common terms used to distinguish forms of memory: short-term memory (STM), WM and LTM.⁴ While these labels are used slightly differently by different scholars, with some controversy about their definition, some scholars propose that the difference between LTM and STM might be that “only short-term memory [demonstrates] (1) temporal decay and (2) chunk capacity limits,” while WM might comprise additional mechanisms that manipulate stored information (e.g., Cowan, 2008). Other researchers, however, question a distinction between STM and LTM (e.g., Brown, Neath, & Chater, 2007; Crowder, 1993; Nairne, 2002; Ranganath & Blumenfeld, 2005; Wickelgren, 1973). Depending on the conditions of learning, a given item will vary in initial strength, and forgetting will vary correspondingly. Crucially, however, memory will not be limited to any specific number of items. Accordingly, STM might in principle have a large capacity.

In fact, LTM has a virtually unbounded memory capacity. For example, Standing (1973) presented participants with up to 10,000 pictures or words presented for 5 seconds each, and tested for recognition two days later. Recognition performance was excellent. Likewise, Brady, Konkle, Alvarez, and Oliva (2008) showed that memory representations for pictures are remarkably precise. After seeing 2,500 categorically unique objects for 3 s each, participants did not only discriminate old objects from novel objects from different categories, but also from objects in the same category, or the same objects in a different state; in each case, discrimination performance approached 90%. Hence, LTM capacity is large. If STM is simply a “weak” form of LTM that is readily forgotten, might it have a larger but still temporary capacity when conditions of acquisition are favorable?

Here, we are concerned with memory stores that temporarily register items. We thus adopt a functional definition of temporary memory: a set of mechanisms that allows people to retain meaningful information over a limited period of time. However, foreshadowing our results, our data are consistent with a unitary account of STM, WM and LTM. Specifically, when items are viewed briefly, the resulting memories are fleeting and disappear over the course of a few minutes, functionally acting as a short-term memory store with a large capacity. When proactive interference is added, one finds the memory limitations of previous visual memory experiments that have been considered limited by WM. Finally, if items are viewed repeatedly or for longer periods of time, the memory representations become consolidated in LTM and are forgotten only slowly. That said, in some cognitive situations (e.g., when performing mental operations on numbers such as comparing them, adding them etc.), there appears to be an effortful and severely constrained form of memory that shows the limitations characteristic of previous WM experiments, that relies on active manipulation of memory items, and that might be limited to as little as a single item that can be placed in the focus of attention (e.g., Oberauer, 2002; Oztekin et al., 2010, but see e.g. Pylyshyn & Storm, 1988; Scholl & Pylyshyn, 1999 for evidence that this is not the case for all forms of attention). The items in this actively maintained system might constitute a separate memory store. Importantly, however, unless items need to be actively manipulated, temporary memory might have a much larger capacity than previously thought.

The current experiments

We assess temporary memory capacity estimates for meaningful everyday objects as well as words, asking whether capacity is always as severely limited as WM research would suggest. We use meaningful items because cognitive processes presumably operate on meaningful items, and because memory capacity is known to be poor for items that cannot be interpreted in terms of meaningful categories (Olsson & Poom, 2005; see also Feigenson & Halberda, 2008 for evidence that conceptual information enhances memory capacity even in infancy). In the General Discussion, we will come back to the issue of how the use of meaningful items might have affected our results.

Our experiments employ a rapid serial visual presentation (RSVP) procedure, where memory items are presented one at a time for presentation durations of the order of a single eye fixation. This method is well suited to investigate the temporary memory store proposed above, for three reasons. First, the presentation time for each item can be controlled and made brief enough to avoid ceiling effects, while allowing participants to retrieve or construct abstract conceptual representations of the items they see (Potter, Staub, & O’Connor, 2004), rather than only lower-level features such as those stored in iconic memory (Sperling, 1960). Encoding stimuli as meaningful items is crucial for them to be useful in a WM-like memory store, because, as mentioned above, cognitive processes presumably operate on conceptual representations as opposed to bundles of low-level features.

Second, observers encode rapidly presented sequences of pictures by non-verbal means. They cannot employ verbal strategies such as rehearsing, because the presentation rate is too high, and because pictures are processed by a fully non-verbal route in such paradigms (Endress & Potter, 2012).

Third, an RSVP procedure allows us to directly assess the effects of PI. Specifically, participants were randomly assigned to one of two conditions. In the unique condition, all pictures were unique, and were encountered only once in the experiment. In the repeated condition, pictures were selected from a set of 22 pictures; participants thus saw new combinations of the same pictures repeatedly across trials. As a result, we would expect substantial PI in the repeated condition, while PI in the unique condition should be minimal.

Experiment 1

In Experiment 1, we measured how many items could be remembered when the items were unique and when they were repeated, respectively, asking whether temporary memory storage would be larger than in the WM literature at least when PI is minimized. In each trial, participants saw a sequence of 7, 12 or 17 pictures of familiar everyday objects, presented in sequence for 250 ms per picture, with no interval between pictures.

Participants were then shown a single test picture and had to decide whether it had been presented in the sequence: on half the trials it had been. Crucially, participants were randomly assigned to one of two conditions. In the unique condition, all pictures were unique, and were encountered only once in the experiment. In the repeated condition, pictures were selected from a set of 22 pictures; participants thus saw the same pictures repeatedly across trials, but without repeats within a trial.

If we can store only a fixed number of items that is below the number of items in the sequence, capacity estimates should be constant in both conditions. In contrast, if we have a relatively large temporary storage capacity, capacity estimates should be much larger in the unique condition, increasing when more items are presented — because, without interference from previous trials, participants can remember more items when more items are presented. If PI limits memory capacity, capacity estimates should increase much less in the repeated condition, staying in the range of previously reported WM capacity estimates.

Materials and methods

Participants

Thirty-six participants (24 females, means age 25.2) from the MIT community took part in Experiment 1. They were randomly assigned to the unique and the repeated condition.

Apparatus

Stimuli were presented on a NEC MultiSync FE700+ 17" CRT (refresh rate: 75 Hz; resolution: 640 × 480), using the Matlab psychophysics toolbox (Version 3.0.8; Brainard, 1997; Pelli, 1997). Responses were collected from pre-marked “Yes” and “No” keys on the keyboard.

Materials

Stimuli were color photographs of familiar everyday objects taken fromBrady et al. (2008). Stimuli were randomly selected for each participant from a set of 2,400 pictures. They were presented subtending a visual angle of 12.7 × 12.7 degrees.

Procedure

Participants completed 60 trials per set-size. They started each trial by a key-press and then viewed instructions to look at the pictures for 1000 ms, followed by a fixation cross for 300 ms and a 200 ms blank screen, followed by the sample pictures presented at a duration of 250 ms per picture. Then, they saw a question mark for 800 ms, followed by a blank screen for 900 ms and the test picture presented for 800 ms. “Old” test items (those that occurred in the sample sequence) were randomly sampled from two initial positions (serial positions 2, 3), two final positions (antepenultimate and penultimate) and two middle positions that depended on the set-size (with the exception of set-size 7, where we used only one serial position for medial and 2 serial positions each for initial and final positions). Importantly, the very first and last pictures in the sequence were never tested.

“New” test items, which were presented on 50% of the trials, were entirely new items in the unique condition; in the repeated condition, they were drawn randomly from the set of 22 pictures, excluding those that had been presented in that trial. Trials were presented in random order, with the constraints that not more than three trials could occur in a row that shared the set-size, the correct response (yes/no) or the serial position of “old” test pictures.

Before completing the main experiment, participants were pre-familiarized with pictures. In the repeated condition they were pre-familiarized with the 22 pictures they would see during the main experiment. That is, the pictures were presented 10 times, with presentation durations decreasing from 2000 to 250 ms. Participants in the unique condition were also familiarized with 22 pictures in the same manner, but these pictures were different from those used in the main experiment.

Analysis

We will report the results below using two main measures: memory capacity estimates and the percentage of correct responses. As we will discuss below, the percentage of correct responses is linearly related to the probability of remembering an item; hence, the analyses of the percentage of correct responses hold also for probability of remembering.

WM capacity estimates are typically obtained using the two-high-threshold formula K = N × (H − FA), where K is the capacity, N the number of items, and H and FA the hit rate and the false alarm rate, respectively (e.g., Cowan, 2001; Rouder et al., 2008). This formula assumes that observers report that they recognize an item when the item’s familiarity crosses a certain (memory) threshold, and that they have a second, low, threshold below which they report that the items are new; in between these two thresholds, observers guess (see e.g. Cowan, 2001; Rouder et al., 2008 for discussion). According to this formula, p_retained = H − FA is the probability that an item is retained in memory; multiplying by the number of presented items gives the estimated number of items in memory, K. In our case, with an equal number of “old” and “new” test pictures, p_retained is simply p_retained = 2 × p_cor – 1, where p_cor is the proportion of correct responses (combining hits and correct rejections). For each participant and set-size, we computed capacity estimates separately.

We present the data in terms of capacity estimates for comparison purposes with the previous literature. However, the K measure only makes sense if indeed observers have a fixed capacity that, once it is reached, prevents any further items from being encoded. As will become clear, our data do not conform to this assumption. Hence, we also analyze our results in terms of the proportion of correct responses as a function of the number of items presented. As mentioned above, these analyses are equivalent to those using the proportion of retained items as a dependent measure.

Results

Capacity estimates

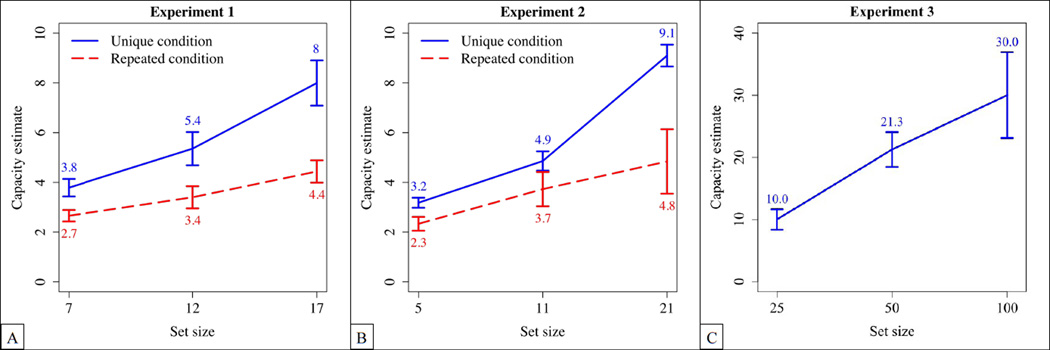
Figure 1(A) shows the results of Experiment 1 in terms of capacity estimates. In the unique condition, capacity estimates increased from 3.8 to 8.0 between set-sizes 7 and 17. In contrast, in the repeated condition, capacity estimates were relatively constant, increasing from 2.7 to 4.4 between set-sizes 7 and 17. An ANOVA with set-size as within-subject factor and condition as between-subjects factor yielded main effects of condition, F(1,34) = 11.45, p = .002, ${\eta }_p^2=.252$, as well as of set-size, F(2,68) = 32.02, p< .0001, ${\eta }_p^2=.449$. Critically, an interaction, F(2,68) = 5.35, p = .007, ${\eta }_p^2=.075$, indicated that capacity estimates increased more with list length in the unique condition, F(2,34) = 25.01, p< .0001, ${\eta }_p^2=.595$, than in the repeated condition, F(2,34) = 7.69, p = .002, ${\eta }_p^2=.311$.

Figure 1.

Results of Experiment 1 (A), 2 (B) and 3 (C).The blue solid lines represent the unique conditions, and the red dotted lines the repeated conditions. Error bars represent SEM. In the unique condition, memory capacity estimates were relatively large. They were higher, and increased more, than in the repeated condition.

Percentage of correct responses

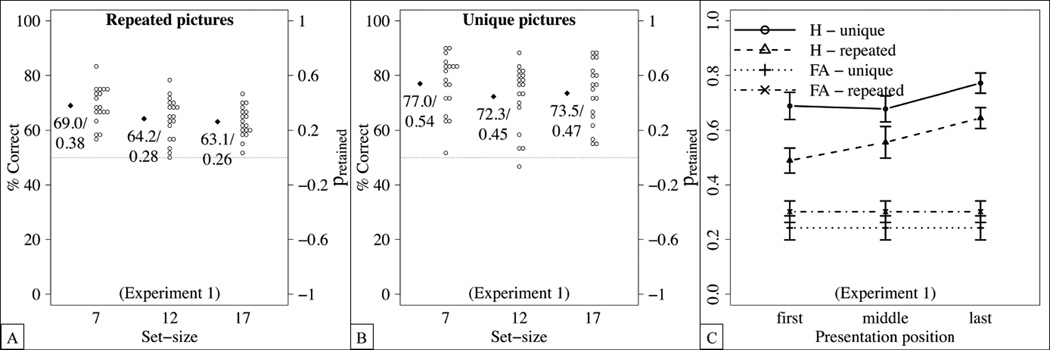
In the unique condition of Experiment 1, we did not observe a fixed capacity limit; instead, estimated capacity increased with set size. To measure the extent of this increase, we analyzed the results in terms of the percentage of correct responses. These results are shown in Figure 2(A) and (B) as a function of set size and condition. (As mentioned above, the analyses for the percentage of correct responses are identical to those for the proportion of items retained, which we show on the right-hand axis of Figure 2.) Participants performed better in the unique condition than in the repeated condition, and performance decreased for larger set-sizes. An ANOVA with the within-subject factor set-size and the between-subjects factor condition yielded main effects of set-size, F(2,68) = 8.45, p = .0005, ${\eta }_p^2=.197$, and of condition, F(1,34) = 10.75, p = .002, ${\eta }_p^2=.24$, but no interaction between these factors, F(2,68) = .52, p = .595, ${\eta }_p^2=0.122$, ns.

Figure 2.

Detailed results of Experiment 1. Dots represent the means of individual participants, diamonds the sample averages, and error bars standard errors from the mean. (A,B) Percentage of correct responses and proportion of retained items in the repeated condition (A) and the unique condition (B). (C) Hit rates for set-size 17 as a function of presentation positions in the repeated and the unique condition, respectively. False alarm rates are calculated for all “new” trials for set-size 17.

Serial position effects

When presented with the larger set-sizes of Experment 1, participants might simply remember the last few items. To address this possibility, we investigated serial position effects for the largest set-size, i.e., 17 items. As mentioned above, “old” items were taken from two initial, medial and final positions each (while the very first and the very last position were never tested). As shown in Figure 2(C), hit rates increased for later presentation positions, yielding a recency effect. This was confirmed by an ANOVA with condition as a between-subjects factor and presentation position as a within-subjects factor, yielding main effects of presentation position, F(2,68) = 7.68, p = .001, ${\eta }_p^2=.180$, and of condition, F(1,34) = 7.58, p= .009, ${\eta }_p^2=.182$, but no interaction between these factors, F(2,68) = .93, p = .401, ${\eta }_p^2=.022$. Importantly, hit rates differed from false alarm rates for all presentation positions (first: t(35) = 8.48, p < .0001, Cohen’s d = 1.4; middle: t(35) = 8.99, p < .0001, Cohen’s d = 1.5; last: t(35) = 15.42, p < .0001, Cohen’s d = 2.6), suggesting that each serial position contributed to item memory.

Discussion

The unique condition of Experiment 1 revealed relatively large capacity estimates, doubling between set-sizes 7 and 17. These results suggest, therefore, that visual temporary memory capacity might be much larger than previously thought. In marked contrast, the repeated condition revealed capacity estimates in the range reported in previous WM experiments, suggesting that PI has a substantial negative effect on memory capacity.

However, these results also show that the data from the unique condition violate the assumption of the capacity estimate formula, which is that capacity is fixed and will not increase once that capacity has been exceeded. In fact, if participants had a capacity of 8 items (as the 17-item condition suggests), they should be at ceiling in the 7-item condition, which was clearly not the case. Hence, it may be more illuminating to look at the data in terms of the percentage of correct responses, as shown in Figure 2. As one can see, the proportion of correct responses declines somewhat as the number presented increases, but it is relatively stable, compared to the same results expressed as capacity. The reason for the apparent capacity increase is, therefore, that, according to the formula for estimating the capacity, a relatively constant number (i.e., the proportion of retained items) is multiplied with a number that grows (i.e., the number of presented items). Our main finding is, therefore, that, without massive PI, the proportion of retained items changes relatively little as a function of the presented items; as a result, participants can retain many more items than past capacity estimates suggest, but they do not seem to have any fixed memory capacity.

We can also exclude that the large capacity estimates in the unique condition might be due to participants noticing that only certain serial positions were tested, and strategically attending to these positions. First, list length was randomized and different serial positions were tested for different list lengths, making it impossible to predict, as a sequence unfolded, when the middle or end of the sequence would occur. Further, within each list length, the critical position of the tested item was randomized. Second, and crucially, if participants strategically attended to certain serial positions, they should preferentially encode the items that appear in serial positions that were tested most regularly. Given that we probed serial positions 2 and 3 in all list length conditions, performance for these positions should be best, leading to a primacy effect. In contrast to this prediction, we observed small but reliable recency effects at each length of list. Hence, we can exclude the possibility that participants strategically attended to specific serial positions.

Experiment 2

In Experiment 2, we tested the generality of the results of Experiment 1 by replicating the experiment using different experimental parameters. Specifically, we kept a total set of 22 items in the repeated condition, but used different set-sizes (5, 11, or 21 items). Further, to test whether the pre-familiarization in Experiment 1 was required for the contrast between the repeated and the unique condition, participants were not pre-familiarized with any pictures.

Materials and methods

Participants

Twenty-four participants (13 females, means age 25.2) from the MIT community were paid for taking part in Experiment 2; none had participated in Experiment 1. They were randomly assigned to the unique and the repeated condition.

Procedure

The procedure was identical to that in Experiment 1, with two exceptions. First, we used different set-sizes of 5, 11, and 21 items, respectively. Second, participants were not pre-familiarized with any pictures.

Results

Capacity estimates

As in Experiment 1, we start by presenting the results of Experiment 2 in terms of estimated memory capacities; while Experiment 1 showed that the capacity estimates did not conform to the hypothesis that estimated capacity remains constant once the number of presented items exceeds estimated capacity, one of the objectives of this research was to provide evidence for this very point. As a result, we present the results in terms of capacity estimates for Experiment 2 as well.

The results of Experiment 2 are shown in Figure 1(B). In the unique condition, memory capacity estimates increased from 3.2 to 9.1 between set-sizes 5 and 21. In contrast, in the repeated condition, capacity estimates remained close to the range reported in previous WM experiments, increasing from 2.3 to 4.8 between set-sizes 5 and 21. An ANOVA with set-size as within-subject factor and condition as between-subjects factor yielded main effects of condition, F(1,22) = 7.50, p = .012, ${\eta }_p^2=.254$, and of set-size, F(2,44) = 40.78, p< .0001, ${\eta }_p^2=.576$. Critically, an interaction, F(2,44) = 8.03, p = .001, ${\eta }_p^2=.113$, indicated that capacity estimates increased more with set-size in the unique condition, F(2,22) = 140.6, p < .0001, ${\eta }_p^2=.927$, compared to the repeated condition, F(2,22) = 4.16, p = .029, ${\eta }_p^2=.274$. Hence, both in the unique and in the repeated condition, the results of Experiments 1 and 2 were very similar.

Percentage of correct responses

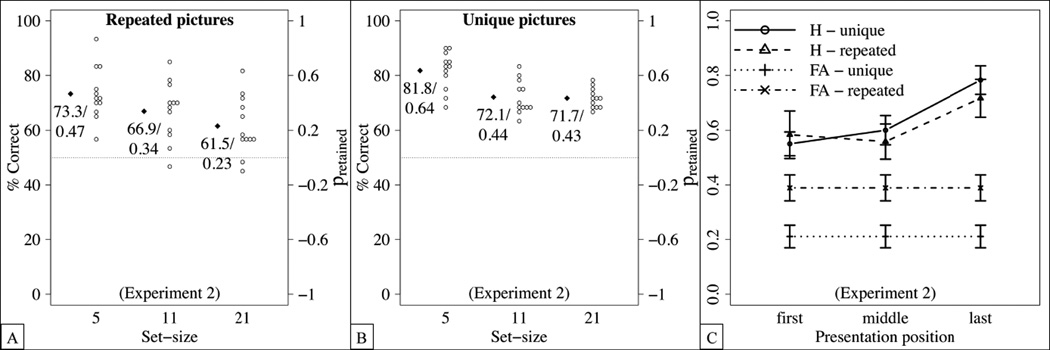
The results in terms of the percentage of correct responses and of the proportion of retained items are shown in Figure 3(A) and (B). Participants performed better in the unique condition than in the repeated condition, and performance decreased for larger set-sizes. An ANOVA with the within-subject factor set-size and the between-subject factor condition yielded main effects of set-size, F(2,44) = 34.96, p < .0001, ${\eta }_p^2=.595$, and of condition, F(1,22) = 6.72, p = .017, ${\eta }_p^2=.234$, but no interaction between these factors, F(2,44) = 1.75, p = .185, ${\eta }_p^2=.03$.

Figure 3.

Detailed results of Experiment 2. Dots represent the means of individual participants, diamonds the sample averages, and error bars standard errors from the mean. (A,B) Percentage of correct responses and proportion of retained items in the repeated condition (A) and the unique condition (B). (C) Hit rates for set-size 21 as a function of presentation positions in the repeated and the unique condition, respectively. False alarm rates are calculated for all “new” trials for set-size 21.

Serial position effects

As in Experiment 1, we investigated the effect of the presentation position on the hit rate for the largest set-size (i.e., 21 items). As shown in Figure 3(C), hit rates increased for later presentation positions, yielding a recency effect. This was confirmed by an ANOVA with condition as a between-subjects factor and presentation position as a within-subject factor, yielding a main effect of presentation position, F(2,44) = 11.99, p < .0001, ${\eta }_p^2=.345$, but no other main effects or interactions. Importantly, however, hit rates differed from false alarm rates for all presentation positions (first: t(23) = 5.6, p < .0001, Cohen’s d = 1.1; middle: t(23) = 6.77, p < .0001, Cohen’s d = 1.4; last: t(23) = 10.47, p = .001, Cohen’s d = 2.1), suggesting that each serial position contributed to the memory capacity.

Discussion

The results of Experiments 1 and 2 suggest that temporary memory for everyday objects does not have the fixed capacity that past WM experiments seem to suggest, and that participants can temporally retain many more items than previously thought. As mentioned above, the capacity estimates in the unique condition are not meaningful; if participants truly had a fixed capacity of about 9, they should be at ceiling for all set-sizes below this limit, which was clearly not the case. Rather, our crucial result is that, in the unique condition, the proportion of correct responses (equivalent to the estimated proportion of retained items) changes only relatively little as a function of the set-size.

In contrast, in the presence of PI, capacity limits remained in the range of WM limitations, although the capacity estimates for large set-sizes were relatively high as well. As mentioned earlier, these results are not due to verbal memory encoding of the pictures, both because the presentation rate is too fast for processes such as rehearsal, and because linguistic processes are remarkably independent from those used to memorize the pictures (Endress & Potter, 2012).

Experiment 3

In Experiment 3, we further explored the memory capacity limits in the unique condition. Experiment 3 was similar to the unique condition of Experiment 2, except that we used set-sizes of 25, 50 and 100.

Materials and methods

Participants

Twenty participants (12 females, means age 21.5) from the MIT community took part in Experiment 3; none had participated in the earlier experiments.

Procedure

Experiment 3 was similar to Experiment 2, with four exceptions. First, the experiment contained only a unique but not repeated condition. Second, we used the set-sizes 25, 50 and 100. Third, participants viewed a progress bar between the last sample picture and the test picture lasting for 1 s.⁵ Fourth, with 2,400 pictures, we could construct only 12 trials per set-size, for a total of 36 trials.

Results

Capacity estimates

As in the Experiments above, we start by presenting the data in terms of capacity estimates. As shown in Figure 1(C), a one-way ANOVA with set-size as within-subject factor revealed that capacity estimates increased between set-sizes 25 and 100, F(2,38) = 5.5, p = .008, ${\eta }_p^2=.223$, reaching a maximum of 30.0 for set-size 100.

Percentage of correct responses

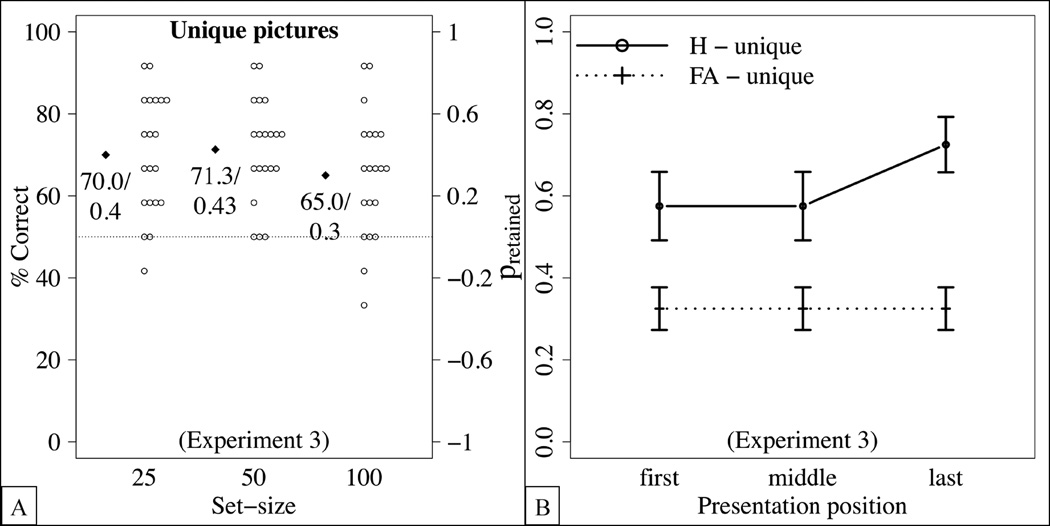
The results in terms of the percentage of correct responses and, equivalently the proportion of retained items are shown in Figure 4(A). In an ANOVA with the within-subject factor set-size, the main effect of set-size was not significant, F(2,38) = 1.2, p = .305, ${\eta }_p^2=.061$, failing to reject the hypothesis that the percentage of correct responses differed across set-sizes, and consistent with the hypothesis that it might be relatively constant irrespective of how many items are presented.

Figure 4.

Detailed results of Experiment 3. Dots represent the means of individual participants, diamonds the sample averages, and error bars standard errors from the mean. (A) Percentage of correct responses and proportion of retained items. (B) Hit rates for set-size 100. False alarm rates are calculated for all “new” trials for set-size 100.

Serial position effects

As in Experiments 1 and 2, we investigated the effect of the presentation position on the hit rate for the largest set-size (i.e., 100 items). As shown in Figure 4(C), hit rates did not differ statistically across presentation positions, F(2,38) = 1.8, p = .182, ${\eta }_p^2=.086$, failing to reject the null hypothesis that the hit rate was the same across serial positions.

Discussion

The unique conditions of Experiments 1 to 3 revealed large capacity estimates. As pointed out above, the large capacity estimates do not reflect fixed memory capacities, but rather indicate that the probability of recognizing an item changes little as a function of how many items are presented, at least up to at least 100 items. This raises the question of what kind of memory system stores the unique items. Plausibly, they might be stored in long-term memory (LTM). After all, participants could, at least in principle, perform their task by deciding whether or not they have ever seen a test stimulus before; if they have, it was in the sequence from the current trial.

At least after consolidation, LTM is relatively stable over time. For example, in an experiment testing LTM for the same pictures as those used here, each of 2500 pictures was presented for 3000 ms. Under these conditions, participants’ recognition performance was excellent after 5.5 h (Brady et al., 2008). Hence, if the unique items that are remembered are stored in a consolidated form of LTM, we would expect the corresponding memory to be relatively stable over time.

In contrast, if memory items are stored in a temporary form of memory, the resulting representations should be fleeting, and should not show the temporal stability of consolidated LTM representations. That is, even if the memory representations are fleeting, they might still be stored in an unconsolidated form of LTM that might be fleeting. For the current purposes, however, we just aim to show that the temporary memory store is indeed temporary, rather than to exclude a contribution from LTM.

In Experiment 4, we explored the temporal stability of the memory store. Experiment 4 was similar to Experiments 1 and 2, with two crucial changes. First, we introduced variable delays between the end of the sample sequence and the test item of either 1.5 s (similar to Experiments 1 and 2) or 7.5 s. If probe items that are successfully recognized are stored in a stable form of memory, there should be no difference between the two delay conditions. Second, after participants had completed all the probe trials, they were unexpectedly tested on their long-term retention of the pictures they had seen. If memory in the unique condition depends on a stable form of memory, we should observe recognition performance in the surprise memory test that is comparable to immediate recognition. Given that the specific objects participants saw were novel, and that participants’ long-term ability to remember specific objects is excellent even when pitted against foils of the same category (Konkle, Brady, Alvarez, & Oliva, 2010a, 2010b), we would expect little change in the probability of remembering an item between the immediate tests and the tests at the end of the experiment about 30 min later, if both depend on a stable form of memory. Further, Experiment 4 will also rule out a contribution of sensory or iconic memory (Sperling, 1960), because iconic memory would not survive a 1.5 s and certainly not a 7.5 s delay.

Experiment 4

Materials and methods

Participants

Twenty-four participants (20 females, means age 23.5) from the MIT community took part in Experiment 4; none had participated in previous experiments. They were randomly assigned to the unique and the repeated condition.

Procedure

Experiment 4 was similar to Experiment 2, with three crucial exceptions. First, we used just two set-sizes, 6 and 17, presented for a total of 192 trials. Second, we introduced variable delays between the end of the sample sequence and the test item. As before, participants started each trial by a key-press, viewed instructions to look at the pictures for 1000 ms, followed by a fixation cross for 300 ms and a 200 ms blank screen, followed by the sample pictures presented at a duration of 250 ms per picture. Then, they saw a blank screen for 200 ms, following by a progress bar of either 1 s or 7 s, followed by a fixation cross for 300 ms, and the test picture presented for 800 ms. In total, the delay between the last picture of the sample sequence and the test picture was 1.5 or 7.5 s (compared to a total delay of 1.7 s in Experiments 1 and 2). Third, after they had completed these trials, participants were tested on their long-term retention of the pictures they had seen. For each picture, they had to indicate whether or not they had seen it before in the experiment. Pictures were presented with the constraint of not having more than three “old” items or foils in a row. In the unique condition, the 96 “old” pictures tested for long-term retention each came from one of the 96 trials that had been tested with a new picture, counterbalanced over set-sizes and three serial positions (early, middle, or late). The 96 “new” pictures in the final test were intermixed with the old pictures. The old pictures were presented in the order in which they had appeared during the temporary memory part of the experiment. In the repeated condition, participants were shown all 22 pictures they had seen, mixed with 22 foils, presented one at a time. The pictures were presented in random order. The long-term retention test started immediately after the RSVP phase of the experiment; as the RSVP phase lasted about 30 min and the long-term retention test took no more than 5 min (less in the repeated condition), the LTM retention interval was between 30 and 35 min.

Results

Capacity estimates

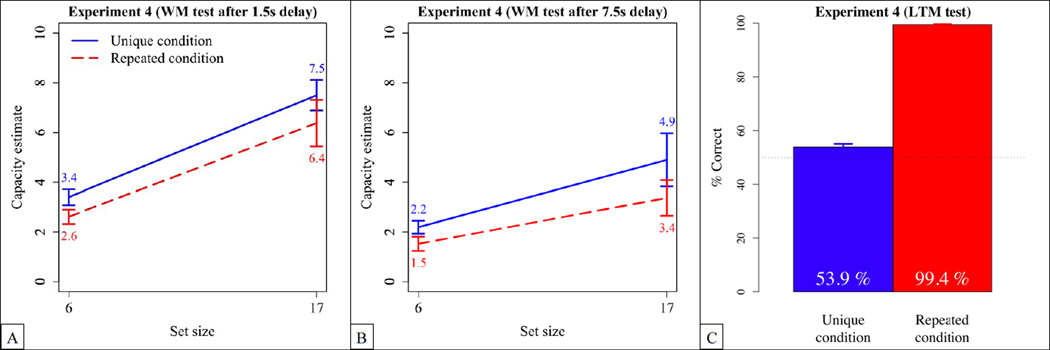
The results of Experiment 4 with 1.5 s and 7.5 s delays are shown in Figure 5(A) and (B). In the unique condition, capacity estimates increased from 3.4 to 7.5 between set-sizes 6 and 17 in the short delay condition, and from 2.2 to 4.9 in the long delay condition. In the repeated condition, capacity estimates increased from 2.6 to 6.4 between set-sizes 6 and 17 in the short delay condition, and from 1.5 to 3.4 in the long delay condition. An ANOVA with set-size and delay as within-subject factors and group as between-subjects factor yielded main effects of delay, F(1,22) = 28.9, p < .0001, ${\eta }_p^2=.567$, as well as of set-size, F(1,22) = 62.0, p < .0001, ${\eta }_p^2=.733$. The main effect of group failed to reach significance, F(1,22) = 2.7, p = .114, ${\eta }_p^2=.109$. We also observed an interaction between delay and set-size, F(1,22) = 5.4, p = .03, ${\eta }_p^2=.195$, suggesting the effect of set-size was more pronounced for short delays, F(1,22) = 64.2, p < .0001, ${\eta }_p^2=.744$, than for long delays, F(1,22) = 15.9, p = .0006, ${\eta }_p^2=.414$. There were no other significant interactions.⁶

Figure 5.

Results of Experiment 4. (A) Memory capacity estimates with a 1.5 s interval between the end of the sample sequence and the test image. (B) Memory capacity estimates with a 7.5 s interval between the end of the sample sequence and the test image. (C) Retention performance during the surprise memory test at the end of the experiment. The blue solid lines represent the unique conditions, and the red dotted lines the repeated conditions. Error bars represent SEM.

The results of the long-term retention test are shown in Figure 5(C). In the long-term retention test of the unique condition, participants performed significantly but only slightly above chance (M = 53.9%, SD = 4.0%), t(11) = 3.4, p = .006, Cohen’s d = .97, CI_:95 = 51.4%, 56.5%. In the repeated condition, participants were virtually perfect (percentage of correct responses: M = 99.4%, SD = 1.0%), t(11) = 166.6, p < .0001, Cohen’s d = 48.0, CI_:95 = 98.8%, 100.1%.

Percentage of correct responses

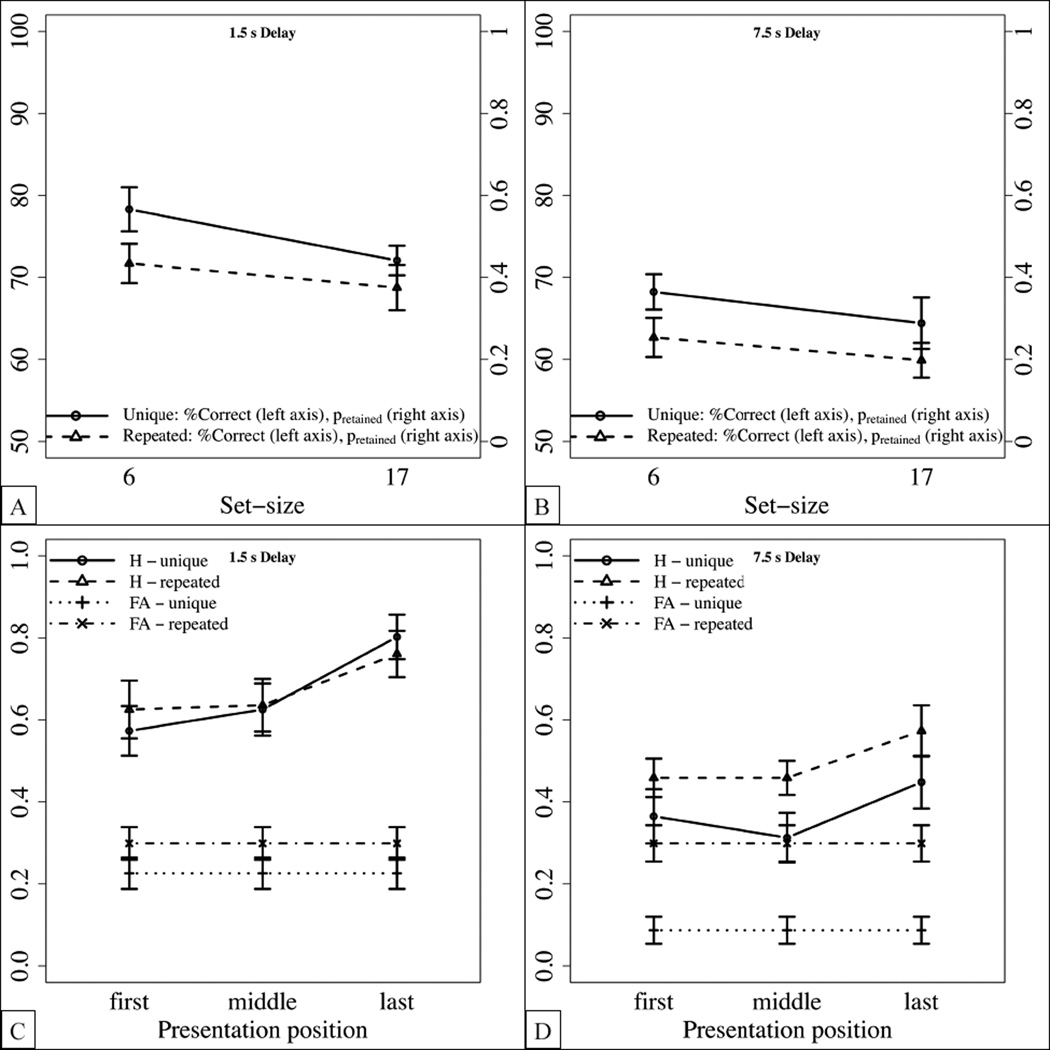
The results in terms of the percentage of correct responses are shown in Figure 6(A) and (B). Participants performed better after the short delay than after the long delay, and performance decreased for larger set-sizes. An ANOVA with the within-subject factors set-size and delay, and the between-subjects factor condition yielded main effects of set-size, F(1,22) = 12.6, p = .002, ${\eta }_p^2=0.355$, and delay, F(1,22) = 39.2, p< .0001, ${\eta }_p^2=.641$, but no effect of condition, F(1,22) = 3.6, p = 0.073, ${\eta }_p^2=0.139$, ns. There were no other main effects or interactions.

Figure 6.

Detailed results of Experiment 4. Error bars standard errors from the mean. (A,B) Percentage of correct responses and proportion of retained items after the short delay (A) and the long delay (B). (C,D) Hit rates for set-size 17 as a function of presentation positions after the short delay (C) and the long delay (D). False alarm rates are calculated for all “new” trials for set-size 17, separately for the long and the short delay, respectively.

Serial position effects

As in Experiment 1, we investigated the effect of the presentation position on the hit rate for the largest set-size (i.e., 17 items). As shown in Figure 6(C) and (D), hit rates increased for later presentation position, yielding a recency effect. This was confirmed by an ANOVA with condition as a between-subjects factor, and presentation position and delay as within-subjects factors. We observed main effects of presentation position, F(2,44) = 13.75, p < .0001, ${\eta }_p^2=0.382$, and delay, F(1,22) = 43.48, p< .0001, ${\eta }_p^2=0.639$, but not of condition, F(1,22) = 1.26, p = 0.274, ${\eta }_p^2=0.054$. We observed no other interactions. Importantly, hit rates differed from false alarm rates for all presentation positions and delay conditions, suggesting that each serial position contributed to the memory capacity.

Discussion

Experiment 4 investigated the temporal stability of the memory mechanism underlying participants’ performance in Experiments 1 to 3. In the repeated condition, long-term retention performance was almost perfect. This result is rather unsurprising, given that participants saw each item frequently not only in the sequences, but also as test items during the first phase of the experiment and, therefore, for presentation durations long enough to yield long-term retention.

The unique condition, in contrast, revealed two crucial results. First, long-term retention of the pictures was almost at chance, suggesting that participants did not encode items in a stable form of long-term memory. Second, in the test after each sequence, participants performed worse after the longer delay, suggesting again that they did not encode the items they had just seen in a stable form of memory.⁷ That being said, given that forgetting curves tend to be negatively accelerated (e.g., Jost, 1897; Rubin & Wenzel, 1996; T. D. Wickens, 1998), it is possible that the main forgetting takes place in the first few seconds; even in this case, however, a stable LTM representation should not all but disappear in half an hour. In the General Discussion, we will come back to potential relations between this temporary memory store and LTM. Specifically, drawing on recent research casting doubt on a clear dissociation between short-term memory and LTM (for a review, see e.g. Ranganath & Blumenfeld, 2005), we will suggest that our large-capacity, temporary memory store reflects early and unconsolidated LTM traces that decay over time.

The results so far suggest that we have a temporary visual memory store for meaningful stimuli with no fixed storage capacity, and that PI associated with repeated items can reduce capacity estimates to the typical range of WM experiments. However, some previous results using verbal stimuli have found an advantage for lists of repeated items. Specifically, participants were presented with a list of words, and had to repeat them back in order. Performance was better when the words were sampled from a limited set of items on all trials compared to when new words were used on all trials (Coltheart, 1993; Conrad, 1963; Roodenrys & Quinlan, 2000).⁸ At first sight, these experiments seem to contradict the findings presented here. However, these experiments used words as stimuli, and there is extensive evidence that verbal memory has different properties from other forms of memory (e.g., Fougnie & Marois, 2006; Baddeley, 1996, 2003). Phonological encoding permits words to be rehearsed, and increased familiarity with words might make it easier to encode them in a phonological format and to rehearse them more efficiently.

To address this issue, we replicated Experiment 2, but using words as stimuli and, importantly, presenting them at a rate too fast to permit rehearsal. Experiment 5 was similar to Experiment 2 except that visually presented words were used as stimuli instead of pictures, the duration of each word was 120 ms, and participants in the repeated condition were pre-familiarized with the words.

Experiment 5

Materials and methods

Participants

Thirty-two participants (17 females, means age 24.5) from the MIT community took part in Experiment 5; none had participated in the previous experiments. They were randomly assigned to the unique and the repeated condition.

Materials

We selected 2381 nouns from the CELEX database (a frequency database for English words) with the constraints that each noun (i) had between 4 and 10 letters; (ii) had one or two syllables; (iii) had a minimum frequency of 100 of out 17.9 million words; (iv) was unique in the final list (e.g., words that differed only in plural markers were removed); (v) was not specific to British English; (vi) was not a proper noun; (vii) was not a swear word or otherwise offensive. Words were presented in a font size of 22 in Courier lower-case font.

Procedure

The procedure was identical to Experiment 2, with three exceptions. First, participants were presented with written words instead of pictures. Second, as in Experiment 1, participants were pre-familiarized with the words they would see during the actual experiment (in the repeated condition), or with words that would not appear during the actual experiment (in the unique condition). Third, words were presented at a rate of 120 ms per word. We chose this rate because pilot testing revealed that participants would be likely to be at ceiling for slower presentation rates, and at chance for faster presentation rates.

Results and discussion

Capacity estimates

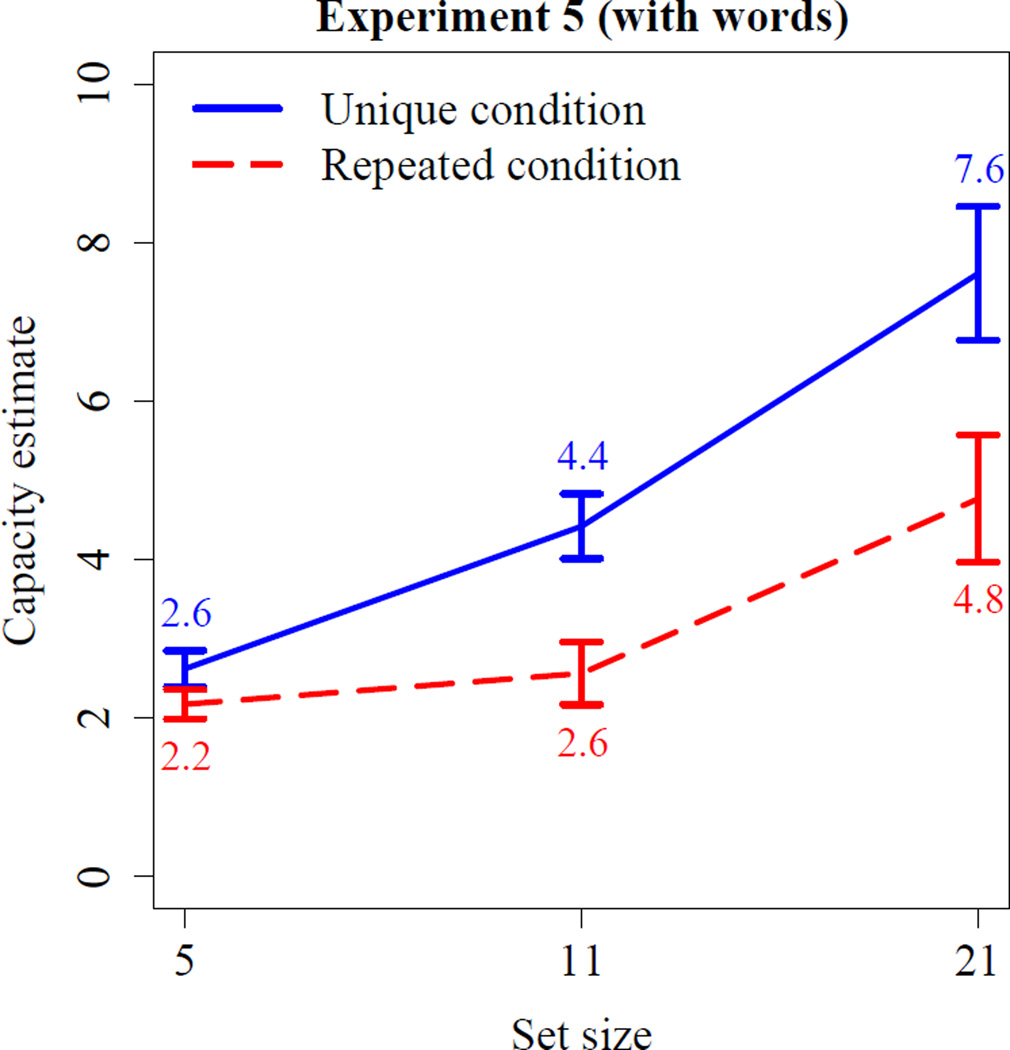
As in the experiments above, we start by presenting the data in terms of capacity estimates. In the unique condition of Experiment 5, as shown in Figure 7, capacity estimates increased from 2.6 to 7.6 between set-sizes 5 and 21. In contrast, in the repeated condition, capacity estimates increased from 2.2 to 4.8 between set-sizes 5 and 21. An ANOVA with set-size as within-subject factor and condition as between-subjects factor yielded main effects of the condition, F(1,30) = 8.9, p = 0.006, ${\eta }_p^2=0.229$, as well as of set-size, F(2,60) = 39.4, p< .0001, ${\eta }_p^2=0.538$. Critically, an interaction, F(2,60) = 3.7, p = 0.029, ${\eta }_p^2=0.051$, indicated that capacity estimates increased more in the unique condition, F(2,30) = 39.5, p < .0001, ${\eta }_p^2=0.725$, compared to the repeated condition, F(2,30) = 8.68, p = 0.001, ${\eta }_p^2=0.367$. Hence, irrespective of whether words or pictures are used as stimuli, humans seem to have a temporary memory store for meaningful information with a relatively large capacity, and PI from repeated items is sufficient to reduce memory capacity to levels reported in previous WM experiments.

Figure 7.

Results of Experiment 5. The blue solid line represents the unique condition, and the red dotted line the repeated condition. Error bars represent SEM.

While the main effect of condition was highly significant, the interaction between condition and set-size was only marginally significant (p = .029). To assess whether the interaction was weaker than in Experiment 2, we performed a joint analysis of Experiments 2 and 5 with set-size as the within-subject factor and condition and experiment as between-subject factors. We observed main effects of set-size, F(2,104) = 78.88, p < .0001, ${\eta }_p^2=0.553$ and condition, F(1,52) = 16.43, p = 0.0002, ${\eta }_p^2=0.233$, as well as an interaction between these factors, F(2,104) = 10.0, p = 0.0001, ${\eta }_p^2=0.0702$, but no other main effects or interactions. The participants’ behavior is, therefore, qualitatively the same in Experiments 2 and 5.⁹

Percentage of correct responses

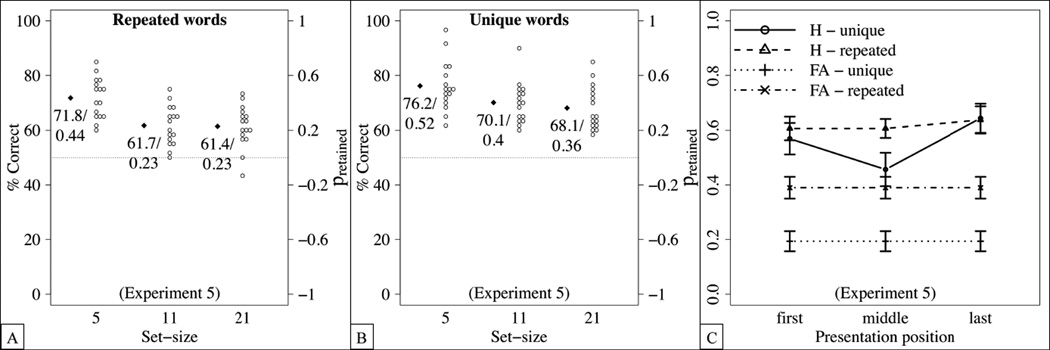
The results in terms of the percentage of correct responses and the proportion of retained items are shown in Figure 8(A) and (B). Participants performed better in the unique condition than in the repeated condition, and performance decreased for larger set-sizes. An ANOVA with the within-subject factor set-size and the between-subjects factor condition yielded main effects of set-size, F(2,60) = 27.7, p < .0001, ${\eta }_p^2=0.471$, and of condition, F(1,30) = 8.3, p = 0.007, ${\eta }_p^2=0.216$, but no interaction between these factors, F(2,60) = 1.1, p = 0.35, ${\eta }_p^2=0.0182$, ns.

Figure 8.

Detailed results of Experiment 5. Dots represent the means of individual participants, diamonds the sample averages, and error bars standard errors from the mean. (A,B) Percentage of correct responses and proportion of retained items in the repeated condition (A) and the unique condition (B). (C) Hit rates for set-size 21 as a function of presentation positions in the repeated and the unique condition, respectively. False alarm rates are calculated for all “new” trials for set-size 21.

Serial position effects

As in Experiment 1, we investigated the effect of the presentation position on the hit rate for the largest set-size (i.e., 21 items). As shown in Figure 8(D), hit rates increased for later presentation position, yielding a recency effect. This was confirmed by an ANOVA with condition as a between-subjects factor and presentation position as a within-subjects factor, yielding a main effect of presentation position, F(2,60) = 4.1, p = 0.021, ${\eta }_p^2=0.114$, but no other main effects or interactions. Importantly, hit rates differed from false alarm rates for all presentation positions (first: t(31) = 6.9, p< .0001, Cohen’s d = 1.2; middle: t(31) = 5.9, p< .0001, Cohen’s d = 1.0; last: t(31) = 7.8, p < .0001, Cohen’s d = 1.4), suggesting that each serial position contributed to the memory capacity.

General discussion

In the experiments presented here, we start to address two conflicting intuitions about the memory capacity available to cognitive processes. While many WM experiments have revealed striking capacity limitations that correlate with important cognitive abilities, many other everyday situations seem to call for a much larger memory for temporary storage.

Participants were shown rapidly presented pictures of real-world objects or of words. Each item was presented at most for a duration equivalent to a single eye fixation (e.g., Rayner, 1998). We asked whether memory capacity would show the severe limitations observed in WM experiments, and whether memory capacity limitations would depend on the presence of proactive interference (PI) among items. Half of the participants saw each item only once throughout the experiment; the remaining participants were shown items from a limited set of 22 items, leading to PI among pictures or words. For the unique group, results of Experiments 1, 2, and 5 revealed large capacity estimates of up to 9.1, and capacity estimates increased when more items were presented, up to an average of 30.0 pictures out of 100 in Experiment 3. In other words, when participants were given the opportunity to memorize more items, they did so. These results should not be taken to imply that participants have an actual capacity of, say, 30 items. As mentioned above, if they had such a capacity, they should be at ceiling for all set-sizes below 30, which was clearly not the case. Rather, these results show that the proportion of retained items depends only mildly on the set-size. Even in this case, however, observers can temporarily store many more items than past capacity limits seem to suggest.

In contrast, PI clearly limited memory capacity; when items were reused across trials, capacity estimates were reduced, remained in the higher range of estimates reported in previous WM experiments, and increased much less as a function of the set-size. Further, Experiment 4 showed that participants did not store the briefly presented items in a temporally stable form of memory, but rather in a form of memory that began to decay over the course of a few seconds, and disappeared almost completely after a few minutes.

Together, these results suggest that temporary storage for meaningful items has a much larger capacity than in typical WM experiments, and that PI is sufficient to reduce capacity estimate to the range observed in previous WM experiments.

Meaningfulness of the items

One reason for the relatively large capacity estimates we found in the unique condition might have been that we used meaningful as opposed to meaningless items or simple visual features. In fact, there is substantial evidence that prior knowledge allows observers to encode more items in WM (see Brady, Konkle, & Alvarez, 2011 for a review and references therein), an observation that has been made even in the earliest discussions of memory capacity limitations (Miller, 1956). In fact, familiarity of items or conceptual information seems to increase capacity estimates (e.g., Feigenson & Halberda, 2008; Jackson & Raymond, 2008).

However, memory capacity limitations have not only been observed with meaningless features such as those used in change-detection experiments following Luck and Vogel (1997). In fact, the earliest discussion of capacity limitations involved memory for meaningful stimuli such as words (e.g., Miller, 1956; Baddeley, 1996; see also Cowan, 1995, for a review). Further, working memory limitations are routinely observed with meaningful non-verbal stimuli such as faces and agents (e.g., Curby & Gauthier, 2007; Curby, Glazek, & Gauthier, 2009; Wood, 2008, 2009; Wong, Peterson, & Thompson, 2008). Hence, the large capacity estimates in the unique condition are not a mere by-product of using meaningful stimuli as opposed to simple features.

That being said, we would not expect the results from the unique conditions to hold up for meaningless simple features such as colors or shapes, for two related reasons. First, memory for items that are not readily categorized is known to be extremely poor (Olsson & Poom, 2005), and there clearly is a limit to how many meaningless items can be categorized. For example, we cannot encode thousands of color hues categorically, as would be required for our experiments. Second, and relatedly, given that a large number of meaningless items is unlikely to be encoded categorically, many of the items will appear extremely similar to each other, and it is well known that confusability severely impairs memory performance (e.g., Baddeley, 1966; Conrad, 1963; Conrad & Hull, 1964; Viswanathan, Perl, Visscher, Kahana, & Sekuler, 2010).

Hence, while we would not expect our results to hold up for meaningless items due to how these items are encoded in the first place, previous reports of working memory limitations with meaningful stimuli clearly show that large capacity estimates for temporary memory are not a mere side effects of using meaningful items as stimuli.

Previous estimates of WM capacity

While we did not observe an upper bound to how many items could be temporarily retained, these results should not be taken to imply that traditional WM measures are invalid because they are taken from conditions that promote PI. Indeed, as noted earlier, some authors have argued that a crucial function of WM is to counteract the effects of such interference (Engle, 2002). Moreover, there is evidence that the processes recruited to counteract interference are active. For example, Kane and Engle (2000) showed that, while high-span individuals are less prone to PI than low-span individuals, this difference disappears when participants have to perform an attentionally demanding secondary task. Further, measures of WM correlate with important aspects of our mental lifes, including intelligence, language comprehension, reasoning, and educational achievement (e.g., Barrouillet, 1996; Daneman & Carpenter, 1980; Daneman & Green, 1986; Engle et al., 1999, 1991, 1992; Fukuda et al., 2010; King & Just, 1991; Kyllonen & Christal, 1990). It thus seems that there are important cognitive situations that require active and effortful manipulation of items, perhaps limiting our ability to juggle more than three or four items, or even permitting us to hold no more than a single item in the focus of attention (e.g., Oberauer, 2002; Oztekin et al., 2010). Crucially, however, our results suggest that, in other cognitive situations, we might not face such stringent memory limitations, and have essentially unbounded capacity available to temporarily store meaningful information, limited only by the rate of decay of the items or the inevitable interference that even unrelated items exert in memory.

Relatedly, we do not have a theory of why capacity estimates in previous experiments often lie between 3 and 4 items; we just refer to previous proposals that the specific limitations coincide with limitations of visual attention (see Cowan, 1995, for a review), but our results do not speak to this issue.

A unitary memory store?

What, then, is the basis for the large-capacity but temporary memory shown here? At first sight, the results seem to fit with many models holding that items in WM are simply the subset of LTM that is currently active and (mentally) attended (e.g., Cowan, 2005; Conway & Engle, 1994; Oberauer, 2002; Oztekin et al., 2010). For example, in tasks where participants have to memorize lists of digits, all digits clearly have entries in LTM, and, within a few trials, all will be activated from LTM. In such models, WM limitations might arise from limited-capacity attentional processes that are required to represent the items on the current list in a form that shields them from interference from other recently activated digits (e.g., Cowan, 2005; Conway & Engle, 1994; Oberauer, 2002; Oztekin et al., 2010). If so, capacity estimates might become much larger when items do not need to be attended and rehearsed to avoid PI.

However, there are other considerations suggesting that our results do not necessarily reflect the same construct as WM. First, WM supposedly relies on active maintenance, and there is no evidence in our experiments for active maintenance or selective attention to a subset of items. For example, complex span tasks such as the sentence span task (e.g., Daneman & Carpenter, 1980), where participants read a sequence of sentences and have to remember the last word of each, clearly require active maintenance of the memory items (e.g., Kane & Engle, 2000). For other WM tasks, however, the evidence for active maintenance is less clear. For example, Fougnie and Marois (2006) asked participants to memorize an array of colors. Before being tested on their memory for the colors, they had either to complete a task that is known to tax attention (i.e., to track multiple objects moving around a display; Pylyshyn & Storm, 1988; Scholl & Pylyshyn, 1999), or to memorize a second array. Memory performance for the first array was much more impaired by memorizing a second array than by a multiple object tracking task, suggesting that attentional capacity and WM capacity are at least partially independent. It thus seems fair to conclude that the evidence for active maintenance is stronger for some WM tasks than for others, and that it is not clear whether and where in this spectrum the (presumably) passive maintenance in our experiments falls.

Second, while the aforementioned models assume that WM items are also represented in LTM, the results of Experiment 4 show that the memory items in the unique condition are not encoded in a temporally stable form of memory. Indeed, LTM is generally assumed to be stable over time (see e.g., Brady et al., 2011; Cowan, 2008; Luck, 2007; Sternberg, 2009; see also Craik & Lockhart, 1972, for a compilation of traditional differences between long-term memory and short-term memory), and should not show decay within a few seconds or minutes. Hence, our results suggest that the memory items reside in a form of memory that is distinct from LTM as commonly conceived. Another possibility, however, is that LTM traces vary in strength and can be very short-lived. The latter hypothesis is in line with recent studies casting doubt on a clear-cut distinction between STM and LTM (for a review, see e.g. Ranganath & Blumenfeld, 2005), and is also consistent with earlier proposals that STM and LTM might be closely related (e.g., Brown et al., 2007; Craik & Lockhart, 1972; Crowder, 1993; Nairne, 2002; Ranganath & Blumenfeld, 2005; Wickelgren, 1972, 1973), and might show common forgetting functions (e.g., Rubin & Wenzel, 1996; T. D. Wickens, 1998; Wixted & Ebbesen, 1991).

For example, some evidence for continuity between STM and LTM comes from another set of experiments using a method similar to the unique condition of Experiment 4, in which participants were first tested on their immediate retention of items presented in a RSVP sequence, and subsequently on their long-term retention of the items they had seen. Crucially, however, some of the rapidly presented pictures were intermittently repeated across trials, but were not tested until the end of the experiment. As in Experiment 4, participants showed almost no long-term retention for items presented once. However, memory for the repeated pictures gradually increased as the number of repetitions increased, so that later long-term recognition performance for a picture presented just eight times was as good as recognition performance in the immediate test (Endress & Potter, under review). These results show that fleeting memories can be gradually consolidated into stable LTM representations, indicating that there is continuity between STM and LTM.

This being said, presenting an item for a longer time, or repeating it more often (which, we assume, has similar effects), is not necessarily sufficient for it to be encoded in stable long-term memory representations. While, at least in the short-term domain, presentation duration clearly has an effect on retention rates (e.g., Intraub, 1980; Keppel & Underwood, 1962; Potter & Levy, 1969; Vogel, Woodman, & Luck, 2006), Craik and Watkins (1973) also showed that time in memory is not the only determinant of LTM encoding, and that processes like elaborative rehearsal or directed forgetting also affect how well or poorly an item is remembered. Be that is it might, the experiments reviewed above show that presenting items more often clearly results in memory representations that are too stable to be in the STM domain although a single presentation does not result in a stable memory representation.

We surmise that memory in the unique condition relies on a short-lived and unconsolidated form of LTM that functions as a temporary memory store. If so, our results would be consistent with the following model. Memory for items viewed briefly is fleeting and disappears over the course of a few minutes, but the capacity of this temporary memory store is large. Adding proactive interference results in the memory limitations of previous WM experiments. Finally, if items are viewed repeatedly or for longer periods of time, the memory representations become consolidated in LTM. In addition to this large capacity temporary memory store, there appears to be an effortful and severely constrained form of memory that shows the limitations characteristic of previous WM experiments, and that relies on active manipulation of memory items. It is presumably this limited-capacity WM that shows the individual differences in WM that have been associated with measures of intelligence and life success. How this capacity-limited, active form of WM works in tandem with the large-capacity but more passive temporary memory seen in the present experiment has yet to be explored.

Whatever the case, the present results demonstrate that meaningful items can be stored in a form of memory that does not show the temporal stability associated with LTM and yet has a much larger capacity than past WM capacity estimates. Some important cognitive activities such as logic and mental arithmetic or even just remembering a phone number might involve the interference associated with changing combinations of a small set of items (e.g., numbers) that limits capacity. However, this might not be the case for many other everyday cognitive activities, such as foraging, decision making, following a conversation, or even understanding a lecture. A memory capacity of three or four items might well be insufficient in many of these cases, calling for a form of temporary memory that operates on meaningful items, that does not rely on active maintenance, and that has a relatively large capacity limit. The present results suggest that we have just such a form of memory.

Appendix

Interference across trials

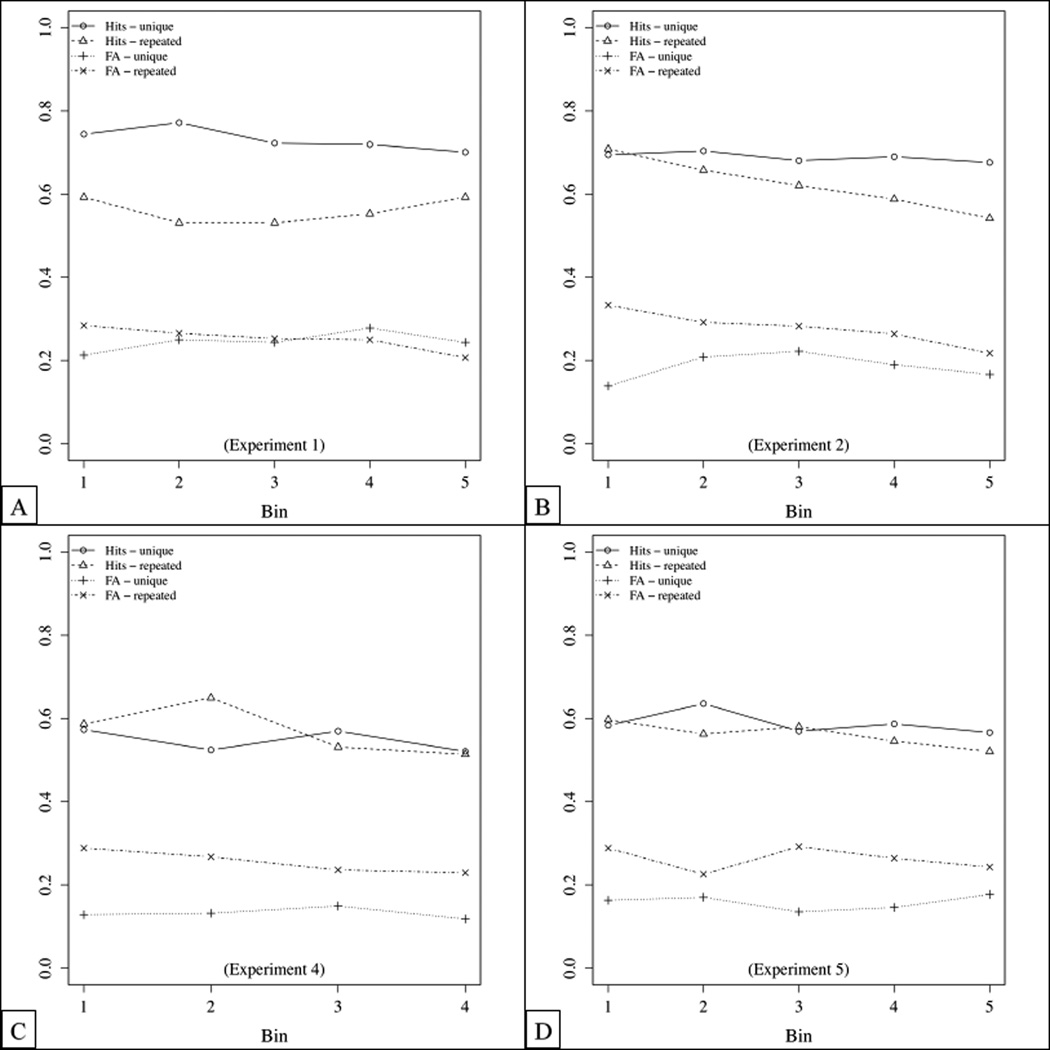
To examine the effect of proactive interference over the course of entire experiments, we analyzed the hit and correct rejection rates as a function of the trial number in Experiments 1, 2, 4 and 5. (We omitted Experiment 3 because it did not comprise a repeated condition.) Specifically, we organized data into bins of 6 trials, separately for each set-size and for “old” and “new” trials. (We opted for bins of 6 trials because 6 was the smallest divider of the total number of trials for which the resulting curves looked relatively smooth; while the results with fewer trials per bin were similar, they were more noisy.) In Experiment 4, we thus collapsed the data across the two delay conditions.

We collapsed the binned data across set-sizes, and submitted it to an ANOVA with the proportion of correct responses as the dependent variable. We included the condition (unique vs. repeated) as between-subject predictor and test type (“old” vs. “new”) and bin as within-subject predictors.

The results for Experiment 1 are shown in Figure A1(A). (In Experiment 1, we used set-sizes of 7, 12 and 17 items, and prefamiliarized participants with pictures, in the repeated condition with the pictures they would experience during the experiment, and in the unique condition with pictures that would not appear during the experiment.) We observed main effects of condition, F(1,34) = 10.75, p = 0.002, ${\eta }_p^2=0.24$, and test type, F(1,34) = 6.53, p = 0.015, ${\eta }_p^2=0.147$, as well as a marginal interaction between these factors, F(1,34) = 4.01, p = 0.053, ${\eta }_p^2=0.09$. There were no other main effects or interactions. In line with Keppel and Underwood’s (1962) and D. D. Wickens et al.’s (1963) finding that PI effects arise extremely quickly, these results suggest that the pre-familiarization might have been sufficient to lead to a high level of PI throughout the experiment.

Figure A1.

Results of Experiment 1, 2, 4 and 5 as a function of the trial number. Trials were organized into bins of 6 trials, separately for each set-size and for “old” and “new” trials.

In Experiment 2, we used set-sizes of 5, 11 and 21, but no pre-familiarization. The results of the by-bin analyses are shown in Figure A1(B). The data were analyzed as for Experiment 1. We observed main effects of condition, F(1,22) = 6.72, p = 0.017, ${\eta }_p^2=0.234$, and test type, F(1,22) = 5.28, p = 0.031, ${\eta }_p^2=0.193$. Critically, we also observed an interaction between test type and bin, F(4,88) = 2.88, p = 0.027, ${\eta }_p^2=0.104$, as well as a triple interaction between condition, test type and bin, F(4,88) = 2.81, p = 0.030, ${\eta }_p^2=0.10$.

We follow up on these interactions by separately analyzing the unique and the repeated condition. For the unique condition, we observed a non-significant main effect of test type, F(1,11) = 3.60, p = 0.084, ${\eta }_p^2=0.247$, ns, and no other main effects or interactions. For the repeated condition, we observed an interaction between test type and bin, F(4,44) = 5.62, p = 0.001, ${\eta }_p^2=0.338$. For “new” items, there was no significant effect of bin, F(4,44) = 1.75, p = 0.157, ${\eta }_p^2=0.137$, ns. In contrast, for “old” items, performance decreased as a function of the bin number, F(4,44) = 4.11, p = 0.006, ${\eta }_p^2=0.272$.

In Experiment 4, we presented participants with different retention delays, but collapsed the analyses below across delays. The ANOVA revealed only a marginal effect of condition, F(1,22) = 3.55, p = 0.073, ${\eta }_p^2=0.139$, a main effect of test type, F(1,22) = 31.05, p = .00001, ${\eta }_p^2=0.557$, and marginal interactions between test type and bin, F(3,66) = 2.57, p = 0.062, ${\eta }_p^2=0.095$, and between condition, test type and bin, F(3,66) = 2.55, p = 0.063, ${\eta }_p^2=0.094$. Hence, as in the analyses of Experiment 4 reported above, the results of Experiment 4 are somewhat weak, presumably due to the inclusion of the long test delay.

In Experiment 5, we tested participants’ memory for words after pre-familiarization with the words. The results are shown in Figure A1(D). We observed only main effects of condition, F(1,30) = 8.27, p = 0.007, ${\eta }_p^2=0.216$, and of test type, F(1,30) = 33.37, p = .00001, ${\eta }_p^2=0.518$, but no other main effects or interaction. Hence, we did not have sufficient temporal resolution to detect the build-up of PI over the course of the experiment.