Perceptual classification in a rapidly-changing environment

SUMMARY

Humans and monkeys can learn to classify perceptual information in a statistically optimal fashion if the functional groupings remain stable over many hundreds of trials, but little is known about categorisation when the environment changes rapidly. Here, we used a combination of computational modelling and functional neuroimaging to understand how humans classify visual stimuli drawn from categories whose mean and variance jumped unpredictably. Models based on optimal learning (Bayesian model) and a cognitive strategy (working memory model) both explained unique variance in choice, reaction time and brain activity. However, the working memory model was the best predictor of performance in volatile environments, whereas statistically optimal performance emerged in periods of relative stability. Bayesian and working memory models predicted decision-related activity in distinct regions of the prefrontal cortex and midbrain. These findings suggest that perceptual category judgments, like value-guided choices, may be guided by multiple controllers.

INTRODUCTION

The intertwined problems of how agents learn about the environment and decide how to act are of central importance in the behavioural, cognitive and neural sciences. One fundamental question is whether decisions rely on an internal model of the environment, replete with statistical information about the likely causes of outcomes or sensations, or whether they rely on simpler mechanisms, such as learning the value of one action over another (Daw et al., 2005; Glascher et al., 2010; Sutton and Barto, 1998). All decisions are perturbed by multiple sources of uncertainty, but decision-making is most demanding when the environment can change rapidly and without warning. An agent that explicitly encodes higher-order statistical information about the changing stimulation history, such as the transitional probabilities among hidden or observable states (Green et al., 2010), their variability (Preuschoff et al., 2008), and rates of change (Behrens et al., 2007), can tailor decision policy to account for this uncertainty, for example by discounting past rewards more steeply when the world changes faster (Rushworth and Behrens, 2008), or by selecting a sure prospect over an equal-valued but risky one (Christopoulos et al., 2009). Recent research has begun to map the neural structures that represent the changing value of states and stimuli, with a focus on the ventromedial prefrontal cortex (Hampton et al., 2006), and one recent postulate is that related neural circuits, for example in the midbrain or insular cortex, may encode the uncertainty associated with a prospect (e.g. outcome variance, or risk) (Schultz et al., 2008). These findings have bolstered the view that, contrary to classic assumptions in behavioural economics (Kahneman et al., 1982), human voluntary choices are fundamentally rational, and can be described in a probabilistic framework that explicitly represents choice uncertainty in order to maximise favourable outcomes.

Much of this research has employed economic tasks where individuals choose among goods or gambles whose value can jump, drift or reverse unexpectedly (Behrens et al., 2007; Boorman et al., 2009; Daw et al., 2006; Green et al., 2010; Hampton et al., 2006). In these tasks, the stimuli are typically simple and readily discriminable (e.g. coloured squares or symbols), but the choice value (e.g. the conditional probability that an action will be rewarded, given the stimulus, and possibly a hidden state) is uncertain, and has to be computed from the past reward history (outcome uncertainty, or risk). Critically, however, outside of the laboratory, observers additionally have to deal with uncertainty pertaining to the functional groupings (or categories) to which sensory stimuli belong. For example, a foraging animal not only has to update the changing calorific value of a food source throughout the changing seasons (e.g. are nuts good to eat now?), but also has to learn to accurately and efficiently classify items as belong to that food category (e.g. is this is a nut?). An exceptionally rich tradition has investigated the cognitive mechanisms by which perceptual information is detected, discriminated and categorised (Ashby and Maddox, 2005; Swets et al., 1964), and recent neuroscientific research has offered important insights into the brain mechanisms mediating perceptual choice (Freedman and Miller, 2008; Gold and Shadlen, 2007; Li et al., 2009; Seger and Miller, 2010). Behavioural work has emphasised that perceptual classification in humans can mimic that of a rational agent that explicitly encodes not only the category mean (e.g. a prototype) but also the category variability (i.e. uncertainty about class membership). For example, psychophysical detection (Stocker and Simoncelli, 2006), multidimensional discrimination (Ashby and Gott, 1988), multifeature integration (Michel and Jacobs, 2008) and exemplar clustering (Anderson, 1991) can all be described with an ideal observer models, such as signal detection theory (Swets et al., 1964), general recognition theory (Ashby and Townsend, 1986), or with related Bayesian approaches (Anderson, 1991).

Importantly, however, observers in these studies are typically allowed many hundreds of training trials to learn stable and predictable category information. With overtraining, rational models of categorical choice are difficult to distinguish from simpler, habit-based accounts, because highly-trained participants can produce a pattern of choices that resembles optimal responding by associating portions of the decision space with a particular action through extensive stimulus-response learning (Blair and Homa, 2003). Indeed, an influential framework suggests that model-free mechanisms, that capitalise on the extended learning history to assign value to actions, may take precedence in control of action in stable, overlearned environments (Daw et al., 2005; Dickinson and Balleine, 2002). It thus remains unknown (i) whether observers learn about the uncertainty associated with category membership (category variance), and use it to inform their decisions, and (ii) which neural structures might encode category variability. The purpose of the current study was to address these questions.

One important feature of unpredictable, fast-changing environments is that observers are obliged to distinguish between unexpected events that occur because of noise (i.e. an outlier), and those that occur because of a state change in the environment (Yu and Dayan, 2005). For example, a bus might be late because of the vagaries of morning traffic (noise), or because new roadworks have introduced a fundamental delay that should be budgeted for when estimating subsequent journey times (a state change). When economic estimates change rapidly, new learning quickly becomes outdated, and so past category information should be discounted more steeply when choices are made (Nassar et al., 2010; Rushworth and Behrens, 2008). Observers do indeed update their estimates of mean reward rate more rapidly when the environment is more volatile, a computation that has been associated with the anterior cingulate cortex (ACC) (Behrens et al., 2007). Model-based learning about the environment (e.g. explicitly encoding category uncertainty) will be most useful in a volatile world, as it allows observers to distinguish optimally between outliers and those events that herald a change of state. On the other hand, in a volatile environment estimates of category variance will be of limited precision, and expensive to compute. It thus remains unknown whether rational strategies will predominate during periods of environmental stability, or volatility. One efficient way of dealing with a volatile world would be to simply maintain the most recent information about each category in short-term memory - equivalent to updating category values in the frame of reference of the stimulus (rather than action) with a learning rate that equals or approaches one.

In pursuit of the question of how category information is learned, represented, and used to inform classification judgments, thus, we asked participants to classify sequentially occurring stimuli (oriented gratings) drawn from categories whose mean and variability (over angle) changed unpredictably and without warning. Recording brain activity during the task with functional magnetic resonance imaging (fMRI) allowed us to compare observed choices, decision latencies, and brain activity to those predicted by three computational models that embodied different hypotheses about how humans learn about and choose between categories. The first model learned the mean and variance of the categories in an optimal Bayesian framework (Bayesian model), the second model learned the value of action in a given state, i.e. angle (Q-learning model) and the third model simply maintained the most recent category information in memory (working memory model). These models allow us to compare the hypotheses that category judgments in an unpredictable environment are driven by strategies that rely on ‘model-based’ optimal estimation of uncertainty (Bayesian), ‘model-free’ habit learning (Q-learning), or a cognitive strategy based on short-term maintenance (working memory).

We report a number of new findings. Firstly, both the Bayesian and the working memory models encoded unique variance in choice, reaction time (RT) and brain activity, suggesting that participants use a mixture of model-based categorisation strategies. Secondly, participants’ tendency to use a decision policy that incorporated category variance depended on the volatility of the environment, with the Bayesian model approximating human performance more closely in relatively unchanging environments, and neural signatures of choice and learning modulated by category variability only during stable periods; by contrast, the working memory model prevailed when the environment was more volatile. Finally, different strategies were associated with dissociable patterns of decision-related brain activity, with fMRI signals predicted by the Bayesian model observed in the striatum and medial PFC, but brain activity predicted by the working memory strategy activating visual regions, and the dorsal frontal and parietal cortex. Together, these results suggest that participants use cognitive strategies involving the short-term maintenance of information when making decisions in volatile environments, but gradually come to rely on information about category uncertainty to make more optimal choices as learning progresses.

RESULTS

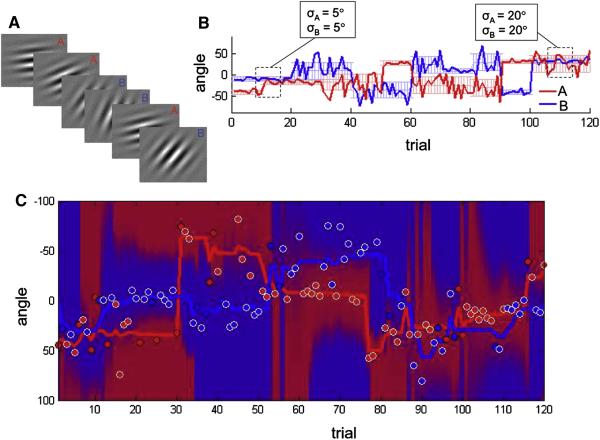
On each of 600 trials, 20 participants viewed an oriented stimulus (full-contrast Gabor patch) that was drawn from one of two categories defined by orientation, with angular means on trial i of ${\widehat{\mu }}_i^a$ and ${\widehat{\mu }}_i^b$ and variances ${\widehat{\sigma }}_i^a$ and ${\widehat{\sigma }}_i^b$ (figure 1a). Subjects received no instructions regarding the categories, but were required to learn about them by trial-and-error, via an auditory feedback tone following each decision epoch of 1500 ms. Generative distributions over angle for the two categories changed unpredictably every 10-20 trials (4 episodes of 10 trials, 4 episodes of 20 trials, randomly intermixed), to a new mean value drawn from a uniform distribution (between −90° and 90°) with a standard deviation of either 5° or 20° (figure 1b). Overall, the task was challenging, with subjects responding correctly on 68.6 ± 3.9% of trials (range 59% to 74%), and overall mean reaction times (RTs) of 697 ± 131 ms. Subjects failed to respond within the deadline on an average of 9.6 ± 4.1 (range 5-22) trials, and these trials were excluded from all further analyses.

Figure 1.

A. Participants viewed a succession of oriented stimuli (Gabor patches) and responded to each with a button press. Stimuli were drawn from one of two categories, A or B (red/blue labels in A not shown to participants). B. Category values for an example block (120 trials), for categories A (red line) and B (blue line). Underlying lighter bars show the generative mean and variance for each category. Dashed boxes highlight periods of common or differing category variance. C. Circles show angular values of stimuli presented in an example block (red circles, A; blue circles, B). White-ringed circles were responded to correctly by this subject; black-ringed circles provoked an error. Red and blue lines show the category mean estimated by the Bayesian model. Red/blue background shading indicates the choice probability landscape across angle,with more red shading indicating angles for which A was the better choice, and blue shading favouring the response B, according to the Bayesian model.

We built three competing computational models of categorical choice and compared them to subjects’ behavioural performance. (1) The Bayesian model learned trial-by-trial means and variances of each category, and their rates of change, in an optimal Bayesian framework. On each successive trial, the model updated a probability space defined by the possible (angular) values of ${\widehat{\mu }}_i^a$, ${\widehat{\sigma }}_i^a$, ${\widehat{\mu }}_i^b$ and ${\widehat{\sigma }}_i^b$ as well as their respective rates of change, and marginalised over the space to estimate current ‘best-guess’ category means and variances of A and B. Choice values reflected the relative likelihood of A and B given current stimulus angle Y_i:

$$p\left(A\right)=\frac{p(Y_i\mid {\widehat{\mu }}_i^a,{\widehat{\sigma }}_i^a)}{p(Y_i\mid {\widehat{\mu }}_i^a,{\widehat{\sigma }}_i^a)+p(Y_i\mid {\widehat{\mu }}_i^b,{\widehat{\sigma }}_i^b)}$$ (1)

(2) The Q-learning model learned the value of choices A and B given the state (stimulus angle), with a single learning rate as a free parameter; choice probability values were calculated as the relative value of responding A vs. B:

$$p\left(A\right)=\frac{Q(s,a)}{Q(s,a)+Q(s,b)}$$ (2)

The learning rate was set to be the best-fitting value across the cohort, α=0.8; in theory, this extra free parameter gave the Q-learning (QL) model an advantage, but in practice it was the poorest-performing of the three models. (3) The working memory model updated the category means ${\widehat{\mu }}_i^a$ and ${\widehat{\mu }}_i^b$ using a delta-rule with a learning rate of 1, i.e. resetting category means on the basis of the most recently viewed category member. Choice probabilities reflected the relative distance of the stimulus to these current estimates of A and B:

$$p\left(A\right)=\frac{\mid Y_{\mathrm{i}+1}-{\widehat{\mu }}_i^a\mid }{\mid Y_{\mathrm{i}+1}-{\widehat{\mu }}_i^a\mid +\mid Y_{\mathrm{i}+1}-{\widehat{\mu }}_i^b\mid }$$ (3)

For simplicity, we refer to these values as p(A) i.e. the probability of choosing A over B. Full details of the models are provided in the Materials and Methods section below.

Predicting choice

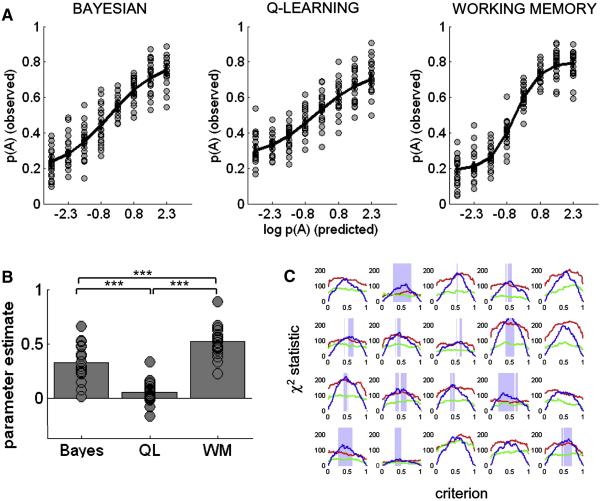
We estimated choice values p(A) under each model for successive stimuli in the trial sequence. Trials were sorted into bins according to their value of p(A), and observed mean choice probability was calculated for each bin (figure 2a). To quantify which model was the best predictor of observed choice data, we used multiple regression; parameter estimates are shown in figure 2b. Entering all three models together into the regression, each explained some unique variance in choice behaviour (Bayesian model: t₍₁₉₎ = 8.77, p < 1 × 10⁻⁷; QL model t₍₁₉₎ = 2.4, p < 0.02; working memory model: t₍₁₉₎ = 16.6, p < 1 × 10⁻¹²). However, across the subject cohort, the working memory model was a reliably better predictor than the Bayesian model (t₍₁₉₎ = 4.07, p < 1 × 10⁻³) or the Q-learning model (t₍₁₉₎ = 10.2, p < 1 × 10⁻⁸). To interrogate the data further, we fit a decision criterion c (0.01 < c < 0.99) to the choice probability values under each model, and compared the resulting binary trial classification (model choices) to human choices. Resulting χ² values for each model across values of c are shown for individual subjects in figure 2c. Comparing models under best-fitting values of c, the working memory model again out-performed the Bayesian (t₍₁₉₎ = 2.69, p <0.05) and the Q-learning models (t₍₁₉₎ = 2.87, p <0.01) in pair-wise comparison at the group level.

Figure 2.

A. The probability of choosing category A plotted as a function of the log of p(A) calculated by the Bayesian (left panel), Q-learning (middle panel) and working memory (right panel) models. Grey circles show data from individual participants; the black line shows the best-fitting 4-parameter sigmoidal function. B. Parameter estimates from the probit binomial regression of model-derived estimates of choice probability [p(A)] on human observers’ actual choices, for the three models (QL = Q-learning model, WM = working memory model). Grey circles show data from individual participants. Stars indicate that comparisons among regressors are all significant at p<0.001. C. Lines show χ² values for each model (red = Bayes, green = QL, red = WM) reflecting the overlap between participants choices and model choices. Model choices were calculated by applying a criterion (0.01 < c < 0.99) on p(A) values (x-axis). Each plot is an individual participant. Blue shading shows criterion values for which the WM model is more successful than the other two models.

The task was structured such that the true category statistics jumped every 10 or 20 trials. We wanted to determine whether participants learned this periodic jump structure, because if so, this could have disadvantaged the Bayesian model, which has no way of inferring the periodic structure of the task. Our approach was twofold. First, we asked whether learning rates (fit by a simple delta rule) differed for the first 8 trials following switch (when an observer with full knowledge of the 10-trial cycle should not learn any new information), relative to trials 9-13 following a switch. In fact, participants learned faster immediately following a switch (t₍₁₉₎ = 3.15, p < 0.004) – behaviour that is well captured by the working memory model, but which would could not be approximated with a variant of the Bayesian model that optimally inferred the cyclic task structure. Secondly, we compared learning rates for different phases of a 10-trial harmonic across each run (i.e. trials 3-7, 13-17, 23-27… etc. vs. trials 1-2, 8-12,18-22…, irrespective of when jumps occurred). These revealed almost identical learning rates (0.73 vs. 0.69, t₍₁₉₎ < 1). If participants had been explicitly using knowledge about the structure of the sequence (to which the current Bayesian model has no access), then we would expect them to learn faster in period where jumps were more probable. Together, these two results strongly suggest that participants do not learn the periodic structure of the task, and that the Bayesian model is not unfairly disadvantaged by being blind to the 10-20 trial jump cycle. In fact, because the Bayesian model outperforms the human participants, and a model with perfect knowledge of the jumps would perform even better, so that it would approximate human behaviour yet more poorly.

Predicting RT

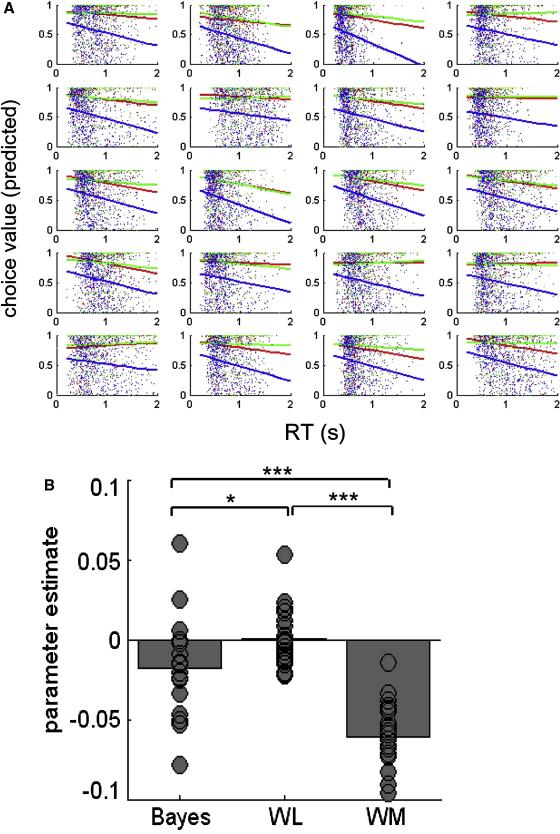
We converted choice probability values into a quantity that scales with the probability of making a correct response (methods) and correlated these choice values with trial-by-trial RT values for each participant (figure 3a). Slopes were more negative for the working memory model than the Bayesian (t₍₁₉₎ = 11.2, p < 1 × 10⁻⁹) and QL models (t₍₁₉₎ = 15.9, p < 1 × 10⁻¹²), suggesting that choice values from the working memory model captured the most variability in RT (indeed, the slope for the QL model did not deviate significantly from zero: p = 0.48). This was confirmed by regression analysis (figure 3b), which revealed parameter estimates for the working memory model that were significantly more negative than for both competing models (Bayesian model, t₍₁₉₎ = 5.76, p < 1 × 10⁻⁵ ; QL model, t₍₁₉₎ = 8.81, p < 1 × 10⁻⁷).

Figure 3.

A. Scatter plots of choice values against reaction time (RT) in seconds for individual participants, with best fitting linear trend lines for the Bayesian (red), Q-learning (green) and working memory (blue) models. B. Parameter estimates for the regression of choice values on RT for the three models. Grey circles are individual participants. More negative values indicate a better prediction of RT, i.e. when choice values are closer to 1, RT is faster. Stars indicate the significance of the comparison between betas: *p < 0.05, *** p < 0.001.

Predicting decision-related fMRI activity: expected value

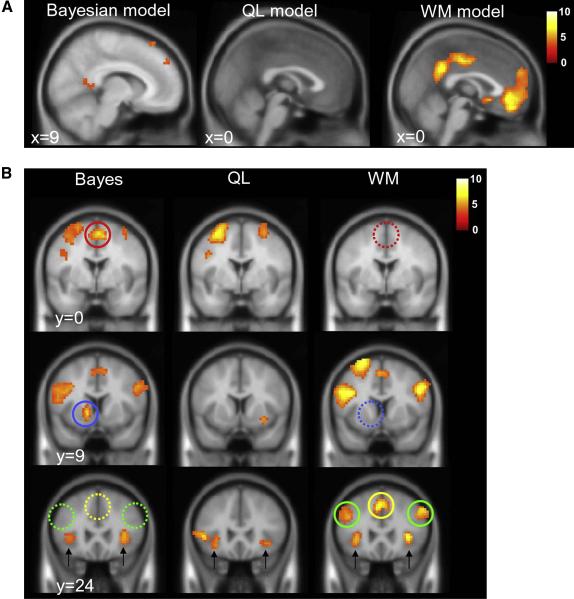
Subsequently, we used the three models to generate trial-by-trial predictions about the BOLD response, by modelling fMRI data with parametric regressors scaled by predicted choice values from each model. Again, we included predictions from all three models in a single design matrix, allowing them to compete for variance in brain activity at each voxel across the brain during the decision epoch (figure 4a and table S1). Our results thus reflect the unique contribution of each model to fMRI signals (the common contribution is shown in supplemental materials, figure S1). Because estimated choice values reflect the probability that positive feedback will be obtained, we focussed our initial analyses on brain regions known to respond to positive outcomes, such as the ventromedial prefrontal cortex (vmPFC), and the posterior cingulate cortex (PCC) (Rushworth et al., 2009). Activity in both of these regions was predicted by the working memory model (PCC: 9, −51, 27; t₍₁₉₎ = 9.15, p < 1 × 10⁻⁸; vmPFC, 6, 45, −18, t₍₁₉₎ = 7.87, p < 1 × 10⁻⁶), and more modestly by the Bayesian model (PCC: 9, −57, 15, t₍₁₉₎ = 4.02, p < 0.001, vmPFC: 12, 60, 0, t₍₁₉₎ = 3.51, p < 0.002). No such prediction was observed for the QL model.

Figure 4.

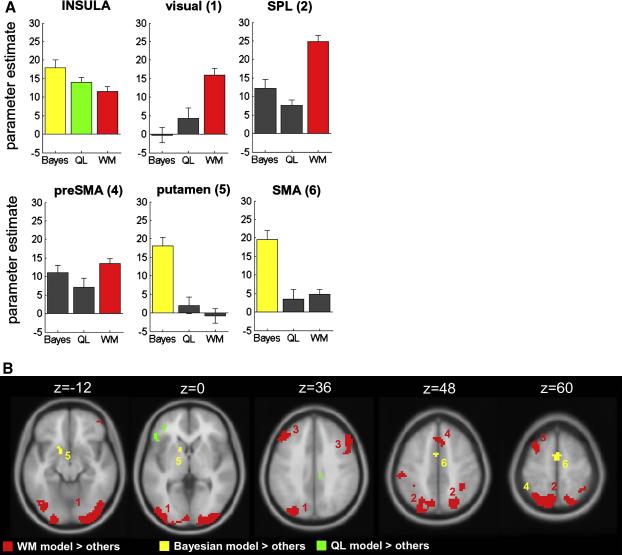
A. Voxels for which BOLD signals are stronger when choice values from the Bayesian (left panel), QL (middle panel) and WM (right panel) models are higher (i.e. when the probability of a correct response is greater) rendered at a threshold of p < 0.001 onto a template brain (saggital slice). B. Voxels for which BOLD signals are stronger when choice values from the three models are lower (e.g. when p(A) is closest to 0.5, the probability of correct is lowest, and decision entropy is highest), shown on three coronal slices. Full coloured circles highlight clusters that are specific to either the Bayesian or WM models; dashed models signal the absence of the corresponding cluster for the other model (red, SMA; blue, striatum; green, anterior dorsolateral PFC; yellow, pre-SMA). Black arrows highlight activation in the anterior insula, which was present in all three condition (see also figure 5a). In both A and B, the red-white render scale indicates the t value at each voxel.

Predicting decision-related fMRI activity: decision entropy

The inverse contrast identified voxels that correlated with the entropy (or conflict) associated with the decision, i.e. how close the probability of a choosing A over B was to chance (p = 0.5) under each model (figures 4-5 and table S2). We modelled the predictions of each model with a unique parametric regressor and entered these simultaneously into the design matrix, allowing the identification of voxels that responded (i) to the predictions of all three models (shown in figure 4), and (ii) to predictions of one model alone. We defined the latter as voxels where t-values were positive-going for decision entropy, and exceeded those for the other two models by at least 3.09 (p < 0.001) in both cases (shown in figure 5). These analyses offer complementary information: the former identifies voxels that correlate with each model for a given threshold, and the latter identifies voxels that differ in their degree of correlation with each model (although this analysis is limited by the extent to which regressors are correlated). Firstly, we found that decision-related BOLD signals in the anterior insular cortex were robustly predicted by all three models (figure 4b and 5a). Secondly, activity predicted by the working memory model, but not the other models, was mainly observed in the extrastriate visual cortex (peak: −21, −96, −9, t₍₁₉₎ = 9.29, p < 1 × 10⁻⁸), including the superior occipital lobe (peak: −30, −81, 33, t₍₁₉₎ = 8.01, p < 1 × 10⁻⁷), as well as dorsal fronto-parietal sites such as the superior parietal lobule (peak: 24, −69, 54, t₍₁₉₎ = 15.09, p < 1 × 10⁻¹¹) dorsolateral prefrontal cortex (peak: −48, 6, 30, t₍₁₉₎ = 7.97, p < 1 × 10⁻⁷), and pre-SMA (peak: 6, 15, 48, t₍₁₉₎ = 7.17, p < 1 × 10⁻⁶).

Figure 5.

A. Mean parameter estimates for the correlation with decision entropy predicted by the Bayesian (left panel), Q-learning (middle panel) and working memory (right panel) models, averaged over voxels falling within independent regions of interest. Bars are coloured when parameter estimates are significantly greater than zero at a threshold of p < 0.001. Numbers in the titles correspond to clusters shown in B. B. Voxels that correlate with decision entropy for the Bayesian model alone (yellow), the QL model alone (green) and the WM model alone (red), rendered onto axial slices of a template brain. Voxels were deemed to respond to one model alone if the voxel was positive-going for decision entropy, and the relevant t-value was greater than that for the other two models by at least 3.29 (p < 0.001). Numbers refer to brain regions referred to in the text: 1, extrastriate visual regions; 2, superior parietal lobule; 3, dorsolateral prefrontal cortex; 4, pre-SMA; 5, striatum; 6, SMA.

The Bayesian model was also associated with unique patterns of brain activity, but these fell in the left striatum (peak: −12, 9, −3, t₍₁₉₎ = 6.09, p < 1 × 10⁻⁵), and the supplementary motor area (SMA) (peak: 3, 0, 57, t₍₁₉₎ = 6.26, p < 1 × 10⁻⁵). The SMA cluster fell immediately caudal to the pre-SMA cluster identified by the working memory model; the juxtaposition of the two clusters is shown in supplementary materials. Finally, activity in the left ventrolateral prefrontal cortex (peak: −48, 24, 3, t₍₁₉₎ = 6.45, p < 1 × 10⁻⁵) was uniquely predicted by the QL model. These results are shown in detail in figures 4 and 5.

Correlation with volatility

We reasoned that participants’ tendency to employ the simple working memory strategy rather than higher-order model-based strategies might depend on the volatility in the environment. One possibility is that participants use information about the variance of the categories only when the environment is stable and predictable, when more resources are available for computationally intensive decision strategies. Alternatively, probabilistic information might be deployed when it is most useful, i.e. in volatile environments, where the category means are changing fast, and there is more ambiguity about whether unexpected events are outliers, or reflect a change in the generative mean. We arbitrated among these possibilities using the behavioural data by estimating trial-by-trial errors in the fit of each model to choice data, and correlating this with the estimated volatility of the sequence (methods). Statistically reliable positive correlations were observed for the Bayesian (t₍₁₉₎ = 3.13, p < 0.003) and QL (t₍₁₉₎ = 2.46, p < 0.02) models, suggesting that these models fit the observed data better [lower residual error] when volatility was low. No such correlation was observed for the working memory model (p = 0.58). In a further analysis, we separated trials into quartiles on the basis of the estimated volatility, and re-ran the regression analysis separately for the 25% most volatile and 25% least volatile trials. The advantage for the WM model over the Bayesian model on high volatile trials (t₍₁₉₎ = 3.81, p < 0.001) was eliminated on low volatile trials (p = 0.34). In other words, observers were more likely to base their decisions on information about the category variance when the trial sequence was stable than when it was volatile.

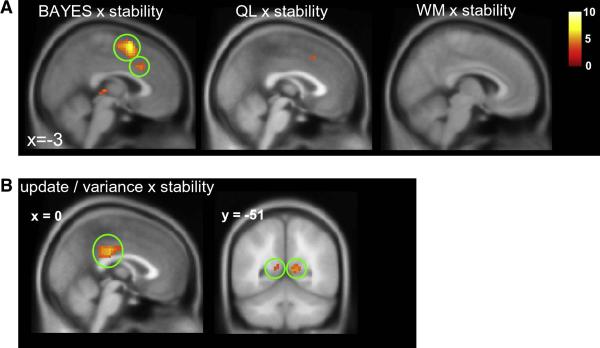
This finding prompted us to search for voxels where fMRI signals correlated better with Bayesian or QL estimates of decision entropy under low than high volatility. We identified voxels in the SMA and anterior cingulate cortex that displayed such a pattern for estimates of decision entropy predicted by the Bayesian model (ACC peak: 3, 21, 33, t₍₁₉₎ = 4.54, p < 0.001; SMA peak: 0, 9, 60, t₍₁₉₎ = 4.54, p < 1 × 10⁻⁶) as well as a small cluster in the ACC for the interaction between volatility and entropy predicted by the QL model (peak: 3, 15, 45, t₍₁₉₎ = 3.96, p < 0.001). No such voxels were identified for the working memory model. These results are shown in figure 6a and table S3. This finding at the time of the decision is complementary to, but does not contradict, the previous finding that ACC signals scale with increasing volatility at the time of the outcome.

Figure 6.

A. Voxels responding to the interaction between decision entropy and volatility, i.e. voxels that predict decision-related activity more successfully when the environments is stable than volatile, for the Bayesian, QL and WM models. Green rings encircle the SMA and ACC. B. Voxels responding to the three-way interaction of update, category variance, and volatility, in the posterior cingulate cortex and retrosplenial cortex. For A and B, activations are rendered onto a template brain, and the red-white scale indicates the t-value associated with each voxel.

fMRI signals for category updating

The above analysis of behavioural and brain imaging data at the time of the decision suggests that observers display a greater tendency to use optimal decision strategies when the environment is more stable. This led us to ask whether neural signals reflecting updating of information at the time of feedback are modulated by variance and volatility. In our task, an observer should update his or her beliefs about the categories on the basis of the angular disparity between the stimulus presented and the current estimate of the mean of the category from which that stimulus was drawn. For example, if an observer who estimates the mean of category A to be 45° responds B to a stimulus presented at 90° and receives negative feedback, that observer will probably want to substantially revise his or her beliefs about category A. However, an observer who is using a statistical decision strategy will revise this estimate more when category variance is low than high (Preuschoff and Bossaerts, 2007). We thus searched for voxels that reflected the angular updating signal normalised by its variance under low, but not high, volatility.

Accordingly, when we constructed predictors that encoded these three factors and their two- and three-way interactions (methods), along with regressors encoding the main effect of stimulus, feedback, and reward. These were then regressed against brain activity at the time of feedback. The results are shown in figure 6b and table S4. Critically, a three-way interaction between these factors was observed in the posterior portion of the cingulate gyrus (peak: 3, −30, 27; t₍₁₉₎ = 6.03, p < 1 × 10⁻⁵) extending into the posterior cingulate on the right (peak: 12, −54, 9; t₍₁₉₎ = 5.15, p < 1 × 10⁻⁴) and left (peak: −15, −48, 6; t₍₁₉₎ = 4.76, p < 1 × 10⁻⁴), as well as the supplementary motor area (peak: 6, 9, 63; t₍₁₉₎ = 5.57 p < 1 × 10⁻⁴). Moreover, when we tested for significance within an a priori region of interest centred on the dorsal ACC region previously found to respond to scale prediction errors by volatility (Behrens et al., 2007), we found an additional cluster (peak: 3, 30, 18; t₍₁₉₎ = 2.98, p < 0.004).

DISCUSSION

We asked healthy human participants to classify visual stimuli in a rapidly-changing environment, with a view to describing the computational strategies they use to learn about, and choose between, perceptual categories. Our analyses compared three models: the Bayesian model learned the statistics of the environment (e.g. the mean and variance of category information), the Q-learning model learned the value of actions, and the working memory model simply stored the last piece of information learned about each of the categories, and used that as a benchmark for future choices. These models embody different strategies that observers could use during categorisation, strategies that differ in terms of what is encoded (first-order, or higher-order information about the categories), and the rate at which past information is devalued (immediately, in the working memory model; or according to environmental volatility, in the Bayesian model). Surprisingly, we found that the simple, ‘working memory’ model was the best predictor of choice, RT, and brain activity across the experiment. This suggests that in our task, human participants favour a fast and frugal categorisation strategy that does not overly tax systems for storage and processing of decision-relevant information. Indeed, the working memory model was many orders of magnitude more economical than the Bayesian model. For example, where n is the sampling resolution of the decision space (over angle), our computer based-implementation of the working memory model demanded the storage of 2n bits of information per trial, compared to 2n⁴ bits for the Bayesian model (although of course these values may not reflect the true neural cost of each model).

Our fMRI analyses also identified specific neural circuits associated with this simple, memory-based decision strategy. For example, working memory model was the best predictor of decision-related activity in a dorsal fronto-parietal network previously implicated in working memory maintenance (D’Esposito, 2007; Wager et al., 2004), and superior occipital regions implicated in storing iconic traces in visual short-term memory (Xu and Chun, 2006). Together, these data points reveal that a simple, memory-based process can be used to solve a seemingly complex and challenging categorisation problem, and suggest that visual and fronto-parietal regions are engaged to do so.

However, we know that participants did not rely exclusively on this cognitive strategy to make categorical choices, because the other models – in particular, the Bayesian model – explained unique variance in choice, RT and BOLD activity. In other words, participants switched between different strategies for categorisation, and in the process, preferentially activated distinct brain regions. The dissociable patterns of voxels that were observed to correlate with decision entropy under each model offer clues to the strategies involved. For example, in the medial and lateral prefrontal cortex (PFC), decision-related brain activity predicted by the WM model fell systematically more anterior to that predicted by the Bayesian model, activating rostral regions of the lateral PFC (BA 9/46) that are typically recruited when decision-relevant information has to be maintained in the face of distraction over a prolonged behavioural episode (Koechlin et al., 2003; Sakai et al., 2002). By contrast, both models were associated with decision-related activity in middorsolateral PFC regions falling at the intersection of BA 8 and 44 (the ‘inferior frontal junction’) (Brass et al., 2005), where activity tends to reflect the demand of selection, conditioned on the context (Koechlin and Summerfield, 2007), and from where category-related information can be decoded independent of physical input (Li et al., 2009). Similarly, in the medial PFC, the Bayesian model predicted decision-related activity in the SMA, and the WM model in the pre-SMA. Although the relative functional significance of the SMA and pre-SMA remains controversial (Nachev et al., 2008), one possibility is that there exists a rostro-caudal gradient in the medial PFC, by which more anterior regions responding more vigorously when decisions are based on motivational information that is more conditionally complex (Badre and D’Esposito, 2009; Nachev et al., 2009), or that arose further in the past (Kouneiher et al., 2009; Summerfield and Koechlin, 2010). One interpretation of these findings is that cognitive strategies for categorisation in a volatile environment involve maintaining recent exemplar-based representations active across several intervening trials at the expense of their competitors, and thus recruit PFC structures known to support cognitive and motivational control across a discrete behavioural episode.

By contrast, when decisions are made without the benefit of explicit working memory information, but based on approximations of the mean and variance of the categories, recruit more posterior zones within the PFC, as well as the striatum. The latter finding is surprising from the perspective of theories that have emphasised a role for the basal ganglia in habit learning (Daw et al., 2005; Dickinson and Balleine, 2002), but squares well with the finding that the risk associated with an economic prospect (i.e. the variance of the outcome) scales with signals in both caudate and putamen (Preuschoff et al., 2006; Schultz et al., 2008). Indeed, dopaminoceptive neurons of the striatum are known to encode uncertainty associated with an economic decision, in addition to its value (Bunzeck et al., 2010; Fiorillo et al., 2003; Tobler et al., 2007); our results imply that this may extend to situations where the uncertainty pertains to the category of the stimulus. Finally, the Q-learning model activated preferentially the left ventrolateral prefrontal cortex, in tune with a substantial literature implicating this region in stimulus-response learning (Toni et al., 2001).

Our analysis of the interaction between model fits and environmental stability/volatility offered insight into the factors that prompt participants to switch between memory-based and higher-order learning strategies for categorical choice. Specifically, the Bayesian model (but not the working memory model) fit the choice data better when the environmental volatility is low, as if participants gradually acquired information about category variances. In our task, ‘stable’ environments consisted of runs of 20-30 trials in which the category mean remained constant – a far shorter training interval than the hundreds or even thousands of trials offered in many categorisation or sensorimotor tasks (Ashby and Gott, 1988; Kording and Wolpert, 2004). It is thus perhaps unsurprising that overall, the working memory model provided a better fit to human choices than an ideal observer model. However, our data chart clearly the emergence of optimal decision-making as observers are offered a chance to become familiar with the category statistics.

This notion was also supported by fMRI analyses, which identified voxels that responded to the interaction between volatility and decision entropy predicted by the Bayesian model in the anterior cingulate cortex (ACC). One interpretation of these data is that the ACC contributes to choices that are informed by information about the rate of change of the environment, in line with previous lesion (Kennerley et al., 2006) and fMRI (Behrens et al., 2007) work implicating this region in making optimal use of past reward history to inform decisions. Analysis of brain activity at the time of the feedback also supported this contention. Using an ROI-based analysis, we found that the ACC region activated in concert with environmental volatility at the time of feedback in (Behrens et al., 2007) was sensitive to ‘optimal updating’ signals defined by the three-way interaction between angular update, estimated variability, and volatility. One interpretation consistent with previous work is that at outcome time the volatility of the environment is encoded in the ACC in a fashion that dictates the extent that subjects will learn from each outcome (Behrens et al., 2007), in the decision period, ACC activity is only modulated by the optimal level of uncertainty at times when subjects employ this optimal strategy (in this task, when the environment is stable). We additionally found strong optimal updating signals at the time of feedback in the posterior cingulate gyrus, a brain region implicated in the representation of uncertainty about rewards (McCoy and Platt, 2005), and in the choice to make exploratory decisions (Pearson et al., 2009) in the non-human primate.

Admittedly our current data do not indicate the mechanism by which, or the cortical locus at which, participants switch between strategies. Indeed, one possible candidate is the anterior insular cortex, where decision-related fMRI signals were predicted by all three strategies, and which has been previously implicated in controlling the switch between behavioural modes (Sridharan et al., 2008). However, this remains a topic for future investigation.

Together, our findings suggest that participants adapt their decision strategy to the demands of the environment, moving towards statistically optimal behaviour when the environment permits learning about stable and predictable categories (Nisbett et al., 1983). By contrast, in volatile environment agents adopt a cognitive strategy that is fast and computationally frugal, and relies on maintainence processes subserved by the prefrontal cortex.

EXPERIMENTAL PROCEDURES

Subjects

Twenty healthy participants aged between 18 and 37 with no history of psychiatric or neurological disorder, and normal or corrected-to-normal vision, participated in the experiment. Participants were paid ~80 Euros for their participation.

Procedure

In each of 5 scanning sessions of ~8 minutes each, subjects viewed 120 successive, full-contrast Gabor patches that were oriented at between −90° and 90° degrees relative to the vertical meridian. Each stimulus was visible for 1500 ms, during which period subjects were required to make a categorization judgement by pressing the right or left button on the response pad. Auditory feedback consisted of an ascending (400/800 Hz) or descending (800/400 Hz) tone of 200 ms, and followed stimulus onset by a variable interval in the range of 3-7 seconds. On 25% of trials, correct or incorrect feedback engendered a small monetary gain or loss, which was totalled up and supplemented subjects’ compensation (range 20 to 30 Euros). An interstimulus interval of x intervened between feedback and the subsequent stimulus. Stimuli were drawn randomly from category A (60 trials) or B (60 trials) with no constraints, and response-category assignments were counterbalanced across subjects. Category means and variances were unstable and independent, and jumped unpredictably every 10 or 20 trials (4 episodes of 10 trials, 4 episodes of 20 trials, randomly intermixed) to a new mean drawn from a uniform random distribution with a variance of either 5° or 20°.

Modelling

Values representing the probability of choosing category A over B under the Bayesian model were estimated using a hierarchical Bayesian learner that calculates best-guess estimates of the generative mean and variance of each category in a Markovian fashion. For each category, a generative model of the observations is assumed as follows (see supplementary info of Behrens et al. 2007 a more extensive description of a related model): At each trial i, after the true category has been revealed the probability of observing the orientation i, given any possible mean and variance may be written:

$$p(Y_i\mid {\mu }_i,{\sigma }_i)\sim N({\mu }_i,{\sigma }_i)$$ (4)

Hence each new data point contains information about the underlying mean and variance. However, the mean and variance are constant over runs of trials before jumps, or change-points occur. Hence the prior distribution, conditional on the previous trial, may be written as follows:

$$p({\mu }_i,\mid {\mu }_{i-1},J_i)=\{\begin{array}{cc}\delta ({\mu }_i-{\mu }_{i-1})\hfill & J_i=0\hfill \\ U(0,180)\hfill & J_i=1\hfill \end{array}$$ (5)

This equation states that the underlying category mean at trial i will be the same as that at trial i-1 if there has not been a jump (J=0), or could take on any value if there has been a jump (J=1). A similar equation may be written to describe the dynamics of σ, which varied in a log space.

$$p({\sigma }_i,\mid {\sigma }_{i-1},J_i)=\{\begin{array}{cc}\delta ({\sigma }_i-{\sigma }_{i-1})\hfill & J_i=0\hfill \\ U(2,40)\hfill & J_i=1\hfill \end{array}$$ (6)

Jumps J occur at random with probability v, termed the volatility.

$$p\left(J_i\right)=\nu$$ (7)

This allows us to marginalise over J to rewrite the conditional priors:

$$p({\mu }_i\mid {\mu }_{i-1},\nu )=(1-\nu )\delta ({\mu }_i-{\mu }_{i-1})+\nu U(0,180)$$ (8)

$$p({\sigma }_i\mid {\sigma }_{i-1},\nu )=(1-\nu )\delta ({\sigma }_i-{\sigma }_{i-1})+\nu U(2,40)$$ (9)

This generative model may then be inverted at each trial using Bayes’ rule, with the posterior distribution from the previous trial acting as the prior for the current trial (See Behrens et al. 2007 for a formal proof):

First compute the joint distribution over μ and σ parametered from trials i and i-1

$$p({\mu }_i,{\mu }_{i-1},{\sigma }_i,{\sigma }_{i-1},\nu \mid Y_{1:i-1})=p({\mu }_i\mid {\mu }_{i-1},\nu )p({\sigma }_i\mid {\sigma }_{i-1},\nu )p({\mu }_{i-1},{\sigma }_{i-1},\nu \mid Y_{1:i-1})$$ (10)

Where this last distribution p(μ_i−1,σ_i−1,ν∣Y_1:i−1) is the posterior distribution taken from the previous trial.

Next marginalise over the parameters from the previous trial:

$$p({\mu }_i,{\sigma }_i,\nu \mid Y_{1:i-1})=\iint p({\mu }_i,{\mu }_{i-1},{\sigma }_i,{\sigma }_{i-1},\nu \mid Y_{1:i-1})d{\mu }_{i-1}d{\sigma }_{i-1}$$ (11)

Lastly incorporate the new information from the current observed angle:

$$p({\mu }_i,{\sigma }_i,\nu \mid Y_{1:i})=\frac{p(Y_i\mid {\mu }_i,{\sigma }_i)p({\mu }_i,{\sigma }_i,\nu \mid Y_{1:i-1})}{\int \int \int p(Y_i\mid {\mu }_i,{\sigma }_i)p({\mu }_i,{\sigma }_i,\nu \mid Y_{1:i-1})d{\mu }_{i}d{\sigma }_{i}d\nu }$$ (12)

All integrals are performed using numerical grid integration.

Under the Bayesian model, choice probability values were estimated by comparing the expected probability that the stimulus Y was drawn from distributions A and B

$$p\left(A\right)=\frac{p(Y_i\mid {\widehat{\mu }}_i^a,{\widehat{\sigma }}_i^a)}{p(Y_i\mid {\widehat{\mu }}_i^a,{\widehat{\sigma }}_i^a)+p(Y_i\mid {\widehat{\mu }}_i^b,{\widehat{\sigma }}_i^b)}$$ (13)

The Q-learning model learned the value of state-action pairings as previously described (Watkins and Dayan, 1992), where R is the feedback [correct = 1, incorrect = 0] and t is trial.

$$Q(s_{i+1},a_{i+1})=Q(s_i,a_i)+\alpha \times [R-Q(s_i,a_i\left)\right]$$ (14)

Under this formulation, states (n=18) reflect the angle of orientation of the stimulus in bins of 10 degrees, i.e.

$$s_i=\lceil Y_i∕10\rceil$$ (15)

The choice rule was then simply

$$p\left(A\right)=\frac{Q(s,a)}{Q(s,a)+Q(s,b)}$$ (16)

The working memory model simply updated a single value for A and B whenever new information was received, i.e. where feedback indicated that a stimulus Y was from the category A

$${\widehat{u}}_i^a=Y_i$$

Allowing choice probability values to be calculated for the subsequent trial i+1 as

$$p\left(A\right)=\frac{\mid Y_{i+1}-{\widehat{\mu }}_i^a\mid }{\mid Y_{i+1}-{\widehat{\mu }}_i^a\mid +\mid Y_{i+1}-{\widehat{\mu }}_i^b\mid }$$ (17)

The values calculated in the equations above are in the space of A vs. B, i.e. p(A) > 0.5 predicts that the subject should choose A, and p(A) < 0 predicts that B should be chosen. These values were used for behavioural analyses concerned with predicting choice. For RT analyses, and for all fMRI analyses, however, we calculated an absolute choice value estimate for each trial, directly related to the likelihood of being correct:

$$\text{choice value}=2\times \mid p\left(\mathrm{A}\right)-0.5\mid$$

Here, choice value = 0 means each option is equally valued, e.g. p(correct) =0.5. We used choice values because we had no reason to believe that subjects would be faster, or the brain more active, when the subject chose A over B.

fMRI data acquisition

Magnetic resonance images were acquired with a Siemens (Erlangen, Germany) Allegra 3.0T scanner to acquire gradient echo T2*-weighted echo-planar images with blood oxygenation level-dependent contrast as an index of local increases in synaptic activity. The image parameters used were as follows: matrix size, 64 × 64; voxel size, 3 × 3 mm; echo time, 40 ms; repetition time, 2000 ms. A functional image volume comprised 32 contiguous slices of 3 mm thickness (with a 1 mm interslice gap), which ensured that the whole brain was within the field of view.

fMRI data preprocessing

Data were preprocessed using SPM2 (Wellcome Department of Cognitive Neurology, London). Following correction for head motion and slice acquisition timing, functional data were spatially normalized to a standard template brain. Images were resampled to 5-mm cubic voxels and spatially smoothed with a 10-mm full-width at half maximum isotropic Gaussian kernel. A 256 s temporal high-pass filter was applied in order to exclude low-frequency artifacts. Temporal correlations were estimated using restricted maximum likelihood estimates of variance components using a first-order autoregressive model. The resulting non-sphericity was used to form maximum likelihood estimates of the activations.

fMRI statistical analysis

Data were analysed in a modified version of SPM2. By default, SPM2 orthogonalises each parametric regressor in turn with respect to those already entered; we ensured that no orthogonalisation was used in any analysis. We analysed our fMRI data via two design matrices. In the first, we entered (1) the main effect of stimulus presentation; (2-4) parametric regressors for choice value predicted by the Bayesian, QL, and working memory models; (5) the main effect of volatility; (6-8) the interaction between volatility and choice value for the three models; (9) the main effect of feedback; (10) a parametric regressor encoding the valence of the feedback; (11-13) parametric regressors encoding prediction error signals predicted by the Bayesian, QL and working memory models; (14) a nuisance regressor encoding the mean fMRI signal from 1000 randomly selected voxels from outside the brain; (15-20) nuisance regressors encoding realignment parameters (see figure S2 for an example design matrix). Analyses described in figures 3 (expected value/decision entropy) pertain to regressors 2-4 (note that decision entropy = 1-choice value); analyses described in figures 4 (interaction with volatility) pertain to regressors 5-8. Note that main effects of decision- and feedback-related activity for each model, and their interaction with volatility, are all entered simultaneously into this design matrix and so the results described reflect unique variance associated with each of these predictors. Results for the common variance can be seen in supplemental materials (figure S1).

For the second design matrix, we entered (1) the main effect of stimulus, (2) the main effect of reward, (3) the log of the main effect of volatility log(V_A) (4) where the out come revealed the stimulus to be from category A, the absolute angular difference between the current mean of that category and the stimulus ${\widehat{\mu }}_i^a-Y_i$; (5) this difference divided by the standard deviation of category A $\frac{{\widehat{\mu }}_i^a-Y_i}{\sqrt{{\widehat{\sigma }}_i^a}}$; (6) This value multiplied by the log volatility $\frac{({\widehat{\mu }}_i^a-Y_i)\times \ln \left({\nu }_i^a\right)}{\sqrt{{\widehat{\sigma }}_i^a}}$ Analyses described in figure 5b (optimal updating) pertain to .

Our analysis strategy was as follows. (1) we calculated whole-brain SPMs corresponding to the relevant contrasts, reporting voxels that survive p < 0.001 uncorrected. We report clusters where the peak exceeded at least p < 0.0001 uncorrected, except in two cases: (i) that of the volatility × decision entropy interactions in the anterior cingulate cortex, where we relaxed the threshold to p < 0.001, on the basis of strong a priori predictions that optimal updating signals would be observed there (Behrens et al., 2007; Kennerley et al., 2006), and (ii) that of the correlation of brain activity with choice value predicted by the Bayesian model, where marginal [p < 0.001/0.002 uncorrected] signals were observed in a priori predicted regions [PCC and vmPFC]. Full details of voxels surviving a threshold of p < 0.001 uncorrected are described in supplemental tables 1-4 in the supplemental online materials.

Highlights.

• Human categorisation judgements are guided by both Bayesian and cognitive strategies

• Decision strategy varies with environmental volatility

• Distinct prefrontal and midbrain regions are activated by different strategies