Genetic regulatory network motifs constrain adaptation through curvature in the landscape of mutational (co)variance

Abstract

Systems biology is accumulating a wealth of understanding about the structure of genetic regulatory networks, leading to a more complete picture of the complex genotype-phenotype relationship. However, models of multivariate phenotypic evolution based on quantitative genetics have largely not incorporated a network-based view of genetic variation. Here we model a set of two-node, two-phenotype genetic network motifs, covering a full range of regulatory interactions. We find that network interactions result in different patterns of mutational (co)variance at the phenotypic level (the M-matrix), not only across network motifs but also across phenotypic space within single motifs. This effect is due almost entirely to mutational input of additive genetic (co)variance. Variation in M has the effect of stretching and bending phenotypic space with respect to evolvability, analogous to the curvature of space-time under general relativity, and similar mathematical tools may apply in each case. We explored the consequences of curvature in mutational variation by simulating adaptation under divergent selection with gene flow. Both standing genetic variation (the G-matrix) and rate of adaptation are constrained by M, so that G and adaptive trajectories are curved across phenotypic space. Under weak selection the phenotypic mean at migration-selection balance also depends on M.

Introduction

Recent years have seen an explosion in the functional understanding of genetic interactions, including mapping of large genetic regulatory and metabolic networks (Dieckmann and Doebeli 1999; Stuart et al. 2003; Huang et al. 2007; Dixon et al. 2009; Costanzo et al. 2010; Zhang et al. 2011). These data have led toward a more comprehensive understanding of complex phenotypes, and emphasize the complexity and non-linearity of the genotype-phenotype relationship (Benfey and Mitchell-Olds 2008; Mitteroecker 2009; Tøndel et al. 2011; Travisano and Shaw 2013). In particular, pleiotropy and functional epistasis are ubiquitous in genetic regulatory networks (Tyler et al. 2009), and this has important consequences for the evolution of complex phenotypes.

However, traditional quantitative genetic models of multivariate adaptation typically assume phenotypic traits to be affected by a large number of loci with largely independent, additive effects (Lande and Arnold 1983; Turelli 1985; Arnold et al. 2001; Roff 2006; Arnold et al. 2008). While pleiotropy and statistical epistasis are sometimes included in these models (e.g. Jones et al. 2003; Jones et al. 2007; Alvarez-Castro et al. 2009), the effects of specific genetic regulatory network architectures on quantitative genetic predictions of adaptation are not well understood. Incorporation of a network-level functional view of genetic interactions into models of multivariate phenotypic evolution represents a new synthesis in biology, enabled by a new wealth of empirical data (Zhu et al. 2009; O'Malley 2012).

An initial step toward this synthesis is to explore the consequences of simple network motifs on patterns of dominance, pleiotropy, and epistasis, considering the equilibrium expression level of a gene in the network as the phenotype (Omholt et al. 2000; Gjuvsland et al. 2007; Aylor and Zeng 2008). Here we apply a similar modeling approach to multivariate phenotypic space. In multivariate evolution, mutational and genetic correlation among traits can either constrain or facilitate adaptation, depending on the relationship between the direction of selection and genetic correlation (Schluter 1996; Hansen and Houle 2008; Agrawal and Stinchcombe 2009; Walsh and Blows 2009). Such correlations are expected to result from factors including the pleiotropy and epistasis inherent in genetic networks. Moreover, non-linearity in the genotype-phenotype map resulting from genetic network architecture means that the patterns of mutational correlation may change across phenotypic space, even when the mutational process at the genotypic level remains constant (Mitteroecker 2009). This variation across phenotypic space could substantially affect both adaptive and neutral evolutionary trajectories (Steppan et al. 2002; Arnold et al. 2008). However, the ways in which genetic regulatory network architecture may induce this variation have not been well quantified.

Here we consider a set of two-node network motif models, covering all basic types of regulatory interactions, in which the phenotypes of interest are the expression levels of the two loci. The mathematical form we use to model regulatory interactions is general to Michaelis-Menten kinetics as well as other modes of gene regulation (Omholt et al. 2000; Gjuvsland et al. 2007), and we explore the complete set of possible two-node interactions in this form. The two nodes in the network, while described below as single loci, may also be interpreted as well-connected modules in a larger network that interact in relatively simple ways. We model the interactions in these networks with differential equations describing dynamic gene expression, where the phenotypes are equilibrium gene expression levels. We assess whether simple network motifs lead to non-linearity in the genotype-phenotype map that is sufficient to create not only mutational and genetic correlation, but also variation in patterns of that correlation across phenotypic space. Using simulations of adaptive divergence with gene flow between two populations, we test whether the resulting curvature in phenotypic space constrains rates and trajectories of adaptation.

Methods

Modeling Gene Regulatory Networks

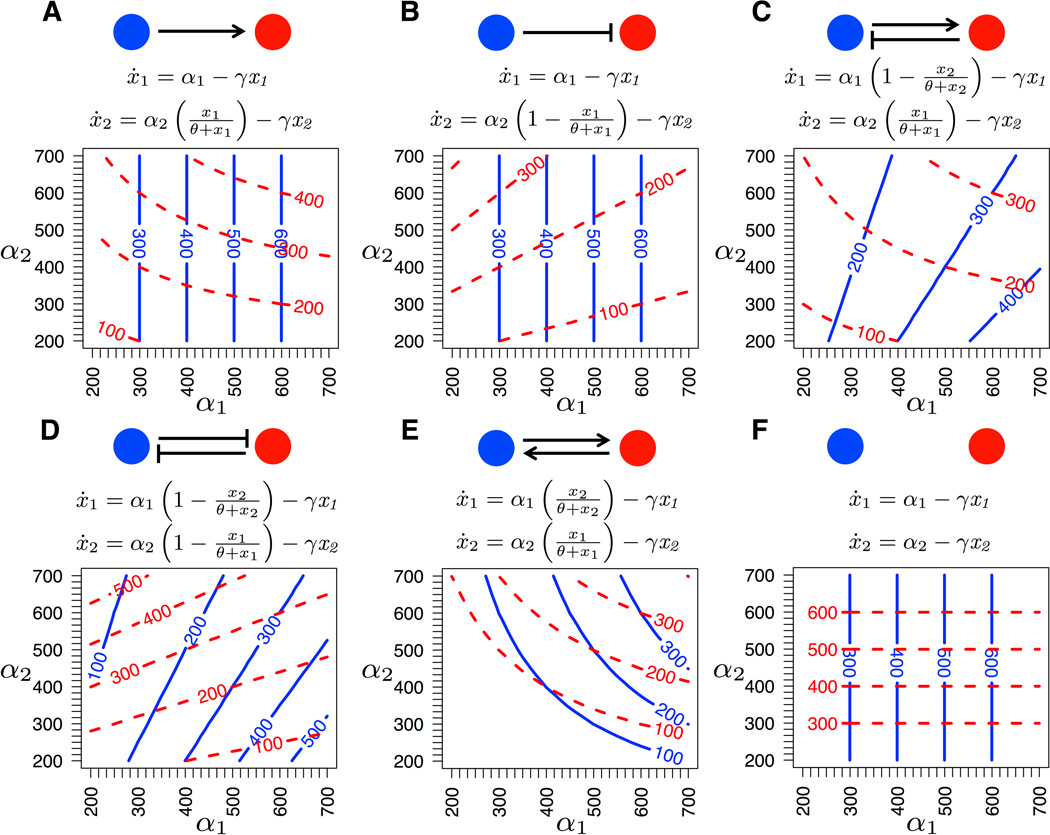
We modeled a set of six two-node gene regulatory networks using systems of ordinary differential equations (ODEs) describing gene expression levels. These two-locus ODEs are analogous to Gjuvsland et al.'s (2007) three-locus models, and they describe the rate of change of the concentrations of gene products x₁ and x₂ given the genotypic values α₁ and α₂ and the parameters θ and γ. These ODE systems reach stable equilibrium levels of expression, and we use the equilibrium expression levels of gene products x₁ and x₂ as the two phenotypic traits for any instance of a network motif. We do not explicitly model transcription and translation or specify what type of gene product is involved, in order to apply the models to any type of regulatory signal that could lead to interactions between loci or between tightly connected modules in a genetic network. Our model uses diploid individuals but does not contain any dominance, so we define the “genotypic value” α_i at each locus as the sum of allelic effects for the two alleles. Positive or negative gene regulation was modeled as a sigmoid function (Figure 1). For example, concentration of gene product x₁ has a positive effect on dynamic expression levels of locus 2 in the second equation of Figure 1A, so locus 1 positively regulates locus 2. The parameter θ represents the amount of regulator needed to get half of the maximum expression rate and γ is the decay rate of expressed gene product (Gjuvsland et al. 2007). For simplicity in the current study, these two parameters were fixed (θ = 300, γ = 1).

Figure 1.

Gene regulatory network motifs. Below each motif are the system of ordinary differential equations governing gene expression levels x_i and a graphical depiction of the genotype-phenotype map. Parameters are genotypic value α_i, the sum of allelic values at locus i; θ, concentration of the regulator at which half of the maximum activation level is reached; and γ, gene product decay rate. All motifs reach a single stable equilibrium gene expression level given a pair of genotypic values. Contours represent these phenotypic trait values x₁ (solid blue) and x₂ (dashed red) as a function of genotypic values.

Setting the ODEs for each motif to zero and solving for x₁ and x₂ yields unique solutions for the gene expression levels at equilibrium as a function of the genotypic values, θ, and γ (see Supporting Information). We assume no environmental variation; therefore, for a given genotype in a particular network motif we can calculate both equilibrium expression levels – i.e. the phenotypic trait values – directly. We assessed stability of equilibrium expression levels by calculating the Jacobian matrix linearization of the ODEs at equilibrium points. Equilibrium trait values are stable for all motifs when allelic effects and trait values are positive, conditions that are assumed throughout this study (see Supporting Information). For each regulatory motif we also solved for genotypic value (sum of the allelic values at each locus) as a function of equilibrium expression levels. These solutions are unique, so that the genotype-phenotype map is 1:1 at the level of genotypic values for all motifs across positive gene expression levels.

Estimating M, G, and epistatic (co)variance

We estimated the matrix of mutational (co)variance M across phenotypic space for each motif using a linear approximation to the genotype-phenotype map as follows. For each motif we calculated the 2×2 Jacobian matrix J_i of the genotype-phenotype map. Then for motif i, M_i = J_i Σ J_i^T, where Σ is the matrix of mutational variance introduced per generation at the level of genotypic values. We assumed Σ to have zero covariance (i.e. no correlation in mutation between loci) and equal variance terms 2σ, where σ² = 17.3 is the per-allele mutational variance in allelic value following a continuum of alleles model (Kimura 1965). This per-allele mutational variance effectively scales the total size of M, but does not affect the covariance structure of M at all. To validate the linear transformation approximation of M against the M-matrix that would occur in a polymorphic population, we also estimated M numerically by creating populations centered at nine points in a grid across phenotypic space (at x₁ = 200, 300, 400 and x₂ = 200, 300, 400) for each motif. We randomly sampled phenotypic values for 10,000 individuals from a bivariate Gaussian distribution with standard deviation of 20 phenotypic units. We mutated each allele in all 10,000 individuals by adding a random deviate, sampled from a Gaussian distribution with variance σ² = 17.3, and calculated M as the (co)variance of phenotypic deviations resulting from allelic mutation. The resulting M matrices were indistinguishable from those calculated above, so the linear approximation method was used for all calculations below.

We also estimated the G-matrix of additive (co)variance and the epistatic (co)variance matrix for the nine populations in each motif described above, using the animal model (Kruuk 2004; Wilson et al. 2010). Each population was evenly split into males and females, and 100 sires were randomly mated to 10 dams each resulting in 1000 offspring, with independent assortment between loci. Using the resulting pedigree information, we obtained breeding values for individuals and population estimates of the G-matrix by fitting a generalized linear mixed model with the R package MCMCglmm (Hadfield 2010; R Development Core Team 2012). Because our model includes no dominance (alleles are purely additive within each locus) and no random environmental effects on phenotype, the population-level residual (co)variance matrix includes solely epistatic (co)variance. For the random effects prior, we set the variance component equal to the phenotypic (co)variance and set the parameter “nu” to 2. To the speed up convergence and chain mixing properties we used parameter expanded methods (Liu et al. 1998) with prior means for the working parameter “alpha” set to (0,0) and variances set to 1,000 with zero covariance. For the residual effects prior, we set the variance component of the inverse Wishart distribution to 1,000 along the diagonal with zero covariance and nu to 0.002. We ran the Markov Chain for 12,000 generations following a 1,000-generation burn-in period, sampling every 25 generations to reduce autocorrelation.

Evolvability depends on mutational variation, so phenotypic space can be re-scaled by the mutational distance between phenotypes. To the extent that adaptation is mutation-limited, this re-scaling reflects the “evolutionary distance” traveled during adaptation to a novel phenotype. Mathematically, this distance between phenotypic values is the Mahalanobis distance scaled by the local value of M, so that the inverse of M is a Riemannian metric tensor (Jost 2011). We created visualizations of mutation-scaled phenotypic space using an iterative algorithm for deforming a grid of bivariate phenotypes. The algorithm first scaled the grid by mutational variance along single phenotypic axes by multiplying distances from each point to its 4 nearest neighbors by the square root of the corresponding diagonal elements of M⁻¹, estimated at each grid point as described above. It then incorporated mutational covariance by sequentially adjusting the position of each point on the grid so that its Euclidean distance to its 8 nearest neighbors (horizontal, vertical, and diagonal) matched as closely as possible to the Mahalonobis distance between phenotypes, scaled by the local M-matrix. Code to perform this deformation was written in R (R Development Core Team 2012) and is available from the authors.

Simulating divergent selection with gene flow

We used R to create individual-based simulations to determine the effect of varying gene regulatory network motifs on adaptation under a model of divergence with gene flow. Each simulation replicate included two populations, each of size n = 2,000, exchanging migrants at rate m in an island model (Wright 1931). To initialize each population, we used the Phenotype-to-Genotype equations (see Supporting Information) to obtain the genotypic values α₁ and α₂ that correspond to a phenotype of x₁ = 300 and x₂ = 300 for each network. We then generated allelic variation by randomly drawing allelic values for each individual using a Gaussian distribution centered at half of the genotypic value and with a variance of 200. We then imposed divergent selection on the two populations by selecting toward two optimum phenotypes. The phenotypic optima for populations 1 and 2 were set to phenotypic points (x₁ = 150, x₂ = 450) and (x₁ = 450, x₂ = 150), respectively. Thus divergent selection was imposed along the axis representing negative correlation between the two traits, and selection on the two populations was symmetrical in terms of distance to the optimum and strength of selection.

We used a Gaussian fitness function to calculate individual fitness, w:

$$w={\mathit{\text{exp}}}^{-\frac{1}{2}{(\mathit{x}-{\mathit{x}}_{\mathit{\text{opt}}})}^T{\mathbf{\Omega }}^{-1}(\mathit{x}-{\mathit{x}}_{\mathit{\text{opt}}})}$$ (1)

where x is a column vector containing trait values, x_opt is a column vector of phenotypic optima for each trait, and Ω is a symmetrical 2-by-2 matrix describing the landscape of stabilizing selection, analogous to a (co)variance matrix. For simplicity, we assume equal strengths of stabilizing selection for each trait (i.e. the diagonal elements of Ω are ω = ω₁₁ = ω₂₂) and no correlational selection (ω₁₂ = ω₂₁ = 0). Individuals were randomly chosen to mate with a probability proportional to their relative fitness $(w=\frac{w}{w_{\mathit{\text{max}}}})$.

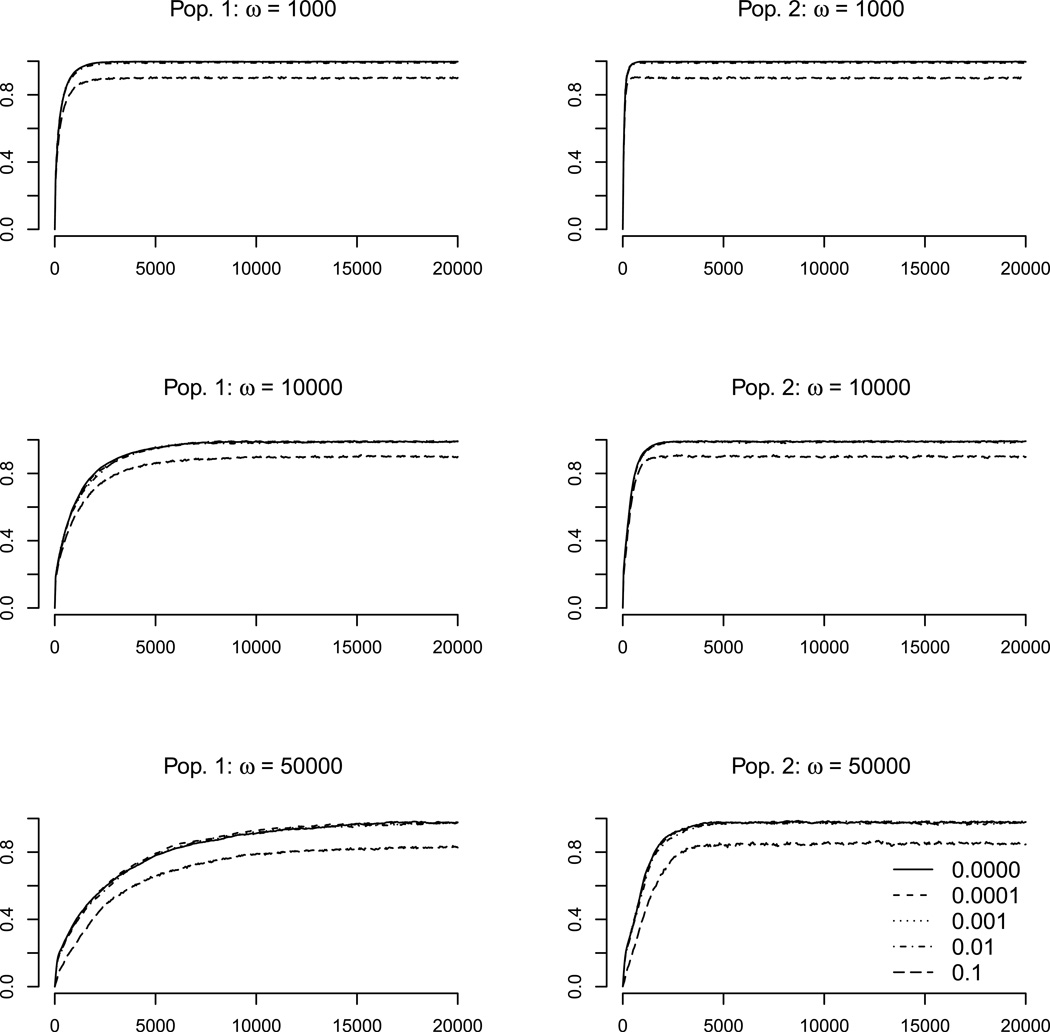
Offspring randomly received one allele per locus from each parent, with independent assortment between loci. This process was continued, sampling with replacement from the parental generation, until the new population's size equaled the parental size, so that generations were non-overlapping. During meiosis there was a probability μ that an allele mutates. In this case the new allelic value was the sum of the original allelic value plus a random value centered at zero with variance σ² = 17.3. For these simulations μ was set to 0.01, so total allelic variance introduced by mutation per generation per allele was 0.173. Note that this represents less total mutational variance, but identical covariance structure, compared to the M-matrices calculated above. Migration between populations followed mating. Individuals (from both populations) were chosen to migrate with probability m, then pooled and redistributed randomly back to one of the populations. To characterize the effects of network motif on adaptation, we simulated 10 replicates of population pairs for each motif for 1,000 generations with parameter values m = 0.001 and ω = 10,000. To explore the effects of selection strength and migration rate, we simulated 10 replicates of population pairs for motif C across multiple parameter values (m = 0, 0.0001, 0.001, 0.01; ω = 1000, 10,000, 50,000). We ran these simulations for 20,000 generations to characterize equilibrium levels of adaptation. For reference, at selection strengths of ω = 1000, 10,000, and 50,000, fitness of individuals 10 phenotypic units away from the optimum is 90%, 99%, and 99.8% of the fitness at the optimum, respectively. Initial selection during the simulations was strong; mean-standardized selection gradients per trait (Hansen and Houle 2008) for the null motif at the initial population mean would be +/− 25, 2.94, and 0.60, respectively.

Quantifying genetic variation and adaptation

We estimated the G-matrix of additive genetic (co)variance at generations 50, 100, 500, and 1000 for the shorter simulations, and additionally at generation 20,000 for the longer simulations. Before the mating phase of each of these generations, we conducted a “side experiment” in which 100 sires were mated to 10 dams each to produce 1000 offspring, and we estimated G using MCMCglmm (Hadfield 2010; R Development Core Team 2012) as described above. Note that this pedigree data was produced independent of fitness, and these offspring were not those used for the next generation of the simulation.

We used several metrics to quantify adaptation and the structure of G during the course of divergence with gene flow. The extent of adaptation was calculated as:

$$𝒜=1-\frac{D_{\mathit{\text{opt}},t}}{D_{\mathit{\text{opt}},\mathit{\text{ini}}}}$$ (2)

where D_opt,ini is the Euclidean distance between the initial starting position (300, 300) and the phenotypic optimum, and D_opt,t is the Euclidean distance between a given population's mean phenotype at time t and its phenotypic optimum. Equation 2 represents a ratio where a value of 1 can be interpreted as a population being well-adapted to its respective phenotypic optimum. We quantified aspects of G with four metrics (Jones et al. 2003): i) size Σ, calculated as the sum of the eigenvalues, equal to the sum of the variance terms; ii) eccentricity or shape ε, calculated as the smaller eigenvalue divided by the larger eigenvalue; iii) orientation φ, calculated as the angle between the leading eigenvector g_max and the axis of x₁, and iv) effective dimensionality n_D, calculated as the total variance divided by the leading eigenvalue (Kirkpatrick 2009).

Results

Genotype-phenotype map under simple network motifs

We modeled a set of six genetic regulatory network motifs (Figure 1). For all motifs, the genotype-phenotype map was 1:1 at the level of genotypic values, although not allelic values (see Supporting Information). In the absence of any interlocus interaction (null motif; Figure 1F) each phenotype equaled the genotypic value at the corresponding locus. In all other cases, both pleiotropy and epistasis were evident in the genotype-phenotype maps. Pleiotropy resulted from unidirectional (motifs A and B) and bidirectional (motifs C, D, E) regulation between loci, because the genotypic value at a single locus affected the expression levels of both loci. In contrast, the nature of epistasis in allelic effects on phenotypes depended on the type of interaction. Negative regulation led to linear contours on the genotype-phenotype map for the expression level of the downstream gene – but note that where the contours are not parallel, the relationship between multivariate genotypes and phenotypes is still nonlinear (e.g. Figure 1B,D; see Supporting Information). In contrast, positive regulation led to hyperbolic curved contours in the genotype-phenotype map for the downstream gene (e.g. Figure 1A). In both cases, the non-linearity in mapping from genotype to phenotype for one or both traits indicates statistical epistasis; that is, the phenotype resulting from allelic substitutions at both loci differs from the expectation based on the independent additive effects of the alleles considered separately (Phillips 2008).

Landscape of mutational variation

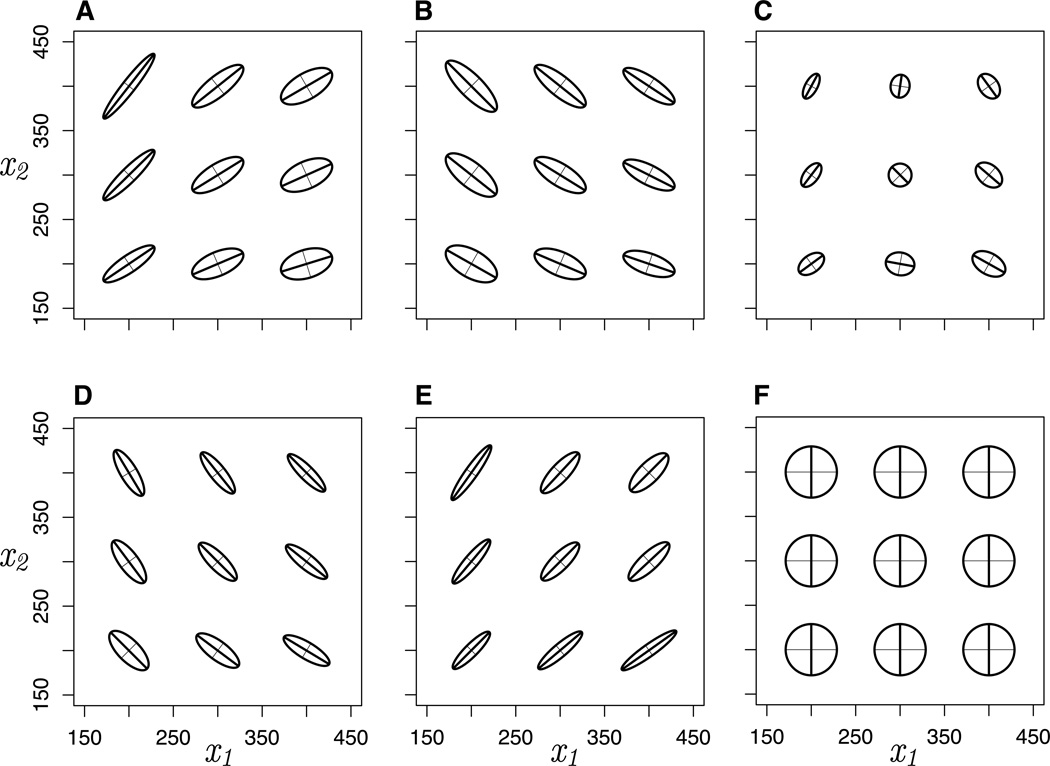
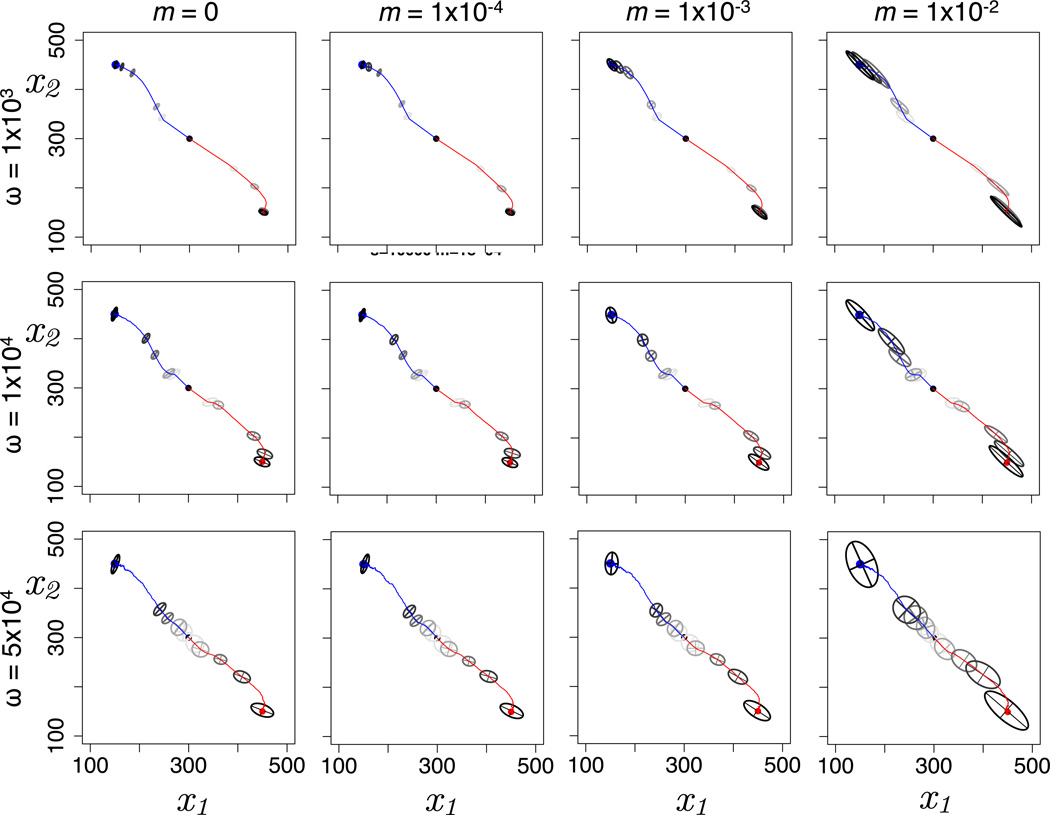
We assessed the landscape of mutational variation using the M-matrix of quantitative genetics, a (co)variance matrix of the phenotypic variation across multiple traits produced by mutation per generation. The motifs produced a wide range of mutational variance in each trait and, with the exception of the null motif (F), correlation between traits (Figure 2). Moreover, M exhibited striking variation across phenotypic space even when network motif and all other parameters were held constant for all but the null motif. The overall size of M -- the total amount of phenotypic variance produced by mutation -- varied across motifs as well as across phenotypic space within motifs. The magnitude of mutational correlation, and thus the effective dimensionality of M, varied across phenotypic space for all but the null motif (Figures 2, S1). The sign of the correlation also shifted under the negative feedback loop motif (Figure 2C), leading to the most extreme variation in dimensionality (Figure S1C).

Figure 2.

The mutational (co)variance matrix M across phenotypic space. For each network motif (A–F, labeled as in Figure 1), M-matrices for nine populations are plotted as 95% confidence ellipses around mutational variation produced per generation, scaled up by a factor of 2.5 for visualization. Axes within each ellipse represent the first (thick line) and second (thin line) eigenvectors, or principal components, of mutational variation.

Although the network motifs exhibit strong functional epistatic interactions between loci and statistical epistasis in the genotype-phenotype map, the patterns of (co)variance in M were essentially the result of additive genetic (co)variance with only negligible epistatic (co)variance. We estimated additive genetic and epistatic (co)variance for the two traits across phenotypic space for each motif (Figures S2–3). Matrices of epistatic (co)variance were much smaller in total magnitude than the G-matrix of additive genetic (co)variance, and the pattern of covariance was similar to G. Total epistatic variance represented a negligible contribution to total phenotypic variance, such that narrow-sense heritability was greater than 0.99 for both traits in all motifs, for those populations at the center of phenotypic space. Because additive variation contributes most directly to the response to selection, the covariance patterns in M are predicted to have a strong effect on adaptation to the extent that evolution is mutation-limited. If this is so, we can get relative estimates of mean evolvability (Hansen and Houle 2008) from M. This also varied widely across phenotypic space (Figure S4).

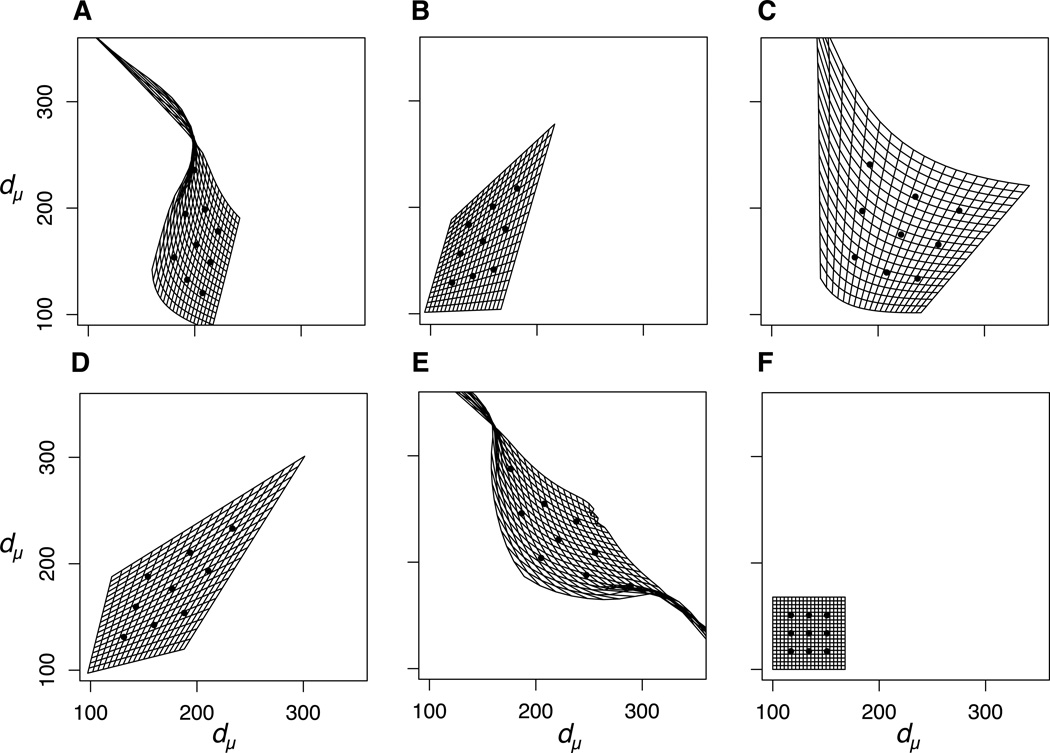
Because M varied across phenotypic space for all but the null model of network motifs, re-scaling by mutational distance induced curvature in the phenotypic landscape (Figure 3). Note that this re-scaled, curved phenotypic landscape may be best represented as an n-dimensional manifold (for n traits) embedded in a higher-dimensional space, but the 2-dimensional projection of this manifold is shown in Figure 3. Phenotypic space was generally stretched for all motifs relative to the null. Phenotypic space was also stretched, as expected, in directions of positive correlation between traits in the case of negative gene regulation (Figure 3B,D) and directions of negative correlation between traits in the case of positive regulation (Figure 3A,E). The extent of deformation varied across network motifs as well as across phenotypic space. Deformation was particularly pronounced in regions of low genotypic value for the upstream gene and high genotypic value for the downstream gene in positive regulation (upper left corners in Figures 3A,C, upper left and lower right corners in Figure 3E). To the extent that evolution is mutation-limited, these are predicted to be regions of phenotypic space in which adaptation may be particularly constrained.

Figure 3.

Phenotypic space re-scaled by mutational (co)variance for each motif. Phenotypic values from 100–500 are represented as a grid that is deformed such that distances between phenotypes, d_μ, in this new depiction represent equal amounts of mutational variation. For visual reference, the locations of the nine populations from Figure 2 are plotted as black dots in this new mutational space. Note that this re-scaling may cause the 2-dimensional phenotypic space to curve outward into higher dimensions, but it is represented here as the projection of this curved manifold onto a plane.

Adaptation under divergent selection

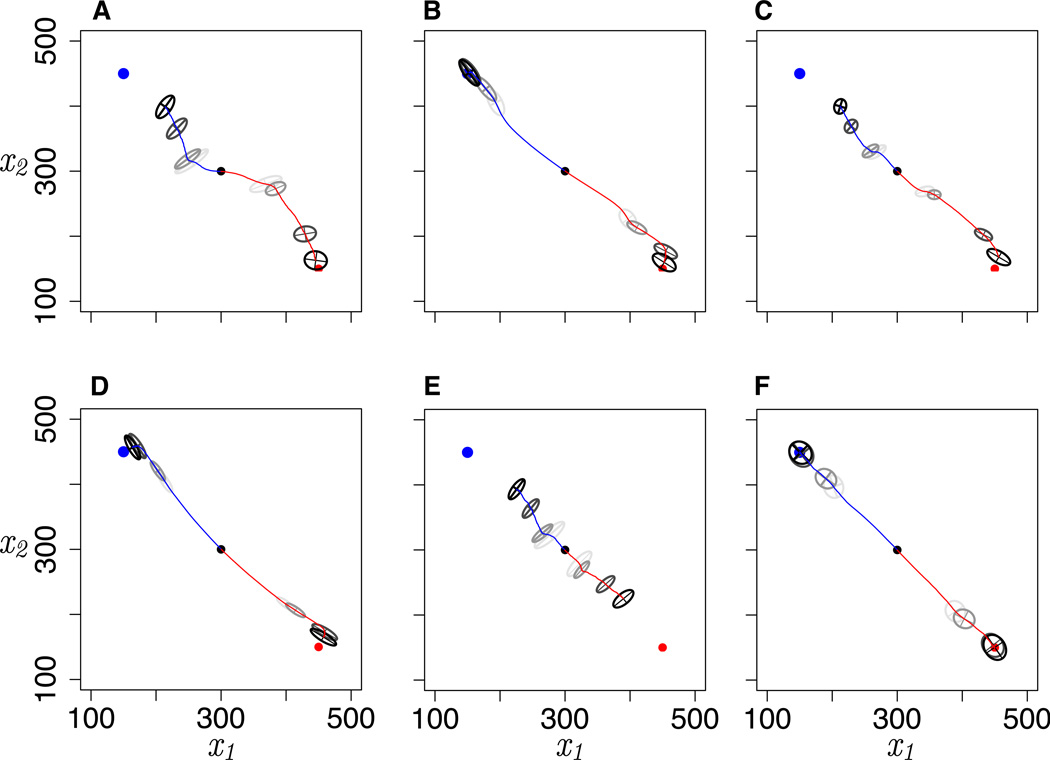
To test the effect of network-induced curvature in phenotypic space on trajectories of adaptation, we simulated pairs of populations evolving from a common ancestor toward separate phenotypic optima with migration between them, with replicate simulations to minimize stochastic differences (Figure 4). Network motifs had a strong influence on both the rate and the trajectories of adaptation. In terms of adaptation rate, most striking is the constraint on adaptation in the direction of negative correlation between traits when gene regulation is positive (Figures 4A,C,E). This corresponds to the reduced mutational variation and stretching of evolutionary distance in these regions of phenotypic space illustrated in Figures 2 and 3. Conversely, adaptation is relatively rapid under negative gene regulation (Figure 4D). Network motifs also produced curved trajectories of adaptation through phenotypic space, most notably early in adaptation for motif A and close to the optima for motifs B, C, and D. Curved trajectories represent the tension between the orientation of directional selection and the orientation of additive genetic variation, summarized by the G-matrix (Lande 1979; Arnold et al. 2008). The effects of mutational variation on adaptation rates and trajectories depend on G (Figure 4), and G in our simulations was strongly affected by M. Adaptation was constrained when the major axis of M, and thus the major axis of G, is perpendicular to the orientation of directional selection, and adaptation was facilitated when M and G align with directional selection.

Figure 4.

Evolution during 1,000 generations in response to divergent selection with migration across network motifs. Blue and red lines track the phenotypic means of the two populations evolving toward selective optima at the blue and red points, respectively, averaged across 10 independent replicates for each motif. G-matrices are drawn as 95% confidence ellipses at 4 time points (50, 100, 500, and 1,000 generations; darker ellipses denote more recent G-matrices). Parameter values are m = 0.001, ω = 10,000, μ = 0.01, size of each population = 2,000.

To further explore the interactions among migration, selection, drift, M, and G, we focused on the negative feedback loop represented in motif C, extending the simulations of divergent selection to reach equilibrium and varying strength of selection and migration rate. Motif C showed striking differences in the degree and direction of mutational correlation across phenotypic space (Figure 2C). This is expected to lead to regions of elevated and depressed evolvability (e.g., compare upper left and lower right regions in Figure 3C, respectively, and the two populations in Figure 4C). As expected, we found that selection strength generally increased and migration generally decreased both the rate and equilibrium extent of adaptation (Figures 5 and 6; Table 1). As seen in the trajectories of adaptation across all motifs (Figure 4), the rate of adaptation toward the selective optimum was lower in regions of phenotypic space where mutational variance in the direction of selection was limited for the negative feedback motif, and this effect was consistent across selection strengths and migration rates (Figures 5, 6, and S5–S9). Thus adaptation was slower in the phenotypic region around the optimum of population 1 as opposed to the region around the optimum of population 2.

Figure 5.

Extent of adaptation through time for the negative feedback network (motif C). Rows denote different selection strengths and columns denote either population 1 (left) or 2 (right). Within each panel are 5 different migration rates between the two populations. Plotted is the mean adaptation ratio across 10 simulated replicates for each parameter combination.

Figure 6.

Adaptive divergence for the negative feedback network (motif C). Each plot shows the average of 10 replicates of two populations diverging from the initial starting position (black dot) to either the blue or red phenotypic optima for a given combination of strength of stabilizing selection ω and migration m. Blue and red lines track phenotypic means through the course of the 20,000-generation simulation. G-matrices are drawn as 95% confidence ellipses at 5 time points (50, 100, 500, 1,000, and 20,000 generations; darker ellipses denote more recent G-matrices).

Table 1.

Adaptation and G-matrix summary statistics for motif C at migration-selection balance (20,000 generations; see Figure 5). For each combination of migration m and selection strength ω, means and standard errors (in parentheses) are provided for population 1 (first row) and population 2 (second row) averaged over 5 simulated replicates. 𝒜, the extent of adaptation (see Equation 2); G_ij, the i^th by j^th component of G; n_D, dimensionality of G; φ, the angle of the leading eigenvector of G relative to trait axis x₁; Σ, the sum of the two eigenvalues of G; and ε, a measure of the eccentricity of G (see Methods).

m	ω	𝒜	G11	G12	G22	nD	φ	Σ	ε
0	103	0.997 (4e-04)	0.9 (0.1)	2.5 (0.2)	8.3 (0.4)	1.01 (0.002)	72.9 (0.5)	9.2 (0.5)	0.01 (0.002)
		0.997 (4e-04)	11.2 (0.4)	−3.9 (0.2)	3.4 (0.2)	1.14 (0.004)	157.7 (1.2)	14.6 (0.5)	0.14 (0.004)
10−4	103	0.997 (5e-04)	1.0 (0.1)	2.7 (0.1)	8.9 (0.3)	1.01 (0.002)	73.0 (0.4)	9.8 (0.4)	0.01 (0.002)
		0.996 (5e-04)	11.7 (0.5)	−3.9 (0.2)	3.6 (0.2)	1.15 (0.005)	158.2 (0.8)	15.3 (0.6)	0.15 (0.005)
10−3	103	0.997 (5e-04)	16.3 (6.5)	−13.2 (6.7)	24.7 (6.7)	1.03 (0.009)	92.1 (7.5)	41.0 (13.2)	0.03 (0.009)
		0.997 (5e-04)	45.1 (12.4)	−37.6 (12.3)	37.4 (12.3)	1.09 (0.016)	148.4 (2.9)	82.5 (24.7)	0.09 (0.016)
10−2	103	0.990 (8e-04)	214.4 (22.4)	−214.2 (22.1)	225.0 (22.7)	1.01 (0.002)	134.2 (0.1)	439.4 (45.1)	0.01 (0.002)
		0.989 (8e-04)	256.0 (16.0)	−245.9 (15.7)	242.2 (15.4)	1.01 (0.002)	135.8 (0.1)	498.2 (31.4)	0.01 (0.002)
10−1	103	0.901 (0.0022)	2291.4 (57.7)	−2301.0 (58.3)	2320.9 (58.7)	1.00 (0.001)	134.8 (0.0)	4612.3 (116.2)	0.00 (0.001)
		0.901 (0.0021)	2469.6 (71.3)	−2424.1 (67.9)	2410.7 (68.0)	1.00 (0.002)	135.3 (0.1)	4880.3 (139.0)	0.00 (0.002)
0	104	0.992 (9e-04)	5.0 (0.4)	10.7 (0.8)	35.1 (1.9)	1.04 (0.004)	72.3 (0.9)	40.1 (2.2)	0.04 (0.004)
		0.990 (0.0016)	46.1 (2.6)	−14.3 (1.0)	16.0 (1.0)	1.19 (0.005)	158 (1.5)	62.1 (3.3)	0.19 (0.005)
10−4	104	0.989 (0.0016)	4.6 (0.4)	10.0 (0.9)	31.7 (2.2)	1.04 (0.004)	72.1 (0.9)	36.3 (2.6)	0.04 (0.004)
		0.988 (0.0015)	47.4 (2.3)	−17.0 (1.5)	18.1 (1.5)	1.18 (0.004)	155.9 (1.3)	65.5 (3.6)	0.18 (0.004)
10−3	104	0.990 (0.0012)	20.0 (6.5)	−5.8 (6.9)	49.0 (6.6)	1.1 (0.028)	89.1 (6.4)	68.9 (13.0)	0.10 (0.028)
		0.987 (0.0020)	83.2 (13.5)	−50.9 (12.7)	51.1 (12.5)	1.13 (0.015)	150.4 (2.9)	134.3 (25.9)	0.13 (0.015)
10−2	104	0.988 (0.0015)	217.4 (22.6)	−210.3 (22.8)	252.1 (23.2)	1.06 (0.006)	132.3 (0.3)	469.5 (45.7)	0.06 (0.006)
		0.984 (0.0018)	295.1 (16.6)	−260.9 (16.1)	257.9 (15.5)	1.03 (0.003)	137.1 (0.1)	552.9 (32)	0.03 (0.003)
10−1	104	0.900 (0.0033)	2302.5 (58.1)	−2298.4 (60.7)	2360.1 (62.1)	1.01 (0.001)	134.6 (0.1)	4662.7 (119.6)	0.01 (0.001)
		0.897 (0.0023)	2471.5 (67.8)	−2430.3 (65.2)	2424.1 (69.5)	1.00 (0.002)	135.3 (0.1)	4895.7 (137)	0.00 (0.002)
0	5×104	0.978 (0.0037)	13.7 (1.4)	26.2 (2.8)	80.2 (7.2)	1.05 (0.005)	71.1 (1.0)	93.9 (8.4)	0.05 (0.005)
		0.977 (0.0023)	108.6 (8.3)	−31.9 (4.2)	36.9 (4.2)	1.19 (0.005)	159.9 (1.9)	145.5 (11.7)	0.19 (0.005)
10−4	5×104	0.978 (0.0024)	11.7 (1.1)	22.3 (2.4)	73.5 (5.1)	1.05 (0.007)	72.2 (1.3)	85.2 (5.9)	0.05 (0.007)
		0.974 (0.0035)	116.9 (6.5)	−40.8 (2.5)	45.2 (2.4)	1.19 (0.009)	155.6 (1.6)	162.1 (7.9)	0.19 (0.009)
10−3	5×104	0.977 (0.0027)	29.9 (6.2)	7.7 (8.1)	104.6 (8)	1.17 (0.037)	85.2 (4.2)	134.5 (13.5)	0.17 (0.037)
		0.977 (0.0035)	155.4 (13.6)	−79.6 (13.8)	87.5 (13.6)	1.16 (0.013)	150.4 (2.7)	242.9 (26.5)	0.16 (0.013)
10−2	5×104	0.976 (0.0035)	274.9 (22.0)	−194.5 (28.7)	526.1 (30.6)	1.27 (0.025)	116.2 (2.2)	801.0 (49.4)	0.27 (0.025)
		0.970 (0.0027)	474.2 (19.4)	−353.8 (20)	385.2 (21.6)	1.09 (0.01)	138.9 (0.7)	859.4 (38.2)	0.09 (0.010)
10−1	5×104	0.829 (0.0059)	2567.8 (57.1)	−2264.7 (51.9)	4815.8 (93.0)	1.19 (0.006)	121.8 (0.6)	7383.6 (130.7)	0.19 (0.006)
		0.853 (0.0050)	3563.5 (81.6)	−3183 (76.2)	3766.6 (109.2)	1.07 (0.004)	134.1 (0.3)	7330.1 (174.9)	0.07 (0.004)

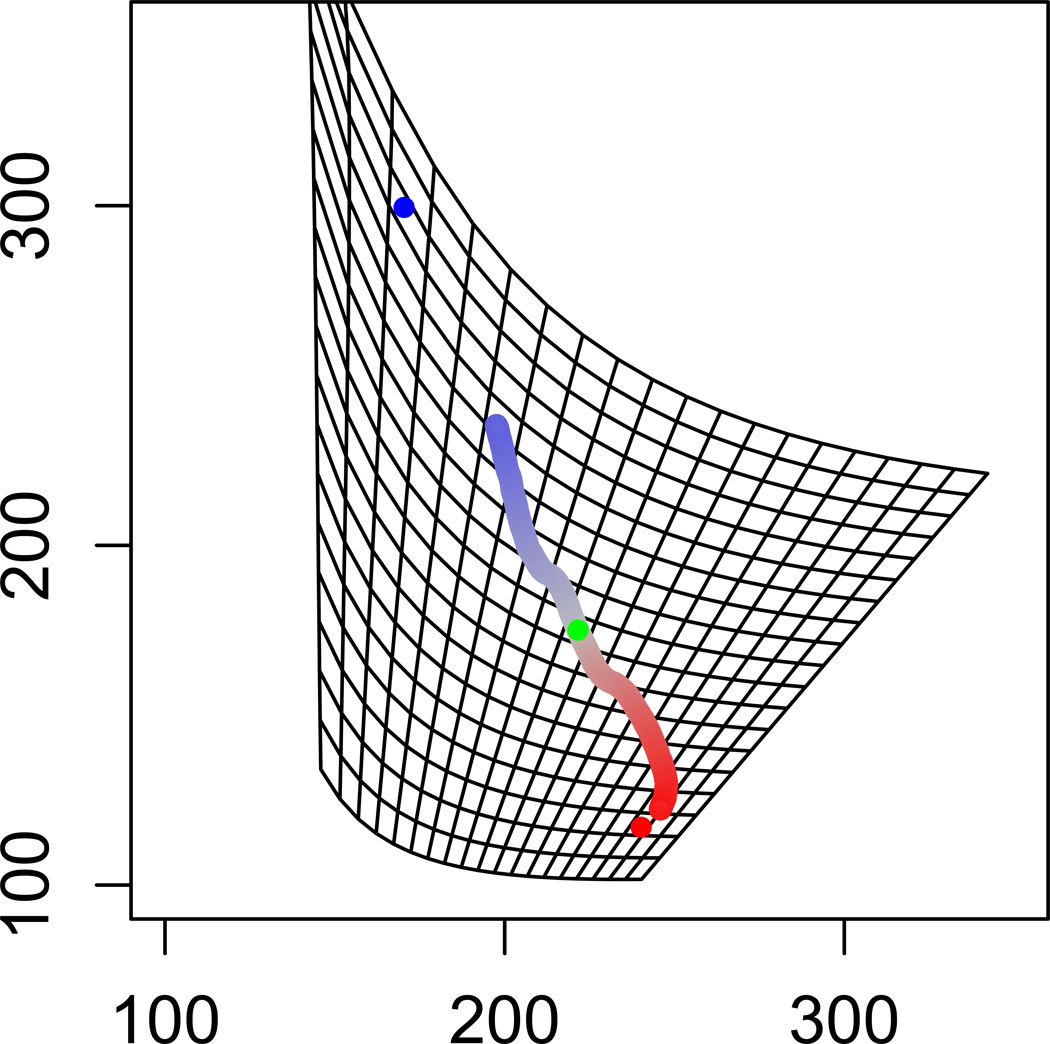
Re-scaling phenotypic space by mutational distance makes this difference clear: the two populations are seen to travel roughly the same mutational distance over the course of 1000 generations, but the optimum of population 1 is simply farther away from the starting point in mutational distance (Figure 7). Accordingly, the distance traveled in phenotypic space by population 1 was much less than that traveled by population 2, despite the entirely symmetrical directional selection, migration, and genetic drift acting on each (Table 2). However, the distance traveled by the two populations was much more similar in mutation-scaled space. In fact, population 1 traveled farther in this re-scaled space, as a result of a steeper selection gradient acting during the simulation because population 1 remained farther from its respective optimum than population 2.

Figure 7.

Single simulation run for motif C, plotted in the re-scaled space shown in Figure 3. Parameter values for this run are as in Figure 4.

Table 2.

Alternative distance metrics for quantifying the amount of evolutionary change over the two 1000-generation evolutionary trajectories shown in Figure 7. Rescaled space uses the M-matrix as a metric tensor, normalizing phenotypic change by the amount of mutational variance along a trajectory Populations 1 and 2 are those whose phenotypic optimum is at point (150, 450) and (450, 150) in phenotypic space, respectively.

	Population 1	Population 2
Euclidean distance traveled in phenotypic space	132.7	204.5
Total length of trajectory in phenotypic space	150.5	221.1
Euclidean distance traveled in rescaled space	64.8	57.9
Total length of trajectory in rescaled space	78.6	71.4

With weaker selection, genetic drift had a larger effect, causing higher levels of variation across replicate simulations (Figures S5–S9). Over longer time scales, in the case of weak selection, an equilibrium reflecting drift/migration/selection/mutation balance was reached farther from the optimum for population 1 compared to population 2, particularly at higher migration rates (Table 1).

The G-matrix is affected not only by mutation but also selection and migration. For the negative feedback motif (C), the structure of G varied widely across phenotypic space and across simulation parameters (Table 1; Figure 6). In general, stronger selection produced smaller G matrices (lower overall genetic variance; see Table 1), and higher migration rates shifted the pattern of genetic correlation within populations so that the major axis aligned with the direction of divergence between populations (Figure 6). G also varied strongly between the two populations within simulations, showing the effect of variation in M across phenotypic space. Thus the tenuous balance between selection, migration, and mutational variance led to shifts in the sign of genetic correlation across multiple factors: phenotypic space, migration rates, and strength of selection.

Discussion

Curvature of the landscape of mutational variation

The M-matrix of mutational variance and covariance plays a central role in quantitative genetic models of multivariate evolution. M provides the ultimate source of additive genetic variation, summarized by the G-matrix, which in turn determines the response to selection (Lande 1979). However, while increasing attention has focused on both empirically estimating G in natural populations and gaining a theoretical understanding of its stability and response to evolutionary forces (Arnold et al. 2008; Björklund et al. 2013), the M-matrix has received relatively less attention in part because of the difficulty of directly measuring it (Houle et al. 1996; Houle 1998; Houle et al. 2010). One exception is Houle and Fierst (2013), who recently estimated M for wing traits in a set of inbred Drosophila lines subject to mutation accumulation. They found significant variation in M between lines, both in total size of M and in mutational covariance structure, although some similarity in M was maintained across lines. While the functional genetic basis of these wing traits is unknown, differences in mutation rates between the lines may account for some of the differences in M, particularly overall size (Houle and Fierst 2013).

In the absence of shifts in mutational rates or process at the molecular level, one way in which M can evolve and differ across genotypes or populations is through shifts in the architecture of genetic regulatory networks – for example, appearance or disappearance of regulatory connections between genes (Wagner and Altenberg 1996; Lynch 2007). An additional way is through changes in allelic values and/or allele frequencies at loci that influence other loci in a regulatory network. In this case, substantial additive genetic variation can be produced by mutation even when genes have strong interactions at the molecular level of genes and their products, termed functional epistasis (Stadler et al. 2000; Gibson and Dworkin 2004; Phillips 2008). Here we explored shifts in the structure of mutational variation caused by functional epistasis with simple but explicit network motif models, holding the network architecture of regulatory connections constant while allowing population variation in allelic values and frequencies. We found striking variation in M at multiple levels, which influenced adaptation under divergent selection in simulation. Our models lead to several conclusions about the effect of genetic regulatory network motifs on mutational and genetic variation and on trajectories of adaptation.

First, we found that positive gene regulation produces more complex patterns of statistical epistasis (Phillips 2008) than negative regulation, illustrated by the hyperbolic versus linear contours on the genotype-phenotype map (Figure 1). This is consistent with the results of Gjuvsland et al. (2007), who found that positive regulation produces greater and/or more complex patterns of statistical epistasis than negative regulation in a three-locus, one-trait network model. This is also consistent with previous work showing higher mutational robustness resulting from negative feedback (Acar et al. 2010; Paulsen et al. 2011; Denby et al. 2012).

Second, despite the functional epistasis modeled in the network motifs and the statistical epistasis evident in the genotype-phenotype map, epistatic (co)variance at the population level was negligible. Narrow-sense heritability was greater than 0.99 for both traits in all motifs. This is in contrast to the results of Gjuvsland et al. (2007), who found moderate levels of epistatic variance across some parameter combinations in their network model. Why the discrepancy between statistical epistasis in the genotype-phenotype map and the lack of epistatic (co)variance at the population level? It appears that the genotype-phenotype map for these models, while curved, is smooth enough that within the phenotypic range of a population it is close to linear. Thus genetic variation within a population is nearly all additive. At this scale, pleiotropy maintains the key role in producing sometimes strong genetic covariance. As populations evolve across phenotypic space in response to directional selection, statistical epistasis then results in shifts in the covariance structure of additive variation, but not a substantial contribution of epistatic (co)variance.

Third, we found that simple network motifs produce striking variation in patterns of mutational variation, even when the mutational process is held constant at the allelic level. The M-matrix exhibits strong correlation as a result of network interactions, as expected. Moreover, the total amount of mutational variation and the sign and degree of mutational correlation depend also on the phenotypic mean, leading to variation in M across phenotypic space for a given network. To the extent that evolution depends on genetic variation provided by mutation, variation in patterns of mutational (co)variance effectively bends and stretches phenotypic space. The effect is analogous to the bending of space-time by gravitation under general relativity, so that the inverse of M acts as a Riemannian metric tensor that can be used to integrate mutational distance along evolutionary trajectories (Figure 7, Table 2), analogous to inertial body trajectories in gravitational fields (Jost 2011). Compared to traditional metrics based on phenotypic units, this type of analysis provides an alternative way of quantifying the pace of adaptation. Re-scaling of phenotypic space by mutational distance is straightforward when the genotype-phenotype map is 1:1, as it is for the simple network motifs examined here.

All network interactions that we examined stretched phenotypic distance overall relative to the null model of no interaction. Phenotypic space was especially stretched in directions of low mutational variance (i.e. axes of M with small eigenvalues). These axes of low mutational variance correspond to directions in which phenotypic change is relatively small given some amount of mutational input, i.e. axes of mutational robustness. Thus network motifs differ from each other in mutational robustness, but motifs also induce differences in mutational robustness both across phenotypic space and along different axes of phenotypic change from a single initial phenotype. Thus the concept of mutational robustness, like genetic variation (Walsh and Blows 2009), requires a multivariate view to provide explanatory power for phenotypic evolution.

Fourth, in our model the availability of mutational variation in the direction of selection constrains the speed of adaptation toward a selective optimum, curves the trajectory of adaptation toward the optimum, and shifts the position of the population mean under migration-selection balance. The effect of genetic (co)variance, and by extension mutational (co)variance, on these aspects of adaptation has been previously established (Jones et al. 2003; Jones et al. 2007; Jones et al. 2012). What is new in the current results is the variation in this effect of M on adaptation across phenotypic space. While the process of adapting toward a selective optimum can shift the pattern of G given constant M (Jones et al. 2004), our network model shows that the process of evolving through phenotypic space can also shift G because the population experiences different M-matrices. In addition, curvature in trajectories of adaptation caused by mis-alignment of G and directional selection is the result of the orientation of M across phenotypic space.

Fifth, some theoretical work has predicted that the major axis of the G-matrix in populations experiencing gene flow should align with direction of divergence between them, but this alignment depends on a balance with selection and migration rate (Guillaume and Whitlock 2007). Our results are consistent with this prediction, with the addition of network-induced changes in M across phenotypic space shifting the resulting orientation of G as well. It is worth noting that under weak selection, population 1 shows slightly higher rates of adaptation at intermediate migration rates, compared to either higher or lower migration rates. This may be an instance of adaptive introgression; i.e. a low level of migration supplying genetic variation along the axis of divergence between populations, which facilitates the response to selection (Guillaume and Whitlock 2007; Arnold and Martin 2009; Abbott et al. 2013). Accordingly, the dimensionality of G is highest at intermediate migration rates in this case (Table 1). More generally, attention has focused on the question of the stability of G over time and among related taxa. Empirically, G is observed to change over short time-scales (Björklund et al. 2013), but also retain some aspects of its structure over longer time-scales and among populations (Arnold et al. 2008). Drift, selection, and migration are factors that can de-stabilize G, and now we can add network-induced shifts in M across phenotypic space to this list.

Extension of simple network motif models

The models above are most simply described in terms of two loci that regulate each others' expression level under Michaelis-Menten-like kinetics. However, these network motifs are general enough to apply to pairs of loci with multiple types of gene regulation (reviewed by Gjuvsland et al. (2007)), and also to two well-defined, interacting modules in a larger regulatory network. As larger regulatory networks are being empirically mapped, it is possible to abstract features of these networks corresponding to such higher-level motif architecture, and to map these aspects of network architecture to phenotype (Tøndel et al. 2011). This extraction of larger-scale network motifs may suggest general features of mutational and genetic (co)variance that emerge from genetic regulatory networks and that could impact adaptation. It remains to be seen to what extent more complex networks can be approximated by much simpler network models in terms of their influence on mutation and genetic variation, or what degree of network modularity is required for this approximation. The general modeling approach taken here could also be directly extended to larger motifs, using more numerical methods in order to catalog the effects of network architecture on mutational variation and evolutionary constraint.

Traditional quantitative genetics theory deals with epistasis as a source of genetic variation, which is more limited than additive genetic variance in its ability to contribute to adaptive variation (Lande 1979; Lynch and Walsh 1998). However, combining epistatic interactions into a single term obscures the wide range of functionally different forms of epistasis. As we found here, detecting little or no epistatic variance using variance decomposition methods may mask relatively strong functional epistatic interactions at the level of gene regulation (Stadler et al. 2000; Phillips 2008). Despite the lack of epistatic (co)variance within populations, we showed that functional epistasis can still have an impact on adaptation rates and trajectories. Integrating a regulatory network view into the study of epistatic variance would help to link quantitative genetic theory and models of phenotypic evolution to the emerging wealth of data from systems biology (Gjuvsland et al. 2007).

As described above, the genotype-phenotype map in this simple model is 1:1. The actual genotype-phenotype map for nearly any quantitative trait is certainly more complex, including dynamic developmental pathways and interactions with environmental inputs, to the extent that some suggest it may not be helpful to consider it as a “map” at all (Pigliucci 2010; Travisano and Shaw 2013). Even simple network architecture can limit the ability of quantitative trait locus (QTL) mapping, based on standard assumptions about the distribution of genetic variation, to detect loci underlying a trait (Gjuvsland et al. 2007). One approach around this issue is to include network parameters directly in the mapping analysis (Wang et al. 2012). On the other hand, it may be that in the case of large genetic regulatory networks with allelic variation at multiple loci, epistatic interactions average out and locus effects are largely additive, so that new approaches to association mapping can indeed account for much of the observed heritability (Allen et al. 2010; Yang et al. 2010).

Given its complexity, one may ask whether the concept of a genotype-phenotype map is obsolete. We argue that it is not. Factors like network motif architecture, developmental processes, and genotype-by-environment interaction certainly add layers of non-linear complexity in the genotype-phenotype relationship. But in both functional studies and predictive models of evolution, approaches can be used to partition these layers. At the phenotypic end, genotype-by-environment interaction can be partitioned out by considering the “phenotype” to be a functional response to environmental inputs -- a set of function-valued traits (Kingsolver et al. 2001). Network-based models can also explicitly incorporate phenotypic plasticity into the genotype-phenotype map (Draghi and Whitlock 2012). At the genotypic end, it may be possible to explain a large portion of the effect of network architecture on relevant evolutionary features, such as M and G, simply by summarizing complex networks as their canonical motif structure (Tøndel et al. 2011). Explicit models of developmental pathways can also help to focus on particular layers of the genotype-phenotype map (Mitteroecker 2009; Félix 2012). These relationships are clearly difficult to unravel, but rapid advances in technology allowing high-throughput empirical measurement at multiple levels (e.g. genomic sequence, genetic and metabolic network architecture), as well as the promise of high-throughput methods at the organismal phenotype level (Houle et al. 2010), may facilitate progress in revealing these connections between genotype, phenotype, and evolutionary trajectories.

Conclusions

Our models indicate that the architecture of simple network motifs can potentially have a strong impact on adaptation. Network interactions lead to mutational covariance among traits, and this covariance varies across phenotypic space. Moreover, despite strong patterns of both functional and statistical epistasis, the mutational covariance takes the form of additive genetic variation, so it has a direct impact on the response to selection. The effects of epistasis are observed in changing the covariance structure of mutational and genetic variation as populations adapt toward novel phenotypes. As a result, several evolutionary properties – additive genetic (co)variance (the G-matrix), the rate of adaptation toward a selective optimum, and the trajectory of adaptation – are all essentially stretched and curved across phenotypic space.