Reliability of Readmission Rates as a Hospital Quality Measure in Cardiac Surgery

Abstract

Background

Recent policy interventions have reduced payments to hospitals with higher-than-predicted risk-adjusted readmission rates. However, whether readmission rates reliably discriminate deficiencies in hospital quality is uncertain. We sought to determine the reliability of 30-day readmission rates after cardiac surgery as a measure of hospital performance and evaluate the effect of hospital caseload on reliability.

Methods

We examined national Medicare beneficiaries undergoing coronary artery bypass for 2006 to 2008 (n=244,874 patients, n=1,210 hospitals). First, we performed multivariable logistic regression examining patient factors to calculate a risk-adjusted readmission rate for each hospital. We then used hierarchical modeling to estimate the reliability of this quality measure for each hospital. Finally, we determined the proportion of total variation attributable to three factors: true signal, statistical noise, and patient factors.

Results

The median number of coronary artery bypasses performed per hospital over the three-year period was 151 (79–265 cases 25%–75% interquartile range). The median risk-adjusted 30-day readmission rate was 17.6% (14.4%–20.8% interquartile range). 55% of the variation in readmission rates was explained by measurement noise. 4% could be attributed to patient characteristics, and the remaining 41% represented true signal in readmission rates. Only 53 hospitals (4.4%) achieved a proficient level of reliability >0.70. To achieve this reliability, 599 cases were required over the three-year period. Approximately 1/3 of hospitals (33.7%) achieved a moderate degree of reliability >0.5, which required 218 cases.

Conclusions

The vast majority of hospitals do not achieve a minimum acceptable level of reliability for 30-day readmission rates. Despite recent enthusiasm, readmission rates are not a reliable measure of hospital quality in cardiac surgery.

Introduction

In the recent movement to curtail health care spending, considerable attention has been placed on thirty-day readmission rates after hospitalization. The Center for Medicare and Medicaid Services (CMS) introduced the Hospital Readmission Reduction Program in October of 2012 to financially penalize hospitals for excess readmissions for three medical conditions [1]. While initially focusing on medical conditions, the program will likely be extended to surgery, including cardiac procedures, in the near future. Implicit in these penalties is adequate risk-adjustment to ensure that hospitals with high-risk patient populations are not inappropriately penalized. This has been the focus of multiple studies identifying predictors and risk factors for readmission after cardiac surgery [2–6].

However, the role of chance in driving hospital outcomes is also an important factor to be considered. This can be formalized in the measurement of hospital quality by assessing reliability. Reliability reflects the proportion of hospital-level variation attributable to true differences in quality (“signal”), while the remaining variation is attributable to chance or measurement error (“noise”). Measures with low reliability have low probability of being reproduced, i.e. hospital readmission rates will likely vary significantly from year to year. Reliability for hospital outcome rates is influenced by hospital case volume (i.e. sample size). Low hospital caseloads can reduce the reliability of outcome measurement, thus affecting our ability to discriminate between high quality and low quality hospitals and increasing the likelihood of misclassification of hospitals. This may result in undeserved financial penalties and poor public perception for incorrectly labeled hospitals.

Using data from national Medicare beneficiaries undergoing coronary artery bypass graft surgery (CABG), we sought to determine the reliability of 30-day readmission rates as a measure of hospital quality and evaluate the effect of hospital caseload on reliability.

Patients and Methods

Data source and study population

We used 100 percent national analytic files from CMS for calendar years 2006 to 2008. Medicare Provider Analysis and Review (MEDPAR) files, which contain hospital discharge abstracts for all fee-for-service acute care hospitalizations of all U.S. Medicare recipients, were used to create our main analytical datasets. CMS has chosen to report readmissions data over a three-year period to combat the problem of low sample size, and we analogously chose to analyze hospital readmissions over the same time period to be consistent with CMS policy.

Using appropriate procedure codes from the International Classification of Diseases, Ninth Revision (ICD-9), we identified all patients ages 65–99 undergoing CABG (36.10–19). To minimize the potential for case-mix differences between hospitals, we excluded patients with procedure codes indicating that other operations were simultaneously performed with CABG (i.e. valve surgery) (35.00–99, 36.2, 37.32, 37.34, 37.35), as these patients have much higher baseline risks.

Risk-adjusted 30-day readmission rates

We first estimated hospital-specific risk-adjusted 30-day readmission rates. We adjusted for patient age, gender, race, urgency of operation, median ZIP-code income, year of operation, and comorbidities. Patient comorbidities were adjusted using the methods of Elixhauser, a validated tool developed by the Agency for Healthcare Research and Quality to be used for administrative data [7]. This method identifies 29 patient comorbidities from secondary ICD-9 diagnosis codes that are treated as individual dichotomous independent variables. We used logistic regression to predict the probability of readmission at thirty days for each patient. Predicted readmission probabilities were then summed at each hospital to estimate the expected number of readmissions. We then calculated the ratio of observed to expected readmissions and multiplied this by the average readmission rate to determine risk-adjusted readmission rates.

Estimating reliability

We next calculated the reliability of risk-adjusted readmission rates at each hospital. Reliability, measured from 0 to 1, can be described as the proportion of observed hospital variation that can be explained by true differences in quality [8,9]. For example, a reliability of 0.8 means that 80% of the variance in outcomes is due to true differences in performance while 20% of the variance is attributable to statistical “noise” or measurement error. Reliability can also be thought of the probability that the same results will be repeated from year to year. To perform this calculation, we used the following formula: reliability = signal/(signal + noise) [8,9]. A commonly used cutoff for acceptable reliability when comparing performance of groups is 0.7 [8,9].

In order to determine signal, we first performed risk adjustment using the same patient characteristics described previously to combine all patient risk factors into a single predicted risk score. The risk score, expressed as log(odds) of readmission, was then added as a single independent variable in subsequent modeling. We used log(odds) of readmission, rather than predicted probability, because log(odds) are linear with respect to the outcome variables. We then created a subsequent model for readmission using hierarchical logistic regression, an advanced statistical technique that explicitly models variation at multiple levels (i.e. patients, surgeons, hospitals). For this study, we used a 2-level model with the patient as the first-level and the hospital as the second-level. The patient risk score (logodds of readmission) was used as the only patient-level variable. We used the risk score rather than all individual variables to simplify the model and decrease the likelihood of non-convergence (failure to find a model that fits the observed data), which is can be more common in hierarchical models. The hospital identifier was the only second-level variable. In our formula to calculate reliability, signal was defined as the variance of the hospital-level random effect.

Noise was calculated using techniques for determining the standard error of a proportion [8]: the square root of p(1−p)/n, where p is the probability of readmission and n is hospital volume. Signal was defined as the variance in the hospital random effect, and noise analogously was defined as the variance in the error: p(1−p)/n. This formula is expressed in linear units. For log(odds) units used in our analysis, the formula adjusts to: Noise = 1/(p(1−p))*(1/n).

Attributing variation to noise, signal, and patient factors

We then estimated the proportion of hospital variation attributable to patient factors, noise, and signal. The proportion of variation due to noise was calculated as 1-reliability, where reliability was described as above. To estimate the proportion of variation due to patient factors, we used two sequential random effects models. The first (“empty”) model was estimated with a random hospital effect but no patient characteristics. A second random effects model was performed that included patient characteristics. Using standard techniques, we calculated the proportion of variation due to patient factors from the change in the variance of the random effect: (variance model 1 − variance model 2)/variance model 1. To graphically demonstrate the proportion of variation due to each factor, we stratified hospitals into five equal groups according to CABG volume. We then determined the amount of variation due to patient factors, noise, and true differences in hospital quality (signal). Statistical analyses were conducted using STATA 12 statistical software (College Station, TX).

Results

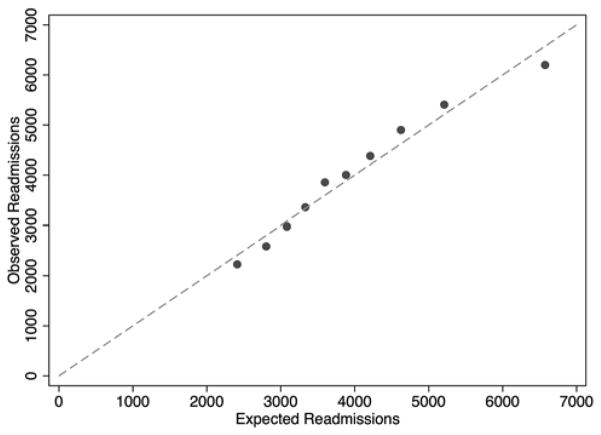
From 2006 to 2008, a total of 244,874 patients from 1,210 hospitals underwent CABG. The median number of coronary artery bypasses performed per hospital over the three-year period was 151 (79–265 cases 25%–75% interquartile range). The median risk-adjusted 30-day readmission rate was 17.6% (14.4%–20.8% interquartile range). Patient demographics are listed in Table 1. Readmitted patients were slightly older, more likely to be non-white and operated on more urgently. Comorbidites were also more prevalent in readmitted patients. All of these patient factors were incorporated into our logistic regression. The c-statistic of our model was 0.60. The Hosmer-Lemeshow test is not reported as a measure of calibration because of its sensitivity to sample size. With large sample sizes, the null hypothesis will inevitably be proven false, given that all such models are only approximations [10]. As an alternative, Figure 1 plots observed versus expected readmissions within deciles of predicted risk.

Table 1.

Characteristics of Medicare Beneficiaries Undergoing Coronary Artery Bypass for 2006–2008

Preoperative Characteristics	Readmitted n=41,410 (16.9%)	Non-Readmitted n=203,464 (83.1%)	p-value
Mean Age (SD)	74.9 (6.1)	74.0 (5.8)	<0.001
Male (%)	66.2	68.7	<0.001
Non-white (%)	10.8	9.7	<0.001
Elective procedure (%)	43.6	49.8	<0.001
Low socioeconomic status (%)	26.1	24.5	<0.001
Comorbidities
Hypertension (%)	58.8	65.5	<0.001
Congestive heart failure (%)	17.6	12.9	<0.001
Valvular disease (%)	8.0	7.4	<0.001
Pulmonary circulation disorders (%)	1.7	1.4	<0.001
Peripheral vascular disease (%)	11.6	11.2	0.02
Chronic lung disease (%)	23.7	18.9	<0.001
Diabetes without complications (%)	24.8	26.2	<0.001
Diabetes with complications (%)	5.1	3.7	<0.001
Renal failure (%)	15.6	10.4	<0.001
Coagulopathy (%)	9.6	8.7	<0.001
Fluid and electrolyte disorders (%)	19.6	17.0	<0.001

Figure 1.

Calibration plot of observed vs. expected readmissions within deciles of predicted risk for patient level logistic regression model of 30-day readmissions.

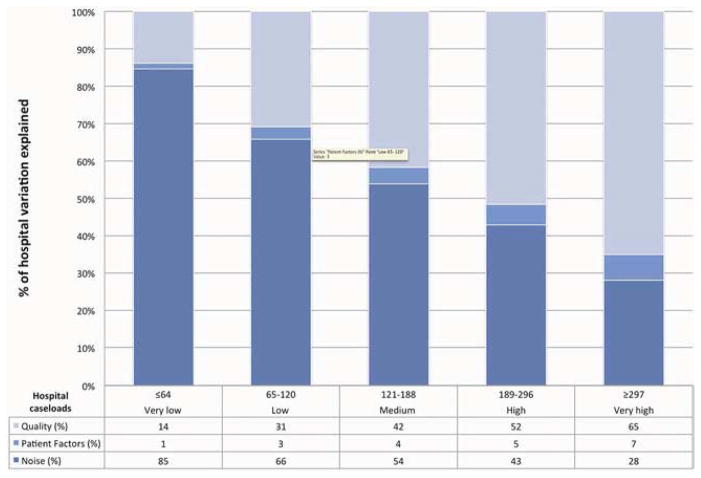
The majority of the overall variation was due to noise (55%). 4% of the variation was due to patient characteristics, and 41% represented true differences in hospital readmission rates. When hospitals were divided into very low (≤64 cases), low (65–120), medium (121–188), high (189–296) and very high (≥297) volume, the proportion of variation explained by patient factors varied across quintiles, ranging from 1% to 7% (Figure 2). The proportion of variation explained by noise decreased as caseload increased from 85% in the very low volume quintile to 28% in the very high volume quintile. The number of patients in each group was 8,137 (very low), 22,439 (low), 37,283 (medium), 57,537 (high), and 119,478 (very high).

Figure 2.

The proportions of hospital variation in risk-adjusted post-CABG 30-day readmission rates attributable to “noise” or measurement error, patient factors, and hospital performance.

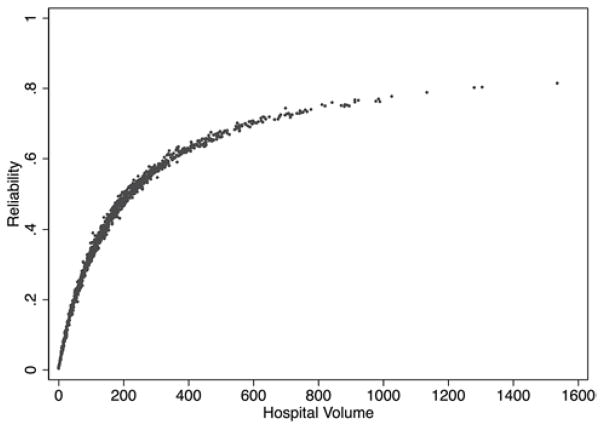
When reliability was graphed against hospital caseload, there was increased reliability with increased hospital volume (Figure 3). In order to achieve a cut-off of 70% reliability, a minimum of 599 cases had to be reported. Only 53 hospitals (4.4%) had enough cases to have excellent reliability. To achieve a minimum of 50% reliability, a minimum of 218 cases had to be reported. 408 hospitals (33.7%) were able to achieve this level of reliability.

Figure 3.

Relationship between reliability of post-CABG readmission rates and hospital volume of CABG based on national Medicare beneficiaries for 2006–2008.

Comment

This study demonstrates the lack of statistical reliability of using 30-day readmission rates as a measure of hospital quality. We found that the majority of variation between hospital readmission rates is attributable to statistical noise. Reliability is primarily determined by the number of cases and frequency of outcomes [8, 9]. The majority of cardiac surgery centers do not perform enough CABGs to generate a reliable readmission rate.

Although no prior studies have evaluated the reliability of readmissions as a quality measure, reliability has been assessed for other outcomes in surgery. In Vascular Surgery, Osborne and colleagues demonstrated that a large proportion of variation in mortality after vascular surgery was also due to statistical noise [11]. Kao and colleagues examined surgical site infection rates after colon surgery and concluded that infection rates could reliably be used as a hospital quality measure when an adequate number of cases could be evaluated (94 cases) [12].

The concept of reliability has also been previously explored in cardiac surgery. Shahian and colleagues studied hospital mortality rates, and demonstrated that traditional logistic regression led to inaccurate hospital rankings when making hospital report cards in Massachusetts [13]. As a result of this work, the state of Massachusetts uses advanced statistical techniques that account for small sample sizes (i.e. hierarchical modeling) to profile hospitals. Our study adds to the previous literature by extending the examination of reliability of outcome rates to another outcome: readmissions. This is particularly policy-relevant given Medicare’s increasing focus on profiling hospitals based on readmissions.

This study has important implications for policy. CMS is already assessing financial penalties to hospitals for excess readmissions for medical conditions and will likely extend this to surgery in the near future. When designing payment reform that directly targets hospitals with financial penalties, it is important to consider the reliability of hospital quality measures. Prior studies evaluating outcome rates in other surgical populations have demonstrated that poor reliability can substantially misclassify hospitals [11, 14]. This misclassification can have substantial implications on public perception and hospital finances. CMS has attempted to address concerns regarding the reliability of readmission rates by analyzing hospital readmissions over a three-year period. This may help reduce the noise due to low sample size in some hospitals, but it will not overcome it in many cases. Despite aggregating data over three years, our analysis suggests that readmission rates are still not reliable enough to discriminate hospital performance as much of the variation is due to chance variation. Thus, the proposed financial penalties will largely be determined by chance, and not true differences in hospital quality.

This study also has important implications for how we measure outcomes in surgery. Given the general lack of statistical precision for outcomes including readmissions, we must ensure that we guard against being fooled by chance. Traditional methods to do this are with p-values and confidence intervals. However, these may be misleading or difficult to interpret. Another approach would be to use advanced hierarchical modeling strategies that are already implemented in the STS composite measures for CABG and aortic valve replacement or CABG report cards in Massachusetts to adjust for reliability [13, 15, 16]. Prior analysis in surgical populations has demonstrated that these modeling strategies reduce statistical noise and improve the ability to forecast future performance and help patients select best hospitals [17]. Though these methods have been applied for surgical process measures and outcomes like morbidity and mortality, thus far they have not been applied for readmission rates.

One important consideration in this study is the use of administrative data in our analysis. Although our analysis is adjusted for patient demographics and comorbidities, the clinical robustness of Medicare claims data is suboptimal; it does not capture important clinical details that may play a major role in predicting readmissions. Furthermore, Medicare claims data only capture patients older than 65. A comprehensive assessment of risk-factors for readmission using a clinically rich database with a broader cohort of patients such as the STS National Adult Cardiac Surgery Database is an important area of further research. However, the performance of this model may still be sub-optimal compared to other well-established STS risk models for mortality and other outcomes [18]. Even in clinical registry data, many factors that may influence readmissions (e.g. living alone, unmet functional needs, limited education, lack of self-management skills) may not be captured [19]. Furthermore, the Hospital Readmissions Reduction Program is specifically designed and executed using Medicare claims data. Our data source is consistent with the methodology that will be utilized for this policy.

This study has additional limitations. First, only isolated CABG data were included in the analysis. We did not examine valvular surgery, CABG in conjunction with another procedure, or other cardiac procedures. As the volume of aortic valve replacement is expanding, extending this analysis to valvular surgery is an important next step. However, isolated-CABG is the most common cardiac procedure. Other procedures are performed with less frequency and higher reported readmission rates. Thus, including other cardiac procedures in the analysis would likely further decrease the reliability of readmission rates, which we have demonstrated to already be statistically unreliable. Additionally, our hierarchical model only examined variation at the hospital and patient level. We did not incorporate an intermediate surgeon-level into our modeling. However, surgeon volumes are only a fraction of a total hospital’s case volume. We have already demonstrated hospital-level readmission rates are unreliable. To incorporate an intermediate surgeon-level would only further decrease the reliability of readmission rates.

Conclusions

We have demonstrated that risk-adjusted 30-day post-CABG readmission rates are not a statistically reliable measure of hospital quality in cardiac surgery. The majority of hospitals do not achieve a high enough procedural volume of coronary artery bypass to achieve a minimum acceptable level of reliability. Consideration should be given to advanced statistical methods that account for small sample size (i.e. hierarchical modeling) to adjust for the reliability of measured outcomes, particularly given the implications of misclassifying hospitals and surgeons based on performance.