Dynamic Interactions of Gas Exchange, Body Mass, and Progressive Exercise in Children

Abstract

Purpose

Cardiopulmonary exercise testing (CPET) is increasingly used as a biomarker of fitness in children. Maximal or peak values remain the most common variables obtained in CPET, but these physiologically challenging high-intensity work rates are often not achieved. We hypothesized that interactions of gas exchange, heart rate (HR), and work rate (WR) CPET variables (slopes) could yield useful mechanistic and clinical insights that might enhance the clinical utility of CPET in children. We further hypothesized that the dependence of the slope on body mass could be predicted by first-principle analysis of body size and physiological response.

Methods

One hundred sixty-nine healthy participants (8–18 years old, BMI<95^th percentile, 82 females) underwent dual X-ray absorptiometry scan to estimate lean body mass (LBM) and performed a ramp-type progressive cycle ergometry exercise protocol with breath-by-breath measurement of gas exchange. Linear regression was used to calculate the slopes among $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2,\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2,{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}$, HR, and WR.

Results

ΔWR/ΔHR (r=0.87) and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}(\mathrm{r}=0.96)$ were strongly correlated with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, while $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}(\mathrm{r}=0.42)$ and $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2(\mathrm{r}=-0.51)$ were mildly correlated with peak values. LBM was more highly correlated than was total body mass with those slopes predicted to be body size dependent (p<0.0001).

Conclusion

The data largely supported our original hypotheses. Unlike peak or maximal values, which are derived from no more than a few data points at the end of a progressive exercise test, the CPET slopes were calculated from a much larger data set obtained throughout the test. Analysis of these slopes might ultimately prove useful clinically and in research studies when peak values are not achieved.

INTRODUCTION

Children are naturally physically active (25;35) and, therefore, quantifying physical fitness through formal exercise testing is increasingly useful as a biomarker in a variety of pediatric conditions (4). Physiological parameters obtained at maximal or peak exercise (most notably, maximal oxygen uptake-$\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$ or peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$) remain the most widely used type of laboratory test in pediatric clinical trials and research. As outlined below, true plateaus or reductions in oxygen uptake despite increasing work rate (WR), the hallmark of $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$, occur only in a minority of children. Cardiopulmonary exercise testing (CPET) is minimally invasive, rendering it suitable for studies in children. CPET is typically performed with cycle ergometers or treadmills, in which the work input increases progressively until the child reaches the limit of his or her tolerance (10).

Maximal exercise tests are, by definition, highly dependent on the willingness of each child to continue exercise at relatively high work rates when dyspnea, muscle fatigue, and other stress sensations are commonly experienced. Not surprisingly, the “cheerleading” abilities of the laboratory personnel contribute to the achievement of a true maximal response in CPET. Despite its proven clinical and research utility, $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$, as noted, only occurs in a minority of exercise tests even in otherwise healthy children and maybe less so in children with chronic disease or disability. For example, in a recent large study of children and adolescents (mean age 12.3 years old) who had undergone the Fontan correction for congenital heart disease during childhood, only 166 of 411 patients (40%) achieved an acceptable $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$ using current criteria (31). This is one reason why many clinicians and researchers choose to use the “peak” $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ rather than $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$.

Most modern commercially available CPET devices measure gas exchange variables ($\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, carbon dioxide output-$\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$, ventilation-${\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}$) and heart rate (HR) quite frequently (e.g., breath-by-breath or with mixing chamber gas collection devices in regular intervals multiple times per minute), and these data are collected well before maximal exercise is achieved. Thus, when a child does not reach an exercise level in CPET that can be classified as maximal, the whole test may be deemed a failure despite the wealth of data successfully collected. Such data could shed light on fitness and other specific indicators of cardiac, pulmonary, or metabolic disease even in the absence of a true $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$. The purpose of this study was to test hypotheses focused on key determinants of CPET data based on dynamic components of the gas exchange and heart rate physiological responses. We used rates of change of gas exchange variables and HR (“slopes”–see Figure 1) which, in contrast to peak or maximal $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, incorporate the bulk of data collected during CPET, rather than just a relatively few data points at the end of the test. Finally, we related the slope analysis to lean body mass (LBM) as an estimate of muscle mass, the essential metabolic determinant of oxygen utilization during exercise.

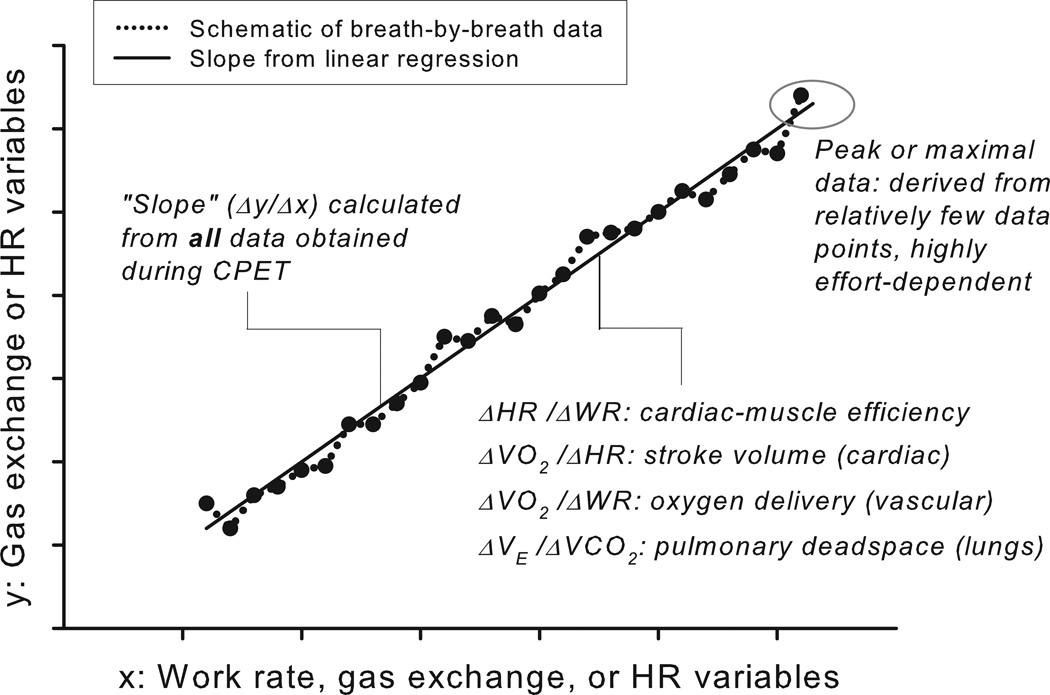
Figure 1.

A schematic generalization of the determination of slopes of key CPET variables from a ramp-type, cycle ergometry, progressive exercise protocol. Unlike the peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ or $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$, which rely on a relatively small set of data obtained during very heavy exercise, the slopes are derived from a much larger set of data obtained throughout the exercise protocol.

Based on a theoretical framework suggested earlier (6) and outlined below, we hypothesized that:

1. Certain slopes (notably, ΔWR/ΔHR and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$) would correlate closely with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. Other slopes (e.g., $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ and $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$) would not correlate with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$.

2. The slopes that correlate closely with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ would also correlate closely with body size and the correlation would be greater with LBM than with body weight, i.e. total body mass (TBM).

Theoretical Framework

Gas Exchange Response to Ramp Forcing Function

A ramp protocol is used extensively in CPET in adults and children, and is so named because exercise is performed on a cycle ergometer and work rate increases linearly in a ramp-type pattern until the participant reaches the limit of his or her tolerance. Whipp and coworkers (42) elegantly outlined the theoretical and experimental framework that predicted and demonstrated the largely linear response of $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ to the steady increase in work rate during ramp exercise protocols. Their model assumed a system with first-order linear dynamics, an assumption which is accurate for low-intensity exercise. A number of studies have attempted to determine the value of τ (the time constant for the first-order linear equation) for gas exchange and HR variables in children (7;26). Factors such as maturational status and the presence of disease and obesity appear to play a role (32;39). After the initial minutes of the ramp test, $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ approaches a linear increase as the ramp progresses. We do recognize that system dynamics become more complex when exercise is performed at high intensities (23). In children, much additional work is needed to examine the maturation of the kinetics of CPET variables during growth and maturation.

Body Size and CPET Variables

Body size and muscle mass change rapidly in children, presenting key challenges to the interpretation of CPET. The noted comparative biologist A. A. Heusner (20) set out a paradigm for scaling biological systems in general. His approach has particular relevance to exercise in children. Heusner conceptualized the concept that thermodynamic systems can be descripted by either extensive or intensive properties. An extensive property is one whose magnitude depends on the size of a system (mass, surface area, volume, energy, heat capacity, etc.); an intensive property is one whose magnitude is size-independent (density, pressure, temperature, etc.)

This approach is useful in determining which exercise-associated physiological variables intrinsically change during the process of growth. Simple scaling equations, such as

$$\mathrm{P}\propto {\mathrm{M}}^{\mathrm{b}}$$

where P is a metabolic variable, M is body mass, and b is the scaling factor, can be useful in this context. In extensive exercise metabolic variables, b is close to 1 suggesting a dependence on body mass itself. Extensive aerobic parameters of exercise likely include peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, which is determined in large measure by the mass of oxygen used in oxidative phosphorylation, which, in turn, is highly dependent on muscle mass. Indeed, peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ in children is highly dependent on body size and muscle mass. Moreover, it is likely that muscle mass, the metabolically active tissue during exercise, would be more highly correlated with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ than would fat mass, whose metabolism changes very little during brief exercise. Consequently, we expected a closer correlation between peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and LBM than between peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and TBM, which includes both fat and lean tissue.

In contrast, one might expect that physiological frequencies, such as HR, would be far less dependent on body mass per se. Indeed, despite the differences in body mass and peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ between adults and children, rest-to-peak HR changes during CPET are quite similar in children and young adults (41).

Our hypotheses were based on the idea that muscle mass would be the predominant determinant of the slopes in healthy children. As a starting point, we used simple linear approximations (y=α+β·x in which β is the slope and α is the y-intercept) to examine the following representative relationships using Heusner’s concept of size-dependent and size-independent properties of thermodynamic systems:

1. WR−HR: HR = α+β·WR, where HR is size-independent and WR is size-dependent;

2. $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2-\mathrm{H}\mathrm{R}:\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2=\alpha +\beta ·\mathrm{H}\mathrm{R}$, where $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ is size-dependent and HR is size-independent;

3. $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2-\mathrm{W}\mathrm{R}:\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2=\alpha +\beta ·\mathrm{W}\mathrm{R}$, where $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and WR are both size-dependent;

4. ${\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}-\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2:{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}=\alpha +\beta ·\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$, where${\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}$ and $\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ are both size-dependent.

Since only one side of the equation in 1) and 2) is size-dependent, it follows that ΔWR/ΔHR (inverse of ΔHR/ΔWR) and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ are dependent on body mass. In contrast, both sides of the equation in 3) and 4) are size-dependent, thus the body mass factor is canceled out, leading to the assumption that $\mathrm{\Delta }\mathrm{W}\mathrm{R}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ are independent of body mass.

METHODS

Volunteers

From five UC Irvine Institutional Review Board-approved pediatric exercise research studies where a CPET was performed in our laboratory, we identified children and adolescents aged 8–18 with no serious health conditions, non-asthmatic, non-obese (BMI < 95^th percentile), and who had a dual X-ray absorptiometry (DXA) measurement within 30 days of the exercise protocol to be studied in this paper. There is currently no validated, universally accepted respiratory exchange ratio (RER) cutoff in children for the determination of peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. We used RER ≥1.0, a criterion recently used in a large study by Rowland and coworkers (34). For subjects who participated in more than one study, one test was randomly selected. Appropriate assents and consents were obtained from each participant and his or her parent or guardian by each study.

Anthropometric Measurement and Body Composition

Standard, calibrated scales and stadiometers were used to determine TBM and height. Body composition, including LBM, fat mass, and percent body fat (% fat) were determined by DXA using a Hologic QDR 4500 densitiometer (Hologic Inc., Bedford, MA). Participants were scanned in light clothing while lying supine. On the day of each test, the DXA instrument was calibrated using the procedures provided by the manufacturer and DXA scans were performed and analyzed using pediatric software.

Measurement of Peak $\stackrel{•}{V}{O}_{\mathit{2}}$ and Slopes

Each participant performed a ramp-type progressive cycle ergometry using the SensorMedics metabolic system (Ergoline 800S, Yorba Linda, CA) and gas exchange was measured breath-by-breath. We used peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ which was calculated as the maximum of 30-second averages (moving average of every 6 seconds) over the last 2 minutes of exercise. From the WR, HR, and gas exchange measurements obtained during CPET, the slopes were calculated using standard linear regression as described under Theoretical Framework using all data obtained during CPET.

Physiologically abnormal data for HR and gas exchange (e. g., HR<50 beat/min or >230 beat/min, $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2=0\mathrm{L}/\text{min}$ or >5 L/min) and outliers, based on each subject, are occasionally observed in breath-by-breath CPET data obtained in children. These data were identified and excluded for peak or slope calculation.

Statistical Analysis

Descriptive statistics are presented with mean and standard deviation (SD). Bivariate relationships between CPET measurements, including peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and slopes, and body mass indices were calculated using Pearson’s correlation (r) and the corresponding 95% confidence interval (CI) was obtained using Fisher’s z transformation (17). The procedure described by Meng et al. (29) was utilized to compare correlations of CPET variables with TBM and LBM. Analysis of covariance (ANCOVA) was applied to evaluate gender difference in slopes using age at CPET as a covariate. All analyses were performed using SAS 9.2 (Cary, NC) and the significance level was set at 0.05.

RESULTS

Participants Characteristics

A total of 388 participants (age range 8 to 18 years old) were identified from five studies and 302 subjects had a DXA measurement within 30 days of the exercise protocol. From this group, 18 were excluded because they were asthmatic, 85 were excluded because of morbid obesity, 10 were excluded because their maximum RER was less than 1.0, 9 were excluded due to technical problems, such as incomplete data collection, loose HR electrodes, or leaks in the mouth piece. We also excluded 11 CPETs because they were repeats from the same individual. Eventually, a total of 169 participants (82 girls) were included in this study. Among them, 27 (15.6%) were overweight (BMI ≥ 85^th percentile), 30 (17.8%) were Asian, 3 (1.8%) were African-American, 102 (60.4%) were Caucasian, 33 (19.5%) were Hispanic, and one did not provide race information. The summary statistics of anthropometrics, body composition, and CPET outcome variables by gender and age are presented in Table 1. Of the participants included for analysis, only 30 (17.8%) achieved a plateau consistent with a true $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$, 14 (8.3%) had a RER < 1.05, and 109 (64.5%) had a RER ≥1.1. Also note that 55 (32.5%) subjects had less than 5% abnormal breath-by-breath data excluded, 8 (4.7%) subjects had 5–10% data excluded, and only 2 (1.2%) subjects had more than 10%, but less than 13%, data excluded.

Table 1.

Summary Statistics of Anthropometrics, Body Composition, and CPET Variables

		Age (years-old)
		8–10	11–13	14–15	16–18
Number of Subject	Female	27	17	22	16
	Male	30	19	18	20
Height (cm)	Female	137.4 ± 8.7	154.1 ± 9.5	163.3 ± 7.5	165.8 ± 5.9
	Male	138.9 ± 6.6	155.5 ± 12.1	170.6 ± 10.5	175.7 ± 6.3
Weight (kg)	Female	31.8 ± 6.3	45.0 ± 10.2	56.9 ± 10.4	59.3 ± 7.4
	Male	33.4 ± 5.9	45.8 ± 11.2	61.8 ± 12.9	68.8 ± 11.2
BMI (kg/m2)	Female	16.7 ± 1.9	18.8 ± 3.1	21.3 ± 3.2	21.6 ± 2.5
	Male	17.2 ± 2.1	18.7 ± 2.7	21.0 ± 2.6	22.2 ± 2.5
BMI %tile	Female	45.1 ± 27.2	50.0 ± 34.6	57.7 ± 30.3	54.1 ± 25.2
	Male	53.0 ± 28.4	51.7 ± 31.1	59.6 ± 25.2	55.1 ± 25.1
LBM (kg)	Female	23.9 ± 4.4	33.7 ± 7.1	42.5 ± 6.7	43.5 ± 5.2
	Male	25.6 ± 3.5	36.1 ± 9.5	51.2 ± 9.8	59.0 ± 8.6
Fat mass (kg)	Female	8.1 ± 2.7	11.5 ± 5.0	14.6 ± 6.0	15.7 ± 4.5
	Male	7.8 ± 3.2	9.9 ± 5.3	10.9 ± 5.4	9.9 ± 4.0
% Fat	Female	25.1 ± 4.9	24.9 ± 7.0	24.8 ± 6.9	26.3 ± 5.6
	Male	22.6 ± 5.6	21.2 ± 8.6	17.0 ± 6.0	14.1 ± 3.8
Exercise Time (minute)	Female	9.1 ± 1.2	9.2 ± 1.7	9.6 ± 1.4	9.6 ± 1.6
	Male	9.6 ± 1.7	10.9 ± 2.2	10.7 ± 1.6	11.5 ± 1.8
Ramp Level (watt/min)	Female	10.5 ± 1.4	14.7 ± 3.1	18.9 ± 3.8	19.3 ± 4.1
	Male	11.0 ± 1.9	14.8 ± 3.9	21.1 ± 5.1	23.4 ± 3.6
Max WR (watt)	Female	93.9 ± 15.8	131.8 ± 35.4	177.7 ± 36.3	181.9 ± 42.9
	Male	101.7 ± 16.5	155.9 ± 40.3	220.1 ± 50.8	266.9 ± 54.6
Peak HR (beat/min)	Female	188.8 ± 10.6	191.3 ± 11.9	186.9 ± 8.3	186.4 ± 10.4
	Male	187.7 ± 8.5	189.1 ± 7.8	187.4 ± 11.0	194.0 ± 10.0
Peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ (L/min)	Female	1.1 ± 0.2	1.6 ± 0.6	2.1 ± 0.5	2.1 ± 0.5
	Male	1.4 ± 0.3	2.0 ± 0.6	2.8 ± 0.7	3.2 ± 0.9
Peak $\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ (L/min)	Female	1.3 ± 0.3	1.9 ± 0.7	2.4 ± 0.6	2.5 ± 0.7
	Male	1.5 ± 0.3	2.3 ± 0.7	3.1 ± 0.8	3.9 ± 1.2
Peak ${\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}$ (L/min)	Female	47.6 ± 7.8	63.3 ± 15.3	73.5 ± 16.6	75.0 ± 17.0
	Male	53.5 ± 8.2	72.7 ± 17.0	94.3 ± 29.6	111.6 ± 32.3
Peak RER	Female	1.12 ± 0.05	1.13 ± 0.05	1.16 ± 0.07	1.18 ± 0.07
	Male	1.09 ± 0.06	1.14 ± 0.07	1.14 ± 0.08	1.20 ± 0.05

Values are mean ± SD.

Relationship Between Peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and Slopes

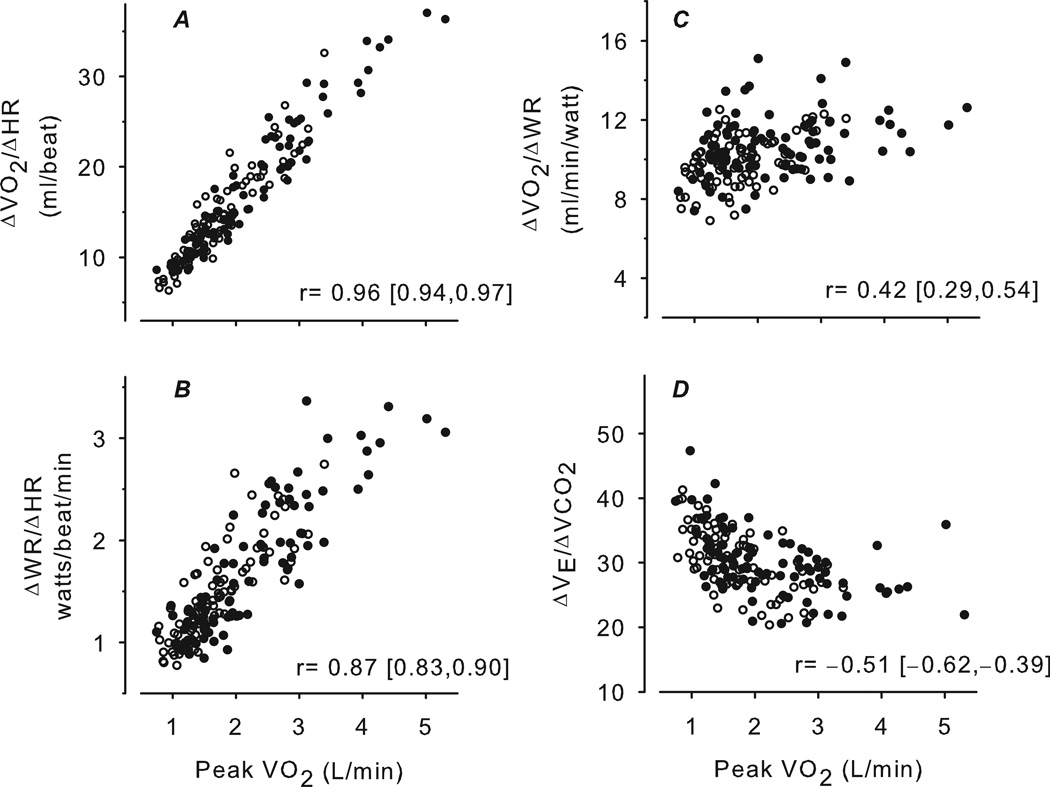
As seen in Figure 2, peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ was correlated strongly with $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ and ΔWR/ΔHR but with $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$. The correlation was negative between peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$. In addition, ΔWR/ΔHR and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ were highly correlated with each other (r=0.93 [95% CI: 0.90, 0.95]) and both negatively correlated with $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ (ΔWR/ΔHR: −0.45 [−0.57,−0.33]; $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$: −0.52 [−0.62,−0.40]). $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ had no correlation with ΔWR/ΔHR (0.08 [−0.07, 0.23]), but was mildly correlated with $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ (0.41 [0.28,0.53]).

Figure 2.

Scatter plots of CPET variables predicted to be relatively body size-dependent (A, B) and body size-independent (C, D) versus peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. Females are shown as open circles, males as closed circles. The correlation and corresponding 95% CI are shown for each plot. The body size-dependent CPET variables, $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ and ΔWR/ΔHR, were highly correlated with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. Since these variables do not require achievement of a maximal or near maximal effort, they may be useful as surrogates for peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ (or $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$) for subjects who are unable to achieve an acceptable peak or maximal $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. In contrast, the body size-independent variables, $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ and $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$, were mildly correlated with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. The value of these slopes is not as a surrogate for peak $\stackrel{•}{\mathrm{V}}\mathrm{O}2$, but rather a useful additional biomarker for abnormal respiratory or cardiovascular function that may only be detected with exercise.

Peak $\stackrel{•}{V}{O}_{\mathit{2}}$ and Slopes Versus Age and Body Size

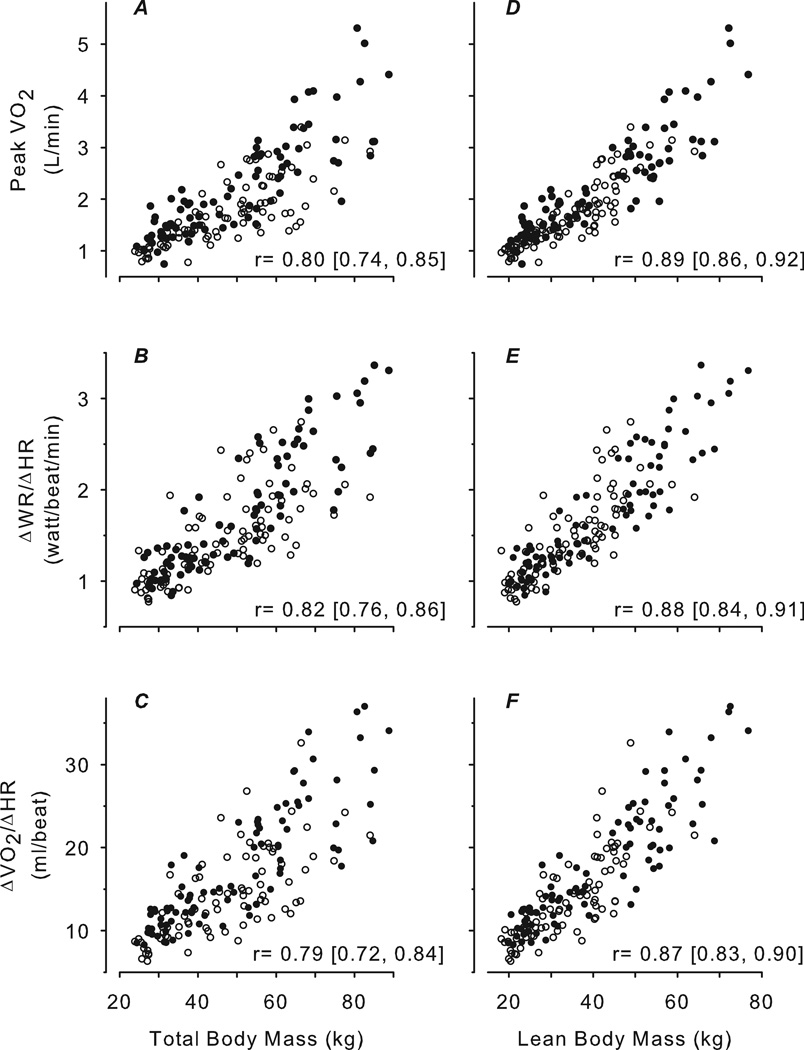
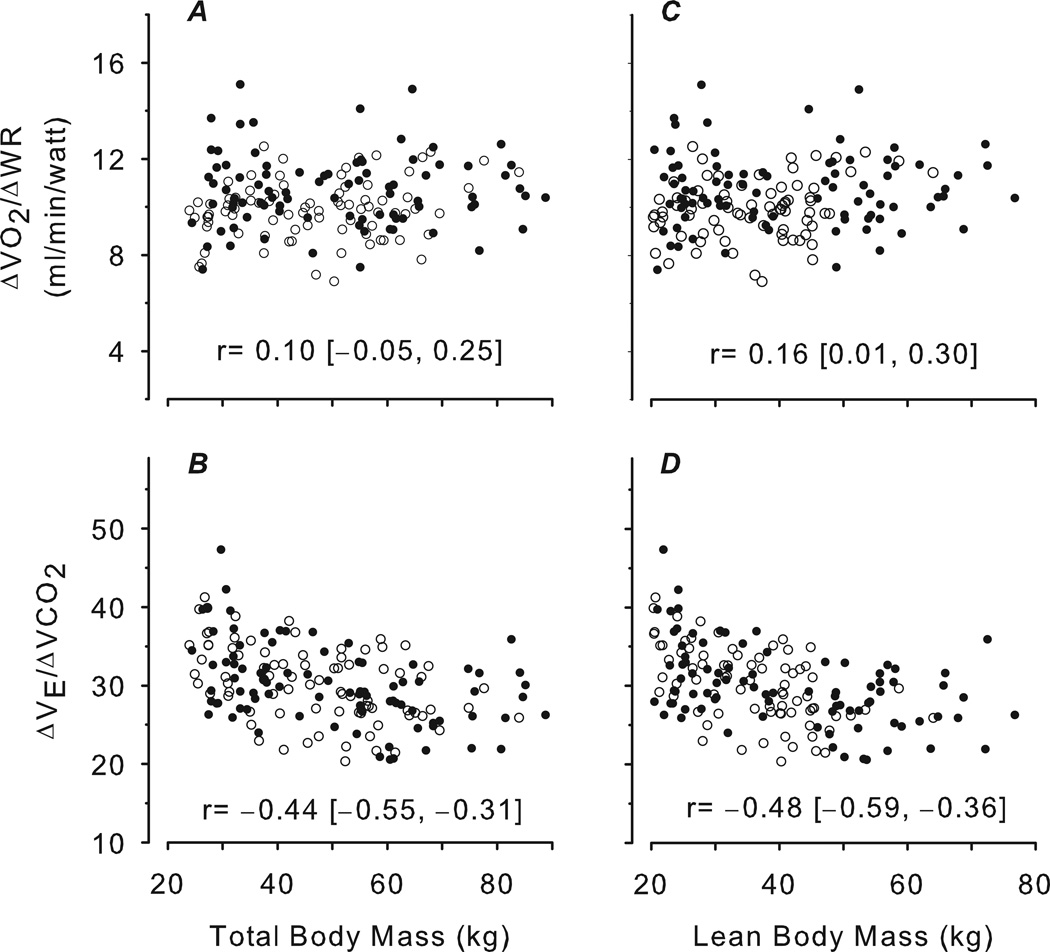
Figure 3 shows that peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, ΔWR/ΔHR, and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ were highly correlated with TBM and LBM, and the correlation with LBM was significantly higher than with TBM (p<0.0001). Figure 4 shows that $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ was negatively correlated with body mass and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ had no correlation with body mass. Peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, ΔWR/ΔHR and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ were also moderately correlated with age (r: 0.69–0.73), highly correlated with height (0.81–0.83), weakly correlated with fat mass (0.14–0.24), and inversely correlated with %fat (−0.48 – −0.39).

Figure 3.

Scatter plots of CPET variables predicted to be relatively body size-dependent versus TBM determined by standard scale (A, B, C) and LBM determined by DXA (D, E, F). Females are shown as open circles, males as closed circles. The correlation and corresponding 95% CI are shown for each plot. In all cases, the correlations with TBM were high but were significantly improved with LBM.

Figure 4.

Scatter plots of CPET variables predicted to be relatively body size-independent versus TBM determined by standard scale (A, B) and LBM determined by DXA (C, D). Females are shown as open circles, males as closed circles. The correlation and corresponding 95% CI are shown for each plot. As predicted, the correlations with both body size were weak or mild. The data indicate that CPET slopes such as $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ may be useful to corroborate the integrated accuracy of the CPET ergometers and gas exchange measuring devices for laboratories that test participants with a wide range of body size. The negative correlation of $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ with body size has been observed before and might indicate a progressive reduction in physiological deadspace and/or increase in the CO₂ respiratory control set-point as children grow and mature.

Gender Difference in Slopes

In a post hoc analysis, we examined the effect of gender on CPET slopes. The ANCOVA results showed that boys had significantly higher ΔWR/ΔHR (p=0.0003), $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ (p<0.0001), and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ (p=0.0003) than girls after controlling for age. Table 2 presents the summary statistics of slopes by gender and age groups.

Table 2.

Summary Statistics of CPET Slope Variables

		Age
		8–10	11–13	14–15	16–18
ΔWR/ΔHR* (watt/beat/min)	Female	1.1 ± 0.2	1.4 ± 0.3	1.8 ± 0.4	1.8 ± 0.4
	Male	1.1 ± 0.2	1.5 ± 0.3	2.3 ± 0.6	2.4 ± 0.5
$\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$* (mL/beat)	Female	9.6 ± 2.3	13.9 ± 3.9	17.8 ± 5.7	16.9 ± 3.5
	Male	11.3 ± 2.2	15.8 ± 4.5	23.0 ± 5.6	24.3 ± 6.9
$\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$* (mL/min/watt)	Female	9.6 ± 1.2	10.1 ± 1.3	10.0 ± 1.2	9.9 ± 1.1
	Male	10.6 ± 1.7	10.9 ± 1.5	10.6 ± 1.4	10.5 ± 1.4
$\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$	Female	33.0 ± 4.5	31.7 ± 4.2	28.0 ± 4.4	27.8 ± 3.6
	Male	33.3 ± 5.2	29.5 ± 3.7	28.6 ± 4.3	26.8 ± 3.9

Values are mean ± SD.

^*Significantly different between boys and girls after controlling for age using ANCOVA.

DISCUSSION

We found that certain CPET slopes showed robust correlations with body size in children and adolescents similar to correlations found for the classical CPET variables like peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ Unlike peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, which is derived from no more than a few data points at the end of a progressive exercise test, the CPET slopes were calculated from a response continuum of gas exchange, WR, and HR variables throughout a large portion of the progressive exercise test. Our hypotheses based on biological concepts of intrinsic and extrinsic (size-dependent and size-independent biological variables) could be applied to an analysis of slopes derived from CPET. The hypotheses were largely substantiated by the experimental data in a very large cohort of children and adolescents. Using DXA measurements, we showed that body size (most prominently, lean body mass) is a critical determinant of some CPET outcome variables while having little or no effect on others.

Study Limitations

Although we treated the response to the ramp-work rate input of key CPET variables ($\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2,\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$, and HR) as if they were first-order and linear, there is evidence suggesting a more complex dynamic. For example, the well-recognized abrupt increase in the slope of the $\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$-WR relationship somewhere between 40–60% of maximal work signifies additional $\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ resulting from buffering of lactic acid produced during exercise beyond muscle-derived, work- related CO₂ production (40). While such alterations in the pattern of gas exchange are clear in well-trained volunteers, they become more difficult to identify in children, in whom respiratory “noise” is more prominent. Moreover, as the complexity of the mathematical model used to fit a data set increases, so does the volume of data required to achieve robust estimates of model parameters (24). Thus, in the present study, we treated the whole breath-by-breath gas exchange response in a relatively simple fashion, one that would yield straightforward parameters of CPET response, useful as biomarkers in research and clinical evaluation. We recognize that more complex analyses of CPET data may prove useful as well [e.g., the oxygen uptake efficiency slope introduced by Baba et al. (2)], and in future studies, the fit of specific physiologically based mathematical models should be tested.

$\stackrel{•}{V}{O}_{\mathit{2}}$-WR Relationship

As hypothesized, $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ was largely independent of body size determined either by TBM or LBM. This observation corroborates a recent study by Ten-Harkel et al. (37) in 175 healthy Dutch school children. In their classic 1969 publication, Whipp and Wasserman (43) delineated the thermodynamic underpinnings of efficiency with regard to the muscular work associated with physical exercise. They later showed how the work efficiency could be calculated from $\mathrm{\Delta }\mathrm{W}\mathrm{R}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ measured during a ramp test (42). Because the primary determinant of work efficiency is the relatively stable interaction among molecular work, ATP rephosphorylation, and oxygen transport and delivery (a function of the vascular system) at the level of the muscle cell, it is not surprising that in healthy subjects, $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ in our study (Figure 4), or $\mathrm{\Delta }\mathrm{W}\mathrm{R}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ in previous studies (12), was independent of muscle mass per se.

The body size independence of the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ and its relatively low coefficient of variation (about 13%, Table 2) point toward its role as a robust screening tool for the quality and comparability of individual CPETs. For example, the finding that the average $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ for normal volunteers in a pediatric exercise laboratory was greater than 2SD above established norms (e.g., 12 or 13 ml O₂/min/watt vs. about 10 ml O₂/min/watt) might prompt an exploration of technical or calibration problems (n.b., this example actually occurred, personal communication, DMC).

Of equal importance is the potential for using the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ as a biomarker for disease. Since Whipp and Wasserman’s conceptualization of work efficiency during exercise, subsequent investigators have shown that this slope is altered when O₂ delivery is abnormal, such as occurs in cardiovascular disease in both adults and children (19;33). As noted earlier, $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$ is often difficult to achieve in patients with heart disease. Consequently, the finding of an abnormal $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$, which can be measured without the subject’s achieving $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$, might be a useful biomarker of underlying cardiovascular disease in children and adolescents.

There was a weak correlation between $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ and peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ (Figure 2). Participants with greater $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ generally achieved greater peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$. Combining this finding with the converse observation noted above, namely, that patients with impaired oxygen delivery from heart disease have lower slopes, would suggest that one’s ability to increase cardiac output (e.g., through larger stroke volume) or to better deliver oxygen to the working muscle (e.g., through greater muscle capillarization) may prove to be a determinant of fitness that is independent of LBM in children and adolescents. In addition, the small but significantly greater value of $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ in boys compared with girls (Table 2) may reflect the larger stroke volumes typically seen in males. $\mathrm{\Delta }\mathrm{W}\mathrm{R}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, previously thought to be equivalent to the thermodynamic work efficiency, is, in fact, altered by factors that influence oxygen delivery. Thus, using $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ as a surrogate for the total energy used (an assumption of the calculation of the thermodynamic work efficiency from the $\mathrm{\Delta }\mathrm{W}\mathrm{R}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ slope of the ramp protocol) may not hold true in the presence of disease.

WR-HR Relationship

In contrast to the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$, we hypothesized that the ΔWR/ΔHR would be highly dependent on body size. Indeed, this was the case. Moreover, like peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, ΔWR/ΔHR was more highly correlated with LBM than with TBM (Figure 3). Finally, ΔWR/ΔHR was, as expected, highly correlated with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$.

Related to ΔWR/ΔHR is the physical work capacity (PWC) test in which the outcome variable is the work rate measured when the subject reaches a preset HR during a progressive exercise test (most commonly, 170 bpm-PWC170). The PWC is extensively used in both children and adults in a wide variety of clinical conditions. It is often used to estimate $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$ in which a submaximal exercise protocol can replace a maximal exercise protocol, thereby avoiding the additional complexity and expense of measurements involving gas exchange (3).

An analysis of the Fick equation identifies the key determinants of ΔHR/ΔWR:

$$\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2=\mathrm{\Delta }[\mathrm{S}\mathrm{V}•\mathrm{H}\mathrm{R}•(\mathrm{a}-\mathrm{v̄})\mathrm{d}{\mathrm{O}}_2]$$

where SV is stroke volume and (a-v̄)dO₂ is the arterio-mixed venous difference in O₂ content. Further,

$$\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2=\mathrm{\Delta }\mathrm{W}\mathrm{R}/\mathrm{W}\mathrm{E}$$

where work efficiency (WE) is a thermodynamic constant. Thus, the ΔWR/ΔHR and the PWC will reflect an individual’s ability to increase stroke volume and widen the arteriovenous O₂ content difference during exercise. Consistent with the relationships outlined above in the Fick equation, PWC170 values are lower in patients with the presence of, or increased risk for, cardiovascular diseases (14;15).

$\stackrel{•}{V}{O}_{\mathit{2}}$-HR Relationship

Given that $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{W}\mathrm{R}$ is close to a constant, it was not surprising to find a high correlation between the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ and ΔWR/ΔHR. In addition, the pattern of correlations between these two slopes and CPET variables and indices of body size were quite similar. The fundamental relationship between $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and HR has long been recognized and was used by Åstrand and Rhyming in 1954 to create an algorithm to estimate $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$ from the measurement of HR alone during exercise (1).

A related, but conceptually distinct, variable often used in CPET is the O₂-pulse. The latter is defined as the ratio of $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ to HR at any given time point during a progressive exercise test. The difference between the O₂-pulse and the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ is subtle but substantial. While the relationship between $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and HR during progressive exercise is largely linear, its x-intercept is never 0; consequently, the shape of the O₂-pulse curve will be hyperbolic and the slope of its asymptote will be equal to the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ (11). Because the O₂-pulse changes throughout a progressive exercise test, it is often expressed as a single value, typically as percent predicted O₂-pulse at maximal exercise.

As would be expected from the analysis of the Fick equation, the O₂-pulse is abnormal in patients with cardiovascular disease (22). Recent data suggest that in children with congenital heart disease, pervasive reductions in stroke volume may be responsible for limited exercise capacity (28). A possible advantage of the $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$ compared with the O₂-pulse max (as percent predicted or as an actual values) is that the potential confounding variable of whether the subject achieved a maximal level is eliminated.

${\stackrel{•}{V}}_E-\stackrel{•}{V}C{O}_{\mathit{2}}$ Relationship

We had hypothesized that $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ would be an intrinsic, size-independent CPET variable. However, we did observe a weak correlation with TBM and LBM. This was not entirely surprising as $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ has been previously shown to change with body size in children by a number of investigators (8;37), albeit using smaller sample sizes.

As has been described in greater detail earlier (8), analysis of the alveolar gas equation indicates that $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ is determined by ventilatory factors such as physiological deadspace, CO₂ storage capacity, and the PaCO₂ set point (the concentration of CO₂ that is homeostatically maintained despite changes in CO₂ production). $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ is abnormal in children with chronic lung diseases like cystic fibrosis, in which ventilatory deadspace is known to be increased (30), and was recently found to be an independent predictor of mortality in adult patients with chronic obstructive pulmonary disease undergoing surgery for non-small-cell lung cancer (38). Thus, analysis of $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ in children with chronic lung diseases may provide specific information about lung function not readily determined from maximal exercise values alone.

CPET Exercise Variables, Slopes, and Body Size: Implications for CPET in Children

The data presented here from children and young adults are particularly useful because gas exchange and HR measurements were made in combination with state-of-the-art determinations of body composition. There was a very strong correlation between LBM and both peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ and the extrinsic, size-dependent CPET slopes (ΔWR/ΔHR and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$). Further, the lack of an effect of % fat corroborates an earlier study of the importance of muscle mass (measured by magnetic resonance imaging) as a determinant of CPET biomarkers in adolescents (16).

We found that % fat per se, to a very small degree, inversely correlated with peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$, ΔWR/ΔHR, and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$–this in marked contrast to the strong positive correlation of these CPET variables with LBM. In most exercise studies of obese children and adolescents, peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ in absolute terms is larger in obese children, but differences between obese and normal-weight children largely disappear when muscle mass is taken into account. Peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ has been found to be predominantly dependent on fat-free mass with little or no influence of fat mass (18). Our finding that a small degree of impaired exercise response was observed in the CPET slopes could indicate a more pervasive impact of body fat on exercise in children and adolescents. Brun and coworkers (5) recently demonstrated interactions between abdominal obesity, circulating lipids, and increased blood viscosity. The latter phenomenon could potentially inhibit oxygen delivery. Other factors, such as impaired peripheral nervous system function associated with obesity (21), could also explain the small effect of body fat per se on exercise.

In the case of $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$, the correlation with % fat mass was positive (0.30 [0.15,0.43]) in contrast to the negative correlations observed with LBM, reflecting maturational differences in ventilatory deadspace, CO₂ storage, and/or the PaCO₂ set point. In an earlier publication, we had demonstrated that the response times for ${\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}$ and $\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ at the onset of constant work-rate exercise (n.b., measured at the mouth) were slower in obese children compared with normal-weight controls, even though the $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ kinetics in the obese participants were not prolonged. (9). This discrepancy could be explained by increased CO₂ stored in body fat delaying the transport of metabolically produced CO₂ from the working muscles to the circulation and lungs (in contrast to CO₂, very little O₂ is soluble in fat). Mismatching of ventilation and perfusion in obesity (27) as well as bronchial hyper-responsiveness (36) might have contributed to the small positive correlation between $\mathrm{\Delta }{\stackrel{•}{\mathrm{V}}}_{\mathrm{E}}/\mathrm{\Delta }\stackrel{•}{\mathrm{V}}\mathrm{C}{\mathrm{O}}_2$ and % fat.

There is a growing body of literature supporting the use of lean body mass as a reference value in interpreting CPET in adults. For example, Crespo and coworkers (13) recently reviewed three separate studies conducted at the Oschner Clinic focused on independent predictors of survival in adult patients with chronic heart failure. These authors reached the conclusion that LBM-corrected CPET variables, especially peak oxygen consumption and oxygen pulse, had greater prognostic value than when the variables were normalized to TBM.

In our data, we found, as expected, that traditional CPET biomarkers like peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ were highly correlated (0.89) with LBM and that the correlations with LBM were greater than with TBM. New observations in this study include our findings that non-traditional CPET slopes (ΔWR/ΔHR and $\mathrm{\Delta }\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2/\mathrm{\Delta }\mathrm{H}\mathrm{R}$) have similarly strong correlations with LBM and peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$.

Our initial analysis suggests that information derived from the analysis of the CPET slopes may augment peak $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2$ data by identifying specific determinants of the exercise response that relate uniquely to ventilatory and/or cardiovascular clinical status of the child or adolescent undergoing testing. We recognize that many questions remain: What is the optimal range and amount of data necessary to reliably determine slopes in children? How do nonlinearities in gas exchange variables during CPET, such as may occur at the lactate or anaerobic threshold, affect the slope value? And what is the impact of specific pediatric illness or conditions on the determination of slopes? Nonetheless, these data and their analyses might suggest ways to gain insight from CPET data obtained in children when a $\stackrel{•}{\mathrm{V}}{\mathrm{O}}_2\text{max}$ is not achieved, a common occurrence in both healthy children and in children with specific diseases and disabilities.