Parameter Variability and Distributional Assumptions in the Diffusion Model

Abstract

In order for the diffusion model (Ratcliff & McKoon, 2008) to account for the relative speeds of correct responses and errors, it is necessary that the components of processing identified by the model vary across the trials of a task. In standard applications, the rate at which information is accumulated by the diffusion process is assumed to be normally distributed across trials, the starting point for the process is assumed to be uniformly distributed across trials, and the time taken by processes outside the diffusion process is assumed to be uniformly distributed. The studies in this article explore the consequences of alternative assumptions about the distributions, using a wide range of parameter values. The model with the standard assumptions was fit to predictions generated with the alternative assumptions and the results showed that the recovered parameter values matched the values used to generate the predictions with only a few exceptions. These occurred when parameter combinations were extreme and when a skewed distribution (exponential) of nondecision times was used. The conclusion is that the standard model is robust to moderate changes in the across-trial distributions of parameter values.

Diffusion models for simple decision processes have received increasing attention over the last five to ten years (e.g., Bogacz et al., 2006; Busemeyer & Townsend, 1993; Diederich & Busemeyer, 2003; Laming, 1968; Link, 1992; Link & Heath, 1975; Palmer, Huk, & Shadlen, 2005; Pleskac & Busemeyer, 2010; Ratcliff, 1978, 1981, 1988, 2002; Ratcliff & Frank, 2012; Ratcliff & Rouder, 1998, 2000; Ratcliff & Smith, 2004; Ratcliff, Van Zandt, & McKoon, 1999; Roe, Busemeyer, & Townsend, 2001; Stone, 1960; van der Maas et al., 2011; Voss, Rothermund, & Voss, 2004). In research in cognitive psychology, the diffusion model and other sequential sampling models (reviewed by Ratcliff & Smith, 2004) have accounted for more and more behavioral data from more and more experimental paradigms. The models are now being used to address questions about cognition for diverse populations and impairments (e.g., aging, Ratcliff, Thapar & McKoon, 2001, 2003, 2004, 2010, 2011; Spaniol, Madden, & Voss, 2006; development, Ratcliff, Love, Thompson, & Opfer, 2012; ADHD, Mulder et al., 2010; dyslexia, Zeguers et al., 2011; sleep deprivation, Ratcliff & Van Dongen, 2009; hypoglycemia, Geddes et al., 2010; anxiety and depression, White, et al., 2010a, 2010b). In most of these domains, the models have led to new interpretations of well-known empirical phenomena. The models are also being applied to neurophysiological data where they show the potential to build bridges between neurophysiological and behavioral data (Churchland, Kiani, & Shadlen, 2008; Gold & Shadlen, 2001, 2007; Hanes & Schall, 1996; Mazurek, Roitman, Ditterich, & Shadlen, 2003; Purcell et al., 2010; Ratcliff, Cherian, & Segraves, 2003).

Early random walk and diffusion models (in the 1970's and 1980's) could not account for the full range of data in simple two-choice tasks, specifically, response times (RTs) for correct and error responses and the relations between them. However, with the simple assumption that the components of processing identified by the model vary in their values from trial to trial, patterns of differences between error and correct RTs that were previously difficult to model could be explained (e.g., errors slower than correct responses, Ratcliff, 1978; errors faster than correct responses, Laming, 1968; and various cross overs such as fast errors in speed-stress conditions becoming slow errors in accuracy-stress conditions, and slow errors in difficult conditions becoming fast errors in easy conditions; see discussions in Ratcliff & McKoon, 2008; Ratcliff & Tuerlinckx, 2002; Ratcliff, Van Zandt, & McKoon, 1999; Wagenmakers, 2009; Wagenmakers et al., 2008).

In this article, we focus on the diffusion model for two-choice decisions (Ratcliff, 1978; Ratcliff & McKoon, 2008), and we investigate whether and how assumptions about the distributions of trial-to-trial variability affect the model's predictions. In the model, information from a stimulus is accumulated over time from a starting point toward one of two boundaries, one for each of the two choices. A response is executed when the amount of accumulated information reaches one of the boundaries. The rate of accumulation is called “drift rate.” Components of processing outside the decision process (e.g., encoding, response execution) are combined into one parameter of the model, labeled the “nondecision” component, that has mean duration T_er. Variability across trials in the values of drift rates, boundaries, and nondecision processes stems from subjects’ inabilities to hold these parameters constant across nominally identical test items.

In almost all applications of the model to date, it has been assumed that the across-trial variability in drift rate is normally distributed, that the across-trial variability in starting point (assumed to be equivalent to across-trial variability in the boundaries) is uniformly distributed, and that nondecision time is uniformly distributed (for convenience, I term these the “standard” assumptions). These distributions were chosen for simplicity, but the sensitivity of the model to changes in the distributional assumptions is an issue that regularly arises. There are two questions. One is whether the model's predictions for accuracy and RTs change as a function of the distributional assumptions. The other is, if the model with the standard assumptions is fit to predictions that were generated from the model with different assumptions, are the recovered parameter values for drift rates, starting point, and nondecision time similar to the ones used to generate the predictions and do they provide similar interpretations of recovered parameter values. These questions are especially important for investigations of the differences between subjects in drift rates, boundaries, and nondecision processes. (For studies that use the diffusion model to examine differences among individual subjects, see Ratcliff, Thapar, & McKoon, 2006, 2010, 2011; Schmiedek et al., 2007).

For the research described in this article, I generated predictions for RTs and accuracy from the model, changing the assumptions about across-trial variability one at a time, then fitting the model with the standard assumptions to the predictions. If the precise forms of the distributions of variability are not critical, then the recovered values of drift rate, boundary separation, and the nondecision component should match those used to generate the predictions.

For a two-boundary diffusion process with no across-trial variability in any of the parameters, the equation for accuracy is given by

$$P(v,a,z)=\frac{e^{-2va∕s^2}-e^{-2vz∕s^2}}{e^{-2va∕s^2}-1}$$ Equation 1

and the cumulative distribution of finishing times is given by

$$G(t,v,a,z)=P(v,a,z)\frac{\pi s^2}{a^2}{e}^{\frac{-vz}{s^2}}\sum _{k=1}^{\infty }\frac{2k\sin \left(\frac{k\pi z}{a}\right)e^{-\frac{1}{2}\left(\frac{v^2}{s^2}+\frac{k^2{\pi }^2{s}^2}{a^2}\right)t}}{\left(\frac{v^2}{s^2}+\frac{k^2{\pi }^2{s}^2}{a^2}\right)}$$ Equation 2

, where a is the boundary separation (top boundary at a, bottom boundary at 0, and the distribution of finishing times is at the 0 boundary), z is the starting point, v is drift rate, and s is the SD in the normal distribution of within-trial variability (square root of the diffusion coefficient). The predictions from the model are obtained by integrating these equations over the distributions of the model's across-trial variability parameters using numerical integrations. In the standard model, the SD in the normal distribution of drift rate across trials is η, the range in the uniform distribution of starting points is s_z, and the range in the uniform distribution of nondecision time is s_t. The predicted values are “exact” numerical predictions in the sense that they can be made as accurate as necessary (e.g., 0.1 ms or better) by using more and more steps in the infinite sum and more and more steps in the numerical integrations.

In some situations, it is important to generate predictions by simulation because simulated data can show the effects of all the sources of variability on a subject's RTs and accuracy (for some models, this is the only way to generate predictions). The number of simulated observations can be increased sufficiently that the data approach the predictions that would be determined exactly from the numerical method. However, for the studies reported here, the questions being asked concerned exact (numerical) predictions, and so numerical methods were used, not simulations.

Parameters of the Model

To generate predictions for RTs and accuracy, I selected combinations of parameter values that span the range of those that have been observed in fits to real data (cf, Matzke & Wagenmakers, 2009; Ratcliff & Tuerlinckx, 2002). The distance between the boundaries, a, was 0.06, 0.12, or 0.30, and the starting point, z, was the value of a multiplied by 0.3, 0.5, or 0.7 (giving nine combinations). There were three drift rates, v= −0.3, 0.1, and 0.4, the same three for each of the nine combinations of a and z. Different drift rates correspond to different conditions of an experiment, where those conditions differ in difficulty. When the model was fit to predictions, it was fit to the three conditions simultaneously (as would be the case for a real experiment). For the mean duration of nondecision processes (T_er), only one value was used, 400 ms, because changes in this parameter simply shift all the RTs by a constant amount.

There were two values for the SD in drift across trials, η, 0.08 and 0.25, and two values for the range of nondecision time, s_t, 0.1 s and 0.25 s. Adding these four combinations to the combinations of a and z produced 36 combinations.

For each of these 36 combinations, one value of the range of the starting point was small, 0.005. Another value was larger and depended on the value of a. With a=0.06, the range was 0.015; for a=0.12, it was 0.03; and for a=0.30, it was 0.075. With these ranges for a and with z set at 0.3a, 0.5a, or 0.7a, there could be no starting point outside a boundary. However, for z=0.5a, this resulted in ranges that covered only a relatively small proportion of the distance between z and the boundaries. For this reason, I added 12 more combinations of parameters (for a total of 84). For each combination of a (0.06, 0.12, 0.30) with z (0.5a), η (0.08, 0.25), and s_z (0.1 s, 0.25 s), the range in starting point was set at 2a/3. The full set of combinations is shown in Table 1.

Table 1.

Parameter Values Used to Generate Predictions

Index	a	η	sz	st	z/a	Index	a	η	sz	st	z/a	Index	a	η	sz	st	z/a
1	.06	.08	.005	.10	.5	2	.06	.08	.005	.10	.3	3	.06	.08	.005	.10	.7
4	.12	.08	.005	.10	.5	5	.12	.08	.005	.10	.3	6	.12	.08	.005	.10	.7
7	.30	.08	.005	.10	.5	8	.30	.08	.005	.10	.3	9	.30	.08	.005	.10	.7
10	.06	.25	.005	.10	.5	11	.06	.25	.005	.10	.3	12	.06	.25	.005	.10	.7
13	.12	.25	.005	.10	.5	14	.12	.25	.005	.10	.3	15	.12	.25	.005	.10	.7
16	.30	.25	.005	.10	.5	17	.30	.25	.005	.10	.3	18	.30	.25	.005	.10	.7
19	.06	.08	.015	.10	.5	20	.06	.08	.015	.10	.3	21	.06	.08	.015	.10	.7
22	.12	.08	.03	.10	.5	23	.12	.08	.03	.10	.3	24	.12	.08	.03	.10	.7
25	.30	.08	.075	.10	.5	26	.30	.08	.075	.10	.3	27	.30	.08	.075	.10	.7
28	.06	.25	.015	.10	.5	29	.06	.25	.015	.10	.3	30	.06	.25	.015	.10	.7
31	.12	.25	.03	.10	.5	32	.12	.25	.03	.10	.3	33	.12	.25	.03	.10	.7
34	.30	.25	.075	.10	.5	35	.30	.25	.075	.10	.3	36	.30	.25	.075	.10	.7
37	.06	.08	.005	.25	.5	38	.06	.08	.005	.25	.3	39	.06	.08	.005	.25	.7
40	.12	.08	.005	.25	.5	41	.12	.08	.005	.25	.3	42	.12	.08	.005	.25	.7
43	.30	.08	.005	.25	.5	44	.30	.08	.005	.25	.3	45	.30	.08	.005	.25	.7
46	.06	.25	.005	.25	.5	47	.06	.25	.005	.25	.3	48	.06	.25	.005	.25	.7
49	.12	.25	.005	.25	.5	50	.12	.25	.005	.25	.3	51	.12	.25	.005	.25	.7
52	.30	.25	.005	.25	.5	53	.30	.25	.005	.25	.3	54	.30	.25	.005	.25	.7
55	.06	.08	.015	.25	.5	56	.06	.08	.015	.25	.3	57	.06	.08	.015	.25	.7
58	.12	.08	.03	.25	.5	59	.12	.08	.03	.25	.3	60	.12	.08	.03	.25	.7
61	.30	.08	.075	.25	.5	62	.30	.08	.075	.25	.3	63	.30	.08	.075	.25	.7
64	.06	.25	.015	.25	.5	65	.06	.25	.015	.25	.3	66	.06	.25	.015	.25	.7
67	.12	.25	.03	.25	.5	68	.12	.25	.03	.25	.3	69	.12	.25	.03	.25	.7
70	.30	.25	.075	.25	.5	71	.30	.25	.075	.25	.3	72	.30	.25	.075	.25	.7
73	.06	.08	.04	.10	.5	74	.12	.08	.08	.10	.5	75	.30	.08	.20	.10	.5
76	.06	.25	.04	.10	.5	77	.12	.25	.08	.10	.5	78	.30	.25	.20	.10	.5
79	.06	.08	.04	.25	.5	80	.12	.08	.08	.25	.5	81	.30	.08	.20	.25	.5
82	.06	.25	.04	.25	.5	83	.12	.25	.08	.25	.5	84	.30	.25	.20	.25	.5

Note. Nondecision time was 0.4 s. Drift rates were −0.3, 0.1, and 0.4. a represents boundary separation, z, starting point, s_z the range in a uniform distributions of starting points, s_t the range in a uniform distribution of nondecision time (in units of s), and η the SD in the normal distribution of drifts. There were 84 combinations tested. The conditions in which there were biases in drift rates for exponentially distributed nondecision time (greater than a 15% deviation) are the italicized lines.

Distributions

For each of the 84 combinations of model parameters, I generated predictions for RTs and accuracy with the standard assumptions about across-trial variability. For RTs, the predicted values were the .1, .3, .5, .7, and .9 quantile RTs for correct responses and the .1, .3, .5, .7, and .9 quantile RTs for error responses. Then I generated six more sets of predictions, each with one of the three distributions changed: (1,2) the normal distribution of drift rates was replaced with uniform and beta distributions; (3) the uniform distribution of starting points was replaced with a beta distribution; (4) the uniform distribution of starting points was replaced by independent uniform distributions of the boundaries; (5,6) the uniform distribution of nondecision times was replaced by normal and exponential distributions. In each case, the SD in the new distribution was set to be the same as in the one it replaced.

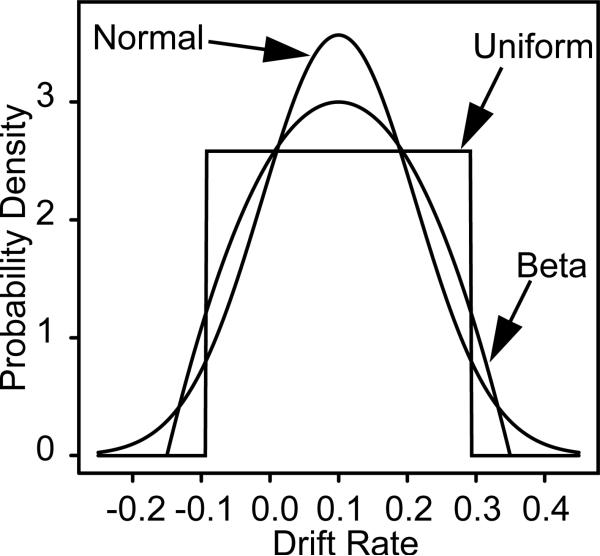
Figure 1 shows uniform, normal, and beta distributions, all with the same SD. The normal and beta look quite similar, and even for the normal and the uniform, the difference between them is smaller than might be expected. Moving from the uniform to the normal requires only that some part of the upper, approximately triangular, portions of the uniform (cut off by the normal, one on each side of the mean) be moved into the peak and the tail of the normal. These upper triangular portions contain only about 20% of the probability density of the uniform distribution.

Figure 1.

Three distributions for across-trial variability with the same SDs.

The beta distribution, with shape parameters 2 (i.e., with α=2 and β=2), was chosen because its shape is similar to that of the normal but, like the uniform, it has a restricted range. The expression for the general beta distribution is

$$f\left(x\right)=\frac{{(x-a)}^{\alpha -1}{(b-x)}^{\beta -1}}{B(\alpha ,\beta ){(b-a)}^{\alpha +\beta -1}}$$ Equation 3

where B is the beta function, which can be seen as a normalization constant used to make the total probability equal 1. a and b are the lower and upper limits of the distribution. The beta distribution with shape parameters set to 2 (α=2 and β=2) produces a density function:

Equation 4

When the uniform distribution of starting points was replaced with independent uniform distributions for each boundary, the ranges of the distributions for the boundaries were set to be the same as the range for starting points. In the standard model, when the starting point varies from trial to trial, variability in the two decision boundaries is correlated: If the starting point is closer to one boundary, it is further away from the other by exactly the same amount. Informal simulations have indicated that when the variability in the starting point is not too large, it mimics independent variability in the decision boundaries. Here, I tested this possibility more formally. The main reason that variability in starting point has been adopted instead of variability in the two boundaries is that it requires only one integration whereas variability in the boundaries requires two. With two integrations compared to one, generating predictions slows by, for example, 20 times when the integration routine approximates the function being integrated with 20 steps.

The model was fit to accuracy values and 5 quantile RTs for correct responses and 5 for error responses, using a standard chi-square method (Ratcliff & Tuerlinckx, 2002). Because accurate predictions were used as input to the fitting program (not simulated data from simulated subjects), the goodness of fit measures do not have a statistical interpretation. The starting points of the parameters used in fitting were those used to generate the predictions from the model.

Results

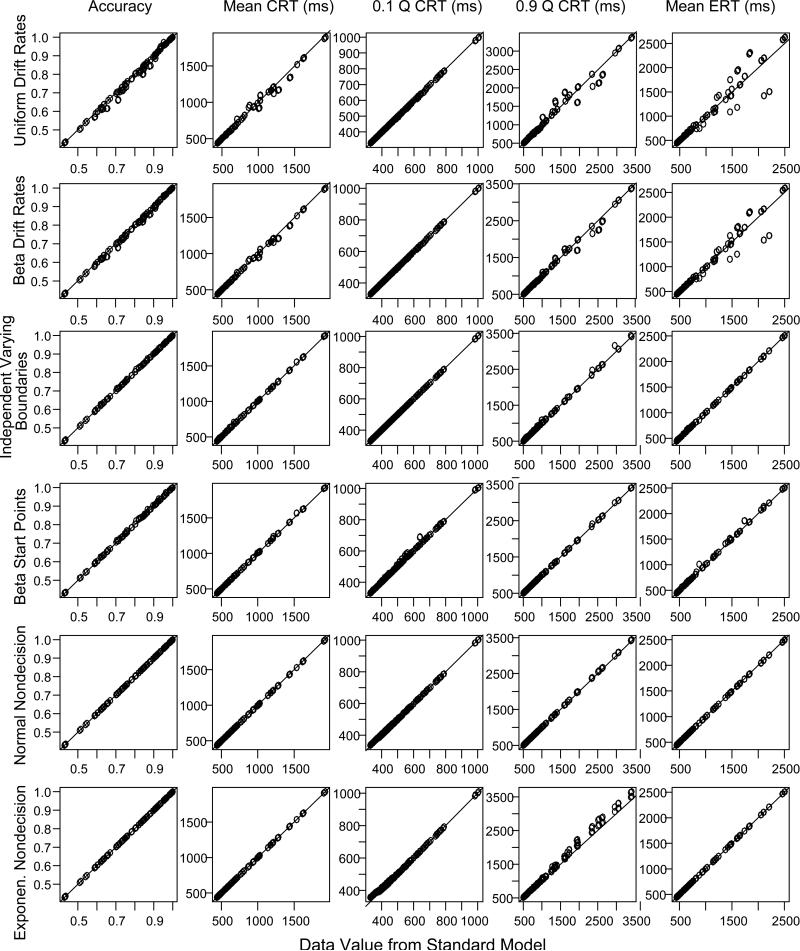
The first question to be addressed is whether the diffusion model's predictions for accuracy and RTs change as a function of the distributional assumptions. In Figure 2, the RTs and accuracy predicted under the standard assumptions are plotted against the RTs and accuracy predicted under the other six combinations of assumptions. There are six rows, one for each of the six combinations. The figure displays accuracy, mean RTs for correct responses, the .1 and .9 quantile RTs for correct responses, and the mean RTs for errors. Apart from the case for which drift-rate variability was uniformly distributed and the case for which nondecision time was exponentially distributed, the match between the predictions with the standard assumptions and the predictions with the other assumptions is good.

Figure 2.

Predicted values of accuracy, mean RT for correct responses (CRT), the .1 and .9 quantile RTs (Q CRT) for correct responses, and mean RT for errors (ERT), for the diffusion model with six alternative assumptions about the distributions of across-trial variability. For the first row, the distribution for drift rates is uniform; for the second, the distribution for drift rates is a beta distribution; for the third, there are independent uniform distributions for the two decision boundaries; for the fourth, the distribution for the starting point is a beta distribution; for the fifth, the distribution of nondecision times is normal; For the sixth, the distribution of nondecision times is exponential.

When across-trial variability in drift rate is normally distributed, mean RTs for errors relative to correct responses depend on the tails of the normal distribution (Ratcliff et al., 1999). For example, suppose the mean for the drift rate distribution was 0.1 (see Figure 1). For trials on which the normal distribution produced a value less than zero, the response would likely be an error. Higher negative values (e.g., −0.1 to −0.2) would lead to faster errors than lower negative values (e.g., 0.0 to −0.1). In contrast, when the distribution of across-trial variability is uniform (and also beta), with the same SD as the normal, there is a lower limit on negative values (−0.1 in Figure 1). This means that a uniform distribution will produce somewhat slower errors than the normal distribution. It is important to note that the fastest responses for errors do not change much across these different assumptions because the fastest responses change little with drift rate (e.g., Figure 2C, Ratcliff, Philiastides, & Sajda, 2009). However, the differences in .9 quantile RTs and error RTs for the different conditions depend on the interaction between across trial variability in starting point and drift rate.

When nondecision time was exponentially distributed, there are systematic changes in the model's predictions from those of the standard model, in particular, the .1 quantile RT is a little higher for the conditions that produce shorter RTs and there is a systematic bias towards longer RTs for all the .9 quantile RTs (Figure 2, bottom row). These biases cause problems for parameter recovery that are discussed later.

The second question is whether interpretations of performance depend on the particular assumptions about across-trial variability. To examine this, the standard model was fit to the predictions generated from each of the six non-standard assumptions. (Note that, strictly speaking, the standard model is a misspecification because the predictions were generated with different assumptions.) First, the drift rate, nondecision time, and boundary separation parameters are examined (because these are more important in applications) and then the variability parameters.

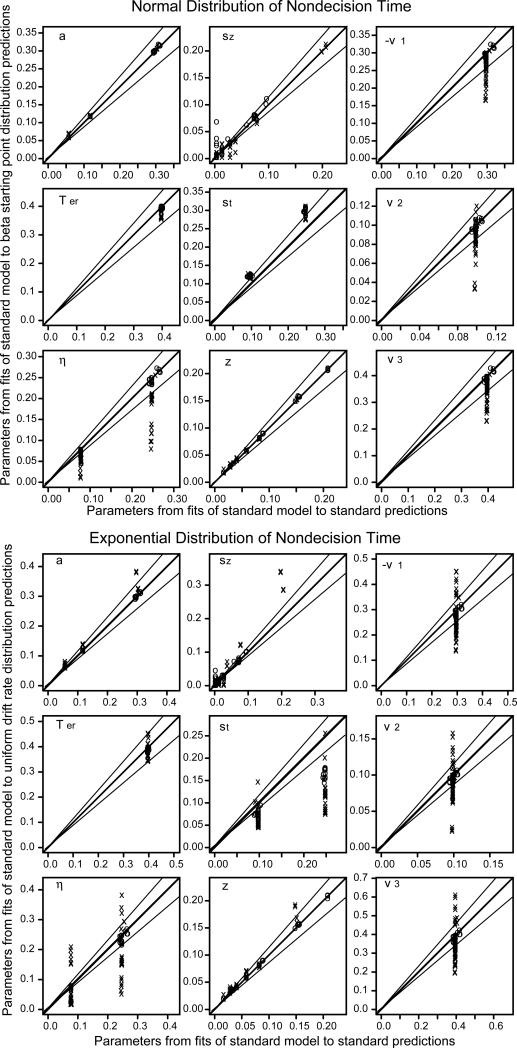
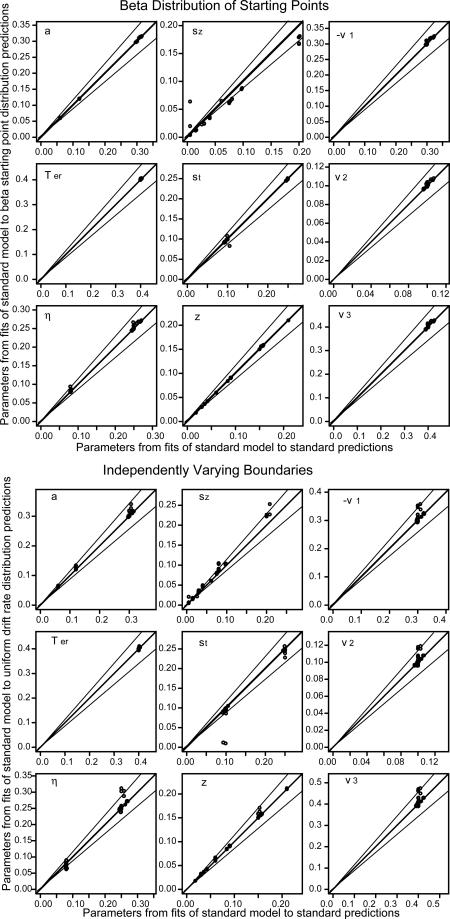
Figures 3, 4, and 5 show the parameter values recovered from fitting the standard model to the predictions from the alternative assumptions plotted against the parameter values recovered from fitting the standard model to the predictions from the standard model. Besides the line of equality, two lines representing 15% deviations are also plotted.

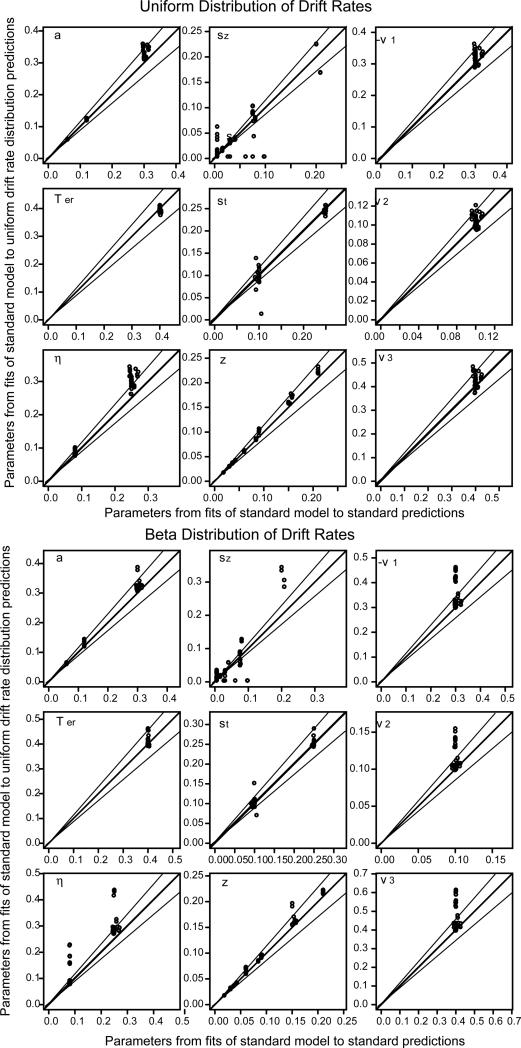
Figure 3.

Plot of diffusion model parameters resulting from fitting the standard model (normally distributed drift rates, uniformly distributed starting points and nondecision times) to predicted values from uniform distributed drift rates (top half) and beta distributed drift rates (bottom half) against parameters recovered from fitting the standard model to predicted values from the standard model (the latter show that the standard model parameters are recovered well when the model is fit to predictions).

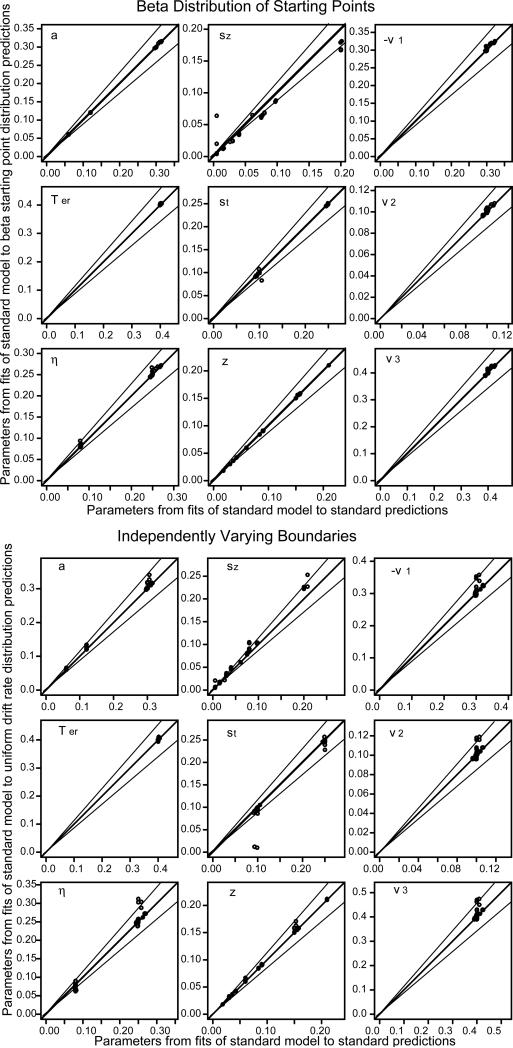
Figure 4.

Same plots as in Figure 3 but with a beta distribution of starting point for the top half and independent uniformly distributed boundaries for the bottom half.

Figure 5.

The same plots as in Figure 3 but with normally-distributed nondecision time in the top half and exponentially-distributed nondecision time in the bottom half. For the normally-distributed nondecision time conditions, the x's are for boundary separation a=0.06. For the exponentially-distributed nondecision time conditions, the italicized parameter values in Table 1 are represented by x's (these have biased estimates of drift rates) and the non-italicized parameter values in Table 1 are represented by o's (see the text for discussion).

For the beta and uniform distributions of drift rates, the beta distribution of starting points, and the case in which there was independent variability in the two decision boundaries, the parameter values recovered by fitting the model with the standard assumptions were nearly the same as those used to generate the predictions (a total of 4 different distributional assumptions and 84 sets of parameter values for each). When the distribution of drift rates was uniform, there were misses of more than 15% only for three values of boundary separation and three values of drift rate. When there was separate variability in the boundaries, there were misses of more than 15% for only three values of drift rate ¹. There were no misses of more than 15% for beta distributions of drift rate or starting point.

For nondecision time, the normal and exponential distributions of nondecision time led to more misses than the alternative assumptions for starting point and drift rate. With a normal distribution of variability in nondecision time, out of 84 sets of parameter values, 14 of the boundary separation values missed by more than 15%, 15 of the sets of drift rate values missed by more than 15%, but none of the nondecision times missed by more than 15%. The misses mainly occurred when boundary separation was small and the SD in nondecision time was large: All except 2 of the misses in drift rates and all of the misses in boundary separation occurred with a=0.06 and s_t=0.25. This combination produces the smallest SD in decision time and the largest SD in nondecision time. This combination is uncommon in fits of the diffusion model to real data.

With an exponential distribution of variability in nondecision time, out of 84 parameter combinations, there were these misses of more than 15%: 22 in boundary separation, 0 in nondecision time, and 35 sets of drift rates. Of these misses, 16 in boundary separation and 13 of the sets of drift rates occurred for the 16 combinations when boundary separation was small and nondecision time variability was large, a=0.06 and s_t=0.25. The other misses occurred when the distance between the boundaries was the middle value (a=0.12) and nondecision time variability was large (s_t=0.25): there were 2 misses in boundary separation and 12 (out of 14 combinations) in the sets of drift rates. The other misses occurred when variability in starting point was large. The misses for the exponentially distributed nondecision time come from the combinations italicized in Table 1.

The size of these misses is shown in Figure 5 with plots of parameter values for the normal and exponential distributions. The x's represent the misfits listed above and the o's are for all the other combinations of parameter values. For the combinations of parameter values other than those listed above, there was only 1 miss in drift rate of more than 15% for the normal distribution and only 3 misses in drift rate of more than 15% for the exponential distribution. Although the symbols overlap in Figure 5, almost all the discernible misses are from the x symbols.

The misfits when the variability in nondecision time was exponential occur because the tail of the exponential merges into the tail of the RT distribution that is generated from the diffusion process; this leads to elongated tails of the distribution (i.e., increased .9 quantile RTs in Figure 2). If the standard model is fit to the predictions, then its parameters are adjusted to attempt to accommodate for this stretching of the tail by lowering drift rate and changing drift rate variability (see Ratcliff & Tuerlinckx, 2002, p.453, for an example of how the model parameters trade off to accommodate perturbations in a single data point).

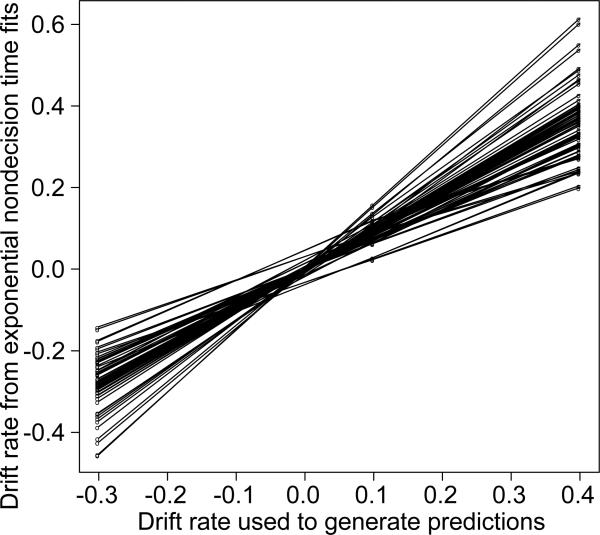
One practical question is whether the ordinal conclusions about drift rate change if variability in nondecision time is exponential but data are fit with uniform variability in nondecision time. Figure 6 shows a plot of drift rates for v₁, v₂, and v₃ against the generating values −0.3, 0.1, and 0.4, for all the 84 functions from the 84 parameter combinations in Table 1. The drift rate functions all fall on straight lines. This means that conclusions based on the ordinal relationships among conditions and the form of the function relating drift rate to the independent variable are maintained even when the estimated parameter values deviate from those used to generate the predictions.

Figure 6.

Plots of recovered drift rates versus values used to generate the predictions for the model with exponentially distributed nondecision time (the values from the bottom part of Figure 5).

In practice, the distribution of nondecision times is not likely to be as asymmetric as the exponential distribution. If one believed in subtractive logic, the distribution of nondecision time is likely to be more like a normal distribution with a slight skew, just as in simple RT (e.g., Figure S2, Ratcliff & Van Dongen, 2011 - even the simple RT task can be modeled with a diffusion process so strict subtractive logic would be suspect). With a distribution of nondecision times like those obtained in simple RT tasks, major deviations would occur only for large variability in nondecision time and very narrow boundaries, conditions that are obtained only in some paradigms under strong speed stress.

Across-trial variability parameters

For the uniform and beta distributions of drift rate, the beta distribution of starting point, and independent variability in the two decision boundaries, the across-trial variability parameters are recovered reasonably well. These parameters have much higher standard deviations of estimation (Ratcliff & Tuerlinckx, 2002), and are sensitive to secondary aspects of data. For example, variability in drift rate and starting point are determined to a large degree by the relative speeds and distributions of correct and error responses, not the global features of overall RT and accuracy values. Thus, if the alternative distributional assumptions change the relationship between correct and error responses, they may have a large effect on the across-trial variability parameters. Therefore, the differences shown in Figures 3 and 4 are probably not of practical significance. Also, significant differences in these parameters across subjects and across subject groups are often not obtained (Ratcliff et al., 2006, 2010, 2011).

With the normal and exponential distributions of nondecision time, there are some rather large misses in the variability parameters. When the drift rates are underestimated, the across-trial variability in drift rate is also underestimated to compensate for reduced accuracy from the lower drift rates. Also, for the exponential distribution, when the across-trial variability in the nondecision component is large, the SD (the mean and SD of an exponential distribution are equal) is underestimated most of the time because the longer RTs from this distribution stretch the tail of the predicted RT distribution. This stretching is not symmetrical-- it is in the right tail-- and this leads to underestimation of the SD and range in the standard model. Figure 5, bottom panel, shows that poor estimation of the variability parameters coincides with poor estimation of the other model parameters (the x symbols).

Discussion

The goal for quantitative models of cognitive processes is to understand the mechanisms that underlie performance on cognitive tasks. With quantitative models, empirical findings can be organized and categorized in ways that do not necessarily correspond to the organization and categorization that might be suggested from a purely empirical perspective. Quantitative models can also be used as tools to understand the effects on processing of clinically relevant manipulations (e.g., Batchelder, 1998; Busemeyer & Stout, 2002; Verbruggen & Logan, 2008; Yechiam, Busemeyer, Stout, & Bechara, 2005). For the diffusion model, these include the effects of sleep deprivation, drug regimens, aging, child development, cognitive ability, injury, and disease. Quantitative models are especially effective when they can provide a coherent account of differences in performance among individuals.

When quantitative models are fit to data, some of the questions of interest concern how components of processing change as a function of experimental conditions or how they change across subject groups. For example, the question might be how the brightness of perceptual stimuli affects the rate of accumulation of information from them (i.e., drift rate). Or the question might be how age affects the amount of information required to make a decision (i.e., boundary positions).

In the absence of ways to identify the form of the across-trial variability distributions, interpretation of the behavior of model components is more credible if the model is robust to the form of the distributions. This study shows that application of the model with the standard assumptions to predictions generated from the model with different assumptions results in recovered parameters that differ little from the generating parameters, although there are some exceptions. The instances in which the recovered parameters differed systematically from the generating parameters occurred when the distribution of nondecision times was normal or exponential and boundary separation was small (so that nondecision time variability was large relative to decision time variability from the diffusion model). The other deviations occurred mainly with combinations of more extreme values of parameters, combinations that are not often observed in fits to real data. For applications to individual differences, it is reassuring that the deviations between parameter values from different distributional assumptions are almost always smaller than the typical differences between subjects (Ratcliff et al., 2006, 2010, 2011). This means that misspecifying the across trial variability distributions would not affect conclusions provided by the model about individual differences.

The conclusion, then, is that the standard model can be used to fit data without too much concern for the exact forms of the across-trial variability distributions (as long as the distributions differ from the standard distributions by not much more than the examples given here). One way to understand why the standard model exhibits robustness to differing assumptions about across-trial variability in drift rate, starting point, and boundaries is to consider the interaction between these and within-trial variability. The amount of within-trial variability must be large in order for the model to produce the wide spread of RTs observed in RT distributions and to produce errors (for a process to end up at the opposite boundary from that toward which it is drifting). This large amount of variability washes out precise distributional assumptions about across-trial variability in drift rate and starting point. In other words, it is the amount of across-trial variability (its SD) that is important, not the precise shape.

There are two limitations of this study. First, I did not fit models with the alternative assumptions to predictions generated with the standard assumptions. However, I would expect the same kinds of results. Second, the standard model was fit to exact predictions from the other models, not to data simulated from them. Even in fitting the standard model to simulated data generated from the standard model, there can be biases in parameter estimates, especially when there are limited numbers of observations per condition, for example, a few hundred or less. This means that if one of the alternative across-trial variability assumptions were correct, and the standard model was fit to experimental data with a limited number of observations, it is not clear whether the results would match those presented here. (But note that simulated data were generated for Ratcliff & Starns, 2009, confidence judgment model and fits of the model back to the simulated data showed robustness to the forms of the distributions of across-trial variability that were examined). To do a simulation study properly, 100 simulations (for example) with each set of parameter values would be needed. The model would have to be fit to each set of simulated data for each set of parameter values, which would lead to 8,400 model fits for the combinations of parameter values that were used here. If this were done, the biases in parameter values along with covariances among parameters and variability in parameter values could be examined (e.g., Ratcliff & Tuerlinckx, 2002).

The conclusion drawn here about robustness for the diffusion model is likely to apply to other two-choice sequential sampling models that can fit data as well as the diffusion model can, such as the leaky competing accumulator model (Usher & McClelland, 2001). However, the linear ballistic accumulator model (Brown & Heathcote, 2008) has no within-trial variability. Thus it is possible that changes in the across-trial variability distributions would change the predictions of the model, but whether or not, and by how much needs, to be determined. A related point is that recent studies (Donkin, Brown, Heathcote, & Wagenmakers, 2011; Ratcliff et al., 2006) have shown that the interpretations of components of processing obtained from applications of the diffusion model are the same as those obtained from applications of the leaky competing accumulator model and the linear ballistic accumulator model. Of course, it would be best if it were possible to find strong differential predictions of the models that would allow some to be ruled out, but as yet, the models seem to mimic each other, at least qualitatively.

In sum, for drift rate and starting point variability, users of diffusion models should be reassured that the interpretations of data provided by the standard model do not depend on specific assumptions about across-trial variability. This is also true when the distribution of nondecision time is normal, except when boundary separation is small and nondecision time variability is large. Only if the distribution of nondecision time is highly skewed might the interpretation of data from using the standard model be different from the interpretation with other distributional assumptions.