Abstract
Objectives
We discuss the problem of computing the standard errors of functions involving estimated parameters and provide the relevant computer code for three different computational approaches using two popular computer packages.
Study Design
We show how to compute the standard errors of several functions of interest: the predicted value of the dependent variable for a particular subject, and the effect of a change in an explanatory variable on the predicted value of the dependent variable for an individual subject and average effect for a sample of subjects.
Empirical Application
Using a publicly available dataset, we explain three different methods of computing standard errors: the delta method, Krinsky–Robb, and bootstrapping. We provide computer code for Stata 12 and LIMDEP 10/NLOGIT 5.
Conclusions
In most applications, choice of the computational method for standard errors of functions of estimated parameters is a matter of convenience. However, when computing standard errors of the sample average of functions that involve both estimated parameters and nonstochastic explanatory variables, it is important to consider the sources of variation in the function's values.
Keywords: Standard errors, variance, estimation, statistics
The questions posed by standard analyses in health services research often require evaluation not only of estimated parameters (e.g., regression coefficients) but also functions of estimated parameters. Common examples of functions of estimated parameters include the predicted value of the dependent variable for a particular subject or set of subjects in the data, and the effect of a change in an explanatory variable on the predicted value of the dependent variable (sometimes referred to as a partial effect, marginal effect, or incremental effect) and elasticities.
While the computation of the function itself often is straightforward, establishing confidence intervals for the function's value can be more difficult. Confidence intervals allow the analyst to test hypotheses about the value of the function—for example, to evaluate the proportion of the function's values that would fall within a given range, if the “experiment” were repeated multiple times.
The construction of confidence intervals requires estimation of the variance of the function, which in turn requires careful consideration of the sources of variation in the function's value. For example, is the variation of interest the variance that arises from inserting different values of the explanatory variables into the function; the fact that coefficients in the function are estimated parameters; or both?
The article begins with a brief note on the distinction between a standard deviation and a standard error. This is a central issue in the question raised in the previous paragraph. We then discuss standard errors in the context of a simple linear model, before turning to more complex nonlinear models. We discuss three methods of computing the standard errors of functions of interest:
The delta method (Greene 2012)
There are other ways to compute standard errors. Some methods are integral to the estimation of the coefficients that subsequently appear in the function of interest, such as the method of moments and Gibbs sampling. In our experience, the three methods that we have chosen to discuss are the most common in the health services research literature and can be applied regardless of the method used to estimate the coefficients in the function of interest.
We discuss the advantages and disadvantages of each method and provide sample computer code for two popular software packages in the Appendix. We end by considering the special case of sample averages of functions of interest.
STANDARD DEVIATIONS AND STANDARD ERRORS
We begin by defining the population standard deviation of a random variable Z, denoted σZ, as the square root of the variance of Z:
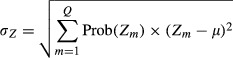 |
where Zm are the Q values that the variable Z can take, μ is the expected value of Z, and Prob (Zm) are the associated probabilities. When Z is a continuous variable, such as income, summation is replaced by integration and the probabilities are replaced by the appropriate density function.
The standard deviation is a measure of the dispersion of the values of Z around its population mean μ. We will focus on functions computed from a random sample of N observations on the variable Z, which will be denoted Zi, i = 1,…, N. It is customary to refer to the variable Z as a random variable and each element of the sample of Zs as a random variable. The term random can be confused with the term stochastic. One of our main objectives is to distinguish a stochastic dependent variable in a regression context (which is stochastic due to the influence of a stochastic error term u) from the nonstochastic explanatory variables whose values are assumed to be fixed in repeated samples. This matters because when the function of interest contains both estimated parameters and the values of explanatory variables, the explanatory variable values are not treated as random (stochastic), but fixed in repeated samples unless explicitly modeled as stochastic variables through measurement error, endogeneity, lagged values of dependent variable, etc.
Estimates of the population mean and standard deviation of Z can be obtained from samples of data. For example, a common estimator of the population mean of Z, denoted 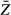 , is:
, is:
and a common estimator of the population standard deviation is:
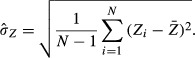 |
Estimators also are variables, but the standard deviation of an estimator is referred to as the standard error. For example, the standard error of 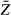 (denoted
(denoted 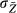 ) is an estimate of the variation in
) is an estimate of the variation in 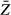 that would arise across many samples. Assuming that the observed values of Z are independently and identically distributed, the standard error of
that would arise across many samples. Assuming that the observed values of Z are independently and identically distributed, the standard error of 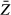 is equal to:
is equal to:
Note that the standard deviation of Z,σZ, is a fixed parameter. The standard error of 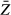 being an estimator of this fixed parameter divided by the sample size, converges to zero as the sample size grows. The sample estimator of the standard deviation of Z,
being an estimator of this fixed parameter divided by the sample size, converges to zero as the sample size grows. The sample estimator of the standard deviation of Z, 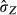 , converges to the parameter that it estimates, the population standard deviation, σZ, a property known as consistency. What is true of estimators also is true of functions of estimated parameters, as explained in the next section.
, converges to the parameter that it estimates, the population standard deviation, σZ, a property known as consistency. What is true of estimators also is true of functions of estimated parameters, as explained in the next section.
FAMILIAR EXAMPLES FROMTHE LINEAR REGRESSION MODEL
Regression Coefficients
In this section, we expand the discussion of standard errors with a simple application: a single regression coefficient. We then consider two common functions of estimated parameters: (a) the estimator of the expected value of the dependent variable conditional on specific values of the explanatory variables and (b) the estimator of the partial effect of an explanatory variable on the expected value of the dependent variable.
Consider analysis of a simple linear regression equation based on data from N individual subjects denoted i = 1,…, N:
| (1) |
where yi is the dependent variable value for the ith subject, xi is a vector of explanatory variables (possibly including a constant term), β is the vector of regression coefficients, ui is the stochastic error, usually assumed to be normally distributed with mean 0 and variance σ2, and σu is the standard deviation of u.
In the regression setting, it is common to assume that the values of the variables in xi are not stochastic but instead are “fixed in repeated samples.”2 That assumption implies that the analyst could collect new data with the same distribution of xi values, but the new data would have different values of yi, because, and only because, the values of ui would be different in the new data. This conceptual experiment is used to understand the nature of and source of variation in the estimators of the parameters of the model.
The coefficients β are estimated from sample data according to some objective function, such as minimization of the sum of squared residuals, 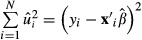 . Minimizing the sum of squared residuals yields the familiar ordinary least squares (OLS) estimator of β. This result can be written in matrix notation as:
. Minimizing the sum of squared residuals yields the familiar ordinary least squares (OLS) estimator of β. This result can be written in matrix notation as:
| (2) |
where the rows of the N×K matrix x are xi′, where K is the number of explanatory variables in equation (1) including the constant term, indexed by k = 1,…,K, and y and u are defined likewise by collecting the values of yi and ui in column vectors. Thus, the OLS estimator of β is a function of both u and x. The standard errors of the individual elements of 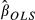 , denoted
, denoted 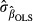 are the diagonal elements of the variance-covariance matrix:
are the diagonal elements of the variance-covariance matrix: 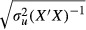 . After the model is estimated,
. After the model is estimated, 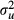 is replaced by a consistent estimator:
is replaced by a consistent estimator:
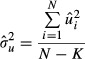 |
The estimated standard errors of 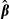 , denoted
, denoted 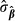 are the diagonal elements of the estimated covariance matrix,
are the diagonal elements of the estimated covariance matrix,
| (3) |
The estimated standard errors of 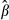 are functions of both
are functions of both 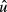 (via
(via 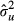 ) and x.
) and x.
Predicted Value of yi
In a simple linear regression setting, the predicted value of the dependent variable y, denoted 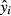 , for a given set of explanatory variable values xi is:
, for a given set of explanatory variable values xi is:
| (4a) |
Assuming that the regression contains a constant term, which is the usual case, this predictor also can be written as:
| (4b) |
In the linear model, we ordinarily have no information to justify assuming the expected value of 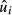 is anything other than zero,3 so
is anything other than zero,3 so 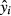 is the value of y that lies on the estimated regression line at point xi. Nevertheless, when deriving an estimator for the sampling variance of
is the value of y that lies on the estimated regression line at point xi. Nevertheless, when deriving an estimator for the sampling variance of 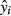 , it is necessary to account for the variation due to ui.4 The estimator of the standard error of the predicted value of y, conditional on a specific vector of x values (xi), is
, it is necessary to account for the variation due to ui.4 The estimator of the standard error of the predicted value of y, conditional on a specific vector of x values (xi), is
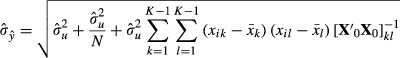 |
(5) |
where the summations are over all variables save for the constant term and x0 is the matrix of variables in x, not including the constant term, expressed in deviations from their means. (See Greene 2012 for this derivation.) The estimated standard error of 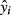 combines four factors:
combines four factors:
The deviation of
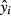 from the sample regression line due to unobserved factors ui;
from the sample regression line due to unobserved factors ui;The deviation of the sample regression line itself from the true regression line;
The sampling variation of x; and
The distance of xi from the sample mean,
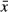 .
.
These points are illustrated in Figure 1. The horizontal axis represents one of the explanatory variables xk holding all the other explanatory variables constant at their specific values xi.
Figure 1.
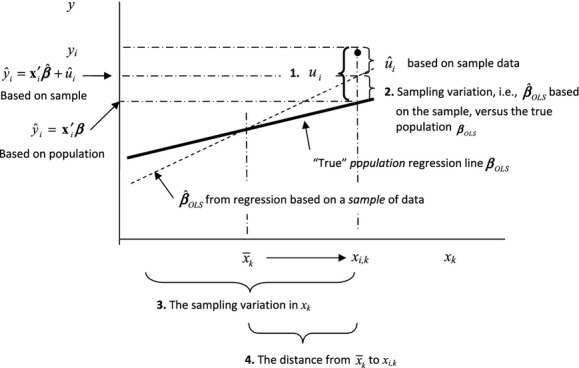
Four Sources of Variation in the Predicted Value of yi
Partial Effects
The partial effect of a specific xk on a function of interest is the change in the function as xk changes by one unit. For example, if xk is a continuous variable, and the function of interest is 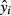 , then the partial effect is referred to in some literatures as a marginal effect. In the linear model with no interaction terms or higher-order terms, the marginal effect is equal to
, then the partial effect is referred to in some literatures as a marginal effect. In the linear model with no interaction terms or higher-order terms, the marginal effect is equal to
| (6) |
If xk is a binary (dummy or dichotomous) variable, the partial effect is often referred to as an incremental effect and is equal (again, if the model has no interaction terms with that binary variable) to the arithmetic difference
| (7) |
with all the other explanatory variables held constant at their xi values. In a linear regression context, this will, once again, be the regression coefficient 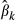 . In case of both discrete and continuous x variables with no interaction or higher-order terms, the standard error of the partial effect is given by equation 3 because the marginal or incremental effect is just the coefficient.
. In case of both discrete and continuous x variables with no interaction or higher-order terms, the standard error of the partial effect is given by equation 3 because the marginal or incremental effect is just the coefficient.
MORE COMPLEX EXAMPLES
Now suppose that instead of a single coefficient we have a function of estimated parameters, and the function might be nonlinear. There are many types of such functions that are common in health services research applications, for which computation of standard errors is more challenging. We consider the following four types of functions:
A nonlinear function for a single observation from a single equation
The sample mean of a function
Functions of parameters from multiple equations
Functions for which the correct covariance matrix of the parameters is not readily available.
We describe each of these in turn. Then we explain how to compute the standard errors of these functions by the delta method, K–R, and bootstrapping.
Nonlinear Functions for a Single Observation from a Single Equation
There are two senses in which a function can be nonlinear. It can be nonlinear in the variables (covariates) and/or nonlinear in the parameters. For example, if the linear regression equation contained a vector of explanatory variables xj plus a variable xk and its squared term, then the equation would be written:
| (8) |
This function is nonlinear in the variable xk, but linear in the parameters. Post-estimation, the marginal effect of a continuous xk would be:
| (9) |
and the estimated standard error of the marginal effect would be:
| (10) |
Alternatively, the function may be nonlinear in the parameters. Suppose that one has estimated a model and subsequently has calculated the value of a function of interest, gi for the ith subject that involves both the explanatory variables xi and the estimated parameters 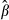 , which we write as
, which we write as 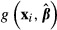 . There is a vast array of models that are used frequently in health services research that are nonlinear in the parameters, including: logit, probit, tobit, semi-log, double-log, count data, survival models, and multipart model for health expenditures. In nonlinear models, most of the functions of interest involving estimated parameters will be nonlinear as well.
. There is a vast array of models that are used frequently in health services research that are nonlinear in the parameters, including: logit, probit, tobit, semi-log, double-log, count data, survival models, and multipart model for health expenditures. In nonlinear models, most of the functions of interest involving estimated parameters will be nonlinear as well.
For example, the predicted probability that yi = 1, conditional on xi, in a logit or probit model is: Estimated Probability
| (11) |
where F is the logistic (logit) or normal (probit) cumulative distribution function. The marginal effect of a continuous xk on the probability that yi = 1 is:
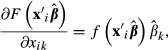 |
(12) |
where f is the corresponding logistic or normal probability density function. The expressions in equations (11) and (12) are nonlinear functions of both the variables and the coefficients. Notice that the marginal effects are evaluated for specific values of x = xi. The values of and derivatives of nonlinear functions generally will be different when evaluated at different values of x. Computing a standard error for a nonlinear function such as that in equation (12) involves more steps than adding up a weighted sum of variances and covariances. We will develop this in detail in the section on computation.
The Sample Mean of a Function
Thus far, we have discussed only functions of interest evaluated for an individual (ith) subject. In nonlinear models, the value of the function of interest usually is different for subjects who have different values of the explanatory variables, and analysts frequently are interested in the values of a function averaged across all subjects in the sample, for example, the average incremental effect of having health insurance on the health expenditures or health outcomes. The sample average of the function 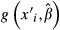 is:
is:
| (13) |
If 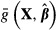 is the average of a function across the observations in the sample, as in equation (13), then the computation of standard errors becomes more complex, as discussed in the section on computation.
is the average of a function across the observations in the sample, as in equation (13), then the computation of standard errors becomes more complex, as discussed in the section on computation.
Function of Parameters from Multiple Equations
In some cases, the function of interest combines the results from more than one estimated equation. A common extension of the logit or probit model in health services research is a two-part model for health expenditures, where the first equation is a probit or logit equation modeling the probability that the subject has some positive value of health care spending, and the second equation models the expected value of health care spending conditional on having a positive level of spending (e.g., a linear or generalized linear model). The predicted value of spending for the ith subject is obtained by multiplying the probability having of a positive level of spending times the expected value of spending given that is positive. The partial effect of an xk on the expected value of spending for the ith subject involves the estimated parameters from both equations and perhaps an estimated retransformation parameter, as well, if the dependent variable in the second equation is the natural log of health expenditures, for example, as is commonly the case.
If the function's parameters come from multiple equations so that computation of the standard errors requires multiple variance-covariance matrices, then bootstrap methods may be the simplest approach, even though the delta method or K–R estimation also would be appropriate.
Functions for Which the Correct Covariance Matrix of the Parameters Is Not Readily Available
As shown in equation (3), in a regression setting, an important ingredient to the calculation of standard errors is the variation in unobserved factors (u). However, to obtain consistent estimators of parameters of interest, it may be necessary to use estimation techniques that result in biased estimates of u, and thus biased estimates of the standard errors of the function of interest.
A simple and familiar example is two-stage least squares (2SLS). Consider the following two equations:
| (14) |
and
| (15) |
where equation (15) is the equation of main interest. If ui and vi are correlated, then xi and ui in equation (15) are correlated, resulting in biased and inconsistent least squares estimates of β. 2SLS proceeds by estimating equation (14) by least squares, then using the predicted values of xi as an instrument for the original x in estimation of β in equation (15). Algebraically, the right result is obtained by replacing the endogenous x in equation (15) with the exogenous prediction. However, the conceptually correct error terms (u) are the deviations of the actual values of y from the actual (not predicted) values of x, which if uncorrected results in a bias in the computation of the covariance matrix of the estimator. This change is made easily and automatically in most software packages once the user alerts the program that 2SLS estimation is required.
Other examples of this type of error term correction are not yet part of familiar statistical software, however. An example is two-stage residual inclusion—another approach to endogenous explanatory variables—in which the estimated residuals (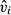 ) from equation (14) are added to equation (15), alongside the endogenous x (Terza 2008; Terza, Bradford, and Dismuke 2008). The standard errors produced from simple OLS estimation of this augmented version of equation (15) will fail to account for the fact that
) from equation (14) are added to equation (15), alongside the endogenous x (Terza 2008; Terza, Bradford, and Dismuke 2008). The standard errors produced from simple OLS estimation of this augmented version of equation (15) will fail to account for the fact that 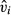 is an estimated variable, and thus the resulting standard errors will be biased.
is an estimated variable, and thus the resulting standard errors will be biased.
If the correct variance-covariance matrix of the parameters is readily available, then any of the three methods can be used to compute the standard errors. If the estimation method does not produce the correct variance-covariance matrix of the parameters, then the analyst must obtain the correct variance-covariance matrix from another source or turn to bootstrap methods.
COMPUTATION
Having described the types of nonlinear functions of estimated parameters that arise frequently in health services research applications, we now describe three approaches to computing the standard errors of those functions: the delta method, Krinsky and Robb, and bootstrapping. (See Hole 2007 for a comparison of methods applied to willingness to pay measures.) The choice often depends on the application. It generally is not the case that one method is appropriate and the others are not. In the most common applications, the choice among these three is based on programming or computational convenience. However, the assumptions underlying each method are important. The properties of the estimators discussed in this section are asymptotic properties and the behavior of the estimators in finite samples can be compromised if the assumptions underlying the estimator are not satisfied.
The discussion in this section is limited to functions involving a single subject, that is, a single vector of variable values 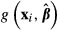 . Functions involving averages of a function's values across all subjects in the sample are discussed in the following section.
. Functions involving averages of a function's values across all subjects in the sample are discussed in the following section.
The Delta Method
The delta method is the most common method of calculating the standard errors of partial effects in most software packages. The delta method uses a first-order Taylor series expansion around 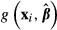 evaluated at specific values of x = xi to estimate the standard error (Greene 2012, pp. 1083–1084). The computational formula is:
evaluated at specific values of x = xi to estimate the standard error (Greene 2012, pp. 1083–1084). The computational formula is:
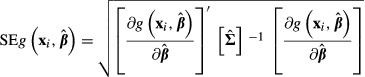 |
(16) |
where 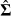 is the estimated variance covariance matrix of
is the estimated variance covariance matrix of 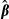 . Equation (16) is derived from the true population values of β and Σ. Empirically, however, β and Σ are replaced with their consistent estimates
. Equation (16) is derived from the true population values of β and Σ. Empirically, however, β and Σ are replaced with their consistent estimates 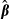 and
and 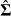 .
.
An advantage of the delta method, shared by K–R, is that the model is estimated only once. We explain this advantage further in the discussion of bootstrap methods, below. There are two disadvantages. First, the delta method assumes that the function 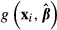 is “locally linear” in the neighborhood of the specific values of the explanatory variables at which the standard error is being computed. If that assumption is not met, then the results can be inaccurate. In practical terms, this problem appears to be extremely uncommon. Second, for some models in some software packages, such as two-stage residual inclusion, the code for
is “locally linear” in the neighborhood of the specific values of the explanatory variables at which the standard error is being computed. If that assumption is not met, then the results can be inaccurate. In practical terms, this problem appears to be extremely uncommon. Second, for some models in some software packages, such as two-stage residual inclusion, the code for 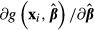 must be supplied by the analyst, introducing the possibility of programming errors. Computing the standard error of the predicted probability that
must be supplied by the analyst, introducing the possibility of programming errors. Computing the standard error of the predicted probability that 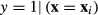 manually would require the analyst to supply the proper derivatives, which in this case are
manually would require the analyst to supply the proper derivatives, which in this case are 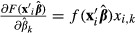 for each of the k = 1,…, K parameters, and then assemble the derivatives into the expression in equation (16). This part of the analysis is automated in some modern programs.
for each of the k = 1,…, K parameters, and then assemble the derivatives into the expression in equation (16). This part of the analysis is automated in some modern programs.
Krinsky and Robb
The K–R method is based on the assumption that the estimators of the model parameters are consistent and have an asymptotically normal multivariate distribution. The K–R method draws multiple vectors of β = βs, s = 1,…,S coefficients from the multivariate normal distribution that has a mean vector equal to the original estimated coefficient vector 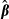 and the same estimated variance-covariance matrix
and the same estimated variance-covariance matrix 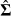 . Each new vector of coefficients, βs, is used to compute a new value of
. Each new vector of coefficients, βs, is used to compute a new value of 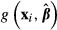 equal to
equal to 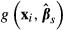 . The standard deviation of the resulting sample of draws of
. The standard deviation of the resulting sample of draws of 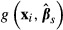 across all values of
across all values of 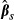 provides an estimate of the standard error of
provides an estimate of the standard error of 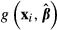 .
.
A reporting issue arises in the K–R method. One might consider reporting the mean of the N different values of 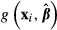 obtained from the K–R draws as the value of
obtained from the K–R draws as the value of 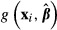 . However, assuming that one has used a consistent estimator to obtain the initial value of
. However, assuming that one has used a consistent estimator to obtain the initial value of 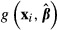 , that is the value that should be reported. We note as well that because of differences in the way different programs generate samples, it often will be impossible to replicate exactly the results obtained from different computer programs.
, that is the value that should be reported. We note as well that because of differences in the way different programs generate samples, it often will be impossible to replicate exactly the results obtained from different computer programs.
Bootstrap Methods
The bootstrap approach (Efron 1979) also applies many “draws” of coefficient vectors βb, to the sample observations, but variation in the coefficient vectors is obtained by re-estimating the model many times on different data samples. Each new data sample is obtained by drawing N observations with replacement from the original sample of data.5 The size of the new sample is set to be equal to the size of the original sample. The model then is re-estimated on the new sample of data, resulting in a new vector of estimated coefficients. Each new coefficient vector then is applied to produce a new value of 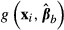 . Again, the standard deviation of the resulting distribution of
. Again, the standard deviation of the resulting distribution of 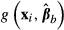 across all values of
across all values of 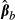 provides an estimate of the standard error of
provides an estimate of the standard error of 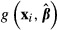 .
.
An important advantage of the bootstrap method is that it is simple to implement and is preprogrammed in many software packages. A disadvantage is that the model must be re-estimated on a different data sample to obtain each new coefficient vector. Maximum likelihood estimation is used for many nonlinear models, and some likelihood functions can have flat areas, making it difficult for the maximization algorithm to find the function maximizing values of the parameters. If the maximization algorithm is unable to find an optimum for any bootstrap sample, the program usually terminates. Even if termination occurs on the last of 1,000 bootstrap samples, the analyst must start over. That possibility alone makes the delta and K–R methods more attractive for some applications.
WHEN THE FUNCTION OF INTEREST IS A SAMPLE AVERAGE
As noted earlier, when the function of interest is the sample average, 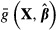
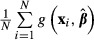 , the analyst must give careful consideration to the sources of variation in that function. For example, it would be incorrect to compute the standard error of
, the analyst must give careful consideration to the sources of variation in that function. For example, it would be incorrect to compute the standard error of 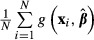 , simply by computing the standard deviation of
, simply by computing the standard deviation of 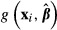 across the sample values then dividing by N. That approach ignores the sampling variation in
across the sample values then dividing by N. That approach ignores the sampling variation in 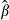 and the fact that the N terms in the sum are obviously not independent — they all use the same
and the fact that the N terms in the sum are obviously not independent — they all use the same 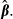
If 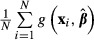 is treated simply as a function and the delta method is applied, then:
is treated simply as a function and the delta method is applied, then:
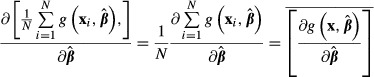 |
(17) |
And the delta method estimate of the standard error of 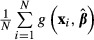 is:
is:
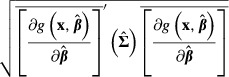 |
(18) |
Instead of 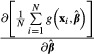 in equation (18), analysts often substitute the sample means of xi as follows:
in equation (18), analysts often substitute the sample means of xi as follows:
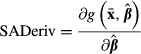 |
(19) |
This approach is unsatisfying for two reasons. First, 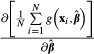 and
and 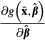 are not equivalent because the expected value of a function (e.g.,
are not equivalent because the expected value of a function (e.g., 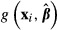 ) generally is not equal to the function evaluated at the expected values of its arguments if the function is nonlinear. Second, substituting the means of x results in the function and the standard error being computed at a point in the data that may not exist or may not be substantively meaningful. For example, no one in the data set will be 60 percent female or 20 percent pregnant.
) generally is not equal to the function evaluated at the expected values of its arguments if the function is nonlinear. Second, substituting the means of x results in the function and the standard error being computed at a point in the data that may not exist or may not be substantively meaningful. For example, no one in the data set will be 60 percent female or 20 percent pregnant.
A question has arisen in the literature regarding the role of the variation in X in equation (18). For example, Basu and Rathouz (2005) add the variance over xi of 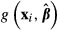 to equation (18). This addition seems incorrect to us. First, it is unclear if the additional term is appropriate. The additional variance term, per se, does not account for the nonlinearity of the function with respect to x. Second, the function
to equation (18). This addition seems incorrect to us. First, it is unclear if the additional term is appropriate. The additional variance term, per se, does not account for the nonlinearity of the function with respect to x. Second, the function 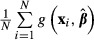 simply is another function of xi and
simply is another function of xi and 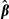 and application of the delta method to
and application of the delta method to 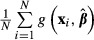 produces equation (18). While it is true that
produces equation (18). While it is true that 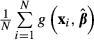 is computed over multiple values of x, the values of x are fixed in repeated samples. Adding more terms to the function does not change the nature of x.
is computed over multiple values of x, the values of x are fixed in repeated samples. Adding more terms to the function does not change the nature of x.
A related issue arises if the standard error of the sample average of a function is calculated by bootstrapping. The earliest work on bootstrap estimation by Efron (1979) recognized the problem of balancing x values that were fixed in repeated samples with the analyst's desire to generate a distribution of parameter values and subsequent functions of those parameters. The response to the problem is a family of bootstraps that come under the headings “bootstrapping regressions” or “resampling residuals.” In the simplest case of homoscedasticity and no autocorrelation, resampling residuals proceeds as follows:
Estimate the model on the original sample of data.
Compute and save both the predicted values of
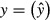 and the computed residuals
and the computed residuals 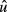 .
.For each
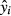 , draw, with replacement, a value of
, draw, with replacement, a value of 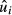 , denoted
, denoted 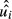 from the distribution of computed
from the distribution of computed 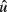 .
.For each observation, construct a new value of yi, denoted
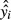 equal to
equal to 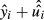 .
.Construct a new dataset consisting of
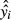 paired with its original values of xi.
paired with its original values of xi.Re-estimate the model, producing a new set of parameter estimates and new values of
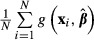 .
.Repeat steps 3 through 6 to obtain a distribution of
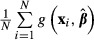 across multiple samples. The standard deviation of
across multiple samples. The standard deviation of 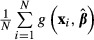 across the samples now provides an estimate of the standard error of
across the samples now provides an estimate of the standard error of 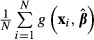 .
.
Notice how this approach differs from standard (paired) bootstrap sampling. The standard bootstrap estimator draws samples of both x and y from the original sample and re-estimates the model. The distribution of x in each sample differs from the distribution of x on which the original estimates of 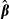 were based. In the “resampling residuals” approach above, the distribution of x is held constant (i.e., “fixed in repeated samples”). The bootstrap sampling is limited to the residuals—the true source of random variation in y.
were based. In the “resampling residuals” approach above, the distribution of x is held constant (i.e., “fixed in repeated samples”). The bootstrap sampling is limited to the residuals—the true source of random variation in y.
If 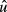 is heteroscedastic or autocorrelated, then simple residual resampling will not preserve the correct variances and dependencies among the residuals. Both problems have been considered in the bootstrap literature. Wu (1986) describes a generalized approach to resampling residuals. Moulton and Zeger (1991) discuss resampling in models with heteroscedasticity, and Politis and Romano (1994) propose a “blocks of blocks” resampling strategy for autocorrelated errors. In those cases, it may be that K–R provides a simpler approach, because the problems of heteroscedasticity and autocorrelation are dealt with “up front” in the initial estimation of
is heteroscedastic or autocorrelated, then simple residual resampling will not preserve the correct variances and dependencies among the residuals. Both problems have been considered in the bootstrap literature. Wu (1986) describes a generalized approach to resampling residuals. Moulton and Zeger (1991) discuss resampling in models with heteroscedasticity, and Politis and Romano (1994) propose a “blocks of blocks” resampling strategy for autocorrelated errors. In those cases, it may be that K–R provides a simpler approach, because the problems of heteroscedasticity and autocorrelation are dealt with “up front” in the initial estimation of 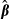 and
and 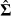 .
.
The K–R method for computing the standard error of the sample average of 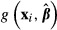 proceeds by drawing a vector of parameters
proceeds by drawing a vector of parameters 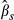 , computing
, computing 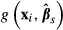 for each subject, and then computing the average value of
for each subject, and then computing the average value of 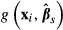 across the entire sample. Those steps are repeated for each new draw of
across the entire sample. Those steps are repeated for each new draw of 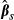 . The standard deviation of the resulting sample averages is the estimated standard error of
. The standard deviation of the resulting sample averages is the estimated standard error of 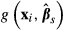 .
.
Despite the speed of modern computers, there can be significant differences in the time required to compute standard errors of sample averages of 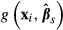 . For example, if one is computing the incremental effect of a binary variable (xk) on the predicted value of yi, using the K–R method, and there are 1,000 subjects in the sample, the program must compute two values of the predicted value of yi for each subject—one with xi,k = 1 and another with xi,k = 0, holding the values of the other variables constant at their values for that subject. Thus, one iteration through the data sample requires 2,000 computations, and 1,000 K–R coefficient draws would result in a total of 2,000,000 computations. The bootstrap approach would take even longer, because the entire model must be re-estimated for each of the 1,000 replications before the computation of the difference
. For example, if one is computing the incremental effect of a binary variable (xk) on the predicted value of yi, using the K–R method, and there are 1,000 subjects in the sample, the program must compute two values of the predicted value of yi for each subject—one with xi,k = 1 and another with xi,k = 0, holding the values of the other variables constant at their values for that subject. Thus, one iteration through the data sample requires 2,000 computations, and 1,000 K–R coefficient draws would result in a total of 2,000,000 computations. The bootstrap approach would take even longer, because the entire model must be re-estimated for each of the 1,000 replications before the computation of the difference 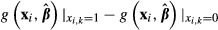 for each subject can begin. In general, the quickest estimation approach will be the delta method.
for each subject can begin. In general, the quickest estimation approach will be the delta method.
COMPUTER CODE
The Appendix contains computer code for calculating the standard errors of some nonlinear functions of estimated parameters. We illustrate the three different methods of computing the standard errors of nonlinear functions of estimated parameters using a fictitious, publicly available dataset—margex.dta.6 The data contain a dichotomous binary {0,1} dependent variable and various demographic explanatory variables for 3,000 observations. The dependent variable is equal to one for about 17 percent of observations. Age ranges from 20 to 60, with a mean of 40. Half the people in the sample are women (female = 1). The interaction between age and female (equal to age × female and denoted agefem) has a mean of 21.8 and ranges from zero to 60. We include only age and female and the interaction of age and female in our model to keep the example simple. The resulting regression equation is:
The observed variable Y is equal to 1 if Y* > 0 and zero if Y* ≤ 0. We assume that u has a logistic distribution and thus the coefficients are estimated by the logit likelihood function:
where F is the logistic cumulative distribution function 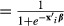 . The predicted value of the probability that y = 1|(x = xi) is:
. The predicted value of the probability that y = 1|(x = xi) is:
| (20) |
and the marginal effect of age, for example, on the probability that y = 1 is:
| (21) |
where f is the logistic probability density function. These functions are nonlinear in both the estimated parameters and the explanatory variables. Thus, the analyst must specify the values of the explanatory variables at which the function is computed. All the point estimates below are calculated for 50-year-old women; there are no other variables in the equation.
We provide the code for two popular software packages, NLOGIT and Stata.7 The choice of these two packages was based primarily on the authors' interests. The calculations can be done with other programs as well, although the degree of difficulty is highly variable. To our knowledge, there are no counterparts to the simulate/partials (NLOGIT) and margins (Stata) commands in other popular statistical packages. However, the computations can be done in less compact fashion with other programs such as SAS.
The packages and the methods produce similar results (see Tables 1–4). The results for the delta method are virtually identical across the two software packages, as expected. The results for K–R and bootstrap differ because the two packages are drawing different samples of coefficients and data.
Table 1.
The Predicted Value of the Probability That y = 1 for a 50-year-old woman
| Delta Method | Krinsky–Robb | Bootstrap | |
|---|---|---|---|
| NLOGIT | 0.33800 (0.01449) | 0.33800 (0.01423) | 0.33800 (0.01483) |
| Stata | 0.3380009 (0.0144851) | 0.3380009 (0.0144782) | 0.3380009 (0.0128234) |
Note.Point estimate (standard error).
Table 4.
The Partial Effect of Age on the Expected Value of the Probability That y = 1 Averaged over the Sample
| Delta Method | Krinsky–Robb | Bootstrap | |
|---|---|---|---|
| NLOGIT | 0.01176 (0.00060) | 0.01176 (0.00055) | 0.01176 (0.00074) |
| Stata | 0.0117612 (0.0006029) | 0.0117612 (0.0007607) | 0.0117612 (0.0006403) |
Note.Point estimate (standard error).
Table 2.
The Partial Effect of Age on the Expected Value of the Probability That y = 1 for a 50-Year-Old Woman
| Delta Method | Krinsky–Robb | Bootstrap | |
|---|---|---|---|
| NLOGIT | 0.02241 (0.00180) | 0.02241 (0.00170) | 0.02241 (0.00199) |
| Stata | 0.022407 (0.0017955) | 0.022407 (0.0018381) | 0.022407 (0.0017938) |
Note.Point estimate (standard error).
Table 3.
The Predicted Value of the Probability That y = 1 Averaged over the Sample
| Delta Method | Krinsky–Robb | Bootstrap | |
|---|---|---|---|
| NLOGIT | 0.16967 (0.00617) | 0.16967 (0.00620) | 0.16967 (0.00717) |
| Stata | 0.1696667 (0.0061658) | 0.1696667 (0.0061082) | 0.1696667 (0.0066586) |
Note.Point estimate (standard error).
SUMMARY AND CONCLUSIONS
Nonlinear functions of estimated parameters are of great interest in health services research applications. Examples include predicted values of the dependent variable and partial effects. Because the coefficients in these functions are estimated, the functions exhibit sampling variation and the confidence intervals for the estimated values of the function allow the researcher to make determinations regarding clinical or policy significance of the estimate. Confidence intervals, in turn, require estimates of the standard error of the function's estimated value. Statistical packages have made computation of standard errors relatively simple, and the methods give similar results. Thus, the choice generally is based on programming and computational convenience.
We have discussed several of the most common models that generate nonlinear functions of estimated parameters that are of interest to researchers, and three different ways of computing the standard errors of those functions. We hope that this discussion and the accompanying examples of computer code for NLOGIT and Stata provide useful information to health services researchers and other analysts.
Acknowledgments
Joint Acknowledgment/Disclosure Statement: William Greene is the developer of LIMDEP and NLOGIT and has an ownership interest in Econometric Software, Inc., the distributor for these programs.
Disclosures: None.
Disclaimers: None.
NOTES
The jackknife method, which is related to bootstrapping, occasionally is used, as well. We focus on the more commonly used bootstrap approach.
Examples of stochastic explanatory variables include variables subject to stochastic measurement error, lagged values of the dependent variable that appear among the explanatory variables, and causally endogenous explanatory variables arising, for example, from omitted variable bias or reverse causality. An example of an obviously nonstochastic explanatory variable is a time trend.
A counter-example is a sample selection model, in which the expected value of 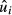 given the sample selection rule, is not zero.
given the sample selection rule, is not zero.
The variance in 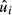 enters the problem in the following way:
enters the problem in the following way: 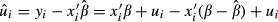 which leads to equation (5).
which leads to equation (5).
The way in which repeated samples of data are drawn must reflect the original sampling process, which could be complex in the case of clustered samples, for example.
This is the same dataset used in Karaca-Mandic, Norton, and Dowd (2012). The data can be downloaded from http://www.stata-press.com/data/r11/margex.dta.
NLOGIT is available from Econometric Software (http://www.limdep.com/). Stata is available from http://www.stata.com).
SUPPORTING INFORMATION
Additional supporting information may be found in the online version of this article:
Computation of Standard Errors Using Two Packages.
Author Matrix.
REFERENCES
- Basu A, Rathouz PJ. Estimating Marginal and Incremental Effects on Health Outcomes Using Flexible Link and Variance Function Models. Biostatistics. 2005;6(1):93–109. doi: 10.1093/biostatistics/kxh020. [DOI] [PubMed] [Google Scholar]
- Efron B. Bootstrap Methods: Another Look at the Jackknife. Annals of Statistics. 1979;7(1):1–26. [Google Scholar]
- Greene WH. Econometric Analysis. 7th Edition. Prentice Hall: Upper Saddle River, NJ; 2012. [Google Scholar]
- Hole AR. A Comparison of Approaches to Estimating Confidence Intervals for Willingness to Pay Measures. Health Economics. 2007;16(8):827–40. doi: 10.1002/hec.1197. [DOI] [PubMed] [Google Scholar]
- Karaca-Mandic P, Norton EC, Dowd BE. Interaction Terms in Non-Linear Models. Health Services Research. 2012;47(1 Part 1):255–74. doi: 10.1111/j.1475-6773.2011.01314.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krinsky I, Robb AL. On Approximating the Statistical Properties of Elasticities. Review of Economics and Statistics. 1986;68(4):715–9. [Google Scholar]
- Krinsky I, Robb AL. On Approximating the Statistical Properties of Elasticities: A Correction. Review of Economics and Statistics. 1990;72(1):189–90. [Google Scholar]
- Moulton LH, Zeger SL. Bootstrapping Generalized Linear Models. Computational Statistics and Data Analysis. 1991;11(1):53–63. [Google Scholar]
- Politis DN, Romano JP. The Stationary Bootstrap. Journal of the American Statistical Association. 1994;89(428):1303–13. [PubMed] [Google Scholar]
- Terza JosephV. Estimating Count Data Models with Endogenous Switching: Sample Selection and Endogenous Treatment Effects. Journal of Econometrics. 2008;84:129–54. [Google Scholar]
- Terza JosephV, Bradford WDavid, Dismuke ClaraE. The Use of Linear Instrumental Variable Methods in Health Services Research and Health Economics: A Cautionary Note. Health Services Research. 2008;43(3):1002–120. doi: 10.1111/j.1475-6773.2007.00807.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu CFJ. Jackknife, Bootstrap, and Other Re-sampling Methods in Regression Analysis. Annals of Statistics. 1986;14(4):1261–95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Computation of Standard Errors Using Two Packages.
Author Matrix.


