Continuous size-based separation of microparticles in a microchannel with symmetric sharp corner structures

Abstract

A new microchannel with a series of symmetric sharp corner structures is reported for passive size-dependent particle separation. Micro particles of different sizes can be completely separated based on the combination of the inertial lift force and the centrifugal force induced by the sharp corner structures in the microchannel. At appropriate flow rate and Reynolds number, the centrifugal force effect on large particles, induced by the sharp corner structures, is stronger than that on small particles; hence after passing a series of symmetric sharp corner structures, large particles are focused to the center of the microchannel, while small particles are focused at two particle streams near the two side walls of the microchannel. Particles of different sizes can then be completely separated. Particle separation with this device was demonstrated using 7.32 μm and 15.5 μm micro particles. Experiments show that in comparison with the prior multi-orifice flow fractionation microchannel and multistage-multiorifice flow fractionation microchannel, this device can completely separate two-size particles with narrower particle stream band and larger separation distance between particle streams. In addition, it requires no sheath flow and complex multi-stage separation structures, avoiding the dilution of analyte sample and complex operations. The device has potentials to be used for continuous, complete particle separation in a variety of lab-on-a-chip and biomedical applications.

INTRODUCTION

Separation of micro particles in suspension, such as cell separation, has been a critical task in many important areas including biomedical research,^{1, 2, 3, 4, 5, 6, 7} food industry,^{8, 9} and clinical applications.^{10, 11, 12, 13, 14} For instance, for a multichannel coulter counting sensor for high-throughput detection of bioactive particles,¹⁵ the sensitivity of the sensor is proportional to the ratio of the particle/channel size;¹⁶ particles of different sizes need to be separated and delivered to different channels with corresponding sizes to achieve high sensitivity and high dynamic range detection. In clinical applications, the separation of rare cells from biological samples is the preconditions for subsequent diagnosis and clinical analysis. One example is that separation of circulating tumor cells (CTCs) and stem cells from other blood cells is critical for cancer diagnoses and disease therapy.^{10, 11, 12, 13}

To date, many microfluidic separation methods¹⁷ have been studied because of numerous advantages, including less sample and reagent need, shorter processing time, higher efficiency, and better precision.¹⁸ These separation methods can be classified into active and passive ones based on the actuation and control mechanism. For active separation methods, externally induced forces are used as the actuation for the high-resolution particle separation. Active separation methods mainly include electrophoresis,^{19, 20} dielectrophoresis,^{21, 22} magnetophoresis,^{23, 24} negative magnetophoresis,^{25, 26} ultrasound,^{27, 28} optical,^{29, 30} and thermal³¹ manipulations. Although active methods can offer high resolution for particle separation, specific physical property of particles is rigorously required by different active separation methods.¹⁷ For example, only the magnetic particles and the magnetically labeled objects can be manipulated with the magnetophoresis.^{23, 24} Additionally, the active separation methods typically require high power consumption, and complex structures to generate external forces for particle separation.

Passive separation methods attract attentions because of the advantages of requiring no external force field, low power consumption, and simple structures for easy fabrication. Existing passive separation methods mainly include hydrodynamic filtration,^{32, 33} deterministic lateral displacement,^{34, 35} Dean flow separation,^{36, 37} and pinched flow fractionation.^{38, 39} Most passive separation methods including hydrodynamic filtration,^{32, 33} deterministic lateral displacement,^{34, 35} and pinched flow fractionation^{38, 39} have very low throughputs (<20 μL/min) because laminar flow in narrow microchannel is needed for the separation. More important, the concentration of particles can not be increased to a significant value.⁴⁰ Dean flow separation method^{36, 37} based on spiral structures can offer a very high particle throughput (10⁶ particles/min). However, this method only works for high speed particle flow. Furthermore, it requires large spiral microchannels which are difficult to be integrated in lab-on-a-chip devices and employed in parallel settings.⁴¹

Recently, inertial methods using parallel expansion-contraction reservoirs⁴² and multi orifice structures^{43, 44, 45} were utilized for particle separation. Due to the inertial migration and microvortices effect, particles of different sizes could be partially separated in these microchannels although complete separation of different sized particles still remains a long-standing problem.⁴⁰ For example, multi orifice fluid fraction (MOFF) method has been studied as a novel passive particle separation method based on the combination of inertial lift force and the momentum changed-induced force.⁴⁵ Plenty of particles can pass through the MOFF microchannel simultaneously, making this method suitable for separating particles with a high concentration.⁴⁰ In addition, the MOFF microchannel is easy to be integrated in lab-on-a-chip devices and employed in parallel settings.⁴⁶ However, particles of different sizes (7 and 15 μm in diameter) can not be completely separated with this method. While a multiple-stage MOFF microchannels (MS-MOFF)⁴⁶ coupled with the use of sheath flows was used to improve the particle separation efficiency, particles of different sizes still could not be completely separated. Further, the use of sheath flow induced the dilution of analyte sample and added complexity in device structure and flow control.

In this paper, we report a new microchannel with a series of symmetric sharp corner structures that can achieve complete size-dependent separation of micro particles with narrow bands of particle streams. The sharp corner structures induce highly curved streamlines in the microchannel and large centrifugal forces on particles passing the sharp corner structures. At appropriate flow rate and Reynolds number (Re), large particles, subjected to stronger centrifugal force than small particles, are focused at the center of the microchannel, while small particles are focused at two side equilibrium positions near the walls under the influence of inertial lift force. Particles of different sizes are thus separated.

WORKING PRINCIPLE

The microchannel designed for particle separation is illustrated in Figure 1, consisting of 100 segments of repeated symmetric sharp corner structures and expansion structures on both sides of the microchannel. Each segment of symmetric sharp corner structures and expansion structures induces a sudden contraction flow region and a gradual expansion flow region. The inlet width between the two symmetric sharp corner structures (W_i) is 40–45 μm. The length of sharp corner structures in the flow direction (L_s) is 80 μm. The length (L_e) and the width (W_e) of the expansion structures are both 200 μm. At the outlet, the width of the microchannel (W_o) is designed to be 800 μm to distinctly observe particle separation. The total length of the microchannel is approximately 39 mm. The microchannel has a uniform height (H) everywhere (50 μm).

Figure 1.

Schematic diagram of the microchannel with a series of symmetric sharp corner structures for micro particle separation.

The working principle of the microchannel with repeated symmetric sharp corner structures is illustrated in Figure 2. Particle's dynamic phenomenon in microchannel is often characterized by Re and particle Reynolds number (Re_p) which are defined as^{44, 47}

$$\mathrm{Re}=\frac{{\rho }_f{D}_{h}U}{\mu },$$ (1)

$${\mathrm{Re}}_p=\frac{{\rho }_f{U}_m{a_p}^2}{\mu D_h},$$ (2)

where ρ_f is the density of the liquid, D_h is the hydraulic diameter of the microchannel, defined as $D_h=\frac{2W_{i}H}{(W_i+H)}$ for a microchannel with contraction and expansion structures,⁴⁵U is the fluid velocity in the microchannel, μ is the dynamic viscosity of the fluid, U_m is the maximum fluid velocity in the microchannel, and a_p is the particle diameter.

Figure 2.

Illustration of working mechanism of particle separation in the microchannel with a series of repeated symmetric sharp corner structures. (a) Dominant forces exerted on the suspended particles. (b) 3-D illustration of particle separation in the microchannel.

When Re_p ≫ 1, in the expansion structure of the microchannel where the streamline changes direction smoothly, a particle in suspension is primarily subjected to the shear-gradient lift force and the wall-effect lift force; the net force of the two forces is the inertial lift force which dominantly drives micro particle away from both the wall and the centerline of the microchannel.^{48, 49, 50, 51, 52} The inertial lift force (F_i) can be estimated by⁵²

$$F_i=C_L{\rho }_f{G}^2{a_p}^4,$$ (3)

where C_L is a non-dimensional lift coefficient which is a function of the normalized cross-section position and Re,⁵² and G = U_m/D_h is the shear rate of the fluid. Particles will migrate towards two side equilibrium positions near the walls of microchannel where the inertial lift force is zero. In the process of particle inertial migration, the inertial lift force will be balanced by Stokes drag force, F_d:

$$F_d=3\pi \mu a_p{U}_s,$$ (4)

where U_s is the relative velocity between the particle and the fluid.

However, in the sudden contraction flow region induced by symmetric sharp corner structures, streamlines are dramatically curved. In addition to the inertial lift force, particles are also subjected to the centrifugal forces (F_c) because of the change of motion directions. From Newton's law, the centrifugal force exerted on a particle can be estimated as⁵³

$$F_c\sim {\rho }_p{v}^2/{\tau }_0=m\frac{v^2}{r}=\frac{\pi {\rho }_p{v}^2{a}_p^3}{6r},$$ (5)

where ρ_p is the density of the particle, v is the velocity of the particle, τ₀ is the time required for the particle to travel through the sharp turn, m is the mass of the particle, and r is radius of particle's trajectory.

The trajectories of suspended micro particles in the microchannel are determined by the competition between the inertial lift force (F_i, driving particles towards the side equilibrium positions near the walls) and the centrifugal force (F_c, driving particles towards the centerline). At low flow rates, because the centrifugal force is weak, particles tend to migrate towards the two side equilibrium positions near the channel walls. At high flow rates, the centrifugal force becomes large due to high flow velocity; particles will be centrifuged to the center of the channel. At the same flow rate, the centrifugal forces on large particles are stronger than those on small particles. Hence, large particles are driven to the center at a lower flow rate, while small particles start to migrate to the center at a higher flow rate when the centrifugal forces are sufficient. Therefore, by selecting an appropriate flow rate, large particles are eventually focused at the center of the microchannel and small particles are focused in the two side equilibrium positions. Note that in the present microchannel, the gap between symmetric sharp corner structures can be designed to be much larger than the size of particles used in the experiment. Particle separation is primarily determined by the effects of inertial lift force and the centrifugal force generated near the sharp corner structures. While for hydrodynamic particle separation, such as pinch-flow based separation, the pinch gap dimension must be designed to be comparable to the particle size so that different sized particles follow different streamlines and hence are separated in the subsequent expansion channel.⁵⁴

In comparison to the multi orifice flow fraction (MOFF) structures used for particle separation,^{45, 46} sharp corner structures used in the current design induce larger streamline curvature, thus generate larger centrifugal forces. At an appropriate flow rate, large particles will be more prone to be focused at the center of the microchannel, while small particles are still focused at two side stream bands (shown in Figure 2). In addition, the sharp corner structures induce gradual flow expansion, generating smaller vortices which may cause fewer disturbances to the focused particle streams by inertial lift force; as a result, the focused particle streams are kept in two narrower bands.

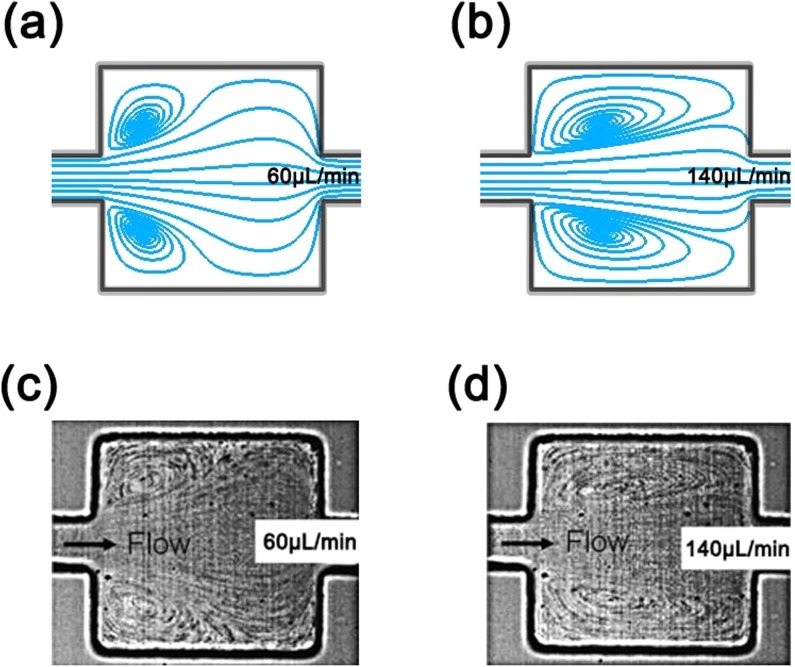
The working mechanism of particle separation in the microchannel with a series of repeated symmetric sharp corner structures was justified by computational fluid dynamics (CFD) simulation using commercial CFD solver Fluent 6.3. Different flow rates ranging from 20 to 200 μL/min were simulated. Similar simulations were also conducted on the MOFF microchannel⁴⁵ to compare particle separation effect; the width and length of the orifice structures in the MOFF microchannel are set the same as W_i and L_s in the present microchannel. While we did not conduct flow field/flow pattern measurements due to lack of experimental apparatus, we simulated the flow field of a MOFF microchannel (Figure 3) and compared the simulation result with the flow pattern measurements reported in Ref. 55. The simulation result matched with the experimental results well, proving the CFD simulations are valid. As an example, the simulated flow fields (streamlines) in the present microchannel and the MOFF microchannel at a flow rate of 100 μL/min are shown in Figures 4a, 4b. Figures 4a, 4b show at the same flow rate the vortices generated in the present microchannel are much smaller than those in MOFF microchannel. The curvature of streamlines near the contraction regions of the microchannels is the key factor for size-dependent particle separation in the microchannels with contraction and expansion structures.⁴⁵ From the simulation results, the average streamline curvature (1/R) near the sharp corners/contraction regions of the microchannels was calculated at various flow rates and plotted in Figure 4c, which clearly shows that the average streamline curvature (1/R) induced by the sharp corner structure is larger than that in the MOFF microchannel. Note that although the streamlines are curved, the flow field simulations (not shown here) show that there is no Dean vortex generated in the current microchannel. Using the average curvature in Figure 4c, we calculated the centrifugal forces (see Figure 4d) on a 15.5 μm polystyrene particle in the two microchannels assuming particle's trajectory follows the streamline and its velocity is the same as the flow velocity. Obviously in the microchannel with sharp corner structures, the centrifugal force exerted on the particle is larger than that in the MOFF microchannel. The larger centrifugal force would quickly focus large particles at the center with a narrower bandwidth, which is necessary for complete size-dependent particle separation.

Figure 3.

Comparison of flow field in a MOFF microchannel obtained from CFD simulation and experiments.⁵⁵ (a) Flow field from CFD simulation at 60 μL/min. (b) Flow field from CFD simulation at 140 μL/min. (c) Measured flow field at 60μL/min. Reprinted with permission from Park et al., Lab Chip 9, 939 (2009). Copyright 2009 Royal Society of Chemistry.⁵⁵ (d) Measured flow field at 140 μL/min. Reprinted with permission from Park et al., Lab Chip 9, 939 (2009). Copyright 2009 Royal Society of Chemistry.⁵⁵

Figure 4.

Simulation results in the present microchannel and the MOFF microchannel. (a) Flow filed in the present microchannel at 100 μL/min. (b) Flow filed in the MOFF microchannel at 100 μL/min. (c) Average curvature of streamline (1/R) in the two kinds of microchannels at various flow rates. (d) Average centrifugal forces exerted on 15.5 μm particles in the two microchannels.

EXPERIMENTAL SECTION

Device fabrication

The microchannel shown in Figure 1 was fabricated using a standard soft lithography technique. First, SU8-2075 photoresist (MicroChem Inc., USA) was spin coated on a silicon wafer with a thickness of 50 μm. Then photolithography was applied to SU8 layer to form the microchannel mold. 10:1 polydimethylsiloxane (PDMS) (Sylgard 184, DowCorning, USA) was poured over the mold, degassed, and cured, to transfer the patterns onto the PDMS layer. Next, the surfaces of the PDMS layer and a pre-cleaned glass slide were treated in air plasma for 40 s at 100 W (Harrick PDC-32G). Finally, the device was completed by bonding the PDMS layer and a pre-cleaned glass slide.

Experimental setup

Fluorescent polystyrene particles 7.32 μm (FS06F/9559, Dragon green, 480/520 nm) and 15.5 μm (FS07F/9277, Dragon green, 480/520 nm) in diameter were used for the particle separation experiments (Bangs Laboratories, Inc., USA), which have similar sizes to erythrocytes and human breast cancer cells (MDA-MB-231), respectively. Separation of human breast cancer cells from erythrocytes in blood and subsequent analysis of cancer cells are important for early stage cancer diagnosis. The densities of both polystyrene particles are 1.062 g/cm³. The standard deviation in diameter distributions is 7.2% and 9.8%, respectively. Two particle solutions were individually prepared with 7.32 and 15.5 μm particles. The 7.32 μm particles were suspended in deionized water with a solid concentration of 3.5–5.5 × 10³ particles/μL, while the 15.5 μm particles were suspended in deionized water with a solid concentration of 0.3–0.5 × 10³ particles/μL. The small solid concentrations were used to avoid the effect of collisions between particles on particle separation. 0.5 wt. % of detergent/surfactant (Tween 20; Sigma-Aldrich Co., USA) was added into the particle solutions to avoid aggregation of particles. Next, the ultrasonic bath was used to sufficiently disperse the particles in suspension for at least 30 min.

The solution prepared with 7.32 μm fluorescent polystyrene particles was first injected into the inlet of the microchannel using a syringe pump (KDS LEGATO270; KD Scientific Inc., USA) equipped with a 10 mL BD syringe at flow rates ranging from 40 to 160 μL/min. The syringe was connected to the microchannel with a PEFE tube. An inverted optical microscope (IX-71, Olympus Co., Japan) was used to observe the migration of particles with a fluorescence mirror unit (U-MNB2, Olympus Co., Japan). Images of particle trajectories were captured with a mono color CCD camera (Qimaging fast 1394, Qicam, USA). Similar processes were conducted on the 15.5 μm fluorescent polystyrene particles solution.

The acquired images of 7.32 and 15.5 μm particles were individually analyzed with ImageJ software (NIH, USA) and Adobe Photoshop (Adobe Systems Inc. USA). Because the 7.32 and 15.5 μm particles fluorescent particles had the same florescence color (Dragon green), to differentiate 7.32 and 15.5 μm particles, ImageJ software was used to add cyan florescence to the images of 7.32 μm particles and green florescence to the images of 15.5 μm particles. To analyze the florescence intensity, first the threshold was set for each image in ImageJ. Then threshold images were converted to the binary ones. Finally, the fluorescence intensity (FI) of particles was quantified with the menu command Analyze. Experiments were also conducted by mixing the 7.32 and 15.5 μm particles in bright light field at selected flow rate to demonstrate the particle separation.

RESULTS AND DISCUSSION

Figures 5a, 5c show typical random particle distributions of 7.32 μm particles and 15.5 μm particles at inlet of the microchannel at a flow rate of 100 μL/min. Note that at all flow rates 7.32 μm particles and 15.5 μm particles exhibited similar random distribution at inlet. Figure 5b shows the migration progress of 7.32 μm particles, and Figure 5d shows the migration progress of 15.5 μm particles at various flow rates ranging from 40 to 160 μL/min (Re from 14.8 to 59.3). The florescence images were taken at selected locations at inlet, upstream (the 10th–12th sharp corner structures), midstream (the 50th–52th sharp corner structures), and outlet (the 98th–100th sharp corner structures) of the microchannel. Re_p at various flow rates are listed in Figures 5b, 5d. For 7.32 μm particles, when the flow rate ranged from 40 to 140 μL/min (Re_p from 0.84 to 2.94) the inertial lift force were dominant; particles were driven to the two equilibrium positions close to the side walls. After passing a series of symmetric sharp corner structures, 7.32 μm particles were focused in two side streams from the midstream to the outlet of the microchannel (Figure 5b). Similar particle migration behaviors were observed by Park et al.^{45, 55} and Sim et al.⁴⁶ in a MOFF microchannel. When the flow rate was increased to 160 μL/min (Re_p = 3.36), the particle velocity increased and so did the centrifugal force, which started to play a role in particle's lateral migration. Some particles originally located near the center were driven to the centerline of the channel. As a result, a new particle stream was formed at the centerline of the channel (see Figure 5b). While we did not conduct experiments at higher flow rates, it can be predicted that with increased flow rate and increased centrifugal force, more particles will be driven to the central particle stream. Eventually, at a sufficient high flow rate, all particles will be focused in a single stream at the centerline. In comparison to the distribution of 7 μm particles in the MOFF microchannel,⁴⁵ the side particle streams have much narrower bandwidth, which might be because the smaller vortices generated in the current microchannel caused fewer disturbances to the focused particle streams (Figures 4a, 4b); as a result, the focused particle streams are kept in narrower bands. Note that the narrower particle streams are desired because they lead to more efficient particle separation.

Figure 5.

Particle migration progress in the microchannel at various flow rates from 40 to 160 μL/min. (a) Particle distribution of 7.32 μm particles at the inlet at a flow rate of 100 μL/min. (b) 7.32 μm particles distribution at upstream, midstream, and outlet of the present microchannel according to various flow rates (Re_p from 0.84 to 3.36). (c) Particle distribution of 15.5 μm particles at the inlet at a flow rate of 100 μL/min. (d) Particle distribution at upstream, midstream, and outlet for 15.5 μm particles (Re_p from 3.73 to 14.94). For clarity, images taken from upstream and midstream are in larger dimension scale than images taken from outlet in (b) and (d).

In the case of 15.5 μm particles, as the flow rate was increased from 40 to 120 μL/min, in addition to the two symmetric particle streams near the side walls, we observed some particles were distributed between the two side particle streams (see Figure 5d). This is possibly because even at the lowest tested flow rate (40 μL/min, Re_p = 3.73), the centrifugal force could be sufficiently large due to the big a_p, driving particles towards the center. At the same time, inertial lift force was also increased (from Eq. 3), which tended to move particles to the two side equilibrium positions. As a result of the competition between the inertial lift force and the centrifugal force, particles originally located near the center were distributed in the region between the two side streams. However, as the flow rate increased, these particles tended to move towards the center because of the increased centrifugal force. When the flow rate was further increased to 140 μL/min (Re_p = 13.05) and 160 μL/min (Re_p = 14.94), the centrifugal force became dominant; starting from the midstream, all particles were focused in a single central particle stream (Figure 5d). In comparison to the distribution of 15 μm particles in the MOFF microchannel,⁴⁵ 15.5 μm particles were focused in a narrower stream at the center of the current microchannel due to the stronger centrifugal force induced by symmetric sharp corner structures.

From the migration behaviors of two-size particles shown in Figure 5, all 15.5 μm particles tended to be focused at the center at a lower flow rate (140 μL/min), while 7.32 μm particles tended to be focused at two side particle streams at low flow rates (40 to 140 μL/min). Hence, two-size particles can be separated in the current microchannel. To show the device's feasibility for two-size particle separation, distributions of 7.32 and 15.5 μm particles at outlet at various flow rates were merged together. The results are shown in Figure 6a.

Figure 6.

(a) Superimposed fluorescence distribution images of 7.32 μm and 15.5 μm particles at various flow rates to show the feasibility of particle separation (cyan florescence for 7.32 μm particles, green florescence for 15.5 μm particles). (b) Bright-field image of separation of the two-size particles at a flow rate of 140 μL/min.

Figure 6a shows 7.32 and 15.5 μm particles could be partly separated at outlet of the present microchannel at low flow rates (40 to 120 μL/min). Complete particle separation can be achieved at the flow rate of 140 μL/min (shown in Figure 6a), where all 15.5 μm particles were focused at the center while the 7.32 μm particles were focused at the two side streams. However, at high flow rates (>140 μL/min), complete two-size particle separation is infeasible because part of the 7.32 μm particles were focused at the center of the microchannel.

To demonstrate the device's capability for complete particle separation, we conducted experiments using a mixture of 7.32 μm and 15.5 μm particles. Because particles of both sizes had the same fluorescence color, a bright-field image at the channel outlet was taken at a flow rate of 140 μL/min (Figure 6b). The picture clearly shows that all 7.32 μm particles were focused in two side particle streams, while all 15.5 μm particles were focused at the center.

To quantitatively analyze the particle stream band for 7.32 and 15.5 μm particles at outlet, we calculated the FI of the two-size particles at various Reynolds numbers from images shown in Figure 6a using ImageJ software. To compare with the particle focusing and separation effectiveness in the MOFF microchannel,⁴⁵ we also plotted the fluorescence intensity from the data at similar Reynolds numbers presented in Ref. 45. The fluorescence intensity distribution curves are shown in Figure 7, where r′ is the dimensionless lateral position from the center of the microchannel defined as r′ = y/r, where y is the Y-coordinate of the focused particle stream and r is half of the local channel width at the outlet (r = 400 μm).

Figure 7.

Fluorescence intensity distribution curves of micro particles in the microchannel with a series of symmetric sharp corner structures and in the MOFF microchannel at various Reynolds numbers: (a) Re ≈ 30; (b) Re = 37; (c) Re ≈ 50; (d) Re = 59.3. r′ is the dimensionless lateral position from the center of the microchannel.

Figures 7a, 7b, 7c show in our microchannel with symmetric sharp corner structures, two symmetric fluorescence intensity peaks for 7.32 μm particles were generated at approximately 0.6r′ with a bandwidth of ∼0.1r′ (40 μm) at the outlet, when Re ranged from 29.6 to 51.8; in comparison, in the MOFF microchannel, two symmetric fluorescence intensity peaks for 7 μm particles were generated at approximately 0.6r′ with an average bandwidth of ∼ 0.5r′ (200 μm) at the outlet within the similar Re range.⁴⁵ These results show that 7.32 μm particles were more tightly focused in two particle streams in the present channel with a narrower bandwidth than 7 μm particles in the MOFF channel. Figure 7d shows when Re = 59.3 and 7.32 μm particles were focused in three particle streams in our microchannel, each with bandwidth of ∼0.05r′–0.1r′ (20–40 μm) at the outlet, while in the MOFF microchannel 7 μm particles were distributed in one wider particle stream with an average bandwidth of ∼1.3r′ (520 μm) at the outlet.⁴⁵ This is possibly because the vortices generated in our microchannel are much smaller than those generated in MOFF microchannel at the same Re (shown in Figures 4a, 4b); the smaller vortices would cause fewer disturbances to the focused particle streams, keeping the tightly focused particle streams in narrower bands.

Figures 7a to 7d also show that in the MOFF microchannel, 15 μm particles were distributed near the center of the channel when Re ranged from 25.9 to 59.3, the bandwidths of the focused 15 μm particle streams ranged from 0.85r′ to 1.35r′ (340 μm to 540 μm) at the outlet; such a large bandwidth made complete particle separation difficult. In comparison, in the present microchannel, at low Reynolds numbers (Re = 29.6 and 37), 15.5 μm particles were focused at three distinctively separated particle streams, with a central bandwidth of ∼0.3r′–0.5r′ (120–200 μm) at the outlet (Figures 7a, 7b; at high Reynolds numbers (Re = 51.8 and 59.3), all 15.5 μm particles were focused in a central stream with a bandwidth of ∼0.5r′ (200 μm) at the outlet, which is much narrower than that in MOFF microchannel at similar Re (Figures 7c, 7d). It is obvious that the present microchannel could tightly focus particles of different sizes in narrower streams than the MOFF microchannel. Furthermore, 15.5 μm and 7.32 μm particle streams were distinctively separated at Re = 51.8 (140 μL/min). The separation distance between the central particle stream (15.5 μm) and side particle streams (7.32 μm) in our microchannel is approximately 0.35r′ (140 μm) at the outlet. In comparison, in the MOFF microchannel, different-size particle streams were partly overlapped with each other.⁴⁵ The result demonstrated that using the microchannel with a series of symmetric sharp corner structures, two-size particles can be completely separated and be collected at the outlet of the microchannel.

In addition, although only particles with diameters of 7.32 μm and 15.5 μm were tested, it can be anticipated that the present microchannel can be applied for separation of two-size particles with larger size difference. Note that the minimum size of particles that can be separated is limited by the widely accepted notion that the particle diameter to the hydraulic diameter ratio (a_p/D_h) should be greater than 0.07.⁵⁶ Based on this notion, particles with diameter smaller than 3 μm would remain unfocused in the microchannel and cannot be separated.

While the present microchannel aims to separate live cells for biomedical applications, the effects of cell deformation^{40, 57} on cell separation in the present microchannel must be considered. Cell deformation could induce a deformability-induced lift force on suspended particles, causing additional lateral migration toward the center of the microchannel.⁵⁸ However, although the deformability-induced lift force tends to drive deformable particles toward the center of the channel, the inertial lift force still plays a dominant role.⁵⁸ As a result, deformable particles/cells were observed to migrate toward two modified symmetric equilibrium positions in the microchannel.^{58, 59} Similar phenomena were also observed in a MS-MOFF microchannel for deformable cell separation.⁴⁴ Based on these observations, it is expected that the present microchannel can be used for separation of deformable cells of different sizes; however, the separation distance between large and small cell streams may become smaller due to the deformability-induced lift force.

Separation devices may also cause damage^{47, 60} of live cells and blockage^{61, 62, 63} of the microchannel. Wall shear stress (τ_w), defined as ${\tau }_w=\mu \frac{\mathit{d}\mathit{U}}{\mathit{d}\mathit{y}}$, is often used to evaluate the extent of cell damage in microchannel.^{47, 60} Recently, Kameneva et al. found when the wall shear stress was less than 300 Pa under laminar flow, the increase in plasma free hemoglobin was very low (indicating very weak cell damage).⁶⁰ This research implied that severe cell damage is less likely to occur when τ_w < 300 Pa under laminar flow. We calculated the wall shear stress in different positions of the present microchannel at 140 μL/min (Re = 51.8), the flow rate where complete particle separation was enabled. The results are shown in Figure 8.

Figure 8.

Wall shear stress (τ_w) distribution in the microchannel with a series of symmetric sharp corner structures at the flow rate of 140 μL/min.

Figure 8 shows wall shear stress is high near the sharp corners; the maximum wall shear stress is 218 Pa and drops to 28 Pa at the expansion region. Hence, cell damage is less likely to occur in the present microchannel. Very recently, separation of live cells in a MS-MOFF microchannel at a flow rate of 144 μL/min was successfully demonstrated without causing cell damages.⁴⁴

Finally, because the present microchannel permits the use of a contraction channel whose size is a few times larger than that of the cell, channel blockage is unlikely to occur. In addition, standard surface treatment methods, such as glutaraldehyde treatment, could be used to improve the cell rigidity before separation to reduce the chance of channel blockage.⁶⁴ From the above mentioned analysis, it is reasonable to predict that the present microchannel with a series of sharp corner structures can be used for live cell separation without causing severe cell damage and channel blockage.

Although we demonstrated complete particle separation using symmetric sharp corner structures with a 45° angle, we anticipate that as the angle becomes smaller/shaper, the current particle separation might be more efficient because sharper corner structure would induce larger centrifugal forces, generating narrower particle stream band at the center for large particles. It is also worthwhile mentioning here that although the device can successfully separate 7.32 μm and 15.5 μm particles, quantitative analysis of inertial lift force and centrifugal force is needed to better understand particle migration behavior, predict the working range of the device, and improve the device design. There are two challenges for the quantitative force analysis: (i) unknown C_L value in Eq. 3 for calculating inertial lift force and (ii) unknown velocities of particles suspended in the microchannel. Recently, Zhou and Papautsky attempted to experimentally study C_L in a microchannel with rectangular cross section by measuring the particle migration distance (L_m) and the focusing length (L).⁶⁵ From the measurement, C_L can be estimated by $C_L=\frac{3\pi \mu D_h^2}{2{\rho }_{f}U{a}_p^3}\times \frac{L_m}{L}$.⁶⁵ Enlightened by this work, we plan to address this problem in our future study by (1) experimentally determining C_L in a microchannel with variable cross sections⁶⁵ and (2) numerically solving particle–fluid interaction by coupling the fluid flow and particle motion equations to accurately calculate the particles' velocity.⁶⁶ Second, the experiments were conducted with small particle volume fractions (3.5–5.5 × 10³ particles/μL for 7.32 μm particles; 0.3–0.5 × 10³ particles/μL for 15.5 μm particles) to avoid the collisions between particles. In the future work, the effect of particle volume fraction on particle separation needs to be studied because the collisions between particles may significantly affect the particle separation in the microchannel. In addition, the experiments were conducted with a fixed length of flow expansion region; further study is needed to investigate the effect of channel dimensions on particle separation in the future. Nevertheless, with the advantages of simple structure, easy operation, and high particle separation efficiency, this method can be potentially used in a variety of lab-on-a-chip applications.

CONCLUSIONS

A microchannel with 100 segments of repeated symmetric sharp corner structures for particle separation was designed and fabricated. Particle separation was based on the combination of the inertial lift force and the centrifugal force induced by the symmetric sharp corner structures in the microchannel. The device was demonstrated by testing 7.32 μm and 15.5 μm micro particles. At appropriate flow rate (140 μL/min) and Reynolds number (Re = 51.8), large particles were focused at the center under the strong influence of centrifugal force, while small particles were focused at two side particle streams primarily driven by the inertial lift force in the microchannel. At the outlet of the microchannel, the bandwidths of the side particle streams (7.32 μm) and the center particle stream (15.5 μm) were approximately 40 μm and 200 μm, respectively. The separation distance between the side streams and the central particle stream is approximately 140 μm. In comparison to the particle separation using MOFF and MS-MOFF microchannels, our device can completely separate two-size particles with narrower stream bandwidth and larger separation distance. In addition, no sheath flow is required, avoiding the dilution of analyte sample and complex flow control. Simple structure used in the present microchannel also induces low flow resistance. With these advantages, this passive particle separation device can potentially benefit a variety of lab-on-a-chip applications that require complete particle separation and simple operations.