Effects of Geometric Parameters on Swimming of Micro Organisms with Single Helical Flagellum in Circular Channels

Abstract

We present a computational fluid dynamics (CFD) model for the swimming of micro organisms with a single helical flagellum in circular channels. The CFD model is developed to obtain numerical solutions of Stokes equations in three dimensions, validated with experiments reported in literature, and used to analyze the effects of geometric parameters, such as the helical radius, wavelength, radii of the channel and the tail and the tail length on forward and lateral swimming velocities, rotation rates, and the efficiency of the swimmer. Optimal shapes for the speed and the power efficiency are reported. Effects of Brownian motion and electrostatic interactions are excluded to emphasize the role of hydrodynamic forces on lateral velocities and rotations on the trajectory of swimmers. For thin flagella, as the channel radius decreases, forward velocity and the power efficiency of the swimmer decreases as well; however, for thick flagella, there is an optimal radius of the channel that maximizes the velocity and the efficiency depending on other geometric parameters. Lateral motion of the swimmer is suppressed as the channel is constricted below a critical radius, for which the magnitude of the lateral velocity reaches a maximum. Results contribute significantly to the understanding of the swimming of bacteria in micro channels and capillary tubes.

Introduction

A variety of stimuli such as the concentration of repellents and attractants, temperature, magnetic field, and light (1,2) can induce bacterial locomotion, or motility, which may be exhibited not only in bulk fluids but also near solid surfaces and in confinements (3–5). Brownian motion randomizes the direction and the position of the cell during a steady swimming period and is coupled with hydrodynamic interactions to alter profoundly the trajectory of bacteria near a planar wall because of variations of the distance from the wall (6). However, the swimming behavior of bacteria in confinements exhibits nearly steady behavior (3). Electrostatic and van der Waals forces are effective and cause adhesion only when the bacteria are very close to the boundary ∼ 10 nm (6).

As demonstrated in previous works (7,8), the swimming characteristics of bacteria with helical tails are vital to understand phenomena such as surface accumulation and mobility in bulk fluids and in porous media. DiLuzio et al. (9) studied the swimming behavior of Escherichia coli (E. coli) cells in confined geometries, reported that the bacteria swim close to porous agar surface than solid polydimethylsiloxane (PDMS) surface, and showed that the motion of cells is affected by the guide material in narrow channels; the percentage of the cells swimming close to the agar surface decreases as the channel height increases, indicating that hydrodynamic interactions diminish (9). In an experimental study with mammalian sperm cells and unicellular green algae, Kantsler et al. (10) demonstrated that flagella-surface interactions are mostly important on the surface scattering mechanism of cells.

Biondi et al. (3) conducted experiments to determine the effects of restricted geometries on the swimming behavior of E. coli in micro channels with heights varying from 2 to 20 μm, calculated the motility coefficients from the single-cell data, and reported that the swimming behavior remains nearly constant in confined geometries. Maximum swimming speed is achieved in the 3-μm channel, but the speed decreases because of increasing drag force attributable to the restriction in the 2-μm channel (3). Berg and Turner (11) conducted experiments with motile and nonmotile bacteria in capillaries of 10 and 50 μm in diameter, reported that drift velocities and diffusion coefficients are higher in a 10-μm capillary than in a 50-μm one, and concluded that bacteria align with the channel's longitudinal axis in restricted geometries. Liu et al. (4) performed experiments with E. coli in a capillary tube with a 50-μm diameter, developed a method to measure chemotaxis parameters at the single-cell level, demonstrated that the swimming speed has a normal distribution, and concluded that there is an optimal viscosity that maximizes the swimming speed (4). Furthermore, the authors also obtained the distribution of turn angles, which exhibits a nonnormal behavior because of geometric restriction (4). Mannik et al. (12) studied the motility of E. coli inside micro channels with a diameter of 2 μm and narrower, which are marginally larger, 30%, than the diameter of the cells. The authors showed that bacterial motion is one-dimensional because of shallowness of the channel and the bacterium swims at the same average speed in the channels with diameters larger than 1.1 μm as in the chamber. The motility of the bacteria vanishes in smaller channels with a diameter of 0.8 μm and smaller, but the bacteria can still pass through these channels by growth and division.

The Reynolds number of the bacterial locomotion is very low, ∼ 10⁻⁵, and the flow is governed by incompressible Stokes equations. Felderhof (13) constructed an approximate solution based on perturbation methods for infinitely long “thick” helical filaments rotating and moving axially inside circular channels, and showed that the confinement leads to increased swimming speed and efficiency depending on the stroke parameters such as the amplitude, wavelength, and the relative radius of the filament with respect to the channel radius.

Boundary element method (BEM) is used in numerical models of the swimming of micro organisms in the bulk fluid (7,14), near planar walls (8,15), and recently in channels (16). Zhu et al. (16) modeled the locomotion of ciliated micro organisms with a spherical squirmer model inside straight and curved capillary tubes with a BEM model, which is tuned for geometric confinements. The authors reported that the confinement and near-wall swimming always decrease the swimming speed of the squirmer with tangential surface deformation, but improve the speed of the squirmer with normal surface deformation, which pushes against the wall (16).

Numerical solutions to Stokes equations, such as finite-element-method (FEM) based computational fluid dynamic (CFD) models are powerful tools to study the effects of the proximity to solid surfaces in the swimming behavior of bacteria and to identify hydrodynamic interactions between the surface and the cell. Temel and Yesilyurt (17) used a three-dimensional CFD model for an actual artificial swimmer used in experiments to study the effect of distance from the wall and the geometry of the helical tail on the swimming speed and the power efficiency, which attain maximum values at a critical distance from the wall compared with center swimming.

A number of studies address the effects of geometric parameters on the swimming of micro organisms near boundaries and in the bulk fluid (7,8). Further study is necessary to understand the swimming behavior of micro organisms in confinements such as circular channels. In this study, we used a model organism with a spheroid head and a rigid helical flagellum to study the locomotion of the organism in circular channels by solving incompressible Stokes equations with the FEM. The numerical model is validated against experimental work reported in the literature. Simulations are performed to demonstrate the effects of the geometrical parameters of flagella on linear and angular velocities and the swimming efficiency of the organism. Effects of the geometric parameters on lateral velocities and wobbling are discussed.

Methodology

The monotrichous bacteria model used in Shum et al. (8) and shown in Fig. 1 is taken as the model organism used in this study and placed at the centerline of the circular channel (parameters shown in Table 1). The flow around the organism inside the channel has a low Reynolds number and is governed by incompressible Stokes equations as follows:

$$-\nabla p+\mu {\nabla }^2\mathbf{u}=0,\nabla \cdot \mathbf{u}=0$$ (1)

where p is pressure, u is the velocity vector, and μ is the dynamic viscosity.

Figure 1.

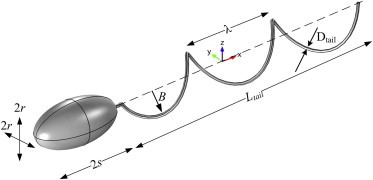
Parameters of the cell geometry; description of the parameters are shown in Table 1. To see this figure in color, go online.

Table 1.

Geometric parameters of the model organism

Symbol	Description
s	Polar radius of spheroid head
r	Equatorial radius of spheroid head
λ	Wavelength of the tail
Nλ	Number of helical turns
B	Wave amplitude
L	Length of the tail
Rtail	Tail radius
Dtail	Tail diameter
f	Frequency
Rch	Channel radius
Lch	Channel length

The helical tail is attached to the cell body with a simple joint as shown in Fig. 1 and rotates in the opposite direction to the rotation of the body. The helical tail is modified with the amplitude growth rate as proposed in Higdon (18). The centerline of the left-handed helical tail is given as follows:

$$X\left(\xi \right)=\left[\xi ,B\left(1-e^{-k_E^2{\xi }^2}\right)\text{sin}\left(k\xi -\phi \right),B\left(1-e^{-k_E^2{\xi }^2}\right)\text{cos}\left(k\xi -\phi \right)\right]$$ (2)

where ξ is the x- coordinate, k is wave number (k = 2π/λ), φ is phase angle that corresponds to the angular position of the tail during its rotation, i.e., φ = ωt, B is the wave amplitude, which is set to equatorial radius of the spheroid head, r, and k_E is the growth rate of the amplitude. Phan-Thien et al. (14) and Shum et al. (8) studied similar geometry of the bacterium as well.

The channel inlet and outlet are sufficiently away from the organism so that the fluid can be assumed stationary with no-slip boundary conditions at the inlet and outlet as well as on the channel wall as follows:

$$\mathbf{u}=0\text{at}x=0,L_{ch}\text{and}\text{at}r=R_{ch}$$ (3)

No-slip boundary conditions on the surface of the organism are expressed as moving wall conditions. Local velocities of the head and the tail of the organism are calculated using angular, Ω, and linear velocities, U_sw, as follows:

$$\begin{array}{l}{\mathbf{u}}_{head}={\mathbf{U}}_{\mathbf{sw}}+\mathbf{\Omega }\times \left(\mathbf{x}-{\mathbf{x}}_{\mathbf{com}}\right),\\ {\mathbf{u}}_{tail}={\mathbf{U}}_{\mathbf{sw}}+{\left[\omega {\text{Ω}}_y{\text{Ω}}_z\right]}^{\prime }\times \left(\mathbf{x}-{\mathbf{x}}_{\mathbf{com}}\right)\end{array}$$ (4)

where ω is the angular velocity of the tail with respect to fixed coordinate frame in the x-direction, subscript “com” represents the center of mass of the bacterium and []′ represents transpose of the vector. The actual center of mass is very close to the midpoint of the spheroid head since the tail is very thin. For the base case bacterium model with λ/s = 3 and L/s = 6, the distance between the center of the spheroid head and the center of mass is about s/10.

For the unknown linear velocity components, U_sw, V_sw, and W_sw in x-, y-, and z-directions, force-free swimming conditions are specified as constraint equations as follows:

$$\mathbf{F}=\underset{S_{sw}}{\int }\sigma \cdot \mathbf{n}dS=0$$ (5)

where σ is the fluid stress tensor, and n is the surface normal vector.

Net torque is equal to zero on the bacterium. The head and tail are rotating in opposite directions about the tail’s axis (x axis). The magnitudes of the x-torques acting on the head and the tail are equal to each other because of the torque balance between the links. Similarly to the force-free swimming constraints used for linear velocities, torque-free swimming constraints are used for angular velocities as follows:

$$\mathbf{\tau }=\underset{S_{sw}}{\int }\left(\mathbf{x}-{\mathbf{x}}_{com}\right)\times \left(\mathbf{\sigma }\cdot \mathbf{n}\right)dS=0.$$ (6)

The swimming efficiency, η, is calculated from the ratio of the rate of work done to propel the organism in the forward direction to the rate of work done to rotate the helical tail with respect to the body of the organism as commonly used in the literature (19) as follows:

$$\text{η}=\frac{F_{body}{U}_{sw}}{{\text{τ}}_{\text{tail}}\left({\text{Ω}}_x+\omega \right)}$$ (7)

where F_body is the drag force on the body, which is calculated by integrating the fluid stresses; U_sw is the forward velocity (in the axial direction of the channel); τ_tail is the tail torque; Ω_x is the angular velocity of the body; and ω is the angular velocity of the tail about x axis.

Results and Discussion

Validation of the CFD Model

Details of the numerical procedure of the CFD model, which is solved by the commercial software COMSOL (20), are provided in the Supporting Material. The CFD model of the bacterial locomotion is validated against the results reported by Goto et al. (7), who developed a BEM model and conducted experiments with individual species of V. algino to study swimming velocity and body rotation rates, which are computed with the CFD model in the current study based on the geometric parameters of cells previously reported (7) and for a channel with a 15-μm radius and 40-μm length, which is sufficiently larger than the average diameter of the cell body and the average length of the cell. The calculated and reported ratios of the swimming velocity to the body rotation rate are shown in Fig. 2. The CFD model results are almost identical with the BEM model results and very close to the measured ones.

Figure 2.

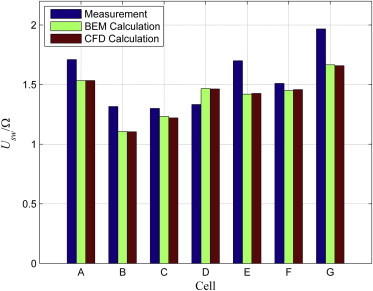
Ratio of the swimming velocity and the body rotation rate: measurements (blue) and BEM calculations (green) reported in Goto et al. (7), CFD results (red) for V. algino species reported in Goto et al. (7) and labeled A to G. To see this figure in color, go online.

In addition to the forward velocity, torques generated by the flagellar motor are computed with the CFD model and compared with the BEM results reported in Goto et al. (7) as shown in Fig. 3 a. Values of the flagellar torque from the CFD model are slightly higher than the ones from the BEM model. To determine if the presence of the channel in CFD simulations may have an effect, we calculated the flagellar torque for different channel radii as shown in Fig. 3 b. The flagellar torque rapidly decreases with increasing channel radius for narrow channels; but for large radii, flagellar torque does not vary with the channel radius significantly. Thus, the channel radius can be deemed sufficiently large. Comparisons with results in Goto et al. (7) indicate that there is ∼ 10% difference between the calculated ones in this study and the previous report.

Figure 3.

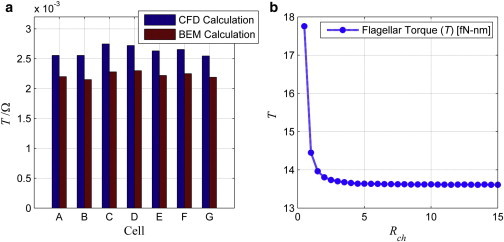
Flagellar torque normalized by the body rotation rate, T/Ω [pN-μm-s]. (a) CFD calculations (blue), BEM calculations (red) reported by Goto et al. (7). (b) Effect of the channel radius, R_ch [μm], on the flagellar torque, T [fN-nm]. To see this figure in color, go online.

Forward velocity

Performance metrics of the flagellar swimming, such as the forward velocity, power efficiency, and the magnitude of lateral velocities vary with geometric parameters of the tail. In the simulations, the radii of the spheroid body in long and short axes are fixed as reference length scales, s = 2r = 1.11 μm, and the tail rotation frequency is set to unity. The radius of the sphere that has the same volume as the spheroid head, a, is 0.7 μm as was also adopted in Shum et al. (8). The tail envelop growth rate that defines the part of tail where it is connected to the spheroid head is taken as k_E = 2π/s.

Inside wide channels, there is a slight improvement in the stroke, which is the distance traveled during a full rotation of the tail, for larger wavelengths especially for shorter tails than inside narrow channels. Shum et al. (8) studied the forward velocity of the cell with the same dimensions near a planar wall and showed that forward velocity reaches its maximum when there is about one full wave on the tail, i.e., for N_λ = 1. Here, the forward velocity becomes maximum for N_λ values between 2 and 3. The forward velocity also exhibits similar dependence on the tail length and the wavelength in narrow and wide channels with slightly varying loci of the optimum (see the black circles in Fig. 4 a for R_ch/r = 3 and Fig. 4 b for R_ch/r = 13.5). Stroke values are slightly larger for swimming inside the wide channel than the ones inside the narrow channel.

Figure 4.

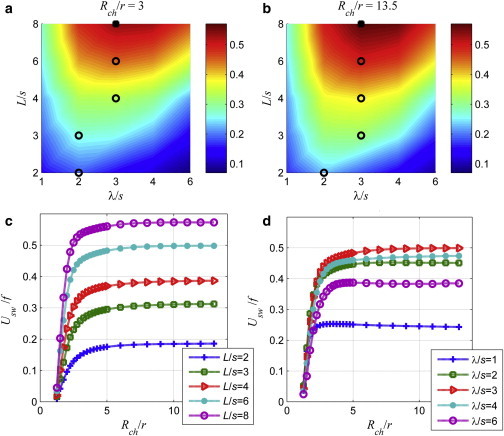
Surface plot of the stroke, U_sw/f [μm], as a function of the wavelength and the length of the tail for (a) narrow channel (R_ch/r = 3) and (b) wide channel (R_ch/r = 13.5). Black circles represent the loci of maximum values of the stroke for each tail length. Solid squares represent the maximum values for all computations. (c) U_sw/f [μm] as a function of the normalized channel radius, R_ch/r, for different tail lengths and the fixed wavelength (λ/s = 3). (d) U_sw/f [μm] as a function of the channel radius, R_ch/r, for different wavelengths and the fixed tail length (L/s = 6). To see this figure in color, go online.

Variation of the stroke with the normalized channel radius is shown in Fig. 4 c for a fixed wavelength, λ/s = 3, and the normalized tail length, L/s, values varying between 2 and 8. As the channel radius increases, the stroke increases rapidly between R_ch/r = 1.25 and R_ch/r = 3, then continues to increase slowly up to R_ch/r = 6, and does not vary significantly for larger values of R_ch/r; in effect, the free-swimming conditions apply for R_ch/r > 6.

For constant tail length, L/s= 6, the variation of the stroke with respect to channel radius is shown in Fig. 4 d, for normalized wavelengths, λ/s, varying between 1 and 6. For λ/s = 1 and 6, as the channel radius increases, the stroke increases rapidly first than decreases slightly. However, for normalized wavelength values equal to 2, 3, and 4, the stroke does not go through a maximum. Moreover, the stroke is the largest for λ/s = 3 for all values of the normalized channel radius.

Decreasing swimming velocity in narrow channels is attributable to the increasing drag force on the body, which is analytically calculated for some objects. For example, Happel and Brenner (22) showed that channel restriction causes increased drag on the sphere that moves axially through a cylindrical tube. As the normalized channel radius approaches to a value of 1, the cell plugs the channel and the displaced fluid in front of the cell cannot flow over the body and results in infinite drag and zero swimming velocity. These results are consistent with previous studies on artificial micro swimmers; Temel and Yesilyurt (17) showed that displaced fluid in front of the swimmer flows over the body and contributes to increased drag. Furthermore, in our previous work on artificial structures with cylindrical bodies swimming in cylindrical channels, as the radius of the body increases, the increasing drag force on the swimmer leads to reduced forward velocity of the swimmer (23).

Moreover, the propulsion force is expected to increase near solid boundaries and result in an increase in swimming velocities as reported in Ramia et al. (15) for swimming between parallel plates, and as observed for λ/s = 1 in Fig. 4 d. The trade-off between the drag on the spheroid body and the flagellar propulsion force leads to small variations in the swimming velocity unless the cell is very close to the wall; however, in some cases, especially for tails with large radii, flagellar force is dominant as discussed in the next section and reported in Felderhof (13).

Power Efficiency

Power efficiency of swimming, which is given by Eq. 7, is calculated as a function of the wavelength and the tail length for wide (R_ch/r = 13.5) and narrow (R_ch/r = 3) channels. For the wide channel, maximum swimming efficiency is 1.27% (Fig. 5 a), whereas it is 2.26% for the narrow channel (Fig. 5 b). For the wide channel, the optimum normalized wavelength is three, λ/s = 3, and the normalized length of the tail is eight, L/s = 8. On the other hand for the narrow channel, the optimal wavelength is four and the optimal normalized tail length is eight, L/s = 8. In the narrow channel (Fig. 5 a), the power efficiency increases monotonically with the normalized tail length up to L/s = 8 for all λ/s. However, for the wide channel (Fig. 5 b), the power efficiency decreases with the tail length for λ/s = 1, 2, and 6 but goes through a maximum for λ/s = 3 and 4. For the wide channel, there is an optimal region, where the efficiency is 1.27% for 3 < λ/s < 4 and 3 < L/s < 8. Shapes of organisms for the four extremes of wavelength and tail length pairs are also shown in Fig. 5 a.

Figure 5.

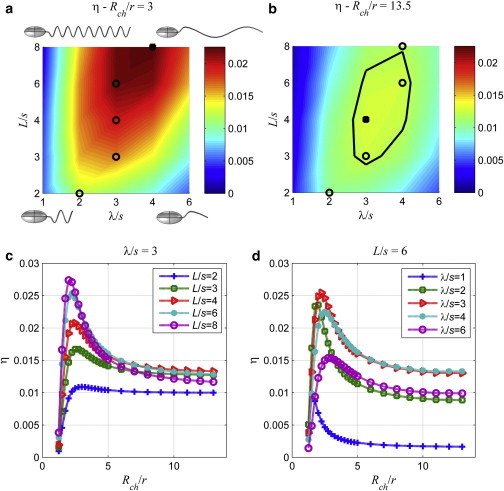
Surface plots of the power efficiency of swimming, η, as a function of the normalized wavelength and the normalized tail length for (a) R_ch/r = 3, and (b) R_ch/r = 13.5. Black circles are the loci of maximum values for normalized tail lengths equal to 2, 3, 4, 6, and 8. Solid squares are the locations of the global maxima. Efficiency plots as function of the normalized channel radius for (c) a fixed wavelength, λ/s = 3, and (d) for fixed tail length L/s = 3. To see this figure in color, go online.

Even though the swimming velocity does not vary significantly for narrow and wide channels, the efficiency is significantly higher in the narrow channel with R_ch/r = 3 than the wide channel with R_ch/r = 13.5. The drag force on the body, which is the same as the propulsion force from the tail, is also higher in the narrow channel than the one in the wide channel. The viscous torque on the body is expected to be higher inside the narrow channel as well. However, the efficiency increase inside the narrow channel indicates that the increase in the torque is not as high as the one in the propulsion force that overcomes the drag. According to Happel and Brenner (22), the drag force on the sphere with the equal volume as the spheroid body of the cell is 2.32 times and the viscous torque is 1.10 times larger in the narrow channel than the wide channel confirming the twofold increase in the efficiency.

The variation of the power efficiency with the channel radius is shown for the fixed wavelength in Fig. 5 c, and for the fixed tail length in Fig. 5 d. There is a critical radius of the channel, which varies between 2 and 3r, for each geometry of the tail that the power efficiency reaches the maximum. For channels with radii smaller than the critical radius, the efficiency declines rapidly and goes to zero as the channel radius approaches to the radius of the body. For channels with radii larger than the critical radius, the efficiency declines rapidly first but then levels out and converges to a limit for the free swimmer in the bulk fluid. Furthermore, the maximum efficiency is larger for longer tails than shorter ones in this study, although there is an optimal tail length for the cell swimming in the bulk fluid.

In Shum et al. (8), the authors report that the efficiency is very close to its maximum for a wide range of wavelength and tail length values as observed in the current paper. Moreover, the optimal range of values does not change substantially for near wall and in free swimming conditions (8). In this study, it is observed that the efficiency in narrow channels can reach a value two times higher than the one in wide channels.

In Fig. 6, the drag force on the body, which is the same as the propulsion force, is plotted against the normalized channel radius: for λ/s = 3 and varying tail lengths in Fig. 6 a; and for L/s = 6 and varying wavelengths in Fig. 6 b. In all cases, drag on the body increases with decreasing channel radius. Dependence of the body drag on the tail geometry is attributable to the effect of hydrodynamic interactions between the body and the tail (24) and increases with the tail length.

Figure 6.

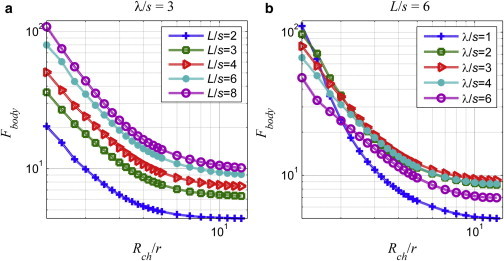
Drag force on the spheroid head, F_body [fN], as a function of the normalized channel radius for (a) the fixed wavelength, λ/s = 3, and (b) tail length, L/s = 6. To see this figure in color, go online.

In Fig. 7, the flagellar torque is plotted with respect to normalized channel radius for λ/s = 3 and varying tail lengths (Fig. 7 a) and for L/s = 6 and varying wavelengths (Fig. 7 b). The flagellar torque increases with the tail length and decreases with the wavelength, or increases with the number of waves on the tail.

Figure 7.

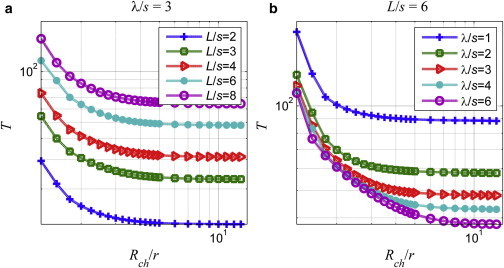
Flagellar torque, T [pN-nm], as a function of the normalized channel radius for (a) the fixed wavelength, λ/s = 3, and (b) tail length, L/s = 6. To see this figure in color, go online.

Lateral velocities

As reported in earlier studies (25,26), bacteria follow helical trajectories during swimming. The radius of the helical trajectory is determined by the magnitude of lateral velocities in perpendicular directions to the forward motion. In this study, we computed the velocities of the cell in lateral directions, (y- and z-directions in Fig. 1), for angular rotations of the tail between π/6 and 2π by π/6 intervals. We observed that there is a π/2 phase angle between the velocities in y- and z-directions (not shown here), which have the same magnitudes, indicating that the cell, in effect, follows a helical trajectory.

In Fig. 8, the effect of the channel radius on the magnitude of the lateral stroke, which is defined as, $V_{lateral}/f=\sqrt{V_{sw}^2+W_{sw}^2}/f$ here, is shown for a fixed tail length, L/s = 6, and for varying values of wavelengths between λ/s = 1 and 6. The lateral stroke increases sharply for the values of the normalized channel radius between 1.5 and 4 and then increases slightly between 4 and 6; further increase in the channel radius does not lead to significant change in the lateral stroke (not shown here). For normalized values of λ/s = 1, 2, 3, and 6, as the wavelength increases the lateral stroke increases. For λ/s = 4, the magnitude of the lateral stroke is larger than the one for λ/s = 1 but smaller than the one for λ/s = 2. The envelop region that defines the smooth increase of the helical radius near the body of the cell contributes to the imbalance in the rotation of the helices with integer number of turns. Shapes of organisms are also shown in Fig. 8 to improve the visualization of the effects of the helical shape.

Figure 8.

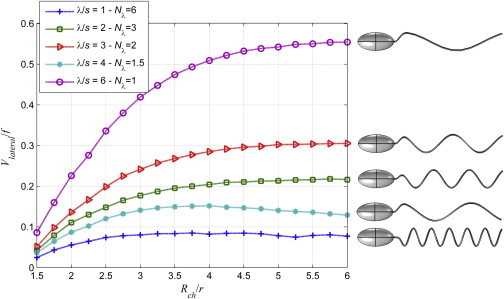
Magnitude of the lateral stroke, V_lateral/f [μm], is plotted as a function of the normalized channel radius, R_ch/r, for different wavelengths and a fixed tail length, L/s = 6. To see this figure in color, go online.

To demonstrate that the effect of the number of turns is an important parameter that governs the lateral stroke, we performed simulations for fixed tail length, L/s = 6 and channel radius, R_ch/r = 4, by varying the number of helical turns, N_λ. In Fig. 9, the effect of N_λ on the magnitude of the lateral stroke, V_lateral/f, is presented. In general, the lateral stroke decreases with the number of helical turns, and goes through peaks and troughs depending on the number of helical turns. Typically peaks are observed at half integers and troughs at full integers in the literature (27). The contribution from the envelop region breaks the symmetry near the joint, thus the lateral stroke achieves local maxima for N_λ = 1, 2, 3, and 4.25, and minima for N_λ = 1.5, 2.5, and 3.75.

Figure 9.

Magnitude of the lateral stroke, V_lateral/f [μm], as a function of N_λ for fixed channel radius, R_ch/r = 4, and tail length, L/s = 6. To see this figure in color, go online.

The effects of solid walls on the motion of micro organisms are well reported in the literature; and observations agree with the results presented in this current study. In particular, there are several studies report that the lateral motion because of Brownian or hydrodynamic effects is suppressed near solid boundaries (8,10,28–30). Berg and Turner (11) report that the bacteria align with the axis of the channel and the lateral motion is suppressed significantly inside channels. Moreover, Liu and Papadopoulos (4) report that that randomness in the locomotion of bacteria is reduced in capillaries compared with the locomotion in the bulk. Our results indicate that lateral motion is also suppressed in narrow channels similarly to the suppression of Brownian motion in capillaries.

Wobbling rate

Angular velocities in lateral directions, Ω_y and Ω_z, indicate the wobbling rate of the bacterium. In Fig. 10, the normalized magnitude of the wobbling rate, ${\text{Ω}}_{wobbling}/\text{Ω}=\sqrt{{\text{Ω}}_y^2+{\text{Ω}}_z^2}/\text{Ω}$, is plotted with respect to normalized channel radius, R_ch/r, and for normalized values of the tail length, L/s, between 2 and 8 and for a fixed wavelength, λ/s =3. In all cases, the magnitude of lateral angular velocities is much smaller than the rotation rate of the tail in the axial direction; for L/s = 2, the maximum is 0.075 for the unit rotation rate of the tail. The magnitude of the wobbling rate decreases as the channel radius decreases, similarly to the effect observed in lateral velocities. It has been reported previously that natural organisms tend to align with the axial direction of the channel as the channel radius decreases consistently with the reduced lateral velocity as well as the wobbling (11).

Figure 10.

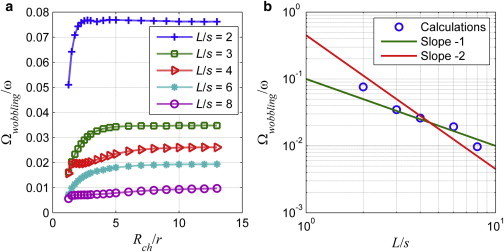
(a) Wobbling rate of the bacterium with respect to the normalized radius of the channel, R_ch/r, for λ/s = 3 and L/s = 2 (blue plus signs), 3 (green squares), 4 (red left-triangles), 6 (cyan stars) and 8 (magenta circles). (b) Relationship between wobbling rate and tail length for wide channels (R_ch/r = 13), blue circles represent the wobbling rates. To see this figure in color, go online.

Furthermore, as the tail length increases the wobbling rate decreases because of increasing resistance to lateral rotations; it is harder to rotate an organism with a longer tail than a shorter one. In fact, the wobbling rate is the highest in the case of the shortest tail, L/s = 2. For L/s = 2, 3, and 6, the wobbling rate increases sharply for 1.5 < R_ch/r < 3, and slowly for R_ch/r > 3. For L/s = 4, and mildly for L/s = 8, there is a slight increase in the wobbling rate for 4 < R_ch/r < 6, because of hydrodynamic interactions between the tail and the channel wall (see Fig. 10 a).

The wobbling behavior of bacteria is also observed during the motion of artificial helical flagella, which are actuated with external magnetic fields (28). Man and Lauga (31) discussed that the visible angle of wobbling is proportional to the wobbling rate for a fixed geometry of the helix and varies inversely with the dimensionless Mason number, Ma, which is defined as the ratio of viscous torques to magnetic torques. At high values of Ma, the swimmer achieves directional propulsion, whereas at low values wobbling prevails (31). In case of micro organisms with helical tails the magnetic torque is replaced by the motor torque and the effective viscous torque increases as the channel diameter decreases, and stabilizes the wobbling (see Figs. 3 b and 10 a). Moreover, for large channels the Ma is smaller (31), and the wobbling rate varies inversely with the square of the tail length (see Fig. 10 b).

Effect of Tail Radius (R_tail)

The combined effects of the radius and the length of the tail and the channel radius are part of the current study, whereas the normalized wavelength is fixed, λ/s = 3. The normalized radius of the tail, R_tail/r, is varied between 0.063, which is the base case, and 0.315; the base case corresponds to 0.05a, where a is the radius of the sphere that has the same volume as the spheroid head as adopted in Shum et al. (8). The stroke increases with the radius of the channel for the base value of the tail radius in Fig. 11 a. However, as the radius of the tail increases, we observed that the stroke goes through maximum at a critical channel radius. The presence of the maximum stroke is distinguishable for L/s = 8 for R_tail/r = 0.126 in Fig. 11 b; and as the tail radius increases further, the maximum stroke is observed for shorter tails as well. In Fig. 11 e, the stroke reaches the maximum for all tails studied.

Figure 11.

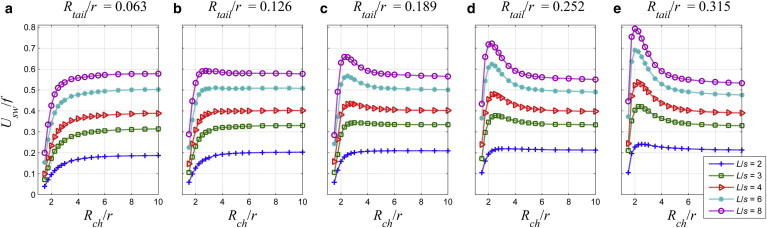
The stroke, U_sw/f [μm], as a function of the normalized channel radius, R_ch/r, and the normalized tail length, L/s, and for (a) R_tail/r = 0.063; (b) R_tail/r = 0.126; (c) R_tail/r = 0.189; (d) R_tail/r = 0.252; and (e) R_tail/r = 0.315. To see this figure in color, go online.

For L/s = 2, the stroke increases with the tail radius for any channel radius in Fig. 12 a. However, for L/s = 8 in Fig. 12 e, there is a crossover: the stroke increases with the tail radius in narrow channels for R_ch/r < 4 and changes the trend in wide channels.

Figure 12.

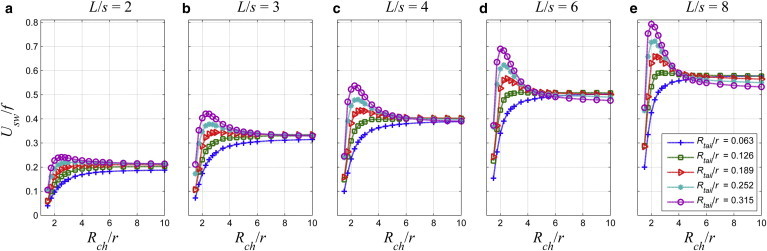
The stroke, U_sw/f [μm], as a function of the normalized channel radius, R_ch/r, for the normalized tail radius, R_tail/r, values varying between 0.063 and 0.315, and for (a) L/s = 2; (b) L/s = 3; (c) L/s = 4; (d) L/s = 6; and (e) L/s = 8. To see this figure in color, go online.

Normalized values of the critical radius of the channel, for which the stroke is maximum, are listed in Table 2; values of the critical radius vary between 2 ≤ R_ch/r ≤ 3. For a given tail length, critical radius of the channel decreases as the radius of the tail increases, but the critical radius is not observed for thinner tails as the length of the tail increases.

Table 2.

Critical channel radii

Critical Rch/r
		Rtail/r
		0.063	0.126	0.189	0.252	0.315
L/s	2	-	-	-	3	2.5
	3	-	-	3	2.5	2.25
	4	-	-	2.75	2.5	2.25
	6	-	3	2.5	2.25	2
	8	-	2.75	2.25	2.25	2

The power efficiency of the bacteria swimming in circular channels is revisited for R_tail/r values varying between 0.063 and 0.315 and for L/s between 2 and 8 in Fig. 13. The efficiency increases with the tail radius in narrow channels but decreases in wide channels. For L/s = 6, the maximum efficiency is observed as 0.0327 for R_tail/r = 0.126, which is considerably higher than 0.0132 for R_tail/r = 0.063 (Fig. 13 e). There is an optimal channel radius, which provides the maximum swimming efficiency. As the tail radius increases, optimal channel radius decreases: for R_tail/r = 0.315, the optimal channel radius is about R_ch/r = 1.75, whereas for R_tail/r = 0.063, the optimal channel radius is R_ch/r = 2.25.

Figure 13.

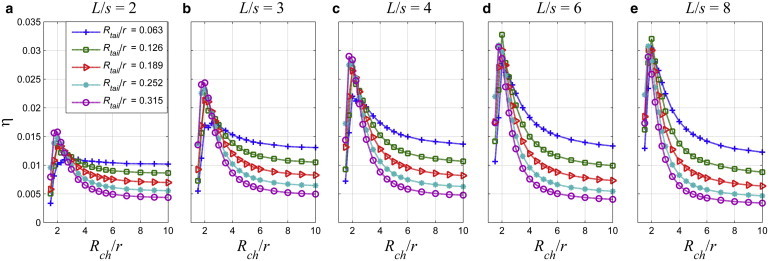
The efficiency as a function of the normalized channel radius, R_ch/r, for the normalized tail radius, R_tail/r, values varying between 0.063 and 0.315, and for (a) L/s = 2; (b) L/s = 3; (c) L/s = 4; (d) L/s = 6; and (e) L/s = 8. To see this figure in color, go online.

The crossover in the efficiency takes place for R_ch/r ≈ 3 for all tails. The increase in the efficiency of helical swimming in circular channels is also discussed in Felderhof (13) based on analytical results obtained from the perturbation theory for infinite helices in channels. Furthermore, inside the channel with R_ch/r = 10 and for L/s = 8, the efficiency for the tail with the smallest radius is 0.0122 and for the one with the largest is 0.0035.

Conclusion

In this study we developed a CFD model to analyze the swimming of singly flagellated bacteria with a spheroid head in circular channels. Force- and torque-free swimming conditions are used in the model to obtain forward and lateral velocities and rotation rates of model organisms. Linear and angular velocities of the organism and swimming efficiencies are computed with the CFD model for varying tail length, wavelength, channel radius, and the tail radius. Maximum forward velocity is obtained for λ/s = 3 and L/s = 8 in both the large channel that mimics free-swimming conditions and the channel with a radius three times the short axis of the spheroid head. The maximum efficiency is obtained for λ/s = 4 and L/s = 8 in the narrow channel, but for λ/s = 3 and L/s = 4 in the large one. Unless inside narrow channels, for which R_ch/r < 3, the forward velocity does not vary significantly, but decreases sharply to almost zero for R_ch/r ≈ 1.5. However, the swimming efficiency is almost twice as much in narrow channels with R_ch/r ≈ 3 as the one in large channels R_ch/r > 10.

For integer number of waves on the tail, the magnitude of the lateral motion attains maximum values, whereas for number of waves (1.5, 2.5, 3.5), the magnitude becomes minimum because of the envelope growth of the amplitude near the joint. In principle, the magnitude of lateral velocities depends on the completion of helical turns that ensures the symmetry of the helix; however, the smooth ramp-up of the helical radius near the joint, which connects the body and the tail, breaks the symmetry. Moreover, the lateral motion and wobbling rate, which is the magnitude of rotation rates of the cell in perpendicular directions to its motion, are suppressed as the radius of the channel decreases, consistent with the observations in literature.

Lastly, the effect of the tail radius is also characterized in conjunction with the effects of the tail length and the channel radius. As the radius of tail is increased, there is a critical channel radius that maximizes the velocity and the efficiency of the swimmer. The normalized critical channel radius, R_ch/r, varies between 2 and 3 depending on the length and the radius of the tail. The forward velocity and the efficiency are higher for thicker tails in narrow channels than thinner tails, and vice versa in wide channels.