Membrane Fluctuations Destabilize Clathrin Protein Lattice Order

Abstract

We develop a theoretical model of a clathrin protein lattice on a flexible cell membrane. The clathrin subunit is modeled as a three-legged pinwheel with elastic deformation modes and intersubunit binding interactions. The pinwheels are constrained to lie on the surface of an elastic sheet that opposes bending deformation and is subjected to tension. Through Monte Carlo simulations, we predict the equilibrium phase behavior of clathrin lattices at various levels of tension. High membrane tensions, which correspond to suppressed membrane fluctuations, tend to stabilize large, flat crystalline structures similar to plaques that have been observed in vivo on cell membranes that are adhered to rigid surfaces. Low tensions, on the other hand, give rise to disordered, defect-ridden lattices that behave in a fluidlike manner. The principles of two-dimensional melting theory are applied to our model system to further clarify how high tensions can stabilize crystalline order on flexible membranes. These results demonstrate the importance of environmental physical cues in dictating the collective behavior of self-assembled protein structures.

Introduction

The assembly of biological subunits into larger, useful structures is a vital function within all organisms. The protein-complex clathrin is one example of a component that assembles to serve a necessary function in eukaryotes (1–4). Clathrin facilitates inter- and intracellular transport by assembling into cagelike structures (5,6) that coat and stabilize cargo-laden vesicles (7–9). This process is central in clathrin-mediated endocytosis—an essential transmembrane cellular transport mechanism (10–12) that also relies on a collection of ancillary proteins (3,13,14). Coated membrane buds and vesicles have also been observed in vitro without these additional components (15), demonstrating clathrin’s robust tendency to form ordered structures on flexible membranes.

The attributes of clathrin structures in vivo are highly dependent on physical and biological conditions, with various sizes, shapes, and lifetimes exhibited depending on cell type and environmental conditions (16–20). A fluorescence microscopy study by Saffarian et al. (21) has parsed through these structural variations to identify two distinct classes within which they fall: curved pits and flat plaques. Small, curved pits are the canonical structures that coat membrane buds, whereas large, flat plaques are internalized at a much slower rate than pits and only with the help of a reorganizing actin cytoskeleton (20–22). No evidence has been found of a unique advantage of slow cargo internalization via plaques, suggesting that such structures arise incidentally as a result of environmental factors and that any prevalence of plaques corresponds to hindered cellular transport (21). Furthermore, plaques are almost exclusively observed on cell membranes that are adhered to a rigid substrate (e.g., a glass coverslip), whereas pits exist on both the adherent and the free cell surface (21). This raises the question: which physical or chemical properties make plaques achievable on adhered membranes but not on free, unadhered ones?

In this article, we develop a physical model for clathrin self-assembly on a flexible membrane. Through simulations of our model system, we show that a simple modification of the physical behavior of a cell membrane is sufficient to stabilize plaque assemblies. Specifically, when the out-of-plane membrane fluctuations are suppressed by an elevated membrane tension, the clathrin lattice adopts an ordered crystalline structure. Alternatively, a highly fluctuating membrane at low tension destabilizes the crystalline structure in favor of a disordered, fluidlike phase. We supplement numerical simulations with arguments based on two-dimensional defect-mediated melting theory to delineate a transition between the crystalline and fluid phases at a critical tension, which is greater than typical physiological values and perhaps brought about by anomalous environmental conditions such as adherence to a solid substrate. These predictions highlight the important role that subtle changes in environmental conditions play in altering the collective behavior of biological assemblies.

Model Description

In this section, we describe the components of our theoretical model, reserving some mathematical details for the Appendix. Our simplified representations of clathrin subunits as elastic pinwheels and the cell membrane as an elastic sheet enable us to address biologically relevant behavior without enduring intractably long computation times, which would arise from models with atomic-level detail.

Clathrin model

A clathrin subunit has a total molecular mass of ∼645 kDa and adopts a three-legged triskelion structure (23). Each of the three flexible legs consists of one heavy chain and one light chain (24), extending outward from a central hub in a puckered pinwheel configuration that is ∼50 nm in diameter (25). We model a clathrin triskelion as a puckered pinwheel consisting of three straight legs emanating from a central hub, as shown in Fig. 1.

Figure 1.

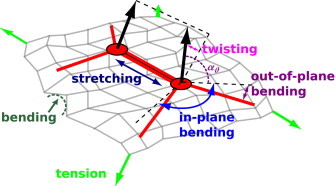
Schematic of two model clathrin triskelia bound to one another and coupled to a deformable membrane. Clathrin and membrane deformation modes are labeled. To see this figure in color, go online.

The model legs are capable of forming and breaking bonds with one another, represented as struts between pairs of hubs. This is a simplification from the physiological scenario. In real clathrin assemblies, each flexible clathrin leg not only binds to the legs of its nearest-neighbor hub with its proximal domain, but its distal domain extends past the near neighbor along an adjacent edge of the assembled structure to interact with additional clathrin legs. In this manner, each edge of a clathrin assembly includes four interwound legs (26). Also, experiments have shown that the multiple coordinated weak interactions between trimerized legs are essential for assembly, as individual leg-leg affinities are too weak to stably dimerize. This would lead to cooperative dynamics within the clathrin lattice assembly, but the omission of these features in the model assembly mechanism will not affect our conclusions on equilibrium condensed lattice phase behavior. We choose a singular leg-leg affinity ϵ = 6.5 k_BT that results in consistently condensed assemblies. This value exceeds a predicted minimum binding strength for stabilizing vesicles in vivo (27) and is half as strong as an estimate based on fitting a thermodynamic model to cage-size distributions in vitro (28). It is also close to an order-of-magnitude estimate of 10 k_BT based on atomic force measurements of triskelion removal from assembled structures (29). Given the approximations inherent in each of these experimental fits and the dependence of the affinity on environmental conditions, our chosen value of 6.5 k_BT is within a realistic range.

Displacement of hubs when they are bound to each other causes the legs to deviate from their minimum-energy configuration, incurring elastic stresses on the pinwheels through four harmonic modes. The stretching modulus k_s gives the resistance to elongation or compression of the inter-hub bonds relative to their equilibrium length r₀, and the twisting modulus k_t governs the resistance to torsion of these bonds. The in-plane bending modulus k_b governs the resistance to distortion of the legs away from an in-plane angle of 120°, and the out-of-plane bending modulus k_o gives the resistance to deformation of the triskelion pucker angle away from an intrinsic value α₀.

In our simulations, we assign k_s = 85 k_BT/r₀² and k_b = k_o = k_t = k_sr₀²/10, where k_BT is the thermal energy. Our previous work shows these elasticities result in a crystalline lattice on a flat membrane (30). Studies of clathrin conformations using electron micrographs (31,32) indicate that the subunit elastic moduli k_s, k_b, k_o, and k_t are slightly larger than our chosen values (see Mehraeen (33) for details). The fundamental physical phenomena presented in this article are not affected by this discrepancy. We set α₀ to be 101°, giving the equilibrium angle between the normal of the hub (defined in the Appendix) and the leg. This value is slightly smaller than those compatible with measurements of lone triskelia radii through dynamic light scattering (34), as well as electron cryomicroscopy measurements of triskelia shape in certain in vitro cages (35,36). However, three-dimensional self-assembly simulations of rigid subunits geometrically similar to ours (α₀ = 101°) have shown aggregation into cages that include ∼50–70 triskelia (37), which is fewer than in most experimentally observed cages (17). This indicates that α = 101° is a degree of puckering that is greater than what is observed in most self-assembled cages, suggesting that α₀ may in fact be smaller than 101°. Our choice of the clathrin natural pucker angle is therefore within this range of experimentally based estimates.

Unbound legs are assumed to adopt the minimum energy configuration, allowing us to fully define the state of our clathrin assemblies by the position and orientation of each central hub and the connectivity of each leg. The clathrin deformation energies are quadratic in the deviation from the undeformed state (i.e., Hookean deformation energy). A full mathematical description of our model appears in the Appendix.

This formulation builds upon our two-dimensional model (30) by adding a three-dimensional position and orientation to the triskelion degrees of freedom. A variation of this model is also employed to study in vitro assembly in the absence of cell membranes (38). Other researchers have developed alternative models for clathrin that provide insight into experimental findings (37,39–41). These models rely largely on patchiness of the individual legs, which are modeled explicitly. Unbound individual legs do not contribute to large-scale lattice stiffness, so we do not treat them as separate degrees of freedom. This reduces the computational load while still predicting experimentally observed structures, as shown in our previous publications (30,38).

Membrane model

The clathrin triskelia self-assemble on a cell membrane, which is modeled as a continuous, elastic sheet of size L_x and L_y in the x and y coordinates, with periodic boundaries. This representation is a valid approximation for studying undulations over length scales significantly greater than the membrane thickness (42,43). We use the Canham-Helfrich Hamiltonian (44–46) and assume the membrane locally exhibits small height fluctuations that are single-valued in the x−y plane, thus employing the Monge representation. The membrane configuration is characterized by a height field $h\left(\overrightarrow{\rho }\right)$ that quantifies its deviation in the z direction from the neutral plane at the x-y coordinate $\overrightarrow{\rho }$. The bending modulus κ gives the resistance to bending curvature, and the tension σ endues a resistance to the generation of area. The membrane energy for a projected area A = L_xL_y is given by

$$E_{\text{mem}}=\underset{A}{\iint }\text{d}\overrightarrow{\rho }\left\{\frac{\kappa }{2}{\left[{\nabla }^{2}h\left(\overrightarrow{\rho }\right)\right]}^2+\frac{\sigma }{2}{\left[\overrightarrow{\nabla }h\left(\overrightarrow{\rho }\right)\right]}^2\right\}.$$ (1)

We discretize the membrane as a rectangular mesh. The distance between mesh points in the x direction is equal to r₀/2, and we set the number of uniformly spaced mesh points in the y direction equal to that in the x direction. This discretization is fine enough to represent short-length membrane deformations that influence clathrin assemblies. First- and second-order central difference formulas are used to compute the gradient and Laplacian terms, respectively, in Eq. 1.

The importance that κ and σ play in dictating the response of $h\left(\overrightarrow{\rho }\right)$ to thermal fluctuations and other external forces (e.g., from associated protein lattices) can be understood by considering the sizes of out-of-plane fluctuations as predicted by the equipartition theorem (46),

$$\langle {\left|h_{\overrightarrow{q}}\right|}^2\rangle =\frac{k_{\text{B}}TA}{\kappa q^4+\sigma q^2},$$ (2)

where $h_{\overrightarrow{q}}$ is the two-dimensional Fourier transform of $h\left(\overrightarrow{\rho }\right)$ as a function of the discrete allowable wave vectors $\overrightarrow{q}$ in our periodic system, and $q=\left|\overrightarrow{q}\right|$. As shown in Eq. 2, the short wavelength (i.e., high q) undulations of membranes are dictated by κ, whereas the long wavelength undulations are dictated by σ. The length scale at which the contributions from both properties are approximately equal is $L_c=\sqrt{\kappa /\sigma }$. This is an important length scale to consider when adjusting model membrane properties. Undulations with a characteristic wavelength much shorter than L_c are not sensitive to changes in tension, whereas long wavelength undulations are insensitive to the bending modulus.

In our simulations, we examine a range of six finite tensions spaced logarithmically between 0.19 k_BT/r₀² and 19,000 k_BT/r₀². Using the estimate of r₀ = 16 nm from electron micrographs (17), this range includes some of the lowest measured physiological tension values (0.003 pN/nm in neuronal growth cones (47)) and exceeds the higher values by more than an order of magnitude (48). We also examine a perfectly flat membrane, representing infinite tension.

The bending modulus of all simulated membranes is kept constant throughout our simulations at a value of 4.7 k_BT, which is on the lower end of the physiological spectrum (49,50). These membrane parameters result in values of L_c in our simulations ranging between 0.02r₀ to 5r₀ at our finite tensions (L_c = 0 at infinite tension). Therefore, across our set of chosen parameters, the membrane undulations separating two neighboring clathrin hubs range from bending-dominated (L_c > r₀) to tension-dominated (L_c < r₀). The decision to vary tension but not bending modulus is based on the fact that resistance to curvature is an inherent physical property, whereas effective tension can be externally modulated. For example, tension is altered by pressure differences across the membrane or by attachment to rigid surfaces (51) such as the glass coverslips used in the observations made by Saffarian et al. (21).

Clathrin-membrane coupling

The final component of our model system is the constraint that clathrin assemblies are attached to the membrane surface. We achieve this in our simulations by fixing the position of each clathrin hub in the z direction to be equal to the height of the membrane mesh point to which it is closest. In this way, membrane conformations directly influence the elastic strain of clathrin lattices by dictating the orientations and positions of the hubs.

The geometric coupling between the membrane shape and the clathrin deformation leads to two important effects that influence the thermodynamic behavior of our clathrin-membrane model. First, the clathrin lattice may have a local honeycomb structure that adopts a flat conformation that is commensurate with the energetically preferred flat membrane conformation, thus increasing the effective rigidity of the membrane. Second, if the local clathrin lattice has defects associated with five- and seven-member ring structures, the clathrin locally prefers to form curved regions that impart a deformation on the membrane. The resulting membrane shape is therefore determined by the local clathrin lattice structure and the balance of deformation energies of the clathrin and membrane. These effects are explored further later in this article and discussed in the context of the thermodynamic behavior of our model.

The physiological mechanism by which clathrin attaches to a cell membrane is in fact very complex and involves dozens of auxiliary proteins (e.g., adaptor protein 2) to both form the reversible membrane-clathrin linkages and localize other endocytic machinery (3,13). Direct linkages between clathrin and these membrane-bound adaptor proteins are formed through weak multivalent interactions, the most typical of which exhibit dissociation constants of ∼10 μM (10 k_BT binding affinity) (52,53). Clathrin in membrane-bound pits in vivo have been observed to exchange regularly with those in the cytoplasm through an ATP-dependent process (e.g., the activity of the ATPase Hsc70) that may be essential for full pit invagination (54).

The ability of clathrin to reversibly associate and dissociate with the membrane will likely affect dynamic predictions of pit or vesicle assembly. In this article, we address the equilibrium behavior of our clathrin model for a fixed number of clathrin on the membrane. A clathrin-binding model can be developed that includes a clathrin reservoir with a fixed chemical potential, effectively converting our equilibrium model to an open ensemble. Results from both the closed and open ensembles would give the same prediction for the equilibrium behavior, so we focus on the more easily implemented closed ensemble in this work. Future work addressing the dynamics of pit formation will incorporate binding and unbinding events as part of the assembly process.

Simulation methodology

We use Monte Carlo (MC) simulations to determine the equilibrium phase behavior of clathrin lattices on membranes at various tensions. The initial configuration is chosen to be a flat, periodic honeycomb lattice of 1972 pinwheels (N = 1972) with perfectly satisfied bonds and nearly square dimensions of 51r₀ × 50.23r₀. A lattice of this size is sufficiently large to avoid size-dependent results, because the observed phase behavior over our tested range of tensions is no different than test cases on a lattice of significantly larger size (N = 2508).

Within each MC step, three types of moves are attempted. The Metropolis algorithm is used to determine the probability of acceptance of each move using Boltzmann-weighted acceptance criteria (55). Specifically, if the resulting total energy change from each individual move ΔE = ΔE_clath + ΔE_mem is negative, then the move is accepted; whereas if ΔE > 0, the acceptance probability P_accept is given by P_accept = exp(−ΔE/k_BT).

The first move selects a randomly chosen membrane mesh point to move up or down in the z direction, shifting the locally attached clathrin hubs with it so that each hub remains coupled to the membrane in the manner described in the last subsection. The orientations of nearby hubs are also adjusted according to the convention described in the Appendix.

The second move translocates a randomly chosen hub in the x-y plane while adhering to the z position of the membrane and updating the orientations of other associated hubs.

The third move alters the binding state of a randomly chosen clathrin leg. If it is bound to another hub, that bond is broken. Alternatively, if the leg is unbound, a new bond is formed with a free leg of another hub that is randomly chosen from the collection of hubs located within a distance of 1.5r₀ from the original hub. The selection probabilities of all membrane moves are influenced by the resulting adjustments to the clathrin lattice configuration, and clathrin moves are influenced by the membrane configuration. Thus, this process ensures that the membrane and clathrin are thermodynamically coupled to each other.

On our system of 1972 triskelia, we carry out 4 × 10⁹ total Monte Carlo steps, for an average of ∼2 × 10⁶ steps per hub. We deem this procedure to be adequate to reach the equilibrium behavior for our model systems, because no discernible changes in the ensemble-averaged clathrin phase behavior occur beyond this many steps. An adaptive-step algorithm is employed to ensure rapid convergence to equilibrium, in which attempted displacement of the membrane grid points and the clathrin hubs are independently adjusted after every 1000 steps if the ratio of accepted moves to total moves over that simulated time frame is less than 0.45 or greater than 0.55. This ensures a roughly 50% overall acceptance ratio, so the hubs are effectively probing both thermodynamically improbable configurations and the varied configurations energetically close to the ground state. Each parameter set is tested by 10 independent MC simulations.

Results

We use our clathrin-membrane model to explore the phase behavior of clathrin lattices on a fluctuating membrane. Clathrin assemblies on membranes exhibit relatively small local out-of-plane fluctuations, resulting in an effectively two-dimensional system capable of possessing long-range crystalline order. Such crystalline order is seen in large clathrin plaques on adhered membrane surfaces (21). These structures are also predicted in our two-dimensional clathrin model (30). Alternatively, a disordered fluid phase would enable the topological reorganization of subunits that can dynamically coat endocytic pits.

To predict the equilibrium phases of clathrin lattices, we examine our systems through the lens of two-dimensional defect-mediated melting theory. This theory states that phase behavior in two dimensions is governed by the creation and interaction of topological defects (56–58). Essentially, systems with high densities of defects that are uncoupled to one another are in a fluid phase, whereas fewer, coupled defects are the trademark of a crystalline phase. A detailed discussion of this theory’s application to our simulated results is presented in the Discussion.

Our clathrin model adopts a perfect lattice of hexagons in the ground state. Defects, induced by thermal excitation, include non-six-sided rings, which are typically pentagons or heptagons. We analyze our results by examining the density and arrangement of these shapes in our lattices. Visualizations of the different macroscale lattice structures, as well as zoomed-in images highlighting lattice structure, are shown in Fig. 2. The crystalline phase contains a few defects that are closely coupled to each other in groups of two heptagons and two pentagons, allowing the bulk of the lattice to adopt an ordered honeycomb structure. In contrast, the fluid phase contains many more defects that are apparently not arranged in any definitive structures, and the lattice only exhibits order over short length scales.

Figure 2.

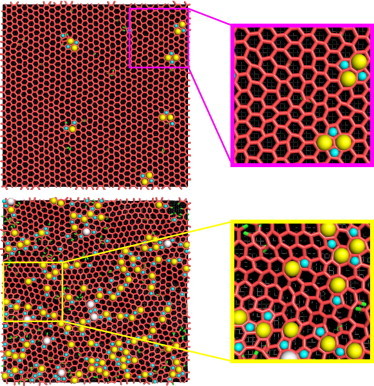
Example images of a crystalline (top) and fluid (bottom) clathrin lattice, with portions magnified to highlight the differences in local order and defect structure. (Yellow spheres) Seven-sided clathrin rings; (cyan spheres) five-sided rings. (White spheres) Eight-sided rings are only observed in the fluid example here. (Red and green) Clathrin legs that are, respectively, bound and unbound to other legs. To see this figure in color, go online.

The identification of defects allows us to visually discern a systematic effect of tension on our model systems. Representative snapshots of our equilibrated simulations with different tensions are shown in Fig. 3. When the membrane tension is very high relative to most physiological values (σ = 190 k_BT/r₀² and above), the associated lattice includes only a few defects, many of which exist as closely coupled sets of two pentagons and two heptagons. Overall, it resembles a honeycomb crystalline state with a few small deviations. As tension decreases and membrane fluctuations increase in magnitude, the prevalence of defects also increases. At σ = 19 k_BT/r₀², there are defect-ridden patches within a mostly connected bulk honeycomb lattice, as well as a greater number of void spaces and free legs. Tensions of 1.9 k_BT/r₀² or lower result in lattices that are significantly different from the ground state. Small patches of regular hexagons appear immersed in a larger population of pentagons, heptagons, other ring structures, and void spaces. These visual observations make it clear that our model clathrin assemblies are qualitatively altered by the size of underlying membrane fluctuations.

Figure 3.

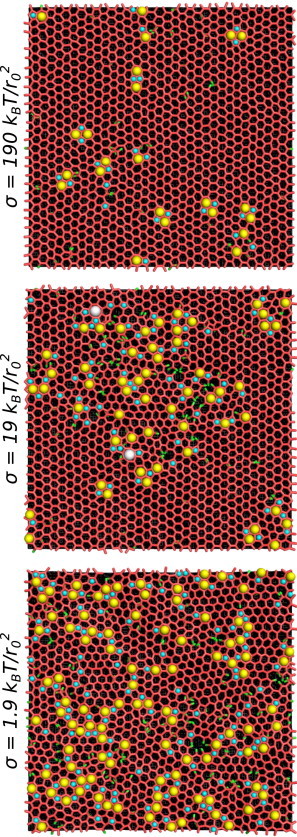
Snapshots of our simulations after 4 × 10⁹ total MC steps (∼2 × 10⁶ MC steps per hub), at different membrane tensions. Defects and free legs are colored as in Fig. 2. To see this figure in color, go online.

To gain insight into the length-scale dependent membrane fluctuations, Fig. 4 shows the effect that a lattice has on the underlying membrane behavior. For σ = 19 k_BT/r₀² and 1.9 k_BT/r₀², we show the simulated average values of the squared difference in membrane height 〈[Δh(P)]²〉 between two membrane points separated by a distance P in the x-y plane with and without associated clathrin lattices. An analytical prediction based on bare membrane parameters (given in Safran (59)) is also shown for comparison.

Figure 4.

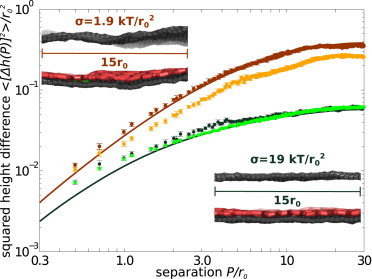
Plot of squared difference in membrane height versus separation in x-y plane. (Light-orange and dark-orange data) σ = 1.9 k_BT/r₀²; (light-green and dark-green data) σ = 19 k_BT/r₀². (Dark-colored dots) Results of simulations with no clathrin attached to the membrane. (Light-colored dots) Simulation results with clathrin. The lines are analytical predictions of the equilibrium height fluctuations in the absence of clathrin, as given in Safran (59) and averaged across all orientations between locations in the x-y plane separated by a distance P. Error bars give the standard error of the mean. Simulated data is averaged over 10 independent samples (with clathrin) or five independent samples (without clathrin). (Insets) Fluctuating portions of the membrane with and without clathrin at the two tensions shown in the plot.

As analytically predicted, the size of membrane fluctuations at all length scales are larger at the low tension than at the high tension. Simulations without clathrin match the analytical predictions at separations greater than several leg lengths. The slight small-separation discrepancy is due to the discretization of our membrane, which is limited to roughly two gridpoints per leg length for ease of computation. When clathrin is associated to the membrane, the simulated fluctuations are smaller than the analytical predictions, due to the stiffening effect that associated clathrin lattices have on membrane elastic parameters. This effect is clearly demonstrated in Fig. 4 at a tension of 1.9 k_BT/r₀² (orange data set), and is discussed in more detail in Melting with Membrane Deformations, found in the Discussion.

We are also able to quantify the increase in defect density that is caused by reducing membrane tension. A histogram of the types of topological structures existing at equilibrium for all our simulated tensions is shown in Fig. 5. At infinite tension, nearly all rings within the lattice are six-sided, with minimal five- and seven-sided rings that are characteristic of defect population. As tension is decreased, resulting in larger membrane fluctuations, the number of five- and seven-sided rings steadily increases at the expense of the six-sided rings, signifying a decay in the regular structure of the lattice.

Figure 5.

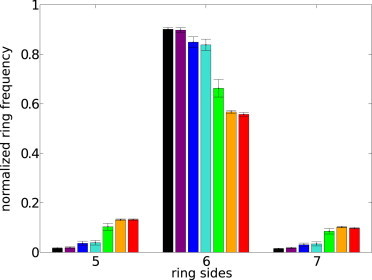
Histogram of the average distribution of ring-sidedness normalized to the number of six-sided rings in a perfect lattice. Simulated tensions include ∞ (black), 19,000 k_BT/r₀² (purple), 1,900 k_BT/r₀² (blue), 190 k_BT/r₀² (turquoise), 19 k_BT/r₀² (lime), 1.9 k_BT/r₀² (orange), and 0.19 k_BT/r₀² (red). Error bars are standard errors of the mean over 10 simulations per parameter set. Rings of fewer than five sides or greater than seven sides are too infrequent to compare on this scale, but are more numerous at lower tensions.

In addition to visual assessment of the state of clathrin lattices based on defect population and arrangement, we also can quantify the degree of orientational order of our clathrin assemblies. The orientational-order correlation function is often used to determine if a two-dimensional system is in a crystalline or fluid state, and we apply it to our quasi-two-dimensional system for this purpose.

Calculating the orientational-order correlation function requires us to map our honeycomb clathrin lattices onto an equivalent hexagonal Bravais lattice, which is constructed of points separated by linear combinations of repetitive primitive vectors. To make this transformation, we first create a Voronoi diagram of the equilibrium lattice configuration projected on the x-y plane (60). The vertices of this diagram are clustered in the centers of the rings of the original clathrin lattice. We delineate the boundaries between clusters by performing an agglomerative hierarchical cluster analysis (61). The dissimilarity between points in this analysis is measured using a Euclidean distance that is normalized to the square-root of half the distance between hexagon centers in each dimension in a perfect lattice. Linkages between clusters are made using the average linkage method. Creating a lattice point at the centers of mass of each of these clusters results in a new array that is sixfold symmetrical in the undeformed state. Note that this new Bravais lattice is hexagonal, owing to the fact that each lattice point is in the center of a hexagon formed by other points, in contrast to our honeycomb-type lattice that lacks such symmetry. The lattice spacing in this new system is also increased from r₀ to $\sqrt{3}{r}_0$.

The local orientational order $\psi \left({\overrightarrow{\rho }}_j\right)$ at the two-dimensional location of the jth point in this new lattice ${\overrightarrow{\rho }}_j$ is given by

$$\psi \left({\overrightarrow{\rho }}_j\right)=\frac{1}{n_j}\sum _{k=1}^{n_j}\text{exp}\left[6i{\theta }_{jk}\left({\overrightarrow{\rho }}_j\right)\right],$$ (3)

in which θ_jk is the angle between the line connecting points j and k and a fixed reference plane, and n_j is the number of near neighbors to point j in the new Bravais lattice. The orientational-order correlation function C₆(P) between points separated by a distance P is given by an average over all points separated by that amount within each system and across an ensemble of simulations, such that

$$C_6\left(P\right)=\langle \psi \left(\overrightarrow{{\rho }_f}\right){\psi }^{\ast }\left(\overrightarrow{{\rho }_i}\right)\rangle ,$$ (4)

where $\left|{\overrightarrow{\rho }}_f-{\overrightarrow{\rho }}_i\right|=P$.

Two-dimensional melting theory shows that C₆ of a crystalline phase tends to a constant at large separation P, whereas fluid phases exhibit either power-law or exponential decays with P (57,58). The behaviors of C₆ with P for our simulated systems at different degrees of membrane fluctuations are plotted in Fig. 6.

Figure 6.

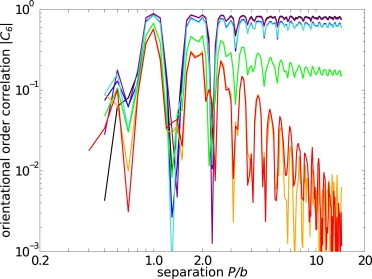
The orientational order correlation function of simulated clathrin lattices, at different membrane tensions. (Colors correspond to the same tensions as in Fig. 5, with higher tensions on the violet end of the visual spectrum and lower tensions on the red end.) Separation is scaled by the magnitude of a standard dislocation Burger's vector b, which is defined in the Discussion.

In agreement with the visual observations shown in Fig. 3, our calculated structural order correlation functions demonstrate a marked effect of membrane fluctuations on clathrin lattices. Membrane tensions ≥190 k_BT/r₀² suppress fluctuations and yield long-range orientational order, shown by the leveling off of C₆, which is consistent with a crystalline phase. Short length-scale oscillations are a natural result of measuring C₆ at points that are displaced from the undeformed lattice points. As the tension decreases, C₆ behavior transitions from staying constant with separation to decaying with separation. At the lowest tested tensions of σ = 1.9 k_BT/r₀² and σ = 0.19 k_BT/r₀², the power law decay of the orientational-order correlation function signifies a fluid phase. The intermediate tension of σ = 19 k_BT/r₀² shows a distinctly intermediate degree of long-range orientational order, which appears to level off in a crystalline-type trend, but our limited simulation length scales do not ensure that this function does not exhibit a power law decay either.

Discussion

Our computational results demonstrate the important role of membrane fluctuations on a system that is ubiquitous in biology. Experiments and simulations of quasi-two-dimensional colloidal systems (i.e., confined to a surface with small deviations) show that out-of-plane fluctuations destabilize the crystalline phase, expanding the range of conditions where a fluid phase prevails (62–64). Out-of-plane fluctuations are modulated in our simulations by the membrane tension. In this section, we show how analytical predictions of quasi-two-dimensional defect-mediated melting theory support the existence of a phase transition at some critical tension σ_f, and that our computational estimate of σ_f is within the range expected from this theory. We also discuss alternative mechanisms for clathrin plaque assembly.

Defect-mediated melting in two dimensions

The theory of two-dimensional defect-mediated melting developed by Kosterlitz and Thouless (56), Nelson and Halperin (57), and Young (58) states that the crystalline-to-fluid transition in two dimensions arises from defect formation and motion within the assembled lattice. The most common defect within a crystal is a dislocation, which is characterized by an insertion of a half lattice-line into an otherwise perfect surrounding lattice. Dislocations can arise in two-dimensional crystals due to thermal excitation, but they only exist in tightly coupled pairs, because the elastic cost of separation outweighs the entropic benefit of defect mobility. Above some finite temperature that is dictated by the elastic properties of the crystal, the entropic benefit of dislocation separation overcomes the elastic cost, and dislocations decouple from one another. This decoupling marks a continuous, second-order phase transition from a crystalline phase to a fluid phase. The predictions of the theory from Kosterlitz and Thouless (56), Nelson and Halperin (57), and Young (58) for two-dimensional melting have been borne out through numerous computational (65,66) and experimental (67,68) systems.

A dislocation pair in our model system consists of two heptagons sandwiched by two pentagons. Two examples of this configuration are shown in the top-right image of Fig. 2. A dislocation pair can be generated by the rotation of a single bond, and subsequent bond rotations lead to decoupling of the pentagon-heptagon (i.e., five-to-seven) dislocations from each other (see Figs. 4 and 5 in Mehraeen et al. (30)). Lone dislocations are confirmed to exist in clathrin lattices in vivo through electron microscopy studies (69). On a flat membrane, dislocation decoupling results in an elastic energy of separation,

$$E_{\text{sep}}=\frac{Y{b}^2}{4\pi }\left(\text{log}\frac{r}{a_0}+c\right),$$ (5)

that scales logarithmically with separation distance r relative to the dislocation core radius a₀ (56,57,70). The two-dimensional Young’s modulus Y dictates the energetic cost of dislocation separation and can be directly related to our model’s in-plane elastic parameters k_s and k_b through (30)

$$Y=\frac{2k_s}{3\sqrt{3}}\frac{6+\eta }{2+\eta },$$ (6)

where η = r₀²k_s/k_b. The magnitude of the dislocation Burger’s vectors b in the present case is related to the lattice constant as $b=\sqrt{3}{r}_0$. The constant c depends on the angle between the Burger’s vector and the line connecting the two dislocations (56,57,70). The in-plane elastic moduli in our simulations correspond to Y ≈ 131 k_BT/b² ≈ 44 k_BT/r₀².

This interaction energy can be used to find a critical Young’s modulus Y_dissoc below which entropic benefits overcome E_sep and a dislocation pair dissociates (71), given by

$$Y_{\text{dissoc}}=\frac{16\pi k_{\text{B}}T}{b^2}.$$ (7)

However, this expression for Y_dissoc does not give the true elasticity at which a phase transition occurs, because this analysis so far neglects fluctuations that give rise to surrounding dislocations at finite temperature. In fact, these fluctuations affect large-scale lattice rigidity. The recursion relations from Kosterlitz and Thouless (56), Nelson and Halperin (57), and Young (58) give the renormalized Young’s modulus Y_R(a) as a function of renormalized dislocation core radius a. Y_R is coupled to the renormalized dislocation fugacity y_R(a), given by

$$y_R\left(a\right)\equiv \text{exp}\left[-E_{cR}\left(a\right)/k_{\text{B}}T\right].$$ (8)

The renormalized dislocation core energy E_cR(a) also depends on Y_R (56–58). As a is increased from a₀ to ∞, the recursion relations from Kosterlitz and Thouless (56), Nelson and Halperin (57), and Young (58) map the bare properties y and Y to large-scale y_R and Y_R. While y_R may increase or decrease with a depending on the bare properties, Y_R is always <Y, and vanishes completely at Y_R = <16π k_BT/b², corresponding to the crystalline-fluid transition. So while any ordered two-dimensional system with Y < Y_dissoc melts into a fluid phase, many systems with Y > Y_dissoc are also fluid. Even with fluctuations, our simulated systems exist well within the crystalline region in purely two dimensions, as Y_R^(2D) > 2Y_dissoc.

Melting with membrane deformations

When an otherwise two-dimensional system allows for out-of-plane deformation, as with clathrin on a cell membrane, the interaction energy of defects is altered, changing the melting criteria significantly. Consider a membrane’s behavior at length scales much less than L_c, a regime that is large at low tension. The membrane may buckle around a dislocation in a way that incurs a bending energy cost, but benefits from a reduction in in-plane elastic strain of the two-dimensional crystal. Seung and Nelson (72) have shown that such buckling around an isolated dislocation can confine the two-dimensional strain to a region characterized by a buckling length that scales as

$$L_b\sim \frac{\kappa }{Yb}.$$ (9)

In other words, E_sep of a dislocation pair on a flexible tensionless membrane adopts the same form as Eq. 5 for separations less than L_b, but is constant above that separation. At sufficiently large system size and no tension, membrane fluctuations enable buckling at any finite temperature, screening dislocations from one another and leading to the destruction of crystalline order with any elastic parameters Y and κ (72,73).

At length scales greater than L_c, tension contributions to membrane behavior overwhelm bending contributions, and the dislocation interactions are altered further. Buckling around a dislocation is resisted by the tension, which seeks to minimize surface area. Morse and Lubensky (74) have shown that the membrane flattens out around a lone defect, counteracting any potential buckling, at some flattening length that scales as

$$L_f\sim \frac{Yb}{\sigma }.$$ (10)

Membrane buckling is therefore enabled at low tension, where L_c ≥ L_b, and suppressed at high tension, where L_c ≤ L_f. These two inequalities are essentially the same condition, as

$$L_c/L_b\sim L_f/L_c\sim Yb/\sqrt{\kappa \sigma }.$$

Ignoring in-plane lattice fluctuations, buckling occurs and dislocation pairs dissociate when the value

$$g\equiv Yb/\sqrt{\kappa \sigma }$$ (11)

exceeds some critical value g_c. Morse and Lubensky (74) have numerically estimated g_c ≈ 80 in the continuum limit. Because fluctuations further soften defect interactions, g_c can be considered the largest possible ratio of in-plane rigidity to out-of-plane rigidity that allows a stable flat crystalline phase when Y_R^(2D) > Y_dissoc. If g > g_c, melting is certain, but it is also possible for cases when g < g_c if Y_R > Y_dissoc. At our lowest simulated tension, σ = 0.19 k_BT/r₀², our system has g = g_c, so melting at that tension is expected, as well as at higher tensions when considering fluctuations. This prediction is confirmed in the Results.

As is found in two-dimensional melting, the presence of in-plane fluctuations significantly effects the melting transition on a flexible membrane. When dislocation-induced buckling is accounted for, the recursion relations from Kosterlitz and Thouless (56), Nelson and Halperin (57), and Young (58) only apply on length scales shorter than L_b or longer than L_f, the regimes in which effects of buckling are outweighed by the two-dimensional interactions between defects. It is therefore necessary to use recursion relations for y_R and Y_R within the regime L_b < a < L_f developed by Morse and Lubensky (74) to bridge the renormalization flow. Unlike in two dimensions, the dislocation fugacity y_R monotonically increases in this regime along with a monotonically decreasing Y_R, because lattice stress does not increase with increasing a around a buckled dislocation for L_b < a < L_f. As a result, many systems that would reach a stable crystalline phase with finite Y_R in two dimensions but have L_f > L_b are driven into a fluid phase when out-of plane deformation is allowed (see Fig. 5 of Morse and Lubensky (74) for further illustration of this effect).

In addition to in-plane lattice fluctuations at finite temperature, the membrane also exhibits out-of-plane fluctuations, which cause the elastic parameters κ and Y to become renormalized as a function of the membrane wavenumber q. These adjustments are only significant on a fluctuating crystalline surface when q⁻¹ is above some nonlinear length $L_{nl}\sim \kappa /\sqrt{Y{k}_{\text{B}}T}$ that is at least several times larger than L_b (73,74), and are weak when q⁻¹ > L_c (75). Therefore, any membrane that has significant renormalization of elastic parameters due to undulations is also subject to buckling around dislocations, as L_b < L_c. Within the regime L_nl < q⁻¹ < L_c, the effective bending modulus κ_R(q) is stiffened at larger wavelength, following κ_R(q) ∼ q^−0.82, and the Young’s modulus Y_R(q) deteriorates as Y_R(q) ∼ q^0.36 (76,77). While the divergence of the bending modulus at large q⁻¹ resists membrane buckling around dislocations, the renormalization of the Young’s modulus still lowers the energetic threshold for dislocation decoupling, the hallmark of melting from a crystalline phase to a fluid phase.

Given these effects of membrane flexibility, in-plane fluctuations, and out-of-plane fluctuations, we predict that our systems will exhibit a crystalline-to-fluid phase transition at some finite tension σ_f. Ignoring membrane fluctuations, this transition is expected when g ≈ g_c and lone dislocations are stabilized by buckling. Because membrane buckling enhances the softening effect of in-plane fluctuations on the renormalized Young’s modulus Y_R, g(Y_R) exceeds g(Y), and σ_f is higher than that which would give g ≈ g_c using bare parameters. The presence of membrane undulations reduces Y_R even more, elevating σ_f further.

Our Monte Carlo simulations have predicted a value of σ_f that is consistent with the theory presented in this section. The lowest simulated tension (σ = 0.19 k_BT/r₀²) decayed to a fluid phase, as expected from the prediction that buckling would occur based on the bare elastic moduli (g ≈ g_c). At tension 10 times higher, fluctuations soften the in-plane elasticity and a fluid phase is once again achieved. Although increasing the tension yet another 10 times appears to restore some order to the system, a crystalline state clearly emerges when tension is raised yet again, to σ = 190 k_BT/r₀². This leads us to the conclusion that the value of σ_f lies somewhere between 1.9 k_BT/r₀² and 190 k_BT/r₀². This range encapsulates the upper end of measured values in normal, resting cells (48,78), which is consistent with the absence of crystalline plaques on freely fluctuating biological membranes. It is also noteworthy that simulations with L_c ≥ r₀ prefer a fluid phase, and simulations with L_c << r₀ have crystalline phases. In other words, when height undulations of wavelength equal to the lattice spacing are dominated by bending as opposed to tension, the crystalline phase is stabilized.

Our estimate of σ_f would be altered for a system in which physical properties differ significantly from the parameter set chosen. For instance, if the membrane bending modulus κ is larger than 4.7 k_BT, as is the case in most cells (50), this will inhibit the ability of the lattice to screen defect interactions through buckling, effectively decreasing σ_f. Different estimates of the clathrin subunit stiffness would also affect the phase boundary, with the out-of-plane bending and twisting moduli (k_o and k_t) of the model clathrin pinwheels supplementing the membrane bending modulus by resisting out-of-plane deformation. Other elastic properties of the subunits affect the phase boundary in a less simple manner. Although increasing their stretching and in-plane bending moduli (k_s and k_b) increases the bare Young’s modulus Y, which stabilizes the crystalline phase in two dimensions, such adjustments have the potential to broaden the buckling window between L_b and L_f if membrane parameters are sufficiently soft, thereby also increasing the likelihood that out-of-plane deformations stabilize a fluid phase. The exact effect of k_s and k_b on σ_f therefore varies based on the membrane properties.

One difference between our model and physiological conditions is the irreversible nature of clathrin-membrane associations. Our treatment fixes the number of clathrin on the membrane, resulting in a density that is sufficiently large to have a single percolated clathrin network in either a fluid or crystalline phase. However, large membrane fluctuations that are shown to induce lattice disorder may also be strong enough to strain the bonds linking adaptor proteins to clathrin and cause their dissociation, resulting in lower density of membrane-bound clathrin. Reducing density is a definitive way to induce a phase transition from a crystal to a fluid (62). These effects could be addressed by either performing a range of simulations with different densities or by performing simulations with clathrin binding and unbinding, i.e., exchanging with a clathrin reservoir with a fixed chemical potential. Fluctuation-induced depletion of clathrin at a fixed chemical potential (i.e., fixed concentration of clathrin in the cytoplasm) would amplify the lattice destabilization from membrane fluctuations that we discuss in this article.

Alternative explanations for clathrin plaques

The stabilization of clathrin plaques due to the suppression of membrane fluctuations suggests that these structures may arise incidentally as a result of experimental conditions, but it does not necessarily rule out their potential to serve a biological function. Plaques have been conjectured as a possible intermediate step on the way to pit formation (79,80), possibly due to frequent electron micrographs showing localization of the two structures neighboring each other on membranes (69,81), and the fact that changes in the cytoplasmic acidity can induce curvature in otherwise flat lattices (18). Computational models of clathrin assembly have shown how a subtle change in the triskelion’s pucker angle could drive the transition from plaques to pits (40). However, live cell imaging has not provided any evidence for this dynamic configurational change, and the extensive molecular rearrangement required for such a transition is considered unlikely (2). Our simulations show that membrane fluctuations are capable of destabilizing plaques without dynamically altering the subunit properties.

Alternative explanations of plaque assembly may be biochemical in nature. For example, the depletion of cholesterol in the plasma membrane (82,83) or interference with intracellular cholesterol trafficking ability (84) has been shown to foster large plaques of clathrin that are resistant to internalization, although the mechanism of this effect is unclear. In the case of cells adhered to solid surfaces, there may be yet unspecified cytoskeletal adjustments made upon adhesion that enable plaque assembly over pit assembly (21). Although such biochemical pathways are not disproven, they are not as simple as membrane properties physically altering the clathrin lattice to determine its preferred phase. In fact, experiments have shown that decreasing membrane tension is correlated with increased endocytosis activity (85), a condition that seems to indicate a prevalence of pits over rigid plaques. Recent numerical computations have also shown that membrane bending rigidity influences the morphology of clathrin pits (86). These examples further demonstrate the principle that membrane properties have a profound impact on associated clathrin structures.

Conclusions

In this work, we show that membrane fluctuations are a critical determinant of whether a clathrin lattice exists in a crystalline structure or a fluid phase. Qualitative visual inspection and quantitative structural order calculations demonstrate a systematic decay of crystalline order as tension is decreased and membrane fluctuations increase, until the point at which crystalline lattices are completely destabilized and enter the fluid phase. Our computations show that crystalline clathrin lattices on a flexible membrane are only stabilized at tensions above normal physiological values. Predictions from quasi-two-dimensional defect-mediated melting theory align with these findings.

Experimental observations in vivo (21) also show agreement with our results, because two distinct phases of biological clathrin assemblies are identified, corresponding to distinct membrane conditions. Large, flat plaques, which slowly internalize with help from the actin cytoskeleton, are much more likely to assemble on membranes that are adhered to solid substrate surfaces. On the other hand, small, curved pitlike structures with nonhexagonal facets are able to form on freely fluctuating cell membranes. These observations compare favorably with our theoretical predictions that membranes restricted in their fluctuations enable the formation and stability of highly ordered crystalline structures.

Based on our findings, the collective behavior of clathrin can be changed from a crystalline phase to a fluid phase by modulating membrane tension. This physical effect represents a simple environmental cue that induces major changes to the properties of a clathrin lattice. The complex process of endocytosis requires the lattice to undergo structural rearrangement to accommodate the specific cargo size and shape with a subsequent stabilization of the lattice when the desired structure is achieved. Our work represents a simple mechanism by which such local changes in behavior can be induced through the local suppression of membrane fluctuations.

Appendix: Clathrin Model

Clathrin triskelia are represented as three-legged pinwheels, shown in Fig. 1. Each unbound leg is capable of forming a bond with an unbound leg of another triskelion, causing a reduction in energy equal to ε. When an individual leg is unbound to any others, it is assumed to adopt an extension and orientation relative to its origin hub that minimizes the triskelion’s elastic energy. However, when two legs are bound together, the position and orientation of their origin hubs can incur elastic stresses on the resulting structures through four harmonic modes. The orientation of hub i is characterized by the vector ${\overrightarrow{n}}_i$ that is normal to the plane created by the ends of its three legs. Specifically, if the location of the end of the mth leg of pinwheel i is given by ${\overrightarrow{r}}_i^{\left(m\right)}$, then this normal vector is defined by

$${\overrightarrow{n}}_i=\frac{\left({\overrightarrow{r}}_i^{\left(2\right)}-{\overrightarrow{r}}_i^{\left(1\right)}\right)\times \left({\overrightarrow{r}}_i^{\left(3\right)}-{\overrightarrow{r}}_i^{\left(1\right)}\right)}{\left|\left({\overrightarrow{r}}_i^{\left(2\right)}-{\overrightarrow{r}}_i^{\left(1\right)}\right)\times \left({\overrightarrow{r}}_i^{\left(3\right)}-{\overrightarrow{r}}_i^{\left(1\right)}\right)\right|}.$$ (A1)

The state of pinwheel i is fully defined by its hub’s position ${\overrightarrow{r}}_i$, ${\overrightarrow{n}}_i$, and the bond connectivity of its three legs, which is characterized by the link indicators L_ij and the leg index indicators λ_i^j for all the hub indices j of the other pinwheels in the model. If hubs i and j are bound, then L_ij = 1, whereas if they are unbound, then L_ij = 0. The leg index indicator λ_i^j gives the leg index (between 1 and 3) of the leg on hub i that connects to hub j, and λ_i^j = 0 if L_ij = 0.

The total energy of a collection of N pinwheels in our model is given by

$$E_{clath}=\sum _{i=1}^{N-1}\sum _{j=i+1}^N\{-\mathit{ϵ}{L}_{ij}+k_{r}H\left(d-r_{ij}\right)\left[{\left(\frac{d}{r_{ij}}\right)}^4-1\right]+\frac{k_s}{2}{\left(r_{ij}-r_0\right)}^2{L}_{ij}+\frac{k_t}{2}{\gamma }_{ij}^2{L}_{ij}\}+\frac{k_b}{2}\sum _{i=1}^N\sum _{j=1}^{N-1}\sum _{k=j+1}^N{\chi }_i^{jk}\left({\lambda }_i^j,{\lambda }_i^k,{\lambda }_i^l\right)L_{ij}{L}_{ik}+\frac{k_o}{2}\sum _{i=1}^N\sum _{j=1}^N{\left({\alpha }_i^j-{\alpha }_0\right)}^2{L}_{ij}.$$ (A2)

A hard-core potential is modulated by the repulsive strength k_r, which is set to 1 k_BT. It imposes steric limitations on the locations of the hubs, and is activated between hubs i and j by the Heaviside step function H(x) only when the separation between the two $\left|{\overrightarrow{r}}_j-{\overrightarrow{r}}_i\right|=\left|{\overrightarrow{r}}_{ji}\right|=r_{ji}$ is less than a cutoff distance d, which is set to 0.8r₀. The stretching modulus, k_s, resists elongation or compression of the interhub bonds relative to their equilibrium length, $r_0$, and the twisting modulus, k_t, resists torsion of these bonds. The twisting angle between hubs i and j, γ_ij, is based on the misalignment of the components of ${\overrightarrow{n}}_i$ and ${\overrightarrow{n}}_j$ that are orthogonal to the unit vector defining their connecting bond ${\overrightarrow{t}}_{ji}={\overrightarrow{r}}_{ji}/r_{ji}$, as given by

$${\gamma }_{ij}={\cos }^{-1}\left[\frac{\left({\overrightarrow{n}}_i\times {\overrightarrow{t}}_{ji}\right)·\left({\overrightarrow{n}}_j\times {\overrightarrow{t}}_{ji}\right)}{\left|{\overrightarrow{n}}_i\times {\overrightarrow{t}}_{ji}\right|\left|{\overrightarrow{n}}_j\times {\overrightarrow{t}}_{ji}\right|}\right].$$ (A3)

The in-plane bending modulus k_b resists distortion of the legs beyond a uniform radial distribution when projected onto their normal plane, i.e., it resists deviation of the in-plane angle θ_jik between legs on hub i that are connected to hubs j and k from a value of 2π/3. Because the configuration of unbound legs is assumed to minimize the elastic energy, the value of the in-plane bending metric χ_i^jk depends on the binding state of all three legs on hub i. Specifically,

$${\chi }_i^{jk}={\left({\theta }_{jik}-\frac{2\pi }{3}\right)}^2$$

if there exists a hub l for which λ_i^l is nonzero, and

$${\chi }_i^{jk}=\frac{3}{2}{\left({\theta }_{jik}-\frac{2\pi }{3}\right)}^2$$

otherwise. To prevent reordering of the legs around the central hub, we measure the angles between them in a counterclockwise fashion from leg 1 to leg 2, leg 2 to leg 3, or leg 3 to leg 1. Therefore, defining ${\overrightarrow{\tau }}_{ji}$ to be the projection of ${\overrightarrow{t}}_{ji}$ in the plane orthogonal to ${\overrightarrow{n}}_i$, and with the example λ_i^j = 1 and λ_i^k = 2, the in-plane angle is calculated to be

$${\theta }_{jik}={\text{cos}}^{-1}\left({\overrightarrow{\tau }}_{ji}·{\overrightarrow{\tau }}_{ki}\right)\text{if}{\overrightarrow{\tau }}_{ji}\times {\overrightarrow{\tau }}_{ki}\ge 0,$$

or

$${\theta }_{jik}=2\pi -{\cos }^{-1}\left({\overrightarrow{\tau }}_{ji}·{\overrightarrow{\tau }}_{ki}\right)\text{if}{\overrightarrow{\tau }}_{ji}\times {\overrightarrow{\tau }}_{ki}<0.$$

The out-of-plane bending modulus, k_o, resists deformation of the triskelion’s pucker angle away from an intrinsic value, α₀. An unpuckered, planar clathrin structure corresponds to α₀ = 90°. The pucker angle contribution α_i^j to hub i from its leg connecting to hub j is given by

$${\alpha }_i^j={\text{cos}}^{-1}\left({\overrightarrow{n}}_i·{\overrightarrow{t}}_{ji}\right).$$