Growth of the eye lens: II. Allometric studies

Abstract

Purpose

The purpose of this study was to examine the ontogeny and phylogeny of lens growth in a variety of species using allometry.

Methods

Data on the accumulation of wet and/or dry lens weight as a function of bodyweight were obtained for 40 species and subjected to allometric analysis to examine ontogenic growth and compaction. Allometric analysis was also used to compare the maximum adult lens weights for 147 species with the maximum adult bodyweight and to compare lens volumes calculated from wet and dry weights with eye volumes calculated from axial length.

Results

Linear allometric relationships were obtained for the comparison of ontogenic lens and bodyweight accumulation. The body mass exponent (BME) decreased with increasing animal size from around 1.0 in small rodents to 0.4 in large ungulates for both wet and dry weights. Compaction constants for the ontogenic growth ranged from 1.00 in birds and reptiles up to 1.30 in mammals. Allometric comparison of maximum lens wet and dry weights with maximum bodyweights also yielded linear plots with a BME of 0.504 for all warm blooded species except primates which had a BME of 0.25. When lens volumes were compared with eye volumes, all species yielded a scaling constant of 0.75 but the proportionality constants for primates and birds were lower.

Conclusions

Ontogenic lens growth is fastest, relative to body growth, in small animals and slowest in large animals. Fiber cell compaction takes place throughout life in most species, but not in birds and reptiles. Maximum adult lens size scales with eye size with the same exponent in all species, but birds and primates have smaller lenses relative to eye size than other species. Optical properties of the lens are generated through the combination of variations in the rate of growth, rate of compaction, shape and size.

Introduction

It has long been known, from casual observation in the laboratory and elsewhere, that there are huge variations, not only in the size, but also in the properties of the eye lens, throughout the animal kingdom. Soft, easily deformed almost spherical lenses are found in the birds while those from most rodents and fish are also almost spherical, but rock-hard. Lenses from the higher order mammals are generally of intermediate hardness and ellipsoid in shape. Optical power varies because of differences in lens curvature and in the refractive index distribution. How such differences arise is not understood and little is known about the nature of factors which determine the final properties of the lens. Allometry offers a means for exploring some aspects of these.

Allometry is the science of scaling growth and/or function for organs and organisms, independent of age. This permits an assessment of the relative sizes and importance of organs to the development and functioning of different species without the complications of age-related changes [1,2].

The simplest approach is to examine organ size relative to bodyweight. This may be done according to the following version of the allometric equation

$$\text{Organ weight=P}\ast {\text{Bodyweight}}^{\text{BME}}$$

Where P is the Proportionality constant and BME is the Body Mass Exponent. For most organs studied, including the brain, organ size scales to bodyweight with a BME of 0.2–0.3. As an extension of the brain, the eye would be expected to be similar. This appears to be the case. Howland et al. [3] collated and analyzed axial length and bodyweight data from 292 vertebrate species, and concluded that groups of related animals have characteristic values of BME and P. For example, primates were reported to have BME=0.117 and p=1.14, while rodents had values of 0.26 and 0.91, respectively. These observations suggest that the primate eye may be relatively smaller than its rodent counterpart. How this relates to lens size is not known.

As part of a long-term study on lens growth, data were collected on lens weights at different ages for a variety of species. Logistic analyses of these data were used in the preceding paper to consider the effects of factors such as gestational period, life span, adult bodyweight and gender on the rate of lens growth [4]. The present study uses allometric analyses to explore the relationship between lens and bodyweight in different aged members of the same species (ontogeny) as well as the relationship between adult bodyweight and the asymptotic lens weights (phylogeny).

Methods

No animal was sacrificed specifically for this project. All tissues processed in the author’s laboratory were by-products from procedures performed by others at other locations and were collected under the auspices of the various local ethics committees.

As described previously [4], substantial data sets on lens wet and/or dry weights, as a function of age, were obtained for 129 species. Details of the numbers and origins of the lenses, arranged into groups, were presented in a table in the appendix to the preceding paper [4]. This Table also lists the maximum (asymptotic) wet (LWW_m) and dry (LDW_m) lens weights which were obtained by extrapolation from plots of these data using the linearized form of the logistic equation (Log W=log W_m - k/A, where W_m is the maximum asymptotic lens weight, A is the time since conception and k is the logistic growth constant). These data were used in the present analyses.

For another 27 species, where insufficient numbers of lenses were obtained to permit construction of a logistic plot, a possible maximum asymptotic weight was estimated using the known-age of the samples and the logistic slope from closely related species.

Information on both lens and bodyweights at different ages, was available for 48 data sets. These data were used to examine ontogenic relationships by plotting log (Lens weight) against log (Bodyweight), according to a linear form of the allometric relationship (log Lens wt=BME*log Body wt + P, where BME is the Body Mass Exponent and P is the Proportionality constant). The data were also used to examine compaction by allometric analysis of the relationship between dry weight and wet weight.

The normal maximum adult bodyweights for the various species were obtained from a variety of sources including the compilations by Altman and Ditmer [5], and Grzimek [6]. These and the maximum (asymptotic) lens weights were combined in allometric plots to obtain the Proportionality constant and the Body mass exponent for grouped species. Where gender was known, the maximum male bodyweights were used. When gender data were mixed, the value for log (bodyweight) could be up to 0.18 lower than that for males only. In the extreme case, when male bodyweight was double that of the female. This would equate to an error of 4% in the BME and would not substantially alter the conclusions presented here.

Lens growth was also compared with eye growth. For this comparison, eye volumes were calculated, assuming a spherical globe, using axial lengths obtained mostly from the data collated by Howland et al. [3]. Lens volumes were calculated from wet and dry weights using the formula

$$\text{Volume=Wet weight-Dry weight}\ast \text{(1-p)}$$

where ρ is the partial specific volume of proteins. The value of 0.73, determined for α-crystallin [7] was used.

Data for related species were grouped and colours were assigned to the groups – bats (black), birds (light blue), carnivores (red), ectothermal species (reptiles, amphibians, fish, yellow with black outline), lagomorphs (purple), marsupials (dark green), primates (light green ), rodents (orange with black outline), tree shrew. (light green with black outline) and ungulates (dark blue).

Results and Discussion

Lens wet and/or dry weights and bodyweights were obtained from the literature and in the author’s laboratory for a total of 157 species. Two types of analyses were performed; ontogenic, in which changes were examined during lifetime growth in a single species, and phylogenic, in which maximum lens size was compared with normal maximum adult body size for different species. Care must be taken not to confuse the phylogeny and ontogeny – the latter indicates how fast lens growth is relative to the body; the former how large the lens can become.

Ontogeny

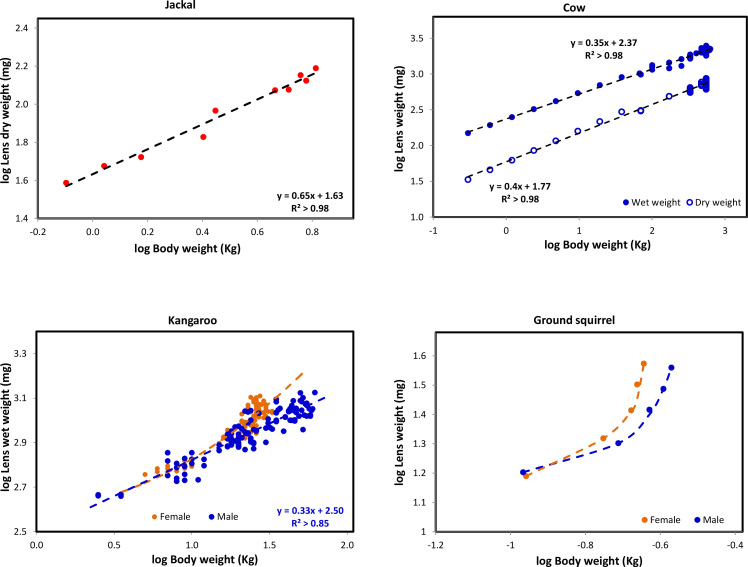
Bodyweights were available for 48 of the data sets permitting an evaluation of the ontogenic relationship with lens weight, i.e., the relative rates at which the lens and body grow, independent of actual age. Bodyweights increased right up to the final age points in all data sets with no suggestion of the decrease often seen in very old animals. Thus, data may not be available for very old animals in some cases. It should be noted that since bodyweights frequently differ between males and females of the same species, the relationships for those where gender is not known will lie somewhere between the two. Where gender was known, the analyses were kept separate but this was only possible for 7 species. Representative examples of the relationship between lens and bodyweight are presented in Figure 1.

Figure 1.

Ontogenic relationship between Bodyweight and lens weight for the jackal, cow, kangaroo and ground squirrel. Data for related species were grouped and colours were assigned to the groups – bats (black), birds (light blue), carnivores (red), ectothermal species (reptiles, amphibians, fish, yellow with black outline), lagomorphs (purple), marsupials (dark green), primates (light green), rodents (orange with black outline), tree shrew. (light green with black outline) and ungulates (dark blue).

For the majority of species examined, linear allometric relationships were obtained. The fits are surprisingly good, given that both lens and bodyweights are variables. No evidence was observed for discontinuous growth due to transitions at physiologic events such as sexual maturation. The BME (slope) for dry weight accumulation in the jackal (0.65) is considerably larger than that for the cow (0.4), indicating that lens growth, relative to body growth is more rapid in the jackal. As can be seen with the cow, the BME for dry weight was always greater than that for wet weight, except the chicken and crocodile, species in which there is no compaction (Table 1). The parameters for the lines of best fit are summarized in Table 1.

Table 1. Ontogenic constants from allometric comparisons of lens weight and bodyweight.

Species (name)		Lens wet weight#			Lens dry weight#
		BME	P	R2	BME	P	R2
baboon female	Papio hamadryas				0.21	32	0.31
baboon male	Papio hamadryas				0.18	29	0.73
howler monkey female	Alouatta caraya				0.16	7	0.63
howler monkey male	Alouatta caraya				0.12	10	0.62
rhesus monkey	Macaca mulatta				0.05	132	0.21
cynomolgus monkey	Macaca fascicularis				0.08	33	0.14
tree shrew	Tupaia glis	1.37	733	0.95	1.69	566	0.98
beaver	Castor canadensis				0.75	5	0.97
cat	Felis silvestris	0.40	417	0.19	0.40	278	0.11
Columbia deer female	Odocoileushemionus columbianus				0.57	62	0.85
Columbia deer male	Odocoileushemionus columbianus	0.58	54	0.93	0.52	66	0.83
corn mouse female	Calomys musculinus				0.96	316	0.99
corn mouse male	Calomys musculinus				0.96	347	0.99
cotton rat	Sigmodon hispidus	0.65	115	0.91
cow	Bos taurus	0.35	234	0.98	0.40	59	0.98
European rabbit	Oryctolagus cuniculus	0.80	391	0.41	0.79	129	0.40
fat tailed dunnart	Sminthopsis crassicaudata				0.17	26	0.05
flying fox	Pteropus poliocephalus				0.69	120	0.91
grey kangaroo female	Macropus giganteus	0.42	263	0.73	0.43	95	0.66
grey kangaroo male	Macropus giganteus	0.39	251	0.91	0.37	105	0.94
guinea pig	Cavia porcellus	0.75	96	0.90
hyrax	Procavia capensis				0.86	51	1.00
jackal	Canis mesomelas Schreber				0.65	43	0.98
Mediterranean pine vole	Microtus duodecimcostatus				1.08	16	0.82
mouse	Mus musculus	0.86	151	0.86	1.08	170	0.97
mule deer	Odocoileus hemionus hemionus				0.40	109	0.79
Norway rat female	Rattus norvegicus	0.58	29	0.98	0.74	11	0.98
Norway rat male	Rattus norvegicus	0.53	28	0.98	0.68	10	0.98
pig male	Sus scrofa	0.49	94	0.57
pig female	Sus scrofa	0.49	94	0.57
Sheep	Ovis aries	0.58	91	0.98	0.66	22	0.98
wild boar	Sus scrofa				0.40	30	0.96
wood buffalo female	Bison bison				0.48	56	0.88
wood buffalo male	Bison bison				0.44	64	0.95
spiny dogfish	Squalus acanthias	1.78	59	0.94

^# Lens weight=P* bodyweight^BME , BME=body mass exponent; p=proportionality constant

Most of the species exhibit negative allometry for both wet and dry weight - i.e., a BME of less than 1.0, indicating that lens weight becomes a smaller proportion of the body with increasing size of an animal. For example, in the cow (wet weight BME, 0.35), the lens wet weight accounts for >10 mg/kg of bodyweight at 1 month but only 3.4 mg/kg at 30 months. By contrast, the tree shrew (BME, 1.37) exhibits positive allometry for lens wet weight, indicating that the lens becomes a greater proportion of bodyweight, increasing from 30 to 39 mg/kg over the same time period.

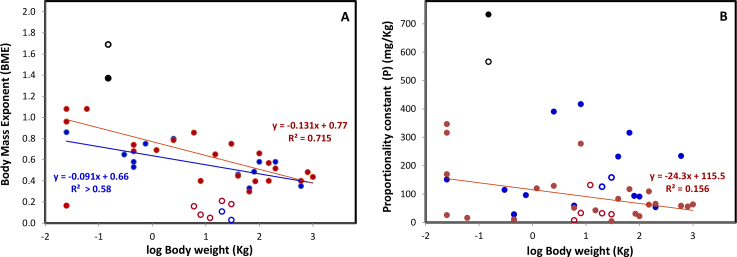
Large difference are seen between the power terms (BME), indicating that there are substantial differences in the rates at which lens and body grow in different species. As can be seen in Figure 2A, for most species examined, BME decreased with increasing animal size. Thus the highest allometric slopes are found with the small rodents and the lowest, with the large ungulates. This is unsurprising since small body sizes are generally associated with short life spans so it is necessary for the lens to rapidly reach its optimal size. The only exceptions are the primates and the dunnart which have very low BMEs for their bodyweights. BME values for the tree shrew are very high compared with the primates, consistent with its classification as a non-primate.

Figure 2.

The relationship between Maximum body weights and (A) the ontogenic body mass exponent (BME) and (B) the Proportionality constants (P) for lens wet (solid circles) and dry weights (open circles) in primates (orange) tree shrews (black ) and other species listed in Table 1 (blue). The values for BME and P were obtained from allometric plots such as those shown in Figure 1.

Differences are observed with gender. For the kangaroo, where male bodyweight may be as much as double that of the female at the same age, there are large differences between BME and P (Table 1; Figure 1). Similar differences were noted with the ground squirrel (Table 1; Figure 1). For the other species where gender was known (buffalo, Columbia deer, corn mouse, Norway mouse and pig) the differences are small, but female BME is always higher than that for the male, consistent with a lower female bodyweight. In all cases, as shown previously [4], male and female lens weights are the same at the same age: only the bodyweights differ.

Nonlinear relationships were observed with the ground squirrel and snow goose (Figure 1). For the ground squirrel part of the reason for the upwards curvature may be that this animal experiences true hibernation. During this time, bodyweight does not increase and may even decrease, whereas the lens keeps growing, unabated. In the preceding paper, it was reported that for the chipmunk, garden dormouse, ground squirrel, hamster and woodchuck, all of which hibernate, lens weights increase continuously and smoothly with age, like all other species, and are unaffected by the hibernation [4]. For the snow goose, it would appear that lens growth is very rapid and independent of body growth, with lens weight reaching over 80% of the asymptotic value within 6 weeks of hatching.

The proportionality constants (P) are listed in Table 1 but it is not clear what they represent when the BMEs differ. Attempts have been made in the past to assign a significance/meaning to this parameter in a variety of studies on other tissues but these have not been successful [1]. As shown in Figure 2B,P for the wet weights does not appear to be related to body size and the relationship for dry weight is weak. This is also the case with gestation period, life span, life style and habitat. In the current study, P corresponds to the weight of the lens in mg when bodyweight is equal to 1 Kg. Clearly, this value is meaningless for species whose bodyweights never reach 1 Kg or for those whose bodies are much heavier. Since the BMEs are different, it is not possible to make any conclusions about the relative sizes of the lenses. One possible interpretation is that P represents the species-specific proportion of bodyweight which is available for the lens. How much of this is actually taken up and the rate at which it is taken up are determined by the BME. This would provide organisms with a variety of options for building lenses, e.g., high BME/high P will result in rapid growth toward the asymptote and a large lens (relative to body size) early in life followed by little growth thereafter. By contrast, low BME/low P leads to a relatively small lens being formed slowly.

Phylogeny and the maximum asymptotic weight

To examine the relationship between lens and body size in different species, allometric analyses were performed using the maximum asymptotic weights determined from logistic analyses and presented in Table 1 of the preceding paper [4]. Maximum lens weights were also estimated for species where insufficient numbers were available to construct logistic plots, using the known-age of the sample and the logistic slope of a closely related species (24 wet and 17 dry weights). In addition, estimates were made for the Asian vole, golden hamster, swamp rabbit and grouse for which reliable ages were not available. These various additional estimates are presented in Table 2. It was noted previously that elephant, giraffe, hippopotamus, human, Spanish ibex and woodchuck lens growth is biphasic [4]. For these species, the maximum asymptotic weights were obtained from the adult logistic growth curve or by extrapolation to the maximum expected life span when adult growth was linear. These estimates are also included in Table 2. In all, wet and dry weight data were available for 66 and 144 species respectively.

Table 2. Estimated maximum lens wet and dry weights densities.

Species		Gestation period days	Life span years	Body wt maximum kg	Dry wt maximum mg	Wet wt maximum mg	Number of lenses n	note	Data source
ebony leaf monkey	Trachypithecus auratus	190	25	15	75	214	4	a	PS
human	Homo sapiens	270	115	75	99	302	520	b	[21], PS
lion tamarin	Leontopithecus rosalia	128	15	0.80	20	62	2	a	PS
mandrill 5 yo	Mandrillus sphinx	175	30	50	64	209	1	a	PS
orang-utan	Pongo pygmaeus	260	50	90	61	173	2	a	PS
African elephant	Loxodonta africana	659	80	5000	980		56	b	[22,23]
fallow deer	Dama dama	230	16	200	715	2015	2	a	PS
giraffe	Giraffa camelopardalis	460	35	2000	1163		34	c	[24]
hippopotamus	Hippopotamus amphibius L	250	55	3000	600		360	b	[25]
Indian antelope	Antelope cerricapra	153	18	50		1500	2	a	PS
Spanish ibex	Capra pyrenaica Schinz, 1838	180	12	120	711		80	c	[26]
African Lynx	Caracal caracal	75	27	20		1150	4	a	PS
grey seal	Halichoerus grypus	350	45	200	897	2480	2	a	PS
maned wolf	Chrysocyon brachyurus	66	20	25		900	2	a	PS
lion	Panthera leo	110	25	150	1000	2500	16	d	PS
red panda	Ailurus fulgens	134	14	6	117	270	2	a	PS
Patagonian cavy	Dolechotis patagonum	85	14	15		500	2	a	PS
Asian Vole	Clethrionomys rufocanus	19	2	0.05	5.0		66	d	[27]
golden hamster	Mesocricetus auratus	16	3	0.10	8.5	15	20	d	[28]
plains rat	Pseudomys australis	30	4	0.07	3		4	a	PS
woodchuck	Marmota monax L	32	6	6	38		14	b	[29,30]
black striped wallaby	Macropus dorsalis	34	15	20		750	3	a	PS
leadbeater possum	Gymnobelideus leadbeateri	16	9	0.20		150	2	a	PS
kowari (marsupial rat)	Dasyuroides byrnei	32	7	0.01	42		2	a	PS
swamp rabbit	Sylvilagus aquaticus	37	9	3	320		145	d	[31]
boobook owl	Ninox novaeseelandiae	35	10	0.30	211	674	2	a	PS
little penguin	Eudyptula minor	35	20	1.0	30	120	6	a	PS
sharp-tailed grouse	Pedioecetes phasianellus	25	13	1.0	40		486	d	[32]
Jackson's chameleon	Chamaeleo jacksonii	170	10	0.08	3	10	2	a	PS
blue fin trevally	Caranx sexfasciatus	365	40	60	3300	7500	2	a	PS
red fish	Sebastes marunus	30	50	20		1360	2	a	PS
snapper	Pagrus auratus	1	35	20	450	1000	6	a	PS
toothfish	Dissostichus Mawsoni	670	100	100	2000	6000	2	a	PS
grass carp	Ctenopharyngodon idella	1	15	20		1399			[33]
silver carp	Hypophthalmichthys molitrix	1		20		1180			[33]

a) Asymptotic weights were estimated using the known age of the samples and the logistic slope from a closely related species. b) Asymptotic weights were obtained by extrapolation to the maximum expected life span when adult growth was linear. c) Asymptotic weights were obtained from the adult logistic growth curve. d) Unreliable age data; asymptotic weights were obtained by assuming largest lens came from adult at 75% of lifespan. PS; present study.

The body and lens sizes are distributed over wide ranges. Among the warmblooded animals studied, the asymptotic lens wet weights range from 8.3 mg for the vesper mouse to >3100 mg for the cow and greater kudu [4]. Dry weights range from 1.1 mg for the guano bat to >1900 mg for the male northern seal. Adult bodyweights varied from 15 g to >5000 kg. In general, the smaller the animal, the greater the proportion of bodyweight occupied by the lens. The ratio of maximum (asymptotic) lens wet weight to adult bodyweight varied from ~1 mg/Kg for the crocodile to >1400 mg/kg for dunnarts.

The data were arranged into groups of closely related species, as used previously [4] and regression analysis was performed on each group as well as on combinations of the groups. Voles and lemmings were found to be different from other rodents and were examined separately. The results are shown in Figure 3.

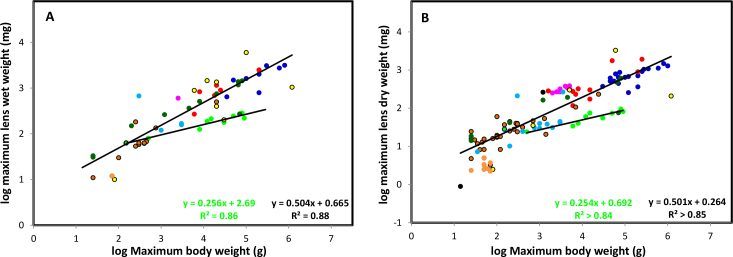
Figure 3.

Allometric comparison of the relationship between maximum bodyweight and maximum lens wet and dry weights. Asymptotic lens wet (Figure 3A) and dry (Figure 3B) weights were obtained from the logistic analysis described previously [5] and from estimates described in Table 2. Primate data were analyzed separately. Data for related species were grouped and colours were assigned to the groups – bats (black), birds (light blue), carnivores (red), ectothermal species (reptiles, amphibians, fish, yellow with black outline), lagomorphs (purple), marsupials (dark green), primates (light green), rodents (orange with black outline), tree shrew. (light green with black outline) and ungulates (dark blue).

Wet weights

Most of the wet weight data (44 species) could be adequately described with a single equation,

$${\text{LensWetWt}}_{\text{m}}=\text{4}\text{.7}\ast {\text{BodyWt}}_{\text{m}}{}^{\text{0}\text{.504}}({\text{R}}^{\text{2}}=0.88)$$

where Wt_m represents the maximum Lens or Bodyweight; the exponent (BME) equals 0.504 and the Proportionality constant (P) is 4.7 mg lens weight/kg bodyweight. The corresponding line is included in the allometric plot (Figure 3A).

The obvious exceptions are the primates, rodents and cold blooded species. Most of the rodents lie below the common line but it appears that the BME (slope) is very similar to that of the other species, suggesting rodent lenses are small for their bodyweights. Nevertheless, lens weight increases, relative to bodyweight, in the same way. No trend can be discerned for the cold-blooded species whereas primates comprise a cohesive group with BME of 0.25 and P of 14.7 (R²=0.86). The primate line of best fit is also included in Figure 3A. It intersects the common line at a point corresponding to a bodyweight of around 150 g. Thus, primates with bodyweights above 150 g have lower lens wet weights than other species with the same bodyweight. The difference increases with increasing bodyweight because of the lower primate BME (0.25 cf 0.5). The tree shrew is near the intersection of the common and primate lines, consistent with its previous classification as a primate, as well as its revised assignment to the order Scandentia.

Dry weights

With the exception of the vole data, the dry weights show similar relationships (Figure 3B). Many of the points appear to lie in the vicinity of a common line with a BME of 0.501, identical to that for wet weight, and P of 1.8 (R²=0.86). The primates again form a separate group (BME 0.25, P, 4.9; R²=0.84) and the slope is the same as that for primate wet weights. Several other groups also differ. These include the lagomorphs and marsupials which lie above the common line while birds lie below. These groups seem to exhibit BMEs very similar to the common line: only P is different. Although only one asymptotic wet weight was available for the lagomorphs, it also lay well above the common line suggesting that lagomorph lenses are larger than might be expected from body size. This is, perhaps, not unexpected since a larger lens is probably needed to achieve the almost 360 degree visual field of the lagomorphs. No trend could be detected for the voles and lemmings for which lens dry weights are substantially below those expected from the common line. The one wet weight available for a vole also lay below the common line, suggesting that vole lenses may be smaller than that expected from body size. Because of their predominantly nocturnal lifestyle, rodents probably do not need a large lens or eye and, instead, rely more on smell and hearing.

Apart from the differences between groups of closely related species, some individuals stand out. For example, the lens of the boobook owl is also much larger than that of other species, including birds, with the same bodyweight. This may be related to the visual requirements of a nocturnal predator. Unfortunately not enough samples were available to assess this possibility. The warthog and domestic pig, on the other hand, appear to have smaller lenses than expected from their bodyweights whereas that of the closely related wild boar is as expected from comparison with the other ungulates.

Compaction

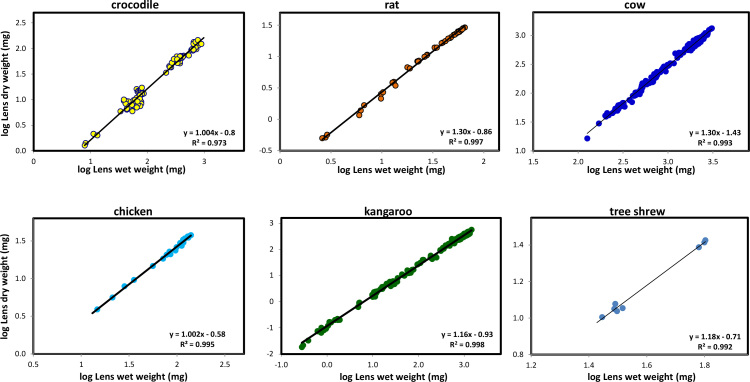
Logisticic analyses of the increases in wet and dry weights with age revealed that dry weight increased more rapidly than wet weight in most species, indicating that compaction was occurring [4]. This can be further assessed using allometry to compare the ontogenic accumulation of wet and dry weights. The crocodile, rat, cow and chicken comparisons are shown in Figure 4.

Figure 4.

Lens compaction as a function of age in the crocodile, rat, cow and chicken, kangaroo and tree shrew. Data for related species were grouped and colours were assigned to the groups – bats (black), birds (light blue), carnivores (red), ectothermal species (reptiles, amphibians, fish, yellow with black outline), lagomorphs (purple), marsupials (dark green), primates (light green), rodents (orange with black outline), tree shrew. (light green with black outline) and ungulates (dark blue).

In each of the examples, a linear relationship is obtained but the allometric constants describing these are quite different. For the crocodile and chicken (Figure 4), the relationship is isometric and the allometric compaction constant (slope of the allometric plot) is 1.00. By contrast, cows, rats (Figure 4) and several other mammals exhibited positive allometry with slopes of around 1.30. Kangaroos and tree shrews were intermediate, with slopes of 1.15 and 1.18. Thus, it would appear that chicken and crocodile lenses do not undergo any compaction whereas the mammalian species compact in the same way with compaction constants of 1.1–1.3. This suggests that accommodation in these species relies on changes in lens shape, made easier by the softness of the lens and/or its position, as demonstrated by Sivak et al. for diving birds [8].

The asymptotic Dry weight/Wet weight ratios for chicken, mallard and little penguin lenses are 0.25–0.27 [4]. Consequently, unlike other species these lenses probably do not have a refractive index gradient, consistent with the conclusion that these birds have monofocal optical systems [9]. By contrast, the boobook owl which has a multifocal system [9] has a ratio of 0.31. The ratio of 0.20 for the crocodile may also indicate monofocal vision.

Further information can be gleaned from the lens/bodyweight comparisons. Since the wet and dry weight allometric slopes (BME) for the bodyweight comparisons are the same for most species, differences in the ratios of dry and wet p values (calculated from the intercepts in Figure 3A,B) will then represent differences in the maximum average concentration of solids in the lens. Thus, most species generate lenses which ultimately have average dry/wet weight ratios of 1.8/4.7=0 38. This suggests lens compaction is similar in most species and the refractive index distributions may also be similar. Differences in lens optical performance at any age will then be determined by differences in lens shape and the rate at which growth occurs.

A small deviation from the average can result in a large difference in dry mass concentration. For example, several rodent lens wet weights are 0.3–0.4 log units below the average whereas their dry weights lie on the common allometric line. The net effect is that these lenses are relatively small but have much higher ratios (>0.5) of dry/wet weight. The laboratory rat lens is a good example of this, having a ratio of ~0.60 (equivalent to an average of 700 mg/ml solids). Bird lens wet weights lie above the wet weight allometric line but dry weights are on the common dry weight line. This indicates that bird lenses are relatively large and have low solid contents. For the species examined in the present study, average dry mass concentrations of the lens varied from 210 (crocodile) to 760 mg/ml (hamster). More detailed data on the dry/wet weight ratios were presented in the preceding paper [4].

Primates appear to be somewhat different with a dry/wet ratio of 0.33, indicating a lower dry weight content, consistent with the conclusions from refractive index measurements on lenses from various species [10]. They also have substantially lower wet and dry lens weights for their bodyweights and the BME is half that of other species. For adults, the relationship between wet and dry weight accumulation is isometric, consistent with the previous conclusion that human lens growth becomes linear not long after birth. These various observations suggest that the regulation of lens size and growth could be different in the primates from that in other species.

It should be remembered that the dry/wet ratios quoted are averages for the whole lens. The ratio will, of course, vary across the lens. In the epithelium, the ratio is probably around 0.17, while in the newly formed fiber cells it is probably close to 0.2. For the species where compaction takes place, the ratio in the nucleus will be substantially larger, as much as 0.9 in the rat [11]. Differences in the ratio across the fiber cell mass are reflected in the different RI gradients observed in different species [10].

It is still not understood what drives the compaction. One attractive hypothesis is that it is related to the concentration of γ-crystallins [12]. This would be consistent with the high concentration of γ-crystallins in fish and rodent lenses which undergo the greatest compaction, the gradient of increasing γ-crystallin toward the nucleus in many species and the complete absence of the protein from bird and crocodile lenses which do not compact.

Determinants of lens size

As a general rule, wet weight data which lie above the common regression line indicate the lens is relatively larger than those from other species while data below the line indicate the lens is smaller. However, such conclusions are complicated by the variable compaction which takes place in the lens with increasing age. This ranges from no compaction in birds up to about fourfold in the rodents and fish. Dry weight is a measure of the number of fiber cells produced but cell size would vary with lens size because of the unique lens growth pattern and hence dry weight would not be useful.

The question remains how final lens size is determined. The closeness of the fit for so many species and the similarities of the BME values suggest that the same regulatory mechanism may be responsible for the control of both lens wet and dry weights. However, since the ratio between wet and dry weights varies substantially between species, it is unlikely that either or both are involved in the regulation. Furthermore, it seems improbable that the eye or body can sense changes in lens wet weight or in the amount of solids (dry weight) accumulated. Therefore, any regulatory mechanism must operate through another property. Lens dimensions and/or volume or optical performance seem more likely since changes in these could be sensed by surrounding tissues. The possible involvement of dimensions and volume can also be examined using allometry.

Very few lens dimensions or measured volumes are available for the different species. However, where data have been obtained for both wet and dry weights, it is possible to calculate the average density and/or volume of a lens using the partial specific volume of proteins, which constitute most of the dry weight. Allometric comparison of the calculated volumes with bodyweight yielded plots where the points lay closer to the common line than for wet weight but not close enough to suggest regulation took place in this way. Given the location of the lens within the eye, it seems more likely that lens size would be sensed by the eye. To examine this, the calculated lens volumes were compared with the globe volumes calculated from published axial lengths, which are reported to scale with body size [3].

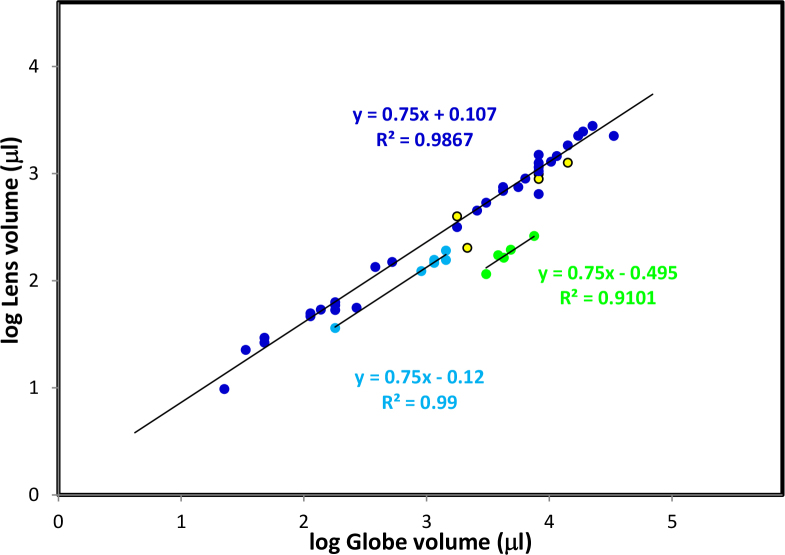
The allometric comparison of eye and lens volumes for 40 species is shown in Figure 5. A linear logarithmic relationship is evident for most but birds and primates form separate groups. Allometric analysis of the data without bird and primate lenses, yielded the relationship

Figure 5.

Allometric analysis of the relationship between eye axial length and lens volume. Lens volumes were calculated from the wet and dry weights using the relationship, volume=wet weight - (1-ρ)dry weight, where ρ is the partial specific volume of proteins. Axial lengths were obtained from the compilation of Howland et al. [4]. Data for related species were grouped and colours were assigned to the groups – bats (black), birds (light blue), carnivores (red), ectothermal species (reptiles, amphibians, fish, yellow with black outline), lagomorphs (purple), marsupials (dark green), primates (light green), rodents (orange with black outline), tree shrew. (light green with black outline) and ungulates (dark blue).

$$\text{Lens volume=0}\text{.83}\ast {\text{Globe volume}}^{0.75}({\text{R}}^2=0.83)$$

The lens-eye exponent of 0.75 is remarkably close to the almost universal scaling constant of 0.66 −0.75 observed on phylogenetic comparison of other organs with bodyweight [13]. The fit of the data are exceptionally good with very few points appearing to differ. The house mouse (with an axial length of 3.5 mm [14] and lens volume of 9 μl) stands out as being quite different and was not used in the regression analysis. The small differences for the other points probably reflect errors in the determination of wet or dry weights or inaccurate axial lengths. Most of the axial length data collated by Howland et al. [3] were obtained from single animals of unknown-age: some were not adults, allowing for the possibility that the axial length had not reached its maximum size. For interspecies allometric comparisons such as this (phylogeny), it is essential that data are obtained from comparably aged animals, preferably adult. Without the ontogenic BME for axial length-bodyweight comparisons, it is not possible to estimate the adult value so using the young values would inadvertently skew the interpretations.

The scaling constants (slopes) for bird and primate lenses appear to be the same as those for the other species but the proportionality constants are lower, indicating that these lenses are smaller relative to eye size than those of other species. By contrast, it was noted earlier that the boobook owl lens was larger than expected from its body size and owl eyes are also larger [3]. These observations suggest that some bird lenses may have been adapted to different lifestyles as noted for eye shape and size [15]. Bird and primate eyes are reported to be 35%–36% larger than those of vertebrates in general [4]. This difference would account for the lateral displacement of the bird data from the common line (Figure 4) but not that of the primates, again demonstrating that primate lens growth is unlike that of all others.

The present data (Figure 5) indicate that the scaling constant for the primate lens/eye allometric comparison is the same as that for all other species. According to Howland et al. [3], “For primates, neither the slope nor the intercept for the eye/body weight allometry differ from those of the vertebrate regression line.” This would lead to the expectation that primate eyes lenses should scale with body size with the same BME as other species. As can be seen in Figure 3, this is clearly not the case. Examination of the data on which the Howland et al. conclusion was based (Figure 2 Figure 4D in [3]) reveals a BME of 0.117 for 11 primates, including the tree shrew which is no longer considered to be a primate, compared to 0.1964 for all vertebrates. Although the difference between the two values was not considered to be statistically significant by the authors, a more realistic interpretation indicates that the eye/body BME for primates is approximately half that of other species, similar to the relationship observed in the present study for the lens/body allometry. If the tree shrew is omitted from the Howland et al. analysis, the BME reduces to 0.09 and P is 1.17 (R²=0.874). It would appear that the reason for the lack of statistical significance in the Howland et al. analyses probably lies in the highly variable axial length data for species other than the primates. This may also reflect the use of data from single animals of unknown-age, referred to earlier.

The identity of the scaling constant for the lens/eye comparison for all species, in contrast to the differences for the lens/body comparison is consistent with the conclusion that lens size is regulated by the eye through the sensing of lens dimensions and/or volume. Whether regulation is mediated through optical signals at the retina or physical contacts through the zonules or iris remains to be established. However, retinal response signals appear unlikely since lens growth in most species involves alterations in both dimensions and refractive index as well as shape changes. The differing signals arising as a result of these various changes in different animals would be extremely complex. Furthermore, studies on experimentally induced myopia have revealed no changes in lens size despite substantial elongation of the globe/axial length [16].

Concluding remarks

The question which still remains unanswered, not only for the lens, but also for other organs is ‘What controls growth and the final size? Most organs appear to stop growing when they reach a genetically predetermined size which may be determined by the competing effects of intrinsic organ factors and extrinsic factors such as the insulin-like growth hormones [17], by the number of progenitor cells laid down during embryogenesis [18] or by the Hippo pathway which stops growth by promoting cell death and restricting cell proliferation through the transcriptional regulation of target genes [19]. These may involve some turnover of cells and/or the accumulation of dead cells when the final size has been reached. However, no evidence for substantial apoptosis or cellular destruction is seen in the lens. It just keeps growing continuously, slowing in most species but at a constant rate in a few. Another model for final size control based on mechanical forces was developed from studies on bird wings [20]. In this model, compression of cells leads to a reduction in proliferation while stretching causes increased proliferation. This might appear to be relevant to the accommodating lens, which is subject to stretching and/or compression forces, but is not consistent with the unabated growth. Further work is required to answer this intriguing question.

It is clear from the data presented here that lens size scales with eye size and not with body size. The scaling constant appears to be the same for all species but different proportionality constants for some species indicate that lens size varies relative to eye size. In particular, primate and bird lenses are small compared with those of other species. How lens size is actually sensed cannot be determined from the present data.