Bayesian Sequential Meta-analysis Design in Evaluating Cardiovascular Risk in a New Antidiabetic Drug Development Program

Abstract

Recently, the Center for Drug Evaluation and Research at the Food and Drug Administration (FDA) released a guidance that makes recommendations about how to demonstrate that a new antidiabetic therapy to treat Type 2 diabetes is not associated with an unacceptable increase in cardiovascular risk. One of the recommendations from the guidance is that Phase II and III trials should be appropriately designed and conducted so that a meta-analysis can be performed. In addition, the guidance implies that a sequential meta-analysis strategy could be adopted. That is, the initial meta-analysis could aim at demonstrating the upper bound of a 95% confidence interval (CI) for the estimated hazard ratio to be < 1.8 for the purpose of enabling a new drug application (NDA) or a biologics license application (BLA). Subsequently after the marketing authorization, a final meta-analysis would need to show the upper bound to be < 1.3. In this context, we develop a new Bayesian sequential meta-analysis approach using survival regression models to assess whether the size of a clinical development program is adequate to evaluate a particular safety endpoint. We propose a Bayesian sample size determination methodology for sequential meta-analysis clinical trial design with a focus on controlling the familywise Type I error rate and power. The partial borrowing power prior is used to incorporate the historical survival meta-data into the Bayesian design. Various properties of the proposed methodology are examined and simulation-based computational algorithms are developed to generate predictive data at various interim analyses, sample from the posterior distributions, and compute various quantities such as the power and the Type I error in the Bayesian sequential meta-analysis trial design. The proposed methodology is applied to the design of a hypothetical antidiabetic drug development program for evaluating cardiovascular risk.

1. Introduction

In December 2008, the Center for Drug Evaluation and Research at the Food and Drug Administration (FDA) released a guidance (www.fda.gov/downloads/Drugs/GuidanceComplianceRegulatoryInformation/Guidances/ucm071627.pdf) that makes recommendations about how to demonstrate that a new therapy to treat Type 2 diabetes is not associated with an unacceptable increase in cardiovascular (CV) risk. The guidance recommends that Phase II/III trials should be appropriately designed and conducted so that a meta-analysis can be performed, and the Phase II/III programs should include patients at higher risk of CV events.

Based on the above recommendations, the plans of meta-analysis assessments should consider the following. Before submission of a New Drug Application (NDA) or Biologics License Application (BLA), one must show that the upper bound of the two-sided 95% confidence interval (CI) for the estimated hazard ratio (HR) for comparing the incidence of important CV events occurring in the investigational agent to that of the control group is less than 1.8. This can be demonstrated either by performing a meta-analysis of the randomized Phase II/III studies or by conducting an additional single, large postmarketing safety trial. If the premarketing application contains clinical data from completed studies showing that the upper bound of the 95% CI is between 1.3 and 1.8 and the overall risk-benefit profile supports approval, a postmarketing trial generally will be necessary to definitively show that the upper bound of the 95% CI is less than 1.3. On the other hand, if the premarketing clinical data show that the upper bound of the 95% CI is less than 1.3, then a postmarketing CV trial generally may not be necessary. This requirement will most likely necessitate the performance of a specific CV outcome study for any new therapy, but would also almost certainly include integrating data across randomized Phase II/III studies.

In light of the above new requirement from the FDA, Ibrahim et al. [1] develop a Bayesian meta-analysis sample size determination method for planning a Phase II/III antidiabetes drug development program. The proposed method not only computes the sample size for multiple studies in a program under the meta-analysis framework by properly accounting for the between study heterogeneity, but also incorporates prior historical information for the underlying risk in the control group via the partial borrowing power prior. The authors explore the operating characteristics of a program design in meeting specific criteria for Type I error and power. That paper investigates the operating characteristics of a program design for a non-sequential meta-analysis with a single, fixed non-inferiority margin of 1.3. However, according to the FDA guidance, after showing non-inferiority for the 1.8 margin (for initial NDA/BLA filing), non-inferiority for the 1.3 threshold can be subsequently tested at the post-marketing setting. This implies that a sequential meta-analysis may be conducted during a drug development program. It raises a challenging multiplicity issue from a statistical point of view with regards to looking at the meta-data multiple times with the sequential testing procedure using the non-inferiority margin of 1.8 and 1.3 at different interim analyses. It is thus crucial to preserve the familywise Type I error rate while maintaining sufficient power in this sequential meta-analysis setting. Family-wise Type I error rate in the context of sequential analyses is the probability of rejecting a true null hypothesis in at least one of the entire collection of interim looks.

The group sequential meta-design provides a solution to a practical challenge in the drug development: when the targeted disease population has a low event rate (e.g., 2% per year), the individual efficacy trials alone generally are not adequately powered to evaluate a particular risk. Another motivation is that it allows the sponsors to make earlier decisions based on interim analysis results for ethical and economical purposes [2]. A drug that is deemed unsafe or inferior would result in stopping a trial/program early. The literature on frequentist statistical methods for group sequential clinical trials with interim monitoring is enormous and too numerous to list here. We refer the reader to the well known book by Jennison and Turnbull [2] for extensive references. The literature on Bayesian methods for group sequential clinical trials is much more sparse and the literature on sequential design methods for meta-analysis is essentially non-existent. Bayesian methods for group sequential clinical trials include [3, 4], who consider frequentist operating characteristics of Bayesian Decision-theoretic designs using backward induction methods. Rosner and Berry [5] examine a Bayesian group sequential design for a proposed randomized clinical trial comparing four treatment regimens, where posterior probability calculations determine the criteria for stopping accrual to one or more of the treatments and frequentist properties of the design are examined. Freedman and Spiegelhalter [6] develop a Bayesian group sequential method with boundaries that may be similar to those obtained from Pocock or O’Brien-Fleming rules, depending on the choice of prior distribution, and they carry out comparisons of their approach with frequentist rules. Spiegelhalter et al. [7] also review many Bayesian group sequential methods in their book. Emerson et al. [8] examine the Bayesian evaluation of group sequential clinical trial design and describe how the Bayesian operating characteristics of a particular stopping rule might be evaluated and communicated to the scientific community. They consider a choice of probability models and a family of prior distributions that allows concise presentation of the Bayesian properties for a specified sampling plan. However, none of these methods consider sequential design in the meta-analysis setting as described here. Moreover, their design and monitoring criteria are quite different from what is proposed here. In this paper, we carry out a meta-analysis sequential design for designing a Phase II/III drug development program in CV risk using a right censored time to event endpoint. We use a meta-analysis exponential survival model with random effects to carry out the proposed design and monitoring plan using a set of novel Bayesian criteria that preserve the Type I error. In addition, we use the fitting and sampling prior ideas of [9] in conjunction with a power prior [10] using historical data to carry out the design. The proposed design is novel and the first of its kind in this setting.

We mention here that there has been some recent work, called “evidence-based methods” for designing studies and planning clinical trials using meta-analysis or sequential meta-analysis methods. Within this framework, Sutton et al. [11] describe an evidence-based algorithm that calculates the required sample size for a planned trial based on the power of an updated meta-analysis. Their approach ensures adequate power to detect a clinically important treatment effect in a meta-analysis including previously completed trials as well as the proposed trial. Rotondi et al. [12] extend the methods of [11] to meta-regression. Higgins et al. [13] propose a sequential method for random-effects meta-analysis using an approximate semi-Bayes procedure. They start with an informative prior distribution that might be based on findings from previous meta-analysis and then update evidence on the among-study variance. We refer to [13] for more references therein on sequential methods for meta-analysis. More recently, Roloff et al. [14] develop a method based on conditional power using a random-effects meta-analysis model for evaluating the influence of the number of additional studies, of their information sizes and of the heterogeneity anticipated among them on the ability of an updated meta-analysis to detect a prespecified effect size. These evidence-based approaches are similar in flavor to what we consider here but with different goals and approaches.

The rest of the paper is organized as follows. Section 2 presents the design of a hypothetical drug development program with two categories of meta-trials and multiple interim analyses for the CV outcome trial and the historical data, which are used to formulate priors for the background rates of the CV events in subjects treated for Type 2 diabetes from the control group. Section 3 presents the log-linear random effects regression models for meta-survival data and the general methodology for the Bayesian sequential meta-analysis design. Section 4 provides a detailed development of the computational algorithms for the predictive data generation, the posterior computation, the Type I error, and power developed in Section 3. In Section 5, we apply the proposed methodology to the meta-analysis sequential design for evaluating CV risk as described in Section 2 and report and discuss the results from our simulation studies. We conclude the paper with discussion and future research in Section 6.

2. Motivating Example

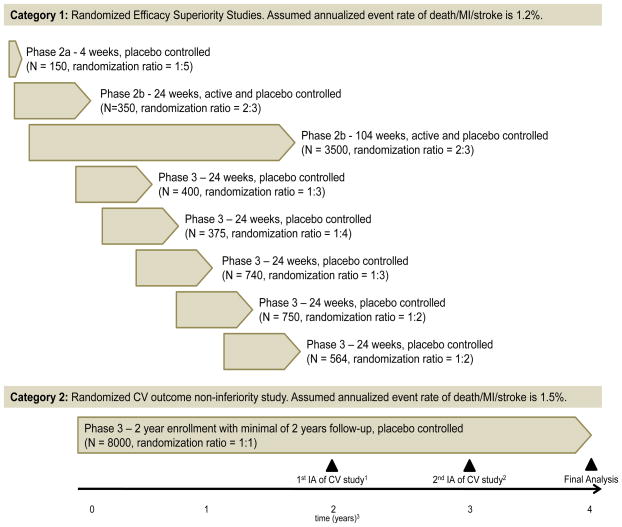
The example in this paper considers a hypothetical drug development program for treating type 2 diabetes mellitus. Our goal here is to appropriately design Phase II/III trials that would facilitate a sequential meta-analysis during the drug development. Figure 1 displays a hypothetical drug development program. The program includes eight randomized controlled efficacy superiority trials (Category 1) and a large randomized controlled CV outcome non-inferiority trial (Category 2). Category 1 trials target subjects with low or moderate CV risk with an assumed annualized event rate of 1.2%. Category 2 targets subjects with high or enriched cardiovascular risk with an assumed annualized event rate of 1.5% as the FDA guidance advocates the inclusion of such a population. The CV outcome non-inferiority trial is a long-term study with scheduled interim analyses. By the time of submission of the NDA/BLA, the Category 1 trials are expected to be complete and Category 2 will undergo its first interim analysis.

Figure 1.

Design of meta studies with two categories and interim analyses (IAs) for evaluating the CV risk. ¹Interim analysis scheduled 2 years after the first subject enrolls in the CV study. Category 1 studies are complete at this time. ²If the upper limit of the 95% CI for the hazard ratio exceeds 1.8 in the first interim analysis, a second interim analysis is scheduled 1 year after the first interim analysis (3 years after the first subject enrolls). ³Time is relative to the start of the CV study. Randomization ratio: control vs treatment.

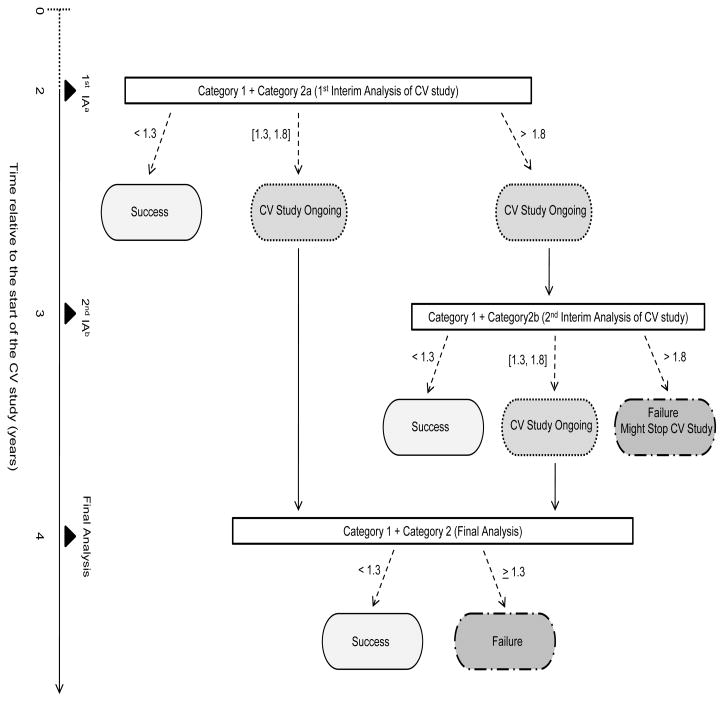
A naïve approach of power calculations is to simply pool the sample size across studies and to use the following approximation: $log(\widehat{\text{HR}})~N(log(\text{HR}))$, 4/total number of endpoints observed from pooled studies). By combining data from the Category 1 studies and the 1st interim analysis of the Category 2 study, 200 events are expected with 100% power to detect the upper 95% CI of the HR < 1.8. By combining data from the Category 1 studies and the 2nd interim analysis of the Category 2 study, 310 events are expected with 100% power to detect the upper 95% CI of the HR < 1.8. The final analysis, combining data from the final analysis of the Category 1 studies and the Category 2 study, is expected to have a total of 462 events with 80% power to detect the upper 95% CI of the HR < 1.3. The problem with this naïve approach is that it does not account for between-study variability. Moreover, simple pooling is susceptible to the issues related to Simpson’s paradox. Historical data could also be considered and incorporated appropriately as implemented using meta-analysis techniques. See Appendix A for published historical data on CV outcome trials in type 2 diabetes patients. The sponsor can also consider decision rules that depend on the outcome and timeline of the integrated analysis (see Figure 2). For example, consider the following possible scenarios and decision rules:

Figure 2.

Diagram of decision rule and timeline for the meta experimental design with interim analyses.

• Scenario 1. If the upper bound of the two-sided 95% CI for HR is < 1.3 for the integrated analysis of Category 1 and Category 2a (first interim analysis of CV study), the sponsor may conclude no elevated CV risk (Success) and decide on submitting the NDA/BLA.

• Scenario 2. If the upper bound of the two-sided 95% CI for HR is ≥ 1.3 and ≤ 1.8, the sponsor may decide to submit the NDA/BLA while continuing the CV study; and if the final analysis (Category 1 + Category 2) shows an upper bound < 1.3, the sponsor may conclude no elevated CV risk (Success).

• Scenario 3. If the upper bound of the two-sided 95% CI for HR is > 1.8, the sponsor may decide to take a 2nd interim analysis at year 3 (Category 1 + Category 2b); if Category 1 + Category 2b shows an upper bound < 1.3, the sponsor may conclude success and submit the NDA/BLA; if Category 1 + Category 2b shows an upper bound between 1.3 and 1.8, the sponsor may decide to submit the NDA and continue to the final analysis to confirm success or failure; and if Category 1 + Category 2b shows an upper bound > 1.8, the sponsor may decide to stop the CV trial for subject safety.

3. The Models and Methods for Bayesian Sequential Meta-analysis Design

3.1. Models for Aggregate Meta-Survival Data

We consider K randomized trials where each trial has two treatment arms (“Control” or “Inv Drug”). Here “Inv Drug” denotes Investigational Drug. Let trt_jk = 0 if j = 1 (control/placebo) and 1 if j = 2 (“Inv Drug”) and also let x_jk denote a trial-level binary covariate, where x_jk = 1 if the k^th trial recruits subjects with low or moderate CV risk for the j^th treatment and x_jk = 0 if the k^th trial recruits subjects with high CV risk for the j^th treatment for j = 1, 2. We further assume that there are a total of I interim analyses, where the I^th interim analysis is the final analysis. Let y_jki and ν_jki denote the total subject year duration, and the total number of events from n_jk subjects for j = 1, 2 and k = 1, …, K at the i^th interim analysis. Write D_Ki = {(y_jki, ν_jki, n_jk, trt_jk, x_jk), j = 1, 2, k = 1, …, K}, which is the observed aggregate meta-survival data available for the i^th interim analysis for i = 1, …, I. We note that D_KI is the aggregate meta-survival data for the final analysis.

Assuming that the individual level failure time follows an exponential distribution with mean 1/λ_jk, the likelihood function of (y_jki, ν_jki) is given by $L({\lambda }_{jk}\mid y_{\mathit{jki}},{\nu }_{\mathit{jki}})={\lambda }_{jk}^{{\nu }_{\mathit{jki}}}exp(-{\lambda }_{jk}{y}_{\mathit{jki}})$. We assume a log-linear random effects regression model for λ_jk:

$$log{\lambda }_{jk}={\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k,{\xi }_k~N(0,{\tau }^2),$$ (3.1)

for k = 1, …, K. In (3.1), τ² captures the between-trial variability and ξ_k also captures the trial dependence between y_1ki and y_2ki. Note that under the exponential model, the design parameter exp(γ₁) is precisely the hazard ratio of the treatment, and θ quantifies the CV risk effect (low or moderate CV risk vs. high CV risk). Let ξ = (ξ₁, …, ξ_K)′ and γ = (γ₀, γ₁)′. Using (3.1), the complete-data likelihood function based on the aggregate meta-survival data D_Ki is given by

$$\begin{array}{l}L(\mathit{\gamma },\theta ,\mathit{\xi },{\tau }^2\mid D_{Ki})=\prod _{k=1}^K\prod _{j=1}^2[exp\{{\nu }_{\mathit{jki}}({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)\}\\ \times exp\left\{-exp({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)y_{\mathit{jki}}\right\}\frac{1}{\sqrt{2\pi }\tau }exp\left(-\frac{{\xi }_k^2}{2{\tau }^2}\right)],\end{array}$$ (3.2)

for i = 1, …, I. We see from (3.2) that under the exponential model, the likelihood function does not depend on the n_jk’s.

3.2. The Key Elements of Bayesian Meta-analysis Design

Let δ₁ denote the interim analysis margin and let δ₂ be the trial success margin for the hazard ratio. The hypotheses for “non-inferiority” testing can be formulated as follows:

$$H_{m0}:exp({\gamma }_1)\ge {\delta }_m\text{versus}{H}_{m1}:exp({\gamma }_1)<{\delta }_m$$ (3.3)

for m = 1, 2. The meta-trial will continue if H₁₁ is accepted and the meta-trials are successful if H₂₁ is accepted. We assume that δ₁ > δ₂. As discussed in Section 1, δ₁ = 1.8 and δ₂ = 1.3 as specified in the FDA guidelines.

Following [9], let π^(s)(γ, θ, τ²) and π^(f)(γ, θ, τ²) denote the sampling and fitting priors, respectively. As discussed in [9] and [15], the meta-survival data D_Ki for i = 1, …, I are simulated from the sampling prior, π^(s)(γ, θ, τ²). The distribution of the predictive datasets D_Ki is considered to be the prior-predictive distribution of the data. Next, the fitting prior, π^(f)(γ, θ, τ²), is updated with the likelihood of the simulated meta-survival data to obtain the posterior distribution of γ, θ, and τ² given the data D_Ki:

$${\pi }^{(f)}(\mathit{\gamma },\theta ,{\tau }^2\mid D_{Ki})\propto \int L(\mathit{\gamma },\theta ,\mathit{\xi },{\tau }^2\mid D_{Ki})d\mathit{\xi }\times {\pi }^{(f)}(\mathit{\gamma },\theta ,{\tau }^2),$$ (3.4)

where L(γ, θ, ξ, τ²|D_Ki) is defined in (3.2). We note that π^(f)(γ, θ, τ²) may be improper as long as the resulting posterior, π^(f)(γ, θ, τ²|D_Ki), is proper. To complete the Bayesian meta-analysis design, we need to specify two proper sampling priors, denoted by ${\pi }_0^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ and ${\pi }_1^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$, defined on the subsets of the parameter spaces induced by hypotheses H₂₀ and H₂₁. To ease the presentation, we consider I = 3. Then, D_K1 is the data from the first interim analysis (Category 1 + Categoriy 2a (1^st Interim Analysis) as shown in Figure 2); D_K2 is the data from the second interim analysis (Category 1 + Category 2b (the second Interim Analysis) as shown in Figure 2); and D_K3 is the data from Category 1 + Category 2, which is used in the final analysis. Corresponding to the four possible paths for trial success as shown in Figure 2, we define

$$\begin{array}{l}{\beta }_{s\ell ,\text{IA}1}^{(n)}=E_{s\ell }\left[1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K1},{\pi }^{(f)})\ge {\phi }_{01}\}\right],\\ {\beta }_{s\ell ,\text{IA}2}^{(n)}=E_{s\ell }\left[1\{P(exp({\gamma }_1)\le {\delta }_1\mid D_{K1},{\pi }^{(f)})<{\phi }_{01}\}1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K2},{\pi }^{(f)})\ge {\phi }_{02}\}\right],\\ {\beta }_{s\ell ,\text{IA}1\Rightarrow \mathrm{F}}^{(n)}=E_{s\ell }[1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K1},{\pi }^{(f)})<{\phi }_{01}\}1\{P(exp({\gamma }_1)\le {\delta }_1\mid D_{K1},{\pi }^{(f)})\ge {\phi }_{01}\}\times 1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K3},{\pi }^{(f)})\ge {\phi }_{02}\}],\\ {\beta }_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}=E_{s\ell }[1\{P(exp({\gamma }_1)\le {\delta }_1\mid D_{K1},{\pi }^{(f)})<{\phi }_{01}\}1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K2},{\pi }^{(f)})<{\phi }_{02}\}\\ \times 1\{P(exp({\gamma }_1)\le {\delta }_1\mid D_{K2},{\pi }^{(f)})\ge {\phi }_{02}\}1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K3},{\pi }^{(f)})\ge {\phi }_{02}\}],\end{array}$$ (3.5)

where 1{A} = 1 denotes the indicator function so that 1{A} = 1 if A is true and 0 otherwise. Then, we propose the following key quantity:

$${\beta }_{s\ell }^{(n)}={\beta }_{s\ell ,\text{IA}1}^{(n)}+{\beta }_{s\ell ,\text{IA}2}^{(n)}+{\beta }_{s\ell ,\text{IA}1\Rightarrow \mathrm{F}}^{(n)}+{\beta }_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}$$ (3.6)

for ℓ = 0, 1. In (3.5), 0 < φ₀₁ < 1 is a prespecified Bayesian credible level for the 1st interim analysis, 0 < φ₀₂ < 1 is a prespecified Bayesian credible level for the 2nd interim analysis and the final analysis, the posterior probabilities, P(exp(γ₁) ≤ δ_j|D_Ki, π^(f)), j = 1, 2, are computed with respect to the posterior distribution of γ₁ given the data D_Ki under π^(f)(γ, θ, τ²), and the expectation E_sl is taken with respect to the predictive distribution of (D_K1, D_K2, D_K3) under ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ for ℓ = 0, 1. We note that the quantities ${\beta }_{s0}^{(n)}$ and ${\beta }_{s1}^{(n)}$ correspond to the Bayesian Type I error and power, respectively. One of the nice features of (3.6) is that φ₀₁ and φ₀₂ play the role of multiplicity adjustments for controlling the familywise Type I error rate in the Bayesian sequential meta-analysis design.

3.3. Specification of the Fitting and Sampling Priors Using Historical Data

Suppose that the historical data are available only for the control arm from K₀ previous datasets. Let y_0k denote the total subject year duration and also let ν_0k denote the total number of events for k = 1, …, K₀. In addition, we let x_0k denote a binary covariate, where x_0k = 1 if the subjects had a low or moderate CV risk and x_0k = 0 if the subjects had a high CV risk in the k^th historical dataset. Suppose that only the trial-level data D_0K0 = {(y_0k, ν_0k, x_0k), k = 1, …, K₀} are available from the K₀ previous datasets. Similar to (3.1), we assume the individual level failure time follows an exponential distribution with mean 1/λ_0k and the log-linear model for λ_0k is given by

$$log{\lambda }_{0k}={\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k},{\xi }_{0k}~N(0,{\tau }^2)$$ (3.7)

for k = 1, 2, …, K₀. Let ξ₀ = (ξ₀₁, …, ξ_0K0)′. Then, the complete-data likelihood function based on D_0K0 is given by $L({\gamma }_0,{\theta }_0,{\tau }^2,{\mathit{\xi }}_0\mid D_{0K_0})={\prod }_{k=1}^{K_0}[exp\{{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}exp\{-exp({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}$ $\times \left(\frac{1}{\sqrt{2\pi }\tau }\right)exp\left(-\frac{1}{2{\tau }^2}{\xi }_{0k}^2\right)]$. Comparing (3.7) to (3.1), we see that the models for the historical data and the current data share the common parameters γ₀ and τ². However, the CV risk effect parameters θ and θ₀ are different in these two models. Thus, strength from the historical data is borrowed through the common parameters γ₀ and τ² and having different parameters θ and θ₀ for the CV risk provides us with greater flexibility in accommodating different CV risk effects in the current and historical data. In addition, we use the partial borrowing power prior of [1] as the fitting prior to control the influence of the historical data on the current study when γ₀ and τ² in the historical data are different than those in the current study.

We now discuss how to specify the sampling prior and the fitting prior. For the sampling prior, ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$, ℓ = 0, 1, we take ${\pi }_{\ell }^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)\propto {\pi }^{(s)}({\gamma }_0){\pi }^{(s)}(\theta ){\pi }^{(s)}({\tau }^2){\pi }_{\ell }^{(s)}({\gamma }_1)$. We first specify a point mass prior for ${\pi }_{\ell }^{(s)}({\gamma }_1)$ with ${\pi }_{\ell }^{(s)}({\gamma }_1)={\mathrm{\Delta }}_{\{{\gamma }_1=log({\delta }_2)\}}$ for ℓ = 0 and Δ_{γ1=0} for ℓ = 1, where Δ_{γ1=γ10} denotes a point mass distribution at γ₁ = γ₁₀, i.e., P(γ₁ = γ₁₀) = 1. We then specify a point mass prior π^(s)(γ₀) at the design value of γ₀. For example, for the meta-design shown in Figure 1, we take Δ_{{γ0=log[−log(1−0.015)]}}, since the annualized event rate for the Category 2 trial is 1.5%. In addition, we specify a point mass prior for each of π^(s)(θ) and π^(s)(τ²). For the meta-design given in Figure 1, we take π^(s)(θ) = Δ_{{θ=−0.225}} and π^(s)(τ²) = Δ_{{τ²=τ̃²}}, where τ̃² is an estimate of τ² from the historical data. For the historical data shown in Table A1, we obtain τ̃² = 0.0537.

Following [1], we specify the fitting prior as follows:

$$\begin{array}{l}{\pi }^{(f)}(\mathit{\gamma },\theta ,{\tau }^2\mid D_{0K_0},a_0)\\ \propto \int \{\int \prod _{k=1}^{K_0}{[exp\{{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}exp\{-exp({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}]}^{a_0}\\ \times \left[\prod _{k=1}^{K_0}\left(\frac{1}{\tau }\right)exp\left(-\frac{1}{2{\tau }^2}{\xi }_{0k}^2\right)\right]d{\mathit{\xi }}_0\}{\pi }_0^{(f)}({\theta }_0)d{\theta }_0{\pi }_0^{(f)}({\gamma }_0,{\tau }^2,{\gamma }_1,\theta ),\end{array}$$ (3.8)

where 0 ≤ a₀ ≤ 1 and ${\pi }_0^{(f)}({\theta }_0)$ and ${\pi }_0^{(f)}({\gamma }_0,{\tau }^2,{\gamma }_1,\theta )$ are initial priors. The parameter a₀ can be interpreted as a relative precision parameter for the historical data D_0K0. One of the main roles of a₀ is that it controls the heaviness of the tails of the fitting prior in (3.8). As a₀ becomes smaller, the tails of (3.8) become heavier. When a₀ = 1 with probability 1, (3.8) corresponds to the update of ${\pi }_0^{(f)}({\gamma }_0,{\tau }^2)$ using Bayes theorem based on the historical data. When a₀ = 0 with probability 1, then the partial borrowing power prior does not depend on the historical data. That is, a₀ = 0 is equivalent to a prior specification with no incorporation of historical data. Thus, the a₀ controls the influence of the historical data on the current study. Such control is important in cases where there is heterogeneity between the historical and current studies. In (3.8), we further specify independent initial priors for (γ₀, γ₁, θ, θ₀, τ²) as follows: (a) a normal prior $N(0,{\tau }_{0f}^2)$ is assumed for each of γ₀, γ₁, θ, and θ₀, where ${\tau }_{0f}^2>0$ is a prespecified hyperparameter; and (b) we specify an inverse gamma (IG) prior for τ², denoted by IG(d_0f1, d_0f2), with density given by ${\pi }_0^{(f)}({\tau }^2)\propto \frac{1}{{({\tau }^2)}^{d_{0f1}+1}}exp\left(-\frac{d_{0f2}}{{\tau }^2}\right)$, where d_0f1 > 0 and d_0f2 > 0 are prespecified hyperparameters. We note here that a different value of ${\tau }_{0f}^2$ may be specified for each of γ₀, γ₁, θ, and θ₀ so that the prior variances for these parameters are different. In (3.8), the parameter a₀ controls the influence of the historical meta-data D_0K0 on the fitting prior for γ₀ and τ² in π^(f)(γ, θ, τ²|a₀, D_0K0). In our prior specification, we consider a fixed a₀. When a₀ is fixed, we know exactly how much historical meta-data are incorporated in the new meta-trial, and also how the Type I error and power are related to a₀. As shown in our simulation study in Section 5, a fixed a₀ provides us additional flexibility in controlling the familywise Type I error rate.

4. The Development of Computational Algorithms

Let T₀ denote the enrollment duration and also let T_i denote the time of the i^th interim analysis for i = 1, …, I. We have T₀ ≤ T₁ < ···< T_I. The assumption T₁ ≥ T₀ implies that the first interim analysis is scheduled only after all patients have been enrolled. Then, we use the sampling prior, π^(s)(γ, θ, τ²), to generate the predictive data D_K1, …, D_KI. We view the distribution of D_Ki as the prior predictive distribution of the data. The algorithm for generating the prior predictive data sets D_K1, …, D_KI is given as follows.

The Predictive Data Generation Algorithm

• Step 1. Generate (γ, θ, τ²) ~ π^(s)(γ, θ, τ²);

• Step 2. Generate ξ_k ~ N(0, τ²) independently for k = 1, …, K;

• Step 3. Compute λ_jk = exp{γ₀ + γ₁trt_jk + θx_jk + ξ_k};

• Step 4. Generate $y_{jk\ell }^{\ast }~\text{Exp}({\lambda }_{jk})$ independently for ℓ = 1, …, n_jk, j = 1, 2, and k = 1, …, K;

• Step 5. Generate accrual times $t_{jk\ell }^{\ast }~U(0,T_0)$ independently for ℓ = 1, …, n_jk, j = 1, 2, and k = 1, …, K;

• Step 6. Compute $c_{\mathit{ijk}\ell }=T_i-t_{\ell jk}^{\ast },y_{\mathit{jki}}={\sum }_{\ell =1}^{n_{jk}}min\{y_{jk\ell }^{\ast },c_{\mathit{ijk}\ell }\}$, and ${\nu }_{\mathit{jki}}={\sum }_{\ell =1}^{n_{jk}}1\{y_{jk\ell }^{\ast }\le c_{\mathit{ijk}\ell }\}$ for j = 1, 2, k = 1, …, K, and i = 1, …, I; and

• Step 7. Set D_Ki = {(y_jki, ν_jki, n_jk, trt_jk, x_jk), j = 1, 2, k = 1, …, K} for i = 1, …, I, which give I sequential meta-data sets.

We note that the above predictive data generation algorithm can be further extended to allow for additional censoring due to the patient withdrawing early from the study. Specifically, Step 6 can be modified as follows:

Step 6^*. Generate $c_{jk\ell }^{\ast }~g(c\mid x_{jk})$ independently, where g(c^*|x_jk) is a pre-specified distribution for the censored random variable, compute $c_{\mathit{ijk}\ell }=min\{T_i-t_{\ell jk}^{\ast },c_{jk\ell }^{\ast }\},y_{\mathit{jki}}={\sum }_{\ell =1}^{n_{jk}}min\{y_{jk\ell }^{\ast },c_{\mathit{ijk}\ell }\}$, and ${\nu }_{\mathit{jki}}={\sum }_{\ell =1}^{n_{jk}}1\{y_{jk\ell }^{\ast }\le c_{\mathit{ijk}\ell }\}$ for j = 1, 2, k = 1, …, K, and i = 1, …, I.

Next, we briefly discuss how to sample from the posterior distributions. Let ξ = (ξ₁, …, ξ_K)′. Using (3.2) and (3.8), the posterior distribution of (γ, θ, τ², ξ, θ₀, ξ₀) given the meta survival data D_Ki available at the i^th interim analysis takes the form

$$\begin{array}{l}{\pi }_i(\mathit{\gamma },\theta ,{\tau }^2,\mathit{\xi },{\theta }_0,{\mathit{\xi }}_0\mid D_{Ki},D_{0K_0},a_0)\propto \{\prod _{k=1}^K[\prod _{j=1}^{2}exp\{{\nu }_{jk}({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)\}\\ \times exp\{-exp({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)y_{jk}\}]\left(\frac{1}{\tau }\right)exp(-\frac{1}{2{\tau }^2}{\xi }_k^2)\}\\ \times [\prod _{k=1}^{K_0}{\left(exp\{{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}exp\{-exp({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}\right)}^{a_0}\\ \times \left(\frac{1}{\tau }\right)exp(-\frac{1}{2{\tau }^2}{\xi }_{0k}^2)]\times {\pi }_0^{(f)}({\theta }_0){\pi }_0^{(f)}({\gamma }_0,{\tau }^2,{\gamma }_1,\theta ).\end{array}$$ (4.1)

We develop the Gibbs sampling algorithm in Appendix B to sample (γ, θ, τ², ξ, θ₀, ξ₀) from the posterior distribution in (4.1) for each of i = 1, …, I.

Finally, we discuss how to compute ${\beta }_{s\ell }^{(n)}$ in (3.6). In this regard, we consider I = 3 and propose the following computational algorithm.

Simulation-based Algorithm for Computing Bayesian Type I Error and Power

• Step 0. Set trt_jk, n_jk, and x_jk for j = 1, 2, and k = 1, …, K, and also set δ₁, δ₂, a₀, φ₀₁, φ₀₂, T₀ ≤ T₁ < T₂ < T₃, M (the Gibbs sample size), and N (the number of simulation runs).

• Step 1. Generate D_K1, D_K2, and D_K3 via the predictive data generation algorithm.

• Step 2. (Interim Analysis 1). Run the Gibbs sampling algorithm to generate a Gibbs sample { ${\gamma }_{11}^{(m)}$, m = 1, …, M} of size M from the posterior distribution in (4.1) given D_K1. Compute ${\widehat{P}}_{11}=\frac{1}{M}{\sum }_{m=1}^{M}1\{exp({\gamma }_{11}^{(m)})\le {\delta }_1\},{\widehat{P}}_{21}=\frac{1}{M}{\sum }_{m=1}^{M}1\{exp({\gamma }_{11}^{(m)})<{\delta }_2\}$, η_f = 1{P̂₂₁ ≥ φ₀₁}, and η_I1 = 1{P̂₁₁ ≥ φ₀₁}. If η_f = 1, go to Step 6.

• Step 3. (Final Analysis (see Figure 2)). If η_f = 0 and η_I1 = 1, run the Gibbs sampling algorithm to generate a Gibbs sample { ${\gamma }_{13}^{(m)}$, m = 1, …, M} of size M from the posterior distribution in (4.1) given D_K3. Compute ${\widehat{P}}_{23}=\frac{1}{M}{\sum }_{m=1}^{M}1\{exp({\gamma }_{13}^{(m)})<{\delta }_2\}$ and recalculate η_f = 1{P̂₂₃ ≥ φ₀₂}. Go to Step 6.

• Step 4. (Interim Analysis 2). If η_f = 0 and η_I1 = 0, run the Gibbs sampling algorithm to generate a Gibbs sample { ${\gamma }_{12}^{(m)}$, m = 1, …, M} of size M from the posterior distribution in (4.1) given D_K2. Compute ${\widehat{P}}_{12}=\frac{1}{M}{\sum }_{m=1}^{M}1\{exp({\gamma }_{12}^{(m)})\le {\delta }_1\},{\widehat{p}}_{22}=\frac{1}{M}{\sum }_{m=1}^{M}1\{exp({\gamma }_{12}^{(m)})<{\delta }_2\}$, and η_I2 = 1{P̂₁₂ ≥ φ₀₂}. Recalculate η_f = 1{P̂₂₂ ≥ φ₀₂}. If η_f = 1, go to Step 6.

• Step 5. (Final Analysis^*). If η_f = 0, η_I1 = 0, and η_I2 = 1, run the Gibbs sampling algorithm to generate a Gibbs sample { ${\gamma }_{13}^{(m)}$, m = 1, …, M} of size M from the posterior distribution in (4.1) given D_K3. Compute ${\widehat{P}}_{23}=\frac{1}{M}{\sum }_{m=1}^{M}1\{exp({\gamma }_{13}^{(m)})<{\delta }_2\}$ and recalculate η_f = 1{P̂₂₃ ≥ φ₀₂}.

• Step 6. Repeat Steps 1–5 N times.

• Step 7. Compute the proportion of {η_f = 1} in these N runs, which gives an estimate of ${\beta }_{s\ell }^{(n)}$.

5. Applications to A Meta-Analysis Sequential Design for Evaluating CV Risk

We consider the meta-analysis sequential design discussed in Section 2. From Figure 1, we have K = 9. Using the historical data shown in Table A1, we have K₀ = 5 and we denote these five historical trials by k = 1, 2, …, 5. Then, we set x_0k = 0 for k = 1, 2 and x_0k = 1 for k = 3, 4, 5. The interim analysis margin and trial success margin were set as δ₁ = 1.8 and δ₂ = 1.3. To ensure that the familywise Type I error rate is controlled under 5%, we considered various values of φ₀₁ and φ₀₂ such as 0.96, 0.97, and 0.98. These values were discussed in [15] and recommended in the 2010 FDA Guidance, “Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials”, released on February 5, 2010 (www.fda.gov/MedicalDevices/DeviceRegulationandGuidance/GuidanceDocuments/ucm071072.htm). In the fitting prior (3.8), we chose an initial prior N(0, 10) for each of γ₀, γ₁, θ, and θ₀, and d_0f1 = 2.001 and d_0f2 = 0.1 for the initial prior for τ². Note that this choice of (d_0f1, d_0f2) leads to a prior variance of 9.98 (about 10) for τ². Thus, we specify relatively vague initial priors for all the parameters.

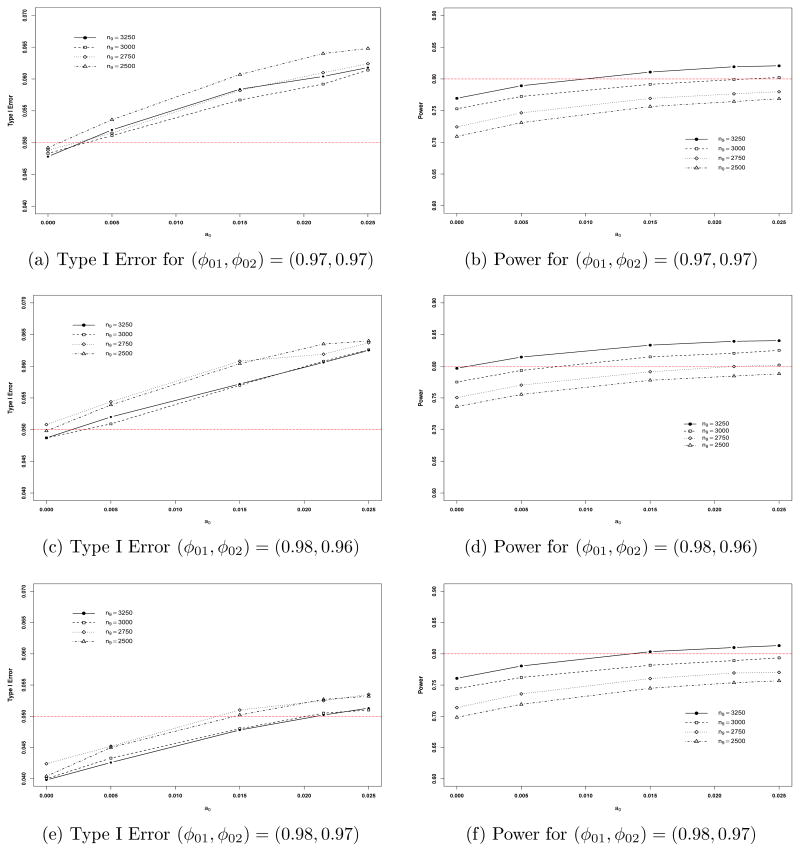
As shown in Figure 1, we have (n₁₁, n₂₁) = (25, 125), (n₁₂, n₂₂) = (140, 210), (n₁₃, n₂₃) = (1400, 2100), (n₁₄, n₂₄) = (100, 300), (n₁₅, n₂₅) = (75, 300), (n₁₆, n₂₆) = (185, 555), (n₁₇, n₂₇) = (250, 500), and (n₁₈, n₂₈) = (188, 376). Then, given the above values of (n_1k, n_2k) for k = 1, …, 8 and various values of n₉ = n₁₉ = n₂₉, we generated D_Ki for i = 1, 2, 3 using the predictive data generation algorithm presented in Section 4 using the sampling priors for (γ₀, γ₁, θ, τ²) specified in Section 3.3. We wish to find the minimum size n₉ and a value of a₀ under various choices of (φ₀₁, φ₀₂) so that the power is at least 80% and the familywise Type I error rate is controlled at 5%. The powers and Type I errors for various values of n₉, (φ₀₁, φ₀₂), and a₀ are shown in Table 1 and plotted in Figure 3. In all computations of the familywise Type I errors and powers, N = 10, 000 simulations and M = 10, 000 with 1000 burn-in iterations within each simulation were used.

Table 1.

Powers and Type I Errors for the Sequential Meta-Design in Figure 1

(φ01, φ02)	a0	Sample Size per Group for Trial 9
		n9 = 2500		n9 = 2750		n9 = 3000		n9 = 3250
		Power	Type I Error	Power	Type I Error	Power	Type I Error	Power	Type I Error
(0.97, 0.97)	0	0.7093	0.0492	0.7244	0.0488	0.7529	0.0483	0.7695	0.0478
	0.0050	0.7310	0.0536	0.7465	0.0515	0.7724	0.0511	0.7893	0.0520
	0.0150	0.7565	0.0607	0.7693	0.0582	0.7915	0.0567	0.8109	0.0584
	0.0215	0.7644	0.0640	0.7765	0.0610	0.7990	0.0592	0.8193	0.0604
	0.0250	0.7688	0.0648	0.7798	0.0624	0.8023	0.0614	0.8208	0.0618
(0.98, 0.96)	0	0.7365	0.0498	0.7506	0.0508	0.7751	0.0487	0.7968	0.0487
	0.0050	0.7555	0.0539	0.7702	0.0544	0.7934	0.0509	0.8145	0.0520
	0.0150	0.7779	0.0604	0.7913	0.0602	0.8148	0.0570	0.8333	0.0572
	0.0215	0.7845	0.0635	0.7996	0.0619	0.8205	0.0608	0.8394	0.0606
	0.0250	0.7881	0.0640	0.8019	0.0637	0.8251	0.0626	0.8404	0.0625
(0.98, 0.97)	0	0.6983	0.0404	0.7139	0.0424	0.7443	0.0400	0.7608	0.0398
	0.0050	0.7191	0.0450	0.7358	0.0452	0.7622	0.0433	0.7805	0.0426
	0.0150	0.7449	0.0502	0.7604	0.0510	0.7817	0.0480	0.8034	0.0478
	0.0215	0.7537	0.0527	0.7693	0.0525	0.7892	0.0505	0.8101	0.0502
	0.0250	0.7568	0.0532	0.7703	0.0535	0.7935	0.0510	0.8132	0.0513

Figure 3.

Plots of Type I error and power versus a₀ for n₉ = 2500, 2750, 3000, and 3250.

From Table 1, we see that with no incorporation of historical meta-survival data, (i) the Type I errors are less than 0.05 for all three values of (φ₀₁, φ₀₂) and the three sample sizes except for one case in which (φ₀₁, φ₀₂) = (0.98, 0.96) and n₉ = 2750, and (ii) for all the three values of (φ₀₁, φ₀₂), the power always increases as n₉ increases. Thus, without incorporation of historical meta-survival data, 80% power was not achieved for n₉ = 2500, n₉ = 2750, and n₉ = 3000 under all three values of (φ₀₁, φ₀₂) and the power was 0.7968, which is very close to 80%, when (φ₀₁, φ₀₂) = (0.98, 0.96) and n₉ = 3250. With incorporation of historical meta-survival data and controlling the 5% familywise Type I error rate, the maximum powers were 0.7449 at a₀ = 0.015 and (φ₀₁, φ₀₂) = (0.98, 0.97) when n₉ = 2500; 0.7358 at a₀ = 0.005 and (φ₀₁, φ₀₂) = (0.98, 0.97) when n₉ = 2750; and 0.7817 at a₀ = 0.015 and (φ₀₁, φ₀₂) = (0.98, 0.97) when n₉ = 3000. Thus, the sample size of n₉ = 3000 or less was not sufficiently large to achieve 80% power while the familywise Type I error rate was controlled at 5% or less. When n = 3250, the maximum power was 0.8101 at a₀ = 0.0215 and (φ₀₁, φ₀₂) = (0.98, 0.97). We also observe from Table 1 that (i) when a₀ = 0.0250, all the Type I errors exceeded 0.05; and (ii) the gains in power were about 4.7%, 2.2%, 3.7%, and 4.9% with incorporation of 1.5%, 0.5%, 1.5%, and 2.15% of the historical data for n₉ = 2500, 2750, 3000, and 3250, respectively, when (φ₀₁, φ₀₂) = (0.98, 0.97).

The four quantities, ( ${\beta }_{s\ell ,\text{IA}1}^{(n)},{\beta }_{s\ell ,\text{IA}2}^{(n)},{\beta }_{s\ell ,\text{IA}1\Rightarrow \mathrm{F}}^{(n)},{\beta }_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}$) for ℓ = 0, 1, defined in (3.5) allow us to examine the power and Type I error contributed from each of the interim analyses and the final analysis. Table 2 shows the results under various choices of (φ₀₁, φ₀₂) and a₀ when n₉ = 3250. We see from Table 2 that when φ₀₁ increases, both the power ( ${\beta }_{s1,\text{IA}1}^{(n)}$) the Type I error ( ${\beta }_{s0,\text{IA}1}^{(n)}$) at the first interim analysis decrease. For example, when (φ₀₁, φ₀₂) = (0.96, 0.97), the Type I errors from the first interim analysis were 0.0390, 0.0466, and 0.0499, which constitute the majority of the familywise Type I errors ( ${\beta }_{s0}^{(n)}$’s), namely, 0.0565, 0.0661, and 0.0705, for a₀ = 0, 0.015, and 0.0215, respectively. On the other hand, when (φ₀₁, φ₀₂) = (0.99, 0.96), the Type I errors from the first interim analysis were 0.0094, 0.0117, and 0.0127; the corresponding powers were 0.2997, 0.3514, and 0.3583; the familywise Type I errors were, 0.0426, 0.0512, and 0.0536; and the overall powers were 0.7915, 0.8265, and 0.8342 for a₀ = 0, 0.015, and 0.0215, respectively. For all of the choices of (φ₀₁, φ₀₂) and a₀, ${\beta }_{s\ell ,\text{IA}2}^{(n)}$ and ${\beta }_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}$ for ℓ = 0, 1 contributed less to the familywise Type I errors and the overall powers than ${\beta }_{s\ell ,\text{IA}1}^{(n)}$ and ${\beta }_{s\ell ,\text{IA}1\Rightarrow \mathrm{F}}^{(n)}$ for ℓ = 0, 1. However, ${\beta }_{s\ell ,\text{IA}2}^{(n)}$ and ${\beta }_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}$ for ℓ = 0, 1 become larger when φ₀₁ increases. The results shown in both Tables 1 and 2, indicate that (i) a smaller value of φ₀₁ leads to a premature termination of the meta CV study and a larger familywise Type I error, (ii) a larger value of φ₀₁ prevents a premature termination but requires a longer waiting time to complete the meta CV study, (iii) (φ₀₁, φ₀₂) = (0.98, 0.97) provides a good overall performance of the Bayesian sequential meta-design under the various scenarios we considered, and (iv) the incorporation of historical data leads to a reduction in sample size. To carry out a sensitivity analysis regarding the use of random effects versus fixed effects models, we fit the fixed effects model to the same predictive data used in Table 1 to recalculate the sample size. The results are reported in Appendix C. The results shown in Table A2 are similar to those shown in Table 1. Thus, the Bayesian sample size calculations are quite robust to the use of random effects or fixed effects models. Although the power, Type I error and sample sizes are the key components, we also examine the posterior summary statistics of the parameters in the random effects model and the results along with detailed discussion are given in Appendix D.

Table 2.

Powers and Type I Errors at Interim Analyses and Final Analysis for the Sequential Meta-Design with n₉ = 3250

	a0	(φ01, φ02)	IA1*	IA2*	IA1 ⇒ Final	IA2 ⇒ Final	Overall
Power	0	(0.96, 0.97)	0.5181	0	0.2580	0.0008	0.7769
		(0.97, 0.97)	0.4681	0.0001	0.2996	0.0017	0.7695
		(0.98, 0.96)	0.4038	0.0006	0.3886	0.0038	0.7968
		(0.98, 0.97)	0.4023	0.0003	0.3553	0.0029	0.7608
		(0.99, 0.96)	0.2997	0.0021	0.4803	0.0094	0.7915
	0.0150	(0.96, 0.97)	0.5758	0	0.2434	0.0004	0.8196
		(0.97, 0.97)	0.5251	0	0.2853	0.0005	0.8109
		(0.98, 0.96)	0.4557	0.0003	0.3749	0.0024	0.8333
		(0.98, 0.97)	0.4557	0.0002	0.3460	0.0015	0.8034
		(0.99, 0.96)	0.3514	0.0010	0.4682	0.0059	0.8265
	0.0215	(0.96, 0.97)	0.5849	0	0.2414	0.0004	0.8267
		(0.97, 0.97)	0.5373	0	0.2816	0.0004	0.8193
		(0.98, 0.96)	0.4654	0.0003	0.3715	0.0022	0.8394
		(0.98, 0.97)	0.4659	0.0002	0.3422	0.0018	0.8101
		(0.99, 0.96)	0.3583	0.0008	0.4696	0.0055	0.8342
Type I Error	0	(0.96, 0.97)	0.0390	0	0.0174	0.0001	0.0565
		(0.97, 0.97)	0.0289	0	0.0188	0.0001	0.0478
		(0.98, 0.96)	0.0190	0	0.0293	0.0004	0.0487
		(0.98, 0.97)	0.0185	0	0.0210	0.0003	0.0398
		(0.99, 0.96)	0.0094	0	0.0324	0.0008	0.0426
	0.0150	(0.96, 0.97)	0.0466	0	0.0195	0	0.0661
		(0.97, 0.97)	0.0368	0	0.0215	0.0001	0.0584
		(0.98, 0.96)	0.0238	0	0.0331	0.0003	0.0572
		(0.98, 0.97)	0.0241	0	0.0235	0.0002	0.0478
		(0.99, 0.96)	0.0117	0	0.0389	0.0006	0.0512
	0.0215	(0.96, 0.97)	0.0499	0	0.0206	0	0.0705
		(0.97, 0.97)	0.0386	0	0.0218	0	0.0604
		(0.98, 0.96)	0.0257	0	0.0347	0.0002	0.0606
		(0.98, 0.97)	0.0255	0	0.0246	0.0001	0.0502
		(0.99, 0.96)	0.0127	0.0001	0.0403	0.0005	0.0536

^*IA1 and IA2 denote the first and second interim analyses, respectively.

The key quantities in (3.5) and (3.6) can be extended to allow for different credible levels at the 2nd interim and final analyses as follows:

$$\begin{array}{l}{\stackrel{\sim }{\beta }}_{s\ell ,\text{IA}1\Rightarrow \mathrm{F}}^{(n)}=E_{s\ell }[1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K1},{\pi }^{(f)})<{\phi }_{01}\}1\{P(exp({\gamma }_1)\le {\delta }_1\mid D_{K1},{\pi }^{(f)})\ge {\phi }_{01}\}\times 1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K3},{\pi }^{(f)})\ge {\phi }_{03}\}],\\ {\stackrel{\sim }{\beta }}_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}=E_{s\ell }[1\{P(exp({\gamma }_1)\le {\delta }_1\mid D_{K1},{\pi }^{(f)})<{\phi }_{01}\}1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K2},{\pi }^{(f)})<{\phi }_{02}\}\\ \times 1\{P(exp({\gamma }_1)<{\delta }_1\mid D_{K2},{\pi }^{(f)})\ge {\phi }_{02}\}1\{P(exp({\gamma }_1)<{\delta }_2\mid D_{K3},{\pi }^{(f)})\ge {\phi }_{03}\}],\end{array}$$ (5.1)

and

$${\stackrel{\sim }{\beta }}_{s\ell }^{(n)}={\beta }_{s\ell ,\text{IA}1}^{(n)}+{\beta }_{s,\text{IA}2}^{(n)}+{\stackrel{\sim }{\beta }}_{s\ell ,\text{IA}1\Rightarrow \mathrm{F}}^{(n)}+{\stackrel{\sim }{\beta }}_{s\ell ,\text{IA}2\Rightarrow \mathrm{F}}^{(n)}$$ (5.2)

for ℓ = 0, 1, where ${\beta }_{s\ell ,\text{IA}1}^{(n)}$ and ${\beta }_{s\ell ,\text{IA}2}^{(n)}$ are given in (3.5) and 0 < φ₀₃ < 1 is a prespecified Bayesian credible level for the final analysis. We note that in (5.1) and (5.2), 0 < φ₀₂ < 1 is a prespecified Bayesian credible level only for the 2nd interim analysis. The Bayesian sequential meta-design with (5.1) and (5.2) is more general and flexible. It is easy to see that when φ₀₁ = φ₀₂ = 1, (5.1) and (5.2) reduces to the one given in Ibrahim et al. (2012), which results in a meta-design without any interim analyses. Using (5.1) and (5.2), we considered (φ₀₁, φ₀₂, φ₀₃) = (0.98, 0.97, 0.96). The resulting powers and familywise Type I errors were 0.7747 and 0.0477, 0.7932 and 0.0512, 0.8148 and 0.0584, 0.8221 and 0.0603, and 0.8243 and 0.0613, respectively, for a₀ = 0, 0.005, 0.015, 0.0215, and 0.025 when n₉ = 3000; and 0.7972 and 0.048, 0.8138 and 0.0507, 0.8332 and 0.0577, 0.8398 and 0.0618, and 0.842 and 0.0623, respectively, for a₀ = 0, 0.005, 0.015, 0.0215, and 0.025 when n₉ = 3250. These results were similar to those shown in Table 1. Thus, our proposed meta-design is quite robust with respect to choices of (φ₀₁, φ₀₂) or (φ₀₁, φ₀₂, φ₀₃). Finally, we considered (φ₀₁, φ₀₂, φ₀₃) = (1, 1, 0.96) and in this case, there were no interim analyses and consequently, there is no multiplicity issue. Under this setting, when n₉ = 3250, the powers and Type I errors were 0.7868 and 0.0394, 0.8037 and 0.041, 0.8225 and 0.0469, 0.8289 and 0.0497, 0.8326 and 0.0503, and 0.8341 and 0.0517, respectively, for a₀ = 0, 0.005, 0.015, 0.0215, and 0.025. These results show that the meta-design without an interim analysis led to about a 2% gain (0.8326 versus 0.8101) in power compared to those with interim analyses while the Type I error is about the same (0.0503 versus 0.0502). However, the meta-design without an interim analysis requires a longer waiting time for the completion of the meta CV study. Therefore, the meta-design with interim analyses offers much more flexibility (e.g., stopping early for safety concerns) while only losing a negligible amount in power.

6. Discussion

The FDA guidance on CV evaluation for diabetes drug development implies that a sponsor may take a two-step development strategy: 1) conducting and completing a set of Phase II/III studies to file an NDA/BLA first by meeting the criterion of the upper bound of 95% CI for HR < 1.8; 2) combining the data from step 1 and another CV outcome trial in order to finally show the upper bound of 95% CI for HR < 1.3. The CV outcome trial should be designed to include the high CV risk patient population, and can start either right after the initial approval or even during the Phase II/III development so that the interim data from the trial can be used as part of the filing data package. There are statistical implications of this sequential meta-analysis design strategy. In this paper, we have extended the work of [1] and developed a novel Bayesian sequential meta-experimental design approach to deal with different statistical challenges in this setting. The approach not only computes the sample size for multiple studies in a drug development program under the meta-analysis framework by properly considering the between study heterogeneity, but also the sample size can be reduced by borrowing historical information for the underlying CV risk in the control population via the partial borrowing power prior. More importantly, the Bayesian approach offers great flexibility in addressing the multiplicity issue in the context of sequential meta-analysis. The operating characteristics of the meta-design against various scenarios and decision rules can be explored easily through the MCMC simulations.

In this paper, we used a hypothetical drug development program with rules and decisions of sponsor to demonstrate our proposed methodology. The example is one of many scenarios that can be posed for a diabetes drug development program. Furthermore, our methodology can be easily extended to other program scenarios for Type 2 diabetes with different study designs, timelines and decision rules, or other diseases with regards to different safety risks. The hypothetical example given in Section 2 contains the information of Categories 1 and 2 (Figure 1). The evaluations of CV risk use the final data from Category 1 and the interim or final data from Category 2 (Figure 2). In practice, many sponsors would like to submit initial filing based on the completed study data from Category 1, while the Category 2 CV outcome study is still ongoing. In this case, it is important to evaluate the CV risk as soon as possible during the initial filing review stage. Thus, it is ideal to understand the CV risk by combining the final data from Category 1 and the interim data from Category 2. This poses several practical considerations from both the operational and regulatory perspectives. The considerations are mainly regarding dissemination of interim results. Two common questions from sponsors are (1) what levels of interim analysis results in Category 2 should be submitted for regulatory evaluations; and (2) If the decision of the market approval includes the evaluations containing the interim data, how it should be addressed in the approved package insert while the Category 2 CV outcome study is still ongoing. To maintain trial integrity of conducting the CV outcome study, one possible approach could be letting the Data Monitoring Committee (DMC) conduct a planned meta-analysis by combining the final data from Category 1 and the interim data from Category 2. The sponsor can share the blinded DMC recommendation with the regulatory agencies afterwards and propose high level blinded information, and clearly specify that it contains the interim data from an ongoing study, in the package insert. Regardless, there are no standard solutions to these questions. Sponsors should proactively discuss these issues with regulatory agencies to get consensus at the pre-filing stage.

In this paper, we have developed a general and flexible Bayesian sequential meta-design with incorporation of historical data. We examined the empirical performance and various characteristics of the proposed meta-design via an extensive simulation study. Our proposed method effectively controls the familywise Type I error rate by selecting appropriate credible levels (φ_0k’s) in the key design quantity given by (3.6) or (5.2). In the types of trials considered in this paper, since the CV event rates are so low, and the patient populations are rare, it appears that meta trial design is the only feasible way to go as mandated by the FDA. It appears that individual trial design is not feasible in this context. A common clinical development plan should have multiple phase 2 and 3 studies. In the area of developing type II diabetes drug, the common practice is to evaluate efficacy from multiple studies enrolling various patients in different disease status and/or background therapies. Meanwhile, the sponsor will continue to cumulate the safety data (either through extension phases of the existing studies, or conduct large scale long term safety studies after certain development milestones). With the need of having multiple studies, the concept of meta-design is a reasonable approach to enhance the evaluations of the integrated safety analysis, which is important for both sponsor and regulatory agents to reduce the risks to the society. This concept is coherent to the regulatory guideline mentioned in Section 1. As far as a₀ is concerned, our experience with the power prior shows that fixed a₀ is just as effective and flexible as random a₀ and is less computationally intensive. Moreover, fixed a₀ has a cleaner interpretation and allows the user more control on the historical data than random a₀. These issues are discussed in [10]. Our recommendation in this paper is to use a meta-trial design due to the study populations and low event rates, and if there is historical data, to incorporate such data via the power prior with fixed a₀. The proposed Bayesian design is flexible, adaptive, and yields excellent operating characteristics.

Throughout the paper, we only considered the exponential regression model, which is one of the limitations of our proposed approach. However, the exponential model is attractive in the sense that the individual patient level survival data is not required. Another major motivation for using the exponential model in this paper is that the historical data itself was only available in aggregate form, thus the exponential model was most natural in this setting, even if we had individual patient level data for the trials themselves. Had we used a different survival model such as the Weibull regression model for the design, individual patient level data would be needed in the design since the likelihood function of the Weibull regression model does indeed depend on subject-level failure times and censoring indicators from n_jk subjects and does not share the same properties as the exponential model. If individual patient level survival data are available, then the proposed methodology can be easily extended to other survival regression models such as piecewise exponential regression models and cure rate regression models in [16]. In addition, in (3.1), the random effect is assumed to be associated only with the trial effect. This assumption implies that the treatment effect is constant across all trials. This assumption may be reasonable since (i) it is not known whether the treatment effects are different across trials; and (ii) as shown in Figure 1, the Category 2 trial has a large sample size, which may play a dominant role in determining the treatment effect. We also note that the historical data are available only for the control arm. Thus, there is no a priori information available about the magnitude of the among-trial variability on the treatment effects from previous trials. This poses a major challenge in the design of a sequential meta-analysis clinical trial. However, our method can be extended to allow for the inclusion of additional random treatment effects. Due to the complexity of the proposed method, we defer this extension to a future research topic to be investigated more thoroughly.

Though our proposed Bayesian meta-experimental design is general and flexible, it is computationally intensive and the key quantities given in (3.5) and (3.6) are certainly not available in closed form. However, the simulation-based algorithms developed in Section 4 are relatively easy to implement. We indeed implemented our methodology using the FORTRAN 95 software with double precision and IMSL subroutines. The FORTRAN 95 code is available upon request. We have written very user-friendly SAS code using PROC MCMC for the fixed effects model discussed in [1]. This software is currently being used by practitioners at Amgen and elsewhere. We are now in the process of generalizing this SAS code to the methodology developed in this paper as well as developing a user-friendly R interface of our available FORTRAN code.

Appendix A: Historical Data to Inform Background Rates for CV Events

Around the time that the FDA CV risk guidance document was published, the final results of the two large scale randomized controlled CV outcome studies in Type 2 diabetes patients were published. The event rates of the controlled groups of these two studies are used as the historical information in the example of this paper (see Table A1). These two studies are described as follows.

Table A1.

Historical Data to Inform Background Rates for CV Events in Subjects Treated for Type 2 Diabetes (Control Arm)

Reference/Control Type	Number of Subjects (N)	Number of CV Events	Total patient years	Annualized event rate
ACCORD (2008) Standard therapy	5123	371	16000	2.29%
ADVANCE (2008) Standard therapy	5569	590	27845	2.10%
Saxagliptin (2009) Total Control	1251	17	1289	1.31%
Liraglutide (2009) Placebo	907	4	449	0.89%
Liraglutide (2009) Active Control	1474	13	1038	1.24%

ACCORD Study

The Action to Control Cardiovascular Risk in Diabetes (ACCORD) trial was designed to determine whether a therapeutic strategy targeting normal glycated hemoglobin levels (i.e., below 6.0%) would reduce the rate of cardiovascular events, as compared with a strategy targeting glycated hemoglobin levels from 7.0 to 7.9% in middle-aged and older people with Type 2 diabetes mellitus and either established cardiovascular disease or additional cardiovascular risk factors. The key result based on 10,251 patients with a mean of 3.5 years of follow-up was published in 2008 [17].

ADVANCE Study

The Action in Diabetes and Vascular Disease: Preterax and Diamicron Modified Release Controlled Evaluation (ADVANCE) trial was designed to assess the effects on major vascular outcomes of lowering the glycated hemoglobin value to a target of 6.5% or less in a broad cross-section of patients with Type 2 diabetes. The key result based on 11,140 patients with a median of 5 years of follow-up was published in 2008 [18].

Moreover, other historical data can be obtained from the briefing documents of the FDA advisory meetings for Saxagliptin and Liraglutide in April, 2009 [19]. For Saxagliptin and Liraglutide, the events were the Major Adverse Cardiac Events (MACE). In Section, we develop a Bayesian method to elicit the priors using these five historical datasets as shown in Table A1.

Appendix B: The Gibbs Sampling Algorithm and Full Conditional Distributions

We use the Gibbs sampling algorithm to sample from the posterior distribution in (4.1) given D_Ki and D_0K0 for i = 1,…, I. The full conditional distributions required in the Gibbs sampling algorithm are (i) [γ|θ, ξ, θ₀, ξ₀, D_Ki,D_0K0, a₀]; (ii) [θ|γ, ξ D_Ki]; (iii) [ξ|γ, θ, τ²,D_Ki]; (iv) [θ₀|γ₀, τ²,D_0K0, a₀]; (v) [ξ₀|γ₀, θ₀, τ²,D_0K0, a₀]; and (vi) [τ²|ξ, ξ₀]. We sample, γ, θ, ξ, θ₀, ξ₀, and τ² from the above full conditional distributions in turn. For (i), using the initial fitting prior in (3.8), the conditional density for [γ|θ, ξ, θ₀, ξ₀,D_Ki, D_0K0, a₀] is given by

$$\begin{array}{l}\pi (\mathit{\gamma }\mid \theta ,\mathit{\xi },{\theta }_0,{\mathit{\xi }}_0,D_{Ki},D_{0K_0},a_0)\\ \propto \prod _{k=1}^K\left[\prod _{j=1}^{2}exp\{{\nu }_{jk}({\gamma }_0+{\gamma }_1{\text{trt}}_{jk})\}exp\{-exp({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)y_{jk}\}\right]\\ \times \prod _{k=1}^{K_0}\left[exp\{a_0{\nu }_{0k}({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})\}exp\{-a_{0}exp({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}\right]\\ \times exp\left(-\frac{1}{2{\tau }_{0f}^2}{\mathit{\gamma }}^{\prime }\mathit{\gamma }\right).\end{array}$$ (B.1)

For (ii) and (iv), the full conditional densities are given, respectively, as follows:

$$\pi (\theta \mid \mathit{\gamma },\mathit{\xi },D_{Ki})\propto \prod _{k=1}^K\prod _{j=1}^2\left[exp({\nu }_{jk}\theta x_{jk})exp\{-exp({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)y_{jk}\}\right]\times exp\left(-\frac{1}{2{\tau }_{0f}^2}{\theta }^2\right)$$ (B.2)

and

$$\pi ({\theta }_0\mid {\gamma }_0,{\tau }^2,D_{0K_0},a_0)\propto \prod _{k=1}^{K_0}\left[exp(a_0{\nu }_{0k}{\theta }_0{x}_{0k})exp\{-a_{0}exp({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}\right]\times exp\left(-\frac{1}{2{\tau }_{0f}^2}{\theta }_0^2\right).$$ (B.3)

For (iii), given, γ, θ, τ², and D_Ki, the ξ_k’s are conditionally independent and the conditional density for ξ_k is given by

$$\pi ({\xi }_k\mid \mathit{\gamma },\theta ,{\tau }^2,D_{Ki})\propto \prod _{j=1}^2\left[exp({\nu }_{jk}{\xi }_k)exp\{-exp({\gamma }_0+{\gamma }_1{\text{trt}}_{jk}+\theta x_{jk}+{\xi }_k)y_{jk}\}\right]\times exp\left(-\frac{1}{2{\tau }^2}{\xi }_k^2\right)$$ (B.4)

for k = 1, …, K. Similarly, for (iv), given γ₀, θ₀, τ², and D_0K0, the ξ_0k’s are conditionally independent and the conditional density for ξ_0k takes the form

$$\pi ({\xi }_{0k}\mid {\gamma }_0,{\theta }_0,{\tau }^2,D_{0K_0},a_0)\propto exp(a_0{\nu }_{0k}{\xi }_{0k})exp\{-a_{0}exp({\gamma }_0+{\theta }_0{x}_{0k}+{\xi }_{0k})y_{0k}\}exp\left(-\frac{1}{2{\tau }^2}{\xi }_{0k}^2\right)$$ (B.5)

for k = 1, …, K₀. It is easy to show that the full conditional distributions in (B.1) to (B.5) are log-concave in each of these parameters. Thus, we can use the adaptive rejection algorithm of [20] to sample (γ, θ, ξ, θ₀, ξ₀). Finally, for (vi), the full conditional distribution [τ²|ξ, ξ₀] is an inverse gamma distribution given by

$${\tau }^2\mid \mathit{\xi },{\mathit{\xi }}_0~\text{IG}\left(d_{0f1}+\frac{K}{2}+\frac{K_0}{2},d_{0f2}+\frac{1}{2}\sum _{k=1}^K{\xi }_k^2+\frac{1}{2}\sum _{k=1}^{K_0}{\xi }_{0k}^2\right),$$ (B.6)

and, hence, sampling τ² is straightforward.

Appendix C: Powers and Type I Errors under the Fixed Effects Model

Following [1], the log-linear fixed effects model for λ_jk assumes log λ_jk = γ₀ + γ₁trt_jk + θ_k for k = 1,…,K. To ensure identifiability, we assume that ${\theta }_K=-{\sum }_{k=1}^{K-1}{\theta }_k$. For the historical trial-level meta-survival data, under the fixed effects model, we assume log λ_0k = γ₀ + θ_0k for k = 1, 2,…,K₀, where ${\sum }_{k=1}^{K_0}{\theta }_{0k}=0$ and ${\theta }_{0K_0}=-{\sum }_{k=1}^{K_0-1}{\theta }_{0k}$. The likelihood function and the partial borrowing fitting prior under the fixed effects model are given in [1]. Under the fixed effects model, the models for the historical data and the current data share only one common parameter, namely, γ₀. We then fit the fixed effects models to the same predictive data used in Table 1 to recalculate the powers and Type I errors. In all calculations, we chose an initial prior N(0, 10) for each of γ₀, γ₁, θ_k, and θ_0k under the fixed effects model. Table A2 shows the power and Type I errors under various values of n₉ and (φ_p1, φ₀₂). Under the fixed effects model, 80% power with the corresponding familywise Type I error of 5% or less was not achieved for n₉ = 2500, n₉ = 2750, and n₉ = 3000. However, 80% power was achieved for n₉ = 3250 when (φ₀₁, φ₀₂) = (0.98, 0.96) and a₀ = 0 or when (φ₀₁, φ₀₂) = (0.98, 0.97) and a₀ = 0.1625. Compared to the random effects model, the fixed effects model allows for more incorporation of the historical data (i.e., a larger value of a₀) in order to achieve 80% power while the familywise Type I error maintains at 5% since the models for the historical data and the current data share only one common parameter, namely, γ₀. These results are consistent with those shown in [1].

Table A2.

Powers and Type I Errors Based on the Fixed Effects Model

(φ01, φ02)	a0	Sample Size per Group for Trial 9
		n9 = 2500		n9 = 2750		n9 = 3000		n9 = 3250
		Power	Type I Error	Power	Type I Error	Power	Type I Error	Power	Type I Error
(0.97, 0.97)	0	0.7138	0.0493	0.7293	0.0489	0.7573	0.0498	0.7748	0.0493
	0.10	0.7395	0.0556	0.7509	0.0523	0.7748	0.0512	0.7932	0.0517
	0.15	0.7602	0.0618	0.7693	0.0573	0.7929	0.0579	0.8099	0.0587
	0.20	0.7765	0.0680	0.7874	0.0631	0.806	0.0631	0.8221	0.0634
(0.98, 0.96)	0	0.7400	0.0502	0.7553	0.0518	0.7807	0.0499	0.8014	0.0494
	0.10	0.7612	0.0553	0.7767	0.0558	0.7953	0.0519	0.8174	0.0537
	0.15	0.7792	0.0606	0.7919	0.0608	0.8116	0.0565	0.8301	0.0581
	0.20	0.7971	0.0672	0.8039	0.0645	0.8255	0.0616	0.8398	0.0636
(0.98, 0.97)	0	0.7039	0.0422	0.7183	0.0434	0.7479	0.0414	0.7651	0.0414
	0.10	0.7274	0.0451	0.7410	0.0469	0.7661	0.0424	0.7853	0.0438
	0.15	0.7466	0.0511	0.7591	0.0508	0.7835	0.0479	0.8006	0.0488
	0.1625	0.7520	0.0534	0.7629	0.0516	0.7859	0.0485	0.8086	0.0500
	0.20	0.7642	0.0581	0.7740	0.0555	0.7954	0.0528	0.8120	0.0540

Appendix D: The Posterior Estimates at Interim and Final Analyses

Due to the nature of the sequential meta-analysis design, we examine the empirical performance of the posterior estimates at each of interim and final analyses under each of the sampling priors ${\pi }_1^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ and ${\pi }_0^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ used in calculating the power and type I error. As discussed in Section 3.3, the design values of (γ₀, γ₁, θ, τ²), denoted by (γ_0,DV, γ_1,DV, θ_DV, ${\tau }_{\text{DV}}^2$), are (−4.192, 0, −0.225, 0.054) and (−4.192, 0.262, −0.225, 0.054) under ${\pi }_1^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ and ${\pi }_0^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$, respectively. To evaluate the performance of the posterior estimates, we generate N = 10, 000 data sets for each of D_K1, D_K2, and D_K3 with n₉ = 3250. For the i^th simulated data set, we compute the posterior means ( ${\widehat{\gamma }}_0^{(i)},{\widehat{\gamma }}_1^{(i)}$, θ̂⁽ⁱ⁾, τ̂²⁽ⁱ⁾), the posterior standard deviations (sd(γ₀)⁽ⁱ⁾, sd(γ₁)⁽ⁱ⁾, sd(θ)⁽ⁱ⁾, sd(τ²)⁽ⁱ⁾), and the 95% highest posterior density (HPD) intervals { $({\gamma }_{0,\text{Low}}^{(i)},{\gamma }_{0,\text{Up}}^{(i)}),({\gamma }_{1,\text{Low}}^{(i)},{\gamma }_{1,\text{Up}}^{(i)}),({\theta }_{\text{Low}}^{(i)},{\theta }_{\text{Up}}^{(i)}),({\tau }_{\text{Low}}^{2(i)},{\tau }_{\text{Up}}^{2(i)})$} for i = 1,…,N. We then calculate the average of the posterior means (EST), the average of the posterior standard deviations (SD), the simulation standard error (SE), the root of the mean squared errors (RMSE), and the coverage probability (CP) of the 95% HPD intervals for each parameter under each simulation setting. Mathematically, for example, for γ₁ (the primary design parameter), EST, SD, SE, RMSE, and CP are defined as follows: $\text{EST}=\frac{1}{N}{\sum }_{i=1}^N{\widehat{\gamma }}_1^{(i)}),\text{SD}=\frac{1}{N}{\sum }_{i=1}^{N}sd{({\gamma }_1)}^{(i)},\text{SE}={\left[\frac{1}{N-1}{\sum }_{i=1}^N{({\widehat{\gamma }}_1^{(i)}-\text{EST})}^2\right]}^{1/2},\text{RMSE}={\left[\frac{1}{N}{\sum }_{i=1}^N{({\widehat{\gamma }}_1^{(i)}-{\gamma }_{1,\text{DV}})}^2\right]}^{1/2}$, and $\text{CP}=\frac{1}{N}{\sum }_{i=1}^{N}1\{{\gamma }_{1,\text{Low}}^{(i)}\le {\gamma }_{1,\text{DV}}\le {\gamma }_{1,\text{Up}}^{(i)}\}$, where the indicator function $1\{{\gamma }_{1,\text{Low}}^{(i)}\le {\gamma }_{1,\text{DV}}\le {\gamma }_{1,\text{Up}}^{(i)}\}=1$ if ${\gamma }_{1,\text{Low}}^{(i)}\le {\gamma }_{1,\text{DV}}\le {\gamma }_{1,\text{Up}}^{(i)}$ and 0 otherwise. These quantities are calculated in a similar fashion for γ₀, θ, and τ. Table A3 shows the simulation results. For the simulated data D_K1 at the 1st interim look, the averages of the posterior means of γ₁ are very close to the corresponding design values, the CP’s of γ₁ are almost 95%, and the SD’s and the SE’s are almost the same when a₀ = 0 or a₀ = 0.0215. For the simulated data sets D_K2 and D_K3 at the 2nd and final looks, the averages of the posterior means of γ₁ are slightly higher than the corresponding designed values, and the SD’s are slightly higher than the SE’s, resulting in the CP’s around 96% to 97%. When a₀ = 0, the averages of the posterior means of γ₀ are slightly higher than the designed value, the SD’s are slight larger than the SE’s, and the CP’s are around 97%. When a₀ = 0.0215, the averages of the posterior means of γ₀ are larger than the designed value, which is expected since the prior mean of γ₀ = −3.807 based on the historical data D_0K0. Based on the design of the predictive data generation, the follow-up times for subjects with high CV risk are always longer than those for subjects with low or moderate CV risk. This unbalanced design leads to biased estimates for θ especially when a₀ = 0.0215. Again, due to a small number of meta studies, the averages of the posterior means for τ² are slightly higher than the designed value and the corresponding SD’s are also high, which leads to high CP’s in all cases.

Table A3.

Summary of the Posterior Estimates at Interim and Final Analyses

Analysis	a0	Para-meter	Under ${\pi }_1^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ for Power					Under ${\pi }_0^{(s)}(\mathit{\gamma },\theta ,{\tau }^2)$ for Type I Error
			EST	SD	SE	RMSE	CP (%)	EST	SD	SE	RMSE	CP (%)
IA1	0	γ0	−4.125	0.318	0.263	0.272	97.32	−4.126	0.314	0.262	0.270	97.21
		γ1	0.005	0.144	0.145	0.145	94.99	0.268	0.136	0.138	0.138	94.93
		θ	−0.325	0.374	0.316	0.332	96.94	−0.321	0.363	0.307	0.322	97.12
		τ2	0.086	0.091	0.033	0.046	99.99	0.084	0.085	0.033	0.045	99.99
	0.0215	γ0	−4.001	0.211	0.129	0.231	91.72	−4.002	0.210	0.130	0.230	91.64
		γ1	−0.016	0.141	0.140	0.141	95.13	0.246	0.133	0.133	0.134	94.93
		θ	−0.431	0.292	0.234	0.312	92.87	−0.426	0.284	0.226	0.303	92.87
		τ2	0.074	0.061	0.023	0.031	100.0	0.073	0.059	0.024	0.030	99.99
IA2	0	γ0	−4.153	0.279	0.250	0.253	96.81	−4.162	0.281	0.252	0.253	97.10
		γ1	0.034	0.123	0.104	0.110	97.25	0.314	0.115	0.099	0.112	95.90
		θ	−0.531	0.336	0.240	0.389	92.35	−0.421	0.327	0.238	0.309	97.02
		τ2	0.068	0.068	0.003	0.015	100.0	0.070	0.066	0.002	0.016	100.0
	0.0215	γ0	−4.024	0.199	0.132	0.214	91.11	−4.029	0.201	0.132	0.210	92.09
		γ1	0.015	0.121	0.101	0.102	97.87	0.295	0.113	0.095	0.100	97.19
		θ	−0.647	0.279	0.139	0.445	75.43	−0.541	0.270	0.140	0.346	89.62
		τ2	0.063	0.050	0.012	0.015	100.0	0.065	0.050	0.012	0.016	100.0
Final	0	γ0	−4.146	0.274	0.245	0.249	96.81	−4.153	0.277	0.247	0.250	97.04
		γ1	0.025	0.105	0.093	0.097	96.88	0.300	0.099	0.089	0.096	95.98
		θ	−0.531	0.333	0.236	0.387	92.92	−0.420	0.325	0.236	0.306	97.12
		τ2	0.068	0.068	0.003	0.015	100.0	0.070	0.066	0.003	0.016	100.0
	0.0215	γ0	−4.025	0.197	0.133	0.213	90.95	−4.028	0.199	0.132	0.211	91.65
		γ1	0.011	0.104	0.091	0.092	97.29	0.286	0.098	0.086	0.089	96.93
		θ	−0.643	0.277	0.137	0.440	75.93	−0.535	0.268	0.138	0.340	90.14
		τ2	0.063	0.050	0.012	0.015	100.0	0.065	0.050	0.012	0.016	100.0