Pseudo-value approach for comparing survival medians for dependent data

Abstract

Survival median is commonly used to compare treatment groups in cancer-related research. The current literature focuses on developing tests for independent survival data. However, researchers often encounter dependent survival data such as matched pair data or clustered data. We propose a pseudo-value approach to test the equality of survival medians for both independent and dependent survival data. The Type I error and power of the proposed method are examined by a simulation study, in which we examine independent and dependent data. The simulation study shows that the proposed method performs equivalently to the existing methods for independent survival data and performs better for dependent survival data. The proposed method is illustrated by a study comparing survival median times for bone marrow transplants.

1. Introduction

Survival analysis is widely used in cancer-related research, for example, bone marrow transplant studies [1]. Survival median is often provided to summarize survival data and to compare treatment groups of interest. Brookmeyer and Crowley [2] proposed a nonparametric test to compare the equality of survival medians (We refer to this method as the Brookmeyer-Crowley test in this paper). They considered a pooled-weighted Kaplan-Meier estimate based on the sample size of each group. Then, the pooled-sample median is calculated by the weighted Kaplan-Meier estimate and linear interpolation. If the survival medians of all groups are the same, the estimated survival rate of each group at the pooled-sample median should be close to 0.5. Thus, a chi-squared test was developed based on the difference between 0.5 and the estimated survival rate of each group at the pooled-sample median. Another chi-squared test was proposed by Rahbar et al. [3] with fewer assumptions than the Brookmeyer-Crowley test. In particular, they considered that the family of the underlying survival distributions or censoring distributions of some groups is different from those of the other groups in the simulation study. Their simulation study indicated that the performance of the Brookmeyer-Crowley test appears to be poor when the survival distribution family differs among groups. However, these two tests are limited to independent survival data.

Another limitation of [3] is that the test requires the existence of survival median for each group because the test statistic is based on the difference between the survival median of each group and the pooled survival median. On the other hand, the Brookmeyer-Crowley test only requires the existence of the pooled survival median. Thus, if the pooled survival median exists, the method is applicable even when the survival medians of some groups do not exist. See Section 4 for a concrete example.

The pseudo-value technique was proposed by Andersen et al. [4]. To explain the details of the pseudo-value approach for clustered or dependent data, we introduce some notations. Let d_j be the sample size of cluster j, j = 1, …, m and n = Σ_j d_j, where m is the number of clusters and n is the total number of individuals. The survival probability S(t) indicates the pooled survival probability at time t based on the total sample and Z_ij represents the covariate vector for the ith individual in the jth cluster. Assuming censoring times are independent of failure times, a pseudo-value at time t of the ith individual in the jth cluster is defined by Y_ij(t) = nŜ(t) − (n − 1)Ŝ_−ij(t), i = 1, …, d_j, j = 1, …, m, where Ŝ(t) is the Kaplan-Meier estimate of S(t) based on the pooled data and Ŝ_−ij(t) is the Kaplan-Meier estimate of survival obtained by omitting the ith individual in the jth cluster. Logan et al. [5] studied marginal cumulative incidence and survival models for clustered data using the pseudo-value approach. Assuming the censoring times are a random sample from a common distribution, they showed that i) Y_ij(t) is approximately independent of Y_kℓ for j ≠ ℓ as n → ∞; and ii) lim_n→∞ E(Y_ij(t)|Z_ij) = S(t|Z_ij). The pseudo-values can be used as a response variable in a generalized estimating equation (GEE) setting as described in [4], [5], and [6]. Since a single fixed time point is only considered in this paper, we illustrate the use of the GEE at a fixed time point τ. To obtain the marginal survival function at time τ given covariate Z, we consider g(S(τ|Z)) = β′Z, where β is a q × 1 parameter vector. Let μ = S(τ|Z) = g⁻¹(β′Z), Y_j = (Y_1j(τ), …, Y_dj,j (τ)), and μ_j = (μ_1j(τ), …, μ_dj,j (τ)), j = 1, …, m. Then, the GEE is defined as follows:

$$\sum _j{\left(\frac{\partial {\mathit{\mu }}_j}{\partial \mathit{\beta }}\right)}^{\prime }{\mathbf{V}}_j^{-1}({\mathbf{Y}}_j-{\mathit{\mu }}_j)\equiv \sum _j{\mathbf{U}}_j(\mathit{\beta })=\mathbf{0},$$ (1)

where V_j is a d_j × d_j working covariance matrix for cluster j. The working covariance matrix V_j can be expressed by ${\mathbf{V}}_j={\mathbf{A}}_j^{1/2}\mathbf{R}(\mathit{\alpha }){\mathbf{A}}_j^{1/2}$, where R(α) is a working correlation matrix and A_j is a diagonal matrix with elements var(Y_ij) = v(μ_ij) for some known variance function v(·). Then, it was shown that $\sqrt{m}(\widehat{\mathit{\beta }}-\mathit{\beta })$ converges in distribution to N(0, Σ) for some covariance matrix Σ, see [5], [7], and [8]. Thus, a Wald chi-square statistic mβ̂′Σ̂⁻¹β̂ converges in distribution to the chi-squared distribution with degrees of freedom q under the assumption that β = 0 for an appropriate estimator Σ̂. To estimate Σ, the sandwich estimator is used:

$${\widehat{\mathrm{\sum }}}_{\mathit{\beta }}=\mathbf{I}{(\widehat{\mathit{\beta }})}^{-1}\widehat{\mathit{Var}}\{\mathbf{U}(\widehat{\mathit{\beta }})\}\mathbf{I}{(\widehat{\mathit{\beta }})}^{-1},$$

where

$$\mathbf{I}(\mathit{\beta })=\sum _j{\left(\frac{\partial {\mathit{\mu }}_j}{\partial \mathit{\beta }}\right)}^{\prime }{\mathbf{V}}_j^{-1}\left(\frac{\partial {\mathit{\mu }}_j}{\partial \mathit{\beta }}\right),\widehat{\mathit{Var}}\{\mathbf{U}(\widehat{\mathit{\beta }})\}=\sum _j{\mathbf{U}}_j(\widehat{\mathit{\beta }}){\mathbf{U}}_j{(\widehat{\mathit{\beta }})}^{\prime }.$$

Therefore, the dependent survival data are readily handled by considering within-cluster correlation between individuals.

We propose a pseudo-value-based method to test the equality of survival medians for independent and dependent data in this paper. In Section 2, we describe the proposed method and its asymptotic distribution. In Section 3, we compare the proposed method to the Brookmeyer-Crowley test and Rahbar et al. [3] in a simulation study. A bone marrow transplant example is illustrated in Section 4. Finally, we have a brief conclusion in Section 5.

2. Method

In this section, we lay out the proposed method. We assume that the censoring times are independent of the failure times and the censoring times are a random sample from a common distribution. The median survival time is given by

$$\zeta =S^{-1}(0.5)=inf\{t:S(t)\le 0.5\}.$$

The Kaplan-Meier estimator Ŝ(t) is consistent even for dependent data under some mild conditions. For the detailed conditions, see [9]. Thus, ζ̂ defined by inf{t : Ŝ(t) ≤ 0.5} is also consistent for dependent data using Lemma 21.2 of [10]. Assume that we have ν groups to compare. Under the null hypothesis, we have ζ₁ = · · · = ζ_ν ≡ ζ₀, where ζ_i is the survival median of group i, i = 1, …, ν. This is equivalent to testing H₀ : S₁(ζ₀) = · · · = S_ν(ζ₀)(= 0.5), where S_i(ζ₀) is the survival rate of group i at time ζ₀. Let ζ̂₀ be an estimate of ζ₀ based on the pooled data.

To compare survival probabilities at ζ₀, we use the pseudo-value approach at a fixed time point ζ₀. Let I_k be an indicator variable for group k such that for k = 1, …, ν,

$$I_k=\{\begin{array}{l}1,\text{if}\text{an}\text{individual}\text{belongs}\text{to}\text{the}k\text{th}\text{group},\hfill \\ 0,\text{otherwise}.\hfill \end{array}$$

Let β = (β₁, …, β_ν)′ be the coefficient vector of the indicator variables in the GEE. To avoid an identifiability issue, without loss of generality we fix β_ν at 0 and estimate β_−ν = (β₁, …, β_ν−1)′. Next, we define pseudo-values Y_ij(ζ̂₀) = nŜ(ζ̂₀) − (n − 1)Ŝ_−ij(ζ̂₀), where Y_ij is a pseudo-value for the ith individual belonging to the jth cluster. Let Y_j = {Y_ij(ζ̂₀); i = 1, …, c_j} and μ_j = {μ_ij(ζ̂₀); i = 1, …, c_j}, which means that Y_j includes all and only individuals belonging to the jth cluster and μ_j is the corresponding mean vector. Then, the GEE is defined as in (1). An identity link function or a logit link function can be used in practice. Assuming Z_ij = I_k, we have lim_n→∞ E(Y_ij(ζ₀)|Z_ij) = S(ζ₀|I_k) = S_k(ζ₀) by [5]. Therefore, the null hypothesis S₁(ζ₀) = · · · = S_ν(ζ₀) is equivalent to testing β_−ν = 0 given ζ₀. Thanks to the consistency of ζ̂₀, the test statistic is given by

$$X^2=m{\widehat{\mathit{\beta }}}_{-\nu }^{\prime }{\widehat{\mathrm{\sum }}}_{{\mathit{\beta }}_{-\nu }}^{-1}{\widehat{\mathit{\beta }}}_{-\nu },$$

where β̂_−ν is found by solving the GEE numerically and Σ̂_β−ν is the corresponding sandwich estimate of the covariance matrix of β̂_−ν. By considering the sandwich estimate for Σ_β−ν, we account for the dependency of survival data. In practice, the independence working correlation matrix was recommended for the pseudo-value approach [6]. Under the null hypothesis, X² converges in distribution to a chi-squared distribution with ν − 1 degrees of freedom by the consistency of ζ̂₀ and [5]. Note that like the Brookmeyer-Crowley test, the proposed pseudo-value approach only requires the existence of the pooled survival median, which is an advantage over [3].

3. Simulation Study

In the simulation study we compared four groups to examine the empirical Type I error rates and rejection rates of the proposed pseudo-value method, the Brookmeyer-Crowley test, and [3] at the significance level α = 0.05. To estimate the density functions of survival distributions for [3], we used bootstrap with 1000 replicates. Survival and censoring times were assumed to have exponential, log-normal, uniform, or Weibull distributions. Three censoring rates were considered: c = 0, 25, and 50 percent. The sample size for each group was fixed at n_i = 100, or 200 for i = 1, …, 4, where n_i is the sample size of group i. All experiments were replicated 5000 times. The logit link was considered for the pseudo-value approach. The independence working correlation matrix was used following the recommendation of [6]. We also examined the exchangeable working correlation matrix and the unstructured working correlation matrix for a portion of the simulation, but there was little difference from the result using the independence working correlation matrix.

Let ζ₀ and c be the survival median and the censoring rate, respectively. The survival times were generated from i) the exponential distribution with mean ζ₀/log(2); ii) the uniform distribution on (ζ₀ − 3, ζ₀ + 3); iii) the log-normal distribution with mean ζ₀ exp(0.5) and variance ${\zeta }_0^{2}exp(1)(exp(1)-1)$; and iv) the Weibull distribution with shape parameter 1.2 and scale parameter ${\zeta }_0^{-1/1.2}/log(2)$. For c > 0, the censoring times were generated from i) the exponential distribution with mean (1 − c)ζ₀/c/log(2) for the exponential survival times; ii) the uniform distribution on (ζ₀ − 3, ζ₀ + 3 + 3(1 − 2c)/c) for the uniform survival times; iii) exp(log(ζ₀) + U) where U was generated from the uniform distribution on (−2, 2 + (2 − 4c)/c) for the log-normal survival times; and iv) the Weibull distribution with shape parameter 1.2 and scale parameter {c log 2/ζ₀/(1 − c)}^−1/1.2 for the Weibull survival times.

Each cluster was assumed to have 8 individuals. The 8 individuals were divided into the 4 groups by 2. Thus, the ith group with n_i = 100 and n_i = 200 consisted of 50 and 100 clusters, respectively. Normal copulas were used to generate correlated survival times of each cluster. The 8 × 8 exchangeable correlation matrix with correlation ρ = 0, 0.25 and 0.5 was used for the normal copulas, i.e.,

$$\mathcal{C}=\left(\begin{array}{cccc}1& \rho & \dots & \rho \\ \rho & 1& \dots & \rho \\ ⋮& ⋮& \ddots & ⋮\\ \rho & \rho & \dots & 1\end{array}\right).$$

Note that ρ = 0 means that the survival times of the four groups are independent. After generating 8-dimensional random vectors on the unit cube [0, 1]⁸ from normal copulas given ρ, the survival times were generated corresponding to their marginal survival distributions. Independent of the survival times, the censoring times were randomly generated using normal copulas with ρ = 0. For the detailed use of copulas, see [11].

Table 1 shows the empirical Type I error rates when the survival time distributions of the four groups were the same. The true survival median was fixed at ζ₀ = 6. ‘PV’, ‘BC’, and ‘Rahbar’ represent the pseudo-value approach, the Brookmeyer-Crowley test, and [3], respectively. ‘Exp’, ‘LN’, ‘Unif’, and ‘WB’ indicate the exponential distribution, log-normal distribution, uniform distribution, and Weibull distribution for survival time distributions. The censoring time distributions were chosen accordingly as discussed previously. Distributions in parentheses are the survival time distributions for four groups. For example, (Exp,Exp,Exp,Exp) indicates that all four groups have the exponential survival distributions. For the independent survival data (ρ = 0), the empirical Type I error rates of all three methods are close to the nominal rate 0.05. For the dependent data (ρ = 0.25 or 0.5), in contrast to the two methods, the pseudo-value approach controls Type I error rates very well. The Brookmeyer-Crowley test and [3] show much less Type I error rates than 0.05 in general. It appears that as the dependency of data increases, the Type I error rates of the Brookmeyer-Crowley test and [3] decreases towards 0.

Table 1.

Simulation 1: Empirical Type I error rates with α = 0.05 when the survival distributions of the four groups are the same. ‘PV’, ‘BC’, and ‘Rahbar’ indicate the pseudo-value approach, the Brookmeyer-Crowley test, and [3], respectively.

ρ	ni	c	(Exp,Exp,Exp,Exp)			(LN,LN,LN,LN)			(WB,WB,WB,WB)			(Unif,Unif,Unif,Unif)
			PV	BC	Rahbar	PV	BC	Rahbar	PV	BC	Rahbar	PV	BC	Rahbar
0	100	0	0.050	0.056	0.063	0.050	0.055	0.057	0.071	0.054	0.063	0.071	0.055	0.066
		0.25	0.044	0.056	0.056	0.050	0.060	0.051	0.065	0.057	0.050	0.062	0.059	0.068
		0.5	0.044	0.061	0.034	0.040	0.056	0.037	0.066	0.062	0.033	0.061	0.057	0.059
	200	0	0.052	0.053	0.054	0.052	0.053	0.052	0.063	0.053	0.055	0.059	0.052	0.059
		0.25	0.044	0.050	0.057	0.050	0.057	0.053	0.062	0.055	0.059	0.066	0.064	0.067
		0.5	0.046	0.055	0.049	0.051	0.058	0.048	0.060	0.061	0.049	0.058	0.055	0.061
0.25	100	0	0.070	0.032	0.033	0.072	0.032	0.028	0.070	0.032	0.033	0.070	0.032	0.036
		0.25	0.064	0.034	0.036	0.062	0.033	0.029	0.071	0.035	0.032	0.066	0.033	0.042
		0.5	0.062	0.042	0.032	0.062	0.037	0.025	0.063	0.042	0.034	0.058	0.035	0.040
	200	0	0.053	0.024	0.032	0.056	0.023	0.031	0.053	0.023	0.033	0.056	0.023	0.037
		0.25	0.058	0.031	0.037	0.060	0.034	0.034	0.057	0.034	0.039	0.060	0.037	0.043
		0.5	0.058	0.035	0.036	0.057	0.036	0.037	0.057	0.035	0.037	0.057	0.035	0.042
0.5	100	0	0.068	0.010	0.013	0.068	0.010	0.012	0.068	0.010	0.013	0.068	0.010	0.014
		0.25	0.069	0.012	0.014	0.064	0.015	0.018	0.067	0.013	0.015	0.062	0.014	0.020
		0.5	0.061	0.021	0.012	0.060	0.024	0.016	0.058	0.021	0.016	0.063	0.023	0.023
	200	0	0.054	0.008	0.013	0.056	0.007	0.011	0.054	0.007	0.013	0.056	0.008	0.012
		0.25	0.062	0.012	0.020	0.060	0.015	0.018	0.061	0.014	0.017	0.065	0.014	0.022
		0.5	0.057	0.021	0.022	0.059	0.025	0.020	0.054	0.020	0.021	0.055	0.021	0.025

Table 2 shows the simulation results of the empirical rejection rates when the survival time distributions of the four groups were the same. Four true survival medians were assumed to be 8, 8, 6, and 6 for (Exp,Exp,Exp,Exp) and (Unif,Unif,Unif,Unif). For (WB,WB,WB,WB) and (LN,LN,LN,LN), the true survival medians were 7.5, 7.5, 6, and 6. For ρ = 0, the pseudo-value approach appears to have higher power than [3] and comparable power to the Brookmeyer-Crowley test. For ρ = 0.25 and 0.5, the pseudo-value approach has greater power than [3] and the Brookmeyer-Crowley test.

Table 2.

Simulation 2: Empirical rejection rates with α = 0.05 when the survival distributions of the four groups are the same.

ρ	ni	c	(Exp,Exp,Exp,Exp)			(LN,LN,LN,LN)			(WB,WB,WB,WB)			(Unif,Unif,Unif,Unif)
			PV	BC	Rahbar	PV	BC	Rahbar	PV	BC	Rahbar	PV	BC	Rahbar
0	100	0	0.379	0.365	0.346	0.325	0.309	0.276	0.343	0.323	0.307	0.575	0.567	0.533
		0.25	0.348	0.338	0.291	0.271	0.264	0.212	0.298	0.281	0.260	0.485	0.494	0.472
		0.5	0.264	0.269	0.175	0.215	0.227	0.134	0.221	0.232	0.161	0.390	0.413	0.357
	200	0	0.653	0.644	0.603	0.552	0.551	0.524	0.587	0.584	0.546	0.867	0.865	0.848
		0.25	0.595	0.600	0.536	0.473	0.476	0.432	0.530	0.531	0.503	0.793	0.804	0.774
		0.5	0.473	0.482	0.411	0.362	0.378	0.306	0.418	0.428	0.539	0.683	0.697	0.650
0.25	100	0	0.452	0.329	0.312	0.377	0.265	0.236	0.395	0.278	0.276	0.653	0.544	0.514
		0.25	0.388	0.304	0.258	0.312	0.230	0.184	0.344	0.258	0.235	0.543	0.462	0.447
		0.5	0.294	0.245	0.148	0.233	0.197	0.121	0.246	0.202	0.141	0.434	0.390	0.343
	200	0	0.732	0.637	0.603	0.643	0.518	0.496	0.661	0.558	0.539	0.918	0.876	0.856
		0.25	0.665	0.580	0.547	0.523	0.437	0.401	0.594	0.504	0.487	0.850	0.801	0.778
		0.5	0.517	0.467	0.386	0.398	0.344	0.291	0.453	0.394	0.347	0.728	0.688	0.653
0.5	100	0	0.523	0.283	0.276	0.458	0.215	0.192	0.468	0.236	0.239	0.758	0.518	0.502
		0.25	0.471	0.264	0.213	0.348	0.187	0.158	0.401	0.206	0.201	0.626	0.437	0.425
		0.5	0.337	0.222	0.127	0.256	0.150	0.101	0.278	0.167	0.125	0.483	0.357	0.324
	200	0	0.833	0.645	0.588	0.746	0.498	0.465	0.770	0.534	0.510	0.970	0.884	0.873
		0.25	0.760	0.571	0.532	0.597	0.407	0.362	0.688	0.477	0.464	0.915	0.803	0.784
		0.5	0.595	0.448	0.376	0.435	0.315	0.251	0.506	0.366	0.314	0.781	0.676	0.640

Although the asymptotics of the proposed method works for a common censoring distribution, the performance is also of interest when some survival distributions or censoring distributions of the groups are different from the others [3]. Table 3 shows the empirical Type I error rates when the two survival time distributions of the four groups were different from the other two survival distributions. For example, (Exp,Exp,LN,LN) is two exponential survival distributions and two log-normal survival distributions. The true survival median was fixed at ζ₀ = 6 as previous. For ρ = 0, the empirical Type I error rates of the three methods are close to 0.05 in general. For ρ = 0.25 and 0.5, in contrast to the other two, the pseudo-value approach controls Type I error rates very well. As in Table 1, the Brookmeyer-Crowley test and [3] show much less Type I error rates than 0.05 in general. Like Table 1, the Type I error rates of the Brookmeyer-Crowley test and [3] decreases to 0 as the dependency of the survival distributions increases.

Table 3.

Simulation 3: Empirical Type I error rates with α = 0.05 when the survival distributions of the two groups are different from those of the other two groups.

ρ	ni	c	(Exp,Exp,LN,LN)			(Unif,Unif,LN,LN)			(Exp,Exp,WB,WB)
			PV	BC	Rahbar	PV	BC	Rahbar	PV	BC	Rahbar
0	100	0	0.051	0.057	0.060	0.052	0.056	0.063	0.072	0.057	0.065
		0.25	0.042	0.053	0.056	0.043	0.059	0.055	0.069	0.054	0.056
		0.5	0.041	0.054	0.034	0.042	0.063	0.047	0.062	0.060	0.043
	200	0	0.052	0.054	0.053	0.055	0.055	0.057	0.062	0.052	0.056
		0.25	0.047	0.051	0.052	0.055	0.060	0.054	0.054	0.053	0.057
		0.5	0.046	0.053	0.042	0.063	0.063	0.053	0.056	0.055	0.050
0.25	100	0	0.074	0.032	0.030	0.074	0.034	0.034	0.074	0.032	0.032
		0.25	0.061	0.030	0.030	0.062	0.034	0.034	0.067	0.030	0.032
		0.5	0.060	0.039	0.026	0.058	0.039	0.035	0.060	0.041	0.028
	200	0	0.055	0.022	0.032	0.057	0.024	0.034	0.057	0.022	0.034
		0.25	0.057	0.031	0.035	0.067	0.035	0.040	0.060	0.030	0.038
		0.5	0.059	0.038	0.032	0.064	0.041	0.038	0.054	0.035	0.036
0.5	100	0	0.073	0.011	0.013	0.074	0.010	0.015	0.075	0.011	0.013
		0.25	0.065	0.016	0.016	0.066	0.016	0.020	0.075	0.014	0.018
		0.5	0.064	0.026	0.014	0.068	0.027	0.020	0.069	0.028	0.019
	200	0	0.057	0.009	0.011	0.060	0.010	0.013	0.057	0.010	0.014
		0.25	0.055	0.011	0.015	0.059	0.016	0.020	0.063	0.015	0.020
		0.5	0.063	0.024	0.019	0.062	0.025	0.025	0.060	0.022	0.023

Table 4 shows the simulation results of the empirical rejection rates when the two survival time distributions of the four groups were different from the other two survival distributions. For (Exp,Exp,LN,LN), survival medians are 8, 6, 8, and 6, respectively. The survival medians of (Exp,Exp,WB,WB) and (Unif,Unif,LN,LN) are 7.5, 6, 7.5, and 6, respectively. For ρ = 0, it appears that the three methods have comparable power. For ρ = 0.25 and 0.5, the pseudo-value approach has greater power than [3] and the Brookmeyer-Crowley test as expected.

Table 4.

Simulation 4: Empirical rejection rates with α = 0.05 when the survival distributions of the two groups are different from those of the other two groups

ρ	ni	c	(Exp,Exp,LN,LN)			(Unif,Unif,LN,LN)			(Exp,Exp,WB,WB)
			PV	BC	Rahbar	PV	BC	Rahbar	PV	BC	Rahbar
0	100	0	0.447	0.431	0.390	0.466	0.442	0.415	0.255	0.277	0.264
		0.25	0.365	0.360	0.312	0.383	0.384	0.343	0.223	0.249	0.237
		0.5	0.283	0.298	0.191	0.296	0.319	0.248	0.170	0.203	0.146
	200	0	0.653	0.754	0.694	0.749	0.741	0.731	0.426	0.504	0.475
		0.25	0.595	0.653	0.599	0.649	0.664	0.617	0.393	0.465	0.422
		0.5	0.473	0.522	0.444	0.528	0.556	0.498	0.301	0.366	0.305
0.25	100	0	0.514	0.395	0.352	0.535	0.414	0.382	0.289	0.235	0.234
		0.25	0.430	0.337	0.285	0.429	0.351	0.316	0.251	0.211	0.202
		0.5	0.310	0.268	0.177	0.309	0.286	0.226	0.191	0.172	0.123
	200	0	0.819	0.735	0.686	0.831	0.742	0.726	0.500	0.481	0.454
		0.25	0.720	0.638	0.595	0.720	0.653	0.627	0.439	0.425	0.395
		0.5	0.566	0.505	0.418	0.562	0.534	0.482	0.326	0.320	0.228
0.5	100	0	0.614	0.360	0.316	0.638	0.379	0.358	0.355	0.187	0.195
		0.25	0.495	0.292	0.250	0.501	0.322	0.297	0.299	0.177	0.161
		0.5	0.347	0.238	0.148	0.350	0.246	0.199	0.213	0.140	0.101
	200	0	0.900	0.735	0.682	0.907	0.746	0.729	0.607	0.446	0.436
		0.25	0.796	0.626	0.589	0.795	0.636	0.614	0.521	0.399	0.369
		0.5	0.630	0.498	0.410	0.627	0.512	0.462	0.447	0.307	0.252

In summary, the proposed pseudo-value approach works properly for independent and dependent data. In particular, it controls Type I error a lot better and has higher power than the other two methods for dependent data. In addition, the proposed method appears to work very well even when some of the survival distributions or censoring distributions are different from the others.

4. Example

The data we considered were collected by the Center for International Blood and Marrow Transplant Research (CIBMTR) [12] and consisted of pediatric patients (< 18 years) with myelodysplastic syndrome undergoing a first allogeneic transplantation from 1993 to 2006. We limited the data to patients with advanced disease status in this example. The study population consisted of 1609 patients at 53 transplant centers. The center size was from 6 to 216 patients and the overall censoring rate was 50%. The data were correlated because a significant center effect (p-value = 0.007) on disease-free survival (DFS) rates was found using the random effect score test of [13]. To test the equality of survival medians, we examined two cases: donor groups and disease groups. Although we found that the choice of the working correlation matrix made little difference in the results under our simulation setting, three working correlation matrices were examined to choose a working correlation matrix based on the quasi-likelihood under the independence model criterion (QIC) [14]: the unstructured correlation matrix, the exchangeable correlation matrix, and the independence correlation matrix.

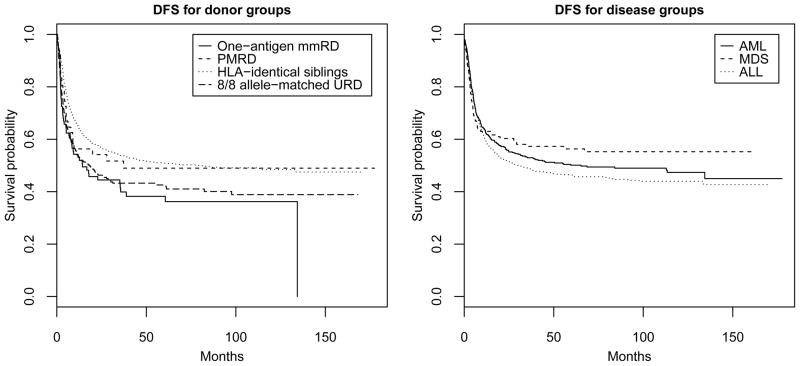
For the donor groups, we considered four donor groups: 97 patients with one-antigen mismatched related donors (mmRD), 51 patients with phenotypically matched nonsibling related donors (PMRD), 1197 patients with human leukocyte antigen (HLA) identical sibling donors, 264 patients with 8/8 allele-matched unrelated donors (URD). The censoring rates of mmRD, PMRD, HLA identical sibling donors, and URD were 42%, 51%, 52%, and 42%, respectively. The left plot of Figure 1 shows the Kaplan-Meier disease-free survival curves of the four donor groups. The DFS distributions of the four groups were different based on [15] (p-value = 0.0001). The estimated survival medians of mmRD, PMRD, HLA identical sibling donors, and URD were 14.2, 27.9, 78.9, and 17.6 months, respectively. It appears that the survival medians of some of the four groups are different. The p-values of the Brookmeyer-Crowley test and [3] are 0.107 and 0.513, respectively. For the pseudo-value approach, the independence working correlation matrix was chosen by QIC. The pseudo-value approach found a significant difference within the four donor groups with p-value 0.004.

Figure 1.

Disease-free survival rates for donor groups and disease groups

To compare different disease groups, we further limited the data to three disease groups: 553 patients with acute myeloid leukemia (AML), 756 patients with acute lymphoblastic leukemia (ALL), and 156 patients with myelodysplastic syndrome (MDS). The censoring rates of AML, ALL, and MDS were 52%, 57%, and 47%, respectively. The right plot of Figure 1 shows the Kaplan-Meier disease-free survival curves of the three disease groups. The estimated survival medians of AML and ALL were 60 and 29 months, respectively. The estimated survival median of MDS did not exist. Although the DFS distributions of the three groups were not different based on [15] (p-value = 0.120), the survival medians of the three disease groups appear to be different to each other. Because the estimated survival median of the MDS group did not exist, [3] was not applicable. The p-value of the Brookmeyer-Crowley test is 0.060. The exchangeable working correlation matrix was selected by QIC for the pseudo-value approach. The pseudo-value approach found a significant difference with p-value 0.031 at the significance level 0.05.

5. Conclusion

We proposed the pseudo-value approach to test survival medians for independent and dependent data. The simulation study showed that the pseudo-value approach performed equivalently to the Brookmeyer-Crowley test and [3] for independent data. For dependent data, the existing methods ignoring dependency were found to be too conservative. However, the pseudo-value approach controlled Type I error satisfactorily and had higher power than the two existing methods for dependent data. Although this paper focuses on the inference of survival median, the proposed method can be readily applied to other survival quantiles. Choosing an appropriate working correlation matrix may improve the performance of the pseudo-value approach [6]. We selected a working correlation matrix by QIC in the example. It may be interesting to investigate whether the working correlation matrix selected by QIC or other criteria such as the correlation information criterion [16] improves the performance of the pseudo-value approach. Exploring a pseudo-value approach for testing the equality of quantiles of cumulative incidence rates for competing risks data may also be an interesting future research question.