Persistent Inter-Excitonic Quantum Coherence in CdSe Quantum Dots

Abstract

The creation and manipulation of quantum superpositions is a fundamental goal for the development of materials with novel optoelectronic properties. In this letter, we report persistent (~80 fs lifetime) quantum coherence between the 1S and 1P excitonic states in zinc-blende colloidal CdSe quantum dots at room temperature, measured using Two-Dimensional Electronic Spectroscopy. We demonstrate that this quantum coherence manifests as an intradot phenomenon, the frequency of which depends on the size of the dot excited within the ensemble of QDs. We model the lifetime of the coherence and demonstrate that correlated interexcitonic fluctuations preserve relative phase between excitonic states. These observations suggest an avenue for engineering long-lived interexcitonic quantum coherence in colloidal quantum dots.

Zero-dimensional semiconductor nanocrystals, or quantum dots (QDs), have size-tunable quantum states that permit the development of useful optoelectronic properties.^1–2 QDs already contribute to imaging,^3–5 quantum information,^6–7 and electronic^8–9 technologies. Quantum confinement in these systems creates discrete, well-separated electron and hole states, shifting the band-edge photoluminescence and establishing distinct absorption features corresponding to specific excitonic states.^10–11 These states can be individually optically addressed, resulting in different dynamic nonlinear responses to excitation.^12–14

Recently, inter-excitonic quantum coherence was reported between the two lowest lying excitonic states in a room temperature QD ensemble.¹⁵ In these two excitonic states, the electron resides its lowest excited state while the hole is in its lowest energy or second lowest energy state. This coherence persisted with a dephasing time of 15 fs, the measurement was perhaps limited by ultrafast charge carrier relaxation due to the high density of states within the hole band or by inhomogeneous, ensemble sources of dephasing.^16–17 Inter-excitonic quantum coherence has been implicated in enhancing energy transfer,^18–21 singlet fission,^22–23 multiple exciton generation,^24–26 and as a platform for quantum information.^{7, 9, 27–31} Creation and optimization of quantum superpositions is desirable for technological applications, and for understanding the fundamental optoelectronic properties of QDs.

In this letter we report direct signatures of quantum coherence between the bandedge excitons and the first excited electron state, probed using continuum two-dimensional electronic spectroscopy (C-2DES). This coherence manifests as discrete, high amplitude oscillations in two-dimensional spectra, which persist for ~80fs. We use “persistent” to describe this coherence because it has a longer lifetime than the ground-excited state coherence as defined by the homogenous linewidth. This relatively long lifetime permits a detailed analysis of this signal using its location on the 2D spectrum, its beat frequency, and its corresponding decay rate. By analyzing a 10% polydisperse sample, we identify coherent oscillations within an ensemble of quantum dots, with distinct size-dependent signatures. Analyzing these beat signatures, we ascertain if the coherence is excitonic or vibrational in nature and develop a simple model which describes the lifetime of the coherence. This model illustrates that intradot correlated fluctuations may maintain relative phase between excited states, and suggests that dephasing is dominated by charge-carrier relaxation. We estimate a cross-correlation coefficient of between 0.89 and 0.99, and finish by discussing how intradot coherence among electronic excited states may be optimized.

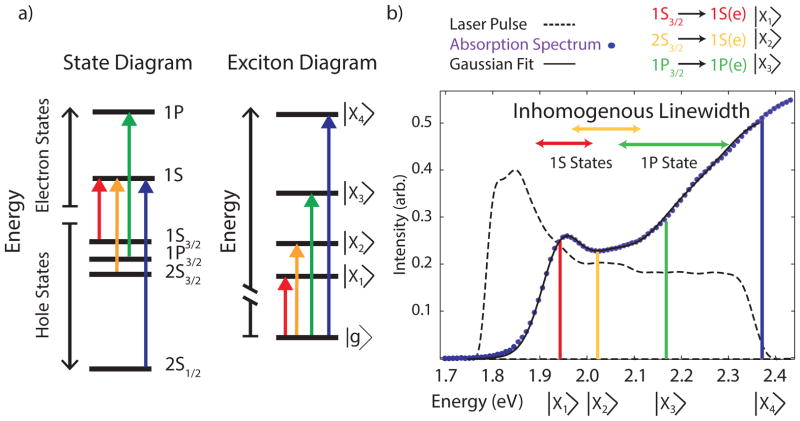
A sample of oleic acid stabilized zinc-blende CdSe QDs (r=3.0±0.3nm) was synthesized following the procedure of Chen et al.³² and characterized using transmission electron microscopy and powder x-ray diffraction (see supporting information and figure S1a and S1b). We study zinc-blende QDs to limit the influence of disorder from excitonic fine structure brought about by crystal field splitting.¹⁰ In figure 1a, we show the first four excitonic states probed in this experiment, and in figure 1b, we plot the absorption spectrum of the sample. We fit this spectrum to a sum of five Gaussians (figure S2), representing the first five excitonic transitions, with energies consistent with previous assignments for dots of this size and comparable to more monodisperse dot preparations.^33–35 The spectrum of the laser pulse overlaps primarily with the first three excitonic features. During optical excitation, an electron is excited to the conduction band, leaving a corresponding hole in the valence band. These features are defined according to the hole (h) and electron (e) excited state that is populated, and labeled |X₁> to |X₄> according to previous conventions as shown in figure 1a.^{1, 35–38} Many theoretical methods have been used to characterize QD excitonic states.^{10–11, 39–40} The simplest approximation, the effective mass model, describes each state with a principle quantum number (1, 2, 3…), an orbital angular quantum number (S, P, D…), and an overall angular moment (3/2, ½).⁴¹ We label the lowest lying, band-edge exciton 1S_3/2(h)→1S(e), |X₁>, followed by 2S_3/2(h)→1S(e), |X₂>, which differs only by the hole state excited. For simplicity, we collectively refer to these states by their electronic character, as 1S. The next transition, 1P_3/2(h)→1P(e), or |X₃>, creates a new electron-hole pair in states that have different angular momentum, which we collectively refer to as 1P. The other 1P states are out of the laser bandwidth. The highest energy excited state likely represents the split-off band, 2S_1/2(h)→1S(e), or |X₄>, though we could not obtain reliable fits of the higher energy states for this ensemble.

Figure 1.

a) We illustrate the QD states and their corresponding exciton transitions probed in this experiment. The first four hole states and first two electron states become the first four dipole allowed transitions. b) Absorption spectrum for zinc-blende CdSe quantum dots, fit to a five-Gaussian function, plotted alongside the laser pulse spectrum. We emphasize the three lowest energy transitions, for which we plot the approximate inhomogeneous linewidths given by equation 2. The 1S states (|X₁>and |X₂>) show some overlap, with separation from the 1P (|X₃>) state. The inhomogeneous linewidth is not centered over the transition, due to the skewed Gaussian described by equation 1.

Both homogenous and inhomogeneous broadening influence discrete features in QD absorption spectra. For example, QDs interact with phonons, ligands and the solvent environment, which leads to pure dephasing of coherence as individual QDs undergo significant fluctuations and relaxation on the time scale of measurement.^42–45 These same interactions also drive charge carrier relaxation which homogenously broadens higher energy features. Furthermore, near the band-edge, charge carriers relax via different mechanisms, with holes displaying size-independent phonon assisted relaxation, while electrons showing size-dependent auger-like energy dissipation via electron-hole correlated motion.^{12, 39, 46}

QDs also display significant static inhomogeneity arising from size and shape polydispersity and unresolved excitonic fine structure.⁴⁷ We can model size inhomogeneity using the particle in a spherical potential model, which neglects valence and conduction band mixing, and overall angular momentum, but captures the effect of polydispersity in particle lineshapes.^{10, 41} If we know the central transition energy for a given state (from prior fitting), the distribution of energies for that state as a function of a Gaussian distribution of radii is given by

$$P(E)=exp\left(-\frac{r_0^2{\left(\sqrt{\mathrm{\Delta }{E}_a/E}-1\right)}^2}{2{\sigma }^2}\right),$$ (1)

where r₀ and σ are the mean and the standard deviation of the particle radius distribution, respectively, and ΔE_a is the difference between the exciton energy and the bulk material band gap. Equation 1 results in a skewed Gaussian inhomogeneous lineshape for a Gaussian distribution of particles. We express the full width half maximum (FWHM) of each statein equation 2, similar to an expression derived by others:⁴⁸

$$\mathit{FWHM}=2\sqrt{2log2}\frac{2\mathrm{\Delta }{E}_a{r}_0^3\sigma }{{\left(a_0^2-2log(2){\sigma }^2\right)}^2}.$$ (2)

Within this model, both the energy of a state above the band-edge and the particle size distribution contribute to ensemble lineshape. Put simply, larger particles have more closely spaced excitonic states than smaller particles, which leads to concomitant effects on ensemble lineshapes, with higher energy states showing far broader inhomogeneous linewidths than lower energy states. This relationship has been confirmed experimentally in size-dependent studies of QD state energies.^35–36 We plot the estimated inhomogeneous linewidth from equation 3 for the first three states in our ensemble of QDs in figure 1, above the absorption spectrum. The two band-edge 1S states show considerable overlap, while the third 1P state is well resolved despite displaying twice the width of the bandedge exciton. In accordance with the particle in a sphere model, large dots have smaller energy gaps between states than small dots. Excitonic coherences induce waiting time-domain oscillations in 2D spectra, at a frequency difference equal to the energy gap between two states; thus, larger dots will result in slower oscillations compared to smaller dots.

In this work, we use 2DES to probe beneath the inhomogeneous lineshape and to resolve particle size dependent signatures of excitonic coherence. 2DES has been extensively reviewed elsewhere, and has recently been applied to study quantum dot dynamics.^{15, 49–52} In this paper we use a variant of 2DES, C-2DES, which utilizes ultrafast filament generation in argon to generate broadband, stable “white” light (0.5% std/mean measured at 10 Hz) as an excitation and probe field. We describe the details of the C-2DES apparatus elsewhere and show a schematic of the apparatus in the supporting information (figure S3).⁵³ We compress the spectral region from 520 to 700nm to sub-10fs pulses, using Multiphoton Intrapulse Interference Phase Scan (MIIPS) with a spatial light modulator; pulse duration is confirmed using transient grating frequency resolved optical gating (figure S4).^54–55 Using beamsplitters, we then create three pulses. Time delays between pulses are systematically varied to generate 2D spectra.^56–59 The evolution of the system during the time, τ, between the first two pulses can be Fourier transformed to determine the energy of the input (the “Coherence Energy” domain). The system then evolves unperturbed as an excited- or ground-state population or as a coherence for a waiting time, T. The third pulse probes the system driving subsequent emission in a phase matched direction that is heterodyned with a local oscillator pulse and spectrally resolved (defining the “Probe Energy” axis). In a typical experiment, signal is collected for τ ranging from −60 to 80 fs, and 2D spectra are measured for T =0 fs to 1000 fs in 5 fs steps (data processing methodology discussed in the supporting information and shown in figure S5). The dynamics during T reflect both relaxation of charge carriers (leading to exponential growth or decrease in signals) and oscillatory dynamics, arising from phonon and electronic superposition states. Using rephasing (τ>0) and non-rephasing signals (τ<0), we can assign features in 2D spectra to ground state bleach, stimulated emission from the excited state, and induced excited state absorption, which represents bi-excitonic features, in analogy to transient absorption measurements.^{15, 60–62} To assign phase to these features, we fit the 2D spectrum to separately collected pump-probe in accordance with the projection slice theorem.^{58, 63} In this work, we focus on coherent dynamics, which appear both in the real (absorptive) 2D spectrum as well as absolute magnitude spectra. All experiments were repeated several times with similar results. We show a replicate trace in figure S6 of the supporting information.

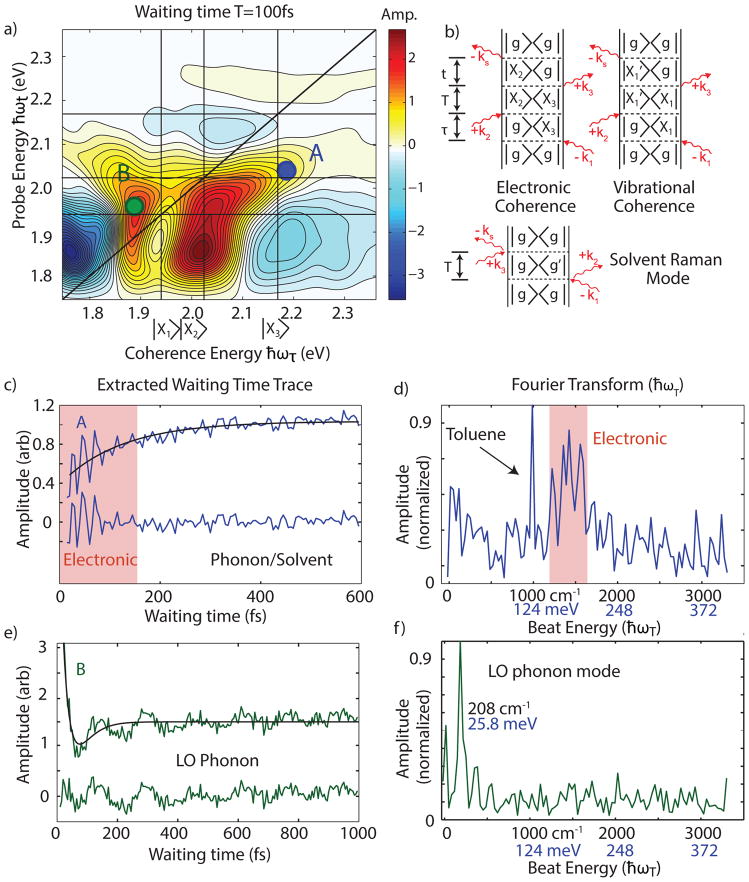
By resolving the excitation frequency, 2DES excels at probing coherent signatures.^{18, 51, 64–72} In figure 2a, we show a typical broadband two-dimensional spectrum of CdSe quantum dots taken at T = 100 fs (additional spectra in figure S7). In this publication, we focus on the coherent dynamics of the 1P/1S crosspeak below the diagonal. This feature appears as the 1P state relaxes to the band-edge.^{12, 46} Briefly, we observe the SE feature grow on a time scale of approximately 167 fs (when the center of the feature is probed) consistent with previous measurements of Auger-like 1P to 1S charge-carrier relaxation for particles of this size.^{12, 46, 73} The recovered time scale provides an estimate of the size-dependent Auger recombination rate that we will use in our model below. Below this feature, we observe a negative signal that we assign to excited state absorption into biexciton states, redshifted and enhanced by increased surface trapping of hot carriers during Auger-like relaxation, similar to signals reported in state-resolved TA measurements.^74–75 The lineshape, and its incoherent dynamics are the topic of a separate manuscript.⁷⁶

Figure 2.

a) Two dimensional spectrum, with A representing the 1P/1S crosspeak, and B highlighting the band-edge feature. b) Feynman diagrams representing stimulated emission coherent oscillatory (rephasing τ>0) contributions to the signal, and coherent solvent response. The arrows represent electric field interactions, which interact with the density matrix of the ensemble. Coherences are off-diagonal elements of the density matrix, which during waiting time create oscillatory signals in 2D spectra. c) We plot the raw signal from A and the residual upon subtraction of a two fit exponentials representing population dynamics during waiting time. This shows large amplitude early time coherent response, followed by smaller amplitude oscillatory signals. d) A Fourier transform of the residual signal showing a broad peak centered at 1500 cm⁻¹, assigned in this work to electronic coherence and a narrow peak near 1000 cm⁻¹ which we assign to the dominant Raman active mode in toluene. We attribute the apparent structure underneath the electronic coherence to additional solvent modes or to experimental noise. e) and f) show the same analysis as c) and d) for the band edge feature B, which oscillates with the longitudinal optical phonon mode.

Double sided Feynman diagrams in Figure 2b show three sources of coherent dynamics in these QDs.^{64, 77} The first diagram describes an electronic coherence in which oscillations arise from direct excitation of a coherent superposition of two excitonic states. These coherences result in oscillations in the amplitude of the 2D spectrum at the spectral coordinates corresponding to excitation into |X₃> and emission from |X₂> as waiting time increases. The oscillation frequency corresponds to the energy difference between the two excitonic states. The second diagram describes vibrational coherences, where a coherent phonon mode modulates the energy gap between electronic states participating in optical excitation. Distinguishing between electronic and vibrational quantum coherences in QDs is much simpler than in molecular or supramolecular systems. Unlike the 3N-6 vibrational modes in a molecule, QDs have a sparser vibrational manifold. The longitudinal optical phonon mode modulates the energy gaps with a frequency of 209 cm⁻¹ in CdSe, and the only other accessible modes are much lower frequency acoustic modes.^{13, 47, 78} Finally, non-resonant solvent signal modulates the overall signal via vibrationally activated optical Kerr effect and also contributes to the 2D signal.^79–80

We observe these three oscillatory signals in 2DES of quantum dots. In figure 2c, we show an extracted waiting time trace from the real part of the 2DES spectrum over the 1P/1S stimulated emission crosspeak (feature A). The signal shows clear biphasic signatures, a large early time oscillatory response for the first 175 fs (~25% of the total signal) followed by a persistent lower amplitude oscillation. We fit this trace to two exponentials to eliminate waiting time dynamics, and then we Fourier Transform (FT) the residual signal. Figure 2d shows that the high amplitude early time signal corresponds to a frequency response around 1500 cm⁻¹ while the low-amplitude oscillations signals manifests in the FT as a narrow peak at 990 cm⁻¹, consistent with the strongest Raman active mode in toluene.⁸¹ Figures 2e and 2f show trace B from the band-edge feature, illustrating modulation consistent with a longitudinal optical phonon mode at 26 meV, but no clear high-frequency features. The differential signatures of longitudinal optical phonon modes are consistent with previous models which show that the 1P state has significantly weaker coupling to the longitudinal optical phonon mode than the 1S state.¹³

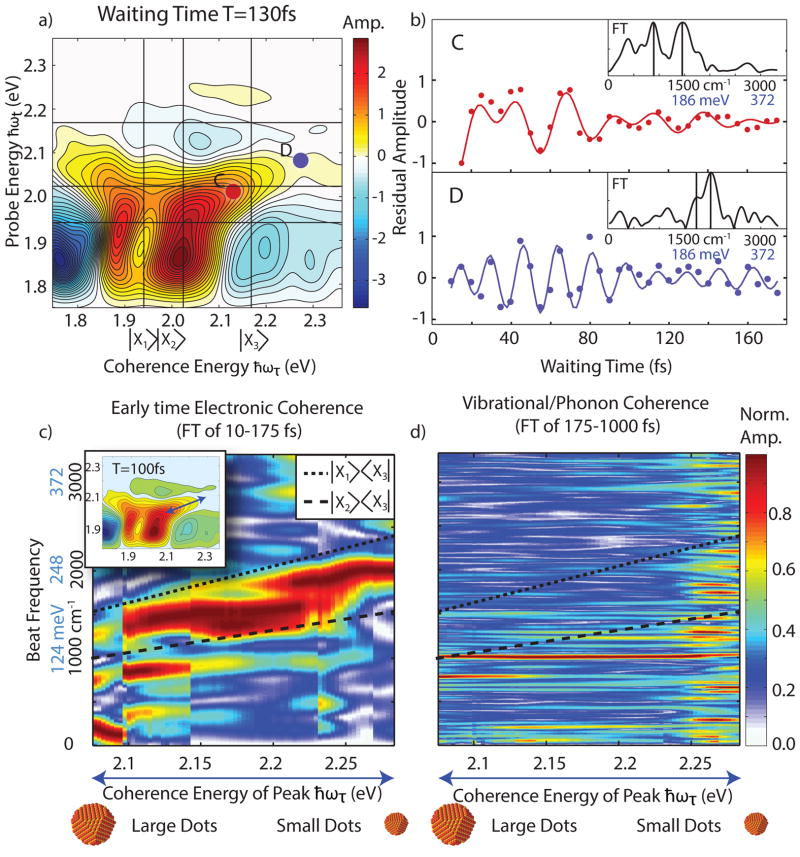
In figure 3, we focus on the early time coherent dynamics of the 1P/1S crosspeak. In figure 3a we show a 2D spectrum from T=130fs, from which we examine two points across the inhomogeneous lineshape of the 1P/1S stimulated emission feature as shown. On the right, we plot the time domain oscillations for the first 175 fs. Similar to previous methods, we fit this oscillation to two exponentially decay sinusoids according the following equation^{15, 82–83}:

$$S(T)=\sum _{n=1}^2{a}_{n}exp\left(-\frac{T}{T_n}\right)sin\left({\omega }_{n}T+{\varphi }_n\right),$$ (3)

Figure 3.

a) 2D spectrum taken from T=130 fs, highlight two regions across the inhomogeneous bandwidth of the 1P/1S SE feature. b) We plot the first 175 fs of the time domain of this feature (solid circles) after exponential subtraction. The solid lines represent the fit to equation 3. In the inset, we plot the Fourier transform of the early time signal, along with two lines represent the dominant fit frequencies. As can be observed, lower frequency oscillations dominate at C vs. higher frequencies at D. We show the parameters of each fit table 1. c) We plot the Fourier spectrum of the residual early waiting time data for the entire inhomogeneous bandwidth of the 1P/1S stimulated emission crosspeak, normalized to each individual FT. Due to changes in phase in the oscillatory signal, vertical discontinuities arise from different exponential best-fit lines. The double-sided arrows in the inset show the region from which we extract the oscillatory signals. We observe a continuous increase in beating frequency ranging from 1300 cm⁻¹ to 2000 cm⁻¹. We overlay the expected energy differences between the 1P and 1S states (|X₃>/|X₂> and |X₃>/|X₁>) across the range of particle sizes in our preparation of QDs (dashed lines). d) We plot the same signal, for the residual trace from 175–1000fs, which shows little difference across the feature, illustrating coherent vibrational and phonon signatures.

We plot the results of this fit in figure 3b, illustrating that the signal is well modeled by equation 3. In table 1, we show the frequencies and decay rates observed. In the insets of figure 3b, we show an FT of the early time data with lines at the dominant fit frequencies to show how the fit conforms to the FT. The fit and the FT demonstrate that at point C, we observe lower frequency signals than at point D, with both showing decay rates on the order of 80 fs. We assign the lowest frequency feature in trace C (ω₂) to the previously discussed toluene mode.

Table 1.

Parameters Derived from Fitting Equations 3 and 4 for Early Time Oscillations from the 1P/1S Crosspeak.

	Amplitude	Frequency	Lifetime	Correlation factor a
C	a1=1.0 ± 0.27b	ω1=1,440 ± 25 cm−1	T1=70 ± 23 fs	C1= 0.97 (0.94 –0.983)
	a2=1.1 ± 0.30c	ω2=946 ± 32c	T2=55 ± 17c	Null
D	a1=0.6 ± 0.29	ω1=1,704 ± 36	T1=85 ± 50	C1=0.97(0.89 –0.99)
	a2=−1.0 ± 0.27	ω2=2,019 ± 20	T2=97 ± 36	C2=0.98 (0.96 –0.99)

^aThe degree of correlation (C) is approximated by fitting equation 4 to reproduce the decay rate estimated by the fit as discussed in the text. The numbers in parentheses represent the correlation needed to reproduce the low and high range for the decay rate.

^bErrors reported are standard deviations for experimental fits.

^cWe assign ω₂ from feature C to a non-resonant toluene solvent mode.

In figure 3c, we present the Fourier transforms of early waiting time data extracted across the 1P/1S SE feature. The dominant frequency varies continuously between 1300 cm⁻¹ and 2000 cm⁻¹ and is proportional to the excitation energy as we progress along this feature. Lower input coherence energies display lower frequency oscillations. We overlay the size-dependent expected energy difference between the 1P and both 1S excitonic states using the model presented in equation 2. Despite the ensemble measurement, we observe clear signatures of sub-ensemble resolved size-based heterogeneity in the coherent response, in particular the slope of the oscillatory frequency across the feature. Put simply, the red-edge of the crosspeak addresses larger dots, which have smaller difference energies, while the blue-edge addresses smaller dots in the ensemble. Thus, the oscillatory signals can be identified as intradot electronic superpositions. Due to limited resolution in time, we cannot conclusively assign the coherence to a specific 1S state, as both appear to contribute to the overall signal. We also plot the FT of the same feature from 175–1000 fs in figure 3d, which shows no coherence energy dependent response, as expected for vibrational coherences.^{72, 84} Finally, in figure S8 we show early time traces taken from the magnitude only spectrum to show that the result does not arise from phasing error; we also plot the analogous upper diagonal feature for nonrephasing, rephasing and combined pathways, showing signals consistent with electronic coherence using the method described by Turner et al.^{15, 72} Thus, the frequency, spectral character, position on the 2D spectrum, and time-domain response allow us to assign the early time oscillation to the presence of a superposition between 1S and 1P excitonic states inside an individual quantum dot.

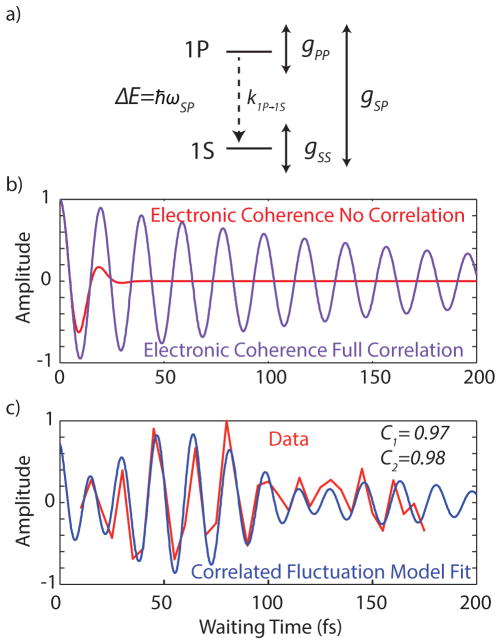
The lifetime of a coherence measures the persistence of relative phase between these states, informing on perturbations to that phase by fluctuations of the constituent energy levels and electronic relaxation.^85–89 It is not surprising that excitonic states fluctuate relative to one another in a manner quite distinct from the ground state.⁹⁰ This effect has been observed in photosynthetic systems, small molecules and polymers.^{18, 91–94} We can understand the coherence lifetime (measured to be ~80fs) between two states, 1S and 1P, using a simple model (shown in figure 4a) which considers fluctuations and relaxation as follows:⁹⁵

Figure 4.

a) A representation of the terms from equation 4; ω_SP represents the energy difference between states, k_1P→1S is the rate of relaxation, g_SS and g_PP are the lineshape functions which represent the fluctuations of each state, and g_SP describes degree to which those fluctuations are shared (or correlated). b) Two extreme cases, where the fluctuations are completely uncorrelated (leading to dephasing on a 10 fs time scale, or completely correlated, leading to dephasing only from population relaxation. c) Data from point D from figure 3, which shows two frequencies, for which we fit the model described in supporting information, given known lineshape parameters. The fit shows a high degree of correlation (C=0.97 or C=0.98 for the two observed modes, respectively) is needed to reproduce the observed excitonic lifetimes.

$${\rho }_{SP}(T)\infty \langle exp[i{\omega }_{SP}T-g_{SS}(T)-g_{PP}(T)+2Re(g_{SP}(T))-(k_{1P->1S}+k_r+k_{nr})T]\rangle$$ (4)

Here, the evolution of the off diagonal element of the density matrix ρ_SP(T) is defined by an oscillatory component (ω_SP) which modulates the signal at the energy difference between 1S and 1P, and several processes which dephase this coherence. We describe fluctuations via the lineshape function for each individual state, (g_SS and g_PP) which dephase the coherence.^96–97 Population relaxation from state P to state S also eliminates coherence and is represented by a rate k_1P→1S. The radiative and nonradiative (k_r and k_nr) rates which goveren 1S relaxation to the ground state are much slower (10–100ns timescale) than population relaxation rate and can be ignored.⁹⁸ The correlation between excitons, described by g_SP, increases the coherent lifetime due to coupling between the exciton states and a shared vibrational bath.⁹⁹

To develop a simple model to estimate the expected lifetime in QDs we make a few approximations and apply them to equation 4. First, we assume that g_SS = g_PP and used previously measured photon echo peaks shift measurements^{44, 100} to estimate homogenous linewidth. We then model the shared correlation as C•2•g_SS, where C represents the correlation of fluctuations in both states due to coupling between the excitons and a shared bath. The expected signal within this model is given by:

$$S(T)=A_{n}exp[i{\omega }_{n}T-2(1-C)•g_{SS}(T)-(k_{1P->1S})T+{\varphi }_n],$$ (5)

where A_n, ω_n, C, and ϕ_n are fitting parameters related to amplitude, frequency, correlation and phase, respectively. We estimate g_ss using the parameters photon echo peak shift parameters reported by Salvador et al.⁴⁴ for the largest dots measured. While these dots are not identical to those used in this experiment, they assist in providing an estimate of the overall correlation. The parameters report on a spectral density from which the lineshape can be estimated using standard methods.⁷⁷ Using the recovered relaxation time from above of 1/k_1P→1S = 167 fs,^{46, 73} we fit C and show the estimates for the range of lifetimes defined in table 1. This method allows for an examination of how C varies within the error of the liftime estimated by equation 3. Our calculation shows that near unity correlation is required to explain the measured coherence lifetimes. If we assume no correlation between sites, the homogenous linewidth dominates, leading to dephasing with a lifetime of approximately 10 fs. In a fully correlated bath, the coherence only dephases due to population relaxation with a lifetime of 167 fs. We plot these extremes, and the fitted correlation in figure 4b and 4c. We believe that due to wave-function overlap, shared fluctuations are likely an intrinsic feature in colloidal QDs, significantly increasing the lifetime of excitonic coherences. This same mechanism has been implicated in anomalously long lifetimes in photosynthetic complexes,^{85, 88} though several other explanations for long-lived coherence have emerged.^101–104 This study demonstrates, that despite homogenous linewidths of approximately 0.1 eV,^{42, 44} correlated fluctuations can significantly enhance the lifetime of quantum coherence in QDs.

Currently, charge carrier relaxation dominates the dephasing process for quantum dots. However, because 1S/1P coherence involves different electronic states, it may be possible to create far longer room temperature QC using core-shell materials. For example, Pandey and coworkers have shown that electron cooling can be significantly slowed by putting a ZnSe shell on a CdSe dot, which decreases electron-hole wavefunction overlap, slowing Auger-like charge relaxation.¹⁰⁵ One can also tune the homogenous linewidth via surface capping and passivation, with such dots showing significantly decreased homogeneous linewidths.^{45, 100} Furthermore, the lifetime reported here represents merely a lower bound for the coherence lifetime because other forms of polydispersity (shape, ligand field, etc.) will lead to ensemble-dephasing of the signal, not distinguishable in our measurement.^106–107 Analysis of more monodisperse preparations, films, and probing the temperature dependence represent avenues for future research.

In summary, we demonstrate the presence of discrete oscillatory signals representing excitonic superpositions in quantum dots between the 1S and 1P states. These signals can be distinguished from other oscillatory signals (such as the longitudinal optical phonon mode) via their early time response, agreement to inter-exciton size dependent frequencies and their spectral position upon excitation of 1P, and subsequently 1S states. The ability to resolve size-dependent inhomogeneity in a polydisperse solution illustrates the utility of C-2DES in resolving in-ensemble heterogeneity. We conclude that the persistent quantum coherence observed requires significant correlation in the fluctuations of each excitonic state.