Abstract
Availability of multi-modal magnetic resonance image (MRI) databases opens up the opportunity to synthesize different MRI contrasts without actually acquiring the images. In theory such synthetic images have the potential to reduce the amount of acquisitions to perform certain analyses. However, to what extent they can substitute real acquisitions in the respective analyses is an open question. In this study, we used a synthesis method based on patch matching to test whether synthetic images can be useful in segmentation and inter-modality cross-subject registration of brain MRI. Thirty-nine T1 scans with 36 manually labeled structures of interest were used in the registration and segmentation of eight proton density (PD) scans, for which ground truth T1 data were also available. The results show that synthesized T1 contrast can considerably enhance the quality of non-linear registration compared with using the original PD data, and it is only marginally worse than using the original T1 scans. In segmentation, the relative improvement with respect to using the PD is smaller, but still statistically significant.
1 Introduction
Synthesizing MRI contrasts is a computational technique that modifies the intensities of a MRI scan in such a way that it seems to have been acquired with a different protocol. It finds application in several areas of neuroimaging. For example, in multi-site studies, an ideal synthesis method would have (in principle) the potential of making it possible to combine scans from different scanner manufacturers in the analysis without affecting the statistical power to detect population differences [1]. Contrast synthesis can also be used in segmentation: many publicly available methods (especially those based on machine learning, e.g. [2]) are MRI contrast specific and rely on absolute voxel intensities. Synthesis allows us to apply them to data with other types of MRI contrast [3].
Synthesis also has potential benefits for cross-modality image registration, for which metrics based on mutual information (MI) are typically used [4]. While MI suffices to linearly register data, it often fails in the nonlinear case when the number of degrees of freedom of the transform is high. On the other hand, highly flexible transforms do not represent a big problem in the intra-modality case, for which metrics such as the sum of squared differences (SSD) or normalized cross-correlation (NCC) have been proven successful [5]. Synthesis can be used to convert an ill-posed inter-modality registration problem into an intra-modality problem that is easier to solve, as recently shown in [6] for microscopic images.
Previous work in synthetic MRI can be classified into three major branches. The first family of approaches, such as [7], is based on the acquisition of a set of MRI scans that make it possible to infer the underlying, physical MRI parameters of the tissue (T1, PD, T2/T2*). While these parameters can be used to synthesize any arbitrary MRI contrast, data acquired with such a protocol is scarce, limiting the applicability of this approach. The second branch uses a single scan to estimate the synthetic image by optimizing a (possibly space dependent) transform that maps one MRI contrast to the other, often in conjunction with registration. The transform model can be parametric, such as [8] (a mixture of polynomials), or a non-parametric joint histogram, as in [9].
The third type of approach is exemplar-based. The underlying principle is to use a pre-acquired database of images from different subjects, for which two modalities are available: source, which will also be acquired for new subjects, and target, that will be synthesized. Given the source of a test subject, the target can be synthesized using patch-matching [10] or dictionary learning approaches [11, 6]. Exemplar-based approaches are particularly interesting as they do not model the imaging parameters and they naturally incorporate spatial context (i.e. neighboring voxels) in the synthesis, as opposed to applying a transform to the intensity of each voxel independently. They are extremely general and produce visually attractive results even with image databases of limited size.
While patch-based synthesis can produce results that are visually impressive, it is unclear if the synthesized images are mere “pastiches” or they can substitute real acquisitions for some tasks in multi-modal MRI analysis. To answer this question, we used a patch-matching driven, exemplar-based approach to synthesize T1 data from PD images, for which T1 images were also available. Then, we used a separate dataset of T1 scans to register and segment: 1. the PD images; 2. the synthetic T1 data; and 3. the true T1 data. These experiments allow us to quantitatively assess whether more accurate registration and segmentation can be obtained using the synthesized T1 images rather than the PD data, as well as the decrease in performance when synthesized T1 images replace the true T1 volumes. Finally, we also compare the performance of the exemplar-based approach with two intensity-transform-based synthesis techniques.
2 Patch-Based Synthesis Method
Here we use a patch-matching algorithm inspired by the methods in [12, 13] and also Image Analogies [10]. Given a source image I, the goal is to synthesize a target image S using a pre-acquired database of coupled images from N different subjects. We define an image patch centered in a spatial location x as Wd(x) = {y : ||y −x||2 ≤ d}. Our method implements patch-matching: for every x, we search the database for the patch in source modality In(Wd(y)) that best resembles I(Wd(x)). Then we use the information in the corresponding patch in target modality Sn(Wd(y)) to generate the synthesized value S(Wd(x)).
Specifically, the search for the most similar patch is formulated as:
| (1) |
This minimization problem provides an estimate for the synthesized patch as S(Wd (x)) = Sn*(Wd (y*)). Because each x is included in more than one patch, the method estimates multiple synthesized intensity values for x, one coming from each patch x is contained in. Let us denote these different estimates with SWd(x′)(x), i.e., the synthetic value at x as estimated by the patch centered in x′. Based on this, we compute the final estimate for S(x) as the average:
| (2) |
where |·| is the cardinality of the set.
The optimization in Equation 1 can be computationally expensive, considering that it needs to be solved if for each voxel x. Two simple cost reduction methods are used here. First, as done in [12], we assume that all images are linearly aligned, which allows us to restrict the search window for y as:
| (3) |
where WD(x) is a patch of size D around x. The second speed-up is to solve the minimization problem in a multi-resolution fashion using a search grid pyramid. At low resolution, a large D can be used. The found correspondences can be carried over to the higher resolution, and the search repeated with a smaller D.
3 Experiments and results
3.1 MRI data
We used two datasets in this study, one for training and one for testing. The training dataset consists of 39 T1-weighted scans acquired with a MP-RAGE sequence in a 1.5T scanner, in which 36 structures of interest were labeled by an expert rater with the protocol in [14]. We note that this is the same dataset that was used to build the atlas in FreeSurfer [15]. The test dataset consists of MRI scans from eight subjects acquired with a FLASH sequence in a 1.5T scanner. Images with two different flip angles were acquired, producing PD-weighted and T1-weighted images in the same coordinate frame. The test dataset was labeled using the same protocol; the annotations were made on the T1 data in order to make them as consistent as possible with the training dataset.
The brain MRI scans were skull-stripped, bias-field corrected and affinely aligned to Talairach space with FreeSurfer. The T1 volumes (both training and test) were intensity-normalized using FreeSurfer. The PD volumes were approximately brought to a common intensity space by multiplying them by a scaling factor that matched their medians to a constant intensity value.
3.2 Experimental setup
We performed two sets of experiments to evaluate the use of synthetic MRI on registration and segmentation. For registration, we first non-linearly registered the training dataset to the test images, and then used the resulting transform to propagate the corresponding labels. The Dice overlap between the ground truth and deformed labels was used as a proxy for the quality of the registrations. To evaluate the algorithms at different levels of flexibility of the spatial transform, we considered two deformation models: one coarse and one fine. As a coarse deformation model, we used a grid of widely spaced control points (30 mm. separation) with B-spline interpolation as implemented in Elastix [16]. As a more flexible model, we used the symmetric diffeomorphic registration method implemented in ANTS [17], with Gaussian regularization (kernel width 3 mm).
Five approaches were tested in this experiment. First, registering the training data to the PD volumes using MI as a metric (computed with 32 bins); Second, registering the training data to the test T1 volumes using NCC, which works better than MI in intramodality scenarios. The output from this method represents an upper bound on the quality of the registration that can be achieved with synthetic MRI. The other three methods correspond to registering the training data to synthetic T1 volumes (generated with three different approaches) using NCC as cost function. The synthesis was carried out in a leave-one-out fashion such that, when synthesizing the T1 volume corresponding to a PD scan, the remaining seven T1-PD pairs were treated as the corresponding database.
The three contrast synthesis algorithms were: 1. the exemplar-based method described in Section 2 (patch size , i.e., 26 neighborhood, and search window size ); 2. an in-house implementation of the algorithm in [8]; and 3. an in-house implementation of [9]. In the corresponding original papers, [8] and [9] use the information from the registered image to estimate the gray level transform and the joint histogram, respectively. Instead, we compute the transforms directly from the information in the training dataset. For [8], we used the monofunctional dependendence with a ninth-order polynomial.
In the segmentation experiments, we fed the real T1 scans as well as their synthetic counterparts (computed with the same three methods) to the FreeSurfer pipeline, which produces an automated segmentation of the brain structures of interest based on an atlas built using the training dataset, i.e. 39 T1 images. As in the registration experiment, the results from the real T1 scans serve as an upper limit of the performance with the synthetic data. As another benchmark, we segmented the PD scans directly as well. Since FreeSurfer requires T1 data, we segmented the PD scans using the sequence-independent method implemented in the software package SPM [18], which is based on a statistical atlas. To make the comparison with FreeSurfer as fair as possible, we used the statistical atlas from this package in the SPM segmentation.
Both in the registration and segmentation experiments, statistical significance was assessed with paired, non-parametric tests (Wilcoxon signed rank). For a more compact presentation of results, we merged right and left labels and used only a representative subset of the 36 labeled structures in the evaluation: white matter (WM), cortex (CT), lateral ventricle (LV), thalamus (TH), caudate (CA), putamen (PT), pallidum (PA), hippocampus (HP) and amygdala (AM).
3.3 Results
Qualitative synthesis results
Figure 1 displays an axial slice of a scan from the test dataset (both in T1 and PD) along with the corresponding T1 images generated from the PD data using the three evaluated synthesis methods. The exemplar-based approach, despite introducing some minimal blurring due to the averaging, produces a visually better synthesis of the ground truth T1 data. In particular, it displays excellent robustness to noise and outliers; for instance, the vessels are interpreted as white matter by the other approaches methods while the exemplar-based method correctly maps them to dark intensities.
Fig. 1.
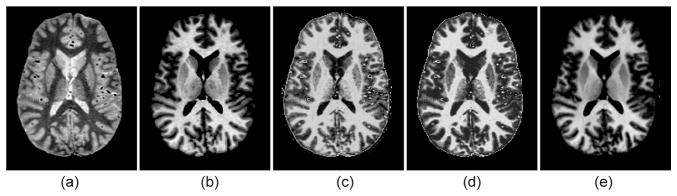
Sagittal slice of a sample MRI scan from the test dataset: (a) PD-weighted volue, (b) T1-weighted volume, (c) T1 volume synthesized from the PD data using [8], (d) synthesized with [9], (e) synthesized with the exemplar-based method.
Registration
Figure 2 show boxplots for the Dice scores achieved by the different approaches using the coarse and fine deformation models. For the coarse model, using T1 data (synthetic or real) has little impact on the accuracy for the white matter, cortex, ventricles, thalamus and caudate. However, it yields a considerable boost for the putamen, pallidum, hippocampus and amygdala. All synthesis approaches outperform directly using the PD volume in non-linear registration. The exemplar-based method produces results as good as the acquired T1, outperforming the other two synthesis approaches.
Fig. 2.
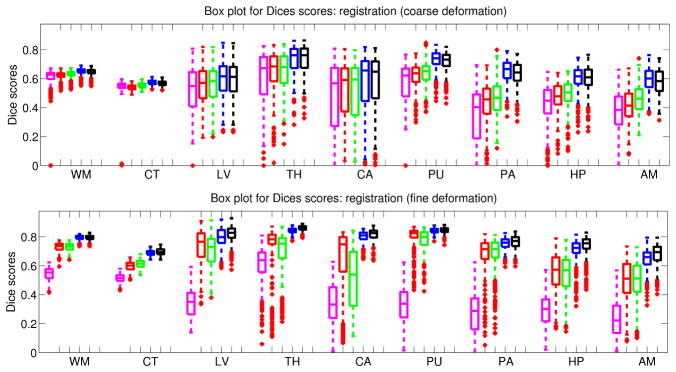
Boxplot of Dice scores in the registration experiment with the coarse (top) and symmetric diffeomorphic (bottom) deformation models. See Section 3.2 for the abbreviations. Color code: magenta = PD registered with MI, red = synthetic T1 from [8], green = synthetic T1 from [9], blue = synthetic T1 from exemplar-based approach, black = ground truth T1. Horizontal box lines indicate the three quartile values. Whiskers extend to the most extreme values within 1.5 times the interquartile range from the ends of the box. Samples beyond those points are marked with crosses. All the differences are statistically significant at p=0.001 (sample size 39 × 8 = 312).
The flexible model is more attractive in practice because it can produce much more accurate deformation fields. However, MI becomes too flexible in this scenario, making the inter-modal registration problem ill posed. Hence, direct registration of T1 to PD data produces poor results. Combining synthesis and NCC yields much higher performance. Again, the exemplar-based approach stays on par with the real T1, outperforming the other two synthesis approaches.
Segmentation
the boxplot for the Dice scores in the segmentation experiment are show in Figure 3, whereas numerical results and p-values for the statistical tests are displayed in Table 1. The decrease in performance of using exemplar-based synthetic T1 with respect to using the acquired T1 is small. However, considering that scores obtained when directly segmenting PD images are high, we conclude that the potential benefits of synthetic MRI in this application are less than in registration. Still, we note that the patch-based approach is able to significantly outperform the segmentation based on the PD data (2% increment in Dice, p = 0.04 despite the small N = 8). This suggests that improving the synthesis method has the potential to make synthesis useful for segmentation.
Fig. 3.
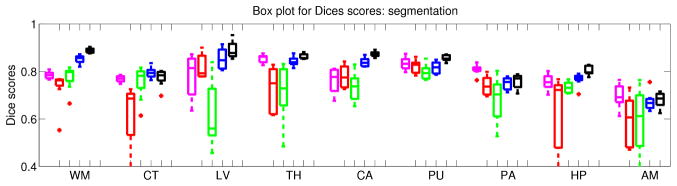
Boxplot of the Dice scores in the segmentation experiment. See caption of Figure 2 for the abbreviations and color code.
Table 1.
Mean Dice score (in %) for each method and brain structure and p-values corresponding to a comparison with the proposed approach. Note that many p-values are the same due to the non-parametric nature of the test.
| Method | WM | CT | LV | TH | CA | PT | PD | HP | AM | All combined |
|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||
| Proposed | 85.2 | 79.5 | 85.3 | 84.2 | 83.9 | 81.6 | 74.9 | 76.6 | 67.3 | 79.8 |
|
| ||||||||||
| PD data [18] | 78.4 | 76.8 | 78.1 | 85.4 | 76.2 | 83.3 | 80.7 | 75.5 | 69.7 | 78.3 |
| p-value | 7.8e-3 | 1.6e-2 | 7.8e-3 | 1.1e-1 | 7.8e-3 | 2.3e-2 | 7.8e-3 | 3.8e-1 | 3.8e-1 | 4.2e-2 |
|
| ||||||||||
| Syn. T1 [8] | 73.2 | 62.1 | 72.9 | 66.6 | 68.8 | 72.3 | 65.3 | 58.2 | 53.6 | 65.9 |
| p-value | 7.8e-3 | 7.8e-3 | 2.3e-2 | 7.8e-3 | 1.6e-2 | 9.5e-1 | 7.4e-1 | 7.8e-3 | 2.3e-2 | 4.5e-10 |
|
| ||||||||||
| Syn. T1 [9] | 77.5 | 75.7 | 61.6 | 71.3 | 66.5 | 71.2 | 63.4 | 66.2 | 55.9 | 67.7 |
| p-value | 7.8e-3 | 7.8e-3 | 7.8e-3 | 7.8e-3 | 7.8e-3 | 3.8e-1 | 2.0e-1 | 7.8e-3 | 1.1e-1 | 3.3e-11 |
|
| ||||||||||
| Real T1 | 88.8 | 77.3 | 89.0 | 86.3 | 87.3 | 85.6 | 75.8 | 80.4 | 68.0 | 82.1 |
| p-value | 7.8e-3 | 2.0e-1 | 7.8e-3 | 1.6e-2 | 7.8e-3 | 7.8e-3 | 3.1e-1 | 7.8e-3 | 6.4e-1 | 3.7e-7 |
4 Discussion
This article tried to answer the question whether synthesizing MRI contrast, in particular with the generic exemplar-based approach based on simple patch-matching, is useful in inter-modal analysis of brain MRI. Our experiments showed that exemplar-based synthesis outperforms methods based on intensity transforms. We also found that, in cross-modality registration, synthesizing a scan that resembles the moving images and using NCC as a metric produces considerably more accurate deformation fields than directly registering across modalities with MI. In segmentation, synthesizing a T1 volume and segmenting it with FreeSurfer was only marginally better than segmenting the original PD data directly. These results suggest that synthesis can be a poor man’s alternative to acquiring new images for cross-subject non-linear registration. Future work will include evaluating how synthesis affects other analyses, e.g., cortical thickness.
Acknowledgments
This research was supported by NIH NCRR (P41-RR14075), NIBIB (R01EB013565, R01EB006758), NIA (AG022381, 5R01AG008122-22), NCAM (RC1 AT005728-01), NINDS (R01 NS052585-01, 1R21NS072652-01, 1R01NS070963), Academy of Finland (133611) and TEKES (ComBrain), and was made possible by the resources provided by Shared Instrumentation Grants 1S10RR023401, 1S10RR019307, and 1S10RR023043. Additional support was provided by the NIH BNR (5U01-MH093765), part of the multi-institutional Human Connectome Project.
References
- 1.Friedman L, Stern H, Brown GG, Mathalon DH, Turner J, Glover GH, Gollub RL, Lauriello J, Lim KO, Cannon T, et al. Test–retest and between-site reliability in a multicenter fmri study. Hum brain mapp. 2007;29(8):958–972. doi: 10.1002/hbm.20440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tu Z, Narr KL, Dollár P, Dinov I, Thompson PM, Toga AW. Brain anatomical structure segmentation by hybrid discriminative/generative models. IEEE Trans Med Im. 2008;27(4):495–508. doi: 10.1109/TMI.2007.908121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Roy S, Carass A, Shiee N, Pham DL, Prince JL. IEEE Int Symp Biom Im (ISBI) IEEE; 2010. MR contrast synthesis for lesion segmentation; pp. 932–935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Maes F, Collignon A, Vandermeulen D, Marchal G, Suetens P. Multimodality image registration by maximization of mutual information. IEEE Trans Med Im. 1997;16(2):187–198. doi: 10.1109/42.563664. [DOI] [PubMed] [Google Scholar]
- 5.Klein A, Andersson J, Ardekani BA, Ashburner J, Avants B, Chiang MC, Christensen GE, Collins DL, Gee J, Hellier P, et al. Evaluation of 14 nonlinear deformation algorithms applied to human brain MRI registration. Neuroimage. 2009;46(3):786. doi: 10.1016/j.neuroimage.2008.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cao T, Zach C, Modla S, Powell D, Czymmek K, Niethammer M. Registration for correlative microscopy using image analogies. In: Dawant B, Christensen G, Fitzpatrick J, Rueckert D, editors. Biomedical Image Registration. Volume 7359 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2012. pp. 296–306. [Google Scholar]
- 7.Fischl B, Salat DH, van der Kouwe AJ, Makris N, Ségonne F, Quinn BT, Dale AM. Sequence-independent segmentation of magnetic resonance images. Neuroimage. 2004;23:S69–S84. doi: 10.1016/j.neuroimage.2004.07.016. [DOI] [PubMed] [Google Scholar]
- 8.Guimond A, Roche A, Ayache N, Meunier J. Three-dimensional multimodal brain warping using the demons algorithm and adaptive intensity corrections. IEEE Trans Med Im. 2001;20(1):58–69. doi: 10.1109/42.906425. [DOI] [PubMed] [Google Scholar]
- 9.Kroon DJ, Slump CH. Mri modalitiy transformation in demon registration. IEEE Int. Symp. Biom. Im. (ISBI); 2009. pp. 963–966. [Google Scholar]
- 10.Hertzmann A, Jacobs CE, Oliver N, Curless B, Salesin DH. Image analogies. Proc Ann Conf Comp Graph and Interac Techniques. 2001:327–340. [Google Scholar]
- 11.Roy S, Carass A, Prince J. A compressed sensing approach for MR tissue contrast synthesis. In: Szekely G, Hahn H, editors. Information Processing in Medical Imaging. Volume 6801 of Lecture Notes in Computer Science. Springer; Berlin Heidelberg: 2011. pp. 371–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Coupé P, Manjón JV, Fonov V, Pruessner J, Robles M, Collins DL. Patch-based segmentation using expert priors: Application to hippocampus and ventricle segmentation. Neuroimage. 2011;54(2):940–954. doi: 10.1016/j.neuroimage.2010.09.018. [DOI] [PubMed] [Google Scholar]
- 13.Rousseau F, Habas P, Studholme C. A supervised patch-based approach for human brain labeling. IEEE Trans Med Im. 2011;30(10):1852–1862. doi: 10.1109/TMI.2011.2156806. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Caviness V, Jr, Filipek P, Kennedy D. Magnetic resonance technology in human brain science: blueprint for a program based upon morphometry. Brain Dev. 1989;11(1):1–13. doi: 10.1016/s0387-7604(89)80002-6. [DOI] [PubMed] [Google Scholar]
- 15.Fischl B, Salat D, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale A. Whole brain segmentation: Automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33:341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- 16.Klein S, Staring M, Murphy K, Viergever M, Pluim J. Elastix: a toolbox for intensity-based medical image registration. IEEE TransMedIm. 2010;29:196–205. doi: 10.1109/TMI.2009.2035616. [DOI] [PubMed] [Google Scholar]
- 17.Avants BB, Epstein C, Grossman M, Gee JC. Symmetric diffeomorphic image registration with cross-correlation: Evaluating automated labeling of elderly and neurodegenerative brain. Med Im Anal. 2008;12(1):26–41. doi: 10.1016/j.media.2007.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ashburner J, Friston KJ. Unified segmentation. Neuroimage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]


