Hybridization gap and Fano resonance in SmB₆

Significance

Quantum entanglement may give rise to emerging phenomena and new states of matter. In the intermediate-valence material SmB₆, this is realized via hybridization between localized 4f and conduction band states that, at sufficiently low temperatures, results in the screening of the 4f local moments by the conduction electrons and produces a so-called Kondo resonance in the density of states. The latter is examined by scanning tunneling spectroscopy down to temperatures well below the Kondo temperature. This atomically resolved spectroscopy allows one to distinguish between reconstructed and pristine surfaces and different surface terminations, all of which influence the spectroscopic results. These insights are vital for other, less local spectroscopic tools in the context of possible topologically protected surface states.

Abstract

Hybridization between conduction electrons and the strongly interacting f-electrons in rare earth or actinide compounds may result in new states of matter. Depending on the exact location of the concomitant hybridization gap with respect to the Fermi energy, a heavy fermion or an insulating ground state ensues. To study this entanglement locally, we conducted scanning tunneling microscopy and spectroscopy (STS) measurements on the “Kondo insulator” SmB₆. The vast majority of surface areas investigated were reconstructed, but infrequently, patches of varying sizes of nonreconstructed Sm- or B-terminated surfaces also were found. On the smallest patches, clear indications for the hybridization gap with logarithmic temperature dependence (as expected for a Kondo system) and for intermultiplet transitions were observed. On nonreconstructed surface areas large enough for coherent cotunneling, we were able to observe clear-cut Fano resonances. Our locally resolved STS indicated considerable finite conductance on all surfaces independent of their structure, not proving but leaving open the possibility of the existence of a topologically protected surface state.

Materials with strong electron correlations continue to draw enormous attention, not only because they may give rise to fundamentally new states of matter or new phenomena but also because of the hope for advanced technological applications. Heavy fermion (HF) materials, i.e., intermetallics of certain rare earths (REs), such as Ce, Sm, and Yb, are model systems to study strong electronic correlations (1). Here, the RE-derived localized 4f states are covalently mixed with the conduction-band states and, thus, acquire a finite lifetime. The associated decay rate in relation to the energy of the localized 4f state corresponds to the valency. In an Sm-based HF system, the valence lies between 3+ (4f⁵) and 2+ (4f⁶), which implies a considerable amount of charge fluctuations. This usually is referred to as intermediate valence (2). In addition to the abovementioned mixing of states and the conduction band, which is well described within the framework of one-electron models, a many-body interaction is operating between the and conduction electrons. This “Kondo effect” (3) eventually leads to a screening of the local moments as a result of particle-hole excitations that are manifested by a narrow Abrikosov–Suhl, or Kondo, resonance at , the width of which is given by the single-ion Kondo temperature .

Because of the periodic arrangement of REs in an HF intermetallic, the Kondo resonances form a weakly dispersive HF or “coherent 4f−” band, resulting in a heavy Fermi liquid state well below . The band interaction between the renormalized 4f and the conduction band generates a so-called hybridization gap, which opens at around . Under certain conditions, may reside inside this gap, characterizing a so-called Kondo insulator (4).

SmB₆ is such a Kondo insulator, with a valence (5), ν being slightly temperature dependent (6, 7). A sharp decrease in the density of states (DOS) at is seen most dramatically in the rise of the resistance over more than three orders of magnitude below ∼40 K (8, 9). Many other measurements, including far-infrared absorption (9) and NMR (10), are consistent with the opening of an activation gap of about 3 meV. The gradual opening of a hybridization gap of about 18 meV below ∼100 K and signatures of interion correlations below ∼30 K recently were reported based on point-contact (11) and angle-resolved photoemission spectroscopy (ARPES) (12–14). However, the gap being caused by hybridization is discussed controversially. For instance, if the hybridization is altered by the application of pressure, a continuous change in the gap is expected (15, 16), although other experiments show a discontinuous change (17, 18). This is relevant because altered atomic distances at the surface (e.g., by valence changes at the surface) then also may result in a conducting surface layer. Moreover, the hybridization usually is discussed in relation to a gap of around 20 meV (11, 13, 19), whereas a thermal activation gap of around 3 meV is referred to in-gap states (9, 20, 21); the relation between the two is not clear.

Intriguingly, unlike in an insulator, the resistance of SmB₆ saturates below about 4 K (22). Recently, it was proposed (23, 24) that SmB₆ may be a strong 3D topological insulator in which the topologically nontrivial insulating state is produced by the hybridization between the conduction band and coherent 4f band. This proposal sparked a flurry of experimental attempts to demonstrate the existence of such topological surface states (25–29). However, ARPES could not unambiguously reveal (12–14, 21) the associated Dirac cones. Our focus, however, is not primarily on these topological properties of SmB₆, yet our atomically resolved surface topographies provide valuable information for nonlocal types of measurements whereas the concomitant spectroscopy indicates a finite low-temperature surface conductance independent of the surface termination.

In an effort to study the DOS, tunneling (30, 31) and point contact spectroscopy (11, 20) were conducted, most of which indicated the opening of a gap of the order of 20 meV. However, as shown below, locally (atomically) resolved information on the DOS is required and may be obtained (32) by scanning tunneling microscopy (STM) on SmB₆. For any surface-sensitive measurement, information on the surface structure is required to draw conclusions on the DOS and the hybridization. Furthermore, in Kondo systems such as SmB₆, tunneling may take place not only into the conduction band, but also into the localized 4f states. The interference of these tunneling processes may give rise to so-called Fano resonances (33–37) and thereby obscure the DOS of interest. We observed two clearly distinct types of surfaces resulting from in situ low-temperature cleavage of SmB₆: large areas of reconstructed surfaces and atomically flat terraces of nonreconstructed areas. These nonreconstructed areas may be of varying size (typically some nanometers, sometimes a few tens of nanometers) and of either B or Sm termination. Tunneling spectroscopy on the latter, nonreconstructed surfaces appears to reveal the DOS of the material within areas of a few nanometers, whereas the quantum-mechanical interference on areas of some ten nanometers yields excellent agreement with the prediction for Fano resonances. Clear indications for hybridization of the coherent 4f and the conduction band, as well as the Kondo effect, are derived in both cases. Furthermore, a finite surface conductance is observed for all types of surfaces.

Results

Topography.

Most of the investigated surfaces appear to be reconstructed, albeit in two different forms (Fig. 1 A and B). On one particular cleave, a surface reconstruction was observed, similar to the results by other groups (21, 32) (Fig. 1A). Here, the bright lines represent chains of Sm atoms on top of a B underlayer (dark). The height difference between Sm and B (i.e., between the bright and dark stripes) can be inferred from the line scan (Fig. 1D) to ∼60 pm, in agreement with the distances expected from the lattice structure (Fig. 1C). However, many of the surfaces (we estimate more than 90% of the surface areas investigated so far) exhibited much more complex topographies, as exemplified in Fig. 1B (see also Supporting Information, Optical Inspection of Cleaved Surfaces and Fig. S1). Such topographies may extend over several micrometers. Because the height difference between the two types of corrugations in Fig. 1B is similar to the one in Fig. 1A, we likewise assume that the bright lines in Fig. 1B represent chains of Sm atoms residing on top of otherwise flat B terraces; we refer to these as chain-like disordered reconstructions, in contrast to the ordered one. Both reconstructions are in good agreement with the proposal of a partly occupied Sm surface layer (38) and clearly attest the simplest solution to avoid the polarization catastrophe associated with polar surface termination planes (39). The presence of Sm and B₆ octahedra in equal amounts and their mixing on short length scales prevents the buildup of long-range electric fields from charged surface areas. Apparently, depending on the cleave conditions, a possible surface reconstruction may be ordered (Fig. 1A) or disordered (Fig. 1B). These surface reconstructions, both ordered and disordered, influence the electronic properties of these surfaces (see discussion at the end of the article). In an effort to minimize such influences, we focus our spectroscopy work on the nonreconstructed surfaces in the following; the ability to do so clearly distinguishes our work from previous tunneling (30–32), point contact (12), and nonlocal studies.

Fig. 1.

Topography overviews on reconstructed surfaces of SmB₆, V = 0.2 V, current set point I_sp = 0.6 nA. (A) reconstructed surface, scan area . (B) More complex reconstructed surface of a different sample, scan area . (C) Cubic crystal structure of SmB₆, lattice constant a = 4.133 Å. (D) Height scan along the line indicated in A. Height scales in A and B are comparable.

Only occasionally was a second type of topography observed that reflects patches of nonreconstructed surface areas. Assuming cleavage along the {001} plane through breaking interoctahedral B–B bonds (40), Fig. 2A exhibits an Sm-terminated surface. This termination is apparent when considering that the white line runs along a 〈110〉 direction; the corresponding height scan is presented in Fig. 2C: The more prominent protrusions indicate Sm atoms (marked by cyan circles in Fig. 2A) spaced about apart; the less pronounced protrusions visualize the topmost atom of the B octahedra centered between the Sm atoms along the 〈110〉 diagonal (magenta circle in Fig. 2A). In contrast, Fig. 2B shows a different area, with the white line pointing along a 〈100〉 direction. The periodicity of the corrugations agrees nicely with the lattice constant a, and no intermediate features are observed. Such surfaces are assigned as B-terminated. These assignments, and specifically the appearance of the B octahedra apex atoms between the Sm atoms, are corroborated by observations on step edges (Supporting Information, Investigation of Step Edges and Fig. S2). We note that—with only the very few exceptions discussed below—these nonreconstructed areas are only a few nanometers in extent. For two of the investigated samples, we did not succeed in finding any nonreconstructed surface areas at all.

Fig. 2.

Topography on small nonreconstructed surface areas of (A) Sm-termination (, I_sp = 0.6 nA) and (B) B-termination. Cyan circles in (A) indicate Sm atoms, the pink one encircles a B atom (compare Fig. 1). (C and D) Height scans along the white line (parallel to 〈110〉) indicated in A and the line parallel to 〈100〉 in B, respectively.

Spectroscopy.

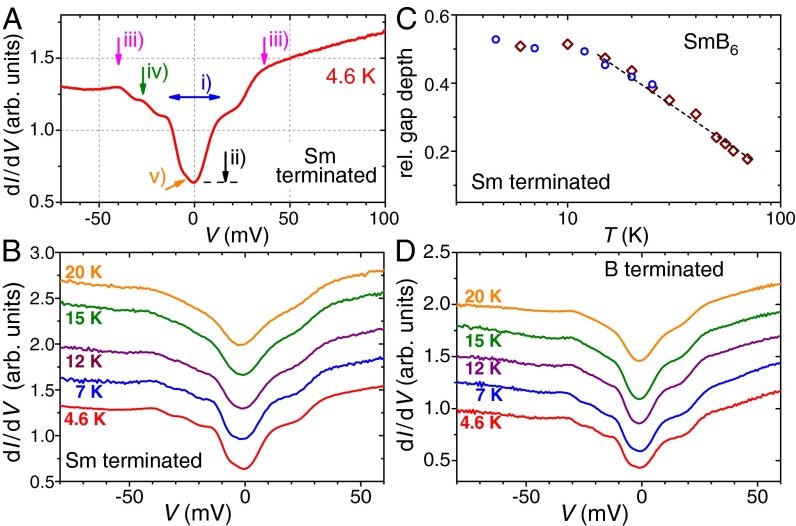
Scanning tunneling spectroscopy (STS) on the above nonreconstructed surfaces is presented in Fig. 3. The exemplary tunneling conductance of Fig. 3A obtained on an Sm-terminated surface at 4.6 K reveals several features: (i) A partial gap of ∼16 meV develops around the Fermi energy . This is consistent with the hybridization gap observed in many other measurements (11–14, 19, 32). (ii) There is a finite 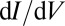-value at , i.e., a finite DOS at . This might indicate an incomplete (or pseudo-) gap, but also is compatible with an additional conductance channel at the surface. (iii) Peaks are observed at around meV. These excitations likely result from a to intermultiplet transition of the Sm²⁺ ion, as seen in neutron-scattering experiments (41). (iv) A small peak at around 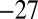meV might be related to crystalline electric field (CEF) excitations (42) between the quartet and the doublet of Sm³⁺, yet no such indications have been found so far in neutron-scattering experiments (43). If we assume a fully developed bulk hybridization gap at low T, then the CEF excitations should take place out of states close to the gap edges, yielding a CEF excitation energy of 11 meV, in line with reported values (44). (v) There seems to be an additional, broadened hump close to meV, i.e., inside the hybridization gap. One may speculate that this feature is related to in-gap states seen in other measurements (19–21, 45–47). Specifically, it is observed only for (Fig. 3B), as seen in many of those measurements.

Fig. 3.

Tunneling spectroscopy on an Sm-terminated surface. (A) Spectroscopy at 4.6 K. Features marked by arrows are discussed in the text using corresponding labels. (B) Temperature-dependent STS on an Sm-terminated surface. -curves for are offset for clarity. (C) Temperature dependence of the zero-bias dip measured on Sm-terminated surfaces of two different samples. The dashed line indicates a logarithmic T-dependence. (D) T-dependent STS on a B-terminated surface. All spectra are averaged over areas of some square nanometers. Parameters before opening the feedback loop for conducting spectroscopy: , .

The temperature evolution of these features on an Sm-terminated surface may be inferred from Fig. 3B. At 20 K, the partial hybridization gap and the intermultiplet transitions, features (i) and (iii), can barely be disentangled (see also spectra at even higher temperature; Fig. S3 in Supporting Information). To investigate the hybridization gap further, we studied the T-dependence of its depth at relative to the tunneling conductance at (Materials and Methods and Fig. S4). The T-dependent closing-up of this partial gap for two different samples is presented in Fig. 3C. The experimental values for the normalized depth of this gap agrees well with results for the single-ion conductance within numerical renormalization group calculations (48) that predict a logarithmic decay, i.e., , for T of order (dashed line). Such a logarithmic T-dependence is a hallmark of Kondo physics and supports a scenario based on the Kondo effect (4, 49). The gap has decayed to half its zero-temperature depth (50) at , in line with other estimates for the opening of the hybridization gap. Deviations from this logarithmic T-dependence due to departure from single-ion behavior, i.e., due to enhanced lattice effects of the Kondo ions, become apparent at , in a regime in which possible in-gap states also appear [feature (v)].

Temperature-dependent -curves obtained on a nonreconstructed B-terminated surface are presented in Fig. 3D. As expected, the hybridization gap exhibits behavior very similar to that on Sm-terminated surfaces. However, all other features appear to be shifted toward smaller absolute values of energy (or ). This highlights the necessity to involve spectroscopic techniques that allow discrimination between differently terminated surfaces when analyzing SmB₆ surfaces. However, the B-terminated surfaces also exhibit a finite conductance at , again compatible with an additional (surface) conductance channel.

Only very rarely did we succeed in locating larger patches of nonreconstructed areas that clearly exceed lateral dimensions of 10 nm² (so far, such patches were found on only two cleaved surfaces), as reported in ref. 51. Two such examples are shown in Fig. 4 A and B. The height scans along the white lines in Fig. 4 A and B, which are presented in Fig. 4 C and D respectively, were conducted parallel to 〈100〉 directions and confirm the expected unit–cell spacing a between the corrugations. There are no discernible intermediate corrugations at any 〈110〉 direction in Fig. 4A. However, they are obvious in Fig. 4B: The height scan along the [110] direction, blue lines marked 2 in Fig. 4 B and D, exhibits corrugations spaced by about , as in Fig. 2A. Consequently, we attribute the surface of Fig. 4A to a B-terminated one, whereas Fig. 4B represents an Sm-terminated surface. The latter surface exhibits dents of about 80 pm in depth (see blue line 2 in Fig. 4D), corresponding to the height difference between Sm and the topmost B atom on an Sm-terminated surface (compare Supporting Information, Investigation of Step Edges). This suggests that these dents are caused by missing Sm atoms, probably ripped out of the Sm surface layer while cleaving the sample. In contrast, on the B-terminated, nonreconstructed surface of Fig. 4A, there are only small height variations of some picometers, resulting in patches of a few lattice constants in extent.

Fig. 4.

Comparison between larger, nonreconstructed B-terminated (Left) and Sm-terminated surfaces (Right). (A and B) Topographies on B-surfaces and Sm-surfaces , respectively. (C and D) Height scans along the lines marked in A and B. White lines are parallel to 〈100〉 directions; blue line 2 in B and D is along 〈110〉 to enable comparison of distances between corrugations to Fig. 2A. (E and F) Tunneling spectroscopies (circles) at 4.6 K on B- and Sm-terminated surfaces, respectively. The lines are fits to the Fano formula; the obtained values of q are indicated.

Discussion

Conducting STS on such an extended nonreconstructed B surface provided -curves such as the one shown in Fig. 4E for . Clearly, such a tunneling conductance indicates a Fano resonance at energy that results from tunneling into two coupled channels (33), namely the conduction band and the 4f quasiparticle states (34, 36, 37). Likely, these nonreconstructed areas are large enough to establish coherence in the two tunneling channels; yet, it also is possible that the position in energy relative to of these two channels or the electronic structure changes accordingly (52). The resulting tunneling conductance may be expressed as (53):

Here, Γ describes the resonance width. The asymmetry parameter q is related to the ratio of probabilities for tunneling into the 4f states vs. into the conduction band as well as the particle-hole asymmetry of the conduction band (36). Eq. 1 was applied successfully to single-impurity (54, 55) as well as Kondo lattice systems (56, 57). Clearly, Eq. 1 also describes our low-temperature data excellently, even without considering details of the DOS (11). The corresponding fit (red line in Fig. 4E) yields mV, a value that agrees well with the width of the hybridization gap discussed above. As to be expected for a B-terminated surface, the value of is smaller than unity, consistent with predominant tunneling into the conduction band. Note that the asymmetry shown here is consistent with other STM measurements on a reconstructed surface (32) but opposite to results from point-contact spectroscopy (11).

An overall very similar behavior is observed for spectra obtained on an Sm-terminated surface (Fig. 4F), with the exception of two additional excitations at around 10 and 25 meV. If these two excitations are ignored, again, a good fit of Eq. 1 to the data is possible (line in Fig. 4F). The value meV thus obtained agrees with that of the B-terminated surface, as expected for the hybridization. However, indicates a more pronounced tunneling into the 4f quasiparticle states, which appears reasonable on an Sm-terminated surface. Both additional excitations also have been seen in earlier point-contact measurements in the tunneling regime (20). One may speculate that the excitation at 25 meV has its counterpart at meV at smaller nonreconstructed Sm surfaces [feature (iv) above], with the respective features at opposite voltage signs masked by other, more pronounced excitations.

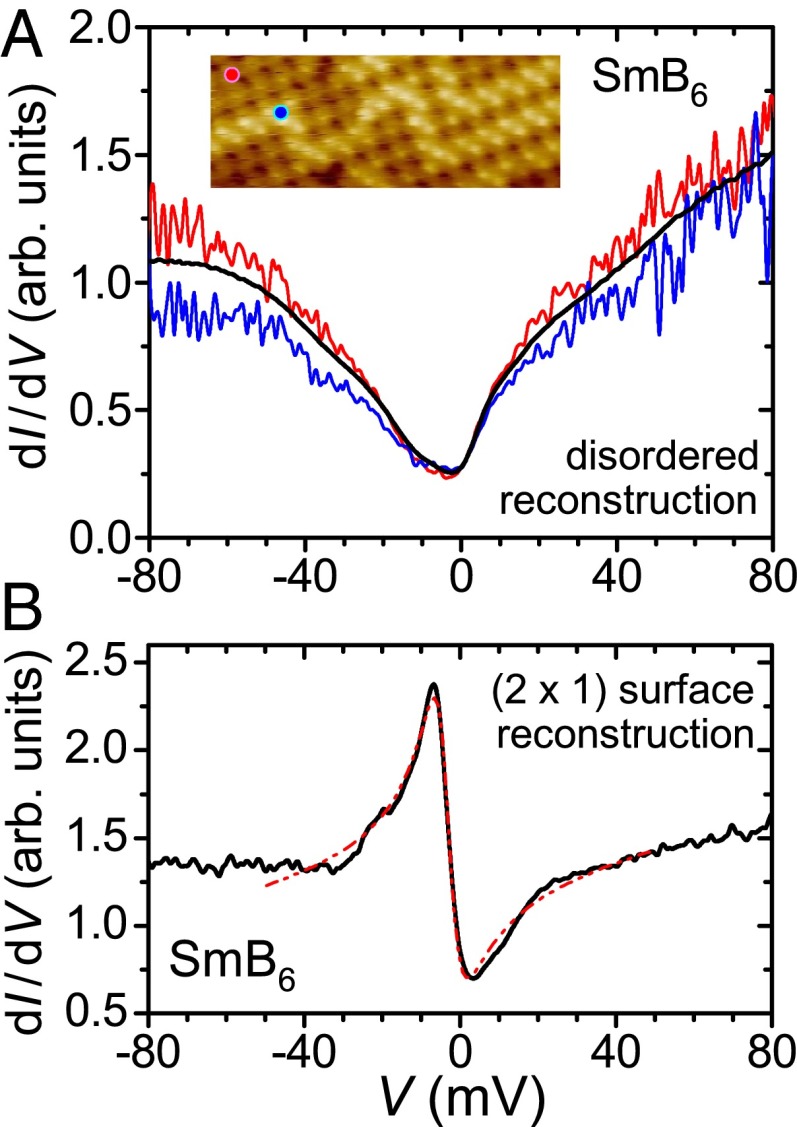
To allow comparison of the tunneling spectra on different surfaces, we also present -curves obtained on reconstructed surfaces, both disordered (Fig. 5A) and ordered [i.e., with reconstruction (Fig. 5B)]. These data were obtained at . Part of a disordered, chain-like surface reconstruction is shown in Fig. 5A, Inset. Two exemplary spectra were taken on top of the chain-like features (speculated to be Sm; blue spectrum and position marked by a blue dot in the topography image) and between these features (speculated to be B terraces; red spectrum and position marked by a red dot). No significant difference is apparent. Moreover, the area-averaged conductance curve (black curve) does not reveal any apparent feature; only a faint, broad hump might be visible at around . This finding reinforces our focus on nonreconstructed surface areas above.

Fig. 5.

Spectroscopy on differently reconstructed surfaces of SmB₆ at 4.6 K. (A) Disordered surface reconstruction as shown in Inset (area of ). The blue curve was taken on top of the chain-like features (likely Sm), the red one between those (positions marked by dots of matching color in the topography Inset). The black spectrum is an area-averaged curve with only very faint features. (B) Spectroscopy on the reconstructed surface of Fig. 1A. The red dashed line is a fit assuming a Fano resonance.

Tunneling conductance obtained within the ordered reconstructed surface shown in Fig. 1A is presented in Fig. 5B. This -curve is similar to other STS results (32) obtained on reconstructed surfaces. Furthermore, it also bears resemblance to the spectra observed on larger nonreconstructed areas (compare Fig. 4 E and F). The red dashed line again results from a fit to a Fano resonance (Eq. 1), yielding and . Clearly, this fit is of inferior quality if compared with fits performed on -curves from nonreconstructed surfaces, specifically on B-terminated surfaces.

We speculate that both surface reconstructions alter the electronic properties at the surface. In case of the disordered surface reconstruction, it may mask the bulk electronic properties. For the ordered reconstruction, we observe a clear shift in the position of the peak in the -curves to approximately mV (Fig. 5B) [in contrast to mV on both nonreconstructed surfaces: B-terminated (Fig. 4E) and Sm-terminated (Fig. 4F)]. Also, it may lead to the reduced value of Γ in the case of reconstruction. There is, of course, the possibility that a description by a Fano resonance may become inappropriate in describing the spectroscopy on the reconstructed surface. Further, one may speculate that such altered electronic properties are one contribution for the need to describe point-contact spectra (11) by a more elaborate scenario going well beyond the simple Fano resonance Eq. 1 used here. This, again, supports our focus on nonreconstructed surfaces, for which a description by a simple Fano resonance works best.

All the investigated surfaces exhibit a finite conductance at . Consequently, our locally resolved measurements show that the surface reconstruction alone cannot account for the surface conductance (51). The robustness of the measured conductance at is consistent with an additional conductance channel, possibly at the surface.

In conclusion, we observed two different types of surfaces: predominantly reconstructed surfaces but occasionally also nonreconstructed ones. For the latter, Sm- as well as B-terminations were found, but larger areas (lateral extension well beyond 10 nm) were encountered only very rarely. STS on nonreconstructed surfaces indicated the formation of a hybridization gap with logarithmic T-dependence and , as well as intermultiplet transitions of Sm²⁺ ions. Spectra on larger nonreconstructed areas showed excellent formation of Fano resonances, establishing the underlying hybridization effect. We speculate that the size of the nonreconstructed surface area is important to establish quantum interference between the two tunneling channels and, hence, Fano resonance. All SmB₆ surfaces exhibited a finite conductance consistent with the existence of a robust surface conducting layer.

Materials and Methods

Single crystals of SmB₆ were grown by using the aluminum flux method. SmB₆ crystallizes in a CaB₆ structure type with space group (221), lattice constant a = 4.133 Å. Reported here are results obtained from nine samples, cleaved in situ at approximately along one of the principal cubic crystallographic axes. STM was conducted in an ultra-high vacuum system (Omicron Nanotechnology) at and with a base temperature of 4.6 K.

The tunneling conductance spectra exhibit a partially developed hybridization gap at sufficiently low temperature. Our estimate of its depth at zero bias was based on the procedure introduced in ref. 49. The good linearity of for and is shown in an exemplary way in Fig. S4. Based on this linearity, we estimate the zero-bias conductance without the effect of a hybridization gap, , i.e., under the assumption of a fully suppressed gap, by linearly extrapolating the data for to (red dashed lines in Fig. S4). The relative gap depth—as shown in Fig. 3C—is then given by , which corresponds to the relative conductance difference between the blue (experimental) data and the red extrapolations at in Fig. S4. For temperatures , additional features were observed in , as discussed in the main text. Therefore, for the linear extrapolations only values for were considered.