Multidimensional spectroscopy of photoreactivity

Significance

Many chemical reactions typically involve ultrafast reaction steps and are highly complex. Thus, one requires special methods to observe the associated atomic movements in real time. Though conventional femtosecond spectroscopy techniques are in principle capable of providing the necessary temporal resolution, they often suffer from the fact that they cannot isolate the overlapping spectral signatures of reactants, intermediates, and products. Here we demonstrate that this issue is unraveled using 2D and 3D electronic spectroscopy that directly visualizes the photochemical connectivity between photoreactive molecular species. Hence, this approach not only provides an intuitive and direct picture for which reactants can be turned into which products, but also exposes the reactive molecular modes connecting them with unprecedented perspicuity.

Abstract

Coherent multidimensional electronic spectroscopy is commonly used to investigate photophysical phenomena such as light harvesting in photosynthesis in which the system returns back to its ground state after energy transfer. By contrast, we introduce multidimensional spectroscopy to study ultrafast photochemical processes in which the investigated molecule changes permanently. Exemplarily, the emergence in 2D and 3D spectra of a cross-peak between reactant and product reveals the cis–trans photoisomerization of merocyanine isomers. These compounds have applications in organic photovoltaics and optical data storage. Cross-peak oscillations originate from a vibrational wave packet in the electronically excited state of the photoproduct. This concept isolates the isomerization dynamics along different vibrational coordinates assigned by quantum-chemical calculations, and is applicable to determine chemical dynamics in complex photoreactive networks.

A basic objective of physical chemistry is to determine the mechanisms underlying chemical reactions. Fundamental insights into these are provided by femtosecond time-resolved spectroscopy, even below the timescale of molecular vibrations (1). The major challenge of ultrafast photochemistry is to identify isolated signatures of reactants, intermediates, and products, whose spectral bands often overlap. Here we show that such ambiguities are unraveled by coherent multidimensional electronic spectroscopy, e.g., 2D and 3D spectroscopy, where the correlation of a system’s excitation and emission frequencies is measured separating features that otherwise superpose. We detect photoreactivity directly via cross-peaks in multidimensional spectra. This opens the broad field of femtochemistry (1) to the multidimensional concept.

Two-dimensional electronic spectroscopy (2–5) was primarily implemented for studying photophysical phenomena such as energy transfer in multichromophore light-harvesting systems or other excitonically coupled systems (6–11). Recently, charge transfer has also been investigated (12, 13). Here we are interested in photochemical processes leading to ground-state product species with a molecular configuration that is different from the initial reactant. As a general extension of 2D spectroscopy, 3D representations provide an even more detailed picture. Coherent 3D spectroscopy has been introduced to infrared spectroscopy (14, 15), and recently to electronic spectroscopy for isolating excitonic coherences (16, 17), for liquid- and gas-phase model systems (18–20), and for analyzing photosynthetic light-harvesting (21, 22). Regarding these approaches, one has to differentiate between fifth-order experiments (14, 15, 19) for effects of higher nonlinearity (e.g., three-point frequency-fluctuation correlation functions) (14) and third-order techniques (20–24), as demonstrated here to unravel photochemical reactions.

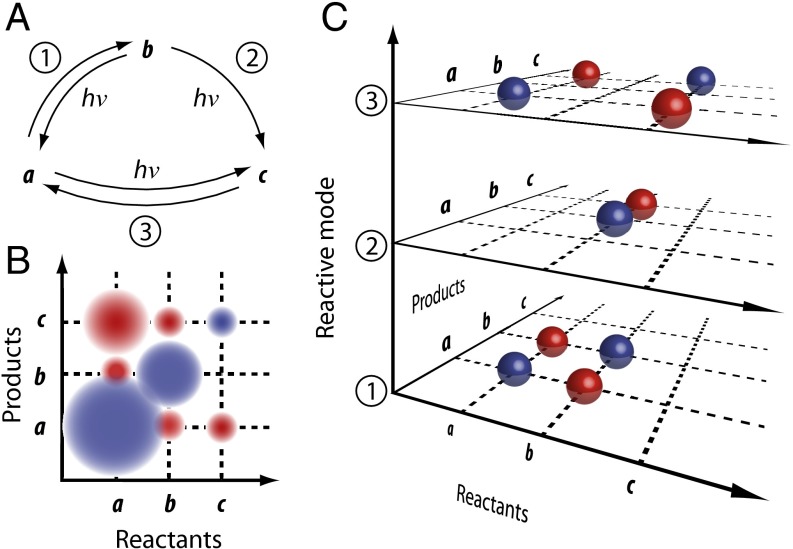
The principal idea of multidimensional spectroscopy for photoreactive processes as used in this work is sketched in Fig. 1. We consider a fictitious “photoreactive network” containing three reactive species a, b, and c connected via reaction channels 1, 2, and 3 (Fig. 1A). In practice, the signatures of reactants and products may strongly overlap in solvent environments. Hence, assigning reaction channels with linear spectroscopy or transient absorption will be unfeasible in many cases.

Fig. 1.

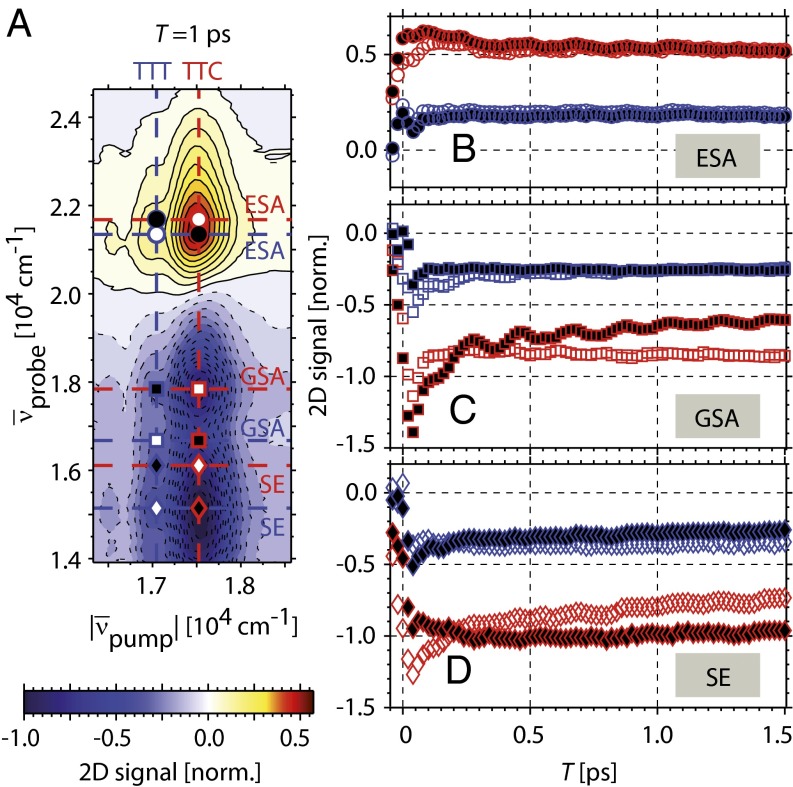
Principle of coherent multidimensional spectroscopy of photoreactivity. (A) For illustration, we assume a photoreactive network composed of three chemical species connected by different reaction channels. (B) 2D frequency spectra of this network visualize the correlations of reactants and products. (C) Involved reactive modes and associated reaction pathways that are still not resolvable from 2D spectra are exposed by introducing a third frequency dimension.

A 2D spectrum (Fig. 1B) visualizes the photochemical connectivity between products and reactants. We have recently proposed how potential photoproducts and the role of higher-lying electronic states can be identified in 2D spectra (25, 26). For long population times T, negative diagonal peaks (blue) describe population loss due to the photoreaction, whereas positive cross-peaks (red) emerge at points connecting reactants and products, disclosing correlations. Thus, at least qualitatively, the 2D spectrum for long T resembles the S-matrix from scattering theory and reveals reactively connected species.

However, a single 2D spectrum provides only a temporal snapshot; dynamics related to T and associated reaction channels remain inaccessible. By introducing an additional frequency axis, we propose that the various reaction paths are separated based on their reactive modes, e.g., vibrations (Fig. 1C). Thus, low-quantum-yield photoreactions could also be disclosed without being obscured by competing signals. In our approach, we isolate these reaction channels by collecting 2D spectra for different T values followed by a Fourier transformation, yielding a third-order 3D electronic spectrum.

To demonstrate this concept, we investigate coherent vibrational dynamics of merocyanine photoisomerization where cross-peaks associated with the ultrafast photoreaction will be isolated by analyzing the global response in terms of vibrational modes. Merocyanines constitute an important class of molecules due to their versatile applicability, e.g., in organic photovoltaics (27) or optical data storage (28). To ensure the functionality in such applications, a profound spectroscopic characterization is crucial to obviate photochemical loss channels that would lower the efficiency of the device.

Absorption Properties of 6-nitro-1′,3′,3′-trimethylspiro[2H-1-benzopyran-2,2′-indoline]

An acetonitrile solution of the ring-open merocyanine of 6-nitro-1′,3′,3′-trimethylspiro[2H-1-benzopyran-2,2′-indoline] (6-nitro-BIPS; see SI Materials and Methods) contains a mixture of two isomers whose photochemical interconversion is the subject of this work. Although photoisomerization has been reported (29, 30), the relevant vibrational reaction coordinates, involved electronic states, and reaction timescales are still unidentified, and the molecule mainly serves as an example to illustrate the general idea of Fig. 1.

The steady-state absorption spectrum (gray-filled curve in Fig. 2) originates from the mixture of two stable merocyanine isomers, which differ in a cis–trans configuration in the methine bridge. The trans–trans–cis isomer (TTC; structure shown in Fig. 2) dominates, absorbing around 557 nm (red dotted line), whereas ∼10% of merocyanine molecules exist in trans–trans–trans (TTT) configuration with a slightly red-shifted absorption around 595 nm (blue dashed line). The used pump laser spectrum is centered at 585 nm (green line) such that it overlaps with both absorption bands. Both isomers also exhibit spectrally separated fluorescence (Fig. S2).

Fig. 2.

Absorption spectrum (gray) of ring-open 6-nitro-BIPS in acetonitrile, which is the sum of the (estimated) contributions of the two displayed isomers (TTC, red dotted line; TTT, blue dashed line). The pump laser spectrum is shown in green.

Two-Dimensional Spectroscopy: Long-Time Dynamics

A subset of absorptive electronic 2D spectra for 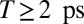is shown in Fig. 3 (see Movie S1 for the complete data set, and SI Materials and Methods for experimental details). The characteristic spectral positions are indicated by red dashed lines for TTC and blue dashed lines for TTT. For (Fig. 3 A–D), strong excited-state absorption (ESA) is observed for 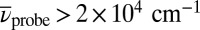, whereas bleaching of the ground-state absorption (GSA) and stimulated emission (SE) are detected between 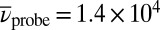and 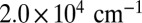. TTC contributions dominate the 2D spectra because the equilibrium isomer ratio in solution is strongly shifted toward TTC (Fig. 2), but also contributions from TTT can be identified, e.g., ESA causing a pronounced distortion of the contour lines toward lower pump wavenumbers (mark I in Fig. 3A).

Fig. 3.

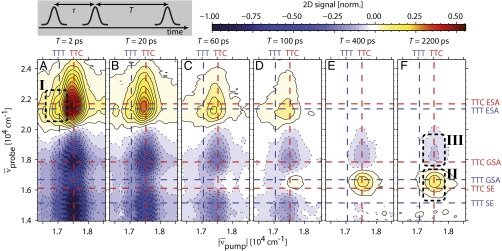
Long-time evolution of absorptive electronic 2D spectra of 6-nitro-BIPS in acetonitrile for various population times T. All spectra are normalized to the minimum of the 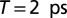spectrum. Negative values (blue) correspond to a decrease of the sample absorption, positive ones (yellow/red) to an increase. Contour lines (dashed for negative, solid for positive values) are drawn in intervals of 4% of the maximum amplitude. Maxima of the TTC contributions are indicated by red dashed lines, those of the TTT isomer by blue dashed lines. A scheme of the employed pulse sequence used to collect 2D/3D spectra in the pump–probe beam geometry is shown in the upper left.

While ESA and SE contributions decrease with T, a positive cross-peak emerges at TTC excitation and TTT GSA probe wavenumbers (mark II) for 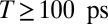(Fig. 3 D–F). A corresponding negative contribution appears blue-shifted at TTC GSA probe wavenumbers (Fig. 3F, mark III). These signals corroborate a decreased TTC amount (Fig. 3F, mark III) and an associated TTT increase (Fig. 3F, mark II) after TTC excitation, unambiguously proving cis–trans photoisomerization. The occurrence of the reversed isomerization reaction (TTT→TTC) can be excluded because no cross-peaks remain on the blue vertical line that would correspond to TTT excitation and reaction (a brief discussion of expected 2D signals for various isomerization scenarios can be found in Fig. S3). In transient absorption, such conclusions cannot be obtained directly because there, only the integral over the 2D spectrum along 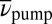is measured.

Two-Dimensional Spectroscopy: Ultrafast Primary Photodynamics

We now extract details on the primary isomerization dynamics, such as their timescale, the associated reaction path, and the involved states. In principle, either an excited-state isomerization followed by photoemission from the photoproduct’s region of the potential energy surface (PES) or ultrafast radiationless isomerization to the electronic ground state (e.g., via a conical intersection) are consistent with the data of Fig. 3. In both cases, cross-peaks indicative of photoproduct formation at early population times would be buried under larger negative contributions due to SE and bleaching of the majority of molecules not undergoing photoisomerization. To overcome this problem, we analyze characteristic molecular vibrations observed during the first picoseconds, leading to the identification of the photoproduct and the relevant electronic state.

Multiple 2D spectra for population times between 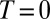and 2.2 ps have been recorded, the one for 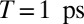is shown exemplarily in Fig. 4A (see Movie S2 for the complete data set). Specific points in 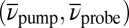space can be associated with different reaction paths. The corresponding temporal evolutions as a function of T are shown in Fig. 4B for contributions arising from ESA (circles); in Fig. 4C for signals at GSA wave numbers (squares); and in Fig. 4D for SE signatures (diamonds).

Fig. 4.

Evolution of the 2D signal up to 1.5 ps after photoexcitation. (A) Exemplary 2D spectrum for 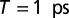. The temporal evolution as a function of population time is shown for (B) ESA (circles), (C) GSA (squares), and (D) SE signals (diamonds). Corresponding 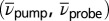coordinates are indicated in A by their associated markers. Red markers represent contributions after TTC excitation, blue ones those after mostly TTT excitation. White filling corresponds to excitation and probing of the same isomer, black filling to different isomers, respectively.

Discriminating between the two isomers solely from ESA signals (Fig. 4B, circles) is not possible because the spectral separation of the two ESA bands is too small. However, a pronounced Stokes shift of the ESA toward higher probe wavenumbers is observed, because the slightly higher energetic part (white-filled red circles) takes longer to reach its maximum compared with the lower energetic part (black-filled red circles) during the first 200 fs.

In the components at GSA wavenumbers (Fig. 4C, squares), strong oscillations with a predominant 190-fs period are found for TTC excitation and TTT GSA probing (black-filled red squares) up to ∼1.5 ps after excitation; they are almost absent at TTC GSA probe wavenumbers (white-filled red and black-filled blue squares) and also substantially decreased when mainly TTT is excited (white-filled blue squares). We assign these oscillations to coherent vibrational wave-packet motion further analyzed below.

Concerning the SE region (Fig. 4D, diamonds), the Stokes shift is evident in the low-energy signal (black-filled red diamonds), reaching its minimum delayed by a few hundred femtoseconds compared with the high-energy emission (white-filled red diamonds).

Third-Order 3D Spectrum

The 2D data are Fourier-transformed along T (see scheme in upper left of Fig. 3) to obtain a third-order 3D spectrum, whose absolute value is shown in Fig. 5A as an isosurface graph. The main contribution is found in a plane at 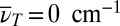, because most of the signal arises from slowly decaying contributions. By contrast, the observed vibrational motion leads to separated cross-peaks in the 3D spectrum. One such isolated cross-peak around 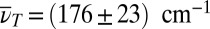reflects the 190-fs vibrational period evident in Fig. 4C [hereafter referred to as lower-frequency mode (LFM)] centered at the crossing of TTC excitation (Fig. 5A, red dashed line) and TTT GSA probing (Fig. 5A, blue dashed line). A second isolated cross-peak—lower in amplitude—shows up around 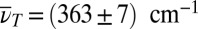[vibrational period 90 fs, higher-frequency mode (HFM)] and is slightly shifted away from the crossing point toward higher excitation frequencies, indicating that more excess energy is required to initiate it. The location in the 3D spectrum reveals that oscillations of cross-peaks connecting the two isomers give rise to these signatures.

Fig. 5.

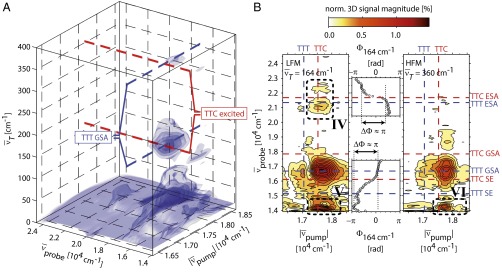
Third-order 3D spectrum. (A) A 3D isosurface representation is used to visualize the absolute value of the 3D spectrum. Iso values of 0.65%, 0.9%, 1.15%, and 1.40% of the maximum amplitude were chosen. Red dashed lines indicate TTC excitation, blue dashed lines the TTT GSA probe wavenumber. (B) Slices of the 3D spectrum in the 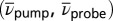plane for 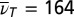(Left) and 360 cm⁻¹ (Right) and the phase for 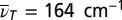at a vertical cut at the TTC excitation wavenumber (Center).

Slices through the 3D spectrum in the 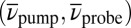plane are shown in Fig. 5B for the two dominating vibrational modes [at 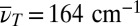for the LFM (Left), and at 360 cm⁻¹ for the HFM (Right)] together with the phase for the LFM along the TTC excitation wavenumber (Center). For both modes, the main contributions are located at TTC excitation and TTT GSA probe wavenumbers.

The formation of the TTT photoproduct involves wave-packet motions on the excited-state PES S₁; this is inferred unambiguously from Fig. 5B as follows: (i) Signatures of the vibrational wave packet can be found in the ESA region of TTT (mark IV). In addition, both modes are observable at the red edge of the SE (marks V and VI). Hence, the oscillatory signatures are associated to excited-state vibrations. (ii) Signals of an oscillating wave packet are typically most pronounced at the inner and outer turning points where the wave packet’s position is strongly localized, and least pronounced at the minimum of the PES (31, 32). Thus, in the case of an excited-state wave packet, the modulations will be smallest at the SE signature of the (vibrationally relaxed) TTT and larger at both red- and blue-shifted wavenumbers (as sketched in Fig. 6D); this is in agreement with the data of Fig. 5B, i.e., both the ESA and the SE show “bimodal” peak shapes. (iii) When the two turning points are probed at these red- and blue-shifted wavenumbers of the TTT ESA and TTT SE, oscillations out of phase (31) and with a distinct phase change of 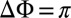in between are observed (Fig. 5B, Center), elucidating excited-state wave-packet motion. All these arguments substantiate that the photoproduct is formed on the timescale of a few vibrational periods in the S₁ state.

Fig. 6.

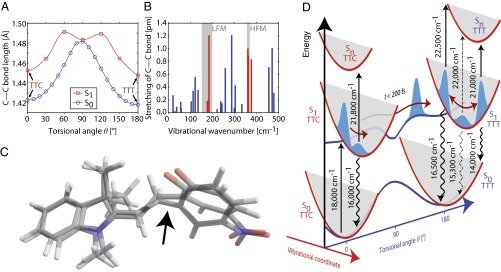
Quantum-chemical analysis of the reaction mechanism and involved vibrational normal modes. (A) The C–C bond around which the cis–trans isomerization occurs (arrow in C) is substantially stretched during the torsional motion both for ground (blue) and first excited state (red). (B) The calculated amplitudes of this C–C stretching for all low-frequency normal modes show strong contributions (red) at the two experimentally observed frequency ranges (gray). (C) The dominant 185 cm⁻¹ mode visualized by overlaying the two reversal point geometries. (D) Simplified picture of signatures arising from a vibrational wave packet in the S₁ state of TTT after TTC excitation. Signal oscillations are most pronounced at the turning points with a phase change of π in between.

The slow dephasing of the oscillations in Fig. 4 support a harmonic character rather than a superposition of excited vibrational states in an anharmonic potential as explanation for the HFM and LFM. The spectral signature of the HFM further reveals that its wavenumber is not just the second harmonic of the LFM, because then its amplitude in the 3D spectrum would not be maximal at the turning points but exactly in between where the wave packet passes twice per vibrational period (31, 33). Therefore, the HFM is a further vibrational mode induced in the photoproduct.

Quantum-Chemical Calculations

An explanation of the experimental data is possible in the framework of a 2D model using the nuclear distortions directly connected to the isomerization as the main coordinate, whereas the effect of all other photoinduced nuclear motions is treated by one additional effective mode. To compute the underlying PESs, the reaction profile of the isomerization on the ground-state S₀ is determined first using a relaxed scan (see SI Materials and Methods for details about the calculations). In this scan, the torsional angle θ (marked in Fig. 2) is varied stepwise while all other degrees of freedom are optimized with respect to the S₀ situation. The solvent influence is included via a polarizable continuum model (34). The computation of vertical excitation energies, incorporating only the electronic polarization of the solvent taking place on a similar timescale as the excitation itself, provides information on the Franck–Condon regions of the excitation (Fig. S4A, solid blue). To take into account excited-state relaxation processes (e.g., stretch and bending modes), the S₁ profile with respect to these coordinates is obtained in a second relaxed scan along the isomerization coordinate θ in which all other coordinates are optimized with respect to the S₁ state (Fig. S4A, dashed blue). In these computations we also account for solvent relaxations taking place on a similar timescale. To disclose possible emission processes, the corresponding S₀ energies are again determined by vertical energy computations. The 2D PESs are finally obtained by assuming a harmonic behavior of the effective mode (Fig. S5). The calculations verify the existence of the two isomers with an angle of 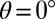(TTC) and 180° (TTT) separated by a rotational barrier of 0.77 eV in S₀. The vertical excitation energy is overestimated, but the difference between the two isomers is reproduced correctly (experimental values given in parentheses): TTC 2.81 (2.23) eV, TTT 2.67 (2.10) eV.

Starting from the Franck–Condon regions of both isomers, a small barrier of less than 0.1 eV is computed along the reaction coordinate on S₁, confirming the existence of the observed photoisomerization. However, modes lying perpendicular to the reaction mode get highly vibrationally excited due to the shape of the surface (Fig. S5). An analysis of variations of geometrical parameters discloses that especially modes involving stretching of the C–C bond around which isomerization is observed are excited, and a pronounced bond elongation at the twisted geometry with 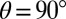occurs during the torsional motion (Fig. 6A); this is substantiated by the calculated C–C bond stretching amplitudes at the twisted geometry for all S₁ normal modes up to 500 cm⁻¹ (Fig. 6B; see Table S1 for the molecular structure and Table S2 for a complete list of all excited-state normal modes), which reveal several strong low-frequency vibrations at 177, 185, 361, 362, and 376 cm⁻¹ (red bars) in the two experimentally observed wavenumber regions (gray shaded areas). The 185-cm⁻¹ vibrational mode, which matches the measured LFM, is illustrated in Fig. 6C by the two overlaid reversal-point molecular geometries. The mode exhibits—apart from the C–C bond stretching—a strong tilting of the benzene ring, supporting the assumption that the LFM is connected to the isomerization upon which the benzene ring is rotated by 180° (other geometry parameters are analyzed in Figs. S6–S8).

At first glance, the calculated PESs (Fig. S5) might indicate the presence of a conical intersection (CI) at around 90°, which would not be in line with the timescale observed in the experiment. However, the molecular orbitals and the coefficients of the leading determinants show no indications for a CI in 6-nitro-BIPS, contrary to theoretical findings for a similar system (35). Beyond, fluorescence cannot occur from the twisted geometry around 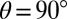, because the oscillator strength is zero (Fig. S4B), but from the shallow excited-state minima at ±180° and 0°. The fluorescence energy is again overestimated, but the small Stokes shift is well reproduced: TTC 2.56 (2.01) eV, TTT 2.44 (1.96) eV.

Conclusion

The combination of experimental 3D spectroscopy and quantum chemistry leads to a comprehensive picture of the ultrafast photoisomerization dynamics, visualized in Fig. 6D where the molecular potential energy is sketched as a function of the main reaction coordinate, i.e., the torsional angle (blue), and a second not-further-specified vibrational coordinate (red). The curves along the torsional angle are based on calculations (Fig. S4), whereas the curves along the vibrational coordinates are approximated by parabolas (harmonic approximation). After TTC excitation, most molecules return to the TTC ground state. However, a smaller portion undergoes cis–trans isomerization on the excited state upon which pronounced wave-packet dynamics are observed. The wave packet moves along the reaction coordinate and oscillates vertically to it, leading to the cross-peaks observed in the 3D spectra, which directly reveal the two involved modes. The SE originates from the shallow minimum at 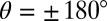in which the wave packet continues to oscillate for several picoseconds.

Moreover, the phase of the vibrational motion corroborates that it indeed proceeds in the S₁ state and that the S_n potential is displaced in the same direction relative to the S₁ potential as S₁ is displaced compared with S₀. Thus, low-energy ESA transitions occur from the same position on S₁ from which low-energy SE originates (and vice versa for the high-energy contributions), as also sketched in Fig. 6D.

In more general terms, we have shown that coherent multidimensional electronic spectroscopy is able to isolate molecular reactive modes involved in an ultrafast photochemical process. Through the emergence of the TTC→TTT cross-peak in the 2D spectra, unidirectional cis–trans photoisomerization was explicitly proven. An even deeper understanding of the reaction was gained by probing the primary photodynamics with high temporal resolution and by evaluating the molecular response via a third-order 3D electronic spectrum, which correlates the signatures of reactants with those of photoproducts and exposes reactive modes connecting them. Using this technique, it has been shown that the photoproduct is impulsively formed in its first excited singlet state, maintaining vibrational coherence during the structural rearrangement. Molecular normal modes in the experimentally detected frequency range have been identified by quantum-chemical calculations and could be associated with the observed photoreaction. Thus, third-order 3D spectroscopy offers great potential for the real-time analysis of complex chemical reaction networks involving a multitude of reactants and products with a variety of reaction quantum yields.

Materials and Methods

Sample.

A 3-mmol/L solution of commercially available 6-nitro-BIPS (ABCR GmbH) in acetonitrile was pumped through a flow cell of 200-μm path length. For investigating the merocyanine form of 6-nitro-BIPS, the sample was continuously illuminated with UV light. More details about the sample are presented in SI Materials and Methods.

Laser System and Experimental Setup.

Laser pulses at 585 nm were generated using a noncollinear optical parametric amplifier (TOPAS-White; Light Conversion, Ltd.) pumped by a Ti:Sapphire amplifier (Solstice; Spectra Physics: 800 nm, 1 kHz, 100 fs), which were compressed to a pulse duration of 17 fs (frequency-resolved optical gating trace shown in Fig. S1) using an LCD-based pulse shaper that was also used to produce the double pulses separated by coherence time τ (see scheme in upper left in Fig. 3) required for 2D spectroscopy in pump–probe geometry (36). The probe continuum (5) was generated by focusing a small portion of the 800-nm pulses into a CaF₂ plate. The pump pulses were delayed with respect to the probe using a computer-controlled motorized stage. Optical density changes between the pumped and unpumped probe volume were measured by blocking every second pump pulse and by a spectrally resolved shot-to-shot detection of the probe.

Data Acquisition and Evaluation.

The 2D data were obtained by measuring the signal as a function of τ for every population time T applying a two-step phase-cycling scheme (37). By Fourier transformation along τ and taking the real part, purely absorptive 2D spectra were generated. The 3D spectrum was obtained by an additional Fourier transformation over T.

Quantum-Chemical Calculations.

For the quantum-chemical calculations, only the ground-state geometry optimizations were performed on the B3LYP/cc-pVDZ level (38). Calibration calculations were performed using the highly accurate SCS-ADC(2)/cc-pVDZ approach as implemented in TURBOMOLE (39, 40). On the basis of these results we selected the CAM-B3LYP (41) functional for the computation of the PESs using Gaussian 09 (42); this was necessary because solvent effects had to be taken into account, which is not possible for SCS-ADC(2). For ground state and excited state, a polarizable continuum model (34) using the integral evaluation formalism was used to include the effect of the solvent (acetonitrile, ϵ = 35.688) as described in more detail in SI Materials and Methods.