Cooperative Binding of Cyclodextrin Dimers to Isoflavone Analogues Elucidated by Free Energy Calculations

Abstract

Dimerization of cyclodextrin (CD) molecules is an elementary step in the construction of CD-based nanostructured materials. Cooperative binding of CD cavities to guest molecules facilitates the dimerization process and, consequently, the overall stability and assembly of CD nanostructures. In the present study, all three dimerization modes (head-to-head, head-to-tail, and tail-to-tail) of β-CD molecules and their binding to three isoflavone drug analogues (puerarin, daidzin, and daidzein) were investigated in explicit water surrounding using molecular dynamics simulations. Total and individual contributions from the binding partners and solvent environment to the thermodynamics of these binding reactions are quantified in detail using free energy calculations. Cooperative drug binding to two CD cavities gives an enhanced binding strength for daidzin and daidzein, whereas for puerarin no obvious enhancement is observed. Head-to-head dimerization yields the most stable complexes for inclusion of the tested isoflavones (templates) and may be a promising building block for construction of template-stabilized CD nanostructures. Compared to the case of CD monomers, the desolvation of CD dimers and entropy changes upon complexation prove to be influential factors of cooperative binding. Our results shed light on key points of the design of CD-based supramolecular assemblies. We also show that structure-based calculation of binding thermodynamics can quantify stabilization caused by cooperative effects in building blocks of nanostructured materials.

Introduction

Cyclodextrins (CDs) are promising building blocks extensively used in the construction of nanostructured materials with sophisticated structures and functions.^1,2 CDs belong to a class of cyclic oligosaccharides with more than six d-glucopyranose residues linked together via α-1,4 glycosidic bonds and arrangement of these residues in a ring endows CDs with a somewhat hydrophobic cavity and a hydrophilic surface.^3,4 This property permits association of varied guest molecules with suitable size to form stable host–guest complexes or supramolecular assemblies, which leads to a variety of fascinating applications in many fields like pharmaceutical research.⁵⁻⁷ In recent years, construction of one- and multidimensional nanoarchitectures using CDs as building blocks has attracted much attention, particularly due to their alluring potential in molecular machines⁸⁻¹⁰ and functional materials.¹¹⁻¹³ CD-based nanostructures integrate together a number of functional groups that have been already captured by CD cavities. These functional groups along with CD cavities provide multiple binding sites for substrates, allowing one to mimic the cooperative multimode complexation existing in biological systems widely. CD-based nanoarchitectures are therefore acknowledged to be ideal candidates for drug or gene carriers¹⁴⁻¹⁶ and artificial enzyme models.¹⁷

Cooperative binding of at least two CD monomers to a template (also known as guest) molecule is the driving force responsible for self-assembly processes in the construction of CD-based nanoarchitectures. For the case without template, the assembly is usually driven by hydrophobic interactions between substituent arms of CD derivatives with the neighboring cavities of other CDs.¹ The following text will focus on the former case with template. Polymer chains such as poly(ethylene glycol) (PEG) and poly(propylene glycol) (PPG) are often used as a template to thread several CD cavities for the construction of one-dimensional nanoarchitectures like (pseudo)polyrotaxanes.^2,14,18 Furthermore, CDs can be grafted covalently to the polymer chain as a bulky stopper for polyrotaxanes, and cooperative binding of two bulky CD cavities to one template molecule (like C₆₀)¹⁹ allows construction of long nanowires based on the polyrotaxanes. Starting from CD-based polyrotaxanes, one can prepare nanotubes by covalent reactions of neighboring CD units with short cross-linking agents such as epichlorohydrin, followed by the cutoff of bulky ends and removal of the polymer thread.²⁰ These tubular polymers are capable of including long guest molecules like 1,6-dimethylhexatriene inside the molecular tube efficiently. Randomly cross-linked CDs without preassembly by a polymer chain cannot form a tube easily and hence do not possess such an inclusion ability.²

Typical CDs used as the building blocks contain 6, 7, and 8 glucopyranose residues, denoted as α-, β-, and γ-CD, respectively. Harada and co-workers characterized topology structures of α-CD/PEG, β-CD/PEG, and β-CD/PPG (pseudo)polyrotaxanes using X-ray crystallography and reported that all CD monomers are oriented as head-to-head (HH) and tail-to-tail (TT) dimers through threading onto the polymer chain.²¹⁻²³ They indicated that secondary hydroxyl groups of CDs hydrogen-bond to each other forming a tight hydrogen-bonding network and that the interactions between primary hydroxyls are weak. Mavridis et al. observed an unusual crystal of β-CD trimers in HH and head-to-tail (HT) fashions which cooperatively bind to two guest molecules.²⁴ HT orientations were found in the crystal packing of γ-CDs as well.²⁵ Figure 1a depicts β-CD dimers in the three orientations of HH, HT, and TT taken from Mavridis’s work;²⁴ head indicates the wide (secondary) rim of β-CD and tail the narrow (primary) rim.

Figure 1.

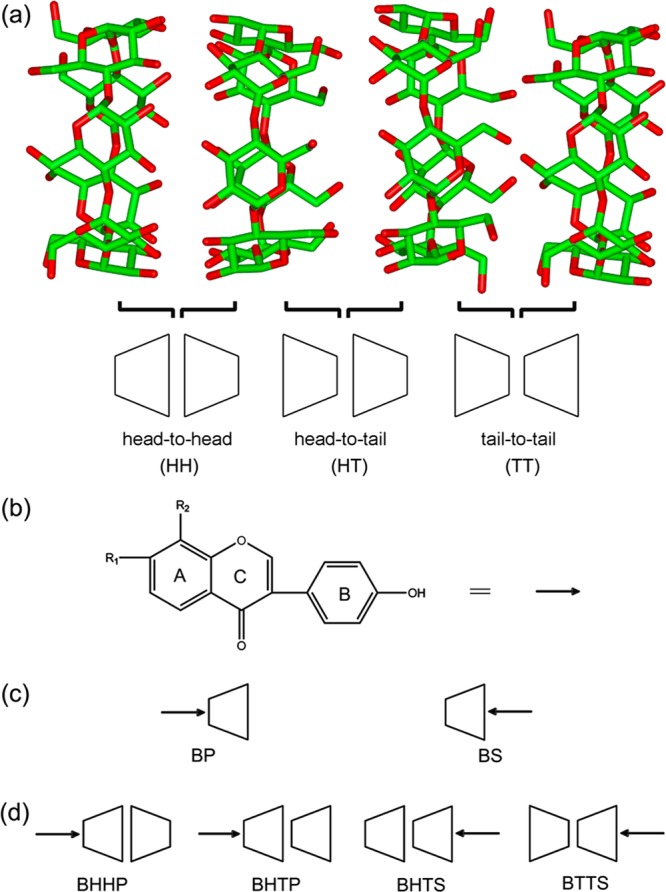
Molecular structure of (a) β-CD dimers and (b) isoflavone guests and possible [host:guest] binding modes with stoichiometric ratios of (c) 1:1 and (d) 2:1. Head means the secondary rim of β-CD and tail the primary rim. The guest molecules include puerarin (R1 = H, R2 = glucose), daidzin (R1 = glucose, R2 = H), and daidzein (R1 = H, R2 = H). A, B, and C denote relevant isoflavone rings. The arrow indicates the guest molecule and the orientation that the guest penetrates into β-CD cavity.

Because of the outstanding performance of CD-based nanoarchitectures, it is highly desirable to find out the mechanism underlying cooperative effects of CD-based assemblies. Molecular dynamics simulation serves as a powerful tool for exploring the mechanism associated with CD-based systems and has contributed valuable explanations for experimental observations.²⁶⁻³⁰ Association of two CD monomers (i.e., dimer) is an essence for cooperative binding of CD cavities. Many theoretical reports focused on the relative stability of noncovalent CD dimers in HH, HT, and TT fashions (Figure 1a) and revealed that hydrogen-bonding (HB) interactions between hydroxyl groups of adjacent CD monomers are a key factor determining the dimer stability.³¹⁻³⁶ Cai and co-workers recently examined dimerization of α-CDs onto a PEG chain using free energy calculations and Monte Carlo simulations.³⁷ They indicated that the dimerization is driven primarily by HB interactions between two α-CDs and that HH is preferred over HT and TT. Pineiro et al. evaluated α-, β-, and γ-CD complexes with sodium dodecyl sulfate (SDS) in ratios of 1:2 and 2:1 through MD simulations and reported that [CD₂:SDS] in the HH orientation seems a potential building block for nanotubular polymers.²⁷ Marrink and co-workers performed potential of mean force (PMF) calculations to investigate the mechanism of cyclodextrin-mediated extraction of cholesterol from model membranes.^38,39 In previous work, we investigated the dissociation of β-CD HH dimer through PMF calculations and concluded that the dimer binding depends on the guest and solvent properties.⁴⁰

Here we present an extensive free energy examination on cooperative binding of β-CD dimers (HH, HT, and TT) to three isoflavone analogues (puerarin, daidzin, and daidzein) through molecular dynamics (MD) simulation. The three isoflavone components (guest molecules) have potential use in medicinal therapies,^41,42 and a more efficient encapsulation of these drugs by β-CD dimers promotes their practical applications. Also, structural properties of the isoflavone skeleton with/without glucose motivated us to choose them as template molecules to examine hydrophobic and hydrophilic interactions that constitute the main driving forces responsible for the construction of CD-based nanostructures. A number of free energy calculations have been implemented to evaluate 1:1 and 2:1 [CD:guest] complexes,^{27,37−40,43−47} while few reports consider all possible cooperative binding of CD cavities. In this work free energy profiles governing all possible formation processes of [β-CD₂:guest] complexes were calculated with umbrella sampling.⁴⁸ Center of mass (COM) pulling⁴⁹ was employed to generate configuration sequences for umbrella sampling simulations. Details on COM pulling and PMF techniques have been presented in refs (46 and 49−54). From PMF and entropy calculations, total and individual contributions from enthalpy and entropy were quantified in detail using a recently proposed method for 1:1 binding.⁵⁵ The results exhibit a comprehensive thermodynamic and energetic characterization for cooperative effects of CD dimers toward guest molecules. As a fundamental step in the construction of nanostructures with cooperatively bound units (like CDs), dimerization of CD molecules studied here offers a generalized picture on molecular assemblies of CDs by cooperative binding to a template. Implications for design of template molecules and CD assembly models in building blocks of nanoarchitectures are discussed at the end of this work.

Methods

The initial coordinates of β-CD dimers (HH, HT, and TT) were taken from the Cambridge Crystallographic Data Center (CCDC no. 648855)²⁴ where β-CD trimers formed a channel-like structure (Figure 1a). Molecular structures of isoflavone guests (puerarin, daidzin, and daidzein) are shown in Figure 1b. All the binding modes of 1:1 and 2:1 [CD:guest] complexes are given in Figures 1c and 1d, respectively. The q4md-CD force field⁵⁶ was used to model β-CD and the generalized Amber force field (GAFF)⁵⁷ for the guests. The rigid model TIP3P⁵⁸ was used for water molecules. All the simulations were carried out at 300 K with GROMACS (version 4.5.5).⁵⁹⁻⁶¹ System equilibrations were performed in the NPT ensemble (P = 1 bar) and production simulations in the NVT ensemble. Other simulation protocols were the same as in the refs (55 and 62).

Each system contained one β-CD dimer, one guest, and approximately 4100 water molecules in a simulation cell of 5 × 5 × 5 nm³. The dimer was centered in the box with Z-coordinates of its glycosidic oxygen atoms approximately located at Z = −0.3 or +0.3 nm for the two monomers, respectively, making the cavity axis of β-CD dimer parallel to the Z-axis. The distance between the center of mass (COM) of the B-ring of the guest and that of 14 glycosidic oxygens of the dimer along the Z-axis was defined as the reaction coordinate ξ. Figure 2 shows the definition of ξ for the HT dimer with daidzein in the BHTS mode (see Figure 1d for nomenclature). Glycosidic oxygen atoms of β-CD dimers were harmonically restrained and used as an immobile reference for pulling simulations. The B-ring of the guest was pulled through the dimer cavity from the primary (P) or secondary (S) rim along the Z-axis over 1 ns with a pulling rate of 0.005 nm ps^–1. All the pulling parameters were the same as in the ref (55) where the 1:1 binding modes (BP and BS, Figure 1c) have been evaluated. In this work, the guest sampled 5 nm covering the entire ξ of [−2.5, 2.5], and a formation process for 2:1 inclusion complexes was detected during the pulling simulation. We then selected 101 windows in the [−2.5, 2.5] interval with a distance equal to 0.05 nm between adjacent positions and these windows were used for umbrella sampling simulations. Following the same procedure, we simulated three guest molecules in the four binding modes of BHHP, BHTP, BHTS, and BTTS (Figure 1d) and therefore obtained 12 PMF profiles in total. The total simulation time for a single PMF was 1.01 μs. For each window the first 2 ns was removed for equilibration, and the rest (2–10 ns) was used for all the data analysis. Details on the calculation of thermodynamic parameters (ΔG, ΔH, or −TΔS) are given in the Supporting Information.

Figure 2.

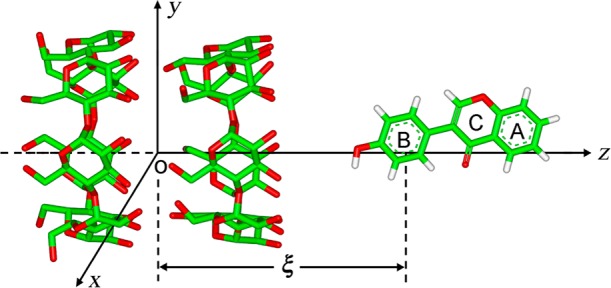
Definition of the reaction coordinate ξ for the BHTS mode with daidzein.

Results

Binding Modes

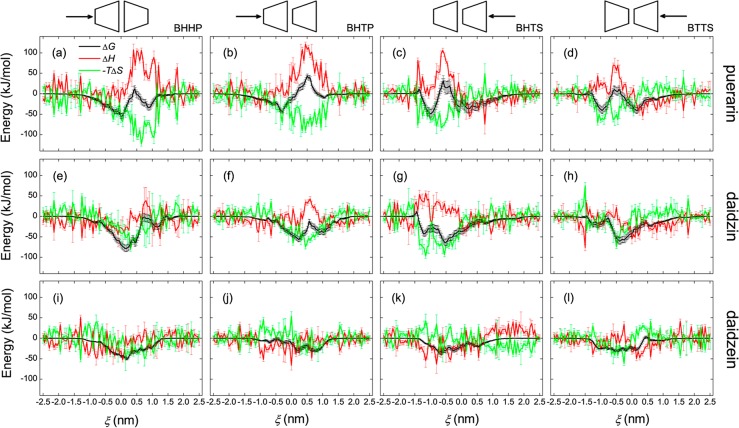
PMF profiles for the formation process of [β-CD₂:guest] inclusion complexes with the three isoflavone guests along ξ in the BHHP mode are shown in Figure 3a. The guest approaches the dimer from the primary rim of β-CD, penetrates into the channel-like cavity, and then gets out of the cavity along the +ξ direction. All the PMFs on both sides of ξ amount to zero and level off corresponding to the completely separated state of the binding partners.

Figure 3.

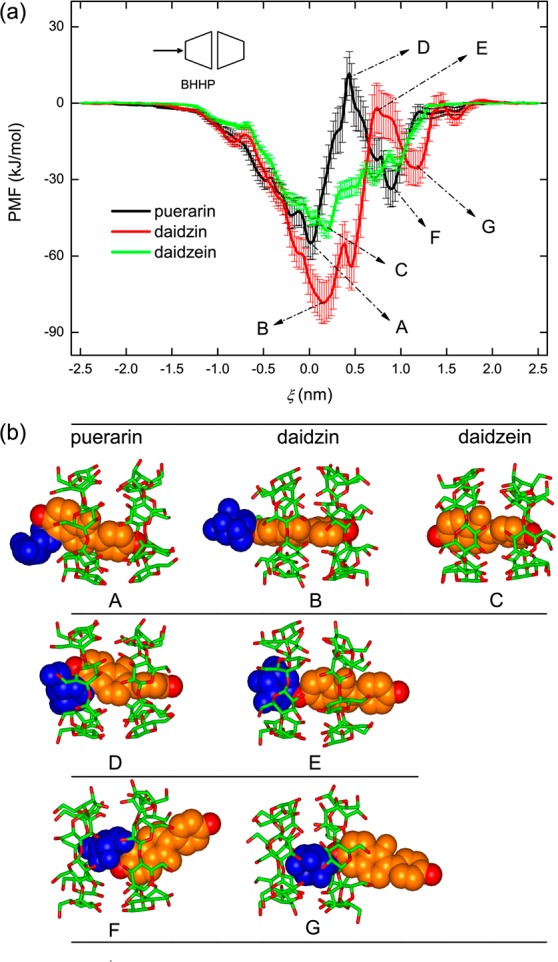
(a) Potential of mean force (PMF) profiles for the [β-CD₂:guest] complex formation in the BHHP binding mode and (b) representative inclusion configurations along ξ. β-CD dimer and guest molecules are shown with stick and space-filling models, respectively. The glucose group of guest is colored in blue and isoflavone skeletons in orange.

Representative configuration states (A–G) in the PMFs are marked in Figure 3a and given in Figure 3b. As the isoflavone skeletons (hydrophobic moieties) of the guests get close to the β-CD cavity, the PMF curves drop and become negative (i.e., thermodynamically favorable). When the isoflavone skeleton is located inside the channel-like cavity, leaving the glucose group (hydrophilic) outside, the most stable inclusion configurations of [β-CD₂:puerarin] and [β-CD₂:daidzin] complexes are sampled, namely the A- and B-states (Figure 3b), respectively. Approaching the cavity for the hydrophilic glucose further results in an upward trend for the PMFs (Figure 3a), revealing a thermodynamically unfavorable state. The most unfavorable states (central maxima in the PMFs) is that with the glucose group being entrapped inside the cavity of one β-CD monomer, while the hydrophobic isoflavone skeleton of the guest still interacts with the β-CD cavity, as in the D- and E-states (Figure 3b). When the hydrophilic glucose stays approximately in the center of mass (COM) of β-CD dimer, such as the F- and G-states (Figure 3b), local favorable minima in the PMFs are observed, indicating that the COM region of the dimer is somewhat hydrophilic. The most stable configuration of [β-CD₂:daidzein] is similar to puerain and daidzein; see the C-state (Figure 3b) where daidzein is almost completely encapsulated by the β-CD head-to-head dimer. Unlike puerarin and daidzin, the PMF for daidzein however does not display an obvious central maximum (Figure 3a). For convenience, the inclusion models similar to A- and B-states are shortened for GO (glucose outside), to D- and E-states for GIM (glucose inside monomer), and to F- and G-states for GID (glucose inside dimer) in the forthcoming text.

PMF profiles (ΔG) for all three guests in the four binding modes of BHHP, BHTP, BHTS, and BTTS are presented in Figure 4. In our simulations all the guests are inserted into the dimer cavity from the primary or secondary rim of β-CD along the +ξ or −ξ direction, respectively, unless stated otherwise. In the PMFs a central maximum resulted from inclusion of the glucose unit inside the β-CD cavity (model GIM) and a local minimum from inclusion of the glucose unit in the dimer center (model GID) are observed for all binding modes of puerarin (Figure 4, panels a–d). Inclusion models for GIM are located approximately at ξ = +0.5 nm or −0.5 nm for BHHP and BHTP or BHTS and BTTS, respectively; models for GID at ξ = ∼1.0 nm or −1.0 nm. For BHHP and BHTP the most stable states are similar to model GO (Figure 4, panels a and b), while for BHTS and BTTS the glucose unit positioned in the COM region of the dimer (model GIM) form the most stable states (Figure 4, panels c and d). Daidzin behaves similar to puerarin, while the most stable states adopt a GO model for all binding modes (Figure 4, panels e–h). The PMFs of daidzein for all binding modes do not show clear central maxima, and the inclusion modes with the isoflavone skeleton completely enclosed in the dimer are the most stable (Figure 4, panels i–l).

Figure 4.

Thermodynamic profiles (ΔG, ΔH, and −TΔS) of the system for the complex formation of β-CD dimers with puerarin, daidzin, and daidzein in the binding modes of BHHP, BHTP, BHTS, and BTTS.

Binding Energetics

Enthalpy (ΔH) and entropy (ΔS) profiles of the system for the [β-CD₂:guest] complex formation along ξ are also given in Figure 4. Here entropy is given as −TΔS. These profiles depict how enthalpy and entropy changes contribute to the binding energy and assist in understanding the thermodynamics of binding. For puerarin and daidzin clear enthalpy loss (positive ΔH) and entropy gain (positive ΔS) are observed in most cases, particularly when the glucose unit of the guest stays inside the β-CD cavity (Figure 4, panels a–h). In some cases the host–guest complexation is enthalpy-driven (negative ΔH), like GO models of puerarin in BHTS and BTTS modes (Figure 4, panels c and d). For daidzein, no obvious entropy changes (ΔS) are observed, and the binding seems to be exclusively driven by ΔH. Notice that the calculations force the guest artificially to access some region of the binding sites that are thermodynamically unstable, like the GIM model of puerarin (Figure 4, panels a–d), which allows us to sample the configuration space as much as possible.

Standard thermodynamic parameters (ΔG⁰, ΔH⁰, and ΔS⁰) for all binding modes of dimer and monomer are given in Table 1 (see eqs S1–S4 in the Suppporting Information for calculation of ΔG⁰, ΔH⁰, and ΔS⁰). For a quantitative evaluation these parameters are weighted by their Boltzmann factors using eq 1

1

where ΔE can be ΔG, ΔH or, –TΔS. The weighted values are listed in Table 1 as well. A good agreement between calculated and experimental ΔG⁰ for 1:1 associations have been shown in the ref (55), which validates the veracity of our calculations. No experimental data for 2:1 associations are available for direct comparison with the calculations yet. Similar to the monomer, the dimer binding to its guest is predominantly enthalpy-driven, and entropy loss cancels out about one-quarter of enthalpy gain. Cooperative binding of the dimer to puerarin does not result in an obvious increase in the binding strength and even in a decrease for the BHTP mode. However, cooperative effects of the two monomers give a clear increase by ∼30% (for daidzin) and 60% (daidzein) in binding free energies (ΔG⁰). BHHP seems the best mode for such guest binding, followed by BHTS and by BHTP and BTTS.

Table 1. Thermodynamic Parameters (kJ/mol) Calculated at 300 K for the Guests Studied.

		dimer				monomera		⟨ΔE⟩b
guest	energy	BHHP	BHTP	BHTS	BTTS	BP	BS	dimer	monomer
puerarin	ΔG0	–30	–19	–31	–27	–26	–32	–30	–32
	ΔH0	–43	–21	–41	–39	–36	–41	–41	–41
	–TΔS0	13	2	10	12	10	9	11	9
daidzin	ΔG0	–38	–31	–36	–29	–24	–29	–37	–28
	ΔH0	–49	–45	–52	–38	–32	–38	–50	–37
	–TΔS0	11	14	16	9	8	9	13	9
daidzein	ΔG0	–35	–18	–20	–18	–19	–22	–35	–21
	ΔH0	–48	–28	–33	–26	–28	–29	–48	–29
	–TΔS0	13	10	13	8	9	7	13	8

^aTaken from ref (55).

^bWeighted on all binding modes using eq 1.

Decomposition of Energy Terms

For a deeper insight into the enthalpy and entropy profiles, ΔH and ΔS are decomposed into individual contributions from the binding partners and solvent environment. The decomposition refers to eqs S6 and S7 in the Supporting Information. Figure 5 shows the ΔH decomposition for [β-CD₂:guest] complexes with puerarin, daidzin, and daidzein along ξ in the BHHP mode. ΔH_host and ΔH_guest are bonded interactions (torsion energies of bond angle and dihedral angle) of host and guest molecules (indicated by black and red lines), respectively. ΔH_host–host and ΔH_{guest–guest} (green and blue) belong to intramolecular nonbonded interactions of the binding partners. These four items quantify the changes in potential energies of host and guest resulting from the fluctuations in atomic positions. Bonded interactions of the rigid TIP3P⁵⁸ water amount to zero and ΔH_sol-sol (cyan) thus contains nonbonded intra- and intermolecular interactions between water molecules only. The other three terms, ΔH_host–guest, ΔH_host–sol, and ΔH_guest–sol (magenta, dark yellow, and orange), describe nonbonded intermolecular interactions between different kinds of molecules.

Figure 5.

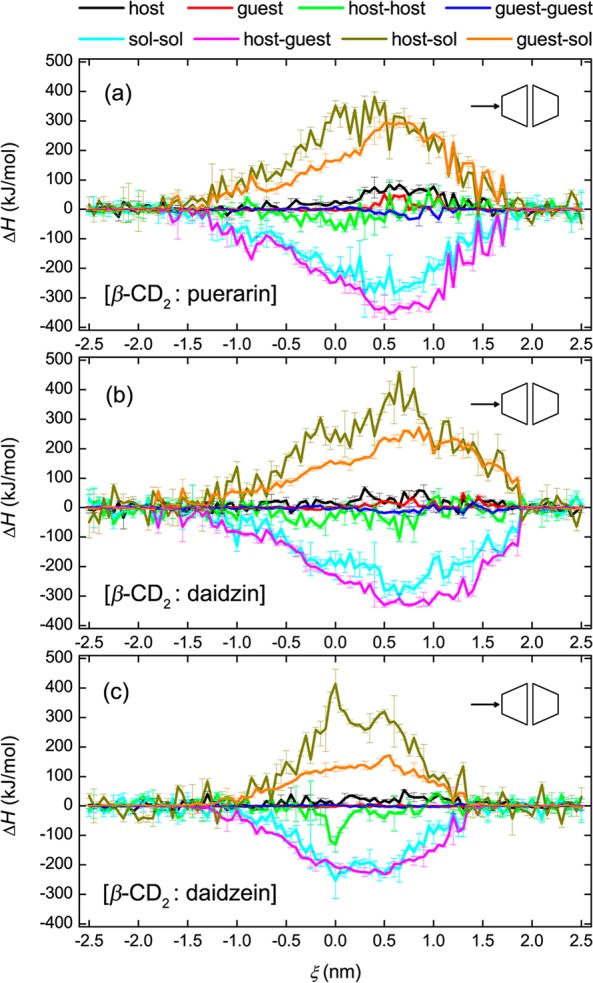
Enthalpy decomposition for the complex formation of β-CD dimers with (a) puerarin, (b) daidzin, and (c) daidzein in the BHHP mode.

As shown in Figure 5a, the bonded items (ΔH_host and ΔH_guest) tend to disfavor [β-CD₂:puerarin] complexation (positive values), while the nonbonded ones of the binding partners (ΔH_host–host and ΔH_{guest–guest}) in contrast favor the complexation (negative). By inclusion of puerarin, the interaction between host and guest is strengthened (negative ΔH_host–guest), and both host and guest molecules are desolvated, as indicated by more positive ΔH_host–sol and ΔH_guest–sol. Water molecules are shown to gain enthalpy (negative ΔH_sol–sol) favoring the binding. Similar observations were found for daidzin (Figure 5b) and daidzein (Figure 5c). Without the glucose unit (Figure 1b), daidzein shows more symmetric profiles and a relatively small change in ΔH_guest–sol, ΔH_host–guest, and ΔH_sol–sol (Figure 5c).

Considering Figures 3 and 5, the most stable [β-CD₂:guest] complexes with puerarin or daidzin (model GO, ξ = 0.0–0.2 nm) do not correspond to the states where the global minima of ΔH_host–guest and ΔH_sol–sol are achieved (ξ = 0.5–1.0 nm). At ξ = 0.5–1.0 nm, the contributions from the unfavorable enthalpy items of ΔH_host, ΔH_guest, ΔH_host–sol, and ΔH_guest–sol seem to be maximized and reduce the enthalpy gain (Figure 5, panels a and b). The most unstable complexes at ξ = 0.4 nm (puerarin) or 0.76 nm (daidzin), such as the D- and E-states (model GIM) in Figure 3, occur in coincidence with the states in which the host desolvation (ΔH_host–sol) reaches its maximum. For the most stable [β-CD₂:daidzein] complex all enthalpy components get very close to their maximum or minimum values, either favoring the complexation or not.

Figure 6 presents the ΔS decomposition for puerarin (Figure 6a), daidzin (Figure 6b), and daidzein (Figure 6c) in the BHHP binding mode. Here configurational entropies of host and guest molecules were calculated from the covariance matrices of atomic fluctuations using the quasi-harmonic approximation.⁶³ A length of at least 8 ns is needed for our simulations to ensure the convergence of such entropy calculations, as shown in Figures S1 and S2 of the Supporting Information. An obvious entropy loss of the host (positive −TΔS) and compensating entropy gain of the solvent (negative −TΔS) is observed. When included inside the CD cavity, daidzin shows a significant entropy loss (Figure 6b), but this is not observed for puerarin (Figure 6a) and daidzein (Figure 6c). As discussed in previous work on the monomer binding,⁵⁵ the glucose rotation of daidzin was affected much more than that of puerarin when entrapped inside the CD cavity, and daidzein did not display any obvious entropy change due to its structural rigidity. In this work, similar entropy changes for these three guests inside the dimer were found (Figure 6). Daidzein gives more symmetric ΔS profiles than either of puerarin or daidzin. As can be seen from Figures 3 and 6, configurational changes of β-CD are greatly affected by guest inclusion (in particular, when the glucose unit of the guest stays inside the cavity), and the most stable complexes (those with the lowest ΔG) do not correspond to the states with maximum or minimum values of the three ΔS components.

Figure 6.

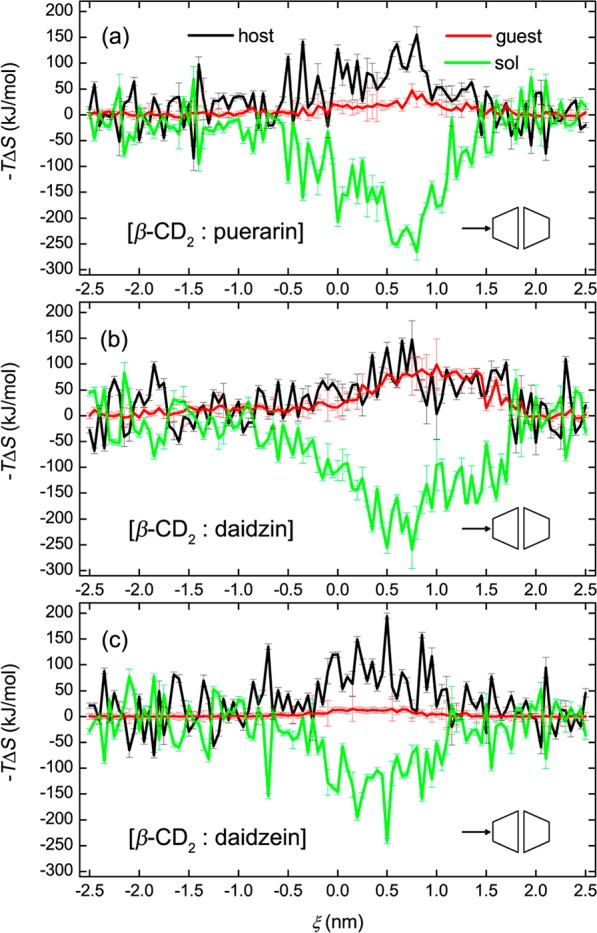
Entropy decomposition for the complex formation of β-CD dimers with (a) puerarin, (b) daidzin, and (c) daidzein in the BHHP mode.

Hydrogen Bonding

Polar moieties of the guests like the glucose units are observed to hydrogen bond to β-CD dimers. The number of hydrogen bonds (HBs) between the binding partners along ξ was analyzed to explore the role of HBs in the complex formation (Figure 7).

Figure 7.

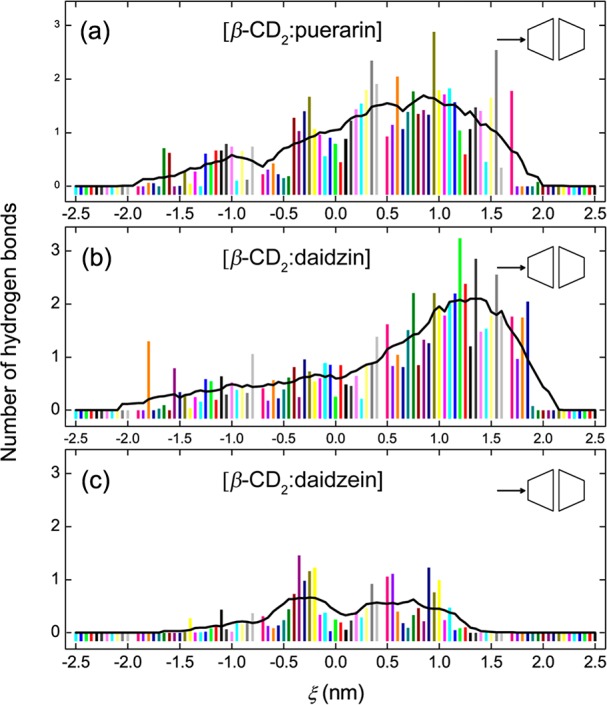
Hydrogen bonding strength during the complex formation of β-CD dimers with (a) puerarin, (b) daidzin, and (c) daidzein in the BHHP mode. The bold black lines represent trend curves smoothed by 10-point-window adjacent averaging.

Here we use a geometrical criterion for HB definition, based on distance and angle cutoffs of 0.35 nm and 30°.⁶⁴ No obvious HB interactions are observed at ξ < −0.5 nm (Figure 7) where the B-ring of the guest approaches the dimer cavity step by step, implying that the hydroxyl group connected to the B-ring contributes little to the binding. For puerarin and daidzin, the most stable states (Figure 3a) have just one HB (ξ = 0.0–0.5 nm in Figure 7, panels a and b). This HB is formed between the glucose unit of guest and the primary rim of β-CD. At the central region of the dimer (ξ = 1.0–1.5 nm), a stronger HB interaction (about two HBs) is observed for puerarin and daidzin (Figure 7, panels a and b) due to efficient contacts between polar moieties of the binding partners. These HB interactions are expected to contribute to the overall stabilization process by lowering down the PMF curves somewhat.⁶⁵ Few influences of HBs on the binding are detected for daidzein (Figure 7c). It should be noted, however, that the stability of HBs, which is the activation energy needed to break HBs, is virtually independent of the environment.⁶⁶

Comparison of Monomer with Dimer

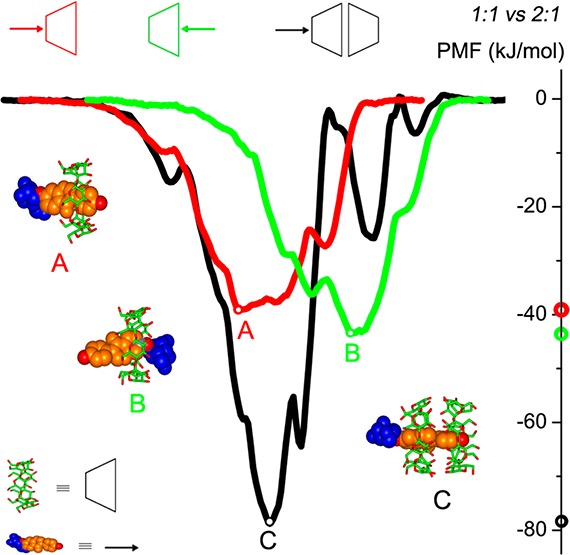
PMF profiles for inclusion complexes of the β-CD monomer in the BP and BS modes and of β-CD dimer in the BHHP mode with the studied guests along ξ are shown in Figure 8. Here the guest passes through the host cavity along +ξ from the primary rim of β-CD for BP and BHHP modes and from the secondary rim for BS. Because of differences in the definition of ξ between the monomer and dimer systems, the PMFs for BP and BS are shifted by 0.3 nm along −ξ and +ξ, respectively, allowing for direct comparison with the dimer. The most stable states for puerarin complexes with the β-CD monomer (BP) and dimer (BHHP) are located approximately in the same position of ξ = ∼0.0 nm, and the dimer only gives a small increase in the binding strength (Figure 8a). However, there exists an obvious enhancement in the binding affinity of the head-to-head dimer to daidzin (Figure 8b) and daidzein (Figure 8c).

Figure 8.

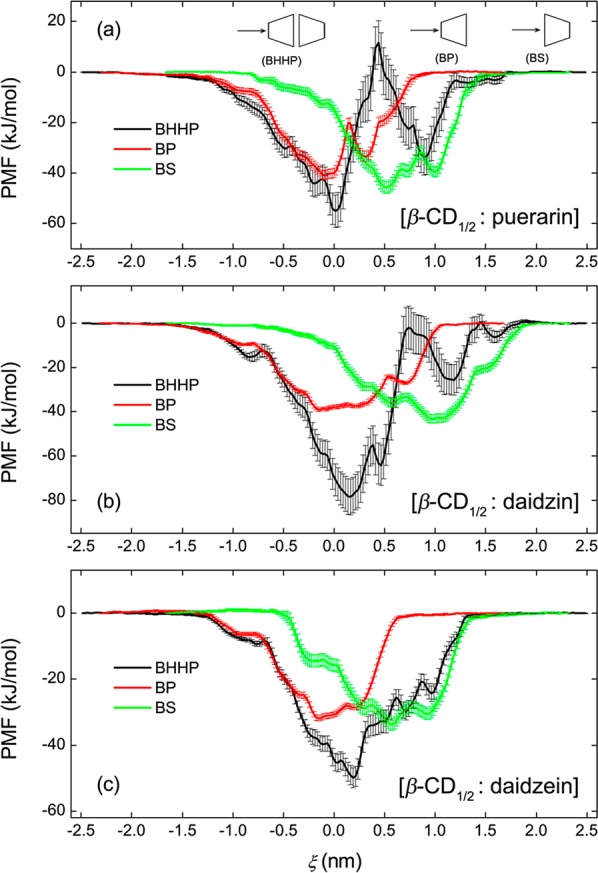
PMF comparison of β-CD monomer in the BP and BS modes with the dimer in the BHHP mode for the complex formation with (a) puerarin, (b) daidzin, and (c) daidzein. PMFs for BP and BS were taken from ref (55).

The cavity of one β-CD monomer does not encapsulate an isoflavone skeleton efficiently, leaving the skeleton in part exposed to the aqueous environment (Figure 3b). The presence of another monomer donating its hydrophobic cavity allows enclosing the exposed moieties of guest. Two β-CD monomers seem enough for encapsulation of such an isoflavone skeleton and cooperative binding of the two monomers forms a more stable inclusion complex (Figures 3 and 8). As seen from panels a and b in Figure 8, approaching the β-CD cavity for the glucose unit of puerarin and daidzin is disfavored thermodynamically (indicated by the central maxima), either in complexation with the monomer or with the dimer, whereas inclusion of the glucose unit inside the cavity seems somewhat favorable (indicated by the local minima). The energy barrier that prevents the glucose unit from further entering the β-CD cavity is higher for puerarin than for daidzin (Figure 8, panels a and b). No significant energy barriers for daidzein binding are detected (Figure 8c).

For evaluation of individual contributions to the binding affinity, the ΔH and ΔS components (see eqs S6 and S7 in the Supporting Information) are weighted by their Boltzmann factors using eq 1 and listed in Table 2. Increment factors (I) relative to the monomer are computed and given in Table 2 as well for comparison. I = 0 means that there is no significant difference between monomer and dimer; I = 1 that the energy contribution is exactly doubled. As shown in Table 2, ΔH_host and ΔH_host–host for the dimer are strengthened significantly with an increment factor (I) larger than 2 in most cases, indicating that atomic positions of host molecules changes obviously (i.e., the host molecule adjusts its configuration for a better encapsulation of its guest), in line with the observed entropy changes of the host (−TΔS_host, I = 1.6–8.3). Configurations of guest molecules do not change that much upon complexation and smaller values for ΔH_guest, ΔH_{guest–guest}, and −TΔS_guest are observed (Table 2).

Table 2. Individual Contributions (kJ/mol) of ΔH and ΔS Weighted by Boltzmann Factors for the BHHP Binding Mode (Standard Deviations in Parentheses).

	puerarin		daidzin		daidzein
⟨ΔE⟩a	BHHP	Ib	BHHP	Ib	BHHP	Ib
ΔHhost	23(3)	14.0	18(3)	17.0	28(4)	27.0
ΔHguest	–3(1)	0.0	3(1)	0.0	0(1)	0.0
ΔHhost–host	–58(6)	2.9	–11(2)	0.3	–37(4)	2.9
ΔHguest–guest	4(2)	5.0	–2(1)	0.0	0(1)	0.0
ΔHsol–sol	–214(9)	0.6	–181(9)	0.5	–203(10)	1.0
ΔHhost–guest	–238(6)	0.4	–254(8)	0.6	–215(8)	0.7
ΔHhost–sol	333(9)	1.1	243(8)	0.7	291(10)	1.4
ΔHguest–sol	165(8)	0.3	152(6)	0.3	131(7)	0.5
–TΔShost	102(5)	2.1	49(3)	1.6	107(6)	8.3
–TΔSguest	17(3)	2.1	32(4)	0.8	13(2)	12.0
–TΔSsol	–181(6)	2.9	–128(4)	2.2	–152(6)	10.7

^aWeighted on all complex states along the entire ξ of [−2.5, 2.5] using eq 1.

^bIncrement I = (d – m)/|m| where d is the energy item for dimer and m the value averaged on monomers BP and BS. Values for the monomers were taken from ref (55).

Water–water enthalpy (ΔH_sol–sol) increases by ∼50% for puerarin and daidzin and doubles for daidzein (I = 1). The cooperative effects of two monomers does not make the interaction between host and guest molecules (ΔH_host–guest) exactly twice as large, with an increment factor of I = 0.4–0.7. Upon binding, two β-CD monomers in the dimer are desolvated more intensively (ΔH_host–sol, I = 1.6–8.3), while the guests just show small desolvation increments (ΔH_guest–sol, I = 0.3–0.5). As a result of the desolvation, the water entropy increases correspondingly (−TΔS_sol, I = 2.2–10.7).

Discussion

Cyclodextrin (CD) dimer is a basic building block for the construction of diversified nanoarchitectures such as inclusion complexes, molecular necklaces, nanotubes, nanowires, and vesicles.^2,8,67−69 The cooperative binding of guest molecules to CD cavities is one of the most important driving forces in the assembly and stabilization of these architectures. In order to achieve such a cooperative effect, two CD monomers can be bridged together by a linker,^47,70−73 mostly through covalent reactions of primary hydroxyls with the linker. Bridged bis(CD)s with functional linkers lead to an increase in the binding strength and molecular selectivity compared to native CD monomers.⁷² Here we focused on the noncovalent case of 2:1 stoichiometry [CD:guest] complexes, which reveals a thermodynamic background for the stabilization of CD assemblies by cooperative binding of CD cavities to a guest (template) molecule.

Three isoflavone analogues (puerarin, daidzin, and daidzein) were tested as template molecules in this work. The former two are isomers belonging to isoflavone glycosides; puerarin is 8-C-glucoside of daidzein and daidzin 7-O-glucoside of daidzein (Figure 1b). The differences in the position of the glucose unit result in different molecule shapes and hence in different binding affinities to the β-CD dimer. Puerarin displays as a branch-like structure and daidzin a stick-like one. The glucose unit induces a high-energy barrier and hinders the tested template from further penetrating into the CD cavity, as indicated by the barriers in the PMFs (Figures 3, 4, and 7). As shown in Table 1 and Figure 8, there is no obvious increase in the binding strength of the dimer to puerarin, indicating that a second monomer is not necessary if a stable inclusion of puerarin is of interest. For daidzin and daidzein, further penetration into another monomer’s cavity is indeed essential for increased stability. Stick-like template molecules are therefore recommended to induce cooperative effects of CD cavities and to offer a stronger binding force for dimerization of CD monomers. The calculated PMFs detect local minima where the glucose unit locates in the COM region of the dimer. Hydrogen bonds (HB) may induce these favorable minima and hence favor the binding to some extent (Figure 7). Hydroxyl groups of adjacent CDs face each other in this region, yielding a somewhat hydrophilic environment. Thus, a hydrophobic stick-like template with a central hydrophilic moiety is expected to give enhanced binding to CD dimers.

For such isoflavone binding, head-to-head (HH) dimer outperforms the other two orientations of head-to-tail (HT) and tail-to-tail (TT). For HH, the two wide rims of β-CDs associate together face to face, thereby maximizing the hydrophobic cavity and allowing efficient encapsulation of template molecules. Thus, BHHP gives the strongest binding. BHTP and BTTS modes disfavor the binding to some extent because the guests encounter two narrow and hydrophilic rims of β-CDs (Figure 1d) when forming an inclusion complex and therefore a barrier to entry which means lower k_on in case binding rates are of importance. Moreover, the wide rim of CDs makes the template binding easier than the narrow rim and template stabilization of CD dimerization using two wide rims is more thermodynamically favorable. The head-to-head packing therefore appears as a better model for building blocks of CD-based nanostructured materials, in line with Pineiro’s report.²⁷

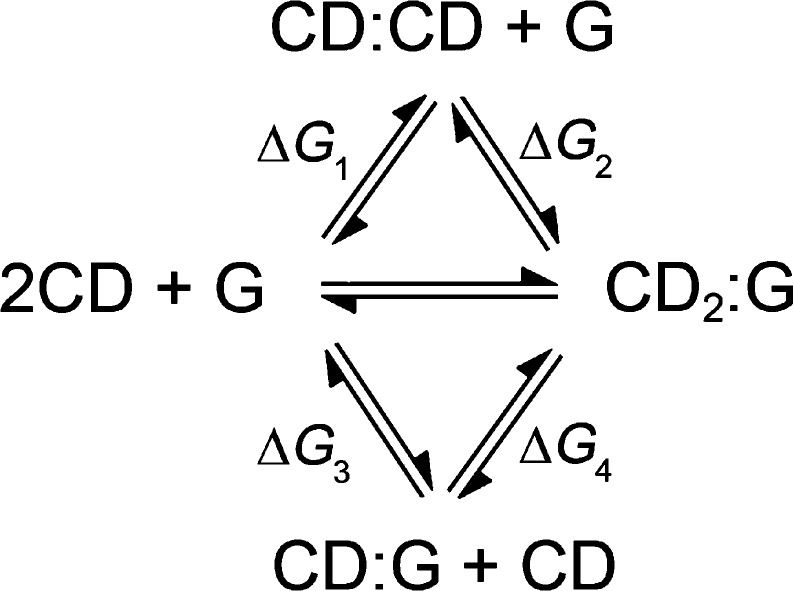
The free energy of head-to-head dimerization of β-CDs in water was calculated to be −12 kJ/mol using the same force field as in this work;⁴⁰ this value is very close to Lopez’s work of −14 kJ/mol (although the force fields used were different).³⁹ Considering the thermodynamic cycle for the binding reaction in Scheme 1, we calculated the binding free energy for each step (Table 3). An obvious cooperative effect for binding of daidzin and daidzein is observed (negative values for ΔG₄ – ΔG₁ = ΔG₂ – ΔG₃ in Table 3). To assess whether the guest (G) is indeed a template for the preferred formation of the CD dimer, one can compare the situation of 2 [CD:G] complexes versus [CD₂:G] complex + G. As shown in the last column of Table 3, we come to a conclusion that only daidzein has a templating effect (ΔG₁ + ΔG₂ – 2ΔG₃ = −5), although an enhanced binding strength was observed for all the three guests in some cases.

Scheme 1. Thermodynamic Cycle for CD Dimer Binding Reactions.

Table 3. Binding Free Energy (kJ/mol) for the Thermodynamic Cycle in Scheme 1.

	ΔG1a	ΔG2b	ΔG3c	ΔG4	ΔG4 – ΔG1d	ΔG1 + ΔG2 – 2ΔG3e
puerarin	–12	–30	–32	–10	2	22
daidzin		–38	–28	–22	–10	6
daidzein		–35	–21	–26	–14	–5

^aHH dimerization.

^bBHHP binding.

^c1:1 binding.

^dCooperative effect.

^eTemplating effect.

Template stabilization of CD assemblies can be quantified by the structure-based calculation of binding, which reveals the thermodynamic foundation of the cooperative effects induced by adjacent CD cavities. Upon host–guest complexation CD and template molecules adjust their configurations to minimize the global free energy, leading to fluctuations in atomic positions. For the binding partner, the bonded and torsion energy terms disfavor the complexation, whereas nonbonded interactions tend to favor the binding. The movements of both CD and template molecules are restricted when associated together, leading to entropy loss. For both 1:1 and 2:1 cases, the simulation captured restricted rotations of glucose unit of the guest inside the CD cavity and showed that entropy contributions from the change in flexibility of the molecules in the binding are of crucial importance for proper prediction of free energy differences. Entropic effects are ubiquitous in molecular assembly; however, reliable estimation of entropy for complex systems remains a challenge.⁷⁴ In order to establish whether there is any correlation between the free energy and entropy changes, we plot ΔG versus −TΔS_host, −TΔS_guest, and −TΔS_sol as well as −TΔS_guest versus −TΔS_host for [β-CD₂:daidzin] in the BHHP mode, as shown in Figures S3a–d, respectively. It is found that the entropy contribution is not correlated to the binding free energy (R² = 0.2). The weak correlation of −TΔS_host with −TΔS_guest (R² = 0.4) seems to agree with the finding that entropy loss of guest molecules is accompanied by entropy loss of host molecules, and vice versa (Figure 6).

Desolvation of the binding partner upon binding occurs as well and induces an enthalpy loss (positive ΔH_host–sol and ΔH_guest–sol). Water molecules that are entrapped inside CD cavity or participate in host and guest solvation are released to the bulk media, yielding a favorable ΔH_sol–sol. The liberation of solvent molecules also allows a greater degree of freedom for water movements and hence an increased ΔS_sol. Both these findings are in agreement with the common principle of hydrophobic effect.^75,76 By comparison of the monomer with the dimer, the enthalpic contributions resulting from structural changes and desolvation of host molecules and the entropy contributions from the binding partners and the solvation environment constitute the crucial factors that affect cooperative binding of β-CD dimers to the template molecules, as indicated by the higher increments in Table 2. These factors need to be considered carefully in the design of CD-based supramolecular assemblies based upon cooperative binding.

Thermodynamic analysis on the tested templates shows that the most stable binding states with β-CD dimers do not always correspond to the states where all (un)favorable energy terms achieve their maxima or minima, which confirms our previous conclusion that calculations neglecting flexibility of the binding partners and/or employing implicit solvent will not be able to predict the thermodynamics of complex binding systematically.^40,55 This finding highlights the complexity in molecular assembly and disassembly of CDs in general and is conducive to the regulation of CD-involved aggregates by e.g. template molecules. An in-depth thermodynamic analysis of the binding process described in the present study sets a theoretical foundation for cooperative binding in building blocks of CD-based nanoarchitectures. Such calculations can readily be applied in the design and construction of nanostructures with cooperatively bound units.

Supporting Information Available

Details on the thermodynamic analysis, convergence of entropy calculations, and correlation between ΔG and ΔS. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.