Attention modulates spatial priority maps in the human occipital, parietal and frontal cortices

Abstract

Computational theories propose that attention modulates the topographical landscape of spatial ‘priority’ maps in regions of visual cortex so that the location of an important object is associated with higher activation levels. While single-unit recording studies have demonstrated attention-related increases in the gain of neural responses and changes in the size of spatial receptive fields, the net effect of these modulations on the topography of region-level priority maps has not been investigated. Here, we used fMRI and a multivariate encoding model to reconstruct spatial representations of attended and ignored stimuli using activation patterns across entire visual areas. These reconstructed spatial representations reveal the influence of attention on the amplitude and size of stimulus representations within putative priority maps across the visual hierarchy. Our results suggest that attention increases the amplitude of stimulus representations in these spatial maps, particularly in higher visual areas, but does not substantively change their size.

Prominent computational theories of selective attention posit that basic properties of visual stimuli are encoded in a series of interacting ‘priority’ maps that are found at each stage of the visual system^1–6. The maps in different areas are thought to encode different stimulus features (e.g. orientation, color, motion) based on the selectivity of component neurons. Two general themes governing the organization of these maps have emerged. First, accurately encoding the spatial location of relevant stimuli is the fundamental goal of these priority maps, as spatial position is necessary to guide saccadic eye movements (and other exploratory and reflexive motor responses). Second, priority maps early in the visual system primarily reflect the physical salience of stimuli in the visual field, whereas priority maps in later areas increasingly index the behavioral relevance of stimuli, independent from physical salience^4,5.

Although many studies have investigated the influence of spatial attention on single unit neural activity over the last several decades^7–17, directly examining the impact of attention on the topographic profile across an entire spatial priority map is a major challenge because single-units have access to a limited window of the spatial scene⁵. This is a key limitation, because the relationship between changes in the size and amplitude of individual spatial receptive fields (RFs; or voxel-level RFs across populations of neurons) and changes in the fidelity of population-level spatial encoding are not related in a straightforward manner (see ref ¹⁸ for a discussion of this issue with respect to population codes for orientation). For example, if spatial RFs are uniformly shrunk by attention while viewing a stimulus, the population-level spatial representation (or priority map) carried by all those neurons might shrink or become sharper, but the code may be more vulnerable to uncorrelated noise (as there is less redundant coding of any given spatial position by the population). Alternatively, a uniform increase in spatial RF size might blur or increase the size of a spatial representation encoded by a population, but such a representation might be more robust to neural noise due to increased redundancy.

Further complicating matters is the observation that spatial RFs have been shown to both increase and decrease in size with attention as a function of where the spatial RF is positioned relative to the attended stimulus. Spatial RFs tuned near an attended stimulus grow, and spatial RFs fully encompassing an attended stimulus shrink^10,19–23. These RF size changes occur in parallel to changes in the amplitude (gain) of neural responses with attention^7–17. Thus, the net impact of all of these changes on the fidelity of population-level spatial representations is unclear, and addressing this issue requires assessing how attention changes the profile of spatial representations encoded by the joint, region-level pattern of activity.

Here, we assessed the modulatory role of attention on the spatial information content of putative priority maps by using an encoding model to reconstruct spatial representations of attended and unattended visual stimuli based on multivariate BOLD fMRI activation patterns within visually responsive regions of occipital, parietal, and frontal cortex. These reconstructions can be considered to reflect region-level spatial representations and they allow us to quantitatively track changes in parameters which characterize the topography of spatial maps within each region of interest (ROI). Importantly, this technique exploits the full multivariate pattern of BOLD signal across an entire region to evaluate the manner in which spatial representations are modulated by attention, rather than comparing multivariate decoding accuracy or considering the univariate response of each voxel in isolation. This approach can be used to examine mechanisms of attentional modulation that cannot be easily characterized by measuring changes in either the univariate mean BOLD signal or decoding accuracy^24–33 (Fig. 1, see also ref ³⁴).

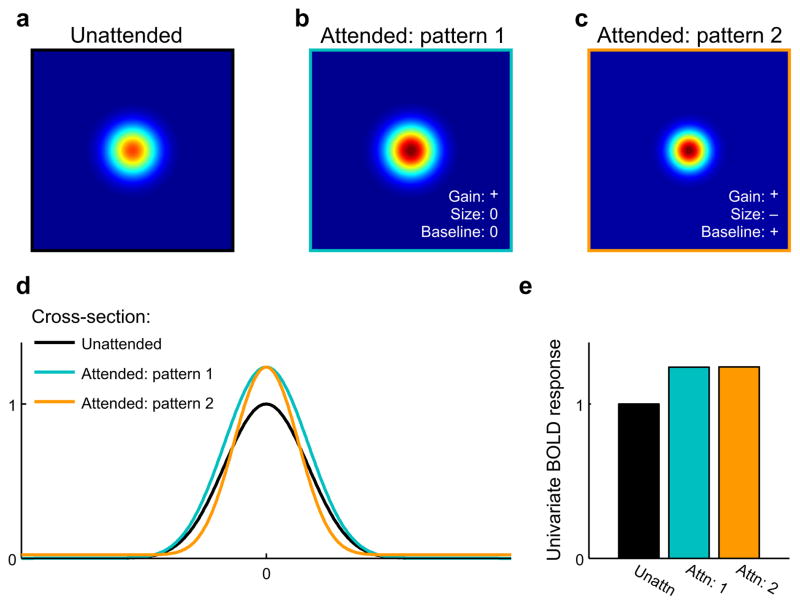
Figure 1. The effects of spatial attention on region-level priority maps.

Spatial attention might act via one of several mechanisms to change the spatial representation of a stimulus within a putative priority map.(a) The hypothetical spatial representation carried across an entire region in response to an unattended circular stimulus. (b) Under one hypothetical scenario, attention might enhance the spatial representation of the same stimulus by amplifying the gain of the spatial representation (i.e. multiplying the representation by a constant greater than 1). (c) Alternatively, attention might act via a combination of multiple mechanisms such as increasing the gain, decreasing the size, and increasing the baseline activity of the entire region (i.e. adding a constant to the response across all areas of the priority map). (d) Cross-sections of panels a–c. Note that this is not meant as an exhaustive description of different attentional modulations. (e) These different types of attentional modulation can give rise to identical responses when the mean BOLD response is measured across the entire expanse of a priority map. Note that simple Cartesian representations, such as those shown in a–c, may be visualized in early visual areas where retinotopy is well-defined at the spatial resolution of the BOLD response. However, later areas might still encode precise spatial representations of a stimulus even when clear retinotopic organization is not evident, so using alternative methods for reconstructing stimulus representations, such as the approach described in Figure 3, is necessary to evaluate the fidelity of information encoded in putative attentional priority maps.

Our results reveal that spatial attention increased the amplitude of region-level stimulus representations within putative priority maps carried by areas of occipital, parietal, and frontal cortex. However, we found little evidence that attention changes the size of stimulus representations in region-level priority maps, even though we observed increases in spatial filter size at the single-voxel level. In addition, the reconstructed spatial representations based on activation patterns in later regions of occipital, parietal, and frontal cortex showed larger attentional modulation than those from early areas, consistent with the hypothesis that representations in later regions increasingly transition to more selectively represent relevant stimuli^4,5. These changes in the gain of spatial representations should theoretically increase the efficiency with which information about relevant objects in the visual field can be processed and subsequently used to guide perceptual decisions and motor plans¹⁸.

Results

To evaluate how task demands influence the topography of spatial representations within different areas of the visual system, we designed a BOLD fMRI experiment that required participants to perform one of three tasks using an identical stimulus display (Fig. 2a). On each trial, participants (n = 8) maintained fixation at the center of the screen (see Online Methods: Eyetracking, Supplementary Fig. 1) while a full-contrast flickering checkerboard was presented in one of 36 spatial locations that sampled 6 discrete eccentricities (Fig. 2b). Participants either reported a faint contrast change at the fixation point (the “attend fixation” condition), reported a faint contrast change of the flickering checkerboard stimulus (the “attend stimulus” condition), or performed a spatial working memory task in which they compared the location of a probe stimulus, T2, with the remembered location of a target stimulus, T1, presented within the radius of the flickering checkerboard(the “spatial working memory” condition, see Fig. 2c). The spatial working memory task was included as an alternate means of inducing focused and sustained spatial attention around the stimulus position³⁵.

Figure 2. Task design & behavioral results.

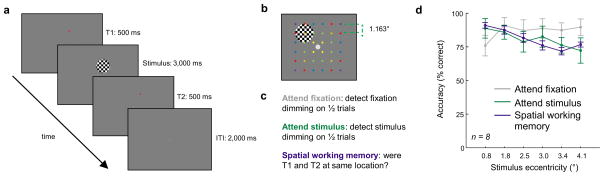
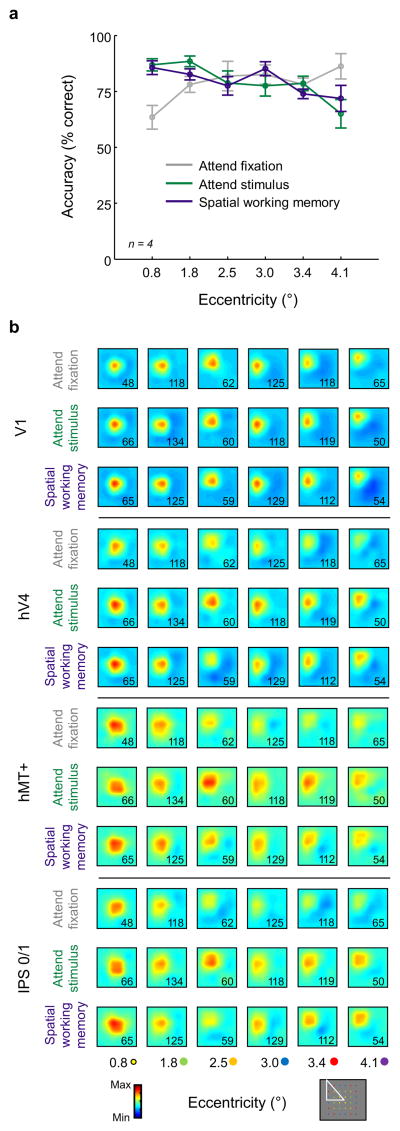
(a) Each trial consisted of a 500 ms target stimulus (T1), a 3000 ms flickering checkerboard (6 Hz, full contrast, 2.34° diameter), and a 500 ms probe stimulus (T2). T1 & T2 were at the same location on 50% of trials, and slightly offset on the remaining 50% of trials. During the stimulus presentation period, the stimulus dimmed briefly on 50% of trials and the fixation point dimmed on 50% of trials (each independently randomly chosen). Participants maintained fixation throughout the experiment, and eye position measured during scanning did not vary as a function of either task demands or stimulus position (see Supplementary Fig. 1). (b) On each trial, a single checkerboard stimulus appeared at one of 36 overlapping spatial locations with a slight spatial offset between runs (see Online Methods). Each spatial location was sampled once per run. This 6 × 6 grid of stimulus locations probes 6 unique eccentricities, as indicated by the color code of the dots (not present in actual stimulus display). (c) On alternating blocks of trials, participants either detected a dimming of the fixation point (attend fixation), detected a dimming of the checkerboard stimulus (attend stimulus), or they indicated if the spatial position of T1 and T2 matched (spatial working memory). Importantly, all tasks used a physically identical stimulus display – only the task demands varied. Each participant completed between 4 and 6 scanning runs of each of the 3 tasks. (d) For the attend fixation task, performance was better when the stimulus was presented at peripheral locations. In contrast, performance declined with increasing stimulus eccentricity in the attend stimulus and spatial working memory conditions. All error bars reflect ±1 S.E.M.

On average, performance in the attend fixation task was slightly, though non-significantly, higher than in the attend stimulus or spatial working memory tasks (Fig. 2d, main effect of condition: F(2,14) = 0.951, p = 0.41; attend fixation: 87.37 ± 6.46%, attend stimulus: 81.00 ± 6.67%, spatial working memory: 80.00 ± 2.09% accuracy, mean ± S.E.M.). However, we observed a different pattern of response errors across the 3 task demands: accuracy for the attend fixation condition was lowest on trials in which the flickering checkerboard stimulus was presented near fixation, whereas accuracy dropped off with increasing stimulus eccentricity for the attend stimulus and spatial working memory tasks (Fig. 2d, condition × eccentricity interaction: F(10,70) = 7.235, p < 0.0001).

To compare spatial representations carried within different brain regions as a function of task demands, we first functionally identified 7 ROIs in each hemisphere of each participant using independent localizer techniques (see Online Methods: Functional localizers; Supplementary Table 1).

Next we used an encoding model³⁶ (see also refs. ^34,37,38) to reconstruct a spatial representation of the stimulus that was presented on each trial using activation patterns from each ROI (Fig. 3). This method results in a “spatial representation” of the entire visual field measured on each trial that is constrained by activation across all voxels within each ROI. As a result, we obtain average spatial representations for each stimulus position for each ROI for each task condition which accurately reflect the stimulus viewed by the observer (Fig 4a). This method linearly maps high dimensional voxel space to a lower-dimensional spatial information space that corresponds to visual field coordinates (see Online Methods: Encoding Model for details).

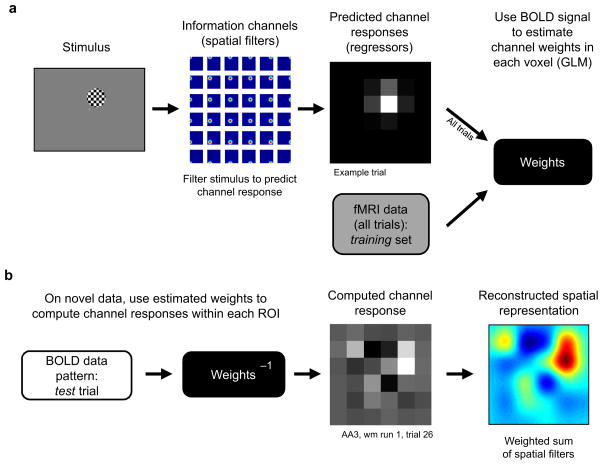
Figure 3. Encoding model used to reconstruct spatial representations of visual stimuli.

Spatial representations of stimuli in each of the 36 possible positions were estimated separately for each ROI. (a) Training the encoding model: a set of linear spatial filters forms the basis set, or “information channels”, that we use to estimate the spatial selectivity of the BOLD responses in each voxel (see Online Methods: Encoding model, Supplementary Figs. 2 & 3). The shape of these filters determines how each information channel should respond on each trial given the position of the stimulus that was presented (thus forming a set of regressors, or predicted channel responses). Then, we constructed a design matrix by concatenating the regressors generated for each trial. This design matrix, in combination with the measured BOLD signal amplitude on each trial, was then used to estimate a weight for each channel in each voxel using a standard general linear model (GLM). (b) Estimating channel responses: given the known spatial selectivity (or weight) profile of each voxel as computed in step a, we then used the pattern of responses across all voxels on each trial in the ‘test’ set to estimate the magnitude of the response in each of the 36 information channels on that trial. This estimate of the channel responses is thus constrained by the multivariate pattern of responses across all voxels on each trial in the test set, and results in a mapping from voxel space (hundreds of dimensions) onto a lower-dimensional channel space (36 dimensions, for mathematical details see Online Methods). Finally, we produced a smooth reconstructed spatial representation on every trial by summing the response of all 36 filters after weighting them by the respective channel responses on each trial. An example of a spatial representation computed from a single trial using data from V1 when the stimulus was presented at the location depicted in (a) is shown in the lower right panel.

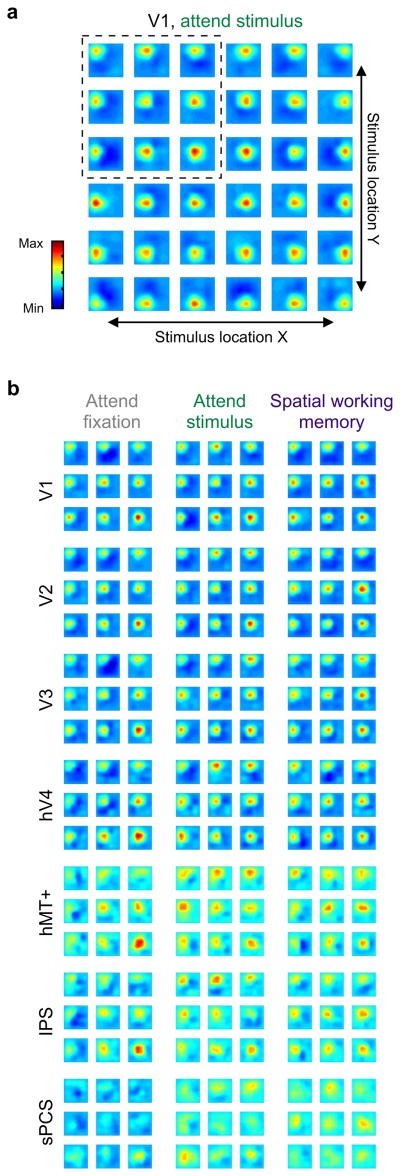
Figure 4. Task demands modulate spatial representations.

(a) Reconstructed spatial representations of each of 36 flickering checkerboard stimuli presented in a 6 × 6 grid. All 36 stimulus locations are shown, with each location’s representation averaged across participants (n = 8) using data from bilateral V1 during attend stimulus runs. One participant was not included in this analysis (AG3, see Supplementary Fig. 4). Each small image represents the reconstructed spatial representation of the entire visual field, and the position of the image in the panel corresponds to the location of the presented stimulus. (b) A subset of representations (corresponding to the upper left quadrant of the visual field, dashed box in a) for each ROI and each task condition. Results are similar for other quadrants (not shown, although see Fig. 5 for aggregate quantification of all reconstructions). All reconstructions in a and b are shown on the same color scale.

As a point of terminological clarification, we emphasize that we are reporting estimates of the spatial representation of a stimulus display based on the distributed activation pattern across all voxels within a ROI. Throughout the Results section, we will therefore refer to our actual measurements as “reconstructed spatial representations”. However, in the Discussion, we will interpret these measurements in the context of putative attentional priority maps that are thought to play a key role in shaping perception and decision making^1–6.

Reconstructed spatial representations of visual stimuli

Reconstructed spatial representations based on activation patterns in each ROI exhibited several qualitative differences as a function of stimulus eccentricity, task demands, and ROI (which we more formally quantify below). First, we note that representations were very precise in V1 (Fig 4a), and became successively coarser and more diffuse in areas of extrastriate, parietal, and frontal cortex (Fig. 4b). Similarly, representations of more eccentric stimuli were more diffuse compared to more foveal stimuli (e.g., compare eccentric to foveal representations within each ROI). We also observed higher fidelity representations of the upper visual field when using only voxels from the ventral aspects of V2 and V3, and higher fidelity representations of the lower visual field when using only voxels from the dorsal aspects of these regions (Supplementary Fig. 5a). This observation, which is consistent with known receptive field locations in non-human primates, confirms that our encoding model method recovered known properties of these visual subregions and that these reconstructions were not merely the result of fitting idiosyncratic aspects of our particular data set (i.e. overfitting noise). We further demonstrated this point by using the model to reconstruct representations of completely novel stimuli (Supplementary Fig. 5b).

Second, the profile of reconstructed spatial representations within many regions also varied with task demands, consistent with the notion that these spatial representations reflect spatial maps of attentional priority. Note that, especially in hV4, hMT+, the intraparietal sulcus (IPS), and superior precentral sulcus (sPCS), the magnitude of the spatial representations increased when the participant was either attending to the flickering checkerboard stimulus or performing the spatial working memory task compared to when they were performing a task at fixation.

Size of spatial representations across eccentricity & ROI

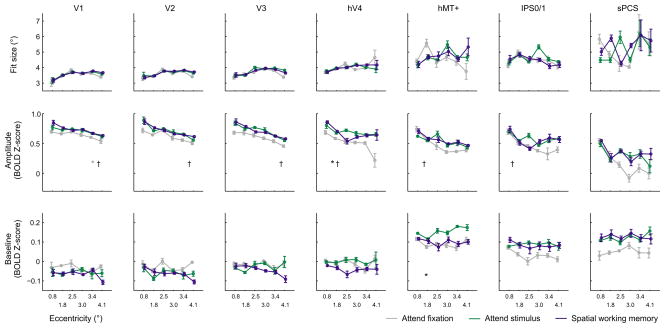
Before formally evaluating the effects of attention on the profile of spatial representations, we first sought to quantify changes in the size of these representations due to stimulus eccentricity and ROI for comparison with known properties of the primate visual system. To this end, we fit a smooth surface to the spatial representations associated with each of the three task conditions separately for each of the 36 possible stimulus locations in each ROI (see Online Methods: Curvefitting and Supplementary Fig. 2). These fits generated an estimate of the amplitude, baseline offset, and the size of the represented stimulus within each reconstructed spatial representation. We averaged the fit parameters obtained from each ROI across stimulus locations that were at equivalent eccentricities and then across participants (yielding 6 sets of fit parameters, one set for each of the 6 possible stimulus eccentricities, see color code in Fig. 2b). We then used these fit parameters to make inferences about how the magnitudes and shapes of spatial representations of stimuli from each ROI varied across stimulus positions.

First, we quantified the accuracy of fits by computing the Euclidean distance between the centroid of the fit function and the actual location of the stimulus across all eccentricities and task conditions. The estimated centroids were generally accurate and closely tracked changes in stimulus location (Fig 4a). However, the distances between fit centroids and the actual stimulus positions in sPCS were nearly double those of the next least accurate region, hMT+ (sPCS: 3.01° ± 0.077°, hMT+: 1.68° ± 0.17°, mean ± S.E.M.). Error distances in all other areas were relatively small (V1: 0.67° ± 0.084°, V2: 0.77° ± 0.12°, V3: 0.75° ± 0.095°, hV4: 1.16° ± 0.13°, IPS: 1.46° ± 0.20°). Thus, the relatively low correspondence between the estimated and actual stimulus position based on data from the sPCS suggests that the resulting fit parameters should be interpreted with caution (we return to this point in the Discussion).

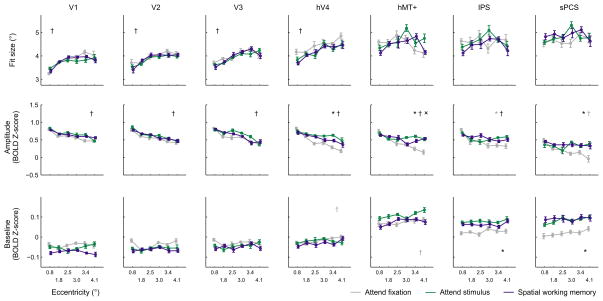
In early visual ROIs V1, V2, V3, and hV4, the size of the reconstructed spatial representations increased with increasing eccentricity, regardless of task condition (Fig. 5, main effect of eccentricity, 2-way ANOVA within each ROI, all p’s < 0.0004; unless otherwise specified, all statistical tests on fit parameters to spatial representations employed a non-parametric permutation procedure and corrected for multiple comparisons, see Online Methods: Statistical Methods). This increase in size with eccentricity is expected, given the use of a constant stimulus size and the well-documented increase in the size of spatial RFs in early visual areas with increasing eccentricity³⁹. In addition, the size of the reconstructed stimulus representations also increased systematically from V1 to sPCS, which is also consistent with the known expansion of mean spatial RF sizes in parietal and frontal cortex^40,41 (3-way ANOVA, significant main effect of ROI on fit size, p < 0.0001).

Figure 5. Fit parameters to reconstructed spatial representations, averaged across like eccentricities.

For each participant, we fit a smooth 2D surface (see Online Methods: Curvefitting) to the average reconstructed stimulus representation in all 36 locations, separately for each task condition and ROI. We allowed the amplitude, baseline, size, and center ({x,y} coordinate) of the fit basis function to vary freely during fitting. Fit parameters were then averaged within each participant across like eccentricities, and then averaged across participants. The size of the best fitting surface varied systematically with stimulus eccentricity and ROI, but did not vary as a function of task condition. In contrast, the amplitude of the best fitting surface increased with attention in hV4, hMT+ and sPCS (with a marginal effect in IPS, see text).

*, ^†, ^× indicate main effect of task condition, eccentricity, and interaction between task and eccentricity, respectively at the p < 0.05 level, corrected for multiple comparisons (see Online Methods: Statistical Procedures). Grey symbols indicate trends at the p < 0.025 level, uncorrected for multiple comparisons. Error bars reflect within-participant S.E.M.

One alternative explanation is that the size of represented stimuli increases with eccentricity because there is more trial-to-trial variability in the center point of the represented stimulus within reconstructions at more peripheral stimulus locations. In turn, this increase in trial-to-trial variability would ‘smear’ the spatial representations, leading to larger size estimates. However, our data speak against this possibility as increased variability in the reconstructed stimulus locations would also result in lower estimated amplitudes, so increases in fit size and decreases in fit amplitude across conditions would always be yoked and correlating the change in amplitude and the change in size within each eccentricity across each condition pair would reveal a negative correlation (e.g., if the size of the spatial representation measured at a given eccentricity increases with attention, then the amplitude decreases). No combinations of condition pair, eccentricity and ROI revealed a significant correlation between change in amplitude and change in size (all p’s > 0.05, corrected using FDR, see Online Methods: Statistical procedures). Furthermore, in a follow-up analysis we computed the population receptive field (pRF) for each voxel⁴², which revealed that voxels tuned to more eccentric visual field positions have a larger pRF size (Supplementary Figs. 8–9; Supplementary Table 2). This combination of analyses supports the conclusion that increases in fit size with increases in stimulus eccentricity are not purely due to increased variability in reconstructed spatial representations.

Effects of attention on spatial representations

Despite being sensitive to expected changes in representation size based on anatomical properties of the visual system, task demands exerted a negligible influence on the size of reconstructed spatial representations, with no areas showing a significant effect (hV4 was closest at p = 0.033, but this did not survive correction for multiple comparisons, and p-values in all other regions were > 0.147).

In contrast, the fit amplitude in hV4, hMT+, IPS, and sPCS is significantly modulated by task condition, with a higher amplitude in the attention and working memory conditions than in the fixation condition (Fig. 5, 3-way ANOVA, main effect of task condition, p = 0.0003). For example, in hV4, the amplitude of the best fitting surface to spatial representations of attended stimuli was higher during the attend stimulus and spatial working memory conditions compared to the attend fixation condition (2-way ANOVA, main effect of task condition, p < 0.0001). Similar effects were observed in hMT+ (2-way ANOVA, p = 0.0007) and sPCS (2-way ANOVA, p = 0.0007). A similar pattern was evident in IPS as well, but it did not survive correction for multiple comparisons (2-way ANOVA, uncorrected p = 0.011). Within individual ROIs, there was a significant interaction between task condition and eccentricity in hMT+ (p = 0.0003) with larger increases in amplitude observed for more eccentric stimuli. It is important to note that this increase in the amplitude of spatial representations with attention corresponds to a focal gain modulation that is restricted to the portion of visual space in the immediate neighborhood of the attended stimulus. Changes in fit amplitude do not result from a global increase in the BOLD signal that equally influences the response across an entire ROI; such a general and widespread modulation would be accounted for by an increase in the baseline fit parameter (see Supplementary Fig. 2; below). Finally, the impact of task condition on the amplitude of reconstructed spatial representations was more pronounced in later visual areas hV4/hMT+/IPS/sPCS compared to earlier areas V1/V2/V3 (3-way interaction between ROI, condition and eccentricity, p = 0.043).

In addition to an increase in the fit amplitude of the reconstructed spatial representations, IPS and sPCS also exhibited a spatially global increase in baseline response levels across the entire measured spatial representation in the attend stimulus and spatial working memory conditions compared to the attend fixation condition (Fig. 5, 2-way ANOVAs, main effect of condition, IPS: p = 0.0014; sPCS: p = 0.0012; see Supplementary Fig. 6). The spatially non-selective increases may reflect the fact that spatial RFs in these regions are often large enough to encompass the entire stimulus display^40,41, so all stimuli might drive some increase in the response, irrespective of spatial position.

Controlling difficulty across task conditions

Slight differences in task difficulty in the first experiment (Fig. 2d) might have contributed to observed changes in the spatial representations. To address this possibility, we ran four participants from the original cohort in a second experimental session while carefully equating behavioral performance across all 3 tasks (Fig. 6a). Overall accuracy during this second session did not differ significantly across the 3 conditions, although a similar interaction is observed between task condition and stimulus eccentricity (Fig. 6a, 2-way repeated-measures ANOVA, main effect of condition: F(2,6) = 0.043, p = 0.96, condition × eccentricity interaction: F(10,30) = 3.28, p = 0.005; attend fixation: 78.8 ± 2.80%, attend stimulus: 80.0 ± 2.60%, spatial working memory: 79.8 ± 1.76%, mean ± S.E.M.). In addition, we also identified IPS visual field maps 0–3 using standard procedures so that we could more precisely characterize the effects of attention on stimulus representations in sub-regions of our larger IPS ROI (refs ^31,32,43,44; see Online Methods: Mapping IPS subregions, Supplementary Fig. 7).

Figure 6. Results are consistent when task difficulty is matched.

(a) Four participants were re-scanned while carefully matching task difficulty across all three experimental conditions. As in Figure 2d, performance is better on the attend fixation task when the checkerboard is presented in the periphery, and performance on the attend stimulus and spatial working memory tasks is better when the stimulus is presented near the fovea. (b) A subset of illustrative reconstructed stimulus representations from V1, hV4, hMT+, IPS 0/1, averaged across like eccentricities (correct trials only, number of averaged trials indicated by inset). See Supplementary Figure 7 for details on IPS subregion identification.

To ensure that behavioral performance was not unduly biasing our results, we reconstructed spatial representations using only correct trials (~80% of total trials, Fig 6a). All representations were co-registered based on stimulus eccentricity before averaging (see Fig. 2b for corresponding eccentricity points). Even though our sample size was smaller (n = 4 vs. n = 8), the influence of attention on the topography of spatial representations was similar to our initial observations (Fig. 6b). In addition, mapping out retinotopic subregions of the IPS revealed that the functionally-defined IPS ROI presented in Figure 5 primarily corresponds to IPS0 and IPS1 (Supplementary Fig. 7a–b).

When examining best-fit surfaces to spatial representations from this experiment (Fig. 7, fits computed using coregistered representations and only correct trials for each participant, see Online Methods: Curvefitting), we found that attention significantly modulated the amplitude across all regions (3-way ANOVA, main effect of task condition, p = 0.0162). When considered in isolation, only hV4 shows a significant change in amplitude with attention after correction for multiple comparisons (2-way repeated-measures ANOVA, p = 0.0022). However, similar trends were observed in V1, V2, and V3 (uncorrected p’s = 0.0243, 0.042, and 0.031, respectively). No significant main effect of task condition on the size of representations was found (all p’s > 0.135, minimum p for hMT+), and overall baseline levels only significantly increased as a function of task condition in hMT+ (p = 0.00197). Across all ROIs, there was a main effect of eccentricity on fit size (3-way ANOVA, p = 0.0016), but no main effect of task condition on fit size (3-way ANOVA, p = 0.423).

Figure 7. Fit parameters to spatial representations after controlling for task difficulty.

As in Figure 5, a surface was fit to the averaged, coregistered spatial representations for each participant. However, in this case task difficulty was carefully matched between conditions, and representations were based solely on trials in which the participant made a correct behavioral response (Fig. 6b). Results are similar to those reported in Figure 5: attention acts to increase the fit amplitude of spatial representations in hV4, but does not act to decrease size. In hMT+, attention also acted in a non-localized manner to increase the baseline parameter. Statistics as in Figure 5. Error bars reflect within-participant S.E.M.

Population receptive fields (pRFs) expand with attention

For these same 4 participants, we computed the population receptive field (pRF, ref ⁴²) for each voxel in V1, hV4, hMT+ and IPS0 using data from the behaviorally-controlled replication experiment. Here, we computed pRFs by first using the initial step of our encoding model estimation procedure (Fig. 3a) to determine the response of each voxel to each position in the visual field (Supplementary Figs. 8–9, Online Methods: population receptive fields). We then fit each voxel’s response profile with the same surface used to characterize spatial representations. By comparing pRFs computed using data from each condition independently, we found that a majority of pRFs in hV4, hMT+ and IPS0 increase in size during either the attend stimulus or spatial working memory condition compared to the attend fixation condition. In contrast, pRF size in V1 was not significantly modulated by attention (Supplementary Fig. 9; see Supplementary Results for statistics).

To reconcile the results that voxel-level pRFs expanded with attention, yet region-level spatial representations remained a constant size, we simulated data using estimated pRF parameters from hV4 (a region for which spatial representations increase in amplitude and pRFs increase in size; see Online Methods: Simulating data with different pRF properties) under different pRF modulation conditions. In the first condition, we generated data using pRFs with sizes centered around two mean values, resulting in a pRF scaling across all simulated voxels (average size across voxels increases, but some voxels decrease in size and others increase). Under these conditions, spatial representations increase in size (Supplementary Fig. 10a–b). In a second pRF modulation scenario, we used the fit pRF values from one participant’s hV4 ROI (Supplementary Fig. 8) to simulate data. In this case, spatial representations remained the same size, but increased in amplitude, consistent with our observations using real data (Figs. 5, 7, Supplementary Fig. 10c–d; this conclusion was also supported when pRF data from the other 3 observers was used to seed the simulation). Thus, the pattern of pRF modulations across all voxels enhances the amplitude of spatial representations while preserving their size.

Discussion

Spatial attention has previously been shown to alter the gain of single-unit responses associated with relevant visual features such as orientation^{7–9,12,13,16,17} and motion direction^11,14,15, as well as to modulate the size of spatial RFs^10,19–23. Here, we show that these local modulations jointly operate to increase the overall amplitude of the region-level spatial representation of an attended stimulus, without changing its represented size. Furthermore, these amplitude modulations were especially apparent in later areas of the visual system such as hV4, hMT+, and IPS, consistent with predictions made by computational theories of attentional priority maps^4,5.

We were able to reconstruct robust spatial representations across a range of eccentricities and for all 3 task conditions in all measured ROIs. Importantly, even though an identical reconstruction procedure was used in all areas, the size of the reconstructed spatial representations increased from early to later visual areas (Fig. 5). Single-unit receptive field sizes across cortical regions are thought to increase in a similar manner^{39–41,45,46}. In addition, representations of stimuli presented at higher eccentricities were larger than representations of stimuli presented near the fovea, which also corresponds to known changes in RF size with eccentricity^39,42. Furthermore, simulating data under conditions in which we uniformly scale the mean size of voxel-level pRFs reveals that such changes are detectable using our analysis method (Supplementary Fig. 10a–b). Thus, this technique is sensitive to detect changes in the size of spatial representations of stimuli that are driven by known neural constraints such as relative differences in RF size across cortical ROIs and eccentricity, even though these factors are not built-in to the spatial encoding model. Together, these empirical and modeling results suggest that at the level of region-wide priority maps, the representation of a stimulus does not expand or contract under the attentional conditions tested here, and underscores the importance of incorporating response changes across all encoding units when evaluating attentional modulations.

The quantification method we implemented for measuring changes in spatial representations across tasks, eccentricities, and ROIs involved fitting a surface defined by several parameters: center location, amplitude, baseline offset, and size (Supplementary Fig. 2). Changes in activation which carry no information about stimulus location (such as changes in general arousal or responsiveness to stimuli presented in all locations due to large RFs) will influence the baseline parameter, as such changes reflect increased/decreased signal across an entire region. In contrast, a change in the spatial representation that changes the representation of a visual stimulus would result in a change in the amplitude or in the size parameter (or both). Here, we demonstrated that attention primarily operates by selectively increasing the amplitude of stimulus representations in several putative priority maps (Figs. 5 and 7), rather than increasing the overall BOLD signal more generally across entire regions.

Interestingly, spatial reconstructions based on activation patterns from sPCS were relatively inaccurate compared to other ROIs, and this ROI primarily exhibited increases in the fit baseline parameter (Fig. 5). This region, which may be a human homolog of the functionally-defined macaque frontal eye fields^47,48 (FEF), may show degraded spatial selectivity in the present study due to the relatively large size of spatial receptive fields observed in many FEF neurons (typically ≥ 20° diameter: see ref. ⁴¹) and the small area subtended by our stimulus display (9.31° horizontally across). Consistent with this possibility, previous reports of retinotopic organization in human frontal cortex used stimuli presented at higher eccentricities in order to resolve spatial maps (≥10°, ref. ⁴⁹ to 25°, ref. ⁴⁵).

Attentional priority maps

The extensive literature on spatial “salience” or “priority” maps^1–6 postulates the existence of one or several maps of visual space, each carrying information about behaviorally relevant objects within the visual scene. Furthermore, priority maps in early visual areas (e.g. in primary visual cortex) are thought to primarily encode low-level stimulus features (e.g., contrast), whereas priority maps in later regions are thought to increasingly weight behavioral relevance over low-level stimulus attributes⁴. While many important insights have stemmed from observing single-unit responses as a function of changes in attentional priority (see ⁵ for a review), these results provide information about how isolated “pixels” in a priority map change under different task conditions.

A previous fMRI study used multivariate decoding (classification) analyses to identify several frontal and parietal ROIs that exhibit similar activation patterns during covert attention, spatial working memory, and saccade generation tasks³². These results provide strong support for the notion that common priority maps support representations of attentional priority across multiple tasks. Here, we assessed how the holistic landscape across these priority maps measured using fMRI changed as attention was systematically varied. Our demonstration that spatial representation amplitude is enhanced with attention in later ROIs, but not earlier ones, supports the hypothesis that priority maps in higher areas are increasingly dominated by attentional factors, and suggests that these attentional modulations of priority maps operate via scaling the amplitude of the behaviorally-relevant item without changing its represented size.

Population receptive fields

In addition to measuring spatial representations carried by the pattern of activation across entire visual regions, we also estimated the voxel-level pRFs⁴² for a subset of participants and ROIs by adding constraints to our encoding model estimation procedure (Supplementary Figs. 8–9; Online methods: population receptive fields). This alternative tool has been used previously to evaluate the aggregate spatial RF profile across all neural populations within voxels across different visual ROIs⁴².

Changes in voxel-level pRFs can inform how a region dynamically adjusts the spatial sensitivity of its constituent filters in order to modulate its overall spatial priority map. First, we replicated the typical result that voxel-level pRFs tuned for more eccentric visual field positions are larger in size (Supplementary Table 2), and that pRFs for later visual regions tend to be larger than pRFs for earlier visual regions (Supplementary Fig. 9). Second, results from this complementary analysis revealed that, in regions which showed enhanced spatial representation amplitude with attention (hV4, hMT+, IPS0), pRF size increased (Supplementary Figs. 8–9), even though the corresponding region-level spatial representations did not increase in size (Fig. 7). This may seem like a disconnect, given that the particular pattern of pRF changes across all voxels within a region jointly shapes how the spatial priority map changes with attention. However, there is not necessarily a monotonic mapping between the size of the constituent filters and the size of population-level spatial representations (see below, Information content of attentional priority maps). Indeed, simulations based on the observed pattern of pRF changes with attention give rise to region-level increases in representation amplitude in the absence of changes in representation size, just as we observed in our data (Supplementary Fig. 10). This finding, together with our primary results concerning region-level spatial representations, provides important evidence that attentional modulation of spatial information encoding is a process that strongly benefits from study at the large-scale population level.

Comparing to previous results

At the level of single unit recordings, attention has been shown to decrease the size of MT spatial RFs when an animal is attending to a stimulus encompassed by the recorded neuron’s RF^19–21 and to increase the size of spatial RFs when an animal is attending nearby the recorded neuron’s RF^20–22. In V4, spatial RFs appear to shift toward the attended region of space in a subset of neurons¹⁰. With respect to cortical space, these single-unit attentional modulations of spatial RFs suggest that unifocal attention may act to increase the cortical surface area responsive to a stimulus of constant size. Consistent with this prediction, our measured pRFs for extrastriate regions hV4, hMT+ and IPS0 increased in size with attention.

In contrast, one previous report suggested that spatial attention instead narrows the activation profile along the cortical surface of visual cortex in response to a visual stimulus⁵⁰. However, this inference was based on patterns of inter-trial correlations between BOLD activation patterns associated with dividing attention between 4 stimuli (one presented in each quadrant). These patterns were suggested to result from a combination of attention-related gain and narrowing of population-level responses⁵⁰; that is, a narrower response along the cortical surface with attention.

We did not observe any significant attention-related changes in the size of the reconstructed spatial representations in either primary visual cortex or other areas in extrastriate, parietal, or frontal cortex. However, the tasks performed by observers and the analysis techniques implemented were very different between these studies. Most notably, observers in the present study and in previous fMRI^24–33 and single-unit studies^10,19–21 were typically required to attend to a single stimulus, whereas population-level activation narrowing was observed when participants simultaneously attended to the precise spatial position of 4 Gabor stimuli, one presented in each visual quadrant⁵⁰. Furthermore, our observation that pRFs increased in size during the attend stimulus and spatial working memory conditions is compatible with the pattern of spatial RF changes in single-units^10,19–23, and our data and simulations show that these local changes can result in a region-level representation that changes only in amplitude, not size (Supplementary Fig. 10).

Collectively, it seems probable that the exact task demands (unifocal vs. multifocal attention) and stimulus properties (single stimulus vs. multiple stimuli) may play a key role in determining how attention influences the profile of spatial representations. Future work using analysis methods sensitive to region-level differences in spatial representations (e.g. applying encoding models like that described here to data acquired when participants perform different tasks), in conjunction with careful identification of neural RF properties across those task demand conditions (e.g., from simultaneous multi-unit electrophysiological recordings or in vivo two-photon Ca²⁺ imaging in rodents and primates), may provide complementary insights into when and how attention changes the shape and/or changes the amplitude of stimulus representations in spatial priority maps and how those changes are implemented in neural circuitry.

Importantly, while our observations are largely consistent with measured RF changes at the single-unit level^10,19–23, we cannot make direct inferences that such single-unit changes are in fact occurring. A number of mechanisms, including a mechanism whereby only the gain of different populations is modulated by attention, could also account for the pattern of results we see both in our region-level spatial representations (Figs. 5 & 7) and our pRF measurements (Supplementary Figs. 8–9). We do note, however, that some neural mechanisms are highly unlikely given our measured spatial representations and pRFs. For example, we would not observe an increase in pRF size if spatial RFs of neurons within those voxels were to exclusively narrow with attention. As a result of these interpretational concerns, we restrict the inferences we draw from our results to the role of attention in modulating region-level spatial priority maps measured with fMRI, and make no direct claims about spatial information coding at a neural level.

Information content of attentional priority maps

One consequence of an observed increase in the amplitude of reconstructed priority maps is that the mutual information (MI) between the stimulus position and the observed BOLD responses should increase (see ref ¹⁸ for a more complete discussion). This increase can occur, in theory, because MI reflects the ratio of signal entropy (variability in neural responses tied systematically to changes in the stimulus) to noise entropy (variability in neural responses that is not tied to changes in the stimulus). Thus a multiplicative increase in the gain of the neural responses associated with an attended stimulus should increase MI because it will increase the variability of responses that are associated with an attended stimulus location, which will in turn increase signal entropy. In contrast, a purely additive shift in all neural responses (reflected by an increase in the fit baseline parameter) will not increase the dynamic range of responses associated with an attended stimulus location, causing MI to either remain constant (under a constant additive noise model), or even to decrease (under a Poisson noise model, in which noise increases with the mean). Previous fMRI work on spatial attention has not attempted to disentangle these two potential sources of increases in the BOLD signal, highlighting the utility of approaches that can support more precise inferences about how task demands influence region-level neural codes^24–33.

The information content of a neural code is not necessarily monotonically related to the size of the constituent neural filters¹⁸. Extremely small (pinpoint) or extremely large (flat) spatial filters each individually carry very little information about the spatial arrangement of stimuli within the visual field. Accordingly, the optimal filter size lies somewhere between these two extremes, and thus it is not straightforward to infer whether a change in filter size results in a more or less optimal neural code (in terms of information encoding capacity). By simultaneously estimating changes in filter size across an entire ROI subtending the entire stimulated visual field, we were able to demonstrate that the synergistic pattern of spatial filter (pRF) modulations with attention jointly constrains the region-level spatial representation to maintain a constant size, despite most voxels exhibiting an increase in pRF size (Supplementary Figs. 8–10). Together, our results demonstrate the importance of incorporating all available information across entire ROIs when evaluating the modulatory role of attention on the information content of spatial priority maps.

Online Methods

Participants

10 neurologically healthy volunteers (5 female, 25 ± 2.11 years, mean ± standard dev.) with normal or corrected-to-normal vision were recruited from the University of California, San Diego (UCSD). All participants provided written informed consent in accordance with the human participants Institutional Review Board at UCSD and were monetarily compensated for their participation. Participants participated in 2–3 scanning sessions, each lasting 2 hours, for the original experiment. Data from 2 participants (1 female) were excluded from the main analysis because of excessive head movement (AJ3) or because of unusually noisy reconstructions during attend fixation runs (AG3, see below).

In the follow-up experiment in which behavioral performance was carefully controlled and IPS subregions were retinotopically mapped, 4 participants of our original cohort were scanned for an additional 2 sessions, each lasting 1.5–2 hrs.

Stimulus

Stimuli were rear-projected on a screen (90 cm width) located 380 cm from the participant’s eyes at the foot of the scanner table. The screen was viewed using a mirror attached to the headcoil.

We presented an identical stimulus sequence during all imaging runs while asking observers to perform several different tasks. Each trial began with the presentation of a small red dot (T1) that was presented for 500 ms, followed by a flickering circular checkerboard stimulus at full contrast (2.34° diameter, 1.47 cycles/°) that was presented for 3 s, followed by a probe stimulus (T2) that was identical to T1. A 2 s intertrial interval (ITI) separated each trial (Fig. 2a). T1 was presented between 0.176° and 1.104° from the center of the checkerboard stimulus along a vector of a random orientation (in polar coordinates, θ₁ was randomly chosen along the range of 0° to 360°, and r₁ was uniformly sampled from the range 0.176° to 1.104°). This ensured that the location of T1 was not precisely predictive of checkerboard location. On 50% of trials T2 was presented in the same location as T1, and the remaining trials, T2 was presented between 0.176° and 1.104° from the center of the checkerboard along a vector oriented at least 90° from the vector along which T1 was plotted (r₂ was uniformly sampled from the range 0.176° to 1.104° and θ₂ was randomly chosen by adding between 90° and 270°, uniformly sampled, to θ₁). Polar coordinates use the center of the checkerboard stimulus as the origin. During the working memory condition (see below), participants based their response on whether T1 and T2 were presented in the exact same spatial position.

The location of the checkerboard stimulus was pseudo-randomly chosen on each trial from a grid of 36 potential stimulus locations, spaced by 1.17°. The stimulus location grid was jittered by 0.827° diagonally either up and to the left or down and to the right on each run, allowing for an improved sampling of space. All figures are presented aligned to a common space by removing jitter (see below).

On each run, there were 36 trials (one trial for each stimulus location) and 9 null trials in which participants passively fixated for the duration of a normal trial (6 s). We scanned participants for between 4 and 6 runs of each task, always ensuring each task was repeated an equal number of times.

Tasks

Participants performed one of 3 tasks during each functional run (Fig. 2c). During attend fixation runs, participants responded when they detected a brief contrast dimming of the fixation point (0.33 s) which occurred on 50% of trials. During attend stimulus runs, participants responded when they detected a brief contrast dimming of the flickering checkerboard stimulus (0.33 s) which occurred on 50% of trials. During spatial working memory runs, participants made a button press response to indicate whether T2 was in the same or a different location as T1. Importantly, all three events (T1, checkerboard, T2) occurred during all runs, ensuring that the sensory display remained identical and that we were measuring changes in spatial representations as a function of task demands rather than changes as a result of inconsistent visual stimulation. For the follow-up behavioral control experiment we dynamically adjusted difficulty (contrast dimming or T1/T2 separation distance) to achieve consistent accuracy of ~75% across tasks.

Eye tracking

Participants were instructed to maintain fixation during all runs. Fixation was monitored during scanning for 4 participants using an ASL LRO-R long-range eyetracking system (Applied Science Laboratories) with a sampling rate of 240 Hz. We recorded mean gaze as a function of stimulus location and task demands after excluding any samples in which both pupil & corneal reflection were not reliably detected (Supplementary Fig. 1).

Imaging

We scanned all participants on a 3T GE MR750 research-dedicated scanner at UCSD. Functional images were collected using a gradient EPI pulse sequence and an 8-channel head coil (19.2 × 19.2 cm FOV, 96 × 96 matrix size, 31 3 mm thick slices with 0 mm gap, TR = 2250 ms, TE = 30 ms, flip angle = 90°), yielding a voxel size of 2 ×2 × 3 mm. We acquired oblique slices with coverage extending from the superior portion of parietal cortex to ventral occipital cortex.

We also acquired a high-resolution anatomical scan (FSPGR T1-weighted sequence, TR/TE = 11/3.3 ms, TI = 1100 ms, 172 slices, flip angle = 18°, 1 mm³ resolution). Functional images were coregistered to this scan. Images were preprocessed using FSL (Oxford, UK) and BrainVoyager 2.3 (BrainInnovations). Preprocessing included unwarping the EPI images using routines provided by FSL, slice-time correction, 3D motion correction (6 parameter affine transform), temporal high-pass filtering (to remove first, second and third order drift), transformation to Talairach space, and normalization of signal amplitudes by converting to Z-scores. We did not perform any spatial smoothing beyond smoothing introduced via resampling during the coregistration of functional images, motion correction, and transformation to Talairach space. When mapping IPS subregions, we scanned those participants using an identical pulse sequence, but instead used a 32 channel Nova Medical headcoil.

Functional localizers

All regions of interest (ROIs) used were identified using independent localizer runs acquired across multiple scanning sessions.

Early visual areas were defined using standard retinotopic procedures^51,52. We identified the horizontal and vertical meridians using functional data projected onto gray/white matter boundary surface reconstructions for each hemisphere. Using these meridians, we defined areas V1, V2v, V3v, hV4, V2d, and V3d. Unless otherwise indicated, data were concatenated across hemispheres and across dorsal/ventral aspects of each respective visual area. We scanned each participant for between 2 and 4 retinotopic mapping runs (n = 3 completed 2 runs, n = 3 completed 3 runs, n = 2 completed 4 runs).

Human middle temporal area (hMT+) was defined using a functional localizer in which a field of dots either moved with 100% coherence in a pseudo-randomly selected direction or were randomly replotted on each frame to produce a visual ‘snow’ display^53,54. Dots were each 0.081° in diameter and were presented in an annulus between 0.63° and 2.26° around fixation. During coherent dot motion, all dots moved at a constant velocity of 2.71°/s. Participants attended the dot display for transient changes in velocity (during coherent motion) or replotting frequency (snow). Participants completed between 1 and 3 runs of this localizer (n = 2 completed 1 run, n = 3 completed 2 runs, n = 3 completed 3 runs).

IPS and superior precentral sulcus sPCS ROIs were defined using a functional localizer which required maintenance of a spatial location in working memory, a task commonly used to isolate IPS and sPCS, which is the putative human FEF^47,49. A flickering checkerboard subtending ½ the visual field appeared for 12 s, during which time two spatial working memory trials were presented. During the flickering checkerboard presentation, we presented a red target dot for 500 ms, followed 2 s later by a green probe dot for 500 ms. After the probe dot appeared, participants indicated whether the probe dot was in the same location or a different location as the red target dot. Here, we limited our definition of IPS to the posterior aspect (Supplementary Table 1). ROIs were functionally defined with a threshold of FDR-corrected p < 0.05 or more stringent when patches of activation abutted one another. Participants completed between 1 (n = 2) and 2 (n = 6) runs of this scan. We also used data from these IPS/sPCS localizer scans to identify voxels in all other ROIs that were responsive to the portion of the visual field in which stimuli were presented in the main tasks since the large checkerboard stimuli subtended the same visual area as the stimulus array used in the main task. All ROIs were masked on a participant-by-participant basis such that further analyses only included voxels with significant responses during this localizer task (FDR-corrected p < 0.05).

Mapping IPS subregions

To determine the likely relative contributions of different IPS subregions to the localized ROI measured for all participants, we scanned the 4 participants who make up the behaviorally-controlled cohort presented in Figures 6 and 7 using a polar angle mapping stimulus and attentionally demanding task.

We used 2 stimulus types and behavioral tasks to define borders between IPS subregions^31,32,43,44. On all runs, we used a wedge stimulus spanning 72° polar angle and presented between 1.75° and 8.75° eccentricity rotating with a period of 24.75 s. On alternating runs, the wedge was either a 4 Hz flickering checkerboard stimulus (black/white, red/green, or blue/yellow) or a field of moving black dots (0.3 °, 13 dots/deg², moving at 5 °/s, changing direction every 8 s). During checkerboard runs, participants quickly responded after detecting a brief (250 ms) contrast dimming of a portion of the checkerboard. During moving dots runs, participants quickly responded after detecting a brief (417 ms) increase in dot speed. Targets appeared with 20% probability every 1.5 s. Difficulty was adjusted to achieve approximately 75% correct performance by changing the magnitude of the contrast dimming (checkerboard) or dot speed increment (moving dots) between runs. On average, participants performed with 84.1% accuracy on the contrast dimming task and 75.4% accuracy on the moving dots task. 2 participants completed 14 (8 clockwise, 6 counter clockwise) runs, and 1 participant completed 10 runs (AC, 5 clockwise, 5 counter clockwise). 1 participant was scanned with 2 different stimulus setups: half of all runs used the parameters described above, and half used a wedge spanning 60° polar angle and rotating with a period of 36.00 s (AB, 6 runs clockwise, 6 runs counter clockwise).

Preprocessing procedures were identical to those used for the main task. To compute the best visual field angle for each voxel in IPS, we shifted signals from counter-clockwise runs earlier in time by twice the estimated HRF delay (2 × 6.75 s = 13.5 s), then removed the first and last full cycle of data (we removed 22 TRs for all participants except AB, for which we removed 32 TRs), then reversed the time series so that all runs are “clockwise”. We then averaged these time-inverted counter-clockwise runs with clockwise runs. We computed power and phase at the stimulus frequency (1/24.75 Hz or 1/36 Hz, participant AB) and subtracted the estimated HRF delay (6.75 s) to align signal phase in each voxel with visual stimulus position. Finally, we projected maps onto reconstructed cortical surfaces for each subject and defined IPS 0–3 by identifying upper and lower vertical meridian responses (Supplementary Fig. 7a). Low statistical thresholds were used (computed using normalized power at the stimulus frequency) to identify borders of IPS subregions. Voxels were selected for further analysis by thresholding their activation during the same independent localizer task used to functionally define IPS and sPCS.

Encoding model

To measure changes in spatial representations under different task demands, we implemented an encoding model to reconstruct spatial representations of each stimulus that was used in the main task³⁶ (see also refs. ^34,37,38). This technique assumes that the signal measured in each voxel can be modeled as the weighted sum of different discrete neural populations, or information channels, that have different tuning properties (see ref. ³⁶). Using an independent set of ‘training’ data, we estimated weights that approximate the degree to which each underlying neural population contributed to the observed BOLD response in each voxel (Fig. 3a). Next, an independent set of ‘test’ data was used to estimate the activation within these information channels based on the activation pattern across all voxels within an ROI on each test trial using the information channel weights in each voxel that were estimated during the training phase (Fig. 3b).

This approach requires specifying an explicit model for how neural populations encode information. Here, we assumed a simple model for visual encoding within each ROI that focused exclusively on the spatial selectivity of visually-responsive neural populations. To this end, we built a basis set of 36 2D spatial filters. We modeled these filters as cosine functions raised to a high power: f(r) = (½ cos(rπ/s) + ½)⁷ for r < s, 0 elsewhere (Supplementary Fig. 2). This allowed the filters to maintain an approximately-Gaussian shape while reaching 0 at a fixed distance from the center (s°), which helped constrain curvefitting solutions (below). The s (size constant) parameter was fixed at 5r_stim, which is 5.8153°. The 36 identical filters formed a 6×6 grid spanning visual space. Filters were separated by 2.094°, with centers tiled uniformly from 5.234° above, below, left and right of fixation (Fig. 3a). The full-width half-maximum (hereafter, FWHM) of all filters was 2.3103° (Supplementary Figs. 2 and 3). This ratio of filter size to spacing was chosen to avoid high correlations between predicted channel responses (caused by too much overlap between channels, which can result in a rank-deficient design matrix) and to accomplish smooth reconstructions (if filters are too small, reconstructed spatial representations are “patchy”, see Supplementary Fig. 3 for an illustration of reconstruction smoothness as a function of filter size:spacing ratio). All filters were assigned identical FWHMs so that known properties of the visual system, such as increasing receptive field size with eccentricity and along the visual stream^39–41, could be recovered without being built-in to the analysis.

To avoid circularity in our analysis, we used a cross-validation approach to compute channel responses on every trial. First, we used all runs but three (1 run of each task condition) to create a ‘training’ set that had an equal number of trials in each condition. Using this training set, we estimated channel weights within each voxel across all task conditions (i.e., runs 1–5 of attend fixation, attend stimulus, and spatial working memory were used together to estimate channel weights, which were used to compute channel responses for run 6 of each task condition). The use of an equal number of trials from each condition in the training set ensures that channel weight estimation is not biased by any changes in BOLD response across task demands. Next, the weights estimated across all task demand conditions were used to compute channel response amplitudes for each trial individually. Trials were then sorted according to their task condition and spatial location.

During the training phase, we created a design matrix which contained the predicted channel response for all 36 channels on every trial (Fig. 3a). These predicted channel responses were computed by convolving each basis function with a mask subtending the area over which the stimulus was presented and normalizing the design matrix to 1, such that reconstruction amplitudes are in units of BOLD Z-scores.

To extract relevant portions of the BOLD signal on every trial for computing channel responses, we took an average of the signal over 2 TRs beginning 6.75 s after trial onset. This range was chosen by examination of BOLD HRFs and was the same across all participants. Qualitatively, results do not change when other reasonable HRF lags are used, such as using 2 TRs starting 4.5 s post-stimulus.

Using this approach, we modeled voxel BOLD responses as a weighted sum of channel responses comprising each voxel^36,38. This can be written as a general linear model of the form:

$${\mathit{B}}_{\mathbf{1}}={\mathit{WC}}_{\mathbf{1}}$$ 1

where B₁ is the BOLD response in each voxel measured during every trial (m voxels × n trials), W is a matrix that maps channel space to voxel space (m voxels × k channels), and C₁ is a design matrix of predicted channel responses on each trial (k channels × n trials). The weight matrix Ŵ was estimated by:

$$\widehat{\mathit{W}}={\mathit{B}}_{\mathbf{1}}{\mathit{C}}_{\mathbf{1}}^{\mathit{T}}{({\mathit{C}}_{\mathbf{1}}{\mathit{C}}_{\mathbf{1}}^{\mathit{T}})}^{-\mathbf{1}}$$ 2

Then, using data from the held out test data set (B₂), the weight matrix estimated above was used to compute channel responses on every trial (Ĉ₂), which were then sorted by task condition and spatial position.

$${\widehat{\mathit{C}}}_2={({\widehat{\mathit{W}}}^{\mathit{T}}\widehat{\mathit{W}})}^{-\mathbf{1}}{\widehat{\mathit{W}}}^{\mathit{T}}{\mathit{B}}_{\mathbf{2}}$$ 3

Reconstructing spatial representations

To reconstruct the region-wide representation of the visual stimulus viewed on every trial, we computed a weighted sum of the basis set, using each channel response as the weight for the corresponding basis function (Fig. 3b, bottom right). Reconstructions were computed out to 5.234° eccentricity across the horizontal and vertical meridians, though visual stimuli only subtended at maximum 4.523° eccentricity across the horizontal or vertical meridians. This was done to avoid edge artifacts in the reconstructions. Additionally, at this stage the reconstructed visual fields were shifted to account for the slight jitter introduced in the presented stimulus locations and align reconstructions from all trials. Runs in which stimuli were jittered up and to the left were reconstructed by moving the centers of the basis functions down and to the right, and runs in which stimuli were jittered down and to the right were reconstructed by moving the centers of the basis functions up and to the left. These shifts serve to counter the spatial jitter of stimulus presentation for visualization and quantification. By including spatial jitter during stimulus presentation, we are able to attain a more nuanced estimate of channel weights by sampling 72 stimulus locations rather than 36.

We averaged each participant’s reconstructions at all 36 spatial locations for each task condition across trials. For Figure 4, all n = 8 participants’ average reconstructions for each task condition were averaged and reconstructions from all ROIs/task conditions visualized on a common color scale to illustrate differences in channel response amplitude across the different task conditions and spatial locations. The 3×3 grid shown in Figure 4b is chosen as it is representative - results are similar for all quadrants.

For the follow-up control experiment, we plotted reconstructed spatial representations from only correct trials by coregistering all representations for trials at matching eccentricities, then averaging across all coregistered representations for each participant at each eccentricity. We coregistered representations for like eccentricities to the top left quadrant (see inset, bottom of Fig. 6b). Representations were rotated in 90° steps and flipped across the diagonal (equivalent to a matrix transpose operation on pixel values) as necessary.

Importantly, this analysis depends on two necessary conditions. First, individual voxels must respond to certain spatial positions more than others, although the shape of these spatial selectivity profiles is not constrained to follow any particular distribution (e.g. it need not resemble a Gaussian distribution). Second, the spatial selectivity profile for each voxel must be stable across time, such that spatial selectivity estimated based on data in the training set can generalize to the held-out test set.

Curvefitting

To quantify the effects of attention on visual field reconstructions we fit a basis function to all 36 average reconstructions for each participant for each task condition for each ROI using fminsearch as implemented in MATLAB 2012b (which uses the Nelder-Mead simplex search method; Mathworks, Inc).

The error function used for fitting was the sum of squared errors between the reconstructed visual stimulus and the function:

$$f(r)=b+a\ast {(½+½\ast cos(r\pi /s))}^7\text{for}r<s,0\text{elsewhere}$$ (4)

where r is computed as the Euclidean distance from the center of the fit function. We allowed baseline (b), amplitude (a), location (x, y), and size (s) to vary as free parameters. The size s was restricted so as not to be too large or too small (confined to 0.5815° < s < 26.17°), and the location was restricted around the region of visual stimulation (x, y lie within stimulus extent borders + 1.36° each side).

Due to the number of free parameters in this function, we performed a two-step stochastic curve-fitting procedure to find the approximate best fit function for each reconstructed stimulus. First, we averaged reconstructions for each spatial location across all 3 task conditions and performed 50 fits with random starting points. The fit with the smallest sum squared error was used as the starting point around which all other starting points were randomly drawn when fitting to reconstructions from each task condition individually (same distributions used around these new starting points). When fitting individual task condition reconstructions, we performed 150 fits for each condition. We used parameters from the fit with the smallest sum squared error as a quantitative characterization of the reconstructed visual stimulus. Then, we averaged fit parameters across like eccentricities within each task condition, ROI, and participant. For the follow-up control experiment, we performed an identical fitting procedure on each of the coregistered representations to directly estimate best fit parameters at each eccentricity.

Excluded participant

For one participant (AG3), reconstructions from the attend fixation runs were unusually noisy and could not be well approximated by the basis function used for fitting. However, both attend stimulus and spatial working memory runs exhibited successful reconstructions (Supplementary Fig. 4). Recall that the estimated channel weights used to compute these stimulus reconstructions were identical across the 3 task conditions, so only changes in information coding across task demands could account for this radical shift in reconstruction fidelity. Because this participant’s reconstructions could not be accurately quantified for the attend fixation condition, their reconstructions and fit parameters for all conditions have been left out of data presented in the Results. However, as noted above, data from this participant are consistent with our main conclusion that attentional demands influence the amplitude of spatial representations.

Evaluating the relationship between amplitude and size

It may be the case that our observation of increasing spatial representation size with increasing stimulus eccentricity is purely a result of intertrial variability in the reconstructed stimulus position. That is, the same representation could be jittered across trials, and the resulting average representation across trials would appear “smeared” – and would be fit with a larger size and smaller amplitude. If this were true, changes in these parameters would always be negatively correlated with one another – an increase in size across conditions would always co-occur with a decrease in amplitude.

To evaluate this possibility, for each eccentricity and each ROI and each condition pair (attend stimulus & attend fixation, spatial working memory & attend stimulus, and spatial working memory & attend fixation) we correlated the change in size with the change in amplitude (each correlation contained 8 observations, corresponding to n = 8 participants). To evaluate the statistical significance of these correlations, we repeated this procedure 10,000 times, each time shuffling the condition labels separately for size and amplitude, recomputing the difference, and then recomputing the correlation between changes in size and changes in amplitude. This resulted in a null distribution of chance correlation values against which we determined the probability of obtaining the true correlation value by chance. After correction for the false discovery rate, no correlations were significant (FDR, all p > 0.05; and note that FDR is more liberal than Bonferroni correction).

Representations from ventral and dorsal aspects of V2 & V3

For Supplementary Figure 5a, we generated reconstructions using an identical procedure to that used for Figure. 4, except we only used voxels assigned to the dorsal or ventral aspects of V2 & V3 instead of combining voxels across dorsal and ventral aspects as was done in the main analysis.

Stimulus reconstructions - novel stimuli

For Supplementary Figure 5b, we estimated channel weights using all runs of all task conditions from the main task as a ‘training set’. We used these weights to estimate channel responses from BOLD data taken from an entirely novel data set, which consisted of responses to a hemi-annulus shaped radial checkerboard (Supplementary Fig 5b, top row).

This new experiment featured 4 stimulus conditions: left-in, left-out, right-in, right-out. Inner hemi-annuli subtended 0.633° to 2.262° eccentricity. Outer hemiannuli subtended 2.262° to 4.523° eccentricity. Stimuli were flickered at 6 Hz for 12 s on each trial while participants performed a spatial working memory task on small probe stimuli presented at different points within the current stimulus.

BOLD signal used for reconstruction was taken as the average of 4 TRs beginning 4.5 s after stimulus onset. This data was used as the ‘test set’. Otherwise, the reconstruction process was identical to that for the main experiment, as were all other scan parameters & preprocessing steps.

Population receptive field estimation

To determine whether the spatial sensitivity of each voxel across all trials and all runs changed across conditions we implemented a novel version of a population receptive field analysis (pRF; refs ^42,55). For this analysis, we estimate the unimodal, isotropic pRF which best accounts for BOLD responses to each stimulus position within every single voxel. This analysis is complementary to the primary analyses described above.

For 4 participants (those presented in Figs. 6 & 7 and Supplementary Fig. 7) and 4 ROIs for each participant (V1, hV4, hMT+, and IPS0, chosen as this set includes both ROIs with [hV4, hMT+ and IPS0] and without [V1] attentional modulation), we used data across all runs within each task condition and ridge regression⁵⁶ to identify pRFs for each voxel under each task condition. We computed these pRFs using a similar method to that used to compute channel weights in the encoding model analysis (Fig. 3a, Online Methods: the univariate step 1 of the encoding model, see equation 1). We generated predicted responses with the same information channels used for the encoding model analysis (Fig. 3a), and reconstructed pRFs for each task condition for a given voxel were defined as the corresponding spatial filters weighted by the computed weight for each channel (Supplementary Fig. 8a).

In the main analysis in which we computed spatial reconstructions based on activation patterns across an entire ROI (Figs. 4 & 6c), any spatial information encoded by a voxel’s response could be exploited; this is true even if the voxel’s response to different locations was not unimodal (it need not follow any set distribution, so long as it responds consistently). However, univariate pRFs computed on a voxel-by-voxel basis cannot be well-characterized by an isotropic function if they are not unimodal⁵⁷. Thus, to ensure that most pRFs were sufficiently unimodal to fit an isotropic function, we used ridge regression^56,57 when computing spatial filter weights for the pRF analysis. The regression equation for computing channel weights then becomes:

$${\widehat{\mathit{W}}}^{\mathit{T}}={({\mathit{C}}_{\mathbf{1}}{\mathit{C}}_{\mathbf{1}}^{\mathit{T}}+\lambda \mathit{I})}^{-1}{\mathit{C}}_{\mathbf{1}}{\mathit{B}}_{\mathbf{1}}^{\mathit{T}}$$ (5)

where I is an identity matrix (k × k). To identify an optimal ridge parameter (λ) we computed the Bayes information criterion (BIC; ref ⁵⁸) value across a range of λ values (0 to 500) for each voxel using data concatenated across all 3 task conditions. This allowed for an unbiased selection of λ with respect to task condition. The λ with the minimum mean BIC value across all voxels within a ROI was selected, and this λ was used to compute channel weights for each of the 3 task conditions separately. An increasing λ value results in greater sparseness of the best-fit channel weights for each voxel, and a λ value of 0 corresponds to ordinary least squares regression.

After computing pRFs for each task condition, we fit each pRF with the same function used to fit spatial representations (Online Methods: Curvefitting) using a similar optimization procedure. We restricted fit size (FWHM) to be at greatest 8.08°, which corresponds to nearly the full diagonal distance across the stimulated visual field. This boundary was typically only encountered for hMT+ and IPS0, and served to discourage the optimization procedure from fitting large, flat surfaces. Then, we computed an R² value for each fit, and used only voxels for which the minimum R² across conditions was greater than or equal to the median of minimum R² across conditions from all voxels in that participant’s ROI (Supplementary Fig. 8a–b).

Because we only have a single parameter estimate for each condition for each voxel, we evaluated whether fit size is more likely to increase or decrease between each pair of task conditions (attend stimulus vs. attend fixation, spatial working memory vs. attend stimulus and spatial working memory vs. attend fixation) for each region for each participant by determining the percentage of voxels which lie above the unity line in a plot of one condition against another (see Supplementary Fig. 8d).

Simulating data with different pRF properties

In order to assess whether our region-level multivariate spatial representation analysis would be sensitive to changes in voxel-level univariate population receptive fields, we generated simulated data using two different pRF modulation models.

For the first model (Supplementary Fig. 10a–b), we randomly generated 500 pRF functions so as to uniformly sample the visual field for each of 2 conditions (Condition A, smaller pRFs, and Condition B, larger pRFs). Across the 2 conditions, each simulated voxel’s pRF maintained its preferred position while its amplitude and baseline were each randomly and independently sampled across conditions from the same normal distribution (amplitude: μ = 0.8513, σ = 0.25; baseline: μ = −0.1952, σ = 0.25; these values were taken from the average fit pRF parameters across all participants for hV4, attend fixation and attend stimulus conditions, Supplementary Fig. 9a). pRF size (FWHM) was sampled from a normal distribution with σ = 0.5 and a mean of μ = 4.405° for Condition A (mean of pRF size for hV4, attend fixation) and μ = 4.89° for Condition B (mean of pRF size for hV4, attend stimulus; an increase of 11%). In our simulation, this resulted in 79% of simulated voxels showing larger pRF sizes in Condition B compared to Condition A. For the second model (Supplementary Fig. 10b), we used the upper median split of fit pRFs for the single participant shown in Supplementary Figure 8c, ROI hV4, to generate simulated BOLD data. This allowed us to simulate region-level BOLD data for each attention condition tested in our experiment, and enabled us to determine whether the changes in univariate voxel-level pRF size we observe (Supplementary Fig. 9) are consistent with the multivariate region-level spatial representations we present in the main text (Figs. 5, 7).

After generating voxel-level pRFs using each of the two models described above, we added noise to the simulated weights (Gaussian noise added independently to each channel weight, σ = 0.1) and presented model voxels with 6 runs of all 36 spatial positions for each condition. We simulated each voxel’s BOLD response as the predicted channel response (response of corresponding spatial filter, Fig. 3a) to each stimulus weighted by the corresponding channel weights. We added Gaussian noise to the resulting BOLD data for each simulated voxel independently (σ = 0.1). Then, all analyses of multivariate spatial representations proceeded identically to those described above. We computed spatial representations using estimated channel weights computed across all conditions within a model (i.e. Condition A & Condition B, Supplementary Fig. 10a–b; or attend fixation, attend stimulus, and spatial working memory; Supplementary Fig. 10c–d), then fit average spatial representations with a smooth surface (see Online Methods: Curvefitting) to determine the amplitude and size of each spatial representation. We then averaged these parameters across all 36 positions.

Statistical procedures

All behavioral analyses on accuracy data were performed using a 2-way repeated-measures ANOVA with task condition and stimulus eccentricity modeled as fixed effects (3 levels and 6 levels, respectively, Fig. 2d, Fig. 6a).

To assess whether fit parameters to reconstructed spatial representations reliably changed as a function of task demands, we performed a multi-stage permutation testing procedure. This non-parametric procedure was adopted because the spatial filters (basis functions) used to estimate the spatial selectivity of each voxel during the ‘training’ phase (Fig. 3a) overlapped, they were not independent (violating a key assumption of standard statistical tests).

For each parameter (rows in Figs. 5 and 7), we first found ROI/parameter combinations which showed an omnibus main effect in a repeated-measures ANOVA (1 factor, 18 levels), corrected using a false discovery rate (FDR) algorithm⁵⁹ across all ROIs. Then, we computed F-scores for a 2-way repeated measures design with eccentricity and condition as factors (6 levels and 3 levels, respectively) for ROIs with significant omnibus main effects.

For all tests, because we had a relatively small n (n = 8 for Fig. 5, n = 4 for Fig. 7 & Supplementary Fig. 7) and the range of parameters was in some cases restricted to be positive (size), we computed an F distribution for the null hypothesis that there is no main effect of omnibus factor (omnibus test) or that there is no main effect of condition, eccentricity, or their interaction (for a follow-up 2-way test) by shuffling trial labels within each participant 100,000 times. For each data permutation, we computed a new F score for the omnibus test, and for ROI/parameter combinations with a significant omnibus effect, a main effect of condition, eccentricity, and their interaction. P-values were estimated as the probability that the F score computed based on the shuffled data was equal to or greater than the F scores computed using the actual data. These additional tests were corrected for multiple comparisons using Bonferroni’s method within each parameter. We also occasionally highlight trends in the data by reporting p-values which do not reach significance under correction for multiple comparisons at this sample size as “marginal effects”, and such p-values are always reported as “uncorrected” in the text. For display, marginally significant tests are reported on Fig. 5 and Fig. 7 at uncorrected p < 0.025.

In addition, we performed a 3-factor repeated-measures ANOVA with ROI, task condition, and eccentricity modeled as fixed effects to determine whether fit parameters changed across ROIs (n = 8, Fig. 5; n = 4, Fig. 7). We implemented the same permutation procedure described above to compute p-values (10,000 iterations).

To determine whether pRF size increases at higher eccentricities, we computed a linear fit to a plot of each voxel’s pRF size vs. its pRF eccentricity for each ROI for each condition for each participant (Supplementary Fig. 8c). To determine whether the slope of the fit line was reliably positive for a given ROI/participant/condition, we computed confidence intervals around the best fit slopes using bootstrapping (resampled all voxels with replacement 10,000 times) and the related p value was defined as the as the probability that the slope was ≤ 0. We used a Bonferroni-corrected significance threshold for 48 planned comparisons (4 ROIs × 4 participants × 3 conditions) of α = 0.001 (see Supplementary Results, Supplementary Table 2 for reported statistics).

To evaluate the statistical significance of the pRF size increase (Supplementary Fig. 9), we first performed a 2-way repeated-measures ANOVA with ROI and condition modeled as fixed effects and participant modeled as a random effect in which we shuffled ROI and condition labels for each participant and recomputed the percentage of voxels which increased in size across each condition pair. We repeated this shuffling procedure 10,000 times and compared F-scores computed using the real labels to the distribution generated using the shuffled labels, as above. Then, we compared whether each condition pairing resulted in a significant change in pRF size for each ROI by computing a T score testing against the null hypothesis that 50% of voxels show an increase in pRF size. As above, we generated a null T distribution by shuffling condition labels within each participant 10,000 times. For this analysis we used a Bonferroni-corrected significance threshold for 12 (4 ROIs × 3 conditions) planned comparisons of α = 0.0042.