Quantum mechanical study of solvent effects in a prototype S_N2 reaction in solution: Cl⁻ attack on CH₃Cl

Abstract

The nucleophilic attack of a chloride ion on methyl chloride is an important prototype S_N2 reaction in organic chemistry that is known to be sensitive to the effects of the surrounding solvent. Herein, we develop a highly accurate Specific Reaction Parameter (SRP) model based on the Austin Model 1 Hamiltonian for chlorine to study the effects of solvation into an aqueous environment on the reaction mechanism. To accomplish this task, we apply high-level quantum mechanical calculations to study the reaction in the gas phase and combined quantum mechanical/molecular mechanical simulations with TIP3P and TIP4P-ew water models and the resulting free energy profiles are compared with those determined from simulations using other fast semi-empirical quantum models. Both gas phase and solution results with the SRP model agree very well with experiment and provide insight into the specific role of solvent on the reaction coordinate. Overall, the newly parameterized SRP Hamiltonian is able to reproduce both the gas phase and solution phase barriers, suggesting it is an accurate and robust model for simulations in the aqueous phase at greatly reduced computational cost relative to comparably accurate ab initio and density functional models.

INTRODUCTION

Ab initio and density functional quantum chemical calculations are powerful tools which can be used for highly accurate predictions of gas phase geometries and reaction energetics.^{1, 2, 3} However, when systems are in a condensed phase environment extensive conformational sampling is required and the computational cost of these quantum mechanical (QM) calculations can pose a practical bottleneck. One strategy to overcome this limitation and obtain QM level accuracy in molecular dynamics simulations at a reduced computational cost is to use a hybrid quantum mechanical/molecular mechanical (QM/MM) potential^{4, 5, 6, 7} where the system is divided into two different regions; a small active site region containing any chemically active atoms with their immediate neighbors to be modeled with QM techniques and then the rest of the system is modeled with classical molecular mechanics (MM). Even within a QM/MM framework, however, when interrogating reaction pathways of large biological systems, where QM regions can be 100 atoms or more and the total system size can be on the order of hundreds of thousands of atoms, traditional QM techniques may still be prohibitive. As a result, the last decade has seen a resurgence of interest in the development of fast, approximate “semi-empirical Hamiltonian” quantum models for use in QM/MM simulations. Specifically parameterized semi-empirical models have shown themselves to be invaluable at exploring different classes of highly specialized reactions.^{8, 9, 10, 11}

This work will outline a procedure for creating an Specific Reaction Parameterization (SRP) quantum model for chlorine within the Austin Model 1 (AM1)¹² Hamiltonian for the symmetric bimolecular nucleophilic reaction (S_N2) of a chlorine anion attacking methyl chloride in both the gas phase and in solution. Simple S_N2 reactions, such as the focus reaction of this study, are some of the most fundamental reactions in organic chemistry and have provided keen insights into gas phase reactivity and aqueous, solvation properties, reaction energetics, and kinetics over the past several decades.^{13, 14, 15, 16, 17} It is well known that S_N2 reactions, when in the gas phase, have an double-well potential energy surface with a single transition state (TS), as seen in Figure 1, bracketed on either side by low wells generated from the formation of a more energetically stable Ion-Dipole Complex (IDC). Then, when the reaction is moved into solution, the reaction profile is likely to be dominated by an enhanced central barrier. This change in the general shape of the reaction energy surface is due to destabilization of the TS and the IDC. Relative to the reactants/products, both of these complexes have an increased solvent-excluded space because they are generally much more diffuse than either of the separated reagents. As a result, solvation strongly favors the reactant state over the TS and IDC, leading to a pronounced single barrier and less prominent IDC stabilization. The solvation stabilization of ionic species and another, possibly dipolar, molecule at infinite separation is much greater than for the TS. Although the TS bears a charge, the solvation cavity it creates is considerably larger than those made from either of the reactants. Also, if the reaction is symmetric, the TS will not have a net dipole moment. Similarly, solvation destabilizes the IDC relative to the reactants, although to a smaller extent than the TS, causing a drastic reduction of the depth of the corresponding minima in the free energy profile.

Figure 1.

Schematic representation of gas and solution phase potential energy surfaces for the symmetric S_N2 reaction of a chloride ion with methyl chloride. The IDC nucleophilic attack distance (d_N), the leaving group distance (d_L), and the TS halide distance (d_H) are labeled.

The study of chloromethane and other small halogenated hydrocarbons are not only of central interest to understanding a wide range of fundamental chemistry, but are of health and environmental interest in themselves.^{18, 19, 20, 21, 22} Having been so extensively studied, by both experimental^{23, 24, 25, 26, 27} and computational^{28, 29, 30, 31, 32, 33, 34, 35, 36} means, lends this class of reactions to be an outstanding starting position for benchmarking and refining new computational methods and techniques. In particular, the chloride/methyl chloride reaction is a strong candidate as a prototype reaction as it has been quite extensively studied in order to understand the exact nature of the transition state in the gas and condensed phases.^{37, 38, 39, 40} Furthermore, by starting out with a small system which has inherently less degrees of freedom in interaction and parameter space, one can refine parameters more easily and then proceed to build on the system from that strong foundation.

Very recently, a similar set of reactions has been the focus of semi-empirical model development and application in QM/MM simulations by Liang and Roitberg.⁴¹ This work performed critical examinations of the S_N2 reactions of chloride and fluoride attacking methanol and develops a new AM1 parameterization using the internal reaction coordinates of each respective gas phase reaction to include reaction energetics and force-matching to MP2 reference data. This strategy has been demonstrated to be a successful one in subsequent QM/MM applications. In the present work, we examine a different reaction and take a different approach in parameterization strategy that includes sets of constrained geometry optimizations at different stages along the reaction coordinate, as well as properties of the isolated reactant species, and demonstrate that it is robust and transferable in application to QM/MM simulations in solution. Results of the simulations provide insight into the origins of solvation effects on the reaction.

COMPUTATIONAL METHODS

The bimolecular identity reaction of a chloride anion attacking methyl chloride via an S_N2 mechanism both in the gas and solution phases is examined for the purposes of creating a SRP semi-empirical Hamiltonian. This manuscript explores the use of a stepwise approach to the parameterization and testing of new models to study chemical reactions in solution. The first step is to perform benchmark gas phase quantum chemical calculations to obtain a target reaction profile, as well as key molecular properties of the reactants and products including geometries, electron affinities, and dipole moments. All values validate the data against available literature values where possible. The second step is to use the most accurate high-level QM results, in conjunction with known experimental values where appropriate, from the methods tested as a training set to parametrize an accurate semi-empirical Hamiltonian model that is orders of magnitude faster than any of the benchmark-level models allowing it to be utilized in molecular dynamics simulations. The parametrization will only focus on recapitulating the gas phase quantum chemical data, with no other modulation of the parameters to better performance in solution. In the third step, the new semi-empirical model will be tested in QM/MM simulations using standard molecular force field van der Waals parameters to capture free energy profiles for the target reaction. Results will be scrutinized against experimental and other semi-empirical data to determine the accuracy of the SRP Hamiltonian for solution phase reactions. Below, the details of the computational methods used for each of these sections are described.

Benchmark quantum chemical calculations

Different quantum models were tested in order to see which best reproduced experimental gas phase reaction data. Hartree Fock (HF) and Second-order Møller-Plesset (MP2)⁴² methods were compared along side a series of density-functionals: BH&HLYP,⁴³ B3LYP,⁴⁴ ωB97x-D,⁴⁵ and M06-2X.⁴⁶

Each of the chosen QM methods performs differently, largely related to their general formulations. It is important to test each and to find which best captures the physics of the reaction of interest. HF has several known issues with chemical bonding⁴⁷ however it does provide the exact exchange while being computationally less demanding than several other ab initio and hybrid density functional methods. MP2 is the only perturbative method chosen for our bench-marking calculations: being fairly widely used and having been shown to be highly accurate, even when given small to moderately sized basis sets, for small molecules and their reactions.⁴⁸ Several different hybrid density functionals were examined: BH&HLYP, B3LYP, ωB97x-D, and M06-2X, each has different strengths, related to each of their formulations and treatment of the exact (HF) exchange. BH&HLYP uses equal parts of the Kohn-Sham exchange energy and of Becke's⁴³ correction to the local spin density approximation (LSDA) while the B3LYP functional contains each of these, with different weightings, while also having three other fit mixing parameters relating to the exchange or correlation energies. M06-2X weights the exact HF exchange more highly than either of the two functionals at 54% in conjunction with several other empirical functions. The ωB97x-D is a long-range corrected (LC) hybrid density functional, which uses 100% of the HF exchange to describe distant electron-electron interactions and then uses parametrized functionals and general gradient approximations (GGA) for shorter, close-range, interactions. To enhance short-range behavior, both the ωB97x-D and M06-2X functionals also use Grimme's⁴⁹ density functional theory dispersion correction with weighting factors of 1.0 and 0.06, respectively. Finally, the M06-2X functional also includes meta-GGA character to further differentiate itself from the other functionals in this test set.

As for why each of these functionals were chosen initially; B3LYP was an obvious choice to test for a model function, as a majority of density functional computational studies today use this method due to its generally good performance and low computational cost. The BH&HLYP was included because other similar studies noted that this functional performs quite well for capturing energy barriers for small reactions, however it has also been noted that BH&HLYP does not correctly predict reaction thermodynamics.³² The ωB97x-D functional has shown superior performance for measuring both bonded and non-bonded interactions in the LC hybrid class of functionals and finally M06-2X is the recommended functional of the M06 suite for main group chemistry, which has been shown to accurately predict thermochemistry, kinetics, and non-covalent interactions for non-multi-reference systems.

To calculate gas phase reaction energies, stationary points of the reaction were determined for the separate reagents, the IDC and the TS. The TS was verified as a first order saddle point through normal mode analysis which reported a single negative eigenvalue in the Hessian, whose mode amplitude and motion were along the predicted reaction pathway. Further, intrinsic reaction coordinate profiles were calculated to ensure that the TS correctly connected the reactant and product minima (see the supplementary material⁷³). All gas phase quantum benchmark calculations were carried out using the Gaussian09 software suite⁵⁰ in conjunction with the GaussView tool.⁵¹ Each of the high-level quantum methods were geometry optimized and their energies evaluated at the 6-311++g(3df,2p) level of theory with tight optimization and self-consistent field (SCF) convergence criteria while using an ultrafine integration grid. This work was carried out using hardware and software provided by the University of Minnesota Supercomputing Institute and the supercomputing facilities at Rutgers, the State University of New Jersey.

After selecting a quantum method to act as the model for the new semi-empirical Hamiltonian, it is used to create gas phase reaction profiles. To create the reaction profiles, constrained optimizations were performed where, departing from the TS, the nucleophile was incrementally pulled away from the carbon which it was attacking until well passed the minima of the IDC. Two constraints are used: one distance constraint between the attacking nucleophile and the carbon center of S_N2 inversion, and another maintaining the attack angle between the nucleophile, the carbon center, and the leaving group at 180°. These two constraints are adequate for this study because the reaction examined in this paper is symmetric; the nucleophile and the leaving group are identical. If this was not the case, it would be important to examine the departure of the leaving group with additional points and constraints during and after the transition state. Additionally, calculations were made of each individual reagent in order to properly calculate the energy of the reactants and products at “infinite separation.” With the listed constraints imposed, geometries of several different points of reaction coordinate progress were optimized using the selected functional at the 6-31+g(d,p) level of theory. Energies were then recalculated at the 6-311++g(3df,2p) level at the previously optimized geometry, each performed using an ultrafine integration grid and tight convergence criteria. After the reaction profile was created, it was verified to be representative of the reaction through cross examination with the intrinsic reaction coordinate (IRC) profile. Comparisons of the two calculations can be found in the supplementary material.⁷³

Where possible, results in the gas phase are compared with computational benchmark results from the W1^′ method by Parthiban et al.³² The W1^′ method is a variation on the Weizmann-1 (W1) procedure to improve performance on second-row compounds, using a combination of high basis set level B3LYP, CCSD, and CCSD(T) calculations to extrapolate to infinite basis set limits and accurately account for an-harmonic zero-point energy, relativistic effects, and other computationally challenging energetics. Typically, this procedure yields results that are accurate within 0.25 kcal/mol for thermochemical data.^{52, 53}

Parametrization of semi-empirical quantum model

Once the high-level reference gas phase reaction profile was obtained, it was used to generate an objective function for the parameterization of the new AM1 Hamiltonian. A weighted chi-squared function was used, taking into account energetics and molecular geometries of each of the points in the reaction profile outlined in Sec. 2A. Including many points along the reaction coordinate allows the new model to capture subtle features over the course of the reaction, such as curvature of the adiabatic energy surface. Identical constraints as those in the benchmark quantum calculations were also imposed on the optimization procedure for regeneration of the gas phase reaction profile. Extra weight was given to the important minima and saddle points in the chi squared function, as recapitulating the reaction barrier was thought of as the most important characteristic to obtain. Reagents and other similar molecules were also included into the objective function. Important physical observables, such as the dipole moments of relevant reagents and electron affinities of select particles, were also taken into account. Full details of the merit function and optimization protocol, used to derive the new parameters, including each molecular species and their starting geometries, the molecular refinement procedure including all constraints, all properties and their reference values, and chi squared weight, can be found in the supplementary material⁷³ as a documented input file which was used to run the calculation. Optimization departed from the original AM1 parameters for chlorine and was accomplished using a direction set method⁵⁴ in conjunction with the MNDO97⁵⁵ software package.

Molecular simulations

After a new Hamiltonian was parametrized, molecular dynamics simulations were carried out using AMBER12.⁵⁶ Potential of Mean Force (PMF) simulations were performed using both the TIP3P⁵⁷ and TIP4P-ew⁵⁸ water models according to the following protocol: (1) Generate structure and solvent box using the leap series of programs. Structures were generated using ANTECHAMBER from optimized TS Gaussian output files and force field modification files for the parameters of methyl chloride and the chloride anion were generated. Lennard-Jones parameters for all chlorine atoms were selected from the Joung and Cheatham's work⁵⁹ for each of their respective solvents because the authors felt that, over the coarse of the reaction, the chlorine atoms maintain a strong chloride-like charge-state and character. All Lennard-Jones parameters used can be seen in Table 1. Using Leap, the solute was given a 15 Å solvent buffer radius in a cubic cell for periodic simulations. (2) Equilibration of the solvent box was performed for 250 ps using an NPT ensemble with the solute harmonically restrained with a 500 (kcal/mol)/Ų force constant. The purpose of this step is to relax the solvent box around the initial state and allow the solvent box density to stabilize. (3) Several different umbrella windows along the reaction coordinate are created. The system is then allowed to equilibrate at each umbrella windows. This step of equilibration was performed for 150 ps in an NPT ensemble. (4) Finally, production was run for 150 ps in an NVT ensemble. Production trajectories were then analyzed using MBAR⁶⁰ in conjunction with a kernel density estimator in order to calculate the solution reaction profile.

Table 1.

Lennard-Jones parameters. Parameters for the chlorine and chloride atoms are taken from the work of Joung and Cheatham.⁵⁹ R_{min, ij} and ε_ij values are in Å and kcal/mol, respectively.

	TIP3P		TIP4P-ew
Element	Rmin, ii/2	εii	Rmin, ii/2	εii
OW	1.7683	0.1520	1.775931	0.16275
HW	0.0000	0.0000	0.0000	0.0000
C	1.9080	0.0860	1.9080	0.0860
H	1.4870	0.0157	1.4870	0.0157
Cl/Cl−	2.5130	0.0355910	2.760	0.0116615

RESULTS AND DISCUSSION

The goal of this manuscript is to create a SRP AM1 Hamiltonian for chlorine for the attack of chloride on methyl chloride. Parameterization was carried out in a straight-forward manner, only relying on the gas phase data for refinement of that Hamiltonian, only testing its performance in solution after augmentation of all parameters was complete. Specific results from SRP parameterization and details of the parameter optimization can be found in the supplementary material.⁷³ The performance results from that Hamiltonian are examined here, in both the gas phase and in solution. All reaction barrier and geometric data are compared to selected existing semi-empirical Hamiltonians and literature experimental data where applicable.

Benchmark quantum chemical calculations

A variety of different mid-to-high level quantum mechanical methods was tested in order to determine a standard on which the new semi-empirical Hamiltonian could be parametrized. The ideal test functional would achieve chemical accuracy for the reaction of interest while reducing the computational cost of parametrization as much as possible. Results comparing the complexation energy (the energy difference between the IDC and the free reagents) and the central attack barrier (the difference between the TS and the IDC) are shown in Table 2. The values shown compare each functional to the experimentally observed value, as well as the high-level W1^′ reference.

Table 2.

Quantum gas phase energetics and geometries. Gas phase stationary point calculations were performed at the 6-311+g(3df,2p) level of theory with a variety of quantum methods describing the attack of chloride anion on methyl chloride. Adiabatic energy results are presented as differences from experiment. Included with the methods tested in this study is the W1^′ functional as a high-level benchmark for readers. All energies and energy differences are reported in kcal/mol. Bond distances are also given for the TS and IDC. All distances are reported in Å.

	Transition state		Ion dipole comp.
Method	dH	Barrier	dN	dL	Energy
Expt.	…	13.6661, 62	…	…	−10.5367
W1′	2.3551	(0.01)	1.8461	3.1911	(−0.05)
HF	2.381	(2.60)	1.818	3.350	(1.49)
MP2	2.287	(2.22)	1.806	3.151	(−0.30)
B3LYP	2.354	(−4.57)	1.844	3.180	(0.71)
BH&HLYP	2.562	(−0.71)	1.816	3.194	(0.59)
ωB97x-D	2.324	(−0.58)	1.817	3.186	(0.04)
M06-2X	2.300	(0.06)	1.817	3.101	(−1.16)
AM1	2.154	(−4.61)	1.785	2.872	(1.97)
MNDO	2.148	(−3.15)	1.830	3.346	(3.25)
MNDO/d	2.173	(5.93)	1.805	3.516	(4.45)
PM3	2.189	(−4.00)	1.806	2.843	(1.65)
MeCl SRP	2.300	(0.04)	1.819	3.088	(−1.12)

¹Geometries calculated at the B3LYP/cc-pVTZ+(X) level of theory.

Looking at the energetics of the chloride/methyl chloride reaction, the experimentally known central reaction barrier of 13.66 kcal/mol^{61, 62} is best reproduced by the high-level benchmark W1^′ model chemistry, which underestimated the barrier by 0.01 kcal/mol. As previously stated, due to the computational cost of this method, it is not an ideal choice to use in the parametrization scheme despite its high accuracy. The next most accurate tested method was the M06-2X functional, which had similarly accurate performance of over estimating the barrier by 0.06 kcal/mol. The binding energy of the IDC is most accurately reproduced by the ωB97x-D functional and W1^′ method with deviations from the experimental value of 0.04 and 0.05 kcal/mol, respectively. All of the tested high-level quantum methods have similar calculated geometries for the various reagents and reaction complexes. A majority of the quantum methods estimated d_H to be approximately 2.3 Å, with the largest deviation from the set being BH&HLYP which estimated that bond length to be about 0.2 Å larger than the other functionals. Likewise, all high-level QM methods performed similarly when evaluating d_N and d_L, with the largest outlier being the HF calculation of d_L, indicating that the distance should be about 0.15 Å longer than the other functionals. The HF d_L distance discrepancy is possibly related to its significantly lower electron affinity for chlorine, as also seen in Table 3, thus requiring longer distances in the IDC because electronic transfer will happen more readily at closer distances than the other methods.

Table 3.

Comparison of experimental and calculated physical properties used in the parameterization of the SRP Hamiltonian. Each of the properties listed were used in the objective function for the selected functional. EA is the electron affinity and BL is the bond length. All energies are reported in kcal/mol, dipole moments are reported in Debye and all distances are reported in Å.

	Cl−	Cl2	MeCl		CCl4
	EA	BL	C-Cl BL	Dipole	C-Cl BL
Expt.	83.3168	1.98869	1.77670	1.87071	1.76972
HF	55.35	1.974	1.781	2.119	1.760
MP2	82.89	1.985	1.773	2.080	1.762
B3LYP	84.90	2.010	1.795	1.950	1.780
BH&HLYP	79.32	1.983	1.777	1.991	1.761
ωB97x-D	84.88	1.986	1.781	1.943	1.768
M06-2X	84.15	1.984	1.779	1.931	1.764
AM1	37.65	1.918	1.741	1.513	1.760
PM3	51.20	2.035	1.764	1.377	1.747
MNDO	83.71	1.996	1.795	1.973	1.782
MNDO/d	83.40	1.984	1.779	1.859	1.786
MeCl SRP	83.65	1.988	1.771	1.817	1.795

As for physical properties and geometries for related compounds, M06-2X reproduced the experimental electron affinity for a chlorine atom as well as the dipole moment of methyl chloride the best among the quantum methods that were surveyed. These results would indicate that the M06-2X most accurately describes the electronic nature of chlorine and chlorine containing molecules, as it is the only density functional which takes into account the second derivative of the electronic density, from the set tested. As a whole, geometries for the relevant small molecules were similarly well reproduced by all functionals with the exception of B3LYP which consistently overestimated carbon-to-chlorine bond lengths by approximately 0.05 Å.

When evaluating QM methods to act as the model function for the parameterization of the SRP semi-empirical Hamiltonian, it is important to consider how accurate the chosen method would perform in capturing overall reaction energies as well as how computationally demanding the method is to perform the needed calculations. The best overall performance in capturing geometries and energies for the entire data set would fall upon ωB97x-D, being able to calculate both the central barrier and IDC energies with sub kcal/mol accuracies and being able to closely recapitulate known geometries for the related molecules. However, the authors felt that the central barrier of the reaction was the most important aspect of the potential energy surface to correctly calculate, especially due to reasons discussed earlier. When in solution, which is the intended medium for which this Hamiltonian is designed, the reagents of a reaction are greatly stabilized by their interactions with the surrounding water while the IDC (if one exists) is destabilized relative to the reagents, all of which is controlled by the molecules’ charge distribution and the atoms’ Lennard-Jones terms. In this regard, the complexation energy is less important to recapitulate in the gas phase as it becomes mostly insignificant when compared to the reaction barrier in solution. As such, the M06-2X functional was chosen. This functional is able to accurately capture the reaction barrier, the key feature the SRP Hamiltonian is targeted to produce, while being more tractable than the W1^′ functional.

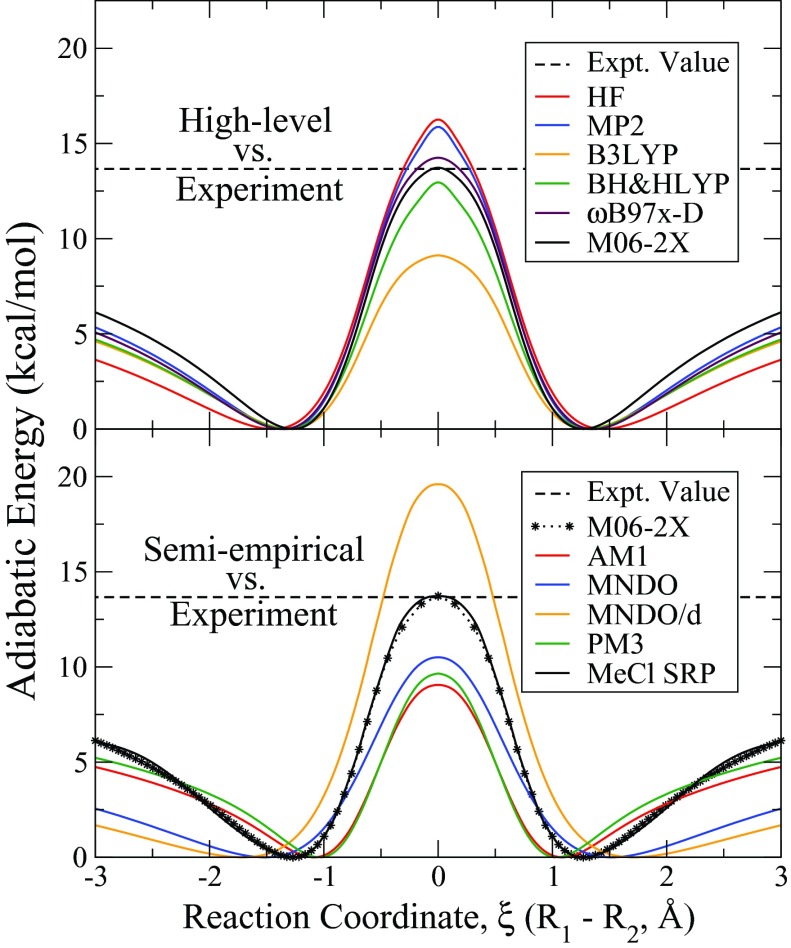
After selection, constrained scans of the chloride attack on methyl chloride, as defined by the distance and angle between them, were performed at a mixed basis set level in order to map out the reduced adiabatic energy surface of the reaction. These scans can be seen in Figure 2.

Figure 2.

Gas phase profiles. Shown are the gas phase attack profiles of a chloride anion reacting with methyl chloride for both a range of different high-level quantum mechanical techniques (top) and with a variety of semi-empirical Hamiltonians (bottom) as compared to the experimentally known barrier. From the high-level data, M06-2X reproduces the barrier most accurately. The newly parameterized semi-empirical Hamiltonian (SRP) closely mimics the higher level data (shown as the dashed line) and captures the experimental barrier.

Parametrization of semi-empirical quantum model

The newly parametrized SRP Hamiltonian is shown to reproduce a higher level QM gas phase profile. Several aspects of the reaction were taken into account including the geometry and energetics of the reaction along several different points, but also several important properties of relevant compounds. For general comparison of gas phase performance of different semi-empirical Hamiltonians for this reaction, gas phase optimization of each the AM1, MNDO, MNDO/d, and PM3 Hamiltonians were performed with an identical protocol as used in the SRP optimization, with constraints on the angle of attack and the distance between the attaching chloride ion and the methyl chloride carbon. Results of this test can be seen in Figure 2. Similarly to the higher level quantum data, differences from experimental reaction barriers and physical properties were collected and can be seen in Table 3.

To accurately capture the reaction barrier in solution, and in order for the results to be physically meaningful, the gas phase profile must be accurately reproduced. To this end a series of standard semi-empirical Hamiltonians were tested in order to determine if a special parametrization was needed for the chloride/methyl chloride reaction and, of the Hamiltonians tested, none of them performed adequately in capturing the reaction barrier in the gas phase. All of the semi-empirical Hamiltonians tested severely underestimated the reaction barrier besides the MNDO/d functional which overestimated the barrier by 5.93 kcal/mol. It should also be noted that all of the semi-empirical Hamiltonians underestimate the energy for forming the IDC, however it is interesting that the slope of the energy surface for the approach of the chloride ion into the IDC is consistently underestimated for all of the semi-empirical Hamiltonians, indicating that while in the gas phase each semi-empirical Hamiltonian predicts that the chloride ion will interact with the methyl chloride at a much longer range than the higher-level M06-2X functional would indicate. This trend is most notable the MNDO-type Hamiltonians. When looking at the physical properties of the semi-empirical Hamiltonians, the AM1 and PM3 Hamiltonians both underestimate the dipole moment of methyl chloride and correspondingly the carbon to chloride distance in the IDC and the TS are too short as compared to the M06-2X model functional.

Due to the lack of accuracy in existing semi-empirical models, a new parametrization must be made. As seen in Table 2 and in Figure 2, the specifically parametrized chlorine Hamiltonian can readily reproduce the stationary point values quite accurately (within less than one tenth of a kcal/mol), and general curvature, of the reaction profile. A comparison of the IRC profiles between the newly parameterized Hamiltonian and the high-level reference can be found in the supplementary material.⁷³ Also noted in Table 3, several of the higher-level properties such as carbon to chlorine bond lengths and the methyl chloride dipole moment are reproduced.

Solution phase reaction barriers in different water models

In order to capture the reaction profile in solution, PMF simulations were performed in solution for each semi-empirical Hamiltonian tested in the gas phase. Results of these simulations can be seen in Figure 3. The profiles are compared to the experimental reaction barrier. The parametrized semi-empirical Hamiltonian performed the best out of the selected Hamiltonians for both the TIP3P and TIP4P-ew water simulations. Errors on reported values are on the order of ±0.1 kcal/mol in the free energy barriers.

Figure 3.

QM/MM free energy profiles. Free energy profiles for the attack of the chloride anion on methyl chloride in both TIP3P (top) and TIP4P-ew (bottom) water are presented. Simulations were performed in AMBER and the free energy profiles were calculated using umbrella sampling in conjunction with MBAR utilizing a kernel density estimator.

The SRP Hamiltonian best captures the experimentally observed solution phase reaction barrier of 26.5 kcal/mol⁶³ from the set of semi-empirical Hamiltonians tested, and did so within statistical error of the simulation. Numerical data from the PMF simulations can be found in Table 4. The standard Hamiltonian results follow much in the same trend as was seen in the gas phase adiabatic profile calculations, however while in the gas phase PM3 more accurately reproduces the experimental barrier than AM1 while in solution phase the opposite was the case. Given that the “size” of the particles involved in the reaction is set using static Lennard-Jones parameters, the differences between the solvation effect of each Hamiltonian can mostly be attributed to their electronic nature. Therefore, it is believed that because the PM3 Hamiltonian drastically underestimated the dipole moment of methyl chloride, it would in turn destabilize the methyl chloride's solvation which would lead to more energetically unfavorable reactants and a shorter central barrier height. Similarly, the MNDO semi-empirical Hamiltonian performed admirably in solution despite drastically underestimating the barrier in the gas phase, this change could be due to the over predicted dipole moment of methyl chloride. As the reagents of the reactant would be more stabilized due to stronger interactions with the surrounding water, the reaction would appear to have an enhanced central barrier.

Table 4.

Solution phase reaction data. Solution phase data are presented for a variety of QM/MM PMF simulations using different semi-empirical Hamiltonians. The carbon to chloride distance (d_H) and the attack barrier (ΔG(ξ)‡) for each are shown. Reaction barriers are reported as differences from experimentally⁶³ known values. Distances are reported in Å and energy barriers are reported in kcal/mol.

	TIP3P		TIP4P-ew
Hamiltonian	⟨dH⟩	ΔG(ξ)‡	⟨dH⟩	ΔG(ξ)‡
Expt. value	…	26.5	…	26.5
AM1	2.170	(−2.6)	2.169	(−2.8)
MNDO	2.170	(−0.9)	2.170	(−1.0)
MNDO/d	2.182	(5.9)	2.181	(5.9)
PM3	2.198	(−3.2)	2.199	(−3.6)
MeCl SRP	2.345	(0.0)	2.346	(0.1)

Bond lengths in solution for the TS, d_H, mimic the same trend as those seen in the gas phase, with the SRP Hamiltonian having a much larger bond length than the other standard Hamiltonians. When moved into solution, all of the semi-empirical Hamiltonians experienced a minor elongation of d_H. This behavior is expected because increased interactions with the surrounding water would favor geometric relaxation of the d_H bond, insomuch as the competing solvent destabilization energy would allow the complex to expand. None of the semi-empirical Hamiltonians showed any strong solution-type dependence in either d_H or the barrier height. Working in an NDDO (neglect of diatomic differential overlap) basis frame work, with non-polarizable chlorine atoms surrounded by non-polarizable waters, relegates the direct interaction between the Hamiltonian and the solvent to be largely electrostatic without any type of electronic response. Given that the Lennard-Jones parameters used were specifically designed to account for changes in the solvent it is not surprising that there is no strong dependence for changes in the solvent.

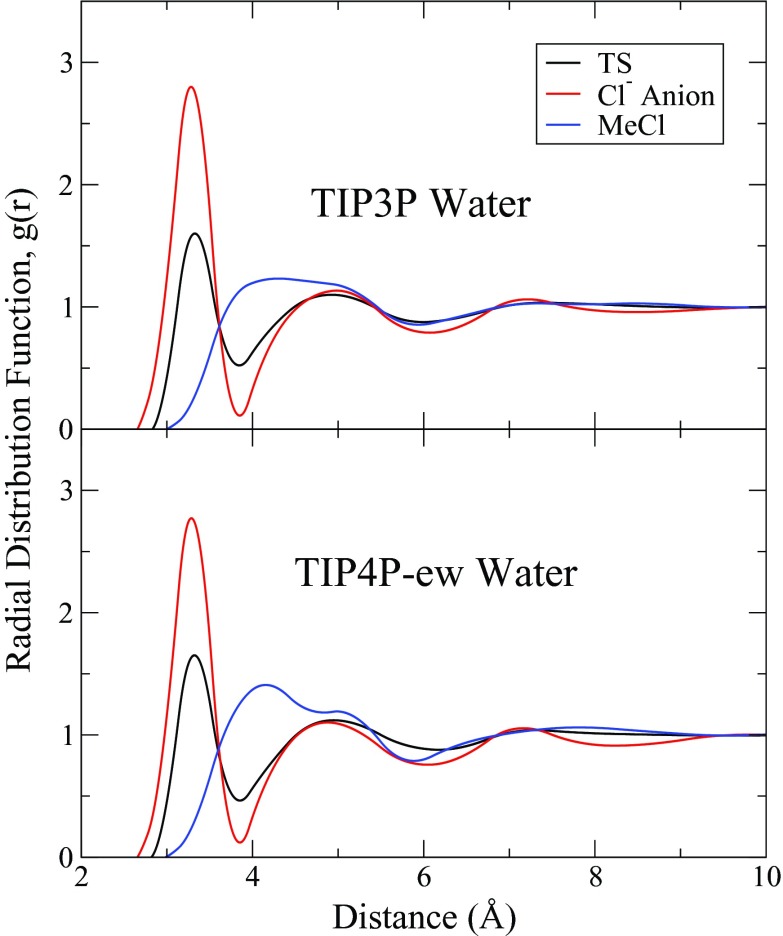
The radial distribution function (RDF), using the SRP Hamiltonian, for the chlorine to oxygen of water (OW), is also included for both the TIP3P and TIP4P-ew simulations, and can be seen in Figure 4. Differences between the two different water models are nominal, however the differences in the number of coordinated water between the chloride anion, around the each chlorine in the TS and methyl chloride are drastic (as seen in Table 5). The calculated coordination number for the chloride anion is 6.93 ± 0.01 and 6.52 ± 0.01 for TIP3P and TIP4P-ew, respectively, which compared favorably to the experimental number range of 6.0 to 6.5 ± 0.5,⁶⁴ and appears to have fairly well organized second and possibly third solvation shells. As the system moves through the transition state the coordination number for the chlorine drops to 3.95 ± 0.08 and 4.05 ± 0.18, as the local charge of the chlorine changes from negative 1.0 to approximately negative 0.7 charge units and the chloride attacks the methyl chloride. The results for methyl chloride are not too meaningful, despite the fact that one would expect the interactions of the chlorine atom to be lessened as the local charge of that atom decreases, because the methyl group attached to the chlorine atom disrupts the RDF in non-trivial ways. As such, the first and second solvation shells around the chlorine atom appear to overlap.

Figure 4.

Radial distribution functions from QM/MM simulations. Shown are the RDF of the chlorine/chloride atoms involved in the S_N2 reaction between chloride and methyl chloride and the oxygen of the surrounding waters. RDF plots are generated from retained simulations in both TIP3P (top) and TIP4P-ew (bottom) water, comparing the solvent structure at the transition state to that of the separate reagents. Functions are generated by integrating the direct count of the species of interest and then smoothed using binned splines. Numerical results from these simulations can be found in Table 5.

Table 5.

Structure of the first solvation shell around chloride in the chloride/methylchloride reaction. r_max and r_min are the positions of the maximum and the minimum of the RDF between chloride and the oxygen of water, respectively. N_crd is the calculated coordinated number of waters in the first solvation shell (between the beginning of the RDF and and r_min). ${\mathrm{r}}_{max}^{*}$ and ${\mathrm{N}}_{crd}^{*}$ are the experimentally known values, taken from the work of Zhang et al.⁶⁴

	TIP3P		TIP4P-ew
	TS	Cl−	TS	Cl−
rmax	3.28 ± 0.03	3.18 ± 0.02	3.26 ± 0.02	3.20 ± 0.02
rmin	3.73 ± 0.02	3.84 ± 0.03	3.75 ± 0.03	3.73 ± 0.01
Ncrd	3.95 ± 0.08	6.93 ± 0.01	4.05 ± 0.18	6.52 ± 0.01
${\mathrm{r}}_{max}^{*}$	…	(3.05-3.25)±0.2	…	(3.05-3.25)±0.2
${\mathrm{N}}_{crd}^{*}$	…	(6.0-6.5)±0.5	…	(6.0–6.5)±0.5

Critical assessment of the model

The new AM1 SRP Hamiltonian performs quite admirably in capturing experimentally known observables in both the gas and solution phases. Nonetheless, one must be critical in evaluating the limitations of the procedure described herein, and acknowledge that the very close agreement with experiment might arise due to a somewhat fortuitous cancellation of errors. Notably, the solvent models used in this study are not explicitly polarizable, and the van der Waals radii used for the chloride ion were derived to accurately reproduce the solvation free energy of a non-polarizable MM chloride ion for use with each specific water model used.⁵⁹ However, due to the minimal basis set used in the QM model employed here, the QM chloride ion when in isolation is also not polarizable due to the lack of available virtual orbitals.

While the model performed well within the current framework, one should expect that as the reaction proceeds through the reaction coordinate the electronic density around the chlorine atoms shifts in accordance to their bonding environment. These changes should be reflected in the repulsive exchange and correlation dispersion potentials, requiring the van der Waals radii to adjust.^{65, 66} The static Lennard-Jones parameters used in this study were developed to obtain solvation free energy of a chloride ion in non-polarizable water, as is the case for the QM/MM system, and do not consider the solvation free energy of methyl chloride. It is therefore likely to be in error. However, in the case of this study, the explicit coupling of polarization and exchange effects might not be necessary in order to obtain an accurate reaction barrier in solution. Thus, recognizing these limitations of the model used in the present work, one must concede that the very close agreement with the experimental barrier in solution is likely a result of the fortuitous cancellation of errors.

CONCLUSION

Accurately predicting reaction barriers in the condensed phase are of pinnacle importance in the fields of computational chemistry and biology. In order to be able to achieve this feat, precise models must be made in a reliable and robust fashion. In this work, such an approach has been applied for the development of SRP quantum model for chloride ion attack to methyl chloride based on gas-phase reaction profiles that are transferable to QM/MM simulations in solution. The new model reproduces many important observables, while being orders of magnitudes faster than conventional high-level QM methods. In the gas phase, reference experimental geometries and dipole moments are recapitulated, as well as the experimental reaction barrier. QM/MM simulations in solution demonstrate that the new model provides excellent agreement with the experimentally observed free energy barrier estimated from kinetic experiments. The overall free profiles show little dependence on the form of the water model (TIP3P versus TIP4P-ew), although there are some differences in the predicted solvent structure along the reaction coordinate. While these results are quite encouraging, one must also be forthcoming with respect to the limitations of the model, and in particular, the use of van der Waals radii that are fixed along the reaction coordinate. Overall, the results of this work provide an accurate SRP model for an important prototype S_N2 reaction in chemistry that can be used in the gas phase to build potential energy surfaces or in QM/MM simulations in solution to build free energy profiles. Analysis of the simulation results provides a detailed characterization of the solvent structure along the reaction coordinate, and insight into the nature of solvation effects on the reaction.