Incorporating single-side sparing in models for predicting parotid dose sparing in head and neck IMRT

Abstract

Purpose: Sparing of single-side parotid gland is a common practice in head-and-neck (HN) intensity modulated radiation therapy (IMRT) planning. It is a special case of dose sparing tradeoff between different organs-at-risk. The authors describe an improved mathematical model for predicting achievable dose sparing in parotid glands in HN IMRT planning that incorporates single-side sparing considerations based on patient anatomy and learning from prior plan data.

Methods: Among 68 HN cases analyzed retrospectively, 35 cases had physician prescribed single-side parotid sparing preferences. The single-side sparing model was trained with cases which had single-side sparing preferences, while the standard model was trained with the remainder of cases. A receiver operating characteristics (ROC) analysis was performed to determine the best criterion that separates the two case groups using the physician's single-side sparing prescription as ground truth. The final predictive model (combined model) takes into account the single-side sparing by switching between the standard and single-side sparing models according to the single-side sparing criterion. The models were tested with 20 additional cases. The significance of the improvement of prediction accuracy by the combined model over the standard model was evaluated using the Wilcoxon rank-sum test.

Results: Using the ROC analysis, the best single-side sparing criterion is (1) the predicted median dose of one parotid is higher than 24 Gy; and (2) that of the other is higher than 7 Gy. This criterion gives a true positive rate of 0.82 and a false positive rate of 0.19, respectively. For the bilateral sparing cases, the combined and the standard models performed equally well, with the median of the prediction errors for parotid median dose being 0.34 Gy by both models (p = 0.81). For the single-side sparing cases, the standard model overestimates the median dose by 7.8 Gy on average, while the predictions by the combined model differ from actual values by only 2.2 Gy (p = 0.005). Similarly, the sum of residues between the modeled and the actual plan DVHs is the same for the bilateral sparing cases by both models (p = 0.67), while the standard model predicts significantly higher DVHs than the combined model for the single-side sparing cases (p = 0.01).

Conclusions: The combined model for predicting parotid sparing that takes into account single-side sparing improves the prediction accuracy over the previous model.

INTRODUCTION

For head-and-neck (HN) cancer radiation therapy, intensity modulated radiation therapy (IMRT) has significant advantage in reducing the severity and incidence of xerostomia over three-dimensional conformal radiotherapy because of improved parotid sparing.^{1, 2, 3} The current consensus clinical guidelines for parotid sparing are derived from population-based toxicity studies, such as the QUANTEC (Ref. ⁴) and RTOG.⁵ Studies have shown that gland function reduction occurs minimally at 10–15 Gy mean dose, gradually increases at 20–40 Gy mean dose range, and becomes severe when mean dose >40 Gy.^{4, 6, 7} The QUANTEC guideline recommends that at least one parotid gland should receive less than 20 Gy mean dose, or both parotid glands should receive less than 25 Gy mean dose. In addition, the mean dose to each parotid gland should be kept as low as possible. The parotid gland dose sparing objectives recommended by RTOG are: at least one parotid gland should receive less than 26 Gy mean dose, or 20 cc of the combined volume of the left and right parotids should receive no more than 20 Gy dose, or alternatively at least 50% of the one gland receive no more than 30 Gy. As we can see, both guidelines include criterion to spare single side parotid as well as to spare bilateral parotids. Meeting either one of them can usually avoid severe xerostomia. The decision of which criterion to use is often left to the clinicians to make during treatment planning.

In clinical practice, the physicians often visually inspect the patient-specific anatomy. In cases where the location of the primary tumor or bulky lymph nodes causes large overlap of one parotid with the planning target volume (PTV) thus it is unlikely to spare both parotid glands, they will choose to reduce or remove the dose constraint to one parotid in exchange for more sparing in the salvageable parotid on the contralateral side for a more favorable radiobiological outcome.⁸ In this paper, we use the term “single-side sparing” to refer to the special consideration used to plan these cases and use the term “bilateral sparing” to refer to the cases where the physicians choose to spare both parotid glands.

A number of methods have been developed to predict the achievable organ-at-risk (OAR) dose sparing in HN IMRT treatment planning based on patients’ anatomical features and past planning experiences.^{3, 9, 10, 11, 12, 13} Our earlier work showed encouraging results using knowledge-based mathematical models to describe the quantitative correlations between patient anatomical features and the achievable dose sparing in a number of OARs.¹² These correlations represent the clinical acceptable tradeoff between PTV dose coverage and the dose sparing in these OARs. However, none of the reported methods considered the sparing of single side parotid in HN IMRT planning. The sparing of single side parotid reflects a “break point” in the normally continuous tradeoff between the left and right parotids and it is a special case of dose sparing tradeoff between different OARs. Our data show that this type of special, discontinuous tradeoff between left and right parotids is actually a common practice in HN IMRT planning.

This study focuses on improving the previously reported knowledge-based model in order to better predict dose sparing in parotid glands.¹² Our new model incorporates single-side sparing considerations so that it can more closely reflect the clinical planning tradeoffs and decisions. This model proposes a quantitative criterion for automatic determination of cases suitable for single-side parotid sparing and accounts for the extra dose sparing in the salvageable parotid of these cases.

MATERIALS AND METHODS

Patient data

Sixty-eight HN patients were retrospectively retrieved for training OAR dose prediction models, under an Institutional Review Board (IRB) approved protocol. The prescription was 44–50 Gy to primary PTV and 66–70 Gy to boost PTV. These cases include oropharynx, oral cavity, hypopharynx, and larynx tumors. Nasopharynx tumor cases are not included in this study because they usually involve an additional set of critical organs different from other HN cancer types and the correlation between parotid sparing and patient anatomical features is also somewhat different. There was no institutional template for dose constraints in HN IMRT planning. Instead, the dose constraints were prescribed case by case by the physicians after careful examination of patient anatomy and indications. In 35 of these 68 cases physicians prescribed single-side sparing preferences, where the dose constraints were indicated as “minimize when possible” or “no constraint” to the unsalvageable side of the parotid. The dose sparing to the salvageable side was prescribed with tighter constraints and was emphasized during planning by finding the highest level of dose sparing for the parotid without sacrificing the PTV coverage.

For model validation, 20 additional cases, 10 cases with physician prescribed single-side sparing preferences and 10 without, were used. These cases had the same characteristics as those used for model training.

Building models to predict parotid DVH

In the previous study, we have successfully built a nonlinear model that predicts OAR DVH sparing using an array of anatomical features.¹² This model did not distinguish single-side sparing cases from bilateral sparing cases; all HN cases were trained together to build a generic OAR sparing model. Implementation of this model was detailed in the previous work.¹² In summary, a number of patient's anatomical and dosimetric features were considered in the model (Table 1). In addition to volume features, the features of distance to target histogram (DTH) were extracted by principal component analysis.¹⁴ The prescriptions for PTV dose coverage and dose homogeneity were included as explanatory factors to account for the tradeoff between PTV coverage and OAR sparing. A step-wise multiple regression method was used to select the most significant patient features which influence the OAR dose sparing in the training plans.¹⁵

Table 1.

List of patient anatomical and dosimetric features in the model.

Anatomical and dosimetric features
Distance to primary and boost target histogram (Refs. 12 and 16)
Position of the OAR relative to the treatment fields
OAR, primary and boost PTV volumes
Fraction of OAR volume overlapping with PTVs (overlap volume)
Fraction of OAR volume outside the treatment fields (out-of-field volume)
PTV dose coverage and dose homogeneity

In the previous work, the primary and boost plans within one treatment course are modeled separately. However, physician's dose constraints are usually prescribed on the summed plans which combine the primary and boost plans for the entire treatment courses. In this study, two predictive models were developed to characterize the dependence of parotid dose sparing on patient anatomical features in the summed plans. The single-side sparing model was trained by using the spared parotids data in physician prescribed single-side sparing cases, while the standard model was trained with the remainder of cases for which the planning objectives is to spare bilateral parotids. The final model is the combination of these two models. Given a patient case, the combined model initially predicts parotid dose sparing using the standard model. Then, if the predicted parotid dose satisfies certain single-side sparing criterion, the combined model will apply the single-side sparing model to provide prediction of the parotid dose that takes into account the effects of single-side sparing.

Establish single-side sparing criterion

In clinical treatment planning, cases with single-side parotid sparing tend to have large overlap between PTV and one side of the parotid, which result in high dose in that parotid. Therefore, in this study we use the median dose (D50) predicted by the standard model as criterion for triggering single-side sparing. The single-side sparing criterion in this study is formulated by median dose instead of mean dose because the physicians prescribe parotid dose sparing constraint in terms of median dose in our institution. Let $D_{50}^{\mathrm{L},\mathrm{Std}}$ and $D_{50}^{\mathrm{R},\mathrm{Std}}$ represent the predicted median dose in the left and right parotids, respectively, and d₁ and d₂ be the thresholds doses for the two parotids. A case is identified as a single-side sparing case if the following condition is satisfied:

$$\begin{array}{ccc}& & \left(D_{50}^{\mathrm{L},\mathrm{Std}}>d_1\mathrm{and}{D}_{50}^{\mathrm{R},\mathrm{Std}}>d_2\right)\mathrm{or}\hfill \\ & & \left(D_{50}^{\mathrm{L},\mathrm{Std}}>d_2\mathrm{and}{D}_{50}^{\mathrm{R},\mathrm{Std}}>d_1\right).\hfill \end{array}$$

The “or” in the above condition specifies that the condition can be triggered either by d₁ applied to right parotid and d₂ to left parotid or vice versa.

To determine the best decision threshold, a receiver operating characteristics (ROC) analysis was performed by varying the threshold values and comparing the model-based classification at different thresholds against physician's single-side sparing prescription.¹⁷ The decision criterion were determined by the point on the ROC curve which maximizes the likelihood ratio,¹⁸ which is defined as: likelihood ratio = sensitivity/(1 − specificity). A larger value of likelihood ratio means the physician is more likely to prescribe a case as single-side sparing case if the case satisfies the criterion.

A previous study has shown strong correlation between portion of parotid volume overlapping with PTV and parotid mean dose.³ It suggests that sparing the parotid which has large overlap with PTV (>21% of parotid volume) may lead to inadequate PTV coverage. Thus, we tested the alternative method to identify single-side sparing cases by directly using the parotid-PTV overlap volume. A case would be identified as a single-side sparing case if the portion of parotid volume which overlaps with the primary PTV were greater than a threshold value. This method was compared with the criterion based on the predicted parotid median dose by a ROC analysis.

The combined model for parotid dose sparing is constructed by combining the single-side sparing criterion, the standard and the single-side sparing models. When a case satisfies the single-side sparing criterion, the parotid with lower predicted D50 is chosen to be further spared and its value is predicted by the single-side sparing model.

Validation of the DVH prediction model

To assess the effectiveness of the final model (the combined model) and its improvement over the standard model, we performed validation tests using the validation dataset. The validation dataset is outside the training database, with ten cases having single-side sparing preferences prescribed by physicians and ten cases not. Both the standard and combined models are applied to these cases. The differences between the model-predicted values and the actual plan values are calculated to evaluate the prediction accuracy.

Two quantitative measures were calculated to compare the differences in the modeled and actual planned DVHs. The first measure uses D50 as an indicator of dosimetric prediction accuracy. For the combined and standard models, respectively, the difference between the predicted D50 and actual clinical values was calculated for each validation case and the distribution of the differences was visualized in box plots. Furthermore, for the two sets of differences computed from the two models, a Wilcoxon rank-sum test was performed to assess the significance of improvements in prediction accuracy.¹⁹

While the median of the parotid median dose differences between the combined model prediction and the actual plan values was utilized to assess the prediction accuracy at a specific dosimetric point, the sum of residues (SR) is used as the second measure to quantify the overall difference of the entire DVH curves between the modeled and the actual plan's. SR, introduced by Appenzoller et al.,¹³ is defined as the sum of the differences between two DVHs over each dose bin (calculated at 1% prescription dose interval):

$$\mathrm{SR}={\sum }_{D=0}^{\infty }[V^{\mathrm{Actual}}\left(D\right)-V^{\mathrm{Model}}\left(D\right)]·\Delta D,$$

where V^Actual(D) and V^Model(D) are the fractional volume values corresponding to normalized dose D on the actual and modeled DVHs, respectively, and ΔD is the dose bin width. A positive SR value indicates the actual clinical DVH is higher than the modeled DVH on average, and vice versa. The Wilcoxon rank sum tests were again performed to show significance of any separation between the two models.

RESULTS

Training of the standard and single-side sparing models

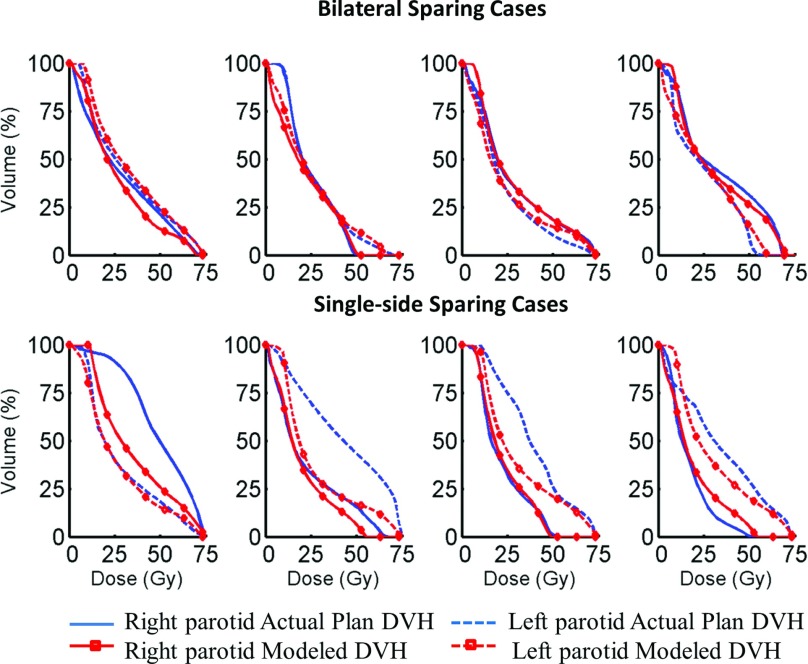
Both standard and single-side sparing models describe the dependency of the first three principal component scores (PCS) of the parotid DVHs on a number of patient factors. The determination coefficients R² of the standard models that account for the first two PCS are: PCS1: 0.81, PCS2: 0.68. Those of the single-side sparing models are: PCS1: 0.72, PCS2: 0.45. Examples of four single-side sparing cases and four bilateral sparing cases from the training data sets are shown in Fig. 1. The actual plan DVHs and model predicted DVHs for both parotids are plotted. The “nonspared” parotids are not used to train the single-side sparing model. They are shown in the figure to demonstrate the trade-off effect.

Figure 1.

The actual plan DVHs and model predicted DVHs of both side parotids in four examples of single-side sparing cases and four examples of bilateral sparing cases from the training data sets. The “nonspared” parotids are not used to train the single-side sparing model. They are shown in the figure to demonstrate the trade-off effect.

Establish single-side sparing decision criterion

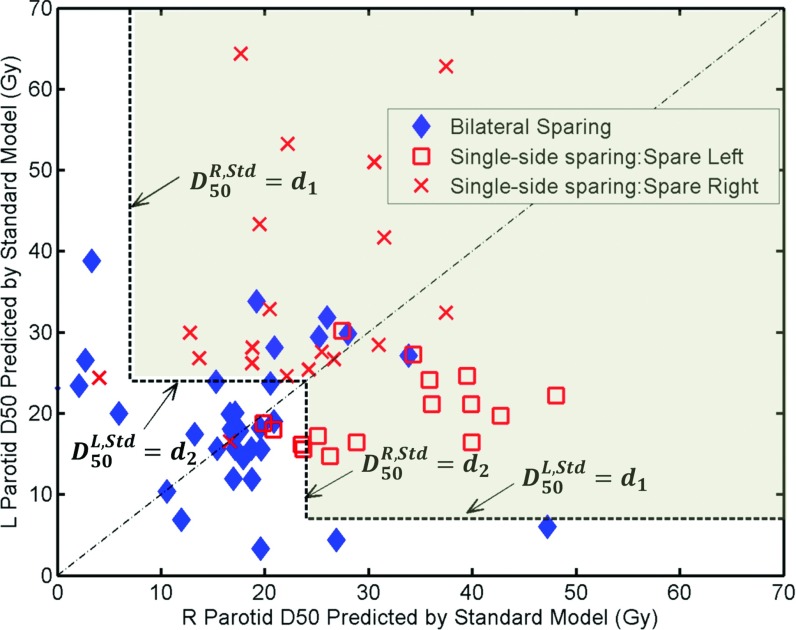
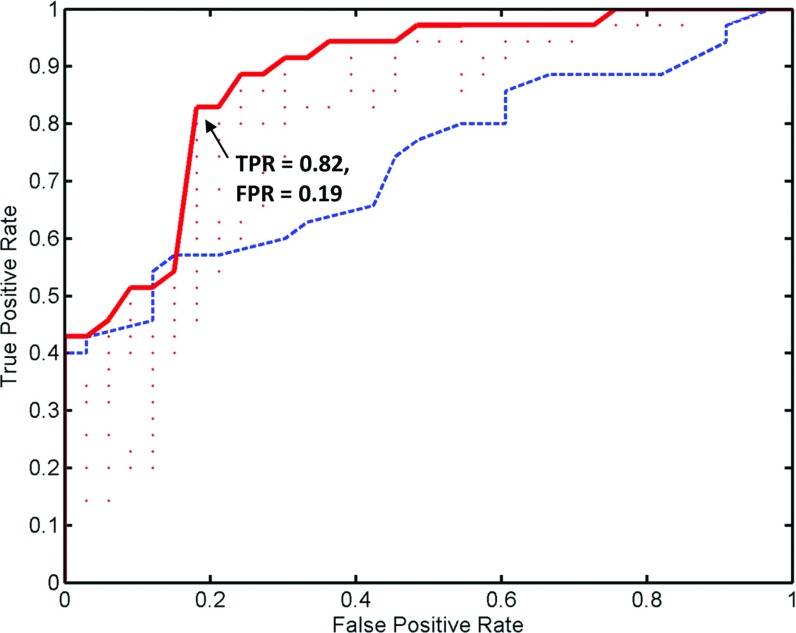
The median dose values predicted by the standard model for the 68 cases are plotted in Fig. 2. The median dose for the left parotid is represented by the Y-axis and that for the right parotid is represented by the X-axis. The single-side sparing thresholds d₁ and d₂ were varied and the true positive rate (TPR) and false positive rate (FPR) were calculated for each pair of thresholds by comparing the model classification against physician prescriptions (ground truth). The ROC curve is plotted in Fig. 3. The area under curve (AUC) for the ROC is 0.87. On the ROC curve, we choose the point with true positive rate and false positive rate of TPR = 0.82, FPR = 0.19. At this point, the likelihood ratio has a maximum at 4.3 and it corresponds to the threshold of d₁ = 24 Gy and d₂ = 7 Gy. Thus, a patient case will be considered a single-side sparing case if (1) the predicted median dose of one side parotid is greater than 24 Gy; and (2) the value for the other side is greater than 7 Gy. This single-side sparing region is visualized in Fig. 2 as the light gray area above the two L-shaped threshold lines.

Figure 2.

The dosimetric criterion for single-side parotid sparing. Each marker represents one patient plan. The single-side sparing region is the light gray area above the two L-shaped single-side sparing threshold lines.

Figure 3.

The ROC curve in solid is constructed by varying the single-side sparing threshold d₁ and d₂ and compare the threshold identified single-side sparing cases with the preidentified cases. Each dot in the figure represents a combination of d₁ and d₂. The dashed curve is the ROC curve for the decisions that use the portion of parotid volume overlapping with PTV as the criterion.

As a comparison, the ROC curve calculated by using the portion of parotid volume overlapping with PTV as criterion is also plotted (Fig. 3). It has an AUC as 0.73. The lower AUC indicates the criterion based on predicted parotid median dose is more consistent with physician's clinical single-side sparing decisions.

With this threshold, 29 of the 35 physicians prescribed single-side sparing cases (square and “X” markers in Fig. 2) are correctly identified as single-side sparing cases, while 27 of the 33 physicians prescribed bilateral sparing cases (diamond markers in Fig. 2) are correctly identified as bilateral sparing cases. Most misclassified cases are close to the diagonal-line of the figure indicating high symmetry of the PTV to the left and right parotids. One single-side sparing case misclassified as bilateral sparing case has very low right parotid D50 (<5 Gy) and a left parotid D50 of about 25 Gy.

Validation of DVH prediction model

Within the ten validation cases which have physician prescribed single-side sparing preferences, seven cases were correctly classified. In those three misclassified cases, the predicted D50 for both parotids are in the ranges of 20–24 Gy. Also, the geometrical relationships of the left and right parotids with the PTV are very similar. This indicates that even though physician has prescribed single-side sparing based on his/her personal estimation, the clinical plan would be able to spare both parotids to less than the critical threshold of 24 Gy.

Within the ten validation cases without physician prescribed single-side sparing, eight cases were correctly classified. In the two misclassified cases, both the right parotid D50 were predicted at about 26 Gy, and the left parotid median doses were predicted at 21 and 19 Gy, respectively. These two cases were just above the single-side sparing threshold of 24 Gy, and were clinically interpreted by physician as bilateral sparing cases.

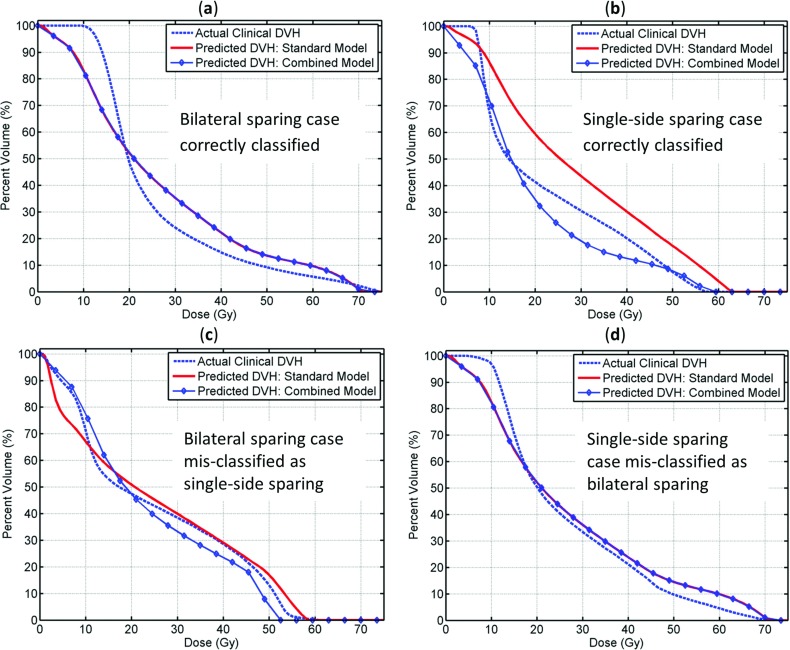
Two examples of correctly classified cases and two examples of misclassified cases are shown in Fig. 4. As shown in the figure, for bilateral sparing cases, both the standard and the combined models predict closely to clinical plan values [Figs. 4a, 4c]. For single-side sparing cases, the combined model is much closer to clinical values when single-side sparing is clearly favored in clinical situations as in Fig. 4b. On the other hand, when single-side sparing is borderline necessary (parotid D50 being close to 24 Gy) as shown in Fig. 4d, both the standard and combined models are close to clinical D50 values.

Figure 4.

Two examples of correctly classified cases and two examples of misclassified cases. (a) and (c) Physician prescribed bilateral sparing cases; (b) and (d) physician prescribed single-side sparing cases.

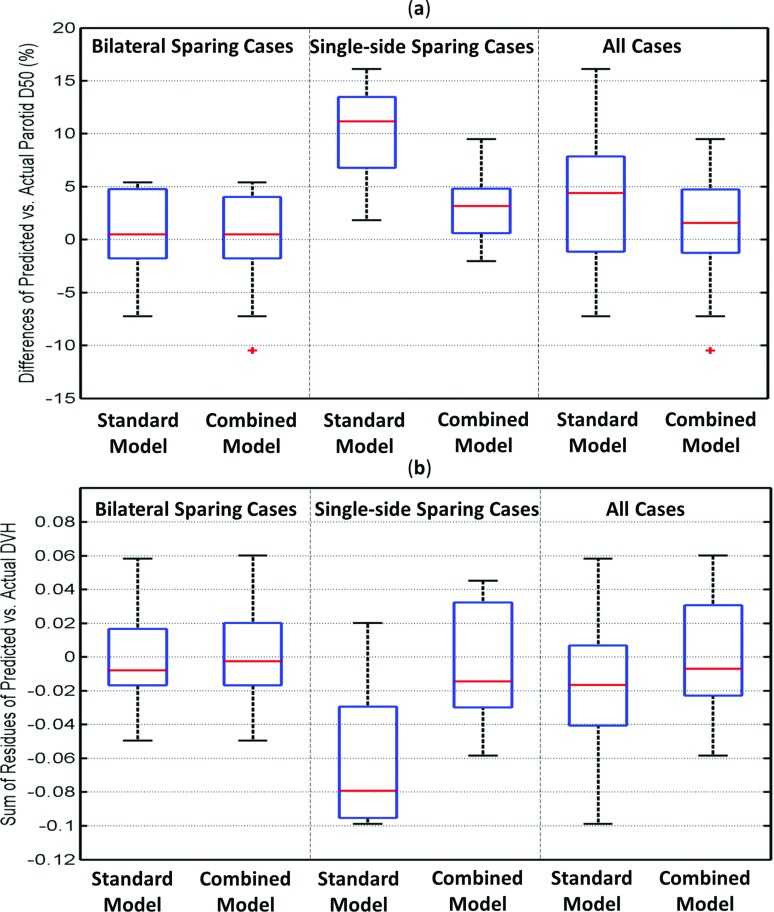
Figure 5a compares the prediction accuracies on parotid medain dose between the standard and the combined model. The prediction error is the difference between the predicted median dose values and the actual planned values, and is visualized in box plots for the bilateral sparing cases, single-side sparing cases, and all cases together. In the figure, the horizontal bars inside the boxes indicate the locations of the median of the distributions, and the boxes represent the interquartile range (IQR) of the distributions (the 25% quartile to 75% quartile).¹⁹ Outliers, represented by crosses, are defined as the points more than 1.5 times IQR away from the box edge. The upper and lower extreme values are represented by the horizontal bars connected to the box.

Figure 5.

Box plot depicting prediction accuracies on parotid median dose (D50) by the standard and the combined model. The prediction error is the difference between the model-predicted values and the actual planned values. (a) Differences of parotid median dose. (b) The sum of residues between the modeled and actual plan DVHs.

For the bilateral sparing cases, the combined and the standard models performed equally well, with the median of the prediction errors being 0.34 Gy by both models (p = 0.81). For the single-side sparing cases, the standard model overestimates the D50 by 7.8 Gy on average, while the predictions by the combined model differ from actual values by only 2.2 Gy (p = 0.005). The differences between these two models are not significant when only the bilateral sparing cases are considered or when both the single-side sparing and bilateral sparing cases are considered together (p = 0.81 and 0.11). However, the difference between these two models is significant (p = 0.005) when single-side sparing cases alone are considered.

The modeled and actual planned DVH curves are compared using the SR index in Fig. 5b. Since the SR calculates the difference of the two DVH curves, a value close to zero indicates a close match between the modeled and the actual planned DVH curves. A positive SR value indicates the actual plan DVH has higher values (hotter) than the modeled DVH on average, and vice versa. The prediction accuracy of the combined model and the standard model is the same for the bilateral sparing cases: the medians of the SR for the two models are −0.002 and −0.009, respectively (p = 0.67). For single-side sparing cases, the medians are −0.08 and −0.015, respectively, and are significantly different (p = 0.01), which indicates the standard model predicts DVHs significantly higher than the actual planned DVHs. When all the cases are considered together, the medians are −0.018 and −0.007, respectively, and not significantly different (p = 0.09).

DISCUSSION

IMRT planning involves many different types of tradeoff situations. In addition to the dose sparing tradeoff between the left and right parotid glands, there are also indications in our dataset that the parotid dose sparing is influenced by other OARs in some cases. For example, we see a lack of oral cavity or larynx constraints comes with a lower parotid dose. While this type of tradeoff between the dose sparing of parotids and other OARs is a very interesting topic, it is outside the scope of this study. Currently the effect of the tradeoff is treated as the standard deviation of the regression model. We also would note that, in most clinical cases, the priorities of sparing organs do follow convention or templates; hence there is high consistency in most cases in terms of the prescriptions for OAR sparing constraints.

Single-side parotid sparing is prescribed to loosen or eliminate dose constraint to one parotid in exchange for lower median (and mean) dose of the salvageable parotid on the contralateral side. In cases where the PTV mainly resides on one side of the neck, the contralateral side parotid will get little dose, thus there is no need to give up the parotid sparing on the ipsilateral side. These cases are shown along the long arms of the two “L” shapes in Fig. 2 (with the dose threshold of 7 Gy). For these cases, physician and planner often do not just spare single-side parotid. The only exception is in one case where sparing right parotid is emphasized by physician (shown as the “X” on the left side of the Fig. 2), with right parotid D50 getting 5 Gy and left parotid D50 getting about 25 Gy in the actual plan. Although single-side sparing is prescribed, the actual plan attempted to spare bilateral parotids and both DVHs agreed with the standard prediction model.

The single-side sparing classifications do not always agree with physician prescriptions. In most of these misclassified cases, the PTVs located at the center of the neck and the left and right parotids have very similar geometrical relationships to the PTVs. For these cases, the D50 are close to the diagonal line in Fig. 2, and are in the range of 20–30 Gy. In this scenario, the standard model and the combined model have very close predictions, as shown in Figs. 4c, 4d. Hence, physician preferences or model classifications will result in minimal dosimetric difference in clinical plans and the predicted DVHs by both models are close to the clinical DVHs. Most of the misclassified cases fall into this scenario and therefore do not significantly influence the final combined model.

Another reason for the misclassification is that the physicians’ clinical prescriptions for single-side sparing are used as the ground truth in this study. However, physicians make the single-side sparing prescriptions based on their clinical judgment using visual inspection of patient anatomy and personal estimation of the dose to the parotids before the final treatment plan and dosimetric data are available. Therefore, the physician preferences can be uncertain in some cases when parotid D50 are close to the 24 Gy thresholds.

If there were more objective and physician-independent criteria that determine exactly when single-side sparing is preferred, we should use those criteria in our model. However, there is currently no consensus clinical criterion to guide the decision whether to spare single side parotid or to spare bilateral parotids. Current models of the radiobiological outcome of parotid sparing are also insufficient to provide an objective criterion. For example, there have been a number of studies to model the correlation between the normal tissue complication probability (NTCP) of parotid gland or salivary gland flow function and the dose volume data.^{6, 20, 21, 22, 23} The mean-dose-exponential model which describes the overall salivary function at 6 month after treatment as the mean of the bilateral parotids adequately fit the data presented in Blanco et al.⁶ However, since both the ipsilateral and contralateral side parotids contribute to the overall salivary function equally in the model, this model cannot account for benefit of preferentially sparing the contralateral parotid which is a common clinical practice. Moiseenko et al. showed orderly dependences of overall whole-mouth salivary function on the mean dose to the highly spared gland for 3 and 12 months data.²¹ A logistic model was used to describe the incidence of Grade 4 xerostomia as a function of the mean dose of the spared parotid gland. While this model can be used to evaluate the biological benefit of single-side parotid sparing, it cannot be used to compare the biological benefit of single parotid sparing vs bilateral sparing because only spared parotid is considered. Our work will benefit greatly from future models that incorporate those outcome data which can differentiate single-side sparing and bilateral sparing.

Our current approach assumes that the high quality prior plans contain fundamentally good decisions made by physicians and seeks to capture the knowledge behind these decisions by learning from physician approved plans. In addition, the model and criterion obtained in this study reflect the clinical experience of multiple physicians in our institution because our dataset consists of plans done by several physicians. We further note that the goal of this work is to improve the accuracy of the ultimate combined models. With a change of threshold dose within 1–2 Gy, the cases which would be misclassified are most likely those with PTVs overlapping both parotids in a similar manner. For these cases, the predictions by the standard model and the combined model are very close, thus the prediction accuracy will not deteriorate significantly. We expect a single-side sparing decision criterion to perform well for a range of different physicians and institutions.

For cases that clearly favor single-side sparing, the results show that the standard model significantly overestimates the parotid median dose. This indicates the different dosimetric features between the single-side sparing and bilateral sparing plans. In IMRT planning, the salvageable parotid achieved extra dose sparing by relaxing the constraint on the ipsilateral side parotid sparing. This extra dose sparing can be quantified by the difference of the standard and the combined model prediction, which is 5.6 Gy on average. By incorporating published guidelines on differential parotid sparing and learning the planning knowledge embedded in prior IMRT plans, we have significantly improved modeling accuracy. The combined model switches between the standard and the single-side sparing models according to the single-side sparing criterion. The residual 2.2 Gy difference between the median dose predicted by the combined model and the actual plan value is an indication of the validation accuracy of the single-side sparing model. The larger validation error by the single-side sparing model is due to the larger case-by-case variation in the resulting parotid sparing when the planner tried to achieve extra sparing for the spared parotid. This variation is also reflected by smaller determination coefficient values of the single-side sparing model compared with the standard model. We expect the variations to decrease and eventually the prediction accuracies of the two models to converge when more cases are added to the training pool.

Prediction models that “mimic” real clinical planning scenario are highly valuable to clinical IMRT planning as it can potentially lead to more efficient planning and optimal dose sparing.^{3, 24} The time and effort spent on trial-and-error process for the search of optimal parotid sparing goals can be greatly reduced, even eliminated with a precise prediction model. Early studies have applied linear relationships between parotid-PTV overlap and mean dose in guiding treatment planning.^{3, 25, 26} For example, Hunt et al. used an OAR-PTV overlap of 21% as an empirical indication for different parotid sparing trend.³ Our model extends these early works by incorporating a combined consideration of patient's anatomy, organ toxicity and sparing guidelines, and physician's personal experience into an advanced model to closely represent clinical reality where different tradeoff options are explored for a given patient. Finally, the modeling technique and the models developed in this study are in general applicable to intensity modulated radiation therapy in any format, including volumetric modulated arc therapy and tomotherapy.

CONCLUSION

An enhanced model for predicting parotid dose sparing in HN IMRT planning is developed to incorporate single-side parotid sparing. Initial validation results demonstrated better performance of this new model in comparison to a standard model that did not consider single-side sparing. Clinical dose criterion is established to guide the preplanning prediction when one of the parotids is favored more sparing for better radiobiological outcome.