The potential of positron emission tomography for intratreatment dynamic lung tumor tracking: A phantom study

Abstract

Purpose: This study aims to evaluate the potential and feasibility of positron emission tomography for dynamic lung tumor tracking during radiation treatment. The authors propose a center of mass (CoM) tumor tracking algorithm using gated-PET images combined with a respiratory monitor and investigate the geometric accuracy of the proposed algorithm.

Methods: The proposed PET dynamic lung tumor tracking algorithm estimated the target position information through the CoM of the segmented target volume on gated PET images reconstructed from accumulated coincidence events. The information was continuously updated throughout a scan based on the assumption that real-time processing was supported (actual processing time at each frame ≈10 s). External respiratory motion and list-mode PET data were acquired from a phantom programmed to move with measured respiratory traces (external respiratory motion and internal target motion) from human subjects, for which the ground truth target position was known as a function of time. The phantom was cylindrical with six hollow sphere targets (10, 13, 17, 22, 28, and 37 mm in diameter). The measured respiratory traces consisted of two sets: (1) 1D-measured motion from ten healthy volunteers and (2) 3D-measured motion from four lung cancer patients. The authors evaluated the geometric accuracy of the proposed algorithm by quantifying estimation errors (Euclidean distance) between the actual motion of targets (1D-motion and 3D-motion traces) and CoM trajectories estimated by the proposed algorithm as a function of time.

Results: The time-averaged error of 1D-motion traces over all trajectories of all targets was 1.6 mm. The error trajectories decreased with time as coincidence events were accumulated. The overall error trajectory of 1D-motion traces converged to within 2 mm in approximately 90 s. As expected, more accurate results were obtained for larger targets. For example, for the 37 mm target, the average error over all 1D-motion traces was 1.1 mm; and for the 10 mm target, the average error over all 1D-motion traces was 2.8 mm. The overall time-averaged error of 3D-motion traces was 1.6 mm, which was comparable to that of the 1D-motion traces. There were small variations in the errors between the 3D-motion traces, although the motion trajectories were very different. The accuracy of the estimates was consistent for all targets except for the smallest.

Conclusions: The authors developed an algorithm for dynamic lung tumor tracking using list-mode PET data and a respiratory motion signal, and demonstrated proof-of-principle for PET-guided lung tumor tracking. The overall tracking error in phantom studies is less than 2 mm.

INTRODUCTION

Motion management during radiotherapy has been vigorously researched over the past several years, but it remains challenging to reduce the effect of motion due to irregular and unpredictable motion patterns.¹ The best strategy for motion management is dynamic tumor tracking (i.e., image-guided real-time tumor tracking), which enables continuous radiation on the target, reducing the treatment setup margins and the effect of motion of the target during treatment.^{1, 2} Commercial instruments have been developed to achieve dynamic tumor tracking, such as the CyberKnife Synchrony system (Accuray, Inc.), the gimbaled linear accelerator (linac), the beacon electromagnetic transponder (Calypso Medical), and magnetic resonance imaging (ViewRay, Inc.).^{3, 4, 5, 6, 7} In almost all cases, for in-room imaging, x-ray imaging (using megavoltage or kilovoltage source) with implanted markers is used for dynamic tumor tracking.^{8, 9, 10} However, implanted markers have potential problems to cause pneumothorax and maker migration.^{11, 12} Markerless tracking techniques are alternative non-invasive methods, but direct tracking is difficult or impossible if the tumor is hidden behind other structures such as the vertebrae, ribs, and heart.

Positron emission tomography imaging has not been incorporated with radiotherapy systems (e.g., linac) despite the potential of biologically based targeting. New methods using on-board PET have been recently proposed for radiation treatment.^{13, 14, 15, 16, 17, 18} Fan et al. evaluated the feasibility of a combined PET-linac system for real-time guidance of radiotherapy for moving targets in Monte Carlo simulations (Fig. 1).^{14, 15} Darwish et al. proposed PET using an open dual ring geometry, which was investigated as an on-board system for functional imaging and PET marker tracking in Monte Carlo simulations, specifically with tomotherapy.¹³ Yamaya et al. developed the first small PET prototype with an open dual ring geometry in order to show a proof-of-principle of PET-guided radiation therapy. Tashima et al. proposed a single-ring PET geometry with an accessible space and investigated the sensitivity of the geometry theoretically.¹⁷ The common feature of all the proposed PET geometries is providing an accessible open space in which a radiation treatment system can be positioned.

Figure 1.

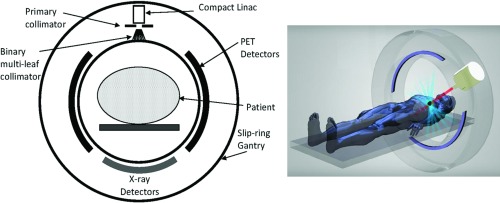
Geometry (left) and schematic (right) of an integrated PET-linac in which the PET signal (coincidence events) can be used to estimate the target position during radiation delivery.¹⁴, ¹⁵

To the best of our knowledge, there have been no previous efforts to evaluate the accuracy of tumor tracking using PET. In the literature, Tashima et al. demonstrated the potential and feasibility of PET-guided tumor tracking using the point source with a 30 s cycle sine curve. However, the simulated motion is not realistic compared to actual human breathing and difficult to be used for tracking accuracy evaluation.¹⁸ The current limitations of PET such as long imaging times and low spatial resolution may explain reasons why FDG-PET has not been considered for PET-guided lung tumor tracking despite the potential of biologically adaptive radiation treatment. Due to the long imaging times and low spatial resolution, respiratory tumor motion degrades the image quality of PET, particularly in thoracic and abdominal images. In PET scans, data are acquired for 3–5 min per bed position. Therefore, PET images are time-averaged over many respiratory cycles (average respiratory period: 4∼5 s) causing motion blurring artifacts. As the result of blurring artifacts, tumor volumes are overestimated in size, and the corresponding standard uptake value (SUV) is underestimated.^{19, 20, 21, 22, 23, 24, 25, 26} Therefore, rather than research PET-guided tumor tracking, previous studies have focused on reducing motion blurring artifacts in PET images.

There are four broad classes to reduce artifacts caused by respiratory motion in PET images: (1) hardware-based gating, (2) software-based gating (Refs. ^{27, 28, 29, 30, 31, 32, 33, 34}), (3) incorporated-motion-model based algorithms (Refs. ³⁵ and ³⁶), and (4) joint estimation (Refs. ³⁷ and ³⁸). In the categories, hardware-based gating is an only clinically approved method based on the assumption that external respiratory motion is a surrogate for motion of internal structures. Devices such as pressure sensors, spirometers, temperature sensors, or the real-time position management (RPM) system are employed to monitor external respiratory motion and generate a trigger signal at a user-predefined phase or displacement.^{19, 20, 21, 25, 39, 40} To reduce lesion blurring, gated PET or four dimensional (4D) PET retrospectively correlates the external respiratory motion with the PET data acquisition to allow image reconstruction at different phases or displacements of the external respiratory signals. PET research regarding motion management has been focused on motion correction such as reducing motion blurring artifacts, not dynamic tumor tracking, because of long scan times and low spatial resolution. However, all the above approaches except IMM-based methods imply the possbility that motion information can be derived from PET raw data or reconstructed images.

This study aims to evaluate the potential and feasibility of PET for dynamic lung tumor tracking during radiation treatment. The research focus is to evaluate tracking accuracy in a commercial PET scanner for a proof-of-principle based on the assumption of real-time processing. We propose a center of mass (CoM) lung tumor tracking algorithm using gated-PET images combined with a respiratory monitoring signal. The geometric accuracy of the proposed algorithm was quantified in a dynamic phantom study.

METHODS

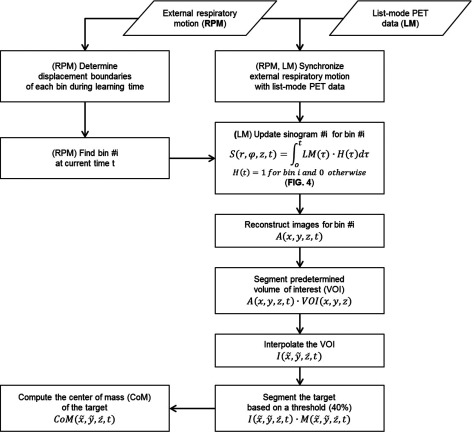
Figure 2 shows the workflow of PET dynamic tumor tracking using external respiratory motion and list-mode PET data. The proposed algorithm estimates the target position information through the CoM of the segmented target volume on gated PET images reconstructed from accumulated coincidence events, which is continuously updated throughout a scan. External respiratory motion and list-mode PET data were acquired from a phantom programmed to move with measured respiratory traces (external respiratory motion and internal target motion) from human subjects, for which the ground truth target position was known as a function of time.⁴¹ (Fig. 3)

Figure 2.

The workflow of PET dynamic tumor tracking using external respiratory motion and list-mode PET data.

Figure 3.

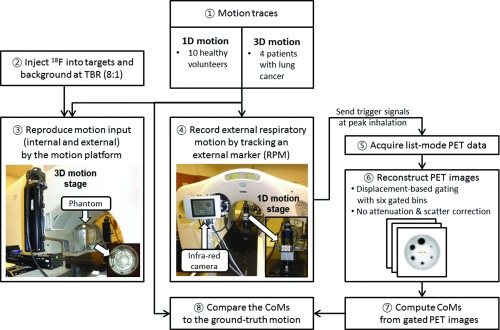
Experimental set-up and process for the PET dynamic tumor tracking phantom studies.

Motion input

PET targeting accuracy using 1D-measured motion from healthy volunteers

We used the external respiratory motion traces of ten healthy volunteers acquired in the Venkat study to reproduce free breathing traces with a programmable motion phantom (4D Phantom).⁴² We assumed a linear one-to-one correlation between the internal target motion (3D motion stage) and external respiratory signals (1D motion stage) and used the same external respiratory traces for both the 3D and 1D motion stages to reproduce free breathing motion. This assumption was based on the combined optical monitoring and fluoroscopic analysis of the abdominal wall and diaphragm motion by Vedam et al.⁴³ They found a correlation of 0.82–0.95 in 60 measurements from five patients. This correlation can be used to predict diaphragm motion, based on the respiration signal to within 0.1 cm. Diaphragm motion is dominant in the superior-inferior (SI) direction and lung motion is strongly dependent on the diaphragm motion, so the assumptions, (1) a linear correlation between internal target motion and external respiratory motion and (2) superior-inferior (SI) direction only for target motion, were reasonable in this phantom study. In general, abdominal organ motion is predominantly in the SI direction, with no more than a 2-mm displacement in the anterior-posterior and lateral directions.⁴⁴ Based on the general characteristics of lung tumor motion, we moved the 3D motion stage in the SI direction only. The SI phantom motion was synchronized with the 1D motion stage, whose motion was only in the AP direction.

PET tracking accuracy using 3D-measured motion from lung cancer patients

In order to test the algorithm on respiratory motion with clinically observed variability, motion traces of higher than average motion magnitudes and complexity were selected from a large abdominal/thoracic tumor motion and respiratory signal database.⁴⁵ These motion traces were 3D-measured motion where the tumor motion and external respiratory signals were different and derived from patient measurements. The selected trajectories were all from lung tumors as previously used by Poulsen et al. and Keall et al. representing typical motion, baseline variations, predominantly left-right motion, and high-frequency breathing.^{6, 10}

Cylindrical phantom

This phantom study followed the standard suggested in the NEMA NU 2–2001 standard document.¹³ The cylindrical phantom consisted of six hollow spheres (10, 13, 17, 22, 28, 37 mm in diameter and 0.5, 1.2, 2.6, 5.6, 11.5, 26.5 ml in volume) of a NEMA IEC body phantom and a cylinder (20.8 cm in inside diameter, 17.5 cm in inside height and 3100 ml in volume) of a Hoffman 3D brain phantom (Fig. 3).⁴⁶ A cylinder of a NEMA ICE body phantom was not used as it exceeded the weight limit of the 3D motion stage of the 4D phantom. Six hollow spheres were positioned symmetrically in the cylinder. We injected ¹⁸F into the six hollow spheres as targets and the cylinder as background. The standard background activity concentration (5.18 kBq/ml) was determined with a typical injection dose (370 MBq) into a 70 kg patient. The target to background ratio was 8:1 as a representative TBR for lung tumors.^{26, 46}

4D Phantom (motion platform)

A 4D phantom was used to reproduce internal target motion and external respiratory motion simultaneously for simulating clinical 4D-PET scans. The 4D Phantom was a programmable motion platform consisting of a 3D-motion stage and a 1D-motion stage (Fig. 3) that simulate tumor motion and abdominal displacement, respectively.⁴⁷ We placed the cylindrical phantom on the 3D-motion stage and scanned it. We positioned an infrared reflective marker box on the 1D-motion stage and measured the vertical motion of the marker box by the RPM system throughout a scan. We set up the 4D phantom outside the scanner, rather than on the scanner table, as it could not be positioned in the scanner bore due to its height.

Data acquisition of list-mode PET and external respiratory motion

We used the data set of ten 1D-motion traces acquired for an audiovisual biofeedback study.⁴¹ For the four 3D-motion traces, the same experimental procedure (Fig. 3) applied to the 1D-motion traces was performed to obtain list-mode PET and external respiratory motion data throughout 4D-PET scans while reproducing the 3D-motion traces. During the 4D-PET scans, the 3D-motion stage and 1D-motion stage reproduced internal target motion and external respiratory motion, respectively, while the RPM system recorded the motion of the 1D-motion stage (external respiratory motion) in real-time. During the recording, the RPM system continuously generated trigger signals at the highest point of each respiratory cycle (peak-inhalation). The trigger signals were transferred to the PET work-station and recorded in the list-mode PET data to facilitate synchronization of the list-mode PET and external respiratory signals in the simulation (Fig. 2).

The 4D-PET scans were performed using a Discovery ST PET/CT scanner (GE Medical Systems, Waukesha, WI).⁴⁸ The 2D scan mode using septa was chosen to minimize the effect of scattering. The PET system has a transaxial field of view (FOV) of 70 cm and an axial FOV of 15.7 cm. The slice thickness (axial sampling interval) is 3.27 mm. The transaxial full width at half maximum (FWHM) is 6.2 mm at 1 cm and 6.8 mm at 10 cm, and the axial FWHM is 4.8 mm at 1 cm and 5.9 mm at 10 cm from the center of FOV. In the 2D scan mode, the sensitivity is 2.0 cps/kBq, the peak noise equivalent count rate (NECR) is 95 kcps at 12 kBq/ml, and the scatter fraction is 19%.

Image reconstruction with displacement-based gating

PET images were reconstructed in the Respiratory Gating Toolbox (RGT, GE Health Care, Milwaukee, WI) which enables the reconstruction of 4D PET images using (1) list-mode PET data acquired from a GE PET system and (2) external respiratory motion data recorded in RPM.

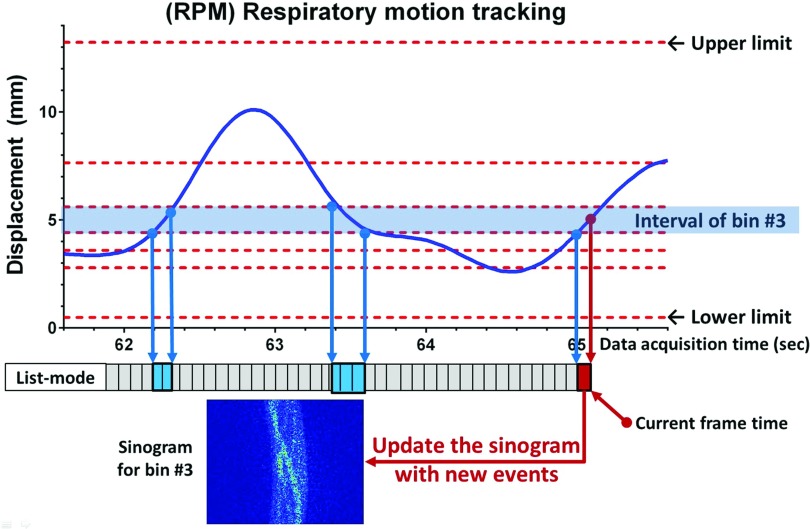
Although phase gating is a clinical protocol for 4D-PET images in the work-station, displacement gating has been shown to be superior to phase gating in general.⁴⁹ As a result, displacement gating was selected as a default gating method for producing gated sinograms from list-mode PET data (Figs. 24). After beginning to collect coincidence events, but before starting to track target motion, a 1 min record of external respiratory motion signals was employed to determine displacement boundaries. One minute was chosen as a reasonable compromise between patient throughput and targeting accuracy. The number of gated bins followed the clinical standard (six bins). The displacement boundaries of six gated bins (bin-1: end inhalation, bin-6: end exhalation) were determined to give each bin the same time duration, based on the recorded external respiratory motion up to 1 min, which caused different gate intervals in displacement.⁴⁹ The equal time duration was maintained for every bin to ensure near uniform counts in each bin for at least 1 min, from which it was reasonable to assume that each bin has approximately the same amount of coincidence events. The upper and lower limits of the boundaries were the maximum and minimum of the used external respiratory signals.

Figure 4.

The procedure of sinogram updating using real-time displacement gating. During learning time (default: 1 min), the displacement boundaries of every bin were determined and initial sinograms were created from accumulated events for every bin. After the learning time, the sinogram corresponding to current time and bin # was updated from new events which were collected during the frame interval (200 ms).

The Ordered Subset Expectation Maximization (OSEM) algorithm (21 subsets, 2 iterations, and 6 mm FWHM Gaussian post filter) was applied for 2D image reconstruction. The corrections for random coincidences, dead time, normalization, and well-counter were included in the reconstruction procedure. However, attenuation and scatter correction using CT images was not applied to avoid any effect of CT images on motion information derived from PET images. The matrix size for an image slice was 128 × 128 with a 4.68 × 4.68 × 3.27 mm³ voxel size. The number of image slices was 47 and the slice thickness was 3.27 mm.

Motion tracking algorithm

Figure 2 shows the workflow of PET dynamic tumor tracking using external respiratory motion and list-mode PET data. The algorithm was developed in MATLAB (MathWorks, Natick, MA) using RGT.

In the current 4D-PET protocol, 4D-PET images are reconstructed retrospectively from list-mode data (and external respiratory motion data in an optional manner). For dynamic target tracking, however, the concept of sinogram updating is proposed, which enables continuous image reconstruction for each gated bin with increasing acquisition time (steps of 200 ms). With the displacement boundaries set as described above, a bin number is continuously updated according to the displacement of external respiratory motion in real-time, and the corresponding sinogram is updated with new coincidence events that are collected during the frame time (200 ms). For example, if the external marker position is in the interval of bin #3, the old sinogram for bin #3 is updated with new events at current time t (Fig. 4). PET images are reconstructed from the sinogram at current time t (Figs. 34):

$$S\left(r,\phi ,z,t\right)={\int }_o^{t}LM\left(t\right)·H\left(t\right)dt,$$ (1)

$$A\left(x,y,z,t\right)=\mathrm{recon}\left\{S\left(r,\phi ,z,t\right)\right\},$$ (2)

where S(r, φ, z, t) is a sinogram for the bin # of time t, and LM(t) is list-mode data at time t. H(t) = 1 for the bin # and 0 otherwise. A(x, y, z, t) is an activity at a voxel (x, y, z) at time t before interpolation.

After the image reconstruction, CoM-based target tracking is employed to estimate the current target position, for which a predetermined volume of interest is segmented and then interpolated with a 1 × 1 × 1 mm³ voxel size:

$$\begin{array}{c}\hfill I\left(\tilde{x},\tilde{y},\tilde{z},t\right)=\mathrm{Interpolate}\left\{A\left(x,y,z,t\right)·VOI\left(x,y,z\right)\right\},\end{array}$$ (3)

where VOI(x, y, z) is a binary mask; VOI(x, y, z) = 1 if (x, y, z) is in a manually predetermined volume of interest, else VOI(x, y, z) = 0. $I\left(\tilde{x},\tilde{y},\tilde{z},t\right)$ is an interpolated volume of A(x, y, z, t) · VOI(x, y, z).

In the VOI, the CoM is computed after segmenting the target based on a threshold (60% for the 10 mm target and 40% for the other targets):^{50, 51}

$$\begin{array}{ccc}& & Co{M}_{\tilde{x}}=\frac{{\sum }_{\tilde{x}}{\sum }_{\tilde{y}}{\sum }_{\tilde{z}=1}^n\tilde{x}·I\left(\tilde{x},\tilde{y},\tilde{z},t\right)·M\left(\tilde{x},\tilde{y},\tilde{z},t\right)}{{\sum }_{\tilde{x}}{\sum }_{\tilde{y}}{\sum }_{\tilde{z}=1}^{n}I\left(\tilde{x},\tilde{y},\tilde{z},t\right)·M\left(\tilde{x},\tilde{y},\tilde{z},t\right)}\hfill \\ & & \mathrm{and}\mathrm{similarly}\mathrm{for}Co{M}_{\tilde{y}}\mathrm{and}Co{M}_{\tilde{z}},\hfill \end{array}$$ (4)

where $M\left(\tilde{x},\tilde{y},\tilde{z},t\right)$ is a binary mask; $M\left(\tilde{x},\tilde{y},\tilde{z},t\right)=1$ if $I\left(\tilde{x},\tilde{y},\tilde{z},t\right)$ is larger than 40% of the maximum voxel value, else $M\left(\tilde{x},\tilde{y},\tilde{z},t\right)=0$. $\left(\tilde{x},\tilde{y},\tilde{z}\right)$ is a new pixel position after interpolation. $\tilde{x}$ direction is corresponding to the left-right direction, $\tilde{y}$ direction is corresponding to the anterior-posterior (AP) direction, and $\tilde{z}$ direction is corresponding to the superior-inferior (SI) direction.

The geometric accuracy of the proposed algorithm was evaluated by quantifying estimation errors between actual motion of targets (1D-motion and 3D-motion traces) and CoM trajectories estimated by the proposed algorithm at time t.^{28, 34} We ignored the data out of upper and lower limits when calculating the errors as this would correspond to a beam pause for clinical implementation. The estimation error at a time frame was quantified by the Euclidean distance between the actual target position and the estimated CoM in three dimensions:

$$\begin{array}{ccc}& & \mathrm{Error}\left(t\right)\hfill \\ & & =\sqrt{{\left(x-Co{M}_x\right)}^2+{\left(y-Co{M}_y\right)}^2+{\left(z-Co{M}_z\right)}^2},\hfill \end{array}$$ (5)

where (x, y, z, t) is the actual position of a target at time t. (CoM_x, CoM_y, CoM_z, t) is the estimated CoM of the target at time t.

RESULTS

Estimation error of 1D-motion traces

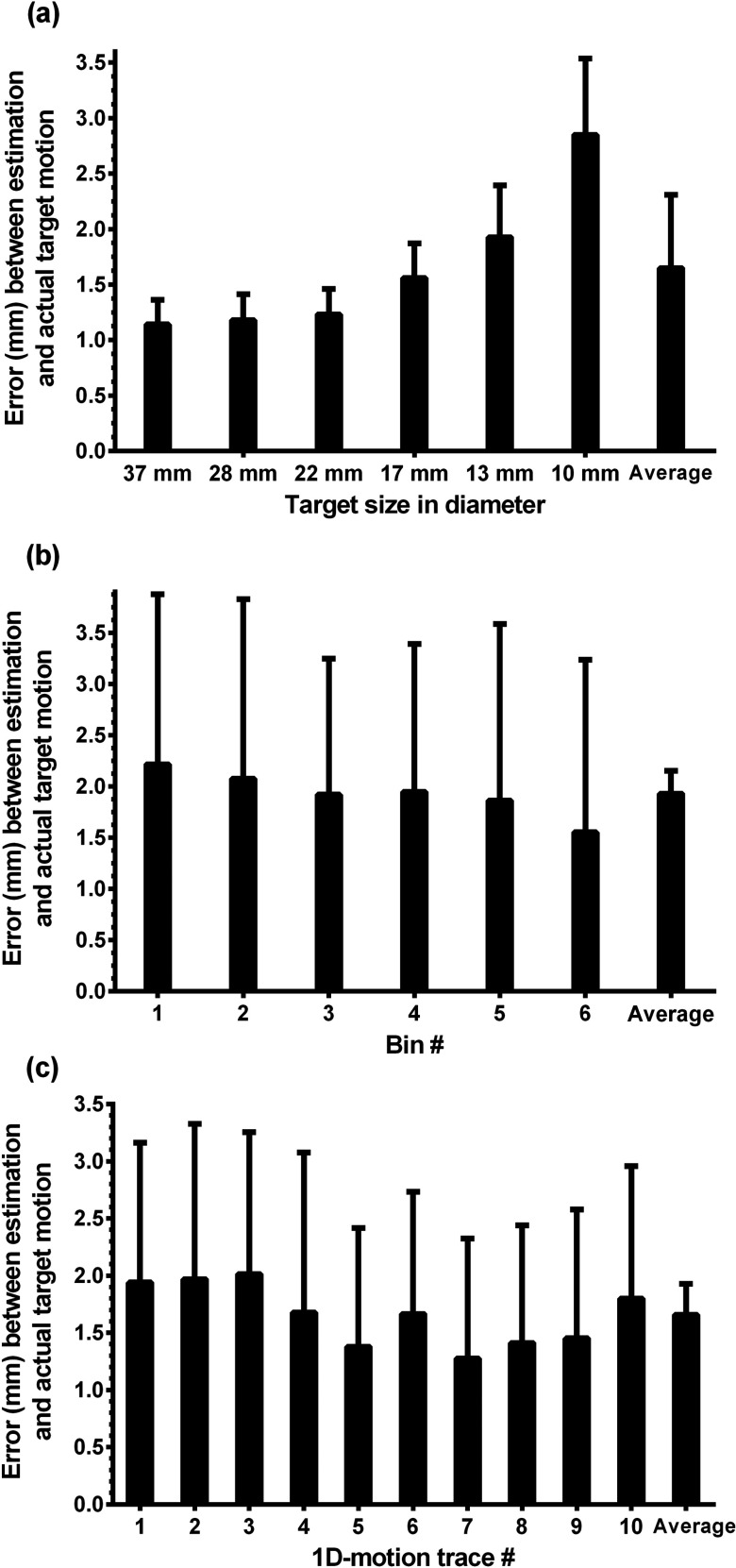
The average error of 1D-motion traces was 1.6 mm, time-averaged over all error trajectories of all targets (10, 13, 17, 22, 28, and 37 mm in diameter). The errors from 60 s to 300 s were used for computing the average error. The first 60 s (1 min) was for learning time or observation time.

The error trajectories decreased with time as coincidence events were accumulated. Figure 5 shows this trend that error decreased with increasing scan time. The overall error trajectory converged to within 2 mm in 300 s [Fig. 5a] for all target sizes. It took approximately 90 s to reach 2 mm error bound in the moving-averaged error trajectory. However, the speed of convergence of error trajectories was dependent on target sizes. The error trajectory of the 37 mm target converged faster than that of the 10 mm target. Specifically, in the moving-averaged error trajectory, it took 35 s to arrive at the 2 mm error bound for the 37 mm target; whereas, 300 s was required for the 10 mm target. This difference can be explained by the higher number of coincidence events and hence lower statistical uncertainty in the larger target.

Figure 5.

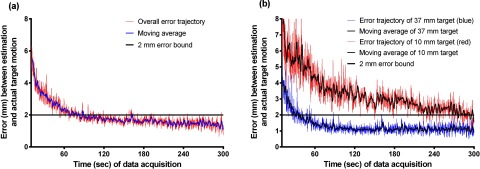
(a) Average errors of 1D-motion traces over all targets in time and (b) average errors of 37 and 10 mm targets with 1D-motion traces in time. The moving average curve is displayed to demonstrate the patterns of convergence.

As expected, improved results were obtained for larger targets [Fig. 6a]. For example, for the 37 mm target, the averaged error over all 1D-motion traces was 1.1 mm; whereas, for the 10 mm target, the average error over the 1D-motion traces was 2.8 mm. There were variations between motion traces and bins such as target sizes in the accuracy of estimation: bin-1 (end inhalation) had the largest average error (2.2 mm) and bin-6 (end exhalation) had the smallest one (1.6 mm) [Fig. 6b]. The overall estimation error of 1D-motion trace 7 was 1.3 mm, but that of 1D-motion trace 3 was 2.0 mm [Fig. 6c].

Figure 6.

Average errors of 1D-motion traces for (a) target sizes, (b) bins, and (c) motion traces. Note that the error bars represent one standard deviation.

Estimation error of 3D-motion traces

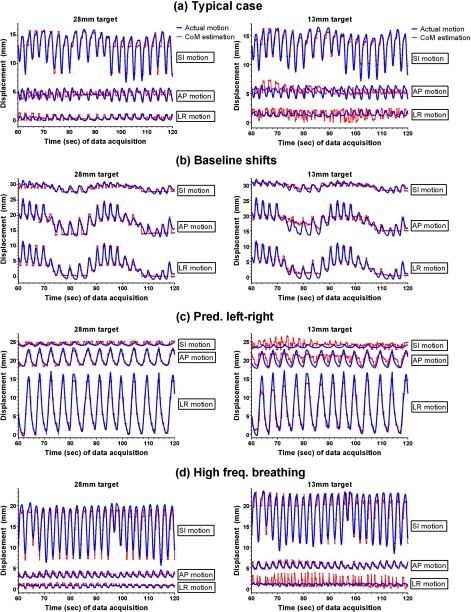
Figure 7 shows trajectories of the actual motion and the CoM estimation of the 28 mm target (2nd largest) and 13 mm target (2nd smallest) in each direction for the 3D-motion traces. As mentioned above, in order to test the accuracy of CoM estimation on tumor motion with clinical variability, the 3D-motion traces selected from the database had higher magnitudes and complexity than average motion. The overall time-averaged error of 3D-motion traces was 1.6 mm, which was comparable to that of 1D-motion traces. There were small variations in the errors for the four traces (Table 1), although they were very different in Fig. 7. The estimation accuracy was consistent for all target sizes except the smallest one.

Figure 7.

Trajectories of the actual motion of targets and the CoM estimation of the 28 mm target and 13 mm target in the three directions. The actual motion trajectories were all from lung tumors, representing (a) typical motion, (b) baseline variations, (c) predominantly left-right motion, and (d) high-frequency breathing. Three directions are SI: superior-inferior, AP: anterior-posterior, and LR: left-right.

Table 1.

The error (Euclidean distance between actual position and CoM estimation) of each target of 3D-motion traces in the three directions.

	Typical	Baseline	Predominantly	High frequency
Target	case	shifts	left-right	breathing
size	Mean error	Mean error	Mean error	Mean error
37 mm	1.1	1.1	1.3	1.9
28 mm	1.1	1.1	1.3	1.7
22 mm	1.1	1.1	1.4	1.8
17 mm	1.2	1.2	1.4	1.7
13 mm	1.2	1.3	2.0	2.0
10 mm	2.3	2.2	2.6	3.9
Overall	1.3 ± 0.5	1.3 ±0.4	1.7 ± 0.5	2.2 ± 0.9

DISCUSSION

This study aims to investigate the potential of PET for dynamic tumor tracking, which demomstrates the proof-of-principle for PET-guided lung tumor tracking. Tumor tracking using PET has potential benefits over other tumor tracking methods, including (1) obviating the need for implanted markers, (2) adapting dose based on tumor biology, and (3) providing a more individualized radiation treatment.⁵² The investigation is focused more on the estimation accuracy of the proposed algorithm than the computational time for two reasons: (1) recent papers have reported that computational power is increasing, which would make real-time PET imaging feasible in the near future, and (2) investigating estimation accuracy is much more important than speeding up the algorithm for the proof-of-principle as the image quality of PET is relatively much poorer than those of X-rays, CT, and MRI. The computational burden of reconstruction time could be a main concern as iterative reconstruction is still computationally challenging; thus, GPU-based acceleration will be mentioned in Sec. 4C.

The variations of tumor position caused by respiratory motion affect PET-guided radiation treatment for lung tumors in all steps of the treatment planning and beam delivery chain. Positional uncertainties are categorized as follows: the treatment planning uncertainty category (systematic uncertainties) and the treatment execution category (random uncertainties); the uncertainties should be included in the treatment margin calculation.⁵³ In terms of systematic uncertainties, 4D treatment planning and patient setup should be elaborated since beam tracking techniques are not matured and a standard for the setup is not crystallized yet.^{54, 55, 56} In the geometry of PET-linac, the setup is described as follows: (1) the planning target volume (PTV) is defined at the tumor delineation (treatment planning) stage, to contain the gross tumor volume (GTV) motion, considering residual tumor motion in each bin; (2) the patient is administered with a PET radiotracer and waits for post-injection scan time (e.g., 1 h); and (3) the patient undergoes setup and registration using megavoltage cone-beam CT (MV cone-beam CT) images after the patient is positioned on the table to align the PTV.^{14, 15, 57} After the setup and the learning time, the proposed algorithm tracks the tumor position through the CoM of the segmented target volume on gated-PET images reconstructed from accumulated coincidence events, throughout a treatment. In terms of random uncertainties, the accuracy of PET-guided tumor tracking is demonstrated by the real-world accuracy of the algorithm (overall time-averaged error ≈2 mm), though the computation time and the impact of tumor location and TBR for estimation accuracy remain as issues (see Sec. 4C). If there are differences between respiratory motion patterns on the date of the imaging study and the date of treatment, 4D treatment planning methods may not account for these differences.⁵⁸ In order to minimize the possibility of mislocalization for the tumor and an increase of toxicity for surrounding healthy tissues, it is necessary to devise a way to compensate for those differences in the stage of patient setup and during treatment. This is beyond the scope of this study.

An approach comparable to PET-guided tumor tracking is magnetic resonance imaging (MRI)-guided tumor tracking.^{7, 59, 60} Although still under development, there are several groups currently developing MRI-linac systems.^{61, 62} Our method for PET-guided tumor tracking is similar to MRI-guided tumor tracking in the sense that both approaches are image-based. However, the concept of biologically based targeting using PET is the most distinguishable feature from that of anatomically based targeting of the other image-based guidance methods (e.g., X-rays, CT, ultrasound, or MRI) as PET has high sensitivity and specificity for tumors.

Analysis

Considering the large spatial resolution of the PET scanner, the performance of the proposed algorithm is demonstrated by the overall time-averaged error 1.6 mm for 1D-motion traces and 3D-motion traces. The error is at least three times smaller than the spatial resolution (axial full width at half maximum) of the PET scanner, which is achievable as multiple voxels are included in the CoM computation.

Convergence of estimation

In the estimation at each frame time, a larger instantaneous error occurred (1) at the beginning of scans and (2) outside of gate boundaries. The reason for these errors was the small number of coincidence events. It is a basic principle of PET that the number of coincidence events are significant for reconstructed image quality. The maximum intensity in the volume of interest changed dynamically at the beginning of scans, which was investigated by Liu et al.⁶³ The general trend is that higher image noise with a small fraction of data causes larger maximum values. For this reason, 1 min was set up as learning time or observation time to collect coincidence events before starting target motion tracking. Regardless of the low number of coincidence events, the overall convergence of the error to the 2 mm error bound was achieved in 30 s after the learning time (Fig. 5), although high frequency noise persisted due to statistical errors. The fast convergence to the error bound can be explained by averaging effects. The CoM tracking involves averaging in computing a target position in each axis over many voxels, which automatically reduces statistical uncertainties or high frequency noise, enabling sub-voxel accuracy.

Target sizes

Target size had a significant influence on the accuracy of estimating target position [Figs. 5b, 6]. In general, targets smaller than two or three times the spatial resolution suffer from the partial volume effect (PVE) around the boundary of the targets.^{26, 64} The signal intensity of smaller targets was further degraded due to respiratory motion and the PVE, which caused the CoM estimation of the smallest target (10 mm) to have higher errors and slower convergence to the error bound.

Bins

Six-bin gating is a default in the PET-CT machine (GE Discovery ST) in which 4D-PET data were acquired. In a dynamic phantom study, Park et al. demonstrated the effect of gating on images by changing the number of bins (1, 2, 5, 10, and 20).²⁶ They concluded that the 5-bin gating method gave the best temporal image resolution with acceptable image noise, which also justified the use of six bins. From the overall average error, bin-6 (end exhalation) had the smallest error, and bin-1 (end inhalation) had the largest error [Fig. 6b]. In general, the breathing patterns around end inhalation have larger fluctuations with a short period, while those around end exhalation are more regular and stable with a longer period.⁴⁴ The CoM of each target for each bin is the mean measured position of the target position in that bin. Thus, the CoM estimation in each bin is stepped, which decreases the estimation accuracy specifically for bin-1.

Motion traces

In addition to the variations of the results according to target sizes and bin number, each motion trace had a specific result due to its specific external and internal respiratory motion (Fig. 7). A perfectly regular trace like a sinusoidal wave would give better results—if regularity was defined by how small variations were between breathing cycles—but it is not possible for humans to breathe regularly without variations of patterns between the cycles. Both the 1D-motion and 3D-motion traces had variations in amplitude, period, and pattern which influenced the performance of the CoM estimation.

Uniqueness

The CoM method for estimating target position has been used previously by several researchers.^{28, 34, 65, 66} Data-driven gating techniques using the CoM method on sinograms or images are possible as motion information is intrinsic to the PET data. The basic idea is to divide the PET raw data into small time frames and estimate the target motion that is assumed to be constant during these frames. The sinogram-based CoM methods by Klein et al. and Büther et al. derive motion information directly from coincidence events (lines of response) which is very time efficient.^{28, 66} However, the disadvantages of this method are: (1) it is only applicable to the axial direction and (2) lines of response that are part of the predetermined VOI include coincidence events from outside the VOI, leading to statistical errors. Whereas, the image-based CoM method by Bundschuh et al. has the advantage of having full 4D (x, y, z, t) motion information of the target without the disadvantages though the image reconstruction time is significant.³⁴

Our proposed algorithm aims to investigate the potential and feasibility of PET for dynamic lung tumor tracking by estimating CoM, based on the assumption that real-time processing is supported. Our method is similar to Bundschuh's approach for PET image reconstruction (not real-time radiotherapy), but is distinct in three respects. It uses (1) image-based target motion tracking (not data-driven gating), (2) sinogram updating using external respiratory signals, and (3) no band-pass filtering. The purpose of Bundschuh's approach is data-driven gating to perform gating retrospectively by using the axial component of CoM without using an external respiratory signal. To enable the image-based CoM estimation dynamically, the real-time sinogram updating is needed for reconstructing PET images continuously (Fig. 4), which requires external respiratory signals for real-time gating. For the real-time sinogram updating, the proposed algorithm accumulates coincidence events in proportion to data acquisition time, which is robust to statistical noise by simply increasing coincidence events in each bin. In the previous CoM methods, the CoM trajectories derived from sinograms or images are filtered retrospectively in order to reduce statistical (high frequency) noise because a short time frame results in a large fluctuation of coincidence events in each frame.

Limitations

Processing time

The main disadvantage of image-based CoM estimation is the long processing time for image reconstruction. On an intel i7 processor with eight cores, the reconstruction time for 3D volume (128 × 128, 47 slices) is about 10 s at each frame time. To apply this method clinically, the total processing time would need to be shorter than the frame time or less to achieve total system latency similar to other guidance methods.^{8, 9, 10} Thus, fast image reconstruction is required to enable image-based CoM estimation for dynamic tumor tracking.

To the best of our knowledge, no algorithm is available for real-time PET image reconstruction. However, the recent publications have given the positive feedback of GPU-accelerated PET image reconstruction toward real-time imaging. In the most recent review paper, Pratx et al. reported the evolution of GPUs: the number of computing cores in GPU processors has increased twofold every 1.4 year; also, the GPU memory bandwidth has increased twofold every 1.7 years.⁶⁷ They stated that the performance of GPUs has been steadily increasing. Cui et al. showed that the GPU-accelerated 3D list-mode OSEM >200 times faster than a CPU implementation for PET image.⁶⁸ Tashima et al. developed a real-time PET imaging system for preclinical studies.¹⁸ They developed the system using the GPU-accelerated list-mode based reconstruction algorithm for real-time visualization, and the processing time of image reconstruction was 0.5 s. The system demonstrated tracking ability with a sine curve (amplitude: 4 mm, period: 30 s) that was not realistic to simulate tumor motion and to investigate the feasibility of PET for tumor tracking.

No effort has yet been made to improve the computation time for the current study, though it is reasonable to expect that large gains could be made by parallelizing the code and using a faster CPU and/or GPU hardware.

PET geometry with an open space

A requirement of PET geometries for dynamic tumor tracking is to provide an accessible open space for the treatment beam. In recent publications, possible open geometries were suggested to satisfy this requirement.¹⁷ Regarding the application of the CoM tracking method, using measurements from a conventional PET scanner and applied to an unconventional PET, our results would be an upper bound on the accuracy. The actual accuracy from a PET geometry with an open space would be limited by the final configuration of the PET ring, which would be designed in such a way as to maximize the PET signal and be as close to a conventional PET scanner as possible.

One institution performed a Monte Carlo simulation regarding the impact of scanner geometry on the quality of PET images. Surti et al. investigated the optimal design of an in situ PET scanner for use in proton therapy using time-of-flight (TOF) information and an iterative reconstruction algorithm through GEANT4 simulations.⁶⁹ It should be noted that the process of positron emission of the in situ PET system (positron emitters produced by proton beams) was different from that of clinical ¹⁸F-FDG PET scanners (positron emitters produced by FDG uptake on tumor cells). However, the science of detection and image reconstruction are consistent with those of clinical PET scanners. Also, a partial-ring PET design was selected in order to avoid interference between PET detectors and proton beams. As ring coverage was reduced, distortions and artifacts increased in images. However, using TOF imaging reduced the image artifacts and distortions through improving the timing resolution. The results indicate that it would be feasible to develop a partial-ring PET scanner, maintaining the similar imaging quality of a full-ring PET scanner.

Displacement gating

The displacement boundaries of each bin for gating were determined from external respiratory motion signals during an initial 1 min learning period. In terms of number of bins, this is a tradeoff between motion resolution and noise level on gated-PET images; increasing the number of bins makes displacement boundaries smaller, which results in increasing tracking accuracy. However, an increased bin number means fewer events per bin, which reduces the precision as there are fewer counts and therefore higher statistical uncertainties in each bin. In terms of gating methods, Dawood et al. evaluated seven gating methods and concluded that the displacement-based gating approaches were superior to the phase-based gating methods.⁴⁹ They also observed that displacement-based gating captured the external respiratory motion best while keeping a constant noise level when equal number of events was sorted into each bin. For this reason, this gating scheme was applied to the proposed algorithm. However, if there is a significant hysteresis in a tumor motion trajectory, the combination of displacement and phase gating could be considered.

In displacement gating, the interval of displacement boundaries of a bin can be much larger than those of the other bins if external respiratory motion is irregular, specifically around end inhalation. In addition, this gating method is not robust to baseline shifts of external respiratory motion, which are not unusual.⁷⁰ As a possible way to improve breathing regularity, the use of an audiovisual (AV) biofeedback system can be considered as the system has a potential to regulate a patient's breathing and to prevent a baseline shift, which is under investigation.^{41, 71, 72} However, even with AV biofeedback respiratory variability will be present, though the variability is potentially of smaller magnitude with breathing training. The AV biofeedback is not suggested as a solution, as not all patients breathe regularly with AV biofeedback, but simply as a method that may reduce the magnitude of breathing variability.

Sensitivity to instantaneous motion

The CoM trajectories estimated by the proposed algorithm converge to actual motion within a reasonable accuracy. However, as data acquisition time is increasing, accumulated data become less sensitive to instantaneous target motion out of displacement boundaries because the estimated position is averaged up to the time that the estimation is performed. However, the approach of accumulating counts in each bin to reduce noise and eliminate the need for image filtering, as opposed to a, e.g., moving window approach where only the counts from the prior fixed time period are included, is a trade-off. To demonstrate the accuracy of the proposed method, we used higher-than-average lung tumor motion measured from four patients with different motion types. The results give an estimate of the real-world accuracy of the method (apart from the computation time issues). As shown in Fig. 7, on average the error is less than 2 mm. To prevent irregular respiratory motion being out of displacement boundaries, an external respiratory guidance such as the AV biofeedback system may help a patient breathe within the displacement boundaries. To maximize imaging sensitivity to present motion, another method could be a weighting scheme to give more weight to coincidence events closer to the present than those further in the past.

Segmentation

In this phantom study, the predetermined binary mask was used to choose the VOI that would be interpolated. The segmentation accuracy is guaranteed since the advantage of phantom studies is to know the ground truth of a target motion and volume. In the VOI, the threshold used for segmenting the 10 mm target (smallest) was 60% that was higher than the 40% value used for segmenting the other targets. The 10 mm target is more susceptible to respiratory motion and blurred out more easily due to the partial volume effect (PVE), which results in smaller TBR and requires a higher percentage threshold.

The segmentation approach using predetermined binary masks and a threshold for the phantom data can be applied to patient data. However, a VOI including a tumor should be selected much more carefully, considering tumor location and TBR.^{51, 73, 74} The accuracy of tumor segmentation is dependent on the location and TBR of the tumor. For instance, if the tumor location is close to or surrounded by an organ whose activity concentration is considerable, TBR may not be enough to distinguish the tumor from surrounding healthy tissues, which may prevent the success of the proposed algorithm. To minimize the possibility of inaccurate segmentation caused by a low TBR, the VOI should be very carefully determined from 4D-CT and 4D-PET images, which can reduce uncertainties in determining the boundary of the tumor.

Attenuation and scatter corrections

In this phantom study, no attempt has been made to compensate for attenuated and scattered events in the procedure of image reconstruction. PET image quality could be further improved by applying attenuation and scatter corrections through an appropriate manner. In terms of attenuation correction, since respiratory phase and displacement in helical CT, a current clinical protocol, are generally different from those in gated PET, the spatial mismatch of within the thorax between the two modalities results in a mismatch of tumor location, which causes inaccurate quantification of tumors in gated-PET images.⁷⁵ For lung tumors with significant motion, in order to match gated-PET images with the corresponding phase of the CT images, averaged-CT or 4D-CT images should be carefully prepared.^{75, 76, 77} In terms of scatter correction, scatter fraction typically ranges from about 15% (2D mode or septa extended) to 40% or more (3D mode or septa retracted), which affects final image quality and leads to image artifacts, specifically for scans performed in 3D mode.⁷⁸

CONCLUSION

We have developed an algorithm using list-mode PET data and external respiratory motion data and investigated the potential and feasibility of PET for dynamic lung tumor tracking. The overall tracking error in phantom studies is less than 2 mm. Although a fast reconstruction algorithm is required for practical implementation, the CoM tracking method using gated-PET images demonstrates the proof-of-principle for PET-guide lung tumor tracking within clinically acceptable accuracy.