Comparison of 2D and 3D gamma analyses

Abstract

Purpose: As clinics begin to use 3D metrics for intensity-modulated radiation therapy (IMRT) quality assurance, it must be noted that these metrics will often produce results different from those produced by their 2D counterparts. 3D and 2D gamma analyses would be expected to produce different values, in part because of the different search space available. In the present investigation, the authors compared the results of 2D and 3D gamma analysis (where both datasets were generated in the same manner) for clinical treatment plans.

Methods: Fifty IMRT plans were selected from the authors’ clinical database, and recalculated using Monte Carlo. Treatment planning system-calculated (“evaluated dose distributions”) and Monte Carlo-recalculated (“reference dose distributions”) dose distributions were compared using 2D and 3D gamma analysis. This analysis was performed using a variety of dose-difference (5%, 3%, 2%, and 1%) and distance-to-agreement (5, 3, 2, and 1 mm) acceptance criteria, low-dose thresholds (5%, 10%, and 15% of the prescription dose), and data grid sizes (1.0, 1.5, and 3.0 mm). Each comparison was evaluated to determine the average 2D and 3D gamma, lower 95th percentile gamma value, and percentage of pixels passing gamma.

Results: The average gamma, lower 95th percentile gamma value, and percentage of passing pixels for each acceptance criterion demonstrated better agreement for 3D than for 2D analysis for every plan comparison. The average difference in the percentage of passing pixels between the 2D and 3D analyses with no low-dose threshold ranged from 0.9% to 2.1%. Similarly, using a low-dose threshold resulted in a difference between the mean 2D and 3D results, ranging from 0.8% to 1.5%. The authors observed no appreciable differences in gamma with changes in the data density (constant difference: 0.8% for 2D vs 3D).

Conclusions: The authors found that 3D gamma analysis resulted in up to 2.9% more pixels passing than 2D analysis. It must be noted that clinical 2D versus 3D datasets may have additional differences—for example, if 2D measurements are made with a different dosimeter than 3D measurements. Factors such as inherent dosimeter differences may be an important additional consideration to the extra dimension of available data that was evaluated in this study.

INTRODUCTION

Quality assurance (QA) for intensity-modulated radiation therapy (IMRT) plans can be performed using a variety of measurement devices and metrics to verify the accuracy of dose distributions. A commonly accepted clinical metric is the gamma (γ) index introduced by Low et al.¹ in 1998. The gamma index quantifies the difference between measured and calculated dose distributions on a point-by-point basis in terms of both dose and distance to agreement (DTA) differences.

Until recently, IMRT QA has mainly consisted of the use of 2D metrics. However, technological advancements in the field of radiation physics have led to the use of new 3D dosimeters and metrics for IMRT QA.^{2, 3, 4, 5} The 3D gamma metric is an extension of the 2D gamma index into another dimension, allowing for consideration and evaluation of the entire volumetric patient dose distribution. Algorithms used for computing 3D gamma values and methods of practical computation are described in the literature,^{6, 7} and numerous authors have reported 3D gamma results.^{2, 3, 4, 5} However, how 3D gamma values and passing rates compare with traditional 2D gamma values and passing rates has yet to be examined. This comparison of 2D results to 3D results is of interest because, as noted by Wendling et al.,⁷ owing to the extra dimension used to search for agreement, the 3D gamma index will always be lower (i.e., produce better agreement) than the 2D index. Therefore, as noted by Persoon et al.,⁸ the implementation of 3D gamma QA using the same acceptance criteria as those for 2D gamma would be expected to lead to a higher passing rate.

The goal of this work was to compare 2D and 3D gamma. In the present study, we compared 2D and 3D gamma results (gamma indices and percentages of pixels passing the gamma criteria) for a variety of acceptance criteria, data density, and dose thresholds for 50 step-and-shoot IMRT plans. We calculated gamma indices by comparing treatment planning system (TPS)-calculated (evaluated) and Monte Carlo (MC)-recalculated (reference) dose distributions. In this study, we evaluate only the impact of the addition degree of freedom for the search. We do not consider or address other possible differences between 2D and 3D data, including different measurement acquisition methods, which, due to inherent dosimeter differences, would also be expected to affect the difference between 2D and 3D gamma results.

METHODS AND MATERIALS

Treatment plans

Fifty IMRT treatment plans recalculated using a homogeneous water phantom data set, hereafter referred to as QA plans, were evaluated. Each plan had dose distributions calculated from the treatment planning system using collapsed-cone (CC) convolution algorithm and a separate MC recalculation which formed the basis for the 2D and 3D gamma comparison.

In addition, to evaluate the effect of calculation geometry used (QA vs patient), the 50 patient plans corresponding to the 50 QA plans used were used for a subset of the study presented. Only a subset of the study was performed on the patient plans as it was thought that the results would be similar and only highlight a difference due to the more complex patient anatomy.

All 100 plans evaluated in this study were clinical cases used at The University of Texas MD Anderson Cancer Center (MDACC). Forty-one of them were head and neck plans, with the remainder consisting of three central nervous system, two mesothelioma, one thoracic, one gastrointestinal, one pediatric, and one genitourinary plan. The plans were chosen randomly from our clinical database. All of the plans were step-and-shoot IMRT generated using the Pinnacle³ TPS (version 7; Philips Healthcare, Fitchburg, WI) with the CC convolution calculation algorithm. Treatment planning for all sites was conducted according to the standard of care at MDACC. For each clinical plan, the corresponding QA plan (calculated on the homogeneous phantom) was calculated in Pinnacle³ using an I’mRT Phantom (IBA Dosimetry, Bartlett, TN) as part of our institution's pre-IMRT QA procedure. The Digital Imaging and Communications in Medicine (DICOM) dose files for all 50 TPS-generated QA plans were exported and used as the evaluated dose distributions for the gamma calculations.

MC simulation

The dose distributions for the 50 QA plans were recalculated using a MC program developed and benchmarked inhouse.⁹ This MC program was based on the BEAMnrc code^{10, 11} and integrated into the Pinnacle³ TPS interface. The MC program begins each simulation by processing the DICOM radiotherapy IMRT plan for needed input parameters and uses the plan CT image of the QA phantom for dose calculation. The beam simulation includes the plan-specific jaw and multileaf collimator (MLC) sequences used in the treatment plan. Yang et al.,⁹ previously validated the MC program against comparisons to ion chamber and TLD measurements in an anthropomorphic phantom.

For use in the gamma calculations, the MC dose distributions were exported as DICOM dose files and used as the reference distributions in the gamma calculations.

Gamma calculation

The Mobius3D software program (Mobius Medical Systems, Houston, TX) was used to calculate the 2D and 3D gamma values for each of the 50 comparisons. 2D gamma calculations were performed based on the traditional definition of gamma by Low et al.,¹ in which γ is quantified using a combined dose-difference and DTA criteria as shown in Eq. 1

$$\gamma \left(r_m\right)=\min \left\{\Gamma \left(r_m,r_c\right)\right\}\forall \left\{r_c\right\}.$$ (1)

Γ in Eq. 1 is defined as shown in Eq. 2

$$\Gamma \left({\mathrm{r}}_{\mathrm{m}},{\mathrm{r}}_{\mathrm{c}}\right)=\sqrt{\frac{r^2\left({\mathrm{r}}_{\mathrm{m}}{,\mathrm{r}}_{\mathrm{c}}\right)}{\Delta {\mathrm{d}}_{\mathrm{M}}^2}+\frac{{\delta }^2\left({\mathrm{r}}_{\mathrm{m}}{,\mathrm{r}}_{\mathrm{c}}\right)}{\Delta {\mathrm{D}}_{\mathrm{M}}^2}},$$ (2)

in which a gamma value of at least 1 indicates a failing region, whereas a gamma value less than 1 indicates a passing region. 3D gamma values were defined using the same equations except that the spatial directions were extended to a third dimension. In this software, all gamma values were capped at a gamma of 2.

For each of the gamma calculations, the Mobius3D software program recast each data set onto a cubic grid of user-defined size. The data were then interpolated using a trilinear interpolation to fill-in missing data.

Gamma tests and analysis

The 2D and 3D gamma indices were calculated using the Mobius3D software program as described above for each QA plan comparison (50 total) in the transverse direction throughout the data set. The 2D analysis was conducted by considering each transverse slice in the phantom geometry as an independent entity. The 3D analysis evaluated the total volume of the QA dataset as well as a slice by slice assessment (with neighboring slices present). This 2D and 3D analysis was conducted using a variety of percent global dose-differences and DTA criteria, low-dose threshold limits (the percent of the maximum dose below which data were excluded), and data densities. For each of the percent dose, DTA, and low-dose threshold variations, the doses were originally cast onto a 1 mm cubic grid for these tests. Then to test the effect of a sparser dataset on gamma, we recast all the data onto 1.5 and 3 mm cubic grids. This test was meant to mimic clinical scenarios such as when different interpolation grids are used for gamma or when no interpolation is employed but different CT slice thickness are used. The following evaluation criteria were used in this study:

1. Dose difference/DTA of 5%/5 mm, 3%/3 mm, 2%/2 mm, and 1%/1 mm using a 1-mm data grid and no low-dose threshold,

2. Dose difference/DTA of 3%/3 mm with 5%, 10%, and 15% low-dose thresholds using a 1-mm data grid,

3. Dose difference/DTA of 3%/3 mm using 1.0-, 1.5-, and 3.0-mm data grid sizes with no low-dose threshold.

The 3%/3-mm criterion was chosen for analyses in (b) and (c) owing to the prevalence of its use in clinical practice. The range of low-dose thresholds (5%, 10%, and 15%) were selected based on a survey of Nelms and Simon¹² who found that more than 70% of institutions used a low-dose threshold between 0% and 10%.

To evaluate the effect of geometry, the 50 patient plans were evaluated using the same dose differences and distances to agreement criteria as listed in (a).

To mimic our own IMRT QA process, transverse slices of data were evaluated in the above comparisons. However, we also evaluated the effect of other spatial directions by considering coronal and sagittal planes. Although, we intuitively expected the results would be the same for other spatial directions, we evaluated a small subset of QA plans (five plans) to check this assumption using all the dose differences and distances to agreement criteria shown in (a) above.

The data output in each comparison included the average 2D and 3D gamma values (weighted per plan according to the number of pixels in each slice) and the number of pixels passing and failing gamma for each complete data set as well as individually for each slice within each respective data set. All data sets for all 2D and 3D comparison tests were analyzed to calculate the percentage of pixels passing gamma, the lower 95th percentile gamma value (i.e., the fifth percentile of data with the worst gamma/percentage of pixels passing), the percentage of pixels passing the gamma criteria, and the percentage of slices in each data set passing gamma.

Additionally, paired-sample t-tests were used to evaluate each set of 2D and 3D gamma values and the percentage of pixels passing gamma to assess whether the differences between the 2D and 3D data was statistically significant (i.e., P < 0.05) using the SPSS software program (version 19; IBM Corporation, Armonk, NY).

RESULTS

2D vs 3D gamma for different QA evaluation criteria

The average gamma value and percentage of pixels passing gamma for the comparisons of 2D and 3D gamma with a variety of dose-difference and DTA criteria for the 50 QA plans and 50 corresponding patient plans are shown in Table 1. Overall, for each acceptance criterion, the 3D gamma was lower than the 2D gamma (i.e., better agreement), on average for both the QA and patient plans with lower 95th percentile gamma values (not shown) that followed the same trend. The QA plans [Table 1(a)] showed a difference between 2D and 3D average gamma values and percentage of pixels passing that increased with tightening gamma criteria from 0.22 vs 0.20 (98.3% vs 98.7%) at 5%/5mm to 1.18 vs 1.10 (79.1% vs 80.9%) at 1%/1mm, for 2D and 3D, respectively. The differences between the average 2D and 3D gamma and percentage of pixels were statistically significant (P < 0.001).

Table 1.

Average 2D vs 3D gammas and percentages of pixels passing gamma criteria for the (a) 50 QA and (b) 50 patient plans at the 5%/5-mm, 3%/3-mm, 2%/2-mm, and 1%/1-mm acceptance criteria with no low-dose threshold and a 1-mm data grid.

			Average 2D	Average 3D
			percentage of	percentage of
Acceptance	Average	Average	pixels passing	pixels passing
criteria	2D gamma	3D gamma	gamma	gamma
5%/5 mm	0.22	0.20	98.3	98.7
3%/3 mm	0.37	0.33	96.6	97.4
2%/2 mm	0.56	0.51	93.2	94.9
1%/1 mm	1.18	1.10	79.1	80.9
(a)
			Average 2D	Average 3D
			percentage of	percentage of
Acceptance	Average	Average	pixels passing	pixels passing
criteria	2D gamma	3D gamma	gamma	gamma
5%/5 mm	0.25	0.22	98.0	98.9
3%/3 mm	0.44	0.37	94.2	96.4
2%/2 mm	0.71	0.59	88.8	91.7
1%/1 mm	1.85	1.58	74.9	77.0
(b)

For the patient plans [Table 1(b)], since the gammas generally exhibited worse agreement, the difference between 2D and 3D gamma was more pronounced than for the QA plans. The difference in gamma value was modest at the least stringent criteria (0.25 vs 0.22 at 5%/5 mm) but increased to 1.85 vs 1.58 as the acceptance criteria tightened to 1%/1 mm (with both 2D and 3D gammas failing on average). Similarly, regarding the percentage of passing pixels in the clinical plans, we observed differences in the average 2D and 3D gamma values of 0.9% and 2.1% at 5%/5 mm and 1%/1 mm, respectively. The difference between the average 2D and 3D gamma and percentage of pixels were statistically significant (P < .001).

We observed the same trend of better 3D gamma values than 2D for the QA plans (Table 1(a)) and the patient plans [Table 1(b)]. The average gamma values and percentages of pixels passing gamma were slightly better for the QA plans than for the patient plans, reflecting better agreement between the TPS CC convolution calculation and MC dose distributions in the simpler geometry of the homogeneous phantom than the patient anatomy. Correspondingly, the difference between the average 2D and 3D gammas was less pronounced for the QA plans than for the clinical plans. Specifically, at 1%/1mm, an improvement of 14.6% was observed for the average gamma in going from 2D to 3D for the clinical plans compared to an improvement of 6.8% for the QA plans, meaning that the average improvement in 3D gamma was greater for the patient data sets than the QA data set. This indicates that the extra search dimension was more important for matching gammas when the average gamma was higher. This finding makes sense because with poorer agreement, the availability of more search points is more important.

Of note, while the results in Table 1 were derived from analysis of the data in transverse planes, 2D and 3D gamma for five of the QA plans analyzed in the coronal and sagittal planes showed nearly identical results.

2D versus 3D gamma: Effect of using a low-dose threshold

The effect of using a low-dose exclusion threshold for 2D and 3D gamma and the average percentage of pixels passing gamma at the 3%/3-mm criteria is shown in Table 2. As above, on average, the 2D results demonstrated worse gamma results than did the 3D results for all QA plans and thresholds evaluated (P < 0.001). While changes were observed with the use of increasing low-dose threshold, generally these changes did not result in greater changes in average gamma and the percentage of passing pixels than did tightening the dose-difference and DTA criteria. The same trends were observed for the results of the lower 95th percentile data (not displayed).

Table 2.

Average 2D vs 3D gammas and percentages of pixels passing gamma criteria for the 50 QA plans at the 3%/3-mm acceptance criteria using 0%, 5%, 10%, and 15% (of the prescription dose) low-dose thresholds and a 1-mm data grid.

			Average 2D	Average 3D
Low-dose			percentage of	percentage of
threshold	Average	Average	pixels passing	pixels passing
(%)	2D gamma	3D gamma	gamma	gamma
0	0.37	0.33	96.6	97.4
5	0.44	0.39	95.5	96.7
10	0.47	0.41	94.9	96.3
15	0.49	0.42	94.6	96.1

The specific effect of excluding low-dose points from the gamma evaluation for the plans was a higher (worse) gamma than that resulting from inclusion of these points, which translated into a lower percentage of pixels passing as the threshold increased. This is because the global dose-difference criteria resulted in very broad local dose-difference criteria in low-dose regions and, therefore, high passing rates in these regions. For example, without a dose threshold in the plans, the average 2D and 3D gamma values were 0.37 and 0.33, respectively, but when we excluded those points with a dose of 15% or lower than the prescribed dose, the average gamma values increased (worsened) to 0.49 and 0.42, respectively. The corresponding percentages of passing pixels decreased by 2% and 1.3% for 2D and 3D, respectively, using a 15% low-dose threshold. As demonstrated in these examples, the 3D gamma value and percentage of passing pixels were less sensitive to the low-dose threshold than were the corresponding 2D values. These differences were also highly significant (P < 0.001).

Effect of data density on 2D and 3D gamma results

The effect of data density (i.e., data grid size) on the 2D and 3D gamma values and the percentages of passing pixels in the QA plans are shown in Table 3. Consistent with all the previous data with changing dose-difference/DTA criteria [Table 1(a)] and low-dose threshold (Table 2), on average, the 3D gamma analysis exhibited better agreement than did the 2D analysis for varying data density, a difference that was highly significant (P < 0.001). However, unlike the other parameters we evaluated, changing the data density via recasting the data on different grid sizes had a relatively small effect on gamma and the percentage of passing pixels. This indicates that the trilinear interpolation used to fill in missing data (for coarse data grids) is performing reasonably well compared to the actual data present with more fine data grids. Increasing the grid size from 1 to 3 mm (i.e., decreasing the amount of data in the dataset) resulted in an increase in the 2D gamma from 0.37 to 0.41 and in the 3D gamma from 0.33 to 0.40. Similarly, we observed a slight change in the percentage of passing pixels, as it decreased by 1.1% in both 2D and 3D plans. In contrast to the results presented in Secs. 3.A and 3.B, neither gamma metric was particularly sensitive to changes in data density. The small change observed indicated that the 3D metric was actually more sensitive to changes in grid size than the 2D metric.

Table 3.

Average 2D vs 3D gammas and percentages of pixels passing gamma criteria for the 50 QA plans at the 3%/3-mm acceptance criteria with 1.0-, 1.5-, and 3.0-mm data grids and no low-dose threshold.

			Average 2D	Average 3D
Interpolated			percentage of	percentage of
grid size	Average	Average	pixels passing	pixels passing
(mm)	2D gamma	3D gamma	gamma	gamma
1.0	0.37	0.33	96.6	97.4
1.5	0.38	0.35	96.4	97.2
3.0	0.41	0.40	95.5	96.3

DISCUSSION

In the present study, we compared 2D and 3D gamma results for a variety of dose-difference and DTA criteria, low-dose thresholds, and data densities. We calculated gamma values for 50 IMRT plans based on TPS CC convolution calculation and MC recalculation of dose distributions. The 3D gamma, in terms of both average gamma value, percentage of pixels passing gamma, and 95th percentile values, resulted in better agreement than did the 2D gamma for every parameter in every plan evaluated. For all parameters, the differences between the 2D and 3D results were highly significant (P < 0.001). Furthermore, the average difference between the 2D and 3D results varied according to the parameter evaluated. Increasing the percentage dose difference and DTA had the greatest effect on gamma results while using a low-dose threshold also played an important role. Contrastingly, the change in the grid size had relatively little effect on gamma results. On average, under all conditions evaluated in this study, the 3D gamma value was 12.7% better (i.e., lower) than the 2D value with an average of 1.5% more pixels passing gamma.

The current study used the same computationally derived dataset, evaluated in 2D and in 3D. Other factors can affect the relationship between 2D and 3D analysis, and different results could be observed with other arbitrary datasets. Most notably, if the 2D and 3D datasets are generated by two different dosimeters (one for 2D measurements and a different one for 3D measurements). The inherent characteristics of the dosimeter will affect the percent of pixels passing, potentially more so than the difference in dimensionality. This was highlighted in a study by Oldham et al.¹³ which found better passing agreement for their 2D portal dosimeter as compared to their 3D Presage dosimeter (96.8% and 94.9%, respectively). These results are directly opposite from ours in that they found better agreement from 2D than from 3D gamma. On the other hand, it is also possible that with a measurement system, one might observe not only our trend of 3D gamma agreeing better than 2D, but even greater differences between 2D and 3D because of the potential impact of setup error. Generally, one would expect to see a larger setup error in 2D results than in 3D because the 2D setup is more sensitive to dose gradients perpendicular to the plane of measurement (because there are no data above and below the plane to allow a DTA analysis to compensate for the setup errors in that dimension). This would result in an even larger difference between 2D and 3D gamma, as shown by Sanghangthum et al.¹⁴ using VMAT plans. Although this study only demonstrated this explicitly for VMAT, it is reasonable to believe the same would hold for other delivery techniques because the same gradient issues exist.

While the literature and current clinical practice indicate that the passing rate of the gamma metric, whether in 2D or 3D form, is commonly used for routine IMRT QA, it should be noted that there is a question in the literature about whether or not the passing rate of the gamma metric alone is useful in IMRT QA for detecting plan errors. Specifically, two independent studies by Kruse¹⁵ and Nelms et al.¹⁶ found that the 2D gamma metric had a low-sensitivity to detect clinically relevant plan errors. More recent studies have called into question the usefulness of passing 2D and 3D gamma rates as they relate to clinically relevant parameters.^{17, 18} Although the usefulness of the gamma metric is not addressed in our study, it is important for the medical physics community to question if the gamma passing rate alone is useful in IMRT QA. Until the community reaches a consensus on this issue, it is likely that gamma will continue to be used for IMRT QA and an understanding of how 3D gamma values compare to 2D values is important.

Another issue regarding common practices in IMRT QA that our study highlights is an issue of higher gamma passing rates associated with the commonly used low-dose thresholds used by the medical physics community. An IMRT QA practices survey by Nelms and Simon¹² showed that all responding institutions used a low-dose threshold of between 0% and 15%, most often a 5%–10% low-dose threshold. Such low-dose thresholds include a large number of low-dose pixels, which, may result in an inflated passing rate when evaluated with a global dose difference criteria. This is consistent with our results that showed an increasing passing rate for both 2D and 3D gamma with a decreasing low-dose threshold (2D and 3D being 94.6% and 96.1% with a 15% low dose threshold, compared to 96.6% and 97.4% with a 0% threshold).

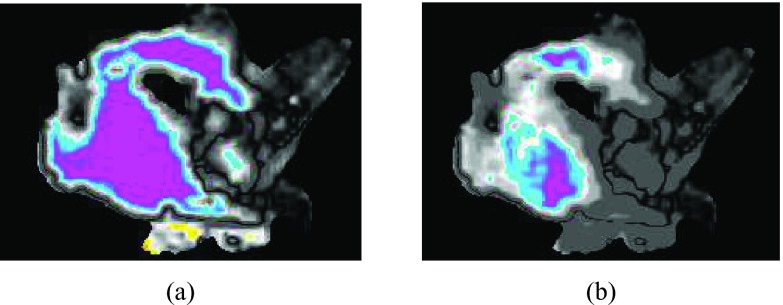
In general, there are many differences between planar and volumetric analysis for IMRT QA. Individual planes in 2D analysis may miss problems that would be identified with 3D analysis, but could also highlight local regions where problems exist. Figure 1 shows a clinical plan in which the same single transverse slice failed 2D gamma QA (γ = 1.04) but easily passed 3D gamma QA (γ = 0.52). This sort of case likely represents a scenario where a plan “failed” based on 2D analysis that should have, in reality, passed, as indicated in the 3D analysis. This observation led us to consider how likely a chosen slice is to pass while others surrounding it fail. We therefore performed additional analysis to determine the percentage of transverse slices that pass gamma at all of the acceptance criteria and dose thresholds previously evaluated for the 50 QA plans. The results demonstrated that on average, a greater percentage of slices passed the 3D criteria than passed the 2D criteria (Table 4). However, as seen in Table 4, with the exception of the 1%/1 mm results, a plane chosen at random would likely provide a passing gamma value consistent with those provided by the majority of other planes. Therefore, at least for our dataset, a single measurement plane was often representative of the entire dataset; however, it was not always representative of the entire patient volume. Overall, there are many clinical questions and considerations to be examined on the larger question of 2D versus 3D analysis, the difference in gamma passing rates being one of those considerations.

Figure 1.

(a) 2D and (b) 3D gamma maps of the same transverse slice of the gamma comparison in patient anatomy showing gamma failure (i.e., γ > 1) in the 2D map (average γ = 1.04) but passing in the 3D map (average γ = 0.52) for the 3%/3-mm acceptance criteria with a 15% low-dose threshold.

Table 4.

Average percentages of transverse slices passing computational gamma QA for the (a) 50 QA plans at the 5%/5-mm, 3%/3-mm, 2%/2-mm, and 1%/1-mm acceptance criteria with no low-dose threshold and a 1-mm data grid and (b) 50 QA plans at the 3%/3-mm acceptance criteria using 0%, 5%, 10%, and 15% (of the prescription dose) low-dose thresholds and a 1-mm data grid.

Acceptance criteria	Average 2D percentage of slices passing gamma	Average 3D percentage of slices passing gamma
5%/5 mm	97.8	98.1
3%/3 mm	97.0	97.5
2%/2 mm	93.1	94.7
1%/1 mm	71.7	76.6
(a)
Low-dose threshold (%)	Average 2D percentage of slices passing gamma	Average 3D percentage of slices passing gamma
0	97.1	97.7
5	91.6	95.9
10	92.0	93.8
15	92.5	95.2
(b)

CONCLUSIONS

In this study, we observed that 3D gamma analysis produced better agreement than the corresponding 2D analysis. The additional degree of searching increased the percent of pixels passing gamma by 0.4%–3.2% in 3D analysis. The greatest difference between 2D and 3D gamma results was caused by increasing the dose difference and DTA criteria. Increasing the low-dose threshold also had an impact.